On the locality of the natural gradient for learning in deep Bayesian networks

Abstract

We study the natural gradient method for learning in deep Bayesian networks, including neural networks. There are two natural geometries associated with such learning systems consisting of visible and hidden units. One geometry is related to the full system, the other one to the visible sub-system. These two geometries imply different natural gradients. In a first step, we demonstrate a great simplification of the natural gradient with respect to the first geometry, due to locality properties of the Fisher information matrix. This simplification does not directly translate to a corresponding simplification with respect to the second geometry. We develop the theory for studying the relation between the two versions of the natural gradient and outline a method for the simplification of the natural gradient with respect to the second geometry based on the first one. This method suggests to incorporate a recognition model as an auxiliary model for the efficient application of the natural gradient method in deep networks.

1 Introduction

1.1 The natural gradient method

Within the last decade, deep artificial neural networks have led to unexpected successes of machine learning in a large number of applications [15]. One important direction of research within the field of deep learning is based on the natural gradient method from information geometry [3, 4, 8]. It has been proposed by Amari [2] as a gradient method that is invariant with respect to coordinate transformations. This method turns out to be extremely efficient within various fields of artificial intelligence and machine learning, including neural networks [2], reinforcement learning [7, 19], and robotics [27]. It is known to overcome several problems of traditional gradient methods. Most importantly, the natural gradient method avoids the so-called plateau problem, and it is less sensitive to singularities (for a detailed discussion, see Section 12.2 of the book [3]; the subject of singularities is treated in [32]). On the other hand, there are significant challenges and limitations concerning the applicability of the natural gradient method [22]. Without further assumptions this method becomes intractable in the context of deep neural networks with a large number of parameters. Various approximate methods have been proposed and studied as alternatives to the original method [20, 23, 26]. In this article, we highlight information-geometric structures of deep Bayesian and, in particular, neural networks that allow for a simplification of the natural gradient. The guiding scheme of this simplification is locality with respect to the underlying network structure [5]. There are several aspects of learning that can be addressed from this perspective:

• 1. Objective function: Typically, learning is based on the optimisation of some global objective function related to the overall performance of the network, which, in the most general context, is evaluated in some behaviour space. On the other hand, if we assume that individual units access information only from their local neighbourhood, then we are naturally led to the following problem. Is it possible to decompose the objective function into individual local objective functions that can be evaluated by the corresponding units?

• 2. Learning I: Assuming that learning is based on the gradient of a global objective function, does the above-mentioned decomposition into local functions imply a corresponding locality of the gradient with respect to the parametrisation? In that case, the individual units would adjust their parameter values, such as the synaptic connection strengths in the case of neural networks, based on local information. This is a typical implicit assumption within the field of neural networks, most prominently realised in terms of Hebbian learning [16], which implies that a connection between two neurons is modified based on their joint activity.

• 3. Learning II: When computing the natural gradient of an objective function, we have to evaluate (the inverse of) the Fisher information matrix. Even if locality of learning is guaranteed for the Euclidean gradient, this matrix might reintroduce non-locality. We will analyse to what extent the natural gradient preserves locality? One instance of this property corresponds to a block diagonal structure of the Fisher information matrix which simplifies its inversion [5, 28].

We are now going to introduce the required formalism and outline the problem setting in more detail.

1.2 Preliminaries and the main problem

We first introduce the notation used in this article. Let $\mathsf {S}$ be a non-empty finite set. We denote the canonical basis of the vector space ${\mathbb R}^{\mathsf {S}}$ by $e_s$, $s \in \mathsf {S}$. The corresponding dual vectors ${\delta }^s \in \left( {\mathbb R}^{\mathsf {S}} \right) ^*$, $s \in \mathsf {S}$, defined by

can be identified with the Dirac measures on $\mathsf {S}$. Each linear form $l \in \left( {\mathbb R}^{\mathsf {S}} \right) ^*$ can be written as $\sum _s l(s) \, \delta ^s$, where $l(s) := l(e_s)$. We denote the open simplex of strictly positive probability vectors on $\mathsf {S}$ by

$$\begin{aligned} {{\mathcal {P}}} (\mathsf {S}) \, := \, \left\{ p = \sum _s p(s) \, \delta ^s \; : \; p(s) > 0 \text{ for } \text{ all } s, \text{ and } \displaystyle \sum _s p(s) = 1 \right\} . \end{aligned}$$

For each point $p \in {{\mathcal {P}}}({\mathsf {S}})$, the tangent space in p can be naturally identified with

$$\begin{aligned} {{\mathcal {T}}}(\mathsf {S}) \, := \, \left\{ A = \sum _s A(s) \, \delta ^s \; : \; \sum _{s} A(s) = 0 \right\} . \end{aligned}$$

The Fisher–Rao metric on ${{\mathcal {P}}}(\mathsf {S})$ in $p = \sum _s p(s) \, \delta ^s$ is defined by

$$\begin{aligned} {\langle A , B \rangle }_p := \sum _{s} \frac{1}{p(s)} \, A(s) B(s), \qquad A, B \in \mathcal {T}({\mathsf {S}}). \end{aligned}$$

(1)

Let us now consider a model ${{\mathcal {M}}} \subseteq {\mathcal P}(\mathsf {S})$ which we assume to be a d-dimensional smooth manifold with local coordinates $\xi = (\xi _1,\dots ,\xi _d) \mapsto p_\xi$, where $\xi$ is from an open domain $\varXi$ in ${\mathbb R}^d$. Below, we will treat more general models, but starting with manifolds allows us to outline more clearly the challenges we face in the context of the natural gradient method. With $p(s ; \xi ) := p_\xi (s)$, we define the vectors $\partial _i (\xi ) := \frac{\partial }{\partial \xi _i} \, p_\xi$, $i = 1,\dots , d$, which span the tangent space $T_\xi {{\mathcal {M}}}$. (Throughout this article, we use the subscript $\xi$, as in $T_\xi {{\mathcal {M}}}$, to denote the point ${p_\xi }$ whenever this simplifies the notation.) From (1) we then obtain the Fisher information matrix $\mathrm{G}(\xi ) = {\left( g_{ij} (\xi ) \right) }_{ij}$, defined by

$$\begin{aligned} g_{i j} (\xi ) \, := \, \left\langle \partial _{i} (\xi ) , \partial _{j} (\xi ) \right\rangle _{\xi } \, = \, \sum _{s} p(s ; \xi ) \, \frac{\partial \ln p(s ; \cdot )}{\partial \xi _i} (\xi ) \frac{\partial \ln p(s ; \cdot )}{\partial \xi _j} (\xi ). \end{aligned}$$

(2)

Given a smooth function ${{\mathcal {L}}}: {{\mathcal {M}}} \rightarrow {\mathbb R}$, its gradient $\mathrm{grad}^{{\mathcal {M}}}_\xi {{\mathcal {L}}} \in T_\xi {{\mathcal {M}}}$ in $p_\xi$ is the direction of steepest ascent. It has the following usual representation in the local coordinates $\xi$:

$$\begin{aligned} \mathrm{grad}^{{\mathcal {M}}}_\xi {{\mathcal {L}}} \; = \; \mathrm{G}^{-1}(\xi ) \, \nabla _\xi {{\mathcal {L}}}. \end{aligned}$$

(3)

As we can see, the gradient depends on the Fisher–Rao metric in $p_\xi$. It is this dependence that makes it natural and the reason for calling it the natural gradient. Let us clarify how to read the equation (3). The LHS is a vector in $T_\xi {{\mathcal {M}}}$, whereas the RHS is a vector in ${\mathbb R}^d$, which appears somewhat inconsistent. The way to read this is the following: As a vector in the tangent space in $p_\xi$, the gradient has a representation $\sum _{i = 1}^d x^i \, \partial _i(\xi )$. The coordinates $x^i$ are then given by the RHS of (3) (see also “Moore–Penrose inverse and gradients” of the Appendix).

In this article, the set $\mathsf {S}$ will typically be a Cartesian product of state sets of units, for instance binary neurons. More precisely, we consider a non-empty and finite set N of units consisting of n visible units V and m hidden units H, that is ${N} = {V} \uplus {H}$. The state sets of the units are denoted by $\mathsf {X}_i$, $i \in N$, and assumed to be non-empty and finite. For any subset $M \subseteq N$, we have the corresponding configuration or state set $\mathsf {X}_M := \times _{i \in M} \mathsf {X}_i$, the set ${{\mathcal {P}}}_M := {\mathcal P}(\mathsf {X}_M)$ of strictly positive probability vectors on $\mathsf {X}_M$, and the tangent space ${{\mathcal {T}}}_M := {{\mathcal {T}}}(\mathsf {X}_M)$. Consider now the restriction $X_M: \mathsf {X}_N \rightarrow \mathsf {X}_M$, $x = (x_M, x_{N \setminus M}) \mapsto x_M$, and its push-forward map

$$\begin{aligned} \pi _M: \; {{\mathcal {P}}}_N \; \rightarrow \; {{\mathcal {P}}}_M, \qquad p \; \mapsto \; \pi _M (p) \, := \, \sum _{x_{M} \in \mathsf {X}_{M}} p(x_M) \, \delta ^{x_M}, \end{aligned}$$

where $p (x_M) := \sum _{x_{N \setminus M} \in \mathsf {X}_{N \setminus M}} p(x_M, x_{N \setminus M})$. This is simply the marginalisation map where $\pi _M(p)$ is the M-marginal of p. We will primarily deal with the case where the subset M is given by the visible units V.

Given a model ${{\mathcal {M}}}$ in ${{\mathcal {P}}}_{V,H} := {{\mathcal {P}}}_N$, we consider the marginal or projected model ${{\mathcal {M}}}_V := \pi _V ({{\mathcal {M}}})$ in ${{\mathcal {P}}}_V$ which will play a major role in this article. With a parametrisation $\xi \mapsto p_\xi$ of ${{\mathcal {M}}}$, we also have a parametrisation of ${{\mathcal {M}}}_V$, simply by mapping $\xi$ to the point $\pi _V (p_\xi ) \in {{\mathcal {M}}}_V$. For $\xi$, we then have the tangent vectors $\partial _i (\xi ) = \frac{\partial }{\partial \xi _i} \, p_\xi$, $i = 1, \dots , d$, in $T_\xi {{\mathcal {M}}}$ and the tangent vectors ${\bar{\partial }}_i (\xi ) := \frac{\partial }{\partial \xi _i} \pi _V (p_\xi )$, $i = 1, \dots , d$, in $T_\xi {{\mathcal {M}}}_V$. The definition (2) of the Fisher information matrix in $\xi$ can now be applied to both models, ${{\mathcal {M}}}$ and ${{\mathcal {M}}}_V$. In order to distinguish them from each other, we write $g_{ij} (\xi ) = \langle \partial _i(\xi ), \partial _j (\xi ) \rangle _{\xi }$ for the components of the Fisher information matrix $\mathrm{G}(\xi )$ in $p_\xi \in {{\mathcal {M}}}$, and correspondingly ${\overline{g}}_{ij} (\xi ) := \langle {\bar{\partial }}_i (\xi ), {\bar{\partial }}_j (\xi ) \rangle _\xi$ for the components of the Fisher information matrix $\overline{\mathrm{G}}(\xi )$ in $\pi _V (p_\xi ) \in {{\mathcal {M}}}_V$.

Notice that we face a number of difficulties already at this point.

• 1. Even if we choose ${{\mathcal {M}}}$ to be a smooth manifold, its projection ${{\mathcal {M}}}_V$ is typically a much more complicated geometric object with various kinds of singularities (to be formally defined in Section 3.1). Therefore, we will allow for more general models without assuming ${{\mathcal {M}}}$ to be a smooth manifold in the first place. However, we will restrict attention to non-singular points only.

• 2. In addition to having a general model ${{\mathcal {M}}}$, we also drop the assumption that the parametrisation $\xi = (\xi _1,\dots ,\xi _d) \mapsto p_\xi$ is given by a (diffeomorphic) coordinate system. This has consequences on the definition of the Fisher–Rao metric in a non-singular point $p_\xi$:

  • (a) In order to interpret the Fisher–Rao metric as a Riemannian metric, the derivatives $\partial _i(\xi ) = \frac{\partial }{\partial \xi _i} p_\xi$, $i = 1,\dots ,d$, have to span the whole tangent space $T_\xi {{\mathcal {M}}}$ in $p_\xi$. (This is often implicitly assumed but not explicitly stated.) Otherwise, the Fisher–Rao metric defined by (2) will not be positive definite. We will refer to a parametrisation that satisfies this condition as a proper parametrisation. Note that for a proper parametrisation $\xi \mapsto p_\xi$ of ${{\mathcal {M}}}$, the composition $\xi \mapsto \pi _V(p_\xi )$ is not necessarily a proper parametrisation of ${{\mathcal {M}}}_V$.

  • (b) Another consequence of not having a coordinate system as a parametrisation is the fact that the number d of parameters may exceed the dimension of the model. Even if we assume ${{\mathcal {M}}}$ to be a smooth manifold and its parametrisation given by a coordinate system, such that d equals the dimension of ${{\mathcal {M}}}$, the corresponding projected model ${{\mathcal {M}}}_V$ can have a much lower dimension. In that case, we say that the model is overparametrised. Such models play an important role within the field of deep learning. The Fisher–Rao metric for such models is well defined in non-singular points. However the Fisher information matrix (2) will be degenerate so that the representation of a gradient in terms of the parameters is not unique anymore. Below, we will come back to this problem.

We use the natural gradient method in order to minimise (or maximise) a function ${{\mathcal {L}}}: {{\mathcal {M}}}_V \rightarrow {\mathbb R}$ which is usually obtained as a restriction of a smooth function defined on ${{\mathcal {P}}}_V$. Therefore, it is natural to use the Fisher–Rao metric on ${{\mathcal {M}}}_V$ which is inherited from ${{\mathcal {P}}}_V$. Assuming that all required quantities are well defined, we can express this natural gradient in terms of the parametrisation as

$$\begin{aligned} \mathrm{grad}^{{{\mathcal {M}}}_V}_{\xi } {{\mathcal {L}}} \; = \; {\overline{\mathrm{G}}}^{+}(\xi ) \nabla _\xi {{\mathcal {L}}}, \end{aligned}$$

(4)

where $\overline{\mathrm{G}}^+(\xi )$ is the Moore–Penrose inverse of the Fisher information matrix $\overline{\mathrm{G}}(\xi )$ (for details on the Moore–Penrose inverse, see “Moore–Penrose inverse and gradients” of the Appendix). If the parametrisation is given by a coordinate system then this reduces to the ordinary matrix inverse. The general difficulty that we face with Eq. (4) is the inversion of the Fisher information matrix, especially in deep networks with many parameters. On the other hand, the model ${{\mathcal {M}}}_V$ is obtained as the image of the model ${\mathcal M}$ which can be easier to handle, despite the fact that it “lives” in the larger space ${{\mathcal {P}}}_{V,H}$. Instead of optimising the function ${{\mathcal {L}}}$ on ${{\mathcal {M}}}_V$ we can try to optimise the pull-back of ${{\mathcal {L}}}$, that is ${{\mathcal {L}}} \circ \pi _V$, which is defined on ${{\mathcal {M}}}$. But this creates a conceptual problem related to the very nature of the natural gradient method. As ${{\mathcal {M}}}$ inherits the Fisher–Rao metric from ${{\mathcal {P}}}_{V,H}$, we can express the corresponding gradient as

$$\begin{aligned} \mathrm{grad}^{{\mathcal {M}}}_{\xi } ({{\mathcal {L}}} \circ \pi _V) \; = \; \mathrm{G}^{+}(\xi ) \nabla _\xi {{\mathcal {L}}} . \end{aligned}$$

(5)

This can simplify the problem in various ways. As already outlined, ${{\mathcal {M}}}_V$ typically has singularities, even if ${\mathcal M}$ is a smooth manifold. In that case, the gradient (5) is well defined for all $\xi$, whereas the gradient (4) is not. A further simplification comes from the fact that ${{\mathcal {M}}}$ is typically associated with some network, which implies a block structure of the Fisher information matrix $\mathrm{G}(\xi )$ in $p_\xi \in {{\mathcal {M}}}$. In Section 2, we will demonstrate this simplification for models that are associated with directed acyclic graphs, where the elements of ${{\mathcal {M}}}$ factorise accordingly. With this simplification, the inversion of $\mathrm{G}(\xi )$ can become much easier than the inversion of $\overline{\mathrm{G}}(\xi )$ (when the latter is defined). On the other hand, if we consider the model ${{\mathcal {M}}}_V$ to be the prime model, where the hidden units play the role of auxiliary units, then we have to use the information geometry of ${{\mathcal {M}}}_V$ for learning. Therefore, it is important to relate the corresponding natural gradients, that is (4) and (5), to each other. This is done in a second step, presented in Sect. 3. In particular, we will identify conditions for the equivalence of the two gradients, leading to a new interpretation of Chentsov’s classical characterisation of the Fisher–Rao metric in terms of its invariance with respect to congruent Markov morphisms [12]. (A general version of this charecterisation is provided in [8].) Based on the comparison of the gradients (4) and (5), we will investigate how to extend locality properties of learning that hold for ${{\mathcal {M}}}$ to the model ${{\mathcal {M}}}_V$. This is closely related to the above-mentioned approximate methods as alternatives to the natural gradient method. Of particular relevance in this context is the replacement of the Fisher information matrix by the unitwise Fisher information matrices as studied in [20, 26]. Note, however, that we are not aiming at approximating the natural gradient on ${{\mathcal {M}}}_V$ by the unitwise natural gradient. In this article, we aim at identifying conditions for their equivalence. Furthermore, in order to satisfy these conditions we propose an extension ${\widetilde{\mathcal {M}}}$ of ${{\mathcal {M}}}$ which corresponds to an interesting extension of the underlying network. This will lead us to a new interpretation of so-called recognition models, which are used in the context of Helmholtz machines and the wake-sleep algorithm [13, 17, 25]. Information-geometric works on the wake-sleep algorithm and its close relation to the em-algorithm are classical [1, 14, 18]. More recent contributions to the information geometry of the wake-sleep algorithm are provided by [10] and [31]. Directions of related research in view of this article are outlined in the conclusions, Sect. 4.

2 Locality of deep learning in Bayesian and neural networks

2.1 Locality of the Euclidean gradient

We now define a sub-manifold of ${{\mathcal {P}}}_{V,H}$ in terms of a directed acyclic graph $G = (N, E)$ where E is the set of directed edges. For a node s, we define the set $pa(s) := \{r \in N \; : \; (r,s) \in E\}$ of its parents and the set $ch(s) := \{t \in N \; : \; (s,t) \in E\}$ of its children. The latter will be only used in “Gibbs sampling” of the Appendix.

With each node s we associate a local Markov kernel, that is a map

$$\begin{aligned} k^s: \; \mathsf {X}_{pa(s)} \times \mathsf {X}_s \; \rightarrow \; (0,1), \qquad (x_{pa(s)}, x_s) \; \mapsto \; k^s(x_s | x_{pa(s)}), \end{aligned}$$

with $\sum _{x_s} k^s(x_s | x_{pa(s)}) = 1$ for all $x_{pa(s)} \in \mathsf {X}_{pa(s)}$. Note that for $pa(s) = \emptyset$, the configuration set $\mathsf {X}_{pa(s)}$ consists of one element, the empty configuration. In this case, a Markov kernel reduces to a probability vector over $\mathsf {X}_s$. (We will revisit Markov kernels from a geometric perspective in Section 3.2.) Given such a family of Markov kernels, we define the joint distribution

$$\begin{aligned} p(x_N) \, = \, \prod _{s \in N} k^s(x_s | x_{pa(s)}). \end{aligned}$$

(6)

The distributions of the product structure (6) form a (statistical) model that plays an important role within the field of graphical models, in particular Bayesian networks [21]. A natural sub-model is given by the product distributions, that is those distributions of the form

$$\begin{aligned} p(x_N) \, = \, \prod _{s \in N} p(x_s). \end{aligned}$$

In order to treat a more general sub-model, in particular one that is given by a neural network, a so-called neuro-manifold, we consider for each unit $s \in N$ a parametrisation ${\mathbb R}^{d_s} \ni \xi _{s} = (\xi _{(s;1)}, \dots , \xi _{(s; d_s)}) \mapsto \kappa ^{s}_{\xi _s}$. This defines a model ${{\mathcal {M}}}$ as the image of the map

$$\begin{aligned} \xi := {(\xi _s)}_{s \in N} \; \mapsto \; p_\xi (x_N) \, = \, \prod _{s \in N} k^s(x_s | x_{pa(s)}; \xi _s ) , \end{aligned}$$

(7)

where $k^s(x_s | x_{pa(s)} ; \xi _s) := k^s_{\xi _s}(x_s | x_{pa(s)})$. In order to use vector and matrix notation, we consider a numbering of the units, that is $N = \{s_1,\dots , s_{n + m}\}$, with $i \le j$ whenever $s_i \in pa(s_j)$. To simplify notation, we can alternatively assume, without loss of generality, $N = \{1,2,\dots , n + m\}$ such that $r \le s$ whenever $r \in pa(s)$. This allows us to write the parametrisation (7) as a mapping from a domain in ${\mathbb R}^d$, $d = \sum _{s = 1}^{n + m} d_s$, to ${{\mathcal {M}}}$, where

$$\begin{aligned} \xi \, = \, (\underbrace{\xi _{(1;1)}, \dots , \xi _{(1;d_1)}}_{ = \xi _1}, \underbrace{\xi _{(2;1)}, \dots , \xi _{(2;d_2)}}_{= \xi _2}, \dots , \underbrace{\xi _{(n+m;1)}, \dots , \xi _{(n+m; d_{n+m})}}_{= \xi _{n + m}}) \end{aligned}$$

(8)

is mapped to $p_\xi \in {{\mathcal {M}}}$.

Now we come to the main objective of learning as studied in this article. Given a target probability vector $p^*\in {\mathcal P}_V$ on the state set of visible units, the aim is to represent, or at least approximate, it by an appropriate element ${\hat{p}}$ of the model ${{\mathcal {M}}}_V = \pi _V ({{\mathcal {M}}}) \subseteq {{\mathcal {P}}}_V$. Such an approximation requires a measure of proximity, a divergence, between probability vectors. Information geometry provides ways to identify a natural choice of such a divergence, referred to as canonical divergence [6]. In the present context, the relative entropy or Kullback–Leibler divergence (abbreviated as KL-divergence)

$$\begin{aligned} D(p \Vert q) = \sum _{x} p(x) \ln \frac{p(x)}{q(x)} \end{aligned}$$

between two probability vectors p and q is the most commonly used divergence. This leads to the search of a probability vector ${\hat{p}} \in {{\mathcal {M}}}_V$ that satisfies

$$\begin{aligned} D(p^*\Vert {{\mathcal {M}}}_V ) \, := \, \inf _{p \in {{\mathcal {M}}}_V} D(p^*\Vert p) \, = \, D(p^*\Vert {\hat{p}}). \end{aligned}$$

(9)

For this search we use the parametrisation (7) of the elements of ${{\mathcal {M}}}$ and define the function

$$\begin{aligned} {{\mathcal {L}}}(\xi ):= & {} D(p^*\, \Vert \, \pi _V(p_\xi )) \nonumber \\= & {} \sum _{x_V} p^*(x_V) \ln \frac{p^*(x_V)}{p(x_V ; \xi )} \nonumber \\= & {} \sum _{x_V} p^*(x_V) \ln \frac{p^*(x_V)}{\sum _{x_H} p(x_V, x_H; \xi )}. \end{aligned}$$

(10)

Minimisation of ${{\mathcal {L}}}$ can be realised in terms of the gradient method. In this section we begin with the Euclidean gradient which is determined by the partial derivatives of ${{\mathcal {L}}}$. It is remarkable that, even though the network can be large, with many hidden units, the resulting derivatives are local in a very useful way (see a similar derivation in the context of sigmoid belief networks in [24]):

$$\begin{aligned} \frac{\partial {{\mathcal {L}}}}{\partial \xi _{(r;i)}} (\xi )= & {} \frac{\partial }{\partial \xi _{(r;i)}} \sum _{x_V} p^*(x_V) \ln \frac{p^*(x_V)}{p(x_V; \xi )} \\= & {} - \sum _{x_V} p^*(x_V) \frac{\partial \ln p(x_V; \cdot )}{\partial \xi _{(r;i)}} (\xi ) \\= & {} - \sum _{x_V} \frac{p^*(x_V)}{p_\xi (x_V)} \sum _{x_H} \frac{\partial p(x_V, x_H; \cdot )}{\partial \xi _{(r;i)}} (\xi ) \\= & {} - \sum _{x_V} \frac{p^*(x_V)}{p_\xi (x_V)} \sum _{x_H} \frac{\partial }{\partial \xi _{(r;i)}} \prod _{s \in N} k^s(x_s | x_{pa(s)} ; \xi _s) \\= & {} - \sum _{x_V} \frac{p^*(x_V)}{p_\xi (x_V)} \sum _{x_H} \prod \limits _{\begin{array}{c} s \in N \\ s \not = r \end{array}} k^s (x_s | x_{pa(s)} ; \xi _s) \frac{\partial k^r (x_r | x_{pa(r)} ; \cdot )}{\partial \xi _{(r;i)}} (\xi _r) \\= & {} - \sum _{x_V} \frac{p^*(x_V)}{p_\xi (x_V)} \sum _{x_H} \prod _{s \in N} k^s (x_s | x_{pa(s)} ; \xi _s) \frac{\partial \ln k^r (x_r | x_{pa(r)} ; \cdot ) }{\partial \xi _{(r;i)}} (\xi _r) \\= & {} - \sum _{x_V,x_H} \frac{p^*(x_V)}{p_\xi (x_V)} p_\xi (x_V, x_H) \frac{\partial \ln k^r(x_r | x_{pa(r)} ; \cdot ) }{\partial \xi _{(r;i)}} (\xi _r) \\= & {} - \sum _{x_V,x_H} p^*(x_V) \, p_\xi (x_H \, | \, x_V) \, \frac{\partial }{\partial \xi _{(r;i)}} \ln k^r(x_r | x_{pa(r)} ; {\xi _r} ). \end{aligned}$$

With $p^*(x_V,x_H ; \xi ) := p^*(x_V) \, p(x_H \, | \, x_V ; \xi )$, we finally obtain

$$\begin{aligned}&{\frac{\partial {{\mathcal {L}}}}{\partial \xi _{(r;i)}} (\xi )} \nonumber \\&\quad = - \sum _{x_V,x_H} p^*(x_V , x_H ; \xi ) \, \frac{\partial }{\partial \xi _{(r;i)}} \ln k^r (x_r | x_{pa(r)} ; {\xi _r}) \nonumber \\&\quad = - \sum _{x_{pa(r)}} p^*(x_{pa(r)} ; \xi ) \sum _{x_r} p^*(x_r | x_{pa(r)} ; \xi ) \, \frac{\partial }{\partial \xi _{(r;i)}} \ln k^r (x_r | x_{pa(r)} ; {\xi _r}). \end{aligned}$$

(11)

We have an expectation value of a function, ${\frac{\partial }{\partial \xi _{(r;i)}}} \ln k^r (x_r | x_{pa(r)} ; {\xi _r})$, that is local in two ways: All arguments of this function, the states and the parameters, are local with respect to the node r. However, the distribution $p^*_\xi$, used for the evaluation of the expectation value, depends on the full set of parameters $\xi$. On the other hand, due to the locality of ${\frac{\partial }{\partial \xi _{(r;i)}}} \ln k^r (x_r | x_{pa(r)} ; {\xi _r})$ with respect to the states $x_{pa(r)}$ and $x_r$, this expectation value depends only on the marginal $p^*(x_{pa(r)}, x_r)$. One natural way to approximate (11) is by sampling from this distribution. This is typically difficult, compared to the sampling from $p_\xi$ which factorises according to the underlying directed acyclic graph G. “One-shot sampling” from $p_\xi$ is possible by simply using $p_\xi$ as a generative model, which here simply means recursive application of the local kernels $k^r_{\xi _r}$ according to the underlying directed acyclic graph. This kind of sampling is also referred to as ancestral sampling [15]. As $p^*_\xi$ incorporates the target distribution $p^*$ on $\mathsf {X}_V$ and does not necessarily factorise according to G, sampling from it has to run much longer. For completeness, the Gibbs sampling method is outlined in more detail in “Gibbs sampling” of the Appendix.

We exemplify the derivative (11) in the context of binary neurons where it leads to a natural learning rule.

Example 1

(Neural networks (I)) We assume that the units $r \in N$, referred to as neurons in this context, are binary with state sets $\{-1,+1\}$. For each neuron r, we consider a vector $w_r = (w_{ir})_{i \in pa(r)}$ of synaptic connection strengths and a threshold value $\vartheta _r$. For a synaptic strength $w_{ir}$, i is referred to as the pre-synaptic and r the post-synaptic neuron, respectively. We set $\xi _{(r;i)} := w_{ir}$, $i = 1,\dots , d_r - 1$, and $\xi _{(r;d_r)} := \vartheta _r$, that is $\xi _r = (w_r, \vartheta _r)$. In order to update its state, the neuron first evaluates the local function

$$\begin{aligned} h_r(x_{pa(r)}) := \sum _{i \in pa(r)} w_{i r} x_i - \vartheta _r \end{aligned}$$

and then generates a state $x_r\in \{-1,+1\}$ with probability

$$\begin{aligned} k^r(x_r | x_{pa(r)}; w_r , \vartheta _r):= & {} \frac{1}{1 + e^{- x_r h_r(x_{pa(r)})}}. \end{aligned}$$

(12)

We calculate the derivatives

$$\begin{aligned} \frac{\partial }{\partial w_{i r}} \ln k^r(x_r | x_{pa(r)}; w_r , \vartheta _r)= & {} \frac{x_i x_r}{1 + e^{x_r h_r(x_{pa(r)})}} , \end{aligned}$$

(13)

$$\begin{aligned} \frac{\partial }{\partial \vartheta _{r}} \ln k^r(x_r | x_{pa(r)}; w_r , \vartheta _r)= & {} - \frac{x_r}{1 + e^{x_r h_r(x_{pa(r)})}} , \end{aligned}$$

(14)

and, with (11), we obtain

$$\begin{aligned} \frac{\partial {{\mathcal {L}}}}{\partial w_{ir}} (w, \vartheta )= & {} - \sum _{x_{pa(r)}} \sum _{x_r} p^*_\xi (x_{pa(r)} , x_r) \, \frac{x_i x_r}{1 + e^{x_r h_r(x_{pa(r)})}}, \end{aligned}$$

(15)

$$\begin{aligned} \frac{\partial {{\mathcal {L}}}}{\partial \vartheta _r} (w, \vartheta )= & {} \sum _{x_{pa(r)}} \sum _{x_r} p^*_\xi (x_{pa(r)} , x_r) \,\frac{x_r}{1 + e^{x_r h_r(x_{pa(r)})}}. \end{aligned}$$

(16)

Equation (15) is one instance of the Hebb rule which is based on the learning paradigm phrased as “cells that fire together wire together” [16]. Note, however, that the causal interpretation of the underlying directed acyclic graph ensures that the pre-synaptic activity $x_i$ is measured before the post-synaptic activity $x_r$. This causally consistent version of the Hebb rule has been experimentally studied in the context of spike-timing-dependent plasticity of real neurons (e.g., [9]). In order to use the derivatives (15) and (16) for learning, we have to sample from $p^*_\xi$. An outline of Gibbs sampling in this context is provided in Example 7 of the Appendix.

2.2 The wake–sleep algorithm

We now highlight an important alternative to sampling from $p^*_\xi$ for the computation of the derivative (11). This alternative is based on the idea that we have, in addition to the generative model ${{\mathcal {M}}}$ of distributions $p_\xi$, a so-called recognition model ${{\mathcal {Q}}}_{H|V}$ of conditional distributions $q(x_H | x_V ; {\eta })$ with which we can approximate $p(x_H \, | \, x_V ; \xi )$. As a consequence, such a recognition model allows us to approximate (11) where we replace $p^*(x_V, x_H ; \xi ) = p^*(x_V) \, p(x_H | x_V ; \xi )$ by $q^*(x_V, x_H ; \eta ) := p^*(x_V) \, q(x_H | x_V ; \eta )$, and correspondingly the marginals on $pa(r) \cup \{r\}$. We obtain

$$\begin{aligned}&{\frac{\partial {{\mathcal {L}}}}{\partial \xi _{(r;i)}} (\xi )} \nonumber \\&\quad \approx - \sum _{x_{pa(r)}} q^*(x_{pa(r)} ; \eta ) \sum _{x_r} q^*(x_r | x_{pa(r)} ; \eta ) \, \frac{\partial }{\partial \xi _{(r;i)}} \ln k^r(x_r | x_{pa(r)} ; {\xi _r}) \end{aligned}$$

(17)

$$\begin{aligned}&\quad = - \frac{\partial }{\partial \xi _{(r;i)}} \sum _{x_{pa(r)}} q^*(x_{pa(r)} ; \eta ) \sum _{x_r} q^*(x_r | x_{pa(r)} ; \eta ) \ln k^r(x_r | x_{pa(r)} ; {\xi _r}) \end{aligned}$$

(18)

$$\begin{aligned}&\quad = \frac{\partial }{\partial \xi _{(r;i)}} \sum _{x_{pa(r)}} q^*(x_{pa(r)} ; \eta ) \sum _{x_r} q^*(x_r | x_{pa(r)} ; \eta ) \ln \frac{q^*(x_r | x_{pa(r)} ; \eta )}{k^r(x_r | x_{pa(r)} ; {\xi _r})} . \end{aligned}$$

(19)

For the evaluation of the gradient of ${{\mathcal {L}}}$ with respect to the $\xi$-parameters we can now use the recognition model, instead of the generative model. This approximation will be the more accurate the smaller the following relative entropy is:

$$\begin{aligned} D(\xi \Vert \eta ) \; := \; \sum _{x_V} p(x_V ; \xi ) \sum _{x_H} p(x_H | x_V ; \xi ) \ln \frac{p(x_H | x_V ; \xi )}{q(x_H | x_V ; \eta )} . \end{aligned}$$

(20)

Ideally, we would like the recognition model to be rich enough to represent the conditional distributions of the generative model. More precisely, we assume that for all $\xi$, there is an $\eta = \eta (\xi )$ so that $q(x_H | x_V ; \eta ) = p(x_H | x_V ; \xi )$. Furthermore, for (20) to be tractable, we assume that $q(x_H | x_V ; \eta )$ also factorises according to some directed acyclic graph $G'$, so that

$$\begin{aligned} q(x_H | x_V ; \eta ) \; = \; \prod _{r \in H} l^r(x_r | x_{pa'(r)} ; \eta _r) , \end{aligned}$$

(21)

where ${pa}'(r)$ denotes the parent set of the node r with respect to the graph $G'$. With the assumption (21), the expression (20) simplifies considerably, and we obtain

$$\begin{aligned}&{\frac{\partial D(\xi \Vert \cdot )}{\partial \eta _{(r;j)}} (\eta ) } \nonumber \\&\quad = - \frac{\partial }{\partial \eta _{(r;j)}} \sum _{x_{pa'(r)}} p(x_{pa'(r)} ; \xi ) \sum _{x_r} p(x_r | x_{pa'(r)} ; \xi ) \ln l^r(x_r | x_{pa'(r)} ; \eta _r) \end{aligned}$$

(22)

$$\begin{aligned}&\quad = \frac{\partial }{\partial \eta _{(r;j)}} \sum _{x_{pa'(r)}} p(x_{pa'(r)} ; \xi ) \sum _{x_r} p(x_r | x_{pa'(r)} ; \xi ) \ln \frac{p(x_r | x_{pa'(r)} ; \xi )}{l^r(x_r | x_{pa'(r)} ; \eta _r)}. \end{aligned}$$

(23)

Note that, while $p_\xi$ factorises according to G so that the conditional distribution $p(x_r | x_{pa(r)} ; \xi )$ coincides with the kernel $k^r( x_r | x_{pa'(r)} ; \xi )$, the conditional distribution $p(x_r | x_{pa'(r)} ; \xi )$ with respect to $G'$ does not have a correspondingly simple structure. On the other hand, we can easily sample from $p_\xi$, and thereby also from $p(x_{pa'(r)} ; \xi )$ and $p(x_r | x_{pa'(r)} ; \xi )$, using the product structure with respect to G.

Let us now come back to the original problem of minimising ${{\mathcal {L}}}$ with respect to $\xi$ based on the gradient descent method. If the parameter $\eta$ of the recognition model is such that $q(x_H | x_V ; \eta ) = p(x_H | x_V ; \xi )$ then the approximation (17) is exact, and we can evaluate the partial derivatives $\partial / \partial \xi _{(r ; i)}$ by sampling from $q^*(x_V, x_H; \eta ) = p^*(x_V) \, q(x_H | x_V; \eta )$. This can then be used for updating the parameter $\xi$, say from $\xi$ to $\xi + \varDelta \xi$ where $\varDelta \xi$ is proportional to the Euclidean gradient. As this update is based on sampling from the target distribution $p^*(x_V)$ and the recognition model $q(x_H | x_V ; \eta )$, it is referred to as the wake phase. After this update, we typically have $q(x_H | x_V ; \eta ) \not = p(x_H | x_V ; \xi + \varDelta \xi )$. In order to use (17) for the next update of $\xi$, we therefore have to readjust $\eta$, say from $\eta$ to $\eta + \varDelta \eta$, so that we recover the identity $q(x_H | x_V ; \eta + \varDelta \eta ) = p(x_H | x_V ; \xi + \varDelta \xi )$. This can be achieved by choosing $\varDelta \eta$ to be proportional to the Euclidean gradient (22) with respect to $\eta$. The evaluation of the partial derivatives $\partial / \partial \eta _{(r ; j)}$ requires sampling from the generative model $p(x_V, x_H ; \xi )$, with no involvement of the target distribution $p^*(x_V)$. This is the reason why the $\eta$-update is referred to as the sleep phase. Alternating application of the wake phase and the sleep phase yields the so-called wake–sleep algorithm, which has been introduced and studied in the context of neural networks in [13, 17, 25]. It has been pointed out that this algorithm cannot be interpreted as a gradient decent algorithm of a potential function on both variables $\xi$ and $\eta$. On the other hand, here we derived the wake–sleep algorithm as a gradient decent algorithm for the optimisation of the objective function ${{\mathcal {L}}}$ which only depends on the variable $\xi$. The auxiliary variable $\eta$ is used for the approximation of the gradient of ${{\mathcal {L}}}$ with respect to $\xi$. In order to have a good approximation of this gradient, we have to apply the sleep phase update more often, until convergence of $\eta$. Only then, we can update $\xi$ within the next wake phase. With this asymmetry of time scale for the two phases, the wake-sleep algorithm is a gradient decent algorithm for $\xi$, which has been pointed out in the context of the em-algorithm in [18].

We have introduced the parameters $\eta$ for sampling and thereby evaluating the derivative (11). However, there is another remarkable feature of the corresponding extended optimisation problem. While the original optimisation function ${{\mathcal {L}}}$, defined by (10), does not appear to be local in any sense, the extended optimisation in terms of a generalised wake-sleep algorithm, which is equivalent to the original problem, is based on a set of local functions associated with the respective units. More precisely, the expressions (18) and (22) are derivatives of local cross entropies, whereas the expressions (19) and (23) are derivatives of local KL-divergences.

We conclude with the important note that a recognition model which, on the one hand, is rich enough to represent all distributions $p(x_H | x_V ; \xi )$ and, on the other hand, factorises according to (21) might require a large graph $G'$ and a correspondingly large number of parameters $\eta _{(r; j)}$ which constitute the vector $\eta$. In practice, the recognition model is typically chosen to be of the same dimensionality as the generative model and does not necessarily satisfy the above conditions.

Example 2

Figure 1a depicts a typical generative network G, which underlies the model $p(x_V | x_H ; \xi )$. It is a directed acyclic network, and we assume that the model is simply given by the set of all joint distributions on $\mathsf {X}_H \times \mathsf {X}_V$ that factorise according to G. In Fig. 1b, we have a typical recognition network $G'$ obtained from the generative network G of Fig. 1a by reverting the directions of all arrows. The corresponding recognition model is given by the set of all conditional distributions $q(x_H | x_V)$ that factorise according to $G'$. However, this model is not large enough to ensure that for all $\xi$, there is an $\eta$ such that $q(x_H | x_V, \eta ) = p(x_H | x_V, \xi )$. Adding further lateral connections, as shown in Fig. 1c, enlarges $G'$, and we obtain a correspondingly enlarged recognition model which now has that property.

Fig. 1

Comparison of generative and recognition networks: a a typical generative network G; b a typical recognition network $G'$ obtained from the generative network G by reverting the directions; c recognition network $G'$ extended by lateral connections

2.3 Locality of the natural gradient

In the previous section, we have computed the partial derivatives (11) which turn out to be local and allow us to apply the gradient method for learning. However, from the information-geometric point of view, we have to use the Fisher–Rao metric for the gradient, which leads us to the natural gradient method. In general, the natural gradient is difficult to evaluate because the Fisher information matrix has to be inverted (see Eqs. (4) and (5)). In our context of a model that is associated with a directed acyclic graph G, however, the Fisher information matrix simplifies considerably. More precisely, we consider a model ${{\mathcal {M}}}$ with the parametrisation (7). The tangent space of ${\mathcal M}$ in $p_\xi$ is spanned by the vectors

$$\begin{aligned} \partial _{(r;i)}(\xi ) \, := \, \frac{\partial }{\partial \xi _{(r;i)}} \, p_\xi , \qquad r=1,\dots ,n+m, \quad i = 1,\dots ,d_r. \end{aligned}$$

(24)

The following theorem specifies the structure of the Fisher information matrix $\mathrm{G}(\xi )$ with the entries $g_{(r;i)(s;j)} (\xi ) = {\left\langle \partial _{(r;i)}(\xi ) , \partial _{(s;j)}(\xi ) \right\rangle }_{\xi }$.

Theorem 1

Let ${{\mathcal {M}}}$ be a model with the parametrisation (7). Then the Fisher information matrix $\mathrm{G}({\xi }) := \left( g_{(r;i)(s;j)}({\xi })\right) _{(r;i)(s;j)}$ decomposes into “local” $d_r \times d_r$ matrices $\mathrm{G}_r({\xi }) := \left( g_{(r;i,j)}({\xi }) \right) _{i,j}$, $r \in N$, with

$$\begin{aligned} g_{(r; i , j)}(\xi ):= & {} \sum _{x_{pa(r)}} p(x_{pa(r)} ; \xi ) \, C(x_{pa(r)}; \xi _r) , \end{aligned}$$

(25)

where

$$\begin{aligned} C(x_{pa(r)}; \xi _r):= & {} \sum _{x_r} k^r(x_r | x_{pa(r)} ; \xi _r) \nonumber \\&\quad \times \frac{\partial \ln k^r(x_r | x_{pa(r)} ; \cdot ) }{\partial \xi _{(r ; i)}}(\xi _r) \, \frac{\partial \ln k^r(x_r | x_{pa(r)} ; \cdot ) }{\partial \xi _{(r ; j)}}(\xi _r) . \end{aligned}$$

(26)

With this, the entries of the Fisher information matrix $\mathrm{G}({\xi })$ are given by $g_{(r;i)(s;j)} (\xi ) = g_{(r; i,j)} (\xi )$ whenever $r = s$, and $g_{(r;i)(s;j)} (\xi ) = 0$ otherwise. Using matrix notation, we have

$$\begin{aligned} \mathrm{G}({\xi }) = \left( \begin{array}{ccc} \mathrm{G}_{1}({\xi }) &{} &{} 0 \\ &{} \ddots &{} \\ 0 &{} &{} \mathrm{G}_{{m+ n}}({\xi }) \end{array} \right) . \end{aligned}$$

Proof

The parametrisation (7) yields

$$\begin{aligned} \ln p(x ; \xi ) \, = \, \sum _{r \in N} \ln k^r(x_r | x_{pa(r)} ; \xi _r) \end{aligned}$$

and therefore

$$\begin{aligned} \frac{\partial \ln p(x ; \cdot ) }{\partial \xi _{( s ; j )}} (\xi ) \, = \, \frac{\partial \ln k^s (x_s | x_{pa(s)} ; \cdot )}{\partial \xi _{( s ; j )}} (\xi _s). \end{aligned}$$

(27)

In what follows, we use the shorthand notation $x_{< s}$ and $x_{> s}$ for $x_{\{i \in N \, : \, i < s\}}$ and $x_{\{i \in N \, : \, i > s\}}$, respectively. With (27) we obtain for $r \le s$:

$$\begin{aligned}&{ g_{(r ; i)(s ; j)}(\xi )} \\&\quad = \sum _{x} p(x ; \xi ) \, \frac{\partial \ln p(x; \cdot ) }{\partial \xi _{( r ; i )}} (\xi ) \, \frac{\partial \ln p(x ; \cdot ) }{\partial \xi _{( s ; j )}} (\xi ) \\&\quad = \sum _{x} p(x ; \xi ) \frac{\partial \ln k^r(x_r | x_{pa(r)}; \cdot )}{\partial \xi _{( r ; i )}}(\xi _r) \frac{\partial \ln k^s(x_s | x_{pa(s)} ; \cdot )}{\partial \xi _{( s ; j )}}(\xi _s) \qquad \quad (\text{ by } ((27))) \\&\quad = \sum _{x_{< s}} \sum _{x_ s} \sum _{x_{>s}} \left\{ \prod _{i< s} k^i(x_i | x_{pa(i)} ; \xi _i) \right\} k^s(x_s | x_{pa(s)} ; \xi _s) \left\{ \prod _{i> s} k^i(x_i | x_{pa(i)} ; \xi _i) \right\} \\&\qquad \qquad \qquad \times \frac{\partial \ln k^r(x_r | x_{pa(r)} ; \cdot )}{\partial \xi _{( r ; i )}} (\xi _r) \frac{\partial \ln k^s(x_s | x_{pa(s)} ; \cdot )}{\partial \xi _{( s ; j )}} (\xi _s) \\&\quad = \sum _{x_{< s}} \left\{ \prod _{i < s} k^i(x_i | x_{pa(i)} ; \xi _i) \right\} \sum _{x_ s} k^s (x_s | x_{pa(s)} ; \xi _s) \underbrace{ \left\{ \sum _{x_{>s}} \prod _{i > s} k^i(x_i | x_{pa(i)} ; \xi _i ) \right\} }_{= 1} \\&\qquad \qquad \qquad \times \frac{\partial \ln k^r (x_r | x_{pa(r)} ; \cdot )}{\partial \xi _{( r ; i )}} (\xi _r) \frac{\partial \ln k^s (x_s | x_{pa(s)} ; \cdot )}{\partial \xi _{( s ; j )}} (\xi _s) \\&\quad = \sum _{x_{pa(s)}} p_\xi (x_{pa(s)}) \sum _{x_ s} k^s (x_s | x_{pa(s)} ; \xi _s) \\&\qquad \qquad \qquad \times \frac{\partial \ln k^r(x_r | x_{pa(r)} ; \cdot )}{\partial \xi _{( r ; i )}} (\xi _r) \frac{\partial \ln k^s(x_s | x_{pa(s)} ; \cdot )}{\partial \xi _{( s ; j )}} (\xi _s) . \end{aligned}$$

If $r \not = s$, this expression reduces to

$$\begin{aligned}&\sum _{x_{pa(s)}} p_\xi (x_{pa(s)}) \frac{\partial \ln k^r(x_r | x_{pa(r)} ; \cdot )}{\partial \xi _{( r ; i )}} (\xi _r) \\&\qquad \qquad \qquad \times \sum _{x_ s} k^s (x_s | x_{pa(s)} ; \xi _s) \frac{\partial \ln k^s(x_s | x_{pa(s)} ; \cdot )}{\partial \xi _{( s ; j )}} (\xi _s) \\= & {} \sum _{x_{pa(s)}} p_\xi (x_{pa(s)}) \frac{\partial \ln k^r (x_r | x_{pa(r)} ; \cdot )}{\partial \xi _{( r ; i )}} (\xi _r) \underbrace{\sum _{x_ s} \frac{\partial k^s (x_s | x_{pa(s)} ; \cdot )}{\partial \xi _{( s ; j )}}(\xi _s)}_{= 0} \\= & {} 0. \end{aligned}$$

This concludes the proof. $\square$

Theorem 1 highlights a number of simplifications of the Fisher information matrix as result of the particular parametrisation of the model in terms of a directed acyclic graph. The presented proof is adapted from [5] (see also the related work [28]):

• 1. The Fisher information matrix $\mathrm{G}(\xi )$ has a block structure, reflecting the structure of the underlying graph (see Fig. 3). Each block $\mathrm{G}_r(\xi )$ corresponds to a node r and has $d_r \times d_r$ components. Outside of these blocks the matrix is filled with zeros. The natural gradient method requires the inversion of $\mathrm{G}(\xi )$ (the usual inverse $\mathrm{G}^{-1}(\xi )$, if it exists, or, more generally, the Moore–Penrose inverse $\mathrm{G}^+(\xi )$). With the block structure of $\mathrm{G}(\xi )$, this inversion reduces to the inversion of the individual matrices $\mathrm{G}_r(\xi )$. The corresponding simplification of the natural gradient is summarised in Corollary 1.

• 2. The terms $g_{(r; i , j)}(\xi )$, defined by (25), are expectation values of the functions $C(x_{pa(r)}; \xi _r)$. These functions are local in two ways. On the one hand, they depend only on local states $x_{pa(r)}$ and, on the other hand, only local parameters $\xi _r$ are involved (see the definition (26)). This kind of locality is very useful in applications of the natural gradient method. Especially in the context of neural networks, locality of learning is considered to be essential. Note, however, that the terms $g_{(r; i , j)}(\xi )$ are not completely local. This is because the expectation value (25) is evaluated with respect to $p_\xi$, where $\xi$ is the full parameter vector. (As only the distribution of $X_{pa(r)}$ appears, parameters of non-ancestors of r do not play a role in the definition of $g_{(r; i , j)}(\xi )$, which simplifies the situation to some extent.) In order to evaluate the Fisher information matrix in applications, we have to overcome this non-locality by sampling from $p(x_{pa(r)} ; \xi )$. As we are dealing with directed acyclic graphs, this can be simply done by recursive application of the local kernels $k^r_{\xi _r}$.

To highlight the relevance of Theorem 1, let us consider a few simple examples.

Example 3

(Exponential families) Consider the model given by local kernels of the exponential form

$$\begin{aligned} k^r(x_r | x_{pa(r)}; \xi _r) \, = \, \frac{\exp \left( \sum _{i = 1}^{d_r} \xi _{(r;i)} \phi ^{(r;i)} (x_{pa(r)}, x_r) \right) }{\sum _{x_r'} \exp \left( \sum _{i = 1}^{d_r} \xi _{(r;i)} \phi ^{(r;i)} (x_{pa(r)}, x_r') \right) }. \end{aligned}$$

(28)

In this case, the expression (25) yields

$$\begin{aligned} {g_{(r;i,j)}(\xi ) } = \sum _{x_{pa(r)}} p( x_{pa(r)} ; \xi ) \, \mathrm{Cov} \Big ( \phi ^{(r;i)} (x_{pa(r)}, \cdot ) , \phi ^{(r; j)} (x_{pa(r)}, \cdot ) \left| x_{pa(r)}; \xi _r \Big )\right. ,\nonumber \\ \end{aligned}$$

(29)

where the conditional covariance on the RHS of (29) is evaluated with respect to $k^r( \cdot | x_{pa(r)}; \xi _r)$.

Example 4

(Neural networks (II)) Neural networks, which we introduced in Example 1, can be considered as a special case of the models of Example 3. This can be seen by rewriting the transition probability (12) as follows:

$$\begin{aligned} k^r(x_r | x_{pa(r)}; w_r , \vartheta _r)= & {} \frac{1}{1 + e^{- x_r h_r(x_{pa(r)})}} \\= & {} \frac{e^{\frac{1}{2} x_r h_r(x_{pa(r)})}}{ e^{\frac{1}{2} x_r h_r(x_{pa(r)})} + e^{- \frac{1}{2} x_r h_r(x_{pa(r)})} } \\= & {} \frac{\exp \left( {\frac{1}{2} \sum _{j \in pa(r)} w_{j r} x_j x_r - \frac{1}{2} \vartheta _r x_r} \right) }{ \sum _{x_r'} \exp \left( {\frac{1}{2} \sum _{j \in pa(r)} w_{j r} x_j x_r' - \frac{1}{2} \vartheta _r x_r'} \right) } . \end{aligned}$$

This is a special case of (28) which only involves pairwise interactions. In order to evaluate the terms (26) we need the derivatives

$$\begin{aligned} \frac{\partial }{\partial w_{i r}} \ln k^r(x_r | x_{pa(r)}; w_r , \vartheta _r)= & {} \frac{x_i x_r}{1 + e^{x_r h_r(x_{pa(r)})}} , \end{aligned}$$

(30)

$$\begin{aligned} \frac{\partial }{\partial \vartheta _{r}} \ln k^r(x_r | x_{pa(r)}; w_r , \vartheta _r)= & {} - \frac{x_r}{1 + e^{x_r h_r(x_{pa(r)})}} . \end{aligned}$$

(31)

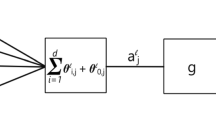
According to Theorem 1, we can evaluate the Fisher information matrix in a local way. More explicitly, we have

$$\begin{aligned} g_{(r; i , j)}(\xi ) \, = \, \sum _{x_{pa(r)}} p_\xi (x_{pa(r)}) \frac{f(x_i, x_j)}{(1+ e^{h_r(x_{pa(r)})})(1+ e^{- h_r(x_{pa(r)})}) } , \end{aligned}$$

where

Fig. 2

Two architectures with the same number of parameters but different complexity of the Fisher information matrix

Example 5

(Shallow versus deep networks) In this example, we demonstrate the difference in sparsity of the Fisher information matrix for architectures of varying depth. Fig. 2 shows two networks with three visible and nine hidden neurons each.

The number of synaptic connections is 27 in both cases, thereby assuming the neuronal model of Examples 1 and 4 (for simplicity, we do not consider the threshold values). If we associate one parameter with each edge, the synaptic strength, then we have 27 parameters in the system, and the Fisher information matrices have $27 \times 27 = 729$ entries. Theorem 1 implies the block diagonal structure of the Fisher information matrices shown in Fig. 3. As we can see, depth is associated with higher sparsity of these matrices. We have at least 486 zeros in the shallow case and at least 648 zeros in the deep case.

This example can be generalised to a network with n visible and $m= l \cdot n$ hidden neurons. As in Fig. 2, in the one case we arrange all m hidden neurons in one layer of width $l \cdot n$ and, in the other case, we arrange the hidden neurons in l layers of width n. In both cases, we have $n \cdot m = n (l \cdot n) = l \cdot n^2$ edges, corresponding to the number of parameters, and therefore the Fisher information matrix has $l^2 n^4$ entries. With the shallow architecture, we have at most $n {(l \cdot n)}^2 = l^2 n^3$ non-zero entries, whereas in the deep architecture there are at most $l \cdot n \cdot n^2 = l \cdot n^3$ non-zero entries. The difference is $l^2 \cdot n^3 - l \cdot n^3 = l \cdot n^3 (l - 1)$. For $n = l = 3$, we recover the difference of the above numbers, $648 - 486 = 162$.

Example 6

(Restricted Boltzmann machine) If we deal with models that are associated with undirected graphs we cannot expect the Fisher information matrix to have a block diagonal structure. Consider, for instance, a restricted Boltzmann machine, as shown in Fig. 4. With each edge $(i,j) \in V \times H$ we associate a weight $w_{ij}$ and denote the full weight matrix by W. The family of all weight matrices parametrises the model ${{\mathcal {M}}}$ consisting of distributions

$$\begin{aligned} p(x_V,x_H; W) \, = \, \frac{e^{\sum _{i \in V, j \in H} w_{ij} x_i x_j}}{\sum _{x_V',x_H'} e^{\sum _{i \in V, j \in H} w_{ij} x_i' x_j'}} . \end{aligned}$$

Note that this deviates somewhat from the setting of a restricted Boltzmann machine as we ignore the threshold values for simplicity.

The Fisher information matrix on ${{\mathcal {M}}}$ is given by

$$\begin{aligned} g_{ij,kl} (W) \, = \, \mathrm{Cov}_{p(\cdot ;W)} \left( X_i X_j , X_k X_l \right) \end{aligned}$$

which has no zeros imposed by the architecture.

Fig. 3

The structure of the Fisher information matrix of size $27 \times 27 = 729$: a the shallow case where we have 486 zeros; b the deep case where we have 648 zeros

Fig. 4

The architecture of a restricted Boltzmann machine

The simplification of the Fisher information matrix, stated in Theorem 1, has several important consequences. As an immediate consequence we obtain a corresponding simplification of the natural gradient of a smooth real-valued function ${{\mathcal {L}}}$ on ${{\mathcal {M}}}$, mainly referring to the function (10), in terms of the parametrisation (7). In order to express this simplification we consider the vectors (24) which span the tangent space of ${{\mathcal {M}}}$ in $p_\xi$. In particular, they allow us to represent the gradient of ${{\mathcal {L}}}$ as a linear combination

$$\begin{aligned} \mathrm{grad}^{{\mathcal {M}}}_{\xi } {{\mathcal {L}}} \; = \; \sum _{r = 1}^{n+m} \sum _{i = 1}^{d_r} x^{(r;i)}(\xi ) \, \partial _{(r;i)}(\xi ). \end{aligned}$$

(32)

Corollary 1

Consider the situation of Theorem 1 and a real-valued smooth function ${{\mathcal {L}}}$ on ${{\mathcal {M}}}$. With

$$\begin{aligned} \nabla _{\xi _r} {{\mathcal {L}}} := \left( \begin{array}{c} \frac{\partial {{\mathcal {L}}}}{\partial \xi _{(r;1)}}({\xi }) \\ \vdots \\ \frac{\partial {{\mathcal {L}}}}{\partial \xi _{(r;d_r)}}({\xi }) \end{array} \right) , \end{aligned}$$

we have the following coordinates of the natural gradient of ${{\mathcal {L}}}$ in the representation (32):

$$\begin{aligned} x^r(\xi ) \; := \; \left( \begin{array}{c} x^{(r;1)}(\xi ) \\ \vdots \\ x^{(r;d_r)}(\xi ) \end{array} \right) \; = \; \mathrm{G}_r^{+}({\xi }) \, \nabla _{\xi _r} {{\mathcal {L}}} , \qquad r = 1,\dots ,n+m. \end{aligned}$$

(33)

Here, $\mathrm{G}_r^+(\xi )$ denotes the Moore–Penrose inverse of the matrix $\mathrm{G}_r(\xi )$ defined by (25) and (26). (It reduces to the usual matrix inverse whenever $\mathrm{G}_r(\xi )$ has maximal rank.)

Note that Theorem 1 as well as its Corollary 1 can equally be applied to the recognition model ${{\mathcal {Q}}}_{H|V}$ defined by (21). In Section 2.2 we have studied natural objective functions that involve both, the generative as well as the recognition model, and highlighted their locality properties. Together with the locality of the corresponding Fisher information matrices, these properties allow us to evaluate a natural gradient version of the wake-sleep algorithm, referred to as natural wake–sleep algorithm in [31].

The prime objective function to be optimised is typically defined on the projected model ${{\mathcal {M}}}_V$. It naturally carries the Fisher–Rao metric of ${{\mathcal {P}}}_V$ so that we can define the natural gradient of the given objective function directly on ${{\mathcal {M}}}_V$. On the other hand, we have seen that the Fisher information matrix on the full model ${{\mathcal {M}}} \subseteq {{\mathcal {P}}}_{V,H}$ has a block structure associated with the underlying network. This implies useful locality properties of the natural gradient and thereby makes the method applicable within the context of deep learning. The main problem that we are now going to study is the following: Can we extend the locality of the natural gradient on the full model ${{\mathcal {M}}}$, as stated in Corollary 1, to the natural gradient on the projected model ${{\mathcal {M}}}_V$? In the following section we first study this problem in a more general setting of Riemannian manifolds.

3 Gradients on full versus coarse grained models

3.1 The general problem

We now develop a more general perspective, which we motivate by analogy to the context of the previous sections. Assume that we have two Riemannian manifolds $({{\mathcal {Z}}}, g^{{\mathcal {Z}}})$ and $({{\mathcal {X}}}, g^{{\mathcal {X}}})$ with dimensions $d_{\mathcal Z}$ and $d_{{\mathcal {X}}}$, respectively, and a differentiable map $\pi : {{\mathcal {Z}}} \rightarrow {{\mathcal {X}}}$, with its differential $d \pi _p: T_p{{\mathcal {Z}}} \rightarrow T_{\pi (p)}{{\mathcal {X}}}$ in p. The manifold ${{\mathcal {Z}}}$ corresponds to the manifold of (strictly positive) distributions on the full set of units, the visible and the hidden units. The map $\pi$ plays the role of the marginalisation map which marginalises out the hidden units and which we will interpret in Sect. 3.2 as one instance of a more general coarse graining procedure. Typically, we have a model ${{\mathcal {M}}} \subseteq {{\mathcal {Z}}}$ which corresponds to a model consisting of the joint distributions on the full system that can be represented by a network. It is obtained in terms of a parametrisation $\varphi : \varXi \rightarrow {{\mathcal {Z}}}$, $\xi \mapsto p_\xi$, where $\varXi$ is a differentiable manifold, usually an open subset of ${\mathbb R}^d$. In general, ${{\mathcal {M}}}$ will not be a sub-manifold of ${{\mathcal {Z}}}$ and can contain various kinds of singularities. We restrict attention to the non-singular points of ${{\mathcal {M}}}$. A point p in ${{\mathcal {M}}} \subseteq {{\mathcal {Z}}}$ is said to be a non-singular point of ${{\mathcal {M}}}$ if there exists a smooth chart $\psi : {{\mathcal {U}}} \rightarrow {{\mathcal {U}}}'$ with an open set ${\mathcal U}$ in ${{\mathcal {Z}}}$ and an open set ${{\mathcal {U}}}'$ in ${\mathbb R}^{d_{{\mathcal {Z}}}}$ such that $p \in {{\mathcal {U}}}$ and, for some k,

$$\begin{aligned}&{\psi ({{\mathcal {M}}} \cap {{\mathcal {U}}})} \nonumber \\&\quad = \{ (x_1,\dots ,x_k, x_{k +1}, \dots , x_{d_{{\mathcal {Z}}}}) \in {{\mathcal {U}}}' \, : \, x_{k +1} = \cdots = x_{d_{{\mathcal {Z}}}} = 0\}. \end{aligned}$$

(34)

Note that k is a local dimension of ${{\mathcal {M}}}$ in p, which is upper bounded by the dimension d of $\varXi$. We denote the set of non-singular points of ${{\mathcal {M}}}$ by $\mathrm{Smooth}({{\mathcal {M}}})$. If a point $p \in {{\mathcal {M}}}$ is not non-singular, it is called a singularity or a singular point of ${{\mathcal {M}}}$ (for more details see [32]). In a non-singular point p, the tangent space $T_p {{\mathcal {M}}}$ is well defined. Throughout this article, we will assume that the parametrisation $\varphi$ of ${{\mathcal {M}}}$ is a proper parametrisation in the sense that for all $p \in \mathrm{Smooth}({{\mathcal {M}}})$ and all $\xi \in \varXi$ with $\varphi (\xi ) = p$, the image of the differential ${d \varphi }_\xi$ coincides with the full tangent space $T_{p} {{\mathcal {M}}}$. This assumption is required, but often not explicitly stated, when dealing with the natural gradient method for optimisation on parametrised models. More precisely, when we interpret the Fisher information matrix (2) as a “coordinate representation” of the Fisher–Rao metric, we implicitly assume that the vectors $\partial _i (\xi ) = \frac{\partial }{\partial \xi _i} p_\xi$, $i = 1,\dots , d$, span the tangent space of the model in $p_\xi$. Note that linear independence, which ensures the non-degeneracy of the Fisher information matrix, is not required and would in fact be too restrictive given that overparametrised models play an important role within the field of deep learning.

We now consider a smooth function ${{\mathcal {L}}}: {{\mathcal {X}}} \rightarrow {\mathbb R}$ and study its gradient on ${{\mathcal {X}}}$ (with respect to $g^{{\mathcal {X}}}$) in relation to the corresponding gradient of ${{\mathcal {L}}} \circ \pi : {{\mathcal {Z}}} \rightarrow {\mathbb R}$ on $\mathrm{Smooth}({{\mathcal {M}}})$ (with respect to $g^{\mathcal Z}$). For a non-singular point of ${{\mathcal {M}}}$, we decompose the tangent space $T_p {{\mathcal {M}}}$ into a “vertical component” $T^{{\mathcal {V}}}_p {{\mathcal {M}}} := T_p {{\mathcal {M}}} \cap \ker {d {\pi }}_p$ and its orthogonal complement $T^{{\mathcal {H}}}_p {{\mathcal {M}}}$ in $T_p {{\mathcal {M}}}$, the corresponding “horizontal component”. (The symbols ${{\mathcal {V}}}$ and ${{\mathcal {H}}}$ should not be confused with the symbols V and H, denoting the visible and the hidden units, respectively.) We have the following proposition where we use the somewhat simpler notation “$\langle \cdot , \cdot \rangle$” for both metrics, $g^{{\mathcal {Z}}}$ and $g^{{\mathcal {X}}}$.

Proposition 1

Consider a model ${{\mathcal {M}}}$ in ${{\mathcal {Z}}}$ and a differentiable map $\pi : {{\mathcal {Z}}} \rightarrow {{\mathcal {X}}}$ and let p be a non-singular point of ${{\mathcal {M}}}$. Assume that the following compatibility condition is satisfied:

$$\begin{aligned} A , B \in T^{{\mathcal {H}}}_p {{\mathcal {M}}} \quad \Rightarrow \quad {\left\langle A, B \right\rangle }_p = {\left\langle {d {\pi }}_p (A), {d {\pi }}_p (B) \right\rangle }_{{\pi }(p)}. \end{aligned}$$

(35)

Then, for all smooth functions ${{\mathcal {L}}}: {{\mathcal {X}}} \rightarrow {\mathbb R}$, we have

$$\begin{aligned} {d \pi }_p \left( \mathrm{grad}^{{\mathcal {M}}}_p ({{\mathcal {L}}} \circ \pi ) \right) = \varPi \left( \mathrm{grad}^{{\mathcal {X}}}_{\pi (p)} {{\mathcal {L}}} \right) , \end{aligned}$$

(36)

where $\varPi$ denotes the projection of tangent vectors in $T_{\pi (p)} {{\mathcal {X}}}$ onto ${d {\pi }}_p (T_p {{\mathcal {M}}})$.

Proof

First observe that $\mathrm{grad}^{{\mathcal {M}}}_p ({{\mathcal {L}}} \circ \pi ) \in T^{{\mathcal {H}}}_p {{\mathcal {M}}}$. Indeed, for all $B \in T^{{\mathcal {V}}}_p {{\mathcal {M}}}$ we have

$$\begin{aligned} {\langle \mathrm{grad}^{{\mathcal {M}}}_p ({{\mathcal {L}}} \circ \pi ), B \rangle }_p \; = \; {d ({{\mathcal {L}}} \circ \pi )}_p ( B ) \; = \; d {{\mathcal {L}}}_{\pi (p)} (\underbrace{{d \pi }_p ( B )}_{= 0}) \; = \; 0. \end{aligned}$$

(37)

Let $A' \in {d \pi }_p(T_p {{\mathcal {M}}}) \subseteq T_{\pi (p)} {{\mathcal {X}}}$. There exists $A \in T_p {{\mathcal {M}}}$ such that ${d \pi }_p ( A ) = A'$. We can decompose A orthogonally into a component $A_1$ contained in $T^{{\mathcal {V}}}_p {{\mathcal {M}}}$ and a component $A_2$ contained in $T^{{\mathcal {H}}}_p {\mathcal M}$. With this decomposition we have $A' = {d \pi }_p (A) = {d \pi }_p (A_1 + A_2) = {d \pi }_p (A_2)$. This implies

$$\begin{aligned} {\langle {d \pi }_p (\mathrm{grad}^{{\mathcal {M}}}_p ({{\mathcal {L}}} \circ \pi )) , A' \rangle }_{\pi (p)}= & {} {\langle {d \pi }_p (\mathrm{grad}^{{\mathcal {M}}}_p ({{\mathcal {L}}} \circ \pi )) , {d \pi }_p (A_2) \rangle }_{\pi (p)} \\= & {} {\langle \mathrm{grad}^{{\mathcal {M}}}_p ({{\mathcal {L}}} \circ \pi ) , A_2 \rangle }_p \qquad (\text{ by } ((37)) \text{ and } ((38))) \\= & {} {d ({{\mathcal {L}}} \circ \pi )}_p (A_2) \\= & {} {d {{\mathcal {L}}}}_{\pi (p)} ({d \pi }_p (A_2)) \\= & {} {\langle \mathrm{grad}^{{\mathcal {X}}}_{\pi (p)} {{\mathcal {L}}} , {d \pi }_p (A_2) \rangle }_{\pi (p)} \\= & {} {\langle \mathrm{grad}^{{\mathcal {X}}}_{\pi (p)} {{\mathcal {L}}} , A' \rangle }_{\pi (p)} . \end{aligned}$$

This proves Eq. (36). $\square$

As stated above, the parametrised model ${{\mathcal {M}}}$ plays the role of the distributions on the full network, consisting of the visible and hidden units. We want to relate this model to the projected model ${{\mathcal {S}}} := \pi ({{\mathcal {M}}})$. The composition of the parametrisation $\varphi$ and the projection $\pi$ serves as a parametrisation $\xi \mapsto \pi (p_{\xi } )$ of ${{\mathcal {S}}}$ as shown in the following diagram.

The map $\pi \circ \varphi$ is a proper parametrisation of ${{\mathcal {S}}}$ if for all $q \in \mathrm{Smooth}({{\mathcal {S}}})$ and all $\xi$ with $\pi (p_\xi ) = q$, the image of the differential ${d (\pi \circ \varphi )}_\xi$ coincides with the full tangent space $T_{q} {{\mathcal {S}}}$. Obviously, this does not follow from the assumption that $\varphi$ is a proper parametrisation of ${\mathcal M}$ and requires further assumptions. One necessary, but not sufficient, condition is the following: Assume that $\pi \circ \varphi$ is a proper parametrisation of ${{\mathcal {S}}}$ and consider a point $p \in \mathrm{Smooth}({{\mathcal {M}}})$ with $\pi (p) \in \mathrm{Smooth}({{\mathcal {S}}})$. With $\xi \in \varXi$, $\varphi (\xi ) = p$, we have

$$\begin{aligned} T_{\pi (p)} {{\mathcal {S}}}= & {} {d (\pi \circ \varphi )}_\xi \left( T_\xi \varXi \right) \qquad \;\,\, (\pi \circ \varphi \text{ proper } \text{ parametristation}) \nonumber \\= & {} {d \pi }_{\varphi (\xi )} \left( {d \varphi }_\xi \left( T_\xi \varXi \right) \right) \;\, \, \, \, \, (\text{ by } \text{ the } \text{ chain } \text{ rule}) \nonumber \\= & {} {d \pi }_{\varphi (\xi )} \left( T_{\varphi (\xi )} {{\mathcal {M}}} \right) \qquad \,\,\, (\varphi \text{ proper } \text{ parametristation}) \nonumber \\= & {} {d \pi }_{p} \left( T_{p} {{\mathcal {M}}} \right) . \end{aligned}$$

(38)

The condition (38) is sufficient for $\pi \circ \varphi$ being a proper parametrisation of ${{\mathcal {S}}}$ if $\pi ^{-1}(\mathrm{Smooth}({{\mathcal {S}}})) \subseteq \mathrm{Smooth}({{\mathcal {M}}})$, which is clearly satisfied if ${\mathcal M}$ is a smooth sub-manifold of ${{\mathcal {Z}}}$ and therefore has no singularities. In any case, the condition (38) is required when dealing with properly parametrised models. We call a point $p \in {{\mathcal {M}}}$ admissible if $p \in \mathrm{Smooth}({{\mathcal {M}}})$, $\pi (p) \in \mathrm{Smooth}({{\mathcal {S}}})$, and (38) is satisfied in p.

We have the following implication of Proposition 1.

Theorem 2

Consider a model ${{\mathcal {M}}}$ in ${{\mathcal {Z}}}$ and a differentiable map $\pi : {{\mathcal {Z}}} \rightarrow {{\mathcal {X}}}$ with image ${{\mathcal {S}}} = \pi ({{\mathcal {M}}})$. Furthermore, assume that the compatibility condition (35) is satisfied in an admissible point $p \in {{\mathcal {M}}}$. Then for all smooth functions ${{\mathcal {L}}} : {{\mathcal {X}}} \rightarrow {\mathbb R}$, we have

$$\begin{aligned} {d \pi }_{p} \left( \mathrm{grad}^{{\mathcal {M}}}_{p} ({{\mathcal {L}}} \circ \pi ) \right) = \mathrm{grad}^{{\mathcal {S}}}_{\pi (p)} {\mathcal L}. \end{aligned}$$

(39)

Proof

This follows directly from (36). For an admissible point p we have ${d\pi }_p \left( T_{p} {{\mathcal {M}}}\right) = T_{\pi (p)} {{\mathcal {S}}}$. Therefore, the RHS of (36) reduces to the orthogonal projection of $\mathrm{grad}^{\mathcal X}_{\pi (p)} {{\mathcal {L}}}$ onto $T_{\pi (p)} {{\mathcal {S}}}$ which equals the $\mathrm{grad}^{{\mathcal {S}}}_{\pi (p)} {{\mathcal {L}}}$. $\square$

Note that, if we do not assume (38), we have to replace the RHS of (39) by $\varPi \left( \mathrm{grad}^{\mathcal S}_{\pi (p)} {{\mathcal {L}}} \right)$, where $\varPi$ denotes the projection of tangent vectors in $T_{\pi (p)} {{\mathcal {S}}}$ onto ${d {\pi }}_p (T_p {{\mathcal {M}}})$. Therefore, it can well be the case that the gradient on ${{\mathcal {M}}}$ vanishes in a point p while the corresponding gradient on ${{\mathcal {S}}}$, that is $\mathrm{grad}^{{\mathcal {S}}}_{\pi (p)} {{\mathcal {L}}}$, does not. Such a point p is referred to as spurious critical point (see [30]). In addition to the problem of having singularities of ${{\mathcal {M}}}$ and ${{\mathcal {S}}} = \pi ({{\mathcal {M}}})$, this represents another problem with gradient methods for the optimisation of smooth functions on parametrised models. However, the problem of spurious critical points does not appear if we are dealing with a proper parametrisation $\varphi$ of ${{\mathcal {M}}}$ for which $\pi \circ \varphi$ is also a proper parametrisation of ${{\mathcal {S}}}$.

We conclude this section by addressing the following problem: If we assume that the compatibility condition (35) is satisfied for a model ${{\mathcal {M}}}$ in ${{\mathcal {Z}}}$, what can we say about the corresponding compatibility for a sub-model ${\mathcal M}'$ of ${{\mathcal {M}}}$? In general we cannot expect that (35) also holds for ${{\mathcal {M}}}'$. The following theorem characterises those sub-models ${{\mathcal {M}}}'$ of ${{\mathcal {M}}}$ for which this is satisfied, so that Theorem 2 will also hold for them.

Theorem 3

Assume that (35) holds for a model ${{\mathcal {M}}}$ in ${{\mathcal {Z}}}$ and consider a sub-model ${{\mathcal {M}}}' \subseteq {{\mathcal {M}}}$. Then (35) also holds for ${{\mathcal {M}}}'$ if and only if for each point $p \in \mathrm{Smooth} ({{\mathcal {M}}}')$ the tangent space $T_p {{\mathcal {M}}}'$ satisfies

$$\begin{aligned} T_p {{\mathcal {M}}}' \, = \, \left( T_p {{\mathcal {M}}}' \cap T^{{\mathcal {H}}}_p {{\mathcal {M}}} \right) + \left( T_p {\mathcal M}' \cap T^{{\mathcal {V}}}_p {{\mathcal {M}}} \right) . \end{aligned}$$

(40)

This theorem is a direct implication of Lemma 1 below which reduces the problem to the simple setting of linear algebra. Let $({{\mathcal {F}}} , {\langle \cdot , \cdot \rangle }_{\mathcal F})$, $({{\mathcal {G}}}, {\langle \cdot , \cdot \rangle }_{\mathcal G})$ be two finite-dimensional real Hilbert spaces, and let $T: {{\mathcal {F}}} \rightarrow {{\mathcal {G}}}$ be a linear map. We can decompose ${{\mathcal {F}}}$ into a “vertical component” ${\mathcal F}^{{\mathcal {V}}} := \ker T$ and its orthogonal complement ${{\mathcal {F}}}^{{\mathcal {H}}}$ in ${{\mathcal {F}}}$, the corresponding “horizontal component”. Now let ${{\mathcal {E}}}$ be a linear subspace of ${{\mathcal {F}}}$, equipped with the induced inner product ${\langle \cdot , \cdot \rangle }_{{\mathcal {E}}}$, and consider the restriction $T_{{\mathcal {E}}}: {{\mathcal {E}}} \rightarrow {{\mathcal {G}}}$ of T to ${{\mathcal {E}}}$. Denoting by $\bot _{{\mathcal {E}}}$ and $\bot _{{\mathcal {F}}}$ the orthogonal complements in ${{\mathcal {E}}}$ and ${{\mathcal {F}}}$, respectively, we can decompose ${{\mathcal {E}}}$ into

$$\begin{aligned} {{\mathcal {E}}}^{{\mathcal {V}}}:= & {} \ker T_{{\mathcal {E}}} \\= & {} {{\mathcal {E}}} \cap \ker T \\= & {} {{\mathcal {E}}} \cap {{\mathcal {F}}}^{{\mathcal {V}}} , \end{aligned}$$

and

$$\begin{aligned} {{\mathcal {E}}}^{{\mathcal {H}}}:= & {} \left( {{\mathcal {E}}}^{{\mathcal {V}}} \right) ^{\perp _{{\mathcal {E}}}} \\= & {} {{\mathcal {E}}} \cap \left( {{\mathcal {E}}}^{{\mathcal {V}}} \right) ^{\perp _{{\mathcal {F}}}} \\= & {} {{\mathcal {E}}} \cap \left( {{\mathcal {E}}} \cap {{\mathcal {F}}}^{{\mathcal {V}}} \right) ^{\perp _{{\mathcal {F}}}} \\= & {} {{\mathcal {E}}} \cap \left( {{\mathcal {E}}}^{\perp _{{\mathcal {F}}}} + {{\mathcal {F}}}^{{\mathcal {H}}} \right) \\\supseteq & {} {{\mathcal {E}}} \cap {{\mathcal {F}}}^{{\mathcal {H}}} . \end{aligned}$$

Note that, while we always have ${{\mathcal {E}}}^{{\mathcal {V}}} \subseteq {{\mathcal {F}}}^{{\mathcal {V}}}$, in general ${\mathcal E}^{{\mathcal {H}}} \not \subseteq {{\mathcal {F}}}^{{\mathcal {H}}}$.

Lemma 1

Assume:

$$\begin{aligned} A, B \in {{\mathcal {F}}}^{{\mathcal {H}}} \quad \Rightarrow \quad {\langle A , B \rangle }_{{\mathcal {F}}} = {\langle T(A) , T(B) \rangle }_{{\mathcal {G}}}. \end{aligned}$$

(41)

Then the following two statements about a subspace ${{\mathcal {E}}}$ of ${{\mathcal {F}}}$ are equivalent:

$$\begin{aligned} (i)&A, B \in {{\mathcal {E}}}^{{\mathcal {H}}} \quad \Rightarrow \quad {\langle A , B \rangle }_{{\mathcal {E}}} = {\langle T_{\mathcal E} (A) , T_{{\mathcal {E}}} (B) \rangle }_{{\mathcal {G}}}. \end{aligned}$$

(42)

$$\begin{aligned} (ii)&{{\mathcal {E}}} \, = \, ({{\mathcal {E}}} \cap {{\mathcal {F}}}^{{\mathcal {H}}}) + ({\mathcal E} \cap {{\mathcal {F}}}^{{\mathcal {V}}}). \end{aligned}$$

(43)

Proof

Let us first assume that (43) holds true. This implies

$$\begin{aligned} {{\mathcal {E}}}^{{\mathcal {H}}} \, = \, \left( {\mathcal E}^{{\mathcal {V}}} \right) ^{\perp _{{{\mathcal {E}}}}} \, = \, \left( {{\mathcal {E}}} \cap {{\mathcal {F}}}^{{\mathcal {V}}} \right) ^{\perp _{{{\mathcal {E}}}}} \, = \, {{\mathcal {E}}} \cap {{\mathcal {F}}}^{{\mathcal {H}}} \, \subseteq \, {\mathcal F}^{{\mathcal {H}}} . \end{aligned}$$

(44)

For all $A, B \in {{\mathcal {E}}}^{{\mathcal {H}}} \subseteq {{\mathcal {F}}}^{{\mathcal {H}}}$, (41) then takes the form

$$\begin{aligned} {\langle A , B \rangle }_{{{\mathcal {E}}}} = {\langle A , B \rangle }_{{{\mathcal {F}}}} = {\langle T(A) , T(B) \rangle }_{{{\mathcal {G}}}} = {\langle T_{{{\mathcal {E}}}}(A) , T_{{{\mathcal {E}}}}(B) \rangle }_{{{\mathcal {G}}}}. \end{aligned}$$

(45)

In order to prove the opposite implication, we assume that (43) does not hold for ${{{\mathcal {E}}}}$. This means that

$$\begin{aligned} {{\mathcal {Q}}} := ({{{\mathcal {E}}}} \cap {{\mathcal {F}}}^{\mathcal H} ) + ( {{{\mathcal {E}}}} \cap {{\mathcal {F}}}^{{\mathcal {V}}} ) \end{aligned}$$

(46)

is a proper subspace of ${{{\mathcal {E}}}}$. We denote the orthogonal complement of ${{\mathcal {Q}}}$ in ${{{\mathcal {E}}}}$ by ${{\mathcal {R}}}$ and choose a non-trivial vector A in ${\mathcal R}$. Such a vector can be uniquely decomposed as a sum of two non-trivial vectors $A_1 \in {{\mathcal {F}}}^{{\mathcal {H}}}$ and $A_2 \in {{\mathcal {F}}}^{{\mathcal {V}}}$. This implies

$$\begin{aligned} {\Vert A \Vert }_{{{\mathcal {E}}}}= & {} {\Vert A \Vert }_{{{\mathcal {F}}}} \\= & {} {\Vert A_1 + A_2 \Vert }_{{{\mathcal {F}}}} \\> & {} {\Vert A_1 \Vert }_{{{\mathcal {F}}}} \\= & {} {\Vert T(A_1) \Vert }_{{{\mathcal {G}}}} \\= & {} {\Vert T(A_1) + T(A_2) \Vert }_{{{\mathcal {G}}}} \\= & {} {\Vert T(A) \Vert }_{{{\mathcal {G}}}} \\= & {} {\Vert T_{{{\mathcal {E}}}}(A) \Vert }_{{{\mathcal {G}}}} . \end{aligned}$$

This means that (42) does not hold for the subspace ${{{\mathcal {E}}}}$. $\square$

3.2 A new interpretation of Chentsov’s theorem

We now come back to the context of probability distributions but take a slightly more general perspective than in Section 1.2. We interpret $X_V$ as a coarse graining of the set $\mathsf {X}_V \times \mathsf {X}_H$ which lumps together all pairs (v, h), $(v', h')$ with $v = v'$. Replacing the Cartesian product $\mathsf {X}_V \times \mathsf {X}_H$ by a general set $\mathsf {Z}$, a coarse graining of $\mathsf {Z}$ is an onto mapping $X: \mathsf {Z} \rightarrow \mathsf {X}$, which partitions $\mathsf {Z}$ into the atoms $\mathsf {Z}_x := X^{-1}(x)$. The corresponding push-forward map is given by

$$\begin{aligned} X_*: \; {{\mathcal {P}}}(\mathsf {Z}) \; \rightarrow \; {\mathcal P}(\mathsf {X}), \qquad p = \sum _{z} p(z) \, \delta ^z \; \mapsto \; X_*(p) = \sum _x \underbrace{\left( \sum _{z \in \mathsf {Z}_x} p(z) \right) }_{=: p(x)} \delta ^x , \end{aligned}$$

with the differential

$$\begin{aligned} d X_*: \; {{\mathcal {T}}}(\mathsf {Z}) \; \rightarrow \; {\mathcal T}(\mathsf {X}), \qquad A = \sum _{z} A(z) \, \delta ^z \; \mapsto \; \sum _x \left( \sum _{z \in \mathsf {Z}_x} A(z) \right) \delta ^x . \end{aligned}$$

Obviously, we have

$$\begin{aligned} {{\mathcal {V}}}_p \, := \, \ker d X_*\, = \, \left\{ \sum _{z} A(z) \, \delta ^{z} \; : \; \displaystyle \sum _{z \in \mathsf {Z}_x} A(z) \, = \, 0 \text{ for } \text{ all } x \right\} , \end{aligned}$$

(47)

and the orthogonal complement

$$\begin{aligned} {{\mathcal {H}}}_p \, := \, {{{\mathcal {V}}}_p}^\perp \, = \, \left\{ {\widetilde{A}} = \sum _{x} \frac{A(x)}{p(x)} \sum _{z \in \mathsf {Z}_x} p(z) \, \delta ^z \; : \; \sum _x A(x) = 0 \right\} \end{aligned}$$

(48)

with respect to the Fisher–Rao metric in p (note that ${\mathcal V}_p$ is independent of p). Given a vector $A = \sum _{z} A(z) \, \delta ^z \in {{\mathcal {T}}}(\mathsf {Z})$, we can decompose it uniquely as

$$\begin{aligned} A = A^{{\mathcal {H}}} + A^{{\mathcal {V}}}, \end{aligned}$$

with $A^{{\mathcal {H}}} \in {{\mathcal {H}}}_p$ and $A^{{\mathcal {V}}} \in {{\mathcal {V}}}_p$. More precisely,

$$\begin{aligned} A^{{\mathcal {H}}}= & {} \sum _x \sum _{z \in \mathsf {Z}_x} \left( \frac{p(z)}{p(x)}\sum _{z' \in \mathsf {Z}_x} A(z') \right) \delta ^z , \end{aligned}$$

(49)

$$\begin{aligned} A^{{\mathcal {V}}}= & {} \sum _x \sum _{z \in \mathsf {Z}_x} \left( A(z) - \frac{p(z)}{p(x)}\sum _{z' \in \mathsf {Z}_x} A(z') \right) \delta ^z . \end{aligned}$$

(50)

For a vector

$$\begin{aligned} {\widetilde{A}} \, = \, \sum _{x} \frac{A(x)}{p(x)} \sum _{z \in \mathsf {Z}_x} p(z) \, \delta ^z \; \in \; {{\mathcal {H}}}_p, \end{aligned}$$

we have

$$\begin{aligned} d X_*({\widetilde{A}}) \, = \, A. \end{aligned}$$

(51)

We now examine the inner product of two such vectors ${\widetilde{A}}, {\widetilde{B}} \in {{\mathcal {H}}}_p$:

$$\begin{aligned} {\langle {\widetilde{A}}, {\widetilde{B}} \rangle }_{p}= & {} \sum _{z} \frac{1}{p(z)} \, {\widetilde{A}}(z) {\widetilde{B}}(z) \nonumber \\= & {} \sum _x \sum _{z \in Z_x} \frac{1}{p(z)} \left( \frac{A(x)}{p(x)} p(z) \right) \left( \frac{B(x)}{p(x)} p(z) \right) \nonumber \\= & {} \sum _x \frac{A(x)}{p(x)} \frac{B(x)}{p(x)} \sum _{z \in Z_x} p(z) \nonumber \\= & {} \sum _x \frac{1}{p(x)} \, A(x) B(x) \nonumber \\= & {} {\langle A , B \rangle }_{X_*(p)} \nonumber \\= & {} {\langle d X_*({\widetilde{A}}) , d X_*({\widetilde{B}}) \rangle }_{X_*(p)}. \qquad \quad (\text{ by } ((51))) \end{aligned}$$

(52)

Thus, the compatibility condition (35) is satsified. Theorem 2 implies that for all smooth functions ${{\mathcal {L}}}: {{\mathcal {P}}}(\mathsf {X}) \rightarrow {\mathbb R}$ and all $p \in {{\mathcal {P}}}(\mathsf {Z})$, the following equality of gradients holds (note that all points $p \in {\mathcal P}(\mathsf {Z})$ are admissible):

$$\begin{aligned} d X_*\left( \mathrm{grad}^{{{\mathcal {P}}}(\mathsf {Z})}_{p} ({{\mathcal {L}}} \circ X_*) \right) \, = \, \mathrm{grad}^{{\mathcal P}(\mathsf {X})}_{X_*(p)} {{\mathcal {L}}} , \end{aligned}$$

(53)

where ${{\mathcal {P}}}(\mathsf {Z})$ and ${{\mathcal {P}}}(\mathsf {X})$ are equipped with the respective Fisher–Rao metrics. Even though this is a simple observation, it highlights an important point here. A coarse graining is generally associated with a loss of information, which is expressed by the monotonicity of the Fisher–Rao metric. This information loss is maximal when we project from the full space ${\mathcal P}(\mathsf {Z})$ onto ${{\mathcal {P}}}(\mathsf {X})$. Nevertheless, the gradient of any function ${{\mathcal {L}}}$ that is defined on ${{\mathcal {P}}}(\mathsf {X})$ is not sensitive to this information loss. In order to study models ${{\mathcal {M}}}$ in ${\mathcal P}(\mathsf {Z})$ with the same invariance of gradients, we have to impose the condition (40), which takes the form

$$\begin{aligned} T_p {{\mathcal {M}}} \, = \, \big ( T_p {{\mathcal {M}}} \cap {\mathcal H}_p \big ) + \big ( T_p {{\mathcal {M}}} \cap {{{\mathcal {V}}}_p} \big ), \qquad p \in \mathrm{Smooth}({{\mathcal {M}}}). \end{aligned}$$

(54)

Definition 1

If a model ${{\mathcal {M}}} \subseteq {{\mathcal {P}}}(\mathsf {Z})$ satisfies the condition (54) in p, we say that it is cylindrical in p. If it is cylindrical in all non-singular points, we say that it is (pointwise) cylindrical.

Of particular interest are cylindrical models with a trivial vertical component. These are the models, for which the coarse graining X is a minimal sufficient statistic. They have been used by Chentsov [12] in order to characterise the Fisher–Rao metric (see Theorem 4). To be more precise, we need to revisit Markov kernels from a geometric perspective. We consider the space of linear maps from ${\mathbb R}^{\mathsf {Z}}$ to ${\mathbb R}^{\mathsf {X}}$, which is canonically isomorphic to $\left( {\mathbb R}^{\mathsf {Z}} \right) ^*\otimes {\mathbb R}^{\mathsf {X}}$, and define the polytope of Markov kernels as

$$\begin{aligned} {{\mathcal {K}}}({\mathsf {Z}} | {\mathsf {X}}):= & {} \Big \{ K = \sum _{x,z} k(z | x) \, \delta ^z \otimes e_x \in \left( {\mathbb R}^{\mathsf {Z}} \right) ^*\otimes {\mathbb R}^{\mathsf {X}} \; : \; \\&\qquad \qquad k(z | x) \ge 0 \text{ for } \text{ all } x,z, and \displaystyle \sum _z k(z | x) = 1\hbox { for all }x \Big \}. \end{aligned}$$

The set ${{\mathcal {P}}}(\mathsf {Z})$ of probability vectors is a subset where each vector p is identified with $k(z | x) := p(z)$. We now consider a Markov kernel K that is coupled with the coarse graining $X: \mathsf {Z} \rightarrow \mathsf {X}$ in terms of $k(z | x) > 0$ if and only if $z \in \mathsf {Z}_x$. Such a Markov kernel is called X-congruent. It defines an embedding $K_*: {{\mathcal {P}}}(\mathsf {X}) \; \rightarrow \; {\mathcal P}(\mathsf {Z})$,

$$\begin{aligned} p = \sum _x p(x) \, \delta ^x \; \mapsto \; \sum _{z} \left( \sum _x p(x) k(z | x) \right) \delta ^z = \sum _{x} p(x) \left( \sum _{z \in \mathsf {Z}_x} k(z | x) \, \delta ^z\right) , \end{aligned}$$

referred to as an X-congruent Markov morphism. We obviously have $X_*\circ K_*= \mathrm{id}_{\mathcal {P}(\mathsf {X})}$. The image of $K_*$, which we denote by ${{\mathcal {M}}}(K)$, is the relative interior of the simplex with the extreme points

$$\begin{aligned} \sum _{z \in \mathsf {Z}_x} k(z | x) \, \delta ^z, \qquad x \in \mathsf {X}. \end{aligned}$$

It is easy to see that ${{\mathcal {M}}}(K)$ is cylindrical. (For $p \in {{\mathcal {M}}}(K)$, we have $T_p {{\mathcal {M}}}(K) = {\mathcal H}_p$. This implies $T_p {{\mathcal {M}}}(K) \cap {{\mathcal {H}}}_p = {{\mathcal {H}}}_p$ and $T_p {{\mathcal {M}}}(K) \cap {{\mathcal V}_p} = \{0\}$, which verifies (54).) Therefore, we have for all smooth functions ${{\mathcal {L}}}: {{\mathcal {P}}}(\mathsf {X}) \rightarrow {\mathbb R}$ and all $p \in {\mathcal M}(K)$,

$$\begin{aligned} d X_*\left( \mathrm{grad}^{{{\mathcal {M}}}(K)}_{p} ({{\mathcal {L}}} \circ X_*) \right) \, = \, \mathrm{grad}^{{\mathcal P}(\mathsf {X})}_{X_*(p)} {{\mathcal {L}}} . \end{aligned}$$

(55)

Comparing the Eq. (55) with (53), we observe that the gradient on the LHS is now evaluated on ${{\mathcal {M}}}(K)$, with respect to the induced Fisher–Rao metric. The gradient on the RHS remains as it is.

The differential of $K_*$ is given by

$$\begin{aligned} {d K_*}: {{\mathcal {T}}}(\mathsf {X}) \; \rightarrow \; {\mathcal T}(\mathsf {Z}), \qquad A = \sum _x A(x) \, \delta ^x \; \mapsto \; \sum _{x} A(x) \left( \sum _{z \in \mathsf {Z}_x} k(z | x) \, \delta ^z\right) , \end{aligned}$$

with the image

$$\begin{aligned} \mathrm{im} \, d K_*\, = \, \left\{ \sum _{x} A(x) \left( \sum _{z \in \mathsf {Z}_x} k(z | x) \, \delta ^z\right) \; : \; \sum _x A(x) = 0 \right\} . \end{aligned}$$

The following simple calculation shows that $K_*$ is an isometric embedding (see Fig. 5):

$$\begin{aligned}&{{\langle d K_*(A), d K_*(B) \rangle }_{K_*(p)}} \nonumber \\&\quad = \sum _x \sum _{z \in \mathsf {Z}_x} \frac{1}{\sum _{x'} p(x') k(z | x')} \left( \sum _{x'} A(x') k(z | x') \right) \left( \sum _{x'} B(x') k(z | x') \right) \nonumber \\&\quad = \sum _x \sum _{z \in \mathsf {Z}_x} \frac{1}{p(x) k(z | x)} A(x) k(z | x) B(x) k(z | x) \nonumber \\&\quad = \sum _x \frac{1}{p(x)} A(x) B(x) \sum _{z \in {{\mathsf {Z}}}_x} k(z | x) \nonumber \\&\quad = \sum _x \frac{1}{p(x)} A(x) B(x) \nonumber \\&\quad = {\langle A , B \rangle }_{p}. \end{aligned}$$

(56)

Fig. 5

X-congruent Markov morphism with the following coarse graining X: $z_1 \mapsto x_1$, $z_2 \mapsto x_2$, $z_3 \mapsto x_3$, $z_4 \mapsto x_3$. The inner product between A and B equals the inner product of $dK_*(A)$ and $d K_*(B)$ (see (56))

The invariance (55) of gradients follows also directly from the invariance (56) of inner products. In fact, $K_*$ being an isometric embedding is equivalent to (55) (for details, see the proof of Theorem 5). A fundamental result of Chentsov [12] characterises the Fisher–Rao metric as the only invariant metric (see also [8]).

Theorem 4

(Chentsov’s theorem) Assume that for any non-empty finite set $\mathsf {S}$, ${{\mathcal {P}}}(\mathsf {S})$ is equipped with a Riemannian metric $g^{(\mathsf {S})}$, such that the following is satisfied: Whenever we have a coarse graining $X: \mathsf {Z} \rightarrow \mathsf {X}$ and an X-congruent Markov morphism $K_*: {\mathcal P}(\mathsf {X}) \rightarrow {{\mathcal {P}}}(\mathsf {Z})$, the invariance (56) holds, interpreted as a condition for $g^{(\mathsf {X})}$ and $g^{(\mathsf {Z})}$. Then there exists a positive real number $\alpha$ such that for all $\mathsf {S}$, the metric $g^{(\mathsf {S})}$ coincides with the Fisher–Rao metric multiplied by $\alpha$.

In order to compute the gradient of a function on an extended space that is equivalent to the actual gradient, we want to use Eq. (39) of Theorem 2. Instances of this equivalence are given by the Eqs. (53) and (55) where we considered two extreme cases, the full model ${{\mathcal {P}}}(\mathsf {Z})$ and the model ${{\mathcal {M}}}(K)$, respectively, which both project onto ${{\mathcal {P}}}(\mathsf {X})$. We know that Theorem 2 also holds for all cylindrical models ${\mathcal M}$, including, but not restricted to, intermediate cases where ${{\mathcal {M}}}(K) \subseteq {{\mathcal {M}}} \subseteq {\mathcal P}(\mathsf {Z})$. How flexible are we here with the choice of the metric? In fact, a reformulation of Chentsov’s uniqueness result, Theorem 4, identifies the Fisher–Rao metric as the only metric for which Eq. (39) holds.

Theorem 5

Assume that for any non-empty finite set $\mathsf {S}$, ${\mathcal P}(\mathsf {S})$ is equipped with a Riemannian metric $g^{(\mathsf {S})}$. Then the following properties are equivalent:

• 1. Let $X: \mathsf {Z} \rightarrow \mathsf {X}$ be a coarse graining, ${{\mathcal {M}}}$ a cylindrical model in ${{\mathcal {P}}}(\mathsf {Z})$, and ${{\mathcal {M}}}_X := X_*({{\mathcal {M}}})$ its image. Then for all smooth functions ${{\mathcal {L}}}: {{\mathcal {P}}}(\mathsf {X}) \rightarrow {\mathbb R}$ and all admissible points $p \in {{\mathcal {M}}}$, we have

  $$\begin{aligned} d X_*\left( \mathrm{grad}^{{\mathcal {M}}}_{p} ({{\mathcal {L}}} \circ X_*) \right) \, = \, \mathrm{grad}^{{{\mathcal {M}}}_X}_{X_*(p)} {{\mathcal {L}}}, \end{aligned}$$

  (57)

  where the gradient on the LHS is evaluated with respect to the restriction of $g^{(\mathsf {Z})}$ and the RHS is evaluated with respect to the restriction of $g^{(\mathsf {X})}$.

• 2. There exists a positive real number $\alpha$ such that for all $\mathsf {S}$, the metric $g^{(\mathsf {S})}$ coincides with the Fisher–Rao metric multiplied by $\alpha$.

Proof

“(1) $\Rightarrow$ (2):” Let $X: \mathsf {Z} \rightarrow \mathsf {X}$ be a coarse graining, and let $K_*: {{\mathcal {P}}}(\mathsf {X}) \rightarrow {{\mathcal {P}}}(\mathsf {Z})$ be an X-congruent Markov morphism. We consider the model ${{\mathcal {M}}}(K)$, as a special instance of a cylindrical model ${{\mathcal {M}}}$ in ${{\mathcal {P}}}(\mathsf {Z})$. In that case, (57) is equivalent to

$$\begin{aligned} \mathrm{grad}_{K_*(p)}^{{{\mathcal {M}}}(K)} ({{\mathcal {L}}} \circ X_*) \; = \; d K_*\left( \mathrm{grad}_p^{{\mathcal P}(\mathsf {X})} {{\mathcal {L}}}\right) . \end{aligned}$$

(58)

We choose $p \in {{\mathcal {P}}}(\mathsf {X})$ and $A,B \in {\mathcal T}(\mathsf {X})$. We can represent A as a gradient of a function ${{\mathcal {L}}}$. More precisely, with

$$\begin{aligned} {{\mathcal {L}}}: \; {{\mathcal {P}}}(\mathsf {X}) \; \rightarrow \; {\mathbb R}, \qquad p \; \mapsto \; {{\mathcal {L}}}(p) \, := \, \sum _x A(x) \cdot \ln p(x) , \end{aligned}$$

(59)

we have

$$\begin{aligned} \mathrm{grad}^{{{\mathcal {P}}}(\mathsf {X})}_p {{\mathcal {L}}} \, = \, A . \end{aligned}$$

(60)

This implies

$$\begin{aligned} {\langle A , B \rangle }_p= & {} \left\langle \mathrm{grad}^{{\mathcal P}(\mathsf {X})}_p {{\mathcal {L}}} , B \right\rangle _p \qquad \qquad \qquad \qquad \qquad \quad \;(\text{ by } ((37))) \\= & {} {d {{\mathcal {L}}}}_p (B ) \\= & {} {d {{\mathcal {L}}}}_p \left( (d X_*\circ d K_*) (B) \right) \\= & {} d ( {{\mathcal {L}}} \circ X_*)_{K_*(p)} ( dK_*(B) ) \qquad \qquad \qquad \,\,\; (\text{ by } \text{ the } \text{ chain } \text{ rule}) \\= & {} \left\langle \mathrm{grad}^{{{\mathcal {M}}}(K)}_{K_*(p)} ({{\mathcal {L}}} \circ X_*) , d K_*(B) \right\rangle _{K_*(p)} \\= & {} \left\langle d K_*\left( \mathrm{grad}^{{\mathcal P}(\mathsf {X})}_p {{\mathcal {L}}} \right) , d K_*(B) \right\rangle _{K_*(p)} \quad \;\;\, (\text{ by } (35)) \\= & {} \left\langle d K_*(A) , d K_*(B) \right\rangle _{K_*(p)}. \end{aligned}$$

This proves the invariance (56). According to Chentsov’s uniqueness result, Theorem 4, this invariance characterises the Fisher–Rao metric up to a constant $\alpha > 0$.

“(2) $\Rightarrow$ (1):” This follows from the compatibility (52), which holds for the Fisher–Rao metric, and Theorems 2 and 3. $\square$

3.3 Cylindrical extensions of a model

Throughout this section, we consider a model ${{\mathcal {M}}}$, together with a proper parametrisation ${\mathbb R}^d \supseteq \varXi \rightarrow {{\mathcal {P}}}(\mathsf {Z})$, $\xi \mapsto p_\xi \in {{\mathcal {M}}}$, satisfying that the composition $\xi \mapsto X_*(p_\xi )$ is a proper parametrisation of ${{\mathcal {M}}}_X := X_*({{\mathcal {M}}})$. This ensures that all tangent spaces in non-singular points of ${{\mathcal {M}}}$ and ${{\mathcal {M}}}_X$, respectively, can be generated in terms of partial derivatives with respect to the parameters $\xi _i$, $i = 1, \dots , d$.

We can easily construct a model ${\widetilde{\mathcal {M}}} \subseteq {{\mathcal {P}}}(\mathsf {Z})$ that satisfies the conditions

$$\begin{aligned} \mathrm{(a)} \;\; {{\mathcal {M}}} \subseteq {\widetilde{\mathcal {M}}}, \quad \mathrm{(b)} \;\; X_*({{\mathcal {M}}}) = X_*({\widetilde{\mathcal {M}}}), \quad \text{ and } \quad \mathrm{(c)} \;\; {\widetilde{\mathcal {M}}} \text{ is } \text{ cylindrical }. \end{aligned}$$

(61)

We refer to such a model as a cylindrical extension of ${{\mathcal {M}}}$. Before we come to the explicit construction of cylindrical extensions, let us first demonstrate their direct use for relating the respective natural gradients to each other. Given an admissible point $p \in {{\mathcal {M}}}$ that is also admissible in ${\widetilde{\mathcal {M}}}$, we can decompose the tangent space $T_p {\widetilde{\mathcal {M}}}$ into the sum $T_p {{\mathcal {M}}} \oplus T^\perp _p {{\mathcal {M}}}$, where the second summand is the orthogonal complement of the first one in $T_p \widetilde{\mathcal M}$. We can use this decomposition in order to relate the natural gradient of a smooth function ${{\mathcal {L}}}$ defined on the projected model ${{\mathcal {M}}}_X$ to the natural gradient of ${{\mathcal {L}}} \circ X_*$:

$$\begin{aligned} \mathrm{grad}^{{{\mathcal {M}}}_X}_{X_*(p)} {{\mathcal {L}}}&{\mathop {\leftarrow }\limits ^{d X_*}}&\mathrm{grad}_p^{{\widetilde{\mathcal {M}}}} ({{\mathcal {L}}} \circ X_*) \nonumber \\= & {} \mathrm{grad}_p^{\top } ({{\mathcal {L}}} \circ X_*) + \mathrm{grad}_p^{\bot } ({{\mathcal {L}}} \circ X_*) \nonumber \\= & {} \mathrm{grad}_p^{{\mathcal {M}}} ({{\mathcal {L}}} \circ X_*) + \mathrm{grad}_p^{\bot } ({{\mathcal {L}}} \circ X_*). \end{aligned}$$

(62)

(Here “$\top$” stands for the projection onto $T_p {{\mathcal {M}}}$ and “$\bot$” stands for the projection onto the corresponding orthogonal complement in $T_p \widetilde{\mathcal M}$.) The difference between the natural gradient on the full model ${{\mathcal {M}}}$ and the natural gradient on the coarse grained model ${{\mathcal {M}}}_X$ is given by $\mathrm{grad}^{\bot }_p ({{\mathcal {L}}} \circ X_*)$ which vanishes when ${{\mathcal {M}}}$ itself is already cylindrical. Thus, the equality (62) generalises (57).

The product extension I Given a non-singular point $p_\xi = \sum _{z} p(z;\xi ) \, \delta ^z$ of ${{\mathcal {M}}}$, the tangent space in $p_\xi$ is spanned by

$$\begin{aligned} \partial _i(\xi ):= & {} \sum _{z \in \mathsf {Z}} \frac{\partial p(z; \cdot )}{\partial \xi _i} (\xi ) \, \delta ^z \nonumber \\= & {} \sum _{z \in \mathsf {Z}} p(z; \xi ) \frac{\partial \ln p(z; \cdot )}{\partial \xi _i} (\xi ) \, \delta ^z, \qquad i = 1, \dots , d. \end{aligned}$$

(63)

Now, consider the projection of $p_\xi$ onto ${\mathcal P}(\mathsf {X})$ in terms of $X_*$, that is $X_*(p_\xi ) = \sum _{x \in \mathsf {X}} p(x;\xi ) \, \delta ^x$ where $p(x;\xi ) = \sum _{z \in \mathsf {Z}_x} p(z; \xi )$. Assuming that this projected point is a non-singular point of ${{\mathcal {M}}}_X = X_*({{\mathcal {M}}})$, the corresponding tangent space $T_{X_*(p_\xi )} {{\mathcal {M}}}_X$ is spanned by

$$\begin{aligned} {\bar{\partial }}^{{\mathcal {H}}}_i(\xi ):= & {} d X_*(\partial _i(\xi )) \nonumber \\= & {} \sum _{x \in \mathsf {X}} \frac{\partial p(x; \cdot )}{\partial \xi _i}(\xi ) \, \delta ^x \nonumber \\= & {} \sum _{x \in \mathsf {X}} p(x; \xi ) \frac{\partial \ln p(x; \cdot )}{\partial \xi _i}(\xi ) \, \delta ^x , \qquad i = 1,\dots , d. \end{aligned}$$

(64)

In addition to the described projection of $p_\xi$ onto the “horizontal” space, leading to ${{\mathcal {M}}}_X$, we can also project it onto the “vertical” space. In order to do so, we define a Markov kernel $K_\xi = \sum _{x,z} p(z |x ; \xi ) \, \delta ^z \otimes e_x$:

(65)

We denote the image of the map $\xi \mapsto K_\xi$ by ${\mathcal M}_{Z|X} \subseteq {{\mathcal {K}}}(\mathsf {Z} | \mathsf {X})$, and assume that $K_\xi$ is a non-singular point of ${{\mathcal {M}}}_{Z|X}$. The corresponding tangent vectors in $K_\xi$ are given by

$$\begin{aligned} {\bar{\partial }}^{{\mathcal {V}}}_i(\xi ):= & {} \sum _{x, z} \frac{\partial p(z |x ; \cdot )}{\partial \xi _i}(\xi ) \, \delta ^z \otimes e_x \nonumber \\= & {} \sum _{x, z} p(z | x; \xi ) \frac{\partial \ln p(z | x; \cdot )}{\partial \xi _i}(\xi ) \, \delta ^z \otimes e_x , \qquad i = 1,\dots , d. \end{aligned}$$

(66)

Note that for all three sets of vectors, $\partial _i(\xi )$, ${\bar{\partial }}^{{\mathcal {H}}}_i(\xi )$, and ${\bar{\partial }}^{{\mathcal {V}}}_i(\xi )$, $i = 1,\dots ,d$, linear independence is not required. In fact, it is important to include overparametrised systems into the analysis, where linear independence is not given.

Now, we can define the product extension ${\widetilde{\mathcal {M}}}^{I}$ of ${{\mathcal {M}}}$ as follows: For each pair $({\xi }, {\xi '}) \in \varXi \times \varXi$, we define $p_{\xi ,\xi '} = p(\cdot ; \xi , \xi ')$ as

$$\begin{aligned} \sum _z p(z; \xi , \xi ') \, \delta ^z:= & {} \sum _{x} \sum _{z \in \mathsf {Z}_x} \left[ p(z ; \xi ) + p(x ; \xi ) \big ( p(z | x ; \xi ') - p(z | x ; \xi ) \big ) \right] \, \delta ^z \nonumber \\= & {} \sum _{x} \sum _{z \in \mathsf {Z}_x} p(x ; \xi ) \, p(z | x ; \xi ') \, \delta ^z . \end{aligned}$$

(67)

The product extension is then simply the set of all points that can be obtained in this way. Obviously, ${{\mathcal {M}}}$ consists of those points in ${\widetilde{\mathcal {M}}}^{I}$ that are given by identical parameters, that is $\xi = \xi '$, which proves (61) (a). Furthermore, $X_*(p_{\xi ,\xi '}) = X_*(p_{\xi })$, and therefore this extension has the same projection as the original model ${{\mathcal {M}}}$ so that (61) (b) is satisfied. The last requirement for ${\widetilde{\mathcal {M}}}^{I}$ to be a cylindrical extension of ${{\mathcal {M}}}$, (61) (c), will be proven below in Proposition 2. We obtain the tangent space of ${\widetilde{\mathcal {M}}}^{I}$ in $p_{\xi ,\xi '}$ by taking the derivatives with respect to $\xi _1,\dots ,\xi _d$ and $\xi '_1,\dots , \xi '_d$, respectively:

$$\begin{aligned}&{\partial ^{{\mathcal {H}}}_i (\xi , \xi ') } \nonumber \\&\quad := \frac{\partial }{\partial \xi _i} \sum _{z} p(z; \xi , \xi ') \, \delta ^z \nonumber \\&\quad = \sum _{z} p(z; \xi , \xi ') \, \frac{\partial \ln p(z; \cdot , \xi ')}{\partial \xi _i} (\xi ) \, \delta ^z \nonumber \\&\quad = \sum _x \sum _{z \in \mathsf {Z}_x} p(z; \xi , \xi ') \, \frac{\partial \ln p(x ; \cdot )}{\partial \xi _i} (\xi ) \, \delta ^z \nonumber \\&\quad = \sum _{x} \sum _{z \in \mathsf {Z}_x} p(x; \xi ) \, p(z | x ; \xi ' ) \, \frac{\partial \ln p(x; \cdot )}{\partial \xi _i} (\xi ) \, \delta ^z \nonumber \\&\quad = \sum _{x} p(x; \xi ) \, \frac{\partial \ln p(x; \cdot )}{\partial \xi _i} (\xi ) \, \left( \sum _{z \in \mathsf {Z}_x} p(z | x ; \xi ' ) \, \delta ^z \right) , \qquad i = 1,\dots ,d. \end{aligned}$$

(68)

A comparison with (64) shows that we have a natural isometric correspondence

$$\begin{aligned} \partial ^{{\mathcal {H}}}_i (\xi , \xi ') \longleftrightarrow {\bar{\partial }}^{{\mathcal {H}}}_i (\xi ), \qquad i = 1,\dots , d , \end{aligned}$$

(69)

by mapping $\delta ^x$ to $\sum _{z \in \mathsf {Z}_x} p(z | x ; \xi ' ) \, \delta ^z$ (this map is given by the X-congruent Markov morhphism discussed above; see also Fig. 5). Now we consider the vertical directions:

$$\begin{aligned}&{\partial ^{{\mathcal {V}}}_i (\xi , \xi ') } \nonumber \\&\quad := \frac{\partial }{\partial \xi _i '} \sum _{z} p(z; \xi , \xi ') \, \delta ^z \nonumber \\&\quad = \sum _{z} p(z; \xi , \xi ') \, \frac{\partial \ln p(z; \xi , \cdot )}{\partial \xi _i'} (\xi ') \, \delta ^z \nonumber \\&\quad = \sum _x \sum _{z \in \mathsf {Z}_x} p(z; \xi , \xi ') \, \frac{\partial \ln p(z | x ; \cdot )}{\partial \xi _i'} (\xi ') \, \delta ^z \nonumber \\&\quad = \sum _{x} \sum _{z \in \mathsf {Z}_x} p(x; \xi ) \, p(z | x ; \xi ' ) \, \frac{\partial \ln p(z | x ; \cdot ) }{\partial \xi _i'} (\xi ') \, \delta ^z, \qquad i = 1,\dots , d. \end{aligned}$$

(70)

A comparison with (66) shows that we also have a natural correspondence

$$\begin{aligned} \partial ^{{\mathcal {V}}}_i (\xi , \xi ') \longleftrightarrow {\bar{\partial }}^{{\mathcal {V}}}_i (\xi '), \qquad i = 1, \dots , d, \end{aligned}$$

(71)

by mapping $\delta ^z \otimes e_x$ to $p(x ; \xi ) \, \delta ^z$, in addition to the above-mentioned correspondence (69). This proves that $(\xi ,\xi ') \mapsto p_{\xi ,\xi '}$ is a proper parametrisation of $\widetilde{\mathcal M}^I$. The situation is illustrated in Fig. 6.

Fig. 6

Extension of ${{\mathcal {M}}}$ to the cylindrical model ${\widetilde{\mathcal {M}}}^{I}$, with the corresponding tangent vectors

Now we consider the natural Fisher–Rao metric on ${\widetilde{\mathcal {M}}}^{I} \subseteq {{\mathcal {P}}}(\mathsf {Z})$ in $p_{\xi ,\xi '}$, assuming that all points associated with $(\xi ,\xi ')$ are non-singular. It follows from Proposition 2 below that ${\langle \partial _i^{{\mathcal {H}}} (\xi , \xi '), \partial _j^{\mathcal V}(\xi ,\xi ') \rangle }_{\xi ,\xi '} = 0$ for all i, j, where ${\langle \cdot , \cdot \rangle }_{\xi ,\xi '}$ denotes the Fisher–Rao metric in $p_{\xi ,\xi '}$. For the inner products of the horizontal vectors we obtain

$$\begin{aligned}&{g^{{\mathcal {H}}}_{ij} (\xi ,\xi ') } \nonumber \\&\quad := {\left\langle \partial ^{{\mathcal {H}}}_i (\xi , \xi '), \partial ^{{\mathcal {H}}}_j (\xi , \xi ') \right\rangle }_{\xi ,\xi '} \nonumber \\&\quad = \sum _x p(x; \xi ) \sum _{z \in \mathsf {Z}_x} p(z | x ; \xi ') \, \frac{\partial \ln p(x; \cdot )}{\partial \xi _i} (\xi ) \, \frac{\partial \ln p(x; \cdot )}{\partial \xi _j} (\xi ) \nonumber \\&\quad = \sum _x p(x; \xi ) \, \frac{\partial \ln p(x; \cdot )}{\partial \xi _i} (\xi ) \, \frac{\partial \ln p(x; \cdot )}{\partial \xi _j} (\xi ) \nonumber \\&\quad = {\left\langle {\overline{\partial }}^{{\mathcal {H}}}_i (\xi ), {\overline{\partial }}^{{\mathcal {H}}}_j (\xi ) \right\rangle }_{\xi } \nonumber \\&\quad =: {{\overline{g}}^{{\mathcal {H}}}_{ij} (\xi )} . \end{aligned}$$

(72)

In particular, these inner products do not depend on $\xi '$. The inner products of the vertical vectors are given by

$$\begin{aligned}&{g^{{\mathcal {V}}}_{ij} (\xi ,\xi ') } \nonumber \\&\quad := {\left\langle \partial ^{{\mathcal {V}}}_i (\xi , \xi '), \partial ^{{\mathcal {V}}}_j (\xi , \xi ') \right\rangle }_{\xi ,\xi '} \nonumber \\&\quad = \sum _x p(x; \xi ) \sum _{z \in \mathsf {Z}_x} p(z | x ; \xi ') \, \frac{\partial \ln p(z | x; \cdot )}{\partial \xi _i'} (\xi ') \, \frac{\partial \ln p(z | x; \cdot )}{\partial \xi _j'} (\xi '). \end{aligned}$$

(73)

This defines two matrices,

$$\begin{aligned} \overline{\mathrm{G}}^{{\mathcal {H}}}(\xi )= & {} {({\overline{g}}^{{\mathcal {H}}}_{ij}(\xi ))}_{1 \le i,j \le d}, \qquad \text{ and } \\ \mathrm{G}^{{\mathcal {V}}}(\xi ,\xi ')= & {} {(g^{\mathcal V}_{ij}(\xi , \xi '))}_{1 \le i,j \le d}, \end{aligned}$$

and the Fisher information matrix $\widetilde{\mathrm{G}}(\xi ,\xi ')$ with respect to the product coordinate system is a block matrix,

$$\begin{aligned} \widetilde{\mathrm{G}}(\xi ,\xi ') = \left( \begin{array}{cc} \overline{\mathrm{G}}^{{\mathcal {H}}}(\xi ) &{} 0 \\ 0 &{} \mathrm{G}^{{\mathcal {V}}}(\xi ,\xi ') \end{array} \right) . \end{aligned}$$

In order to compute the gradient of a function $\widetilde{\mathcal L} : {\widetilde{\mathcal {M}}}^{I} \rightarrow {\mathbb R}$, we have to consider the pseudoinverse of $\widetilde{\mathrm{G}}(\xi ,\xi ')$, and, with the Euclidean gradient $\nabla _{\xi ,\xi '} \widetilde{\mathcal L} = (\nabla _\xi {\widetilde{\mathcal {L}}}, \nabla _{\xi '} {\widetilde{\mathcal {L}}})$, we have

$$\begin{aligned} \mathrm{grad}_{\xi ,\xi '}^{{\widetilde{\mathcal {M}}}^I} {\widetilde{\mathcal {L}}} \; = \; \left( \begin{array}{cc} {\overline{\mathrm{G}}^{{\mathcal {H}}}}^{+}(\xi ) &{} 0 \\ 0 &{} {\mathrm{G}^{{\mathcal {V}}}}^{+}(\xi ,\xi ') \end{array} \right) \left( \begin{array}{c} \nabla _\xi {\widetilde{\mathcal {L}}} \\ \nabla _{\xi '} {\widetilde{\mathcal {L}}} \end{array} \right) . \nonumber \\ \end{aligned}$$

(74)

Now we assume ${\widetilde{\mathcal {L}}} = {{\mathcal {L}}} \circ X_*$, where ${{\mathcal {L}}}$ is a function defined on the model $X_*(\widetilde{{\mathcal {M}}}) = X_*({{\mathcal {M}}}) = {{\mathcal {M}}}_X$. This implies that it only depends on the horizontal variable $\xi$:

$$\begin{aligned} {\widetilde{\mathcal {L}}} (p_{\xi ,\xi '}) \, = \, ({{\mathcal {L}}} \circ X_*) (p_{\xi , \xi '}) \, = \, {{\mathcal {L}}}\left( X_*(p_{\xi , \xi '})\right) \, = \, {{\mathcal {L}}} (p_\xi ) . \end{aligned}$$

This implies $\nabla _{\xi '} {\widetilde{\mathcal {L}}} = 0$ and $\nabla _{\xi } {\widetilde{\mathcal {L}}} = \nabla _{\xi } {\mathcal L}$. With (74), we obtain

$$\begin{aligned} \mathrm{grad}_{\xi ,\xi '}^{{\widetilde{\mathcal {M}}}^I} ({{\mathcal {L}}} \circ X_*) \; = \; \left( \begin{array}{c} {{\overline{G}}^{{\mathcal {H}}}}^{+}(\xi ) \nabla _{\xi } {{\mathcal {L}}} \\ 0 \end{array} \right) . \end{aligned}$$

(75)

This is a confirmation of our more general result that the natural gradient on a cylindrical model, here ${\widetilde{\mathcal {M}}}^I$, is equivalent to the natural gradient on the projected model $X_*({\widetilde{\mathcal {M}}}^I) = {{\mathcal {M}}}_X$ (see Theorem 5). However, Eq. (75) does not imply any simplification of the problem, because $\overline{\mathrm{G}}^{{\mathcal {H}}}(\xi )$ equals the original Fisher information matrix defined on the projected model ${{\mathcal {M}}}_X$ which does not necessarily have a block structure (see Eq. (72)). Assuming that the Fisher information matrix $\mathrm{G}(\xi )$ on the full model ${{\mathcal {M}}}$ has a block structure, we can try to exploit this structure within its product extension ${\widetilde{\mathcal {M}}}^I$. For this, note that the tangent vectors (63) of ${{\mathcal {M}}}$ in $p_\xi$ can be expressed as

$$\begin{aligned} \partial _i(\xi ) \, = \, \partial ^{{\mathcal {H}}}_i (\xi , \xi ) + \partial ^{{\mathcal {V}}}_i (\xi , \xi ) \, \in \, T_\xi {{\mathcal {M}}}, \qquad i = 1, \dots , d. \end{aligned}$$

(76)

This implies $\mathrm{G}(\xi ) = \overline{\mathrm{G}}^{{\mathcal {H}}}(\xi ) + \mathrm{G}^{{\mathcal {V}}} (\xi , \xi )$, and therefore, according to (75), we have to invert $\overline{\mathrm{G}}^{\mathcal H}(\xi ) = \mathrm{G}(\xi ) - \mathrm{G}^{{\mathcal {V}}}(\xi ,\xi )$, a difference of two matrices where the first one has a block structure and the second one does not. This shows that the block structure of $\mathrm{G}(\xi )$ is not sufficient for the simplification of the problem. In what follows, we modify the product extension ${\widetilde{\mathcal {M}}}^I$ and open up the possibility for simplification. The main idea here parallels the idea of introducing a recognition model, in addition to the generative model, as we did in the context of the wake-sleep algorithm in Sect. 2.2.

The product extension II We now generalise the first product extension and replace (67) by $p_{\xi , \eta } = p(\cdot ; \xi , \eta )$ where

$$\begin{aligned} \sum _z p(z; \xi , \eta ) \, \delta ^z:= & {} \sum _{x} \sum _{z \in \mathsf {Z}_x} \left[ p(z ; \xi ) + p(x ; \xi ) \big ( q(z | x ; \eta ) - p(z | x ; \xi ) \big ) \right] \, \delta ^z \\= & {} \sum _{x} \sum _{z \in \mathsf {Z}_x} p(x ; \xi ) \, q(z | x ; \eta ) \, \delta ^z , \end{aligned}$$

denoting by q the elements of a model ${{\mathcal {Q}}}_{Z|X}$ that is properly parametrised by $\eta = (\eta _1,\dots ,\eta _{d'}) \in \mathrm{H} \subseteq {\mathbb R}^{d'}$ and contains the model ${\mathcal M}_{Z|X}$. That is, for each $\xi$ there is an $\eta = \eta (\xi )$ such that $p(z | x ; \xi ) = q(z | x ; \eta )$. This is closely related to the recognition model discussed in Sect. 2.2. For $\eta \in \mathrm{H}$, the tangent space in $T_\eta {{\mathcal {Q}}}_{Z|X}$ is spanned by

$$\begin{aligned} {\bar{\partial }}^{{\mathcal {V}}}_i (\eta ) \, := \, \sum _{x, z} q(z | x ; \eta ) \frac{\partial \ln q(z | x ; \cdot )}{\partial \eta _i}(\eta ) \, \delta ^z \otimes e_x, \qquad i = 1,\dots ,d'. \end{aligned}$$

(77)

Consider a pair $(\xi , \eta ) \in \varXi \times \mathrm{H}$ so that all points associated with it are non-singular points of the respective models. For the horizontal and vertical vectors we obtain, analogous to (68) and (70),

$$\begin{aligned}&{\partial _i^{{\mathcal {H}}}(\xi , \eta )} \nonumber \\&\quad = \sum _{x} p(x; \xi ) \, \frac{\partial \ln p(x; \cdot )}{\partial \xi _i} (\xi ) \, \left( \sum _{z \in \mathsf {Z}_x} q(z | x ; \eta ) \, \delta ^z \right) , \qquad i = 1,\dots , d, \end{aligned}$$

(78)

and

$$\begin{aligned}&{\partial _i^{{\mathcal {V}}}(\xi , \eta )} \nonumber \\&\quad = \sum _{x} \sum _{z \in \mathsf {Z}_x} p(x; \xi ) \, q(z | x ; \eta ) \, \frac{\partial \ln q(z | x ; \cdot ) }{\partial \eta _i} (\eta ) \, \delta ^z , \qquad i = 1,\dots , d'. \end{aligned}$$

(79)

The correspondence (69) of horizontal vectors translates to

$$\begin{aligned} \partial ^{{\mathcal {H}}}_i (\xi , \eta ) \longleftrightarrow {\bar{\partial }}^{{\mathcal {H}}}_i (\xi ), \qquad i = 1,\dots , d , \end{aligned}$$

(80)

this time by mapping $\delta ^x$ to $\sum _{z \in \mathsf {Z}_x} q(z | x ; \eta ) \, \delta ^z$. Furthermore, we obtain the generalisation of (71) as

$$\begin{aligned} \partial ^{{\mathcal {V}}}_i (\xi , \eta ) \longleftrightarrow {\bar{\partial }}^{{\mathcal {V}}}_i (\eta ), \qquad i = 1, \dots , d', \end{aligned}$$

(81)

by mapping $\delta ^z \otimes e_x$ to $p(x ; \xi ) \, \delta ^z$. The situation is illustrated in Fig. 7.

Fig. 7

Extension of ${{\mathcal {M}}}$ to the cylindrical model ${\widetilde{\mathcal {M}}}^{II}$, with the corresponding tangent vectors

We now consider the Fisher–Rao metric on $\widetilde{\mathcal M}^{II} \subseteq {{\mathcal {P}}}(\mathsf {Z})$ in $p_{\xi ,\eta }$. It follows again from Proposition 2 below that ${\langle \partial _i^{{\mathcal {H}}} (\xi , \eta ), \partial _j^{\mathcal V}(\xi ,\eta ) \rangle }_{\xi ,\eta } = 0$ for all i, j, where ${\langle \cdot , \cdot \rangle }_{\xi ,\eta }$ denotes the Fisher–Rao metric in $p_{\xi ,\eta }$. For the inner products of the horizontal and the vertical vectors, respectively, we obtain

$$\begin{aligned} g_{ij}^{{\mathcal {H}}}(\xi , \eta )= & {} \left\langle \partial _i^{{\mathcal {H}}}(\xi , \eta ) , \partial _j^{{\mathcal {H}}}(\xi , \eta ) \right\rangle _{\xi , \eta } \nonumber \\= & {} \sum _{x} p(x ; \xi ) \, \frac{\partial \ln p(x ; \cdot )}{\partial \xi _i} (\xi ) \, \frac{\partial \ln p(x ; \cdot )}{\partial \xi _j} (\xi ) \; = \; {\overline{g}}_{ij}^{\mathcal H}(\xi ) , \end{aligned}$$

(82)

and

$$\begin{aligned} g_{ij}^{{\mathcal {V}}}(\xi , \eta )= & {} \left\langle \partial _i^{{\mathcal {V}}}(\xi , \eta ) , \partial _j^{{\mathcal {V}}}(\xi , \eta ) \right\rangle _{\xi , \eta } \nonumber \\= & {} \sum _{x} p(x ; \xi ) \sum _{z \in \mathsf {Z}_x} \, \frac{\partial \ln q(z | x ; \cdot )}{\partial \eta _i} (\eta ) \, \frac{\partial \ln q(z | x ; \cdot )}{\partial \eta _j } (\eta ) . \end{aligned}$$

(83)

The gradient of a function ${{\mathcal {L}}}$ on ${{\mathcal {M}}}_X$ is given in terms of (75), the formula that we already obtained for the previous product extension, where we have to replace $\xi '$ by $\eta$ and ${\widetilde{\mathcal {M}}}^I$ by ${\widetilde{\mathcal {M}}}^{II}$. However, with the second product extension we can choose the model ${{\mathcal {Q}}}_{Z|X}$ to be larger than ${{\mathcal {M}}}_{Z|X}$. This provides a way to simplify $\overline{\mathrm{G}}^{{\mathcal {H}}}(\xi )$ in (75). In order to be more explicit, consider the parametrisation

$$\begin{aligned} \xi \; \; \mapsto \; \; \sum _z p(z ; \xi , \eta (\xi )) \, \delta ^z \end{aligned}$$

(84)

of ${{\mathcal {M}}}$ which is naturally embedded in ${\widetilde{\mathcal {M}}}^{II}$. For the tangent vectors we now obtain

$$\begin{aligned} \partial _i(\xi )= & {} \sum _z p(z ; \xi , \eta (\xi )) \, \frac{\partial \ln p(z ; \cdot , \eta (\cdot ))}{\partial \xi _i} (\xi ) \, \delta ^z \\= & {} \sum _x \sum _{z \in \mathsf {Z}_x} p(x ; \xi ) \, q(z | x ; \eta (\xi )) \, \left[ \frac{\partial \ln p(x ; \cdot )}{\partial \xi _i} (\xi ) + \frac{\partial \ln q(z | x ; \eta (\cdot ))}{\partial \xi _i} (\xi ) \right] \, \delta ^z \\= & {} \sum _x \sum _{z \in \mathsf {Z}_x} p(x ; \xi ) \, q(z |x ; \eta (\xi )) \, \frac{\partial \ln p(x ; \cdot )}{\partial \xi _i} (\xi ) \, \delta ^z \\&+ \sum _x \sum _{z \in \mathsf {Z}_x} p(x ; \xi ) \, q(z |x ; \eta (\xi )) \sum _k \frac{\partial \ln q(z | x ; \cdot )}{\partial \eta _k} (\eta (\xi )) \, \frac{\partial \eta _k}{\partial \xi _i} (\xi ) \, \delta ^z \\&\text{(by } \text{ the } \text{ chain } \text{ rule) } \nonumber \\= & {} \partial _i^{{\mathcal {H}}}(\xi , \eta (\xi )) + \sum _{k} \frac{\partial \eta _k}{\partial \xi _i} (\xi ) \, \partial _k^{\mathcal V}(\xi , \eta (\xi )) . \end{aligned}$$

This derivation generalises the Eq. (76). For the Fisher information matrix $\mathrm{G}(\xi ) = (g_{ij}(\xi ))_{1\le i, j \le d}$ we obtain

$$\begin{aligned} g_{ij}(\xi )= & {} \left\langle \partial _i (\xi ) , \partial _j(\xi ) \right\rangle _{\xi } \\= & {} \underbrace{\left\langle \partial _i^{{\mathcal {H}}}(\xi , \eta (\xi )) , \partial _j^{{\mathcal {H}}}(\xi , \eta (\xi )) \right\rangle _{\xi , \eta (\xi )}}_{= \; {\overline{g}}^{{\mathcal {H}}}_{ij} (\xi )} \\&\qquad \qquad + \sum _{k,l} \frac{\partial \eta _k}{\partial \xi _i} (\xi ) \, \frac{\partial \eta _l}{\partial \xi _j} (\xi ) \underbrace{\left\langle \partial _k^{{\mathcal {V}}}(\xi , \eta (\xi )) , \partial _l^{{\mathcal {V}}}(\xi , \eta (\xi )) \right\rangle _{\xi , \eta (\xi )}}_{= \; g^{{\mathcal {V}}}_{kl}(\xi , \eta (\xi ))} \\= & {} {\overline{g}}^{{\mathcal {H}}}_{ij} (\xi ) + \sum _{k,l} \frac{\partial \eta _k}{\partial \xi _i} (\xi ) \, \frac{\partial \eta _l}{\partial \xi _j} (\xi ) \, g^{{\mathcal {V}}}_{kl}(\xi , \eta (\xi )) . \end{aligned}$$

Thus, we can insert

$$\begin{aligned} {\overline{g}}^{{\mathcal {H}}}_{ij} (\xi ) \; = \; g_{ij}(\xi ) - \sum _{k,l} \frac{\partial \eta _k}{\partial \xi _i} (\xi ) \, \frac{\partial \eta _l}{\partial \xi _j} (\xi ) \, g^{\mathcal V}_{kl}(\xi , \eta (\xi )) \end{aligned}$$

(85)

into Eq. (75). At first sight, this does not appear to simplify the problem. However, as we will outline in the next section, it suggests conditions for both, the generative model as well as the recognition model, that would be sufficient for a simplification of $\overline{\mathrm{G}}^{{\mathcal {H}}}(\xi )$. These conditions involve locality properties, as we studied in Sect. 2, but also an appropriate coupling between the two models.

We now prove that the second product extension, and thereby also the first one, are indeed cylindrical extensions of ${{\mathcal {M}}}$.

Proposition 2

The product extensions ${\widetilde{\mathcal {M}}}^{II}$ and, as a special case, ${\widetilde{\mathcal {M}}}^I$ are cylindrical extensions of ${{\mathcal {M}}}$. More precisely, we have

$$\begin{aligned} T_{\xi ,\eta } {\widetilde{\mathcal {M}}}^{II} \cap {\mathcal H}_{\xi ,\eta }= & {} \mathrm{span} \left\{ \partial ^{\mathcal H}_i(\xi ,\eta ) \, : \, i = 1,\dots , d \right\} \end{aligned}$$

(86)

$$\begin{aligned} T_{\xi ,\eta } {\widetilde{\mathcal {M}}}^{II} \cap {\mathcal V}_{\xi ,\eta }= & {} \mathrm{span} \left\{ \partial ^{\mathcal V}_i(\xi ,\eta ) \, : \, i = 1,\dots , d' \right\} \end{aligned}$$

(87)

$$\begin{aligned} T_{\xi ,\eta } {\widetilde{\mathcal {M}}}^{II}= & {} \left( T_{\xi ,\eta } {\widetilde{\mathcal {M}}}^{II} \cap {\mathcal H}_{\xi ,\eta } \right) + \left( T_{\xi ,\eta } \widetilde{\mathcal M}^{II} \cap {{\mathcal {V}}}_{\xi ,\eta } \right) . \end{aligned}$$

(88)

Proof

We have to verify the properties (a), (b), and (c) in (61).

• (a) We have assumed that for each $\xi$ there exists an $\eta = \eta (\xi )$ such that $p(z | x ; \xi ) = q(z | x ; \eta (\xi ))$. This implies that each distribution $p_\xi \in {{\mathcal {M}}}$ is also contained in ${\widetilde{\mathcal {M}}}^{II}$:

  $$\begin{aligned} p(z ; \xi ) \, = \, p(x ; \xi ) p(z | x ; \xi ) \, = \, p(x ; \xi ) q(z | x ; \eta (\xi )) \, = \, p(z ; \xi , \eta (\xi )). \end{aligned}$$

• (b) Clearly, from (a) we obtain $X_*({{\mathcal {M}}}) \subseteq X_*({\widetilde{\mathcal {M}}}^{II})$. To prove the opposite inclusion, we consider a point $p_{\xi ,\eta } \in \widetilde{\mathcal M}^{II}$ and show that the point $p_\xi \in {{\mathcal {M}}}$ has the same $X_*$-projection:

  $$\begin{aligned} X_*\left( p_{\xi , \eta } \right)= & {} X_*\left( \sum _{x} \sum _{z \in \mathsf {Z}_x} p(x ; \xi ) \, q(z| x ; \eta ) \, \delta ^z \right) \\= & {} \sum _{x} \left( \sum _{z \in \mathsf {Z}_x} p(x ; \xi ) \, q(z| x ; \eta ) \right) \, \delta ^x \\= & {} \sum _{x} p(x ; \xi ) \, \delta ^x \\= & {} \sum _{x} \left( \sum _{z \in \mathsf {Z}_x} p(x ; \xi ) \, q(z | x ; \eta (\xi )) \right) \, \delta ^x \\= & {} \sum _{x} \left( \sum _{z \in \mathsf {Z}_x} p(x ; \xi ) \, p(z | x ; \xi ) \right) \, \delta ^x \\= & {} \sum _{x} \left( \sum _{z \in \mathsf {Z}_x} p(z ; \xi ) \right) \, \delta ^x \; = \; X_*\left( \sum _z p(z ; \xi ) \, \delta ^z \right) \; = \; X_*\left( p_\xi \right) . \end{aligned}$$

• (c) We have

  $$\begin{aligned} {{\mathcal {H}}}_{\xi , \eta } \, := \, \left\{ {\widetilde{A}} = \sum _{x} A(x) \sum _{z \in \mathsf {Z}_x} q(z | x ; \eta ) \, \delta ^z \; : \; \sum _x A(x) = 0 \right\} \end{aligned}$$

  with the orthogonal complement

  $$\begin{aligned} {{\mathcal {V}}}_{\xi ,\eta } \, := \, \left\{ \sum _{z} A(z) \, \delta ^{z} \; : \; \displaystyle \sum _{z \in \mathsf {Z}_x} A(z) \, = \, 0 \text{ for } \text{ all } x \right\} . \end{aligned}$$

  We first show that the horizontal vectors

  $$\begin{aligned} \partial ^{{\mathcal {H}}}_i (\xi , \eta ) \; = \; \sum _{x} p(x; \xi ) \, \frac{\partial \ln p(x; \cdot )}{\partial \xi _i} (\xi ) \sum _{z \in \mathsf {Z}_x} q(z | x ; \eta ) \, \delta ^z \end{aligned}$$

  are contained in ${{\mathcal {H}}}_{\xi , \eta }$. To this end, we set $A(x) = p(x; \xi ) \, \frac{\partial \ln p(x; \cdot )}{\partial \xi _i} (\xi )$ and verify

  $$\begin{aligned} \sum _x A(x)= & {} \sum _x p(x; \xi ) \, \frac{\partial \ln p(x; \cdot )}{\partial \xi _i} (\xi ) \\= & {} \sum _x \left. \frac{\partial p(x; \cdot )}{\partial \xi _i} (\xi ) \; = \; \frac{\partial }{\partial \xi _i} \sum _x p(x; \cdot ) \right| _{\xi } \\= & {} 0. \end{aligned}$$

  Now we show that the vertical vectors

  $$\begin{aligned} \partial ^{{\mathcal {V}}}_i (\xi , \eta ) \; = \; \sum _{x} \sum _{z \in \mathsf {Z}_x} p(x; \xi ) \, q(z | x ; \eta ) \, \frac{\partial \ln q(z | x ; \cdot ) }{\partial \eta _i} (\eta ) \, \delta ^z \end{aligned}$$

  are contained in ${{\mathcal {V}}}_{\xi ,\eta }$. We set $A(z) := p(X(z); \xi ) \, q(z | X(z) ; \eta ) \, \frac{\partial \ln q(z | X(z) ; \cdot ) }{\partial \eta _i} (\eta )$ and verify

  $$\begin{aligned} \sum _z A(z)= & {} \sum _{x} \sum _{z \in \mathsf {Z}_x} p(x; \xi ) \, q(z | x ; \eta ) \, \frac{\partial \ln q(z | x ; \cdot ) }{\partial \eta _i} (\eta ) \\= & {} \sum _{x} \sum _{z \in \mathsf {Z}_x} p(x; \xi ) \, \frac{\partial q(z | x ; \cdot ) }{\partial \eta _i} (\eta ) \\= & {} \sum _{x} p(x; \xi ) \left. \frac{\partial }{\partial \eta _i} \sum _{z \in \mathsf {Z}_x} q(z | x ; \cdot ) \right| _{\eta } \\= & {} 0. \end{aligned}$$

  In conclusion, we have

  $$\begin{aligned} T_{\xi , \eta } {\widetilde{\mathcal {M}}}^{II}= & {} \mathrm{span} \left\{ \partial ^{{\mathcal {H}}}_i(\xi , \eta ) \, : \, i = 1,\dots , d \right\} + \mathrm{span} \left\{ \partial ^{{\mathcal {V}}}_i(\xi ,\eta ) \, : \, i = 1,\dots , d' \right\} \\\subseteq & {} \left( T_{\xi ,\eta } {\widetilde{\mathcal {M}}}^{II} \cap {{\mathcal {H}}}_{\xi ,\eta } \right) + \left( T_{\xi ,\eta } {\widetilde{\mathcal {M}}}^{II} \cap {{\mathcal {V}}}_{\xi ,\eta } \right) \\\subseteq & {} T_{\xi , \eta } {\widetilde{\mathcal {M}}}^{II} , \end{aligned}$$

  which proves the equalities (86), (87), and (88). $\square$

4 Conclusions: A natural gradient perspective of the wake–sleep algorithm

Information geometry provides two natural geometries associated with a learning system that has visible units V and hidden units H. Typically, the system is given in terms of a model ${{\mathcal {M}}}$ of probability distributions of global states of the full system, ${{\mathcal {P}}}_{V,H}$, but the objective function ${{\mathcal {L}}}$ only depends on the probability distribution of the visible states, giving rise to a projected model ${{\mathcal {M}}}_V \subseteq {{\mathcal {P}}}_V$. Both geometric objects, ${{\mathcal {M}}}$ and ${{\mathcal {M}}}_V$, carry a natural geometry inherited from the respective ambient space. In Sect. 2 we studied various locality properties of the natural gradient based on the first geometry, thereby assuming a factorisation of the elements of ${{\mathcal {M}}}$ according to a directed acyclic graph. These properties simplify the Fisher information matrix for ${{\mathcal {M}}}$ and allow us to apply the natural gradient method to deep networks. The second geometry, the geometry of ${{\mathcal {M}}}_V$, was studied in Sect. 3 where we took a somewhat more general perspective. In what follows, we restate the general problem of comparing the two mentioned geometries within that perspective and summarise the corresponding results.

Consider a model ${{\mathcal {S}}}$ in the set ${\mathcal P}(\mathsf {X})$ of probability distributions on a finite set $\mathsf {X}$, and a smooth function ${{\mathcal {L}}}: {\mathcal P}(\mathsf {X}) \rightarrow {\mathbb R}$. The task is to optimise ${{\mathcal {L}}}$ on ${{\mathcal {S}}}$ in terms of the natural gradient $\mathrm{grad}^{{\mathcal {S}}} {{\mathcal {L}}}$. With no further assumptions this can be a very difficult problem. Typically, however, ${{\mathcal {S}}}$ is obtained as the image of a simpler model ${{\mathcal {M}}}$ of probability distributions on a larger set $\mathsf {Z}$, ${{\mathcal {P}}}(\mathsf {Z})$. More precisely, we consider a surjective map $X: \mathsf {Z} \rightarrow \mathsf {X}$, and the corresponding push-forward map $X_*: {{\mathcal {P}}}(\mathsf {Z}) \rightarrow {{\mathcal {P}}}(\mathsf {X})$ of probability measures. The model ${{\mathcal {S}}}$ is then nothing but the $X_*$-image of ${{\mathcal {M}}}$, that is ${{\mathcal {S}}} = {{\mathcal {M}}}_X = X_*({{\mathcal {M}}})$. Now, instead of optimising ${{\mathcal {L}}}$ on ${{\mathcal {M}}}_X$, we can optimise ${\mathcal L} \circ X_*$ on ${{\mathcal {M}}}$ and aim to simplify the problem by exploiting the structure of ${{\mathcal {M}}}$. This works to some extent. Even though the two problems are closely related, the corresponding gradient fields, $d X_*\left( \mathrm{grad}^{{\mathcal {M}}} ({{\mathcal {L}}} \circ X_*) \right)$ and $\mathrm{grad}^{{{\mathcal {M}}}_X} {{\mathcal {L}}}$, typically differ from each other. Thus, the optimisation of ${{\mathcal {L}}}$ on ${{\mathcal {M}}}_X$, based on the Fisher–Rao metric on ${\mathcal P}(\mathsf {X})$, and the optimisation of ${{\mathcal {L}}} \circ X_*$ on ${{\mathcal {M}}}$, based on the Fisher–Rao metric on ${{\mathcal {P}}}(\mathsf {Z})$, are not equivalent. We can try to improve the situation by replacing the Fisher–Rao metric on ${{\mathcal {M}}}$ and ${{\mathcal {M}}}_X$, respectively, by different Riemannian metrics. While this might be a reasonable approach for the simplification of the problem, from the information-geometric perspective, the Fisher–Rao metric is the most natural one, which is the reason for referring to the Fisher–Rao gradient as the natural gradient. This is directly linked to the invariance of gradients, as we have highlighted in this article. If we request invariance of the gradients for all coarse grainings $X: \mathsf {Z} \rightarrow \mathsf {X}$, all models ${{\mathcal {M}}} \subseteq {{\mathcal {P}}}(\mathsf {Z})$ from a particular class, and all smooth functions ${{\mathcal {L}}}: {{\mathcal {M}}}_X \rightarrow {\mathbb R}$, by Chentsov’s classical characterisation theorem, we have have to impose the Fisher–Rao metric on the individual models (see Theorem 5). Even then, the invariance of gradients is satisfied only if the model is cylindrical in the sense of Definition 1. Given a model ${{\mathcal {M}}}$ that is not cylindrical, we have proposed cylindrical extensions ${\widetilde{\mathcal {M}}}$ which contain ${{\mathcal {M}}}$. The natural gradient of ${{\mathcal {L}}}$ on ${{\mathcal {M}}}_X$ is then equivalent to the natural gradient of ${{\mathcal {L}}} \circ X_*$ on such an extension ${\widetilde{\mathcal {M}}}$.

As an outlook, we want to touch upon the following two related problems:

• 1. Can we exploit the simplicity of the original model ${{\mathcal {M}}}$ in order to simplify the optimisation on ${\widetilde{\mathcal {M}}}$?

• 2. The original model ${{\mathcal {M}}}$ is associated with some network. What kind of network can we associate with the extended model ${\widetilde{\mathcal {M}}}$?

We want to briefly address these problems within the context of Section 2, where $\mathsf {X} = \mathsf {X}_{V}$, $\mathsf {Z} = \mathsf {X}_{V} \times \mathsf {X}_H$, and $X = X_V: (v, h) \mapsto v$. As the cylindrical extension ${\widetilde{\mathcal {M}}}^{II}$ suggests, it can be associated with the addition of a recognition model ${{\mathcal {Q}}}_{H|V}$, assuming that ${{\mathcal {M}}}$ is a generative model. If both models are parametrised by (7) and (21), respectively, then the corresponding Fisher information matrices simplify as stated in Theorem 1. They both have a block structure where each block corresponds to one unit. Outside of these blocks, the matrices are filled with zeros. Being more precise, we consider all parameters that correspond to unit r, the parameters $\xi _r = (\xi _{(r;1)}, \dots , \xi _{(r;d_r)})$ of the generative model ${{\mathcal {M}}}$, and the parameters $\eta _r = (\eta _{(r; 1)} , \dots , \eta _{(r; d_r')})$ of the recognition model ${\mathcal Q}_{H|V}$. With (85) we then obtain

$$\begin{aligned}&{{\overline{g}}^{{\mathcal {H}}}_{(r;i) (s; j)} (\xi )} \nonumber \\&\quad = g_{(r;i) (s; j)}(\xi ) - \sum _{t,u} \sum _{(t;k),(u;l)} \frac{\partial \eta _{(t;k)}}{\partial \xi _{(r; i)}} (\xi ) \, \frac{\partial \eta _{(u;l)}}{\partial \xi _{(s; j)}} (\xi ) \, g^{{\mathcal {V}}}_{(t; k)(u; l)}(\xi , \eta (\xi )). \end{aligned}$$

(89)

We know that $g_{(r;i) (s; j)}(\xi ) = 0$ if $r \not = s$ and $g^{{\mathcal {V}}}_{(t; k)(u; l)}(\xi , \eta (\xi )) = 0$ if $t \not = u$. With the latter property, the sum on the RHS of (89) reduces to

$$\begin{aligned} \sum _t \sum _{(t;k),(t;l)} \frac{\partial \eta _{(t;k)}}{\partial \xi _{(r; i)}} (\xi ) \, \frac{\partial \eta _{(t;l)}}{\partial \xi _{(s; j)}} (\xi ) \, g^{{\mathcal {V}}}_{(t; k)(t; l)}(\xi , \eta (\xi )). \end{aligned}$$

(90)

If all partial derivatives $\partial \eta _{(t;k)} / \partial \xi _{(r; i)}(\xi )$ are local in the sense that they vanish whenever $t \not = r$, then the matrix $\overline{\mathrm{G}}^{{\mathcal {H}}}(\xi )$ inherits the block structure of the matrices $\mathrm{G}(\xi )$ and $\mathrm{G}^{{\mathcal {V}}}(\xi , \eta (\xi ))$. However, this is typically not the case and suggests an additional coupling between the generative model and the recognition model. Without that coupling, the partial derivatives in (90) will “overwrite” the block structure of the matrix $\mathrm{G}(\xi )$, leading to a non-local matrix $\overline{\mathrm{G}}^{{\mathcal {H}}}(\xi )$ with ${\overline{g}}^{{\mathcal {H}}}_{(r;i) (s; j)} (\xi ) \not = 0$ even if $r \not = s$. The degree of non-locality will depend on the specific properties of the partial derivatives $\partial \eta _{(t;k)} / \partial \xi _{(r; i)} (\xi )$.

We conclude this article by revisiting the wake–sleep algorithm of Sect. 2.2. Let us assume that (89) and (90) imply a sufficient simplification so that a natural gradient step in ${\widetilde{\mathcal {M}}}^{II}$ can be made. This will update the generation parameters, say from $\xi$ to $\xi + \varDelta \xi$, and leave the recognition parameters $\eta$ unchanged. (The situation is illustrated in Fig. 8.) Such an update corresponds to a natural gradient version of the wake step. The resulting point $(\xi + \varDelta \xi , \eta )$ in ${\widetilde{\mathcal {M}}}^{II}$ will typically be outside of ${{\mathcal {M}}}$. As the simplification through (89) and (90) only holds on ${{\mathcal {M}}}$, we have to update the recognition parameters, say from $\eta$ to $\eta + \varDelta \eta$, so that the resulting point $(\xi + \varDelta \xi , \eta + \varDelta \eta )$ is again in ${\mathcal M}$. This sleep step will ensure that the next update of the generation parameters benefits from the simplicity of the Fisher information matrix.

Fig. 8

Illustration of the generalised wake–sleep algorithm, taking place on the cylindrical extension ${\widetilde{\mathcal {M}}}^{II}$ of ${\mathcal M}$

Note that it is irrelevant how we get back to ${{\mathcal {M}}}$ within the sleep step, as far as we do not change the generation parameters. Also, it might be required to apply several sleep steps until we get back to ${{\mathcal {M}}}$, which highlights the asymmetry of time scales of the two phases. This asymmetric version has been outlined and discussed in the context of the em-algorithm in [18]. The overall wake-sleep step will typically not follow the gradient of an objective function on $\widetilde{\mathcal M}^{II}$. However, this is not the aim here. The prime process is the process in $\xi$ which parametrises ${{\mathcal {M}}}_V$. Effectively, the outlined version of the wake-sleep algorithm will follow the natural gradient of the objective function with respect to the geometry of ${{\mathcal {M}}}_V$. The natural wake-sleep algorithm with respect to the geometry of ${{\mathcal {M}}}$ has been recently studied in [31].

In Sect. 2.2 we introduced the recognition model as an auxiliary model for the evaluation of the gradient with respect to $\xi$. This work reveals another role of the recognition model in the context of the natural gradient method. It allows us to define an extension of the original model ${{\mathcal {M}}}$ so that we can effectively apply the natural gradient method on the projected model ${{\mathcal {M}}}_V$ within the context of deep learning. The presented results suggest criteria for the coupling between the generative model and recognition model that would ensure the locality of the natural gradient on ${{\mathcal {M}}}_V$. These criteria involve, on the one hand, the structure of the underlying networks (see Example 2) and, on the other hand, the parametrisation of the models. However, in this article they are formulated as sufficient conditions for the simplification of the natural gradient, based on theoretical results. The derivation of explicit design principles for correspondingly coupled models requires further studies.

Appendix

1.1 Moore–Penrose inverse and gradients

We consider a model ${{\mathcal {M}}}$, with a parametrisation ${\mathbb R}^d \supseteq \varXi \rightarrow {{\mathcal {M}}}$, $\xi \mapsto p_\xi$. For a non-singular point $p_\xi \in {{\mathcal {M}}}$, we assume that the tangent space in $p_\xi$, $T_\xi {{\mathcal {M}}}$, is spanned by the vectors $\partial _i(\xi ) := \frac{\partial }{\partial \xi _i} \, p_\xi$, $i = 1,\dots , d$. Note that we do not assume that these vectors are independent. Now consider a function ${{\mathcal {L}}}: {{\mathcal {M}}} \rightarrow {\mathbb R}$ that is smooth in $p_\xi$, and its differential

$$\begin{aligned} {d {{\mathcal {L}}}}_{\xi } : \; T_\xi {{\mathcal {M}}} \; \rightarrow \; {\mathbb R}, \qquad A \; \mapsto \; {d {{\mathcal {L}}}}_\xi (A) = \frac{\partial {{\mathcal {L}}}}{\partial A} (\xi ). \end{aligned}$$

This is a linear form on $T_\xi {{\mathcal {M}}}$. With an inner product $g_\xi$ on $T_\xi {{\mathcal {M}}}$ we can identify ${d {{\mathcal {L}}}}_\xi$ with a vector $\mathrm{grad}^{{\mathcal {M}}}_\xi {{\mathcal {L}}} \in T_\xi {{\mathcal {M}}}$, which points in the direction of maximal infinitesimal increase of ${{\mathcal {L}}}$ in $\xi$. It is uniquely characterised by the equation

$$\begin{aligned} g_\xi (\mathrm{grad}^{{\mathcal {M}}}_\xi {{\mathcal {L}}} , A) \, = \, {d {{\mathcal {L}}}}_\xi (A), \qquad A \in T_\xi {{\mathcal {M}}} . \end{aligned}$$

(91)

Let us now express the gradient in terms of the parameters $\xi$. Clearly, it has a representation

$$\begin{aligned} \mathrm{grad}^{{\mathcal {M}}}_\xi {{\mathcal {L}}} \, = \, \sum _{i = 1}^d x^i(\xi ) \, \partial _i(\xi ) . \end{aligned}$$

(92)

Note that this representation of the gradient in terms of the coefficients $x(\xi ) = (x^1(\xi ),\dots ,x^d(\xi ))$ is not necessarily unique (due to the fact that the vectors $\partial _i(\xi )$, $i = 1,\dots ,d$, need not be independent). We insert the RHS of (92) and $A = \partial _j (\xi )$ into (91) and obtain

$$\begin{aligned} \sum _{i = 1}^d x^i(\xi ) \, g_{ij}(\xi ) \; = \; \frac{\partial {{\mathcal {L}}}}{\partial \xi _j} (\xi ), \qquad j = 1,\dots , d , \end{aligned}$$

(93)

where $g_{ij}(\xi ) = g_\xi ( \partial _i (\xi ), \partial _j (\xi ) )$. This can be written in matrix notation as

$$\begin{aligned} \mathrm{G}(\xi ) \, x(\xi ) \; = \; \nabla _\xi {{\mathcal {L}}} . \end{aligned}$$

(94)

Any coefficient vector $x(\xi ) \in {\mathbb R}^d$ that satisfies (94) will provide an equally valid representation of the gradient in terms of the tangent vectors $\partial _i (\xi )$. Furthermore, we know that there is at least one solution $x(\xi )$ that represents the gradient. In the case where $\mathrm{G}(\xi )$ is of maximal rank this solution is unique and we can simply apply the inverse of $\mathrm{G}(\xi )$ in order to obtain the coefficients of the gradient as $x(\xi ) = \mathrm{G}^{-1}(\xi ) \nabla _\xi {{\mathcal {L}}}$. This is the usual case when we have a local (diffeomorphic) coordinate system around the point $p_\xi$. Even though we interpret a parametrisation of a model as a coordinate system, the number of parameters often exceeds the dimension of the model. In these cases, the matrix $\mathrm{G}(\xi )$ will not be of maximal rank so that we have a non-trivial kernel $\mathrm{ker} \, \mathrm{G}(\xi )$. We can always add to a solution $x(\xi )$ of (94) a vector $y(\xi )$ from that kernel and obtain another solution $x(\xi ) + y(\xi )$. The affine space ${{\mathcal {A}}}(\xi ) = x(\xi ) + \mathrm{ker} \, \mathrm{G}(\xi ) \subseteq {\mathbb R}^d$ of solutions describes all possible representations of the gradient in terms of $\partial _1(\xi ),\dots , \partial _d(\xi )$. They are all equally adequate for describing a learning process that takes place in ${{\mathcal {M}}}$. However, from the perspective of linear algebra there is a natural choice, the element in the affine solution space ${{\mathcal {A}}}(\xi )$ that is orthogonal to $\mathrm{ker} \, \mathrm{G}(\xi )$ (with respect to the canonical inner product in ${\mathbb R}^d$). This defines the Moore–Penrose inverse $\mathrm{G}^+(\xi )$, also called pseudoinverse. In this paper, we were concerned with a number of simplifications of the natural gradient. One simplification was expressed in terms of a block diagonal structure of the Fisher information matrix. For the representation of the natural gradient, we evaluated the pseudoinverse of that block diagonal matrix based on the following simple observation (see, e.g., [11] for more general results related to the pseudoinverse of a block matrix):

$$\begin{aligned} {\left( \begin{array}{ccc} \mathrm{G}_{1} &{} &{} 0 \\ &{} \ddots &{} \\ 0 &{} &{} \mathrm{G}_{|N|} \end{array} \right) }^+ \; = \; \left( \begin{array}{ccc} \mathrm{G}_{1}^+ &{}. &{} 0 \\ &{} \ddots &{} \\ 0 &{} &{} \mathrm{G}_{|N|}^+ \end{array} \right) . \end{aligned}$$

(95)

How natural is the Moore–Penrose inverse? There are two perspectives here. On the one hand, $\mathrm{G}^+(\xi ) \, \nabla _\xi {{\mathcal {L}}}$ is natural in the sense that it represents an object, $\mathrm{grad}^{{\mathcal {M}}}_\xi {{\mathcal {L}}}$, that is independent of the parametrisation. On the other hand, the inner product used for the definition of $\mathrm{G}^+(\xi )$ is the canonical inner product in ${\mathbb R}^d$ which does not have to be at all related to the metric $g_\xi$. In this article, we have chosen the Moore–Penrose inverse as one possible extension of the usual inverse to overparametrised models, following previous proposals (see, e.g., [29]). Note, however, that there are also other possibilities for such an extension. We have some flexibility here which might allow us to further simplify the representation of the natural gradient in terms of a particular choice of the parametrsiation.

1.2 Gibbs sampling

In this section we outline the Gibbs sampling method for the approximation of the derivative (11). By holding the configuration $x_V$ constant, we can sample from $p(x_H | x_V; \xi )$ by randomly selecting a node $s \in H$, and then updating the state of that node according to $p( x_s | x_{H \setminus s}, x_V ; \xi )$. After this update we repeat choosing a node and updating its state. This will generate, after many repetitions, $p_\xi ^*$-typical patterns. The conditional distribution is simple because, due to the local Markov property, it satisfies $p( x_s | x_{H \setminus s}, x_V; \xi ) = p( x_s | x_{bl(s)} ; \xi )$, where bl(s) denotes the Markov blanket of s (see Fig. 9). It is defined as

$$\begin{aligned} bl(s) := pa(s) \cup ch(s) \cup \bigcup _{j \in ch(s)} ( pa(j) \setminus s ). \end{aligned}$$

Note that, in general, the Markov blanket is larger than the parent set and $p( x_s | x_{bl(s)} ; \xi )$ differs from $k^s ( x_s | x_{pa(s)} ; {\xi _s})$. More precisely, for $s \in H$, we have

$$\begin{aligned} p(x_s | x_{bl(s)} ; \xi )= & {} p(x_s | x_V, x_{H \setminus s} ; \xi ) \nonumber \\= & {} \frac{ p(x_V, x_{H \setminus s},x_s ; \xi )}{\sum _{x_s'} p(x_V, x_{H \setminus s},x_s'; \xi )} \nonumber \\= & {} \frac{ \prod _{i \in N} k^i (x_i | x_{pa(i)} ; {\xi _i})}{\sum _{x_s'} \prod _{i \in N} k^i (x_i' | x_{pa(i)} ; {\xi _i} )} \nonumber \\= & {} \frac{ k^s(x_s | x_{pa(s)} ; {\xi _s}) \prod _{i \in ch(s)} k^i (x_i | x_{pa(i)} ; {\xi _i})}{ \sum _{x_s'} k^s(x_s' | x_{pa(s)} ; {\xi _s}) \prod _{i \in ch(s)} k^i (x_i | x_{pa(i) \setminus s}, x_s' ; {\xi _i})}. \end{aligned}$$

(96)

Even though we cannot use the local kernels $k^s ( x_s | x_{pa(s)} ; {\xi _s})$ as a generative model for sampling from $p_\xi ^*$, the kernels $p(x_s | x_{bl(s)} ; \xi )$, which are used for Gibbs sampling, are still local in the sense that they only depend on the Markov blanket of s (see Fig. 9).

Fig. 9

Illustration of the Markov blanket bl(s) of a node s. Its elements are highlighted by thick circles

We exemplify the derivations of this section in the context of binary neural networks, thereby extending Example 1.

Example 7

(Neural networks (III)) In order to evaluate the derivatives (15) and (16) in Example 1, we have to sample from $p^*_\xi$. We use Gibbs sampling based on the expression (96) which, for binary state sets $\{-1,+1\}$, reduces to

$$\begin{aligned} p(x_s | x_V, x_{H \setminus s} ; \xi )= & {} \frac{1}{1 + \frac{k^s (- x_s | x_{pa(s)} ; {\xi _s} )}{k^s(x_s | x_{pa(s)} ; {\xi _s})} {\prod }_{i \in ch(s)} \frac{k^i(x_i | x_{pa(i)\setminus s},-x_s ; {\xi _i})}{k^i (x_i | x_{pa(i)\setminus s}, x_s ; {\xi _i})}}. \end{aligned}$$

Let us analyse the term in the denominator. Using the update rule (12), simple calculations yield

$$\begin{aligned}&{\frac{k^s(- x_s | x_{pa(s)} ; {\xi _s})}{k^s (x_s | x_{pa(s)} ; {\xi _s})} {\prod }_{i \in {ch(s)}} \frac{k^i (x_i | x_{pa(i)\setminus s},-x_s ; {\xi _i})}{k^i (x_i | x_{pa(i)\setminus s}, x_s ; {\xi _i})}} \\&\quad = \frac{e^{-\frac{1}{2} x_s h_s(x_{pa(s)})}}{e^{\frac{1}{2} x_s h_s(x_{pa(s)})}} \\&\quad \quad \times \prod _{i \in {ch(s)}} \frac{e^{\frac{1}{2} x_i \left( h_i(x_{pa(i)}) - 2 w_{si} x_s \right) }}{ e^{\frac{1}{2} x_i \left( h_i(x_{pa(i)}) - 2 w_{si} x_s \right) } + e^{-\frac{1}{2} x_i \left( h_i(x_{pa(i)}) - 2 w_{si} x_s \right) }}\\&\quad \quad \times \,\,\frac{e^{\frac{1}{2} x_i h_i(x_{pa(i)})} + e^{-\frac{1}{2} x_i h_i(x_{pa(i)})}}{e^{\frac{1}{2} x_i h_i(x_{pa(i)})}} \\&\quad = e^{- x_s h_s(x_{pa(s)})} \prod _{i \in {ch(s)}} \frac{e^{- w_{si} x_s x_i } \left( e^{\frac{1}{2} x_i h_i(x_{pa(i)})} + e^{-\frac{1}{2} x_i h_i(x_{pa(i)})} \right) }{ e^{- w_{si} x_s x_i } e^{\frac{1}{2} x_i h_i(x_{pa(i)})} + e^{w_{si} x_s x_i } e^{-\frac{1}{2} x_i h_i(x_{pa(i)})}} \\&\quad = e^{- x_s h_s(x_{pa(s)})} \prod _{i \in {ch(s)}}\frac{e^{\frac{1}{2} x_i h_i(x_{pa(i)})} + e^{-\frac{1}{2} x_i h_i(x_{pa(i)})}}{e^{\frac{1}{2} x_i h_i(x_{pa(i)})} + e^{2 w_{si} x_s x_i } e^{-\frac{1}{2} x_i h_i(x_{pa(i)})}} \\&\quad = e^{- x_s h_s(x_{pa(s)})} \underbrace{\prod _{i \in {ch(s)}} \frac{1 + e^{- x_i h_i(x_{pa(i)})}}{ 1 + e^{2 w_{si} x_s x_i } e^{- x_i h_i(x_{pa(i)})}}}_{=: a_s(x_{bl(s)})} . \end{aligned}$$

This finally implies

$$\begin{aligned} p_\xi (x_s | x_{bl(s)}) \, = \, \frac{1}{1 + e^{- x_s h_s(x_{pa(s)})} a_s(x_{bl(s)})}. \end{aligned}$$

(97)

Comparing this with the update rule (12), we observe that the full Markov blanket is involved in terms of the modulation function $a_s$.