Abstract
This review presents an upgraded wave theory adapted to the high fluctuation level of driven realistic, i.e., non-idealized plasmas. Based on the author’s early publication (H. Schamel, Plasma Phys. 14 (1972) 905) and supported by recent Vlasov–Poisson (VP) simulations, an extended theoretical framework is presented which not only covers the essential features of coherent hole structures, but which also enables to make the necessary corrections to the current wave theory. A linear stability analysis for single harmonic waves that successfully incorporates trapped particle effects (in contrast to previous analyses) shows an unconditional marginal stability independent of the drift between electrons and ions, which irrevocably contradicts Landau’s theory. Moreover, holes of negative energy are of particular interest because they act as attractors in the dynamic system. They are the source for the release of further modes and thus increase the level of intermittent turbulence. In summary, pattern formation in collision-free plasmas is inherently nonlinear, kinetic, and extremely diverse. However, to have a satisfactory, if not yet complete understanding of its processes, a twofold paradigm shift is imperative: one from the conventional linear, discrete wave models to the nonlinear wave models dealing with continuous spectra due to trapping and a second from the BGK to the present method for the correct handling of equilibria.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
First, the reader should be aware that they are unlikely to recognize much of what they have learned about electrostatic plasma waves so far, especially from textbooks. One reason for this is that textbooks mainly refer to linear waves but are less communicative when it comes to the real world of pattern formation that is strictly nonlinear without limitation. This reference to linearity is definitely suitable for waves in the fluid description, in which higher amplitude nonlinear waves emanate from the linear ones. In the kinetic Vlasov description, however, the connection between linear and nonlinear solution is lost due to the phase locking of the coherent structures and the associated trapping nonlinearity, which is absent in fluid theory, but kinetically ubiquitous for structures with phase velocities that are not too high. This premise gives the description a new, largely unexplored dimension.
A second reason is that in the past the wrong method was preferred by the community in the nonlinear regime, namely the BGK method (Bernstein et al. 1957). This method has definitely historical merits as it was the first time that a correct Vlasov–Poisson (VP) solution could be obtained by introducing the trapped particle concept. However, as is explained in more detail also later, the BGK method cannot provide a complete solution, since the phase velocity, the second part of a nonlinear solution of not less importance, remains indefinite. A correct phase velocity is, for example, necessary to set up the decisive evolution equation or to decide on the predominant wave energy. In addition, the shape of the electrical wave potential \(\phi (x)\), which is a prerequisite for handling the BGK method, can no longer be specified mathematically for a typical solution namely when more than one trapping scenario is involved.
Linear theory is thus reserved and applicable for specially prepared, calm plasmas. The first experimental verification of Landau/Langmuir waves by (Derfler and Simonen (1966)), by measuring of the Bohm–Gross dispersion and the damping rate, for example, could only be carried out successfully after they had painstakingly (Footnote 1) created the prerequisites for the validity of the Landau theory, namely a quiet background plasma and a perturbation that satisfies the “topological constraint” \(|\partial _v f_1|<<|\partial _v f_0|\) valid at every moment of evolution. For the “nonlinear Landau damping” (NLD) scenario linear theory only applies in the early phase of evolution, i.e. before saturation on a much lower, but nonlinear level (Manfredi 1997). To the surprise of many, the structure is nonlinear in this late, lowest energy state. Note that this latter, dynamically calmer state is absent from the perturbation analysis by (Mouhout and Villani (2011), Villani (2014)Footnote 2) since trapping effects are neglected by them. The scenario of the NLD is hence only completely solved if coherent nonlinear structures, as we will develop in this article, are included, even if Landau’s prerequisites apply initially. Therefore, to achieve consistency in the NLD scenario, it is imperative to consider trapping.
Because of the paramount importance of this observation, we pause briefly to note the following: This development is in blatant contradiction to the standard wave theory practiced up to now, according to which waves with sufficiently small amplitudes can be described linearly and non-linearity only has to be taken into account for larger amplitudes.
If the topological condition is violated, the damping can be very different or even missing (Korn and Schamel 1996a).
In (Bauer and Schamel (1992)), to present a second well-known example, the two-stream instability, the early phase of linearly dominated, but rather violent nonlinear development (described by mode coupling, including mode slaving and the tendency to wave collapse) is replaced by a sudden calming and saturation of the evolution through particle trapping. This calm phase in the structure formation caused by trapping, to say it again, is our concern in a general context beyond the Landau scenario.
In general, linear wave theory describes pretty well incoherent waves of small amplitudes and random phases but has no chance of meeting the abundance of coherent structures that establish in driven, noisy plasmas triggered for example by seeds or eddies. By localized seeds particle trapping is involved from the very beginning and an a priori linearization of the VP system is no longer useful. The Landau theory is therefore not suitable for describing pattern formation caused by seeds.
The correct view, therefore, is that the Vlasov equation, as a nonlinear equation, must first be solved before the small amplitude limit is taken, and not the other way around. In other words: The smallness of a wave has to be seen as a limiting case of the nonlinear solution and not by solving a wrong equation, the linearly truncated Vlasov equation.The good solvability of the linear Vlasov equation does not necessarily offer a valid ticket to the realm of nonlinear structures.
In the current-driven plasma situation, this premise is justified by comparing both solutions, the linear and the nonlinear. In Fig. 2 of (Schamel (2012)), in which the two distributions are compared with one another in the resonant region, the differences are clearly visible. While the nonlinear solution behaves well, the linear solution involves principal value and delta function singularities in the van Kampen case or manipulations of the background distribution(s) at resonance in the Landau case that should mimic trapped particles. These manipulations are artificial, i.e. not carried out correctly to the end and hence miss nonlinear self-consistency. These differences are retained and do not disappear in the infinitesimal amplitude limit. We will address this point again in Section 3.1.
The main goal of the present paper therefore is to provide the reader with the necessary components of a correct nonlinear wave theory.
In this article, the theory of electron-hole equilibria is unfolded in detail, with an emphasis on its occurrence in collision-free, current-carrying, noisy plasmas. It offers new insights into the dynamics of holes triggered by tiny seeds particularly in linearly subcritical plasmas as seen in the numerical simulations of (Schamel et al. (2017), Mandal et al. (2018), Mandal et al. (2020), Schamel et al. (2020a), Schamel et al. (2020b)). It explains why a hole is suddenly accelerated during its evolution and why it settles on the high energy tail of the distribution where the slope is negative, rather than on the low energy, positively inclined tail, i.e. between the ion and the electron peak, as one would expect from a linear perspective. The existence of privileged electron holes, which exist as nonlinear structures up to the infinitesimal amplitude limit, is discussed in detail and further simplified modes are recovered. The appearance of intrinsic substructures in the trapped particle distribution and in the macroscopic particle densities are further new elements that can be understood as well (Schamel et al. 2017; Mandal et al. 2018, 2020; Schamel et al. 2020a, b). Several new solitary wave types are presented and it is proved that the majority of possible solitary wave solutions refer to mathematically undisclosed potentials \(\phi (x)\) (Schamel 2020a, b). Finally, the negative energy concept associated with these modes offers a new avenue of plasma instability triggered by tiny seeds.
2 Theory of electron hole equilibria
To describe the theory as transparently as possible we study in a first step a two-component, current-driven plasma in which trapping effects refer only to the electrons, i.e. we focus firstly on electron trapping effects for electron holes (EHs) propagating in the electron thermal range. In order not to appear too inflated, ions are allowed to be mobile, but without ion trapping (reflection) effects, which are included in a second step later. Instead, we want to get to know the influence of electron trapping as well as possible.The wavelength of the structure is arbitrary at the beginning, but is later assumed to be infinite in the solitary wave limit.
As said, the Schamel method consists in first solving the Vlasov equation before taking the small amplitude limit, and not vice versa. We therefore start with a stationary solution of the full electron Vlasov equation, which reads in the wave frame where the structure is at rest: \((v\partial _x + \phi '(x) \partial _v)f_e(x,v)=0\). It is solved by any function of the single particle energy \(\varepsilon :=\frac{v^2}{2}-\phi (x)\) valid for the whole velocity range. For free particles there is another (discrete) constant of motion, the sign of the velocity \(\sigma :=v/|v|\), which is needed for traveling holes having a nonzero phase velocity \(v_0\). This, together with the requirement that the electrons without loss of generality obey a shifted Maxwellian in the undisturbed case, results in the following Schamel distribution (Schamel 1972a, 2000, 2020a, b) :
where \(\gamma ,\chi _1, \chi _2, \beta , \zeta\) are free parameters representing the contributions of the trapping scenarios under consideration. The corresponding part of \(f_e(x,v)\) is further on called \(f_{et}(\sqrt{-\varepsilon })\). In this equation \(\theta (x)\) represents the Heavyside step function. We use normalized quantities such that the velocity is normalized by the (unperturbed) electron thermal velocity, the electron potential energy by the electron thermal energy, and the space by the Debye length.
Note that (1) is preceded by two distribution functions. One of them was presented by (Gurevich (1968)), another one by (Montgomery and Joyce (1969)). With his constant distribution for trapped electrons, Gurevich could at least anticipate the \(sech^4\) profile of a solitary wave, although the chosen distribution later turned out to be unsuitable for getting a phase velocity. Montgomery and Joyce, on the other hand, referred for the first time to shifted Maxwell distributions for untrapped electrons and derived double-layer solutions. Due to the application of the BGK method, however, their solutions appear less significant.
Equation (1), to continue, comes from the Galilean shift \({\tilde{v}}_D\) of the Maxwellian given in the unperturbed case by \(f_M(v)=\frac{1}{\sqrt{2\pi }} e^{- (v- {\tilde{v}}_D)^2/2}\) and from the replacement of v by \(\sigma \sqrt{2\varepsilon }\) as an effect of the perturbation. This holds for \(\varepsilon >0\), which represents the free electron region. The gap in between \(\sigma >0\) and \(\sigma <0\) , when \(\varepsilon \le 0\), refers to trapped electrons. The distribution \(f_e(x,v)\) is thus a function of the two constants of motion, \(\epsilon\) and \(\sigma\), and consists of two parts, the contribution of untrapped particles, \(\varepsilon >0\), and the one of trapped particles, \(\varepsilon \le 0\). Trapping is therewith controlled by the five parameters \(\gamma\), \(\beta\), \(\zeta\), \(\chi _1\), \(\chi _2\), the first three refer to a perturbative treatment of trapped particle effects and represent the first three elements of a Taylor expansion around \(\sqrt{-\varepsilon }=0\) of a more general, exponential \(f_{et}(\sqrt{-\varepsilon })\), whereas the fourth and fifth, \(\chi _1\) and \(\chi _2\), are definitely non-perturbative in nature. Note that \(f_e(x,v)\) is continuous across the separatrix and it is assumed that \(0 \le \phi (x) \le \psi<<1\).
The electron density \(n_e(\phi )\) is obtained by a velocity integration.
We mention in passing that studies of finite amplitude, \(\psi \simeq O(1)\), electron holes and strong double layers (Bujarbarua and Schamel 1981; Schamel and Bujarbarua 1983) use a similar but unexpanded distribution of trapped electrons in which case Schamel’s functions \(\mathcal {K}(x,y), \mathcal {H}(x,a,b)\), defined, e.g. in (Schamel (1972a), Bujarbarua and Schamel (1981), Schamel (1982b), Das and Schamel (2005)), are involved. Here we restrict our analysis to weak solutions, \(\psi<<1\). It can either be done by the velocity integration of (1) first and a subsequent Taylor expansion, using \(\phi<<1\), as done, e.g. in (Schamel (1972a), Schamel (1979), Schamel (1982b), Schamel (1986)) or by the Taylor expansion of (1) first, followed by the velocity integration, as done, e.g. in (Schamel (1973), Schamel (1975), Korn and Schamel (1996a), Schamel (2020b)). Both cases yield the same result:
where \(A:=(\Gamma +\frac{a_1}{2}D_1 +a_2D_2)\), \(B:=\frac{16}{15} b(\beta , {\tilde{v}}_D) \sqrt{\psi }\) with \(b(\beta , {\tilde{v}}_D):= \frac{1}{\sqrt{\pi }} (1- \beta - {\tilde{v}}_D^2)e^{- {\tilde{v}}_D^2/2}\) and
\((\Gamma , C, D_1, D_2):=\frac{ \sqrt{\pi }}{2} e^{-\frac{{\tilde{v}}_D^2}{2}}(\gamma , \frac{3\zeta }{4}, \chi _1, \chi _2)\). The constants are given by \(a_1= 2(1-2\ln 2)=-0.773\) and \(a_2=-2+\ln 4(\ln 4-2)+\pi ^2/3 =0.439\). The other quantities are defined by
The function \(Z_r'(x)\) represents the derivative with respect to x of the real part of the plasma dispersion function (Fried and Conte 1961) and is plotted for real x in Fig. 1:
Its zero at \(x=0.924\) will play later an important role in the definition of the “Slow Acoustic Modes”. As usual, prime is defined in the present context as the first derivative with respect to the argument.
Note that all trapping parameters \((A,B,C,D_1,D_2 ; \Gamma )\) in (2) carry the factor \(e^{- {\tilde{v}}_D^2/2}\), i.e. they vanish in the large \(|{\tilde{v}}_D|\) limit.They therefore only influence the pattern formation for moderate and small values of \(|{\tilde{v}}_D|\). As expected, their influence on high-speed Langmuir waves is therefore negligible.
Before we go any further, let us secure this density expression by referring to known special cases.
In case of \(k_0=0\), \({\tilde{v}}_D\)=0 and of zero trapping parameters we find by utilizing \(-\frac{1}{2}Z'_r(0)=1\) and \(-\frac{1}{2}Z'''_r(0)=-4\) the well-known Boltzmann expression for \(n_e(\phi )\): \(n_e(\phi )= 1 + \phi + \frac{1}{2} \phi ^2 + ..\). This particularly confirms the last term in (2) contrary to a different statement found in the literature (Hutchinson 2017).
If we keep (\(k_0\), \({\tilde{v}}_D\), B) but neglect (\(\Gamma\),C, \(D_1\),\(D_2\)) we get
which is identical with (3.9) of Korn and Schamel (1996a). And last but not least, if we just keep \((\Gamma ,D_1,D_2)\) as non-zero, we get
which is the expression (2) of (Schamel (2020a)).
For the ion density we take an expression that incorporates \(O(\psi ^2)\) terms but neglect ion trapping effects and refer to a straightforward extension that reduces to the known expressions in limiting cases:
It reduces in the \(u_0 \rightarrow 0\) limit to \(n_i=1 -\theta \phi +\frac{(\theta \phi )^2}{2} \approx e^{-\theta \phi }\), the expected Boltzmann value. On the other hand, in the “cold ion” or large \(u_0\) limit we receive \(n_i=1 +\frac{\theta \phi }{u_0^2} +\frac{3(\theta \phi )^2}{2u_0^4} \approx \frac{1}{\sqrt{1-\frac{2\theta \phi }{u_0^2}}}\) valid under the constraint \(|\theta \phi /u_0^2|<<1\).
Later in Section 7 we will turn to a more general ion density that also includes ion trapping effects. Notice that the immobile ion case is automatically included in \(n_i\), namely by setting \(\theta =0\).
It should be emphasized that these density expressions are permissible since they are derived from solutions of the Vlasov equation. This is in contrast to some previous publications where the \(\phi\)-dependence is simply imposed without guaranteeing that a valid distribution, especially that for free and trapped particles, stands behind. As long as this justification is lacking, these theories remain essentially unfounded (Cairns et al. 1995; Mamun and Cairns 1996; Guio et al. 2003). Nevertheless, such “theories” may be sometimes useful and more sensitive of an issue and provide good approximations and even predictions of later experimental observations, despite missing more or less justification behind each and every hypothesis.
As said, in case of finite amplitudes and Maxwellian plasmas Schamel’s functions \(\mathcal {K}(x,y), \mathcal {H}(x,a,b)\) (Schamel 1972a; Bujarbarua and Schamel 1981; Schamel 1982b; Schamel and Bujarbarua 1983; Das and Schamel 2005; Goswami et al. 2008) are involved; for nonextensive distributions, however, such as \(\kappa\)-distributions (e.g. Tribeche et al. 2012), a corresponding extension is still missing.
After insertion of the densities (2) and (3) into Poisson’s equation, \(\phi ''(x) = n_e(\phi ) - n_i(\phi )=:- {\mathcal {V}}'(\phi )\), where in the last step the pseudo-potential \({\mathcal {V}}(\phi )\) has been introduced, we get (ignoring a term of \(O(\psi ^2)\) connected with \(k_0^2\))
and by integration with \(\mathcal {V}(0)=0\)
which we abbreviate as: \(-\mathcal {V}_0(\phi )\) since it is used only temporarily. In (5) we have also introduced the quantity \({\tilde{C}}\) which is defined by
(5) reduces to the known expression (4) of (Schamel (2020b)) in case of immobile ions ( \(\theta =0\)), of (\(D_1=D,D_2=0\)) and of a negligible \(O(\phi ^3)\) term.
The necessary constraint of a second zero of \({\mathcal {V}}_0(\phi )\), at \(\phi =\psi\), yields
This expression is identical with (5) of (Schamel (2020a)) and (5) of (Schamel (2020b)) in the appropriate limits. It represents the equation for determining the phase velocity \(v_0\) as a function of the other parameters and is hence the nonlinear dispersion relation (NDR), a relation of eminent importance.
Replacing the first big bracket of (5) by (6) we get:
where r is \(r:=1-a_1 -2\ln \psi =1.773 - 2\ln \psi\). In this form \(\mathcal {V}(\phi )\) automatically satisfies \(\mathcal {V}(\psi )=0\), a form we will call canonical.
To obtain finally the shape \(\phi (x)\) we have to invert
which follows by a quadrature from the pseudo-energy : \(\frac{\phi '(x)^2}{2} + \mathcal {V}(\phi )=0\). The latter itself is derived from Poisson’s equation.
While (6) is the equation that determines the phase velocity \(v_0\), it is (7) that delivers through (8) the wave structure \(\phi (x)\), provided that the integral in (8) and the inversion can be accomplished by known mathematical functions otherwise one has to deal with a numerical evaluation of them.
An important feature of this system is that \(\Gamma\) (or A, respectively) no longer occurs in (7). This special trapping scenario therefore has no influence on the shape. Rather, it is this continuous variable that accounts for the phase velocity \(v_0\) that accordingly belongs to a continuous dispersion relation.
The presence of \(\Gamma\) (or A) in the NDR (and its disappearance in \(\mathcal {V}(\phi )\)) has an interesting consequence. For a given shape \(\phi (x)\) that is determined by the pseudopotential, it provides a continuous band of phase velocities \(v_0\) around the Landau resonance (\(\Gamma =0\)), i.e. it broadens the resonance similar but different to the continuous van Kampen spectrum. In other words, our theory provides the coherent, nonlinearly admissible version of Dupree’s (Dupree 1966, 1972) and Weinstock’s (Weinstock 1968 Weinstock (1968)) resonance broadening and clump theory, which is a perturbation theory that is based on linear, random waves and involves wave-particle scattering and mode coupling effects (Krommes 2015).
It is easily seen that the parameter \(k_0\) stands for periodic waves, namely either from \(\mathcal {V}(\phi )\) or directly from Poisson’s equation. The curvature of \(\phi\) : \(\phi ''(x)=n_e -n_i\), which becomes \(\rightarrow k_0^2\psi\) as \(\phi \rightarrow 0\), vanishes in the solitary wave limit \(k_0 \rightarrow 0\), noting that \(\phi =0\) is the potential minimum. Otherwise the structure is periodic. It is, however, not necessarily the actual wave number k which is defined by \(k=\frac{\pi }{L}\) where 2L is the actual wavelength. The correct relation between k and \(k_0\) is found by the overall charge neutrality condition and becomes (Das et al. 2018; Borah et al. 2018):
where \(\mathcal {N}(k_0, B,...; \varphi ) :=\frac{1}{\psi }\sqrt{-2 \mathcal {V}(\psi \varphi )}= \sqrt{k_0^2\varphi (1-\varphi ) + \varphi ^2 [B(1-\sqrt{\varphi }) + ...]}\) and where the dots stand for the remaining terms in \(\mathcal {V}(\phi =\psi \varphi )\).
Equations (6)–(9) constitute our main result in its most general form.
We emphasize that \(\mathcal {V} (\phi )\) consists of 5 independent contributions, each of which stands for a certain mode structure. Whereas \(k_0\) alone stands for the harmonic wave (or more generally in combination with the other parameters for periodic waves, as said), the other 4 themselves represent specific solitary waves.
It is this central functionality that gives us the opportunity to denote them by an own name: elementary modes. With all 5 terms, however, when playing independently an active role in \(\mathcal {V}(\phi )\), we have through all possible combinations a manifold of 31 (\(\sum _{i=1}^{5}\frac{5!}{i! (5-i)!}\)) wave modes of different provenance (5 single, 10 double, 10 triple, 5 quadruple and 1 quintuple combination(s)), a rather astonishing and up to now unknown variety. In principle the number of modes is doubled by the fact that besides \(k_0=0\) there exists a second limit for \(k_0\) which provides solitary modes (see Sect.4.1 and Sect.5).
Unfortunately most of them are mathematically undisclosed because \(\phi (x)\) can no longer be found analytically. This typically holds when 3 or more combinations are involved, but also some of the double combinations suffer the same fate. Fortunately, all of the elementary modes \(\phi (x)\) can be expressed and analyzed mathematically, an additional signature of their fundamental role. We should however stress that the choice of elementary functions is not unique, as for example other non-perturbative trapping scenarios could be selected and added as well (Schamel 2020a, b).
In the context of the nonlinear world of structure formation, these elementary modes offer via these possible combinations a kind of \({\textbf {superposition}}\) \({\textbf {principle}}\) on the \(\mathcal {V}(\phi )\) level that enable us to get new members, somehow analogous to the superposition principle in linear wave theory. Or more precisely, within the class of potential structures \(\phi (x)\) of given \(\phi _{min}=0\) and \(\phi _{max}=\psi\), the linear combination of two different pseudo-potentials \(\mathcal {V}_1(\phi )\) and \(\mathcal {V}_2(\phi )\) with corresponding \(\phi _1(x)\) and \(\phi _2(x)\) result in a third, \(\phi _3(x)\), which is provided by \(\mathcal {V}_3(\phi )=\mathcal {V}_1(\phi ) +\mathcal {V}_2(\phi )\). This applies as long as the differences in \(\phi _1(x)\) and \(\phi _2(x)\) caused by different trapping parameters are also taken into account in the new NDR valid for \(\phi _3(x)\).
3 The gallery of elementary modes
3.1 The harmonic mode (single wave)
The harmonic, monochromatic or single wave is obtained when \((B,{\tilde{C}},D_1,D_2) \rightarrow 0\). In all five examples, however, we will keep the \(\Gamma\) trapping term which appears in the NDR only. We then have from (7), (8) and by inversion of (8)
The surprising property of this mode is that it remains nonlinear up to the infinitesimal amplitude limit \(\psi \rightarrow 0^{+}\) (Schamel et al. 2020b). The reason is that as long as \(\psi \ne 0\), there exists a non-vanishing trapping area of width \(2 \sqrt{2 \phi }\) in phase space in which \(f_{et}\) behaves regularly. As seen from (1) \(f_{et}\) neither collapses to a \(\delta\)-function (van Kampen) nor does it become a singular principal value function or the more regularized perturbed function that is forced by an artificial and therefore unrealistic flattening of \(f_0 (v)\) at resonance (Landau). In our theory, in which these singularities or artificial interventions are obviously missing, the functional space is well posed.
Consequently, all linearly based single-wave models, as examined exemplarily in (Balmforth, Morrison, Thiffeault 2013 [1]) as an extension of Landau or van Kampen, belong to this category of nonlinearly invalid models and must therefore be discarded.
The NDR (6) becomes in this non-perturbative harmonic wave limit:
Our mode is therefore the correctly upgraded, nonlinear counterpart to Landau (\(\Gamma =0\)) and to van Kampen (\(-\Gamma =\lambda\)). It is moreover for \(\Gamma =0\) the well-known “Thumb-Teardrop” DR which has been studied for \(v_D=0\) in detail by (Trivedi and Ganesh (2018)) mistakenly believing that it is a linear DR. As explained by the author in a comment in (Schamel (2019)), it makes sense only in the nonlinear regime, although formally it exists linearly, too.
On the other hand, a \(\Gamma \ne 0\) provides a new parameter resulting in a continuous spectrum of possible solutions, analogous but of course different to the continuous linear spectrum of van Kampen.
The existence condition for the harmonic wave is that all trapping parameters are zero (except \(\Gamma\)). This particularly means that \(B \sim (1-\beta - {\tilde{v}}_D^2) e^{-{\tilde{v}}_D^2/2} =0\). This is satisfied either for large \(|{\tilde{v}}_D|\) by the exp-function (Langmuir mode) or by \(\beta =1-{\tilde{v}}_D^2\) in case of finite or small values of \(|{\tilde{v}}_D|\). Since the latter is typically larger than unity the trapping parameter \(\beta\) is a negative quantity corresponding to a hole in phase space. The assumption of a flat trapped region, \(\beta =0\), as often anticipated in the literature (e.g. Landau–Lifshitz and related literature), is hence generally inconsistent.
We hence have to conclude that there is no linear analogon of the harmonic wave that can account for the microscopic details.
The two worlds of linear and nonlinear Vlasov equilibria are disconnected with no connection (bridge) between them.
The fact that they agree macroscopically (in shape and velocity for vanishing \(\Gamma\)) does not imply that they are also identical microscopically.
As will be pointed out in detail later (Sect.7.2) this mode is linearly marginally stable (Schamel 2018) for all \(v_D\) in strong contradiction to Landau’s theory. There is no critical drift velocity \(v_D*\) which discriminates between damped and growing perturbations of harmonic equilibria. All harmonic or single mode equilibria, due to their nonlinear character, turn out robust to linear perturbations and propagate undamped with respect to small linear perturbations independent of \(v_D\). If there is any growth it must be due to the higher harmonic part of the spectrum, such as in cnoidal or solitary waves.
It is moreover easily seen that \(k=k_0\) for this harmonic mode, i.e. \(k_0\) is already the exact wavenumber.
3.2 The privileged \({{\,\textrm{sech}\,}}^4(x)\)-solitary mode
The four remaining modes are obtained by setting \(k_0=0\). They are hence solitary in character. We get from (7),(8), by letting \(({\tilde{C}}, D_1,D_2) \rightarrow 0\) the following three expressions:
where the last term represents the shape and follows by inversion of \(x(\phi )\). It must hold: \(B>0\) which determines for given \({\tilde{v}}_D\) the parameter \(\beta\).
This special shape has been known since the earliest times of structure formation (Gurevich 1968; Schamel 1972a, 1973, 1979, 1982b, 1986).
In contrast to the next two solitary modes, which rest on a logarithmic trapping scenario, it stays existent in the low amplitude limit, representing a privilege for this mode.
The phase velocity \(v_0\) is obtained by the NDR (6)
which has depending on B and \(\Gamma\) a wide range of particularly interesting solutions for current-carrying plasmas, as shown next. The only condition is that \(B>0\) whereas \(\Gamma\) can carry either sign. The general solution requires numerical means especially for the continuous branches which, due to B and \(\Gamma\), are a bit more complex than the already complex Thumb-Teardrop DR.
We choose for demonstration two branches that are far apart.
-
(i)
the slow electron acoustic wave branch (SEAW)
This branch is obtained by assuming \(|{\tilde{v}}_D|\sim O(1)\) and \(|B-\Gamma |<<1\) in which case all three terms in (13) are small. Making use of the Taylor expansion of the \(Z_r'(x)\) function: \(-\frac{1}{2} Z_r'(\frac{ {\tilde{v}}_D}{\sqrt{2}}) \sim \frac{1.307 -|{\tilde{v}}_D|}{1.307}\) and of \(\frac{1}{2} Z_r'(\frac{u_0}{\sqrt{2}}) \sim \frac{\delta }{\theta v_0^2}<< 1\) we get \(|{\tilde{v}}_D| = 1.307 ( 1 - B + \Gamma )\). This mode is hence placed on both sides of the shifted Maxwellian at a distance of 1.307 and the phase velocity \(v_0\) is given by \(\qquad v_0= v_D \pm 1.307 (1- B + \Gamma )\).
This mode is acoustic-like and was termed \({\textbf {slow}}\) \({\textbf {electron}}\) \({\textbf {acoustic}}\) \({\textbf {wave}}\) (SEAW) in analogy to the slow ion acoustic wave (SIAW) occurring in the ion case, where the notion “ion acoustic wave” (IAW) has already been taken for the known linear branch (Schamel 1986). Hence the expression “electron acoustic wave” for this mode, as used in the literature, is at least misleading. But it is also wrong because no linear electron acoustic wave exists, as long as one disregards anisotropic temperatures or other background deviations.
In Sect. 4.1 we will treat the periodic extension of this solitary hole, the cnoidal electron hole, for which \(k_0^2 \ne 0\).
-
(ii)
the ion acoustic wave branch (IAW)
In this case \(|{\tilde{v}}_D| \sim O(\sqrt{\delta })<<1\) and \(u_0 \sim \sqrt{\theta }>>1\), i.e. we assume \(\theta>>1\). The Taylor expansions yield \(-\frac{1}{2} Z_r'(\frac{ {\tilde{v}}_D}{\sqrt{2}}) = 1 - {\tilde{v}}_D^2\) and \(\frac{1}{2} Z_r'(\frac{u_0}{\sqrt{2}}) \sim u_0^{-2}\) from which follows \(\qquad u_0=\sqrt{\theta } (1 + \frac{B-\Gamma }{2})\),
which is the ion acoustic branch corrected by B and \(\Gamma\).
The evolution equation for which (12) is a stationary solution is of Schamel type and becomes (assuming \(v_D=0\)) for the SEAW branch (see (17) of Schamel (2020b))
and for the IAW branch (see(49) of (Schamel (1972a)) or (15) of (Schamel (1973))
in which we renormalized t (\(t \rightarrow \sqrt{\delta } t\)), i.e. time is now normalized by the ion plasma frequency. Both equations are of Schamel type and make it possible to track evolutionary changes in the privileged solitary wave during its propagation, especially when overtaking processes or frontal collisions in case of several humps occur.
We, moreover, quote that with (13) the electron density gets the simpler form:
The density expressions for \(n_e\) in (16) and for \(n_i\) in (3) make it easier to approach the measured structures already on the macroscopic level by considering the curvature of \(n_{e,i}\) at potential maximum.
Since it holds \(n_s'(x)=n_s'(\phi )\phi '(x)\) and \(n_s''(x)=n_s''(\phi )\phi '^2(x) + n_s'(\phi )\phi ''(x)\), \(s={e,i}\), it follows that \(n_s''(x=0)=n_s'(\psi )\phi ''(0)\) which is true because of \(\phi '(0)=0\). With \(\phi '' (0) <0\) we see that the sign of \(n_s' (\psi )\) determines the curvature of \(n_s (0)\) in the center, \(s = {e, i}\).
For the ion density we get from (3): \(n_i'(\psi )=\frac{\theta }{2}Z_r'(\frac{ u_0}{\sqrt{2}})\) and for the electron density from (16): \(n_e'(\psi )=\frac{\theta }{2}Z_r'(\frac{ u_0}{\sqrt{2}}) - \frac{7}{8}B\). When the SEH is propagating at ion acoustic speed, i.e. \(\frac{1}{2}Z_r'(\frac{ u_0}{\sqrt{2}})>0\), the curvature of \(n_i(x)\) is unconditionally negative at x=0, whereas \(n_e(x=0)\) changes its sign from negative to positive when B exceeds \(B_c:=\frac{4\theta }{7}Z_r'(\frac{ u_0}{\sqrt{2}})>0\).
The ion density is therefore bell-shaped in x under all circumstances, while the electron density gets a central depression when B exceeds \(B_c\).
As an application we refer to the series of subcritical plasma simulations by (Schamel et al. (2017), Mandal et al. (2018), Mandal et al. (2020), Schamel et al. (2020a), Schamel et al. (2020b)), in which the latter case was omnipresent in all cases considered. As an example we refer to Fig.`1 of (Schamel et al. (2020b)) and the corresponding data:
The NDR (13) is satisfied for \(B=0.48 +\Gamma\) which, due to the presence of a central depression in \(n_e\), has to be larger than \(B_c= 0.59\) from which we conclude that \(\Gamma\) has to exceed 0.11: \(\Gamma >0.11\). In theses simulations the \(\Gamma\) trapping scenario was automatically activated in all runs, which we hence can conclude already on the density, i.e. on the macroscopic level.
The microscopic details still depend on the parameter B. For \(B=1>B_c=0.59\) we get from the B formula:
\(B:=\frac{16}{15} b(\beta , {\tilde{v}}_D) \sqrt{\psi }\) with \(b(\beta , {\tilde{v}}_D):= \frac{1}{\sqrt{\pi }} (1- \beta - {\tilde{v}}_D^2)e^{- {\tilde{v}}_D^2/2}\) and by use of the above data the corresponding value for \(\beta\): \(\beta =-230\). The electron distribution is therefore rather strongly depressed at resonance, a fact that has also be seen numerically, see, e.g. Fig. 5 of (Schamel et al. (2020b)).
However, we should remind the reader that this is not evidence that the identification of the structure is unambiguous, as other trapping scenarios, or combinations thereof, may also be responsible for the settled structure (Schamel et al. 2020a; see also later Sect.4.3, Figs. 4 and 5).
3.3 The Gaussian \(e^{-x^2}\)-solitary mode
In this case \(\Gamma\) and \(D_1\) are the only non-vanishing parameters and we get (Schamel et al. 2020a, b)
valid for \(D_1<0\). This special solitary wave which has mainly been used by space plasma physicists to interpret their data are non-perturbative in nature. This implies that it has no zero-amplitude limit in contrast to the previous privileged \({{\,\textrm{sech}\,}}^4(x)\) solitary electron hole (SEH) as seen by the nonlinear dispersion relation (NDR) which becomes:
B in (13) is, therefore, replaced by \({\hat{B}}:= -D_1(\ln \psi -0.887)\) in (18), which is a negative quantity for small \(\psi\). The discussion of the NDR is, therefore, pretty much the same as the previous one. The only difference is that the new \({\hat{B}}\) is negative instead of positive which can, however, easily be compensated by \(\Gamma\).
Again we can attribute a SEAW branch for which \(\qquad v_0= v_D \pm 1.307 (1- {\hat{B}} + \Gamma )\) and an IAW branch for which \(\qquad u_0=\sqrt{\theta } (1 + \frac{{\hat{B}}-\Gamma }{2})\), and discuss the role of \(\Gamma\).
The evolution equation that relates to the SEAW branch is (see (17) of (Schamel (2020b)))
and similarly for the IAW branch.
Note that the competition between the two solitary structures, B and \({\hat{B}}\), was discussed in (Schamel et al. (2020a)) to explain a numerically measured structure. The first indication of a logarithmic dependence of the trapped electron distribution in the case of a Gaussian SEH was given by (Schamel (1972b)). To distinguish it from other evolution equations we may call it logarithmic Schamel-type equation.
3.4 The second-order Gaussian \(e^{-\sinh ^2(x)}\)-solitary mode
In this case \(\Gamma\) and \(D_2>0\) are non-zero and we get (Schamel 2020a)
where \(r:=1.773-2\ln \psi\). This mode was first considered by the author in (Schamel (2020a)). With this solution we can compare a second, independent, non-perturbative trapping scenario with the usual Gaussian scenario. The effect is that x in the latter simply has to be replaced by \(\sinh (x)\) to arrive at the new structure. That’s why we call it quasi-Gaussian. As extensively investigated in (Schamel (2020a)), it has essentially the same properties as the usual Gaussian SEH and can therefore explain an observation in the same way as the Gaussian.
The NDR becomes:
where \(\hat{ \hat{ B}}:= D_2(-1.326 +1.773 \ln \psi -\ln ^2\psi )\). This variable now takes on the role of B in the NDR discussion, which we leave to the reader. It is clear again that a transition \(\psi \rightarrow 0\) is impossible. Seeds of this type do not allow solutions with infinitesimal amplitudes.
The second-order logarithmic Schamel-type evolution equation reads in this case for the SEAW branch
where \({\hat{r}}= 1 + 2 \ln \frac{\psi }{4}\) and \(\hat{{\mathcal {A}}}\) is an extension of the constant, \(D_2\) independent term in the factor of \(\phi _x\) in (19) inclusively \(\Gamma\), to be derived by the reader.
In the next chapter we will show that the simultaneous presence of \(D_1\) and \(D_2\) belongs to the class of disclosed solutions \(\phi (x)\), i.e. an explicit \(\phi (x)\) can be presented for this pair of trapping scenarios (see Sect.4.3).
3.5 The \({{\,\textrm{sech}\,}}^2(x)\) soliton
In this final case, all trapping terms are assumed zero except (\(\Gamma ,{\tilde{C}}\)). We hence get:
where \(q:=-{\tilde{C}}\psi\) and a solution exists as long as \(q>0\).
The corresponding NDR reads:
The discussion of the NDR therefore proceeds as in III.2 including the two branches SEAW and IAW. We just need to replace B with q, both of which must be positive. Of particular interest is the case of no \(\zeta\)-trapping scenario (C = 0) for which we get: \(q=\frac{1}{24}\bigg (\theta ^2 Z_r'''(\frac{u_0}{\sqrt{2}})-Z_r'''(\frac{{\tilde{v}}_D}{\sqrt{2}})\bigg )\psi\).
For the SEAW branch, \(|{\tilde{v}}_D|=O(1), u_0>>\sqrt{\theta }\), we then get \(q=\bigg (\frac{\theta ^2}{u_0^4} +\frac{1}{6}\bigg )\psi \approx \frac{\psi }{6} >0\) which means that a positive q is automatically satisfied.
For the IAW branch, when it holds \(|{\tilde{v}}_D|=O(\sqrt{\delta }), u_0 \sim \sqrt{\theta }\) and \(v_D=0\), we have \(q=(\frac{\delta ^2}{v_0^4} -\frac{1}{3})\psi =2\psi /3>0\) which is positive either. The common ion acoustic soliton is hence represented by (23). In this case, \(n_e=1 + \phi + \phi ^2/2 +..\) and \(n_i=1 + \phi +3\phi ^2/2 +...\) and we have a complete match with the macroscopic fluid result which is thus recovered within the limits taken. The evolution equation in the IAW case, for which (23) is a solution, is given by
where again time is renormalized by the ion plasma frequency (i.e. \(t \rightarrow \sqrt{\delta } t\)). This is (for \(\Gamma =0\)) the well-known, integrable Korteweg–de Vries equation.
We however stress that microscopically we have an abundance of \({{\,\textrm{sech}\,}}^2\)-solutions belonging to the continuous spectrum not only because \(\Gamma\) may be nonzero but also because of the various additional continuous solutions to the NDR that supplement the SEAW and IAW analytical approach. Moreover, since \(q=-{\tilde{C}} \psi =-\psi \bigg ( \frac{2C}{3} +\frac{1}{24}[ Z_r'''(\frac{ {\tilde{v}}_D}{\sqrt{2}}) -\theta ^2 Z_r'''(\frac{ u_0}{\sqrt{2}})] \bigg )\) there is through the \(Z_r'''\) terms always a nonzero contribution to \({\mathcal {V}}(\phi )\) which stems from the free electron and ion distributions, respectively, even when \(C=2 \zeta /3\) is negligible. Therefore, even if all trapping scenarios are negligible (\(\gamma = \beta = \chi _1=\chi _2= \zeta =0\)) we still have a finite trapped electron region of width \(2\sqrt{2}\psi\) where \(f_{et} \sim \{ 1+...\}\) is nonzero and the \(sech^2\)- solution keeps his microscopic nature. In VP plasmas inhomogeneous equilibria are intrinsically nonlinear and of course microscopic. The embedding of the \({{\,\textrm{sech}\,}}^2\)-fluid solution in the continuous spectrum has to be seen this way, namely as a special microscopic solution. A proof of its existence can hence only be given kinetically.
This section was devoted to isolated single trapping scenarios yielding to what we called elementary modes. As said, by combinations new solutions can be obtained. In the next section examples are presented in which two trapping scenarios are in action at the same time and which lead to new patterns through suitable combinations. As before, \(\Gamma\) is treated independently, since it has disappeared in \({\mathcal {V}} (\phi )\). Three of the possible combinations will have disclosed potentials \(\phi (x)\), whereas one will appear with an undisclosed \(\phi (x)\).
4 Holes caused by two trapping scenarios
4.1 The cnoidal electron hole (CEH) and the solitary hole (SEH) of negative polarity
Periodic EH solutions are obtained by non-zero (\(k_0, B\)) in (7) with vanishing (\(D_1, D_2, {\tilde{C}})\). The trapping scenario \(\Gamma\) in A is retained to obtain maximum variability of the possible phase velocities. We then have from (7):
As shown in (Korn and Schamel (1996a)), equations (3.24)-(3.29), there exist three different regions in which \(\phi (x)\) is represented by Jacobian elliptic functions. They are distinguished by the parameter \({\hat{L}}:=\frac{k_0^2}{4B}\) and are given by : \({\hat{L}} < -\frac{1}{8}\), \(0 \le {\hat{L}} \le 1\), and \(1 < {\hat{L}}\). This implies that negative Bs are now admitted.
Before we continue with the discussion of possible potential profiles \(\phi (x)\), we briefly discuss the nonlinear dispersion relation (NDR) belonging to (26). It reads in the case of immobile ions (\(\theta =0\)), vanishing drift (\(v_D=0, |{\tilde{v}}_D|=v_0\)) and vanishing trapping parameters (\(\Gamma ,A,D_1,D_2,{\tilde{C}}\)) (see (6)): \(k_0^2 -\frac{1}{2} Z_r'(\frac{ v_0}{\sqrt{2}})= B\) and has been discussed thoroughly in Schamel (2012). Fig. 2 (which is identical with Fig. 5 of Schamel (2012)) shows \(\omega _0:=k_0v_0\) as a function of \(\sqrt{2} k_0\).
The special case \(B=0\) represents the Thumb-Teardrop dispersion relation in the immobile ion limit. Note that for \(B>0\) there is a cut-off at lower \(k_0\) given by \(\sqrt{B}=k_0\). The dashed line separates fast from slow waves and is defined by the minimum of \(-\frac{1}{2} Z_r'(\frac{ v_0}{\sqrt{2}})=-0.28\) (see Fig. 1) and yields \(v_0/\sqrt{2}=1.5\). For the slow mode branch we get in the small \(k_0\) limit and for \(B>0\) the phase velocity \(v_0=1.307(1-B)\) which is termed Slow Electron Acoustic Wave (SEAW).
Another characterization, with which we continue our potential profile discussion, can be done by the “steepening” parameter \(S:={\hat{L}}^{-1}\) , (Schamel (1972a)), which varies between -8 and infinity : \(-8 \le S \le \infty\). From \(n_e\) it is seen that one has rarefactive waves when \(S \ge 0\) and compressional waves when \(S<0\). \(S\rightarrow 0\) yields the harmonic wave (10) (no steepening!), and \(S\rightarrow \infty\) results in the hump-shaped solitary EH (12) (maximum steepening!).
Of interest is the lower limit of S: \(S=-8\) or \(B=-2k_0^2\), in which case (26) becomes
\(-\mathcal {V}(\phi )= \frac{k_0^2}{2\sqrt{\psi }}( \phi \psi ^{3/2} -3\phi ^2 \psi ^{1/2}+ 2 \phi ^{5/2}) =\frac{k_0^2 \psi ^2}{2} \varphi (1-\sqrt{\varphi })(1+\sqrt{\varphi } -2\varphi )\) where \(\varphi :=\phi /\psi\). The last expression shows that \(\mathcal {V}\) has a double zero at \(\varphi =1\).
The corresponding \(\phi (x)\) becomes for \(x \ge 0\):
\(\phi (x)= \psi \bigg [\frac{2\sinh \zeta (2\sinh \zeta +\sqrt{3}\cosh \zeta )}{(\sinh \zeta + \sqrt{3} \cosh \zeta }\bigg ]^2\) where \(\zeta :=\frac{\sqrt{3} k_0x}{4}\). It is given by (3.33) in (Korn and Schamel (1996a)) and is rederived in Appendix A, in which we offer an expression that is valid for arbitrary x:
where \(\zeta _0:= \tanh ^{-1} (\frac{1}{\sqrt{3}})=0.65848\).
Figure 3, in which \(\varphi =\phi /\psi\) is plotted in the interval \(-3\le \zeta \le +3\), shows that it has an unexpected negative polarity like a solitary ion hole (Schamel and Bujarbarua 1980; Bujarbarua and Schamel 1981).
We mention that in a recent statistical analysis of more than two thousand “bipolar electrostatic solitary waves” (ESW) Wang et al. (2021) collected from ten quasi-perpendicular Earth’s bow crossings, about 95\(\%\) of the ESWs were found of \({\textbf {negative}}\) polarity. Since the phase velocities were in the order of the local ion-acoustic velocity, the authors argued that these must have been solitary ion holes (Schamel and Bujarbarua 1980; Bujarbarua and Schamel 1981). This determination is too premature, however, as SEHs of negative parity can also come into question, as presented in this section. This interpretation is possibly as relevant as the ion hole interpretation since linear ion–ion streaming instabilities are not necessarily required for both. We remind the reader that Landau theory must not necessarily hold for holes growing out of seeds, but of course larger drifts facilitate their excitation.
Altogether, there is, therefore, an abundance of cnoidal hole solutions that are characterized by a single parameter S and that become solitary-like at both borders with opposite polarity.
The phase velocity \(v_0(u_0)\) follows from the NDR (6), which becomes
It is, therefore, of the same type as the previously discussed cases and the continuous spectrum is again controlled and expanded by the additional trapping parameter \(\Gamma\).
The last step in (28) applies to \(S = -8\), to which we now turn our attention. We provide the corresponding densities and phase velocities for the two analytic branches SEAW and IAW.
For SEAW, when to lowest order \(|{\tilde{v}}_D|\sim 1.307\) and \(u_0\sim \sqrt{\theta /\delta }\), we have \(n_e=1+k_0^2(\psi /2 -3\phi +\frac{5}{2}\phi \sqrt{\phi /\psi })\) and \(n_i \approx 1\), whereas in the IAW case, when \(|{\tilde{v}}_D|\sim O(\sqrt{\delta })\) and \(u_0\sim \sqrt{\theta }\), we have \(n_e=1+k_0^2(\psi /2 -3\phi +\frac{5}{2}\phi \sqrt{\phi /\psi }) + \phi\) and \(n_i=1 +\phi\). In both cases \(n_e\) is hump-like and the electrons experience compression, whereas the ion densities are either nearly constant for SEAW (a too fast phase velocity for the ions to react!) or dip-like for IAW (note that \(\phi =\psi\) is then at infinity!).
To obtain the corresponding evolution equation, for which \(\phi (x-v_0t)\) is a solution, we use the method proposed in (Schamel (2020b)) by “adding two zeros” via a coupling constant c : \([\phi _t +v_0 \phi _x] + c [-{\mathcal {V}}''(\phi ) \phi _x - \phi _{xxx}]=0\).
We only treat a current-less plasma \(v_D=0\).
For SEAW we get with \(v_0=1.307(1 + \Gamma +3k_0^2)\) and c=1.307 the Schamel-type evolution equation for this special solitary EH of negative polarity:
which is nearly identical with (14) despite the different physical background.
For IAW we get with \(v_0=\sqrt{\delta }( 1- \frac{\Gamma +3k_0^2}{2})\) and \(c= -\frac{\sqrt{\delta }}{2}\) the following Schamel evolution equation:
which is equivalent to (15) if we again renormalize time: \(t \rightarrow \sqrt{\delta }t\). Note that in both cases the different polarity of \(\phi (x)\) is reflected in the sign of the nonlinear term.
In both regimes, the corresponding trapping parameter \(\beta\) is a function of \(k_0^2\) and \(\psi\) and follows from \(-2k_0^2= B =\frac{16}{15} b(\beta , v_0) \sqrt{\psi }\) with \(b(\beta , v_0):= \frac{1}{\sqrt{\pi }} (1- \beta - v_0^2)e^{- v_0^2/2}\).
We note that if B is replaced by one of \(D_1, D_2\) or \({\tilde{C}}\), three new series of periodic hole solutions with solitary wave character at the two boundaries for each parameter are obtained.
In Sect. 5, we shall briefly address the whole class solitary electron holes of negative polarity.
4.2 The Schamel–Korteweg–de Vries solitary electron hole (SKdV-SEH)
For the next two-parametric solution we choose B and \(q = - {\tilde{C}} \psi \equiv \frac{2\psi }{3}\) in (7) as the only non-zero parameters and obtain
The corresponding NDR reads
This case has already been treated as early 1972 in (Schamel (1972a)), equations (47), (48), with the result that \(\phi (x)\) is given by
where \(y:=\frac{x}{2}\sqrt{\frac{\psi }{6}(1 + \frac{B}{q})}\) and \(-q < B\).
For \(1<<\frac{B}{q}\) and \(|\frac{B}{q}|<<1\), respectively, this expression reduces to the known cases (12) and (23), respectively, the privileged \({{\,\textrm{sech}\,}}^4(x)\) and the KdV solitary wave. The NDR (32) can be discussed like the previous cases.
In the IAW limit, the following evolution equation, which has (33) as the equilibrium solution, can be easily derived (\(t \rightarrow \sqrt{\delta }t)\):
which is (49) of (Schamel (1972a)). This Schamel–Korteweg–de Vries equation reduces in the appropriate limits to (15) and (25), respectively, as expected.
4.3 The modified second-order Gaussian SEH
In this part we refer to the Gaussian SEH in its first- and second-order version and use
where \(r:=1.773-2\ln \psi\) Schamel (2020a), and get for \(x(\phi )\) with \(s:=r-\frac{D_1}{D_2}>0\)
Its inversion yields
It reduces to the ordinary Gaussian SEH (17) in the limit \(D_2 \rightarrow 0\) (\(sD_2 \rightarrow -D_1\), resp.), and to the second order Gaussian SEH (20) in the limit \(D_1 \rightarrow 0\).
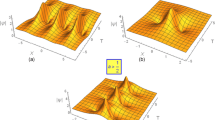
Figures 4 and 5 show the potential distribution \(\phi (x)\) and the corresponding trapped electron distribution \(f_{et}(v)\) at \(\phi =\psi\), respectively, for two values of \(D_2: D_2=0.112\) and \(D_2=0.037\) (Schamel 2020a). The corresponding values of s are: \(s=21.54\) and \(s=64.02\). The other selected parameters are given by \(\theta =10\), \(v_D=0.01 < v_D*=0.053\) (subcritical region), \(\psi =5.2\)x\(10^{-5}\).
Although they differ by a factor of 3, there is hardly any measurable difference. The simultaneous presence of two trapping generations hence establishes a one-parameter continuum spectrum of solitary electron holes that can by appropriate fitting be potential candidates for identifying structures. However, since they lead to macroscopically and microscopically almost identical structures they can no longer be distinguished experimentally. A unique identification of structures, the desired goal expressed in the literature, is therefore not achievable. Origin of this intrinsic ambiguity is the loss of mathematical stringency in the kinetic regime through chaos triggered by the ergodic particle trajectories in the resonant region.
We continue our intention to derive an evolution equation for this second order modified Gaussian SEH. The NDR (6) is simplified in this case of \(k_0=B={\tilde{C}}=0\) and becomes
where \(\hat{B}\) and \(\hat{\hat{B}}\) had been defined in connection with equations (18) and (21), respectively.
The evolution equation for the SEAW branch becomes
where \(\hat{\hat{{\mathcal {A}}}}:=\hat{{\mathcal {A}}} + D_1(2 + \ln {\frac{\psi }{4}})\).
We note that in the three cases treated so far we were able to solve the decisive equation (8) to obtain \(x(\phi )\) by inversion \(\phi (x)\), i.e. our solution \(\phi (x)\) could be expressed by known mathematical functions. It was disclosed. In our final example, we will encounter a situation where this disclosure no longer exists. It represents the general case.
4.4 The undisclosed logarithmic Schamel SEH
This is the case when the two basic trapping scenarios \((B, D_1)\) and only the two are in action simultaneously. The pseudo-potential \({\mathcal {V}}(\phi )\) then reads
a case which has been treated thoroughly in (Schamel (2020b)). The integral for \(x(\phi )\), given by (9) in (Schamel (2020b)), cannot be solved anymore. We can conclude from this that these two trapping channels lead us into an unknown terrain, into an area where only numerically an image of the potential \(\phi (x)\) can be obtained.
This is fortunately not the case for the NDR and the evolution equation, which become
and
with \({\mathcal {A}}\) given by
the latter being valid for the SEAW branch. It may be named for clear identification logarithmic Schamel equation. It is, therefore, worth noting that although the explicit form of \(\phi (x)\) is not known, an evolution equation can still be assigned.
We conclude that a large number of new structures are already coming into play for two trapping channels in action. This is all the more true when more than two scenarios are involved. This abundance of electrostatic structures is a consequence of the nonlinear treatment of the Vlasov equation (s) with no chance of a linear approximation.
In the following two special cases are discussed before their setting in a more general context will be discussed.
5 The class of negatively polarized solitary electron holes (SEHs)
In Sect. 4.1 we learned that by setting the two parameters B and \(k_0 ^ 2\) adequately, SEHs with negative polarity can be obtained. Motivated by its ubiquity in extraterrestrial space (Wang et al. 2021) we extend this two-parametric solution to all five parameters to get the general class of SEHs with negative polarity. The condition for the five parameters \((k_0, B, D_1, D_2, q)\) to achieve a negatively polarized SEH is obtained by setting \(\mathcal {V} '(\psi ) = 0\), such that the double zero point goes from \(\phi =0\) over to \(\phi = \psi\).
This constraint follows from (4) in which we replace the first bracket by (6) and by setting \(\mathcal {V} '(\psi ) = 0\) to get
where \(q:=-{\tilde{C}} \psi\). Replacing \(k_0^2\) in (7) for \(\mathcal {V} (\phi )\) by (31) we get
By replacing \(k_0^2\) in (6) through (31) we get the associated NDR
With the two equations (45) and (46) we have all the ingredients for a complete theory of SEHs with negative polarity. With four independent parameters \((B, D_1, D_2, q)\) we have a 15-fold manifold of different solutions (\(\sum _{i=1}^{4}\frac{4!}{i! (4-i)!}=15\)). Most of them appear as mathematically undisclosed solutions.
Only two special cases are treated further.
One simple case is when only q is present. For \(B=D_1=D_2=0\) we then have \(\mathcal {V} (\phi )=\frac{q\psi ^2}{2} \varphi (1-\varphi )^2\). Since it must be negative we have \(q=-{\tilde{C}} \psi <0\) or \({\tilde{C}}>0\) as a requirement for the existence of a solution. The potential is given by \(\varphi (x)= 1- {{\,\textrm{sech}\,}}^2(\frac{\sqrt{-q}x}{2})\), an expected result (see equation (23) where \(\varphi\) has to replaced by \(1-\varphi\) to yield the new result).
The other simple case is that only \(D_1\) is present, in which case we have \(- \mathcal {V} (\phi )/\psi ^2= \frac{D_1}{2} \varphi (1-\varphi +\varphi \ln \varphi )\). Insertion into \(x(\phi )=\pm \int _{0} ^{\phi }\frac{dt}{\sqrt{{-2 {\mathcal {V}}(t)}}}\) (see Appendix B) yields \(\sqrt{D}_{1} x= \pm 2 \int _{0} ^{\varphi } \frac{dy}{\sqrt{ 1 - y^2 + 2 y^2 \ln y}}\), \(D_1>0\). In contrast to Sect. 3.3, the Gaussian solitary mode, where \(D_1<0\), \(D_1\) must now be positive for a solution to exist. However, we have not been able to solve this latter integral. So it seems that this particular negatively polarized SEH that definitely exists is already part of the plethora of undisclosed potential patterns like most others are.
We will not pursue any further details, leaving it up to the reader to use them in any particular case.
We finally note that this class was obtained by imposing the additional constraint \(\mathcal {V} '(\psi ) = 0\). By setting further restrictions, new structures with different characteristic shapes can be created. An example is the additional constraint \(\mathcal {V} '(0) = 0\) which leads to well-known double layer (DL) (Schamel and Bujarbarua 1983; Schamel 1986). The more trapping parameters are involved, the more constraints can be imposed. So it would be interesting to see which structures the additional conditions \(\mathcal {V}''(0) = 0\) and \(\mathcal {V}''(\psi ) = 0\) lead to. Future scientific generations may take up this problem.
6 The class of ultra-slow SEHs
For a given occasion, we would like to draw our attention to another issue, that of the extremely slow SEHs. In a recently published article (Hutchinson 2021), the opinion was spread that the current theory has flaws which is particularly evident in the lack of ultra-slow SEHs for single humped ion distributions. Here, equipped with the correct method, we show the opposite, namely the existence of ultra-slow SEHs for a single-humped \(f_i\).
For the sake of simplicity, in the following we assume an ordinary SEH, namely one with a positive hump and take \(k_0^2=0\).
The NDR in (6) therefore becomes \(\biggl ( A -\frac{1}{2} Z_r'(\frac{ {\tilde{v}}_D}{\sqrt{2}}) - \frac{\theta }{2} Z_r'(\frac{ u_0}{\sqrt{2}}) \biggr ) - B + {\hat{D}} =0\) where \({\hat{D}}:=[D_1 + (a_1-1)D_2](-\frac{1}{2} +\ln \psi ) + D_2\ln ^2\psi + {\tilde{C}} \psi \biggr ]\) , which in case of a non-propagating structure: \(v_0=0=u_0\) simplifies to
We remember that A was defined by \(A:=(\Gamma +\frac{a_1}{2}D_1 +a_2D_2)\). With given \(v_D\) and \(\theta\) this equation represents the condition which the remaining parameters \((\Gamma , B, D_1, D_2, {\tilde{C}}\) (or q)) have to fulfill. This corresponding 5-parameter solution set again has 31 members and is therefore not insignificant. So there can be no question of a missing solution. Especially due to the presence of \(\Gamma\), a solution can always be found. In case of a vanishing drift \(v_D=0\) and of vanishing parameters \((\Gamma , D_1, D_2, q)\) except B we have \(1+\theta = B =\frac{16}{15}\frac{1}{\sqrt{\pi }} (1- \beta )\) which holds for any \(\theta\) inclusively \(\theta = \frac{T_e}{T_i}<1\). Hence, a \(\beta =-(0.66 +1.66 \frac{T_e}{T_i} )\) and with it a sufficiently excavated trapped electron distribution will do the job. We do not need ion trapping effects to get a solution. (In parenthesis, we state that this does not mean the absence of ion trapping, only the absence of its effects, (\(\alpha =1\) see later)). In a recently conducted VP simulation, such structures could undoubtedly be demonstrated (Mandal et al. 2020).
If ion trapping/reflection effects come into play the NDR is modified and we have to look at altered solutions. But there is no doubt that solutions do exist as well.
The continuous spectrum is extremely rich in elements and provides holes with almost arbitrary phase velocities, which are sustained by appropriately adapted trapping scenarios.
7 Ion trapping effects and ion holes
7.1 Ion trapping effects
In this section, we briefly discuss the effects of ion trapping, which can be important, for example, for the slow propagation of electron holes in the ion thermal range. In addition, we will briefly address the existence of ion holes. The incorporation of ion trapping (reflection) effects can be straightforwardly performed by the following replacements in (1) to get \(f_i(x,u)\), namely \(\varepsilon :=\frac{v^2}{2}-\phi\) by \(\epsilon :=\frac{u^2}{2}-\theta ( \psi -\phi )\) ; \({\tilde{v}}_D\) by \(u_0\) ; a change in the normalization \(1+ \frac{k_0^2 \psi }{2}\) by \(1+ K_i\) and by attaching an index i to the new ion trapping parameters: \(\Gamma _i, B_i, C_i, D_{1i},D_{2i}\). Note that \(\beta\) becomes \(\alpha\). The details of this procedure are found in (Schamel (2000)), especially in Sect.4. We then have
The corresponding density then becomes
where we defined \(A_i:=\Gamma _i + \frac{a_1}{2}D_{1i} + a_2 D_{2i}\) , \(B_i:=\frac{16}{15} b(\alpha , u_0)\sqrt{\psi }\) with \(b(\alpha , u_0):=\frac{1}{\sqrt{\pi }}( 1- \alpha - u_0^2)e^{-u_0^2/2}\) and \((\Gamma _i, C_i, D_{1i}, D_{2i}):= \frac{\sqrt{\pi }}{2} e^{-u_0^2/2} \biggl ( \gamma _i, \frac{3\zeta _i}{4}, \chi _{1i}, \chi _{2i} \biggr )\).
The normalization constant \(K_i\) is determined by the requirement that in the solitary wave limit \(k_0 \rightarrow 0\) both densities \(n_e\) and \(n_i\) should be equal (namely unity) at infinity when \(\phi \rightarrow 0\), which yields:
To check this expression we take the zero limit of \((A_i, D_{1i},D_{2i}, Z_r'''(\frac{u_0}{\sqrt{2}}))\) and get \(1=(1 + K_i)\biggl [1+\biggl ( -\frac{1}{2} Z_r'(\frac{u_0}{\sqrt{2}}) -\frac{5B_i}{4\sqrt{\psi }}\sqrt{\theta \psi } \biggr )\theta \psi \biggr ]\) from which follows \(K_i=\biggl ( \frac{1}{2} Z_r'(\frac{u_0}{\sqrt{2}}) +\frac{5B_i}{4\sqrt{\psi }}\sqrt{\theta \psi } \biggr )\theta \psi\) which is identical with (21) of (Schamel (2000)).
Replacing \(K_i\) in \(n_i\) by this general expression obtained from (50), we can proceed as before: we determine through \(\phi ''(x)=n_e - n_i = -{\mathcal {V}}'(\phi )\) the preliminary form of \(V(\phi )\): \(V_0(\phi )\) (such as in (5)) to get through \(V_0(\psi )=0\) the NDR analogue of (6), we may call (6’). Removing finally the bracket in \(V(\phi )\) which involves \((v_0,u_0)\) through (6’), we can finally find the desired expression for \(V(\phi )\), called (7’), in which both the electron and ion trapping effects are incorporated on equal footing.
We will neither write it down [but may call it (7 ’)] nor deduce the general consequences, leaving this interesting and straightforward but cumbersome procedure to the reader (and perhaps later generations).
Without ionic trapping effects we had 1+4=5 individual terms in \(V(\phi )\) corresponding to \(\sum _{i=1}^{5}\frac{5!}{i! (5-i)!}=31\) possible combinations and hence 31 patterns that can be distinguished. With ion trapping effects the number of free trapping parameters is enhanced by further 4 such that \(\sum _{i=1}^{9}\frac{9!}{i! (9-i)!}=494\) individual modes become vivid, without taking into account the double counting of the solitary waves of positive and negative polarity.
What we finally want to show in this section is the existence of ion holes of positive polarity.
7.2 Ion holes of negative and positive polarity
In the limit of vanishing parameters \((A_s, C_s, D_{1s},D_{2s})\), s = e, i, where the index e refers to the previous electron parameters, and of \(Z_r({\tilde{v}}_D/\sqrt{2}) \simeq 0 \simeq Z'''_r(u_0/\sqrt{2})\), the governing equations simplify to
and
where again \(\varphi = \frac{\phi }{\psi }\), which coincide with (44) and (45) of (Schamel (2000)), respectively. They reduce in case of \(B_i=0\) to our (26), (28) of Sect.4.1. With (51), (52) we now have a situation in which all three trapping scenarios \((k_0 ^ 2, B_e, B_i )\) contribute simultaneously.
From (52), it follows by differentiation
It then follows that at \(\phi =0\) it holds \(-\mathcal {V}'(0) \simeq 0\) and at \(\phi =\psi\): \(-\mathcal {V}'(\psi ) \simeq -2k_0^2- B_e + B_i \theta ^{3/2}\). A positively polarized hole is then given by \(k_0^2=0\) and \(B_e - B_i \theta ^{3/2} > 0\). This yields an extension of our previous elementary \({{\,\textrm{sech}\,}}^4(x)\) solitary electron hole mode (Sect.3.2) by the \(\alpha\)-trapping scenario of ions.
If we only limit ourselves to ion trapping, a positively polarized ion hole is provided by \(k_0^2=0\), \(B_e =0\) and
Together with the corresponding NDR, this forms the basis for \(\textbf{positively}\)-polarized ion holes, a previously unknown and unexplored area. Some more details could be further explored, such as the corresponding Schamel-type evolution equation, but we would like to leave that up to the reader and/or later generations.
Finally, we just want to show that the present formalism includes the usual (negatively) polarized ion hole.
This is achieved by setting \(k_{0-}^2:=2k_0^2 + B_e - B_i \theta ^{3/2}\equiv 0\) (see (48) of (Schamel (2000))). In case of \(B_i=0\) we get back the negatively polarized SEH (27), and for \(B_e=0\) we obtain \(-\mathcal {V}(\phi )/ \psi ^2= B_i \frac{\theta ^{3/2}}{2}(1-\varphi )^2 \bigg (1 - \sqrt{1-\varphi }\bigg )\). This is obviously our familiar negatively polarized ion hole (see (7), (8) of (Schamel and Bujarbarua (1980)) which holds for the dependent variable \({\hat{\varphi }}:=\varphi - 1 \le 0\).
8 Stability
For understandable reasons, the last word cannot be said on the stability of these structures. The dynamics that are triggered by perturbations depend too much on what is happening in the resonance region for a general, conclusive statement to be made. This applies all the more to studies in which such an equilibrium solution was not available. Since the mathematical endeavor turns out to be too complex, we can only outline its general properties, but solve it in the case of a single wave.
To make the analysis as transparent as possible, let us focus on trapping of electrons in its simplest, nontrivial version and on \(\theta = 0\) corresponding to immobile ions\(\left( {{\text{n}}\_{\text{i}} = 1} \right)\).
By the ansatz
where \(f_{0e}(\varepsilon )\) and \(\phi _0(x)\) are our equilibrium functions, we get by linearizing the VP system and using the integration technique along unperturbed orbits (characteristics) of (Lewis and Symon (1979), Schamel (1982a)) a non-local eigenvalue problem for (\(\omega ,\phi _1(x)\)) of the following form:
which is (26) of (Schamel (2018)). We restrict the analysis to the cnoidal electron hole case of Sect.4.1, in which \({\mathcal {V}}(\phi _0)\) is represented by (26), i.e. we ignore for convenience all the other electron trapping scenarios. It then holds to first order in \(S=\frac{4B}{k_0^2}\)
\({\mathcal {V}}\,''(\phi _0)= k_0^2 - B \biggl (1-\frac{15}{8} \sqrt{\frac{\phi _0}{\psi }}\biggr )=k_0^2\biggl (1 -\frac{S}{4}[1-\frac{15}{8}\cos \frac{k_0 x}{2}]\biggr )\), where in the last step we used \(S<<1\).
The eigenvalue problem (55) then becomes
In the harmonic (single) wave limit, when \(S=0\) and \(\phi _1 \sim e^{ikx} + c.c.\), it reduces to the algebraic equation
which is (27) of (Schamel (2018)). The moment \({\mathcal {M}}_n(\phi _0)\) is defined by \({\mathcal {M}}_n(\phi _0)=\int dv v^n \partial _{\varepsilon }f_{0e}\) and it holds the recursion formula \({\mathcal {M}}_{n+2}'(\phi _0)=(n+1){\mathcal {M}}_n(\phi _0)\), which is (29) of (Schamel (2018)). From \({\mathcal {M}}_2(\phi _0)=-\int dv f_{0e}= -n_{e0}(\phi _0)\) and the recursion formula we obtain \({\mathcal {M}}_0(\phi _0)= -n_{e0}'(\phi _0) =\frac{1}{2}Z_r'(\frac{{\tilde{v}}_D}{\sqrt{2}}) + O(\sqrt{\phi _0}, S)\). Whereas the odd moments vanish, the other even moments are of \(O(\phi _0)\) or of higher order. We then get to lowest order \(-k^2 + k_0^2 ={\mathcal {M}}_0+(\frac{k}{\omega })^2{\mathcal {M}}_2=\frac{1}{2}Z_r'(\frac{{\tilde{v}}_D}{\sqrt{2}})-(\frac{k}{\omega })^2\), which is (31) of (Schamel (2018)). Application of the NDR (11) with \(\theta =0=\Gamma\) we hence find \(\omega =1\).
The perturbed eigenmode is an undamped, infinite wavelength Langmuir mode (or a pure plasma oscillation, respectively, (Schamel et al. (2017))), being independent of \({\tilde{v}}_D\).
A harmonic (single-wave) EH is therefore marginally stable, no matter how strong \({\tilde{v}}_D\) is, a result which contradicts Landau theory, where marginal stability holds at threshold \(v_D= v_D*\) only.
Sentences like “the single-wave model ... describes the behavior near the threshold and subsequent nonlinear evolution of unstable plasma waves” (Balmforth et al 2013 [1]) rest on the unproven ad hoc assumption of the validity of the linear Vlasov concept which can, however, not be retained. The underlying single-wave model therein is too simple and simply not applicable. These authors underestimate the effectiveness and need of particle trapping in the real world of coherent structures, an unmistakably nonlinear effect. A similar misunderstanding of the importance of trapped particles is encountered in (Valentini et al. (2012)) (see also (Schamel 2013,Footnote 3)). Here the authors did not realize that their analysis is based on nonlinearly incorrect modes. As in the case of the “Thumb-Teardrop DR”, see Section 3.1, the on- and off-dispersion modes only make sense and become real modes when trapping is built in. The fact that they are also encountered as linear Vlasov modes is correct, but overlooks the fact that the associated distribution functions are no longer valid nonlinearly, as they should.
In contrast to the currently favored wave theory, which is based on Landau’s analysis and is vehemently defended by its protagonists, a nonlinearly permitted single wave is \({\textbf {unconditionally}}\) \({\textbf { marginally}}\) \({\textbf { stable}}\).
For mobile ions we get as an extension of (57):
with \(\mu =\sqrt{\frac{\theta }{\delta }}\) and a corresponding recursion formula for \({\mathcal {M}}_n^{i}(\phi _0)\). It is found that \({\mathcal {M}}_0^{i}(\phi _0)= \frac{1}{\theta }n_{i0}'(\phi _0) =\frac{1}{2}Z_r'(\frac{u_0}{\sqrt{2}}) + O(\phi _0)\) and \({\mathcal {M}}_2^{i}(\phi _0)= -n_{i0}(\phi _0)\) such that to lowest order we have: \(-k^2 + k_0^2 =\frac{1}{2}Z_r'(\frac{{\tilde{v}}_D}{\sqrt{2}})-(\frac{k}{\omega })^2 + \theta \biggl [\frac{1}{2}Z_r'(\frac{u_0}{\sqrt{2}})-(\frac{k}{\omega \mu })^2\biggr ]\), from which follows \(\omega =\sqrt{1 + \delta }\). This is the undamped Langmuir mode with infinite wavelength corrected for the mass ratio as it should be.
In the opposite limit of a maximum distortion, \(k_0 \rightarrow 0\) and \(S \rightarrow \infty\), which is the solitary wave limit, this linear stability problem was attacked by (Schamel (1982b), Hutchinson (2018)). A solution was obtained by an artificial truncation of the series in (55) at \(n=2\), the so-called fluid limit (Lewis and Symon 1979), and by a subsequent representation of \(\phi _1(x)\) in terms of the eigenstates of the \(\Lambda\) operator, which is the operator on the left hand side of (55). The result of a longitudinal stability and a transversal instability has, however, to be questioned because there are hints (Schamel 1986) that this artificial truncation of the series cannot be justified.
This, as well as the stability problem for any S and for all the other trapping scenarios, is hence a great challenge and can occupy many generations.
9 Negative energy states and spontaneous hole acceleration
Another important, if not the most important, aspect is the fact that the total energy of a plasma can be less than that of the undisturbed plasma due to the presence of a hole. This implies that when this state is approached, for example by achieving a higher phase velocity through acceleration, free energy is available which can be the source for the excitation of other modes and thus for a higher degree of intermittent plasma turbulence. As an example I refer to the simulations of (Schamel et al. (2017), Mandal et al. (2018), Mandal et al. (2020)) and the corresponding video [https://youtu.be/-nxIokKORwU] (with gratitude to my coauthors (Schamel et al. (2017), Mandal et al. (2018), Mandal et al. (2020), Schamel et al. (2020a), Schamel et al. (2020b))). A summary of these simulations of holes in subcritical, noisy plasmas will be published by Mandal and Sharma in an upcoming review (Mandal and Sharma 2023).
We see in this video an acceleration that is particularly efficient when \(\theta > 1\), the existence condition for ion acoustic waves. This transition to a higher phase velocity must be a transient, unsteady process, because the NDR (5) written as \(-\frac{1}{2} Z_r '(\frac{u_0}{\sqrt{2}})=c\) exhibits as a stationary NDR a forbidden area or a gap between the slow and the fast branch when \(-0.285< c< 0\) (see section III.B of (Mandal et al. (2020)) or section 4.1 of (Mandal et al. (2018))). For energetic reasons the continuous process of ion sound wave emission during acceleration must hence be associated with a reduction in the hole energy. This process is somewhat similar to the radiation from KdV solitons and Langmuir solitons investigated by ((Karpman (1995)) and references therein) on the basis of an evolution equation. This, therefore, applies to all acoustic propagation structures for which an evolution equation can be set up.
Experimentally a spontaneous acceleration of periodic ion holes was detected by (Franck et al. (2001)) in a double plasma device.
Another process is worth mentioning, the excitation of an energetic plasma oscillation, as can be seen in the behavior of \(\phi (x, t)\) of the simulation. As explained in (Schamel et al. (2017)), this is a relic of two counter-propagating Langmuir waves of the same intensity which can already be understood by a linear fluid approach of the electrons. This plasma oscillation carries most of the excess energy added to the plasma by the initial disturbance.
There is therefore great interest in learning more about the energy associated with a hole which is our last topic. It was developed in a series of papers (Schamel 2000; Grießmeier and Schamel 2002; Grießmeier et al. 2002; Luque and Schamel 2005; Das et al. 2018), to which we refer for a more intensive evaluation. The total energy density w of a plasma that is structurally excited by an equilibrium hole is given in the laboratory system by
where \(x'=x-v_0t\) and a stationary structure of periodicity 2L (\(L\rightarrow \infty\) for solitary holes) is assumed. The distributions are given by (1) for electrons and by (48) for ions, respectively.
Using a straightforward calculation (Schamel 2000; Grießmeier and Schamel 2002; Grießmeier et al. 2002) w is found to be
which is (67) of Luque and Schamel (2005) (in which K stands for \(k_0^2\psi /2\) and A for \(K_i\)). This expression reduces to \(w_H:=\frac{1}{2}(1 + v_D^2 +\frac{1}{\theta })\) in the structureless, homogeneous plasma limit \(\psi \rightarrow 0\). An appropriate renormalization of the electron quantities, which takes into account that \(\frac{1}{2L}\int _{-L}^{+L}n_e dx = 1 + {\tilde{\sigma }}\) can deviate from unity (\(|{\tilde{\sigma }}|<< 1\)) yields \(w_S:=(1-{\tilde{\sigma }})w\), which is (69) of (Luque and Schamel (2005)).
Defining finally \(\Delta w\) by \(\Delta w:=w_S - w_H\) we arrive at the energy (density) difference provided by the structure.
To simplify the further discussion we only consider the \(B_e\) (\(\equiv B\)) and \(B_i\) trapping scenarios (corresponding to (20a,b) of Schamel (2000) and get (see (73) of (Luque and Schamel (2005)))
with \({\hat{\sigma }}:=\frac{{\tilde{\sigma }}}{\psi }= \frac{k_0^2}{2}-\frac{1}{2}Z_r'(\frac{{\tilde{v}}_D}{\sqrt{2}}) \frac{1}{2L}\int _{-L}^{+L}\varphi (x) dx - \frac{5}{4} B_e \frac{1}{2L}\int _{-L}^{+L}\varphi (x)^{3/2} dx\) and \({\hat{K}}_i:=\frac{K_i}{\psi }= \frac{\theta }{2} Z_r'(\frac{u_0}{\sqrt{2}}) +\frac{5}{4}B_i\).
We note that in (61) terms of \(O(\psi ^2)\) have already been neglected which means that the field energy term, the last term in (60), does no longer contribute since it is \(O(\psi ^2)\).
In the solitary, positively polarized electron hole limit (\(k_0^2 \rightarrow 0\)) (61) becomes (see also (77) of (Luque and Schamel (2005)))
which extends (8) of (Grießmeier and Schamel (2002)).
We learn that \(\Delta w\) is only influenced by the ion response and by the ion trapping scenario \(B_i\) whereas \(B_e\) only participates implicitly through the back door via the NDR.
An inspection of (62) shows that to change the sign of \(\Delta w\), \(u_0\) has to be larger than some \(u_0^*\) which is defined by \(\Delta w(u_0^*)=0\) and which only depends on \(B_i/\theta\). In case of \(B_i=0\) it is given by \(u_0^*=2.124\). If \(B_i>0\) \(u_0^*\) will grow monotonically from 1 (\(\theta =0\)) to 2.124 (\(\theta =\infty\)). The dependence of \(u_0^*\) is plotted in Fig. 8 of (Luque and Schamel (2005)) whereas the region of \(\Delta w <0\) in the (\(v_D,\theta\)) plane is exposed in Fig. 10 (for \(B_i=0\)).
This brings us to three basic properties of a structurally excited plasma:
-
1
] \(w_S - w_H=\Delta w= O(\psi )\), the difference in the total energy density is \(O(\psi )\) rather than \(O(\psi ^2)\) as found e.g. by standard linear wave analyses (see Appendix A5 of arXiv:2110.01433v3, (Kruskal and Oberman 1958; Gardner 1963; Morrison and Pfirsch 1994)). The influence of a coherent structure on the energy budget is hence much stronger than predicted by linearly based concepts.
-
2
] By acceleration, a hole can penetrate into areas with negative energy and thus release energy that the plasma can use to generate further waves and hence to increase the level of intermittent turbulence.
-
3
] Due to the multitude of different trapping scenarios, there is a vast, untapped field that many generations of plasma theorists can still benefit from.
10 Two related topics: anomalous transport and holes in synchrotrons
10.1 Coarse grained distributions and anomalous resistivity
The point to be addressed is that the current equilibria still have a weak singularity of cusp type in phase space. At least the free part of the distributions \(f_e\) (and \(f_i\)) exhibits an infinite slope at the separatrix, \(|\partial _v f_e(\varepsilon )| \sim \frac{1}{|\varepsilon |}\) as \(|\varepsilon |\rightarrow 0\) (and similarly for the ions), which is an integrable singularity. In other words, collisional aspects enter near the separatrix and higher moments of the BBGKY hierarchy have to be considered in this region (Krall and Trivelpiece 1973).
Numerically this problem was attacked by the authors (Korn and Schamel 1996a, b; Schamel and Korn 1996; Luque and Schamel 2005) who added a Lorentz-collision operator, \(\nu _e\partial _v[\partial _v + ( v- {\tilde{v}}_D)]f_e\), on the right-hand side of the kinetic equation where \(\nu _e\) is the electron collision frequency. By the inclusion of a homogeneous electric field on the left-hand side, \(E_0=-\nu _e v_D\), they got dissipative structural equilibria of the so-extended Vlasov–Fokker–Planck–Poisson system. We refer to Fig. 6 of (Korn and Schamel (1996b)) for fluid ions and to Sect.2.5 of (Luque and Schamel (2005)) for kinetic ions.
The distribution on the separatrix was smooth in all cases, which corresponded to a coarse-grained distribution, and a single-humped curve could be obtained in the \((\nu _e, v_D)\) space, below which dissipative hole equilibria were time-asymptotically established (see Fig. 9 of (Korn and Schamel (1996b)) and Fig. 23 of (Luque and Schamel (2005))). In turn, ion mobility played a decisive role for the existence of these dissipative structural equilibria. Accordingly, an anomalous resistivity (or conductivity, respectively) could be presented, introduced the quantity.10 and equation (5.13) of (Korn and Schamel (1996b)), which was determined and controlled by the surviving hole structure.
Holes, therefore, play a crucial role in anomalous transport and it is expected that this area will receive more attention in the future.
This approach to intermittent plasma turbulence with surviving structures and coarse grained distributions is supported by another investigation (Schamel and Luque 2005). In this numerical study of a current-carrying, subcritical pair plasma (\(v_D = 2.0 < v_D * = 2.6\)), the nonlinear growth (rather than damping!) of holes in the positive species, which were initially triggered by tiny seeds, could be demonstrated. After saturation a new, steady-state, collisionless, intermittent plasma turbulence state is approached with persistent, albeit somewhat less energetic, holes in it.
We note that in VP simulations and/or PIC simulations such a coarse graining is automatically involved by the artificial phase space diffusion, especially at the separatrix, that is triggered by the numerically necessary discretization of space. We may therefore speculate that the current collisionfree equilibria could be of fundamental importance for the derivation of improved and specially adapted collision operators in weakly collision-free plasmas such as fusion or space plasmas.
10.2 Solitary structures on hadron beams in synchrotrons
Another field of application of our theory of VP structures are the structures that were measured on continuous (coasting) as well as bunched particle beams in circular accelerators, e.g. at RHIC (Blaskiewicz et al. 2003). Our theory, which has been developed over almost a decade (Luque and Schamel 2005; Schamel 1997, 1998; Schamel and Fedele 2000; Grießmeier et al. 2000; Blaskiewicz et al. 2004; Schamel and Luque 2004) combined with the present experience, does predict
-
a)
no threshold for nonlinear structure formation in case of a coherent initial fluctuation spectrum provided that the system is above the transition energy and
-
b)
the existence of long-living stabilized structures that belong to a continuous rather than a discrete spectrum.
The loss of Landau damping, which is seen within these accelerators when at higher intensities the collective frequencies lie outside the incoherent spectrum, is, however, wrongly explained by the beam community (see, e.g. (Burov 2021)) through a tune shift in the sense that there are no longer any particles that can interact resonantly with the wave structure, instead of correctly interpreting this phenomenon through a loss of Vlasov linearity.
In addition, another incorrect interpretation is given (see e.g. (Karpov et al. 2021)) that the observed continuous spectrum after saturation is of the discrete van Kampen type, instead of recognizing that the linearity no longer applies and continuous spectra of the type presented in this work should instead be implied.
We conclude with the expectation that particle trapping, the associated nonlinearities and the various trapping scenarios will certainly find their way into beam physics in the future as well.
11 Summary and conclusions
The aim of this review was to prove that \({\textbf {coherent}}\) \({\textbf { electrostatic}}\) \({\textbf { structures}}\) are due to the (trapping) nonlinearity of the Vlasov–Poisson system. By comparison of exact nonlinear with approximative linear wave solutions of current-carrying plasmas with drift velocity \(v_D\) two fundamentally new results could be obtained:
-
(i)
nonlinearly proper single (harmonic) waves are linearly marginally stable independent of \(v_D\) (see harmonic mode, section 3.1 and stability, section 8) and
-
(ii)
a spontaneous acceleration of a tiny hole is observed, triggered by a gap in the velocity caused by the nonlinear dispersion relation and accompanied by its subsequent approach to a more negative energy state (see section 9).
This necessarily implies that any linear treatment of this system, such as that of Landau or van Kampen (Case), turns out unsuitable for approximating them. Their diversity and mathematical subtleties are a direct result of the various trapping scenarios that are caused by the resonant wave–particle interaction, a problem which is mathematically known to be nonlinear and nonintegrable.
Moreover, due to the occurrence of the \(\Gamma\)-trapping scenario in the nonlinear dispersion relation, the linearly based Dupree-Weinstock resonance broadening and clump theory has received a nonlinear revaluation and justification (see sections 2, 3).
With this work we have thereby laid the basis for a comprehensive description of coherent patterns in current-driven, noisy plasmas, which brings structure and order into the manifold of hole equilibria. They originate from six different electron trapping scenarios that reflect the chaotic single-particle trajectories in the vicinity of the resonance. Thirty-one qualitatively different solutions for the electrostatic wave potential \(\phi (x)\) can be composed which are achieved by all possible combinations of five elementary modes, a manifold that includes thirty different modes of solitary wave character, namely fifteen of positive and fifteen of negative polarity. These elementary modes are: \(\sin (x), {{\,\textrm{sech}\,}}^4(x), e^{-x^2}, e^{-sinh^2(x)}, {{\,\textrm{sech}\,}}^2(x)\). When, in addition, ion trapping effects are taken into account, the result is a three-digit number of modes around five hundred.
In general, however, two combinations of them are already sufficient to prevent the electric wave potential \(\phi (x)\) from being disclosed, i.e. it can no longer be described mathematically by known functions. A distinction between these structures is still possible, however, on the level of the pseudo-potential \({\mathcal {V}} (\phi )\), which is the central variable in the present theory, leading to a \({\textbf {nonlinear}}\) version of the linear superposition principle.
Its utmost generality has the consequence that earlier investigations presented so far are either included as special cases or appear in a corrected, updated form. It offers a profound foundation since it provides a mathematically precise in-depth microscopic derivation. This is in contrast to many studies presented so far, in which such a deepened phase space study is missing. A well-founded study is absent either because for example, the densities are simply given as functions of \(\phi\) rather than being derived, or the studies are wrongly performed without realization that the phase velocity is a necessary part of a complete wave theory. In addition, an intrinsically microscopic process can in generality not be adequately addressed by prescribing a macroscopic potential \(\phi (x)\) as done by the BGK method.
The shortcomings of current methods such as the BGK method (Bernstein et al. 1957) and especially those based on the linear Vlasov theory (van Kampen, Landau) have hence been identified and corrected in favor of the present theory. In noisy plasmas, which are characterized by localized fluctuation nuclei or eddy-like seeds of non-topological character, the linear Landau theory fails, contrary to the popular opinion. The linear Landau theory is undermined by particle trapping, the sibling of coherence, and fails to correctly contribute to the formation of coherent patterns in realistic plasmas because of its resonantly inconsistent distributions.
The present status report was limited to continuous distributions, to a Maxwellian background plasma, to non-relativistic electrons and to non-magnetized plasmas. Various extensions were carried out in the literature with regard to discontinuous distributions by (Schamel (2015), Schamel et al. (2018), Das et al. (2018)), to \(\kappa\) or Fermi–Dirac distributions by (Tribeche et al. (2012), Haas (2021)) and (Schamel and Eliasson (2016)), respectively, to relativistic electrons by (Eliasson and Shukla (2005), Eliasson and Shukla (2006)) and to magnetized plasmas by (Jovanović et al. (2002)).
As pointed out, however, a continuation is still called for because of the cusp singularity at the separatrix, which is inherent in all solutions and which requires an extension of the kinetic Vlasov–Poisson description by incorporation of the higher moments of the BBGKY-hierarchy. This is definitely a new adventure awaiting us in which the mutually dependent chaotic particle behavior and the pair correlations at resonance enter into a liaison with an open outcome, especially for intermittent plasma turbulence and anomalous transport. Such an implementation is still pending and will certainly keep many generations busy.
Other non-trivial challenges are 3D generalization of holes (Jovanović et al. 2002; Chen and Parks 2002) or the incorporation of a second potential, the vector potential, to take into account the additional magnetic island formation, the latter being required, for example, for the propagation of coherent kinetic Alfv\(\acute{e}\)n waves (Karimabadi et al. 2013).
The proximity to the incompressible, non-viscous shear flow in 2D (Rayleigh problem) and more generally to the general fluid theory (Schamel 2012) yields a further application. The “puffs” observed in long pipe flows at high Reynolds numbers (Hof et al. 2008) seem to be closely related to the mentioned phase of hole acceleration and sound emission. The latter is caused by the approach of the system to an energetically lower hole state. This similarity of the coherent vortex dynamics in phase and real space physics, respectively, should definitely deserve further attention in future investigations.
In addition, this analysis can be extended point by point to include collisionfree shocks or double layers. This is achieved in the solitary wave case of \(k_0=0\) by the further constraint: \(\mathcal {V}'(\psi )=0\) or \(n_e(\psi )=n_i(\psi )\) with \(n_e(\phi )\) from (2) and \(n_i(\phi )\) from (49). Accordingly, the variety of shock solutions is unlimited, as in the solitary wave case, being determined by particle trapping.
And of course finite amplitude extensions like that in (Schamel (1972a), Schamel and Bujarbarua (1980), Bujarbarua and Schamel (1981), Schamel and Bujarbarua (1983), Schamel (1982b), Schamel (1986)) remain a gigantic challenge for future generations.
In the case of a bump-in-tail driven plasma such a comparison is still missing because, to my knowledge, no suitable nonlinear solution for comparison is currently available. However, there is no obvious reason why linear wave theory should surprisingly be applicable to coherent structures in this second case, as is practically assumed in the (especially experimental) literature.
We finish by concluding that Landau’s theory is inapplicable to driven plasmas with a non-negligible background of fluctuations. To describe the 1D instability of those plasmas that violate the topological constraint of Landau’s theory, one has to solve the full unabridged Vlasov equation, i.e. without linearization. The pattern formation induced by minute seed fluctuations in collision-free plasmas is thus intrinsically nonlinear since it is governed by particle trapping.
Final note: More details on the loss of the linear Vlasov dynamics are documented in an expanded version of this review, which can be found in arXiv:2110.01433v3.
Data availability statement
The data that supports the findings of this study are available from the corresponding author.
Notes
After a lecture by H. Derfler in Munich at the end of the sixties.
Its small amplitude existence can be seen as a further hint for the need of analytical studies like this, especially in the perturbative trapping regime (\(\beta ,\gamma\)).
It is a misunderstanding of the effectiveness of particle trapping to believe Landau’s onset point of instability can be justified by assuming \(f_0'(v)=0\) for \(v_0-\Delta v \le v \le v_0+\Delta v\), \(\Delta v \ge 0\). Even if this topological constraint applies to a given \(f_0 (v)\), which would correspond to a severe restriction of the permitted background distributions, a f(x, v) of type (1) is nevertheless essential to model the resonant region correctly in a nonlinear manner.
References
N.J. Balmforth, P.J. Morrison, J.-L. Thiffeault, review of modern physics, commissioned (2013)
F. Bauer, H. Schamel, Phys. D 54, 235 (1992)
I.B. Bernstein, J.M. Greene, M.D. Kruskal, Phys. Rev. 108, 546 (1957)
M. Blaskiewicz, J. Brennan, P. Cameron, W. Fischer, J. Wei, A. Luque, H. Schamel, Proceedings of the PAC 2003, Portland, JACoW, CERN, Geneva, (2003)
M. Blaskiewicz, J. Wei, A. Luque, H. Schamel, Phys. Rev. ST Accel. Beams 7, 044402 (2004)
P. Borah, N. Das, H. Schamel, Phys. Plasmas 25, 094506 (2018)
S. Bujarbarua, H. Schamel, J. Plasma Phys. 25, 515 (1981)
A. Burov, Phys. Rev. ST Accel. Beams 24, 064401 (2021)
R.A. Cairns, A.A. Mamun, R. Bingham, R. Boström, R.O. Dendy, C.M.C. Nain, P.K. Shukla, Geophys. Res. Lett. 22, 2709 (1995)
L.-J. Chen, G.K. Parks, Geophys. Res. Lett. 29, 45–1 (2002)
N. Das, H. Schamel, J. Plasma Phys. 71, 769 (2005)
N. Das, P. Borah, H. Schamel, Physics Lett. A 382, 2693 (2018)
H. Derfler, T.C. Simonen, Phys. Rev. Lett. 17, 172 (1966)
T.H. Dupree, Phys. Fluids 9, 1773 (1966)
T.H. Dupree, Phys. Fluids 15, 334 (1972)
B. Eliasson, P.K. Shukla, Phys. Lett. A 338, 237 (2005)
B. Eliasson, P.K. Shukla, Phys. Rep. 422, 225 (2006)
C. Franck, T. Klinger, A. Piel, H. Schamel, Plasma Phys. 8, 4271 (2001)
B.D. Fried, S.D. Conte, The Plasma Dispersion Function (Academic Press, New York and London, 1961)
C.S. Gardner, Phys. Fluids 6, 839 (1963)
K.S. Goswami, K. Saharia, H. Schamel, Phys. Plasmas 15, 062111 (2008)
J.-M. Grießmeier, H. Schamel, R. Fedele, Phys. Rev. ST Accel. Beams 5, 024201 (2000)
J.-M. Grießmeier, H. Schamel, Phys. Plasmas 9, 2462 (2002)
J.-M. Grießmeier, A. Luque, H. Schamel, Phys. Plasmas 9, 3816 (2002)
P. Guio, S. Borve, L.K.S. Daldorff, J.P. Lynov, P. Michelsen, H.L. Pécseli, J.J. Rasmussen, K. Saeki, J. Trulsen, Nonlin. Proc. Geophys. 10, 75 (2003)
A.V. Gurevich, Sov. Phys. JETP 26, 575 (1968)
F. Haas, Plasma Phys. 28, 072110 (2021)
B. Hof, A. de Lozar, D.J. Kulik, J. Westerweel, Phys. Rev. Lett. 101, 214501 (2008)
I.H. Hutchinson, Phys. Plasmas 24, 055601 (2017)
I.H. Hutchinson, J. Plasma Phys. 84, 905840411 (2018)
I.H. Hutchinson, Phys. Rev. E 104, 015208 (2021)
D. Jovanović, P.K. Shukla, L. Stenflo, F. Pegoraro, J. Geophys. Res. 107, 1110 (2002)
H. Karimabadi, V. Roytershteyn, M. Wan, W.H. Matthaeus, W. Daughton, P. Wu, M. Shay, B. Loring, J. Borovsky, E. Leonardis, S.C. Chapman, T.K.M. Nakamura, Phys. Plasmas 20, 012303 (2013)
V.I. Karpman, in Quantum-like models and coherent effects. ed. by R. Fedele, P.K. Shukla (World Scientific, Singapore, 1995), p.392
I. Karpov, T. Argyropoulos, E. Shaposhnikova, Phys. Rev. ST Accel. Beams 24, 011002 (2021)
J. Korn, H. Schamel, J. Plasma Phys. 56, 307 (1996)
J. Korn, H. Schamel, J. Plasma Phys. 56, 339 (1996)
N.A. Krall, A.W. Trivelpiece, Principles of Plasma Physics (McGraw-Hill, 1973)
J.A. Krommes, J. Plasma Phys. 81, 205810601 (2015)
M.D. Kruskal, C. Oberman, Phys. Fluids 1, 275 (1958)
H.R. Lewis, K.R. Symon, J. Math. Phys. 20, 413 (1979)
A. Luque, H. Schamel, Phys. Rep. 415, 261 (2005)
A.A. Mamun, R.A. Cairns, Phys. Plasmas 3, 2610 (1996)
D. Mandal, D. Sharma, to be published (2023)
D. Mandal, D. Sharma, H. Schamel, New J. Phys. 20, 073004 (2018)
D. Mandal, D. Sharma, H. Schamel, Phys. Plasmas 27, 022102 (2020)
G. Manfredi, Phys. Rev. Lett. 79, 2815 (1997)
D. Montgomery, G. Joyce, Plasma Phys. 3, 1 (1969)
P.J. Morrison, D. Pfirsch, Phys. Plasmas 1, 1371 (1994)
C. Mouhout, C. Villani, Acta. Math. 207, 29 (2011)
H. Schamel, Plasma Phys. 14, 905 (1972)
H. Schamel, J. Plasma Phys. 7, 1 (1972)
H. Schamel, J. Plasma Phys. 9, 377 (1973)
H. Schamel, J. Plasma Phys. 13, 139 (1975)
H. Schamel, Phys. Scr. 20, 336 (1979)
H. Schamel, Phys. Rev. Lett. 48, 481 (1982)
H. Schamel, Physica Scripta Vol. T2/1, 228 (1982)
H. Schamel, Phys. Rep. 140, 161 (1986)
H. Schamel, Phys. Rev. Lett. 79, 2811 (1997)
H. Schamel, Phys. Scr. T75, 23 (1998)
H. Schamel, Phys. Plasmas 7, 4831 (2000)
H. Schamel, Phys. Plasmas 19, 020501 (2012)
H. Schamel, Phys. Plasmas 25, 034701 (2013)
H. Schamel, Plasma Phys. 22, 042301 (2015)
H. Schamel, Phys. Plasmas 25, 062115 (2018)
H. Schamel, Phys. Plasmas 26, 064701 (2019)
H. Schamel, Phys. Lett. A 384, 126752 (2020)
H. Schamel, Plasma 3, 166 (2020)
H. Schamel, S. Bujarbarua, Phys. Fluids 29, 2498 (1980)
H. Schamel, S. Bujarbarua, Phys. Fluids 26, 190 (1983)
H. Schamel, B. Eliasson, Plasma Phys. 23, 052114 (2016)
H. Schamel, R. Fedele, Phys. Plasmas 7, 3421 (2000)
H. Schamel, J. Korn, Phys. Scr. T63, 63 (1996)
H. Schamel, A. Luque, New J. Phys. 6, 113 (2004)
H. Schamel, A. Luque, Space Sci. Rev. 121, 313 (2005)
H. Schamel, N. Das, P. Borah, Phys. Lett. A 382, 168 (2018)
H. Schamel, D. Mandal, D. Sharma, Phys. Plasmas 24, 032109 (2017)
H. Schamel, D. Mandal, D. Sharma, Phys. Scr. 95, 055601 (2020)
H. Schamel, D. Mandal, D. Sharma, Phys. Plasmas 27, 062302 (2020)
P. Trivedi, R. Ganesh, Phys. Plasmas 25, 112102 (2018)
M. Tribeche, L. Djebarni, H. Schamel, Phys. Lett. A 376, 3164 (2012)
F. Valentini, D. Perrone, F. Califano, F. Pegoraro, P. Veltri, P.J. Morrison, T.M. O’Neil, Phys. Plasmas 19, 092103 (2012)
C. Villani, Phys. Plasmas 21, 030901 (2014)
R. Wang, I.Y. Vasko, F.S. Moser, S.D. Bale, I.V. Kuzichev, A.V. Artemyev, K. Steinwall, R. Ergun, B. Giles, Y. Khotyaintsev, P.-A. Lindqvist, C.T. Russell, R. Strangeway, J. Geophys. Res. Space Phys. 126, A029357 (2021)
J. Weinstock, Phys. Fluids 68, 1977 (1968)
Acknowledgements
I would like to thank Sarbeswar Bujarbarua for his contributions on holes with finite amplitude and double layers, Jürgen Korn for his contributions and deep insights into weakly collisional and ionic effects on electron holes and anomalous transport (his spectral Fourier–Hermite Vlasov–Fokker–Planck–Poisson Code being still the measure of all things), Alejandro Luque for his contributions on weakly collisional effects on holes and anomalous transport as well as on quantum effects and structure formation in bunched and coasting beams in accelerators, Florian Bauer, Prathana Borah, Nilakshi Das, Bengt Eliasson, Renato Fedele, Kalyan Goswami, Jean-Matthias Grießmeier, Vladimir Karpman and Dusan Jovanovich for their valuable contributions to various hole-related issues, and Debraj Mandal and Devendra Sharma for their series of insightful electron-hole simulations. My thanks also go to Prof. Friedrich Busse for valuable discussions and diverse support. And last but not least, I am very grateful to my wife Helga for keeping my back free over the many decades of our life together.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
I have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
APPENDIX A: Derivation of (27)
APPENDIX A: Derivation of (27)
We start with \(-\mathcal {V}(\phi )= \frac{k_0^2}{2\sqrt{\psi }}( \phi \psi ^{3/2} -3\phi ^2 \psi ^{1/2}+ 2 \phi ^{5/2})\) but use instead of (8) the equivalent expression
\(x(\phi )=\pm \int _{0} ^{\phi }\frac{dt}{\sqrt{{-2 {\mathcal {V}}(t)}}}\) which is better suited because \(\phi =\psi\) occurs at infinity rather than at zero. The +(-) sign holds for \(x\ge 0\) (\(x<0\)). We then have with \(\varphi = \phi /\psi\) :
With the abbreviations \(\zeta :=\frac{\sqrt{3} k_0 x}{4}\) and \(\zeta _0:= \tanh ^{-1} (\frac{1}{\sqrt{3}})=0.65848\) we then have
where again the +(-) sign holds for \(\zeta \ge 0\) \((\zeta < 0)\). This corresponds to (27) and is our main result in this Appendix B. It is easily seen by making use of \(\tanh (x+y)=\frac{\tanh (x) + \tanh (y)}{1 + \tanh (x) \tanh (y)}\) that this main formula agrees with (3.33) of (Korn and Schamel (1996a)) if \(\zeta \ge 0\). (We mention in parenthesis that the application of (3.33) also for negative \(\zeta\) would result in a small additional hump at \(\zeta =-\zeta _0\) which is unphysical because it comes from a wrong handling of the equations.)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Schamel, H. Pattern formation in Vlasov–Poisson plasmas beyond Landau caused by the continuous spectra of electron and ion hole equilibria. Rev. Mod. Plasma Phys. 7, 11 (2023). https://doi.org/10.1007/s41614-022-00109-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s41614-022-00109-w