Kinetic Alfven wave (KAW) eigenmode in magnetosphere magnetic reconnection

Abstract

One prominent signature of collisionless magnetic reconnection in the magnetosphere is the Hall effect. In the ion-scale region of reconnection, ions cannot follow the magnetic field line whereas electrons are still magnetized. The difference in the motions of electrons and ions leads to charge separation, the resulting transverse Hall electric field, the field-aligned streaming of electrons to preserve charge neutrality, and the corresponding Hall magnetic field. Such physics has long been invoked in the discovery of kinetic Alfven waves (KAW) when the perpendicular wavelength becomes comparable to the ion scale. In this review, we present recent progresses in theoretical modeling, numerical simulations and in situ observations that analyze Hall effects in terms of KAW eigenmode. This review will also cover analysis of the impact of KAW eigenmode on the ion acceleration and energy conversion in reconnection. We emphasize that the KAW perspective can provide a unified description of various phenomena in magnetic reconnection, including Hall magnetic fields, Hall electric fields, the field-aligned current, the electric field parallel to B, the non-gyrotropy velocity distribution of ions, and a close connection between Hall fields and a fast reconnection rate ($\sim$0.1). The quantitative description of these aspects is necessary for a Petschek-type model in the era of collisionless reconnection.

1 Introduction

Magnetic reconnection in the magnetosphere is intrinsically characterized by multi-scale physics operating on the global scale, the meso scale, and the kinetic scale (Lee and Lee 2020; Dai et al. 2020). In the global-scale region outside the reconnection sites, the MHD (magnetohydrodynamic) approximation applies. The global-scale flow convection of Earth’s magnetosphere is driven by the operation of magnetic reconnection as described by the Dungey cycle to a zero-order approximation (Fig. 1a) (Dungey 1961).

Within the reconnection site of kinetic-scale, magnetic reconnection occurs when the MHD approximation breaks down (Vasyliunas 1975). In the context of collisionless plasmas, ion-electron collisions are absent so that ions and electrons behave differently at micro-scale. On the ion-motion scale, ions start to become demagnetized whereas electrons are still coupled to the magnetic field. The difference in the ion and electron motion produces charge separation, Hall fields and the associated electric current (Sonnerup 1979; Lu et al. 2022). On the even smaller electron-scale, electrons are demagnetized and correspond to the ‘breaking’ of the field line (Hesse et al. 1999; Lu et al. 2011). Kinetic physics is considered vital to explain the fast rate of collisionless reconnection. The reconnection rate in the conventional resistivity MHD model is usually small unless a large localized or current-dependent resistivity is used (Birn et al. 2001). The kinetic physics corresponding to the fast rate of collisionless reconnection is a long-standing question. Non-gyrotropy particle distributions and the associated off-diagonal term of the pressure tensor have been considered to provide the reconnection electric field at electron-scale (Vasyliunas 1975; Hesse et al. 1999) and ion-scale (Cai and Lee 1997; Dai et al. 2021).

Fig. 1

A schematic of magnetic reconnection in the magnetosphere. a Macro-scale magnetic reconnection in Earth’s magnetosphere. b The micro-scale structure of magnetic reconnection region

Relevance of Hall effects in reconnection is considered important at the ion inertial scale, providing a source for non-ideal reconnection electric field (Vasyliunas 1975). A quadruple Hall magnetic field is proposed to arise in the diffusion region of reconnection (Sonnerup 1979). The quadruple Hall magnetic field is later analyzed as a tearing mode eigenmode of the current layer (Terasawa 1983). The Hall effect introduces a coupling between the tearing mode perturbations ($B_x,B_z$ in Fig. 1b) and shear Alfven mode perturbations ($B_y$ in Fig.1b ) (Terasawa 1983). The Hall effects are identified in a variety of simulations (particle in cell, Hybrid and Hall MHD) as the critical factor for the fast rate in collisionless magnetic reconnection (Birn et al. 2001). In observations, signatures of Hall magnetic fields are used as a working definition of collisionless magnetic reconnection in the Earth’s and planetary magnetosphere (Deng and Matsumoto 2001; Nagai et al. 2001; Øieroset et al. 2001; Paschmann 2008).

The focus of this review is the KAW physics associated with the Hall fields of reconnection. The physics underlying the Hall effect is strikingly similar to that in the discovery of the KAW (Hasegawa 1976, 1975). KAW is the kinetic extension of Alfven waves and has been intensively studied with wide applications(Wu et al. 1996; Chaston et al. 2005; Keiling 2009; Chen and Zonca 2011; Lin et al. 2012; Lysak and Lotko 1996; Chen et al. 2014; Liang et al. 2016; Wang et al. 2019; Cheng et al. 2020; Chen et al. 2021; Wu and Chen 2020). In the case of MHD-scale shear Alfven waves, ions and electrons both follow the ${{\textbf {E}}}\times {{\textbf {B}}}$ drift in the transverse direction, obeying ${{\textbf {E}}}={{\textbf {V}}}_i\times {{\textbf {B}}}$ and ${{\textbf {E}}}={{\textbf {V}}}_e\times {{\textbf {B}}}$. As the perpendicular wavelength of Alfven wave becomes comparable to the ion gyro-radius, the ion can not follow the ${{\textbf {E}}}\times {{\textbf {B}}}$ drift motion. This is because the wave electric field now is non-uniform in the trajectory of ion gyromotion. As a consequence, the ion transverse motion is modified by the finite ion gyro-radius effect. Considering the kinetic correction, the ion actually follows ${{\textbf {E}}}= {{\textbf {V}}}_i\times {{\textbf {B}}}+(1/n_iq_i)\nabla \cdot \overline{\texttt {P}}_i$ in the transverse motion. The finite gyroradius effect is manifested in the ion pressure gradient term (Dai et al. 2017). This makes good sense since the finite ion gyro-radius effect is equivalent to a finite temperate for the ions on the fluid level. At the wavelength of ion-scale wavelength, electrons cannot follow ions in the transverse motion. The difference in the transverse motion of ions and electrons produces a charge separation and coupling to the electrostatic mode (Hasegawa and Uberoi 1978). As a consequence, a quasi-electrostatic electric field is formed in the transverse direction. To remain quasi-neutral condition, electrons quickly move in the direction parallel to the magnetic field. In the parallel direction, these electrons undergo a force balance between a small parallel electric field and the electron pressure gradient in the case of KAW. The parallel motion of electrons created a field-aligned current (FAC) that is a distinct nature of Alfven mode. The FAC induces a wave magnetic field perpendicular to the DC magnetic field. KAW has long been invoked as ingredients for fast reconnection (Kleva et al. 1995; Rogers et al. 2001). KAW physics introduces a new physical scale length $\rho _a^2$, the ion gyroardius based on the electron temperature, for the current layer and outflow layer in fast reconnection (Kleva et al. 1995; Rogers et al. 2001). Through the diffusion region near the X-line, intense KAW turbulence is observed, suggesting that magnetic reconnection is a source of KAW (Chaston et al. 2005, 2009; Huang et al. 2010).

Motivated by the similar physics between Hall fields and KAW, we proposed a quantitative model of Hall fields (Dai 2009; Dai et al. 2017). In this review, we present recent advances in analyzing Hall effects in terms of KAW eigenmode, as well as the impact of KAW eigenmode on energy conversion in reconnection. The KAW perspective of the Hall fields are valuable in many aspects. The spatial profile and strength of Hall fields may rely on the spacecraft trajectory in observations and/or on the parameters in each run in simulations. KAW perspectives can provide a comprehensive knowledge of the spatial profile and strength of Hall fields. These information are important for understanding the diffusion region as well as evaluating the impact of Hall fields on energy conversion in reconnection. A quantitative description of the electromagnetic fields in the reconnection layer and the corresponding impact on the energy conversion are both needed toward a Petschek-type model in the framework of collisionless reconnection.

The rest of the paper is organized as follows. Section 2 presents theoretical rationales, the modeling, relevant observations, and simulation results that analyze Hall fields in terms of KAW eigenmode of the current layer. A variety of aspects of Hall fields are covered, including the scales, the polarity, the strength of Hall fields, the balance of the Hall electric field with the ion pressure gradient, the quasi-electrostatic nature of the Hall electric field, the electric field parallel to B, the field-aligned current and the propagation of Hall fields away from magnetic reconnection. Section 3 examines the impact of KAW eigenmode (Hall fields) on ion acceleration and energy conversion in reconnection. The Hall electric field significantly impacts the acceleration of ions in reconnection. The extent of this effect is determined by the strength of the Hall electric field that is specified by the KAW physics. The analysis indicates a intrinsic link between the Hall electric field, ion acceleration, the ion non-gyrotropy distribution, the off-diagonal effect in the ion pressure tensor, the ion-scale reconnection electric field, and a fast reconnection rate.

2 KAW eigenmode modeling of Hall fields in magnetic reconnection: theory, observations and simulations

2.1 Rationales of the KAW eigenmode model

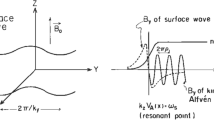
A fundamental rationale for the KAW model of Hall fields is the similarity between KAW and Hall fields in the polarity and scales. Figure 2 illustrates the polarity of the electric field and magnetic field for the shear Alfven waves, KAW and Hall fields.

Fig. 2

A schematic of shear Alfven wave, kinetic Alfven wave(KAW), and Hall fields in reconnection

Figure 2a shows a shear Alfven wave that has a wave vector k in the xz-plane. The perturbation electric field shall oscillate in the ±X direction. The perturbation magnetic field shall oscillate in ±Y in the out-of-plane direction. The electric current of the wave is $\nabla \times \delta {{\textbf {B}}}=i{{\textbf {k}}} \times \delta {{\textbf {B}}}$ and in the xz-plane. The timescale of the variations of the wave fields is much longer than the ion gyroperiod. In both the perpendicular and parallel directions, the spatial scale of the waves 1/k are much larger than ion motion scale. The wave carries a Poynting flux $\delta {{\textbf {E}}} \times \delta {{\textbf {B}}}$ strictly parallel to ${{\textbf {B}}}_o$. The ratio of the wave electric field to the wave magnetic field $|\delta {{\textbf {E}}}|/|\delta {{\textbf {B}}}|$ is exactly one Alfven speed $V_A$.

We consider a KAW with a wave vector k in the xz-plane (Fig. 2b). In many aspects, the KAW is similar to shear Alfven waves. The perturbation electric field is in the ±X direction, the perturbation magnetic field is in ±Y. The electric current of the wave $i{{\textbf {k}}} \times \delta {{\textbf {B}}}$ is still in the xz-plane. The timescale of the variations of the wave field of KAW is much longer than the ion gyroperiod.

Unlike shear Alfven waves, KAW has a perpendicular scale that is comparable to the particle kinetic scale. KAW has a very oblique wave vector $k_\bot>>k_{||}$ so that the wave is not strongly affected by the Landau damping. The spatial scale of the KAW in the perpendicular direction $\sim 1/k_\bot$ is much smaller than that $\sim 1/k_{||}$ in the parallel direction. As illustrated in Fig. 2b, the finite ion gyroradius effect starts to become important as the perpendicular wavelength is comparable to the ion gyromotion (the green circle). Ions can not follow the ${{\textbf {E}}}\times {{\textbf {B}}}$ drift in the electric fields of KAW. This is because ions encounter significantly different electric field in the different phase of the gyromotion. Electrons are still frozen-in in the presence of the wave field. The difference in the ion and electron motion in the perpendicular direction introduces charge separation and coupling to the electrostatic mode (Hasegawa and Uberoi 1978). Because the wave electric field $E_x$ is mainly parallel to the k, $\nabla \times \delta {{\textbf {E}}}=i{{\textbf {k}}} \times \delta {{\textbf {E}}}$ is small and $\nabla \cdot \delta {{\textbf {E}}}=i{{\textbf {k}}} \cdot \delta {{\textbf {E}}}$ is relatively large for KAW. Accordingly, the perpendicular wave electric field $E_x$ is mostly electrostatic in KAW.

Because of charge separation in KAW, electrons need to move along the magnetic field to preserve the charge neutrality. Associated with the parallel motion of electron, a small wave electric field is established. The existence of a parallel electric field is a distinct feature of KAW. The parallel motion of electrons creates the field-aligned current of KAW. As seen from the Ampere’s Law $i{{\textbf {k}}} \times \delta {{\textbf {B}}}=\delta {{\textbf {J}}}$, the field-aligned current $\delta {{\textbf {J}}}_z$ produces a wave magnetic field $\delta {{\textbf {B}}}_y$. As a result, KAW is in fact an electromagnetic mode. The ratio of the wave electric field to the wave magnetic field is $V_A\sqrt{1+k^2_x\rho ^2_i}$ (Stasiewicz et al. 2000). The kinetic correction $k^2_x\rho ^2_i$ introduces a deviation of the ratio $E_x/B_y$ from one $V_A$ as in the shear Alfven waves.

A schematic of the Hall fields in reconnection is shown in Fig. 2c. Hall fields are quasi-steady structures accompanied with a timescale much longer than the ion gyroperiod. The spatial variation of Hall fields is mostly in X, normal to the current layer. The perpendicular scale of the Hall fields is generally considered to be ion-scale. In realistic observations, the perpendicular scale of the Hall fields and current layer can be as small as electron scale as well (Wygant et al. 2005). The parallel scale of the Hall fields are much larger (Wygant et al. 2005; Vaivads et al. 2004). Equivalently, Hall fields are associated with a wave vector k so that $k_x>>k_z$ and $1/k_x$ on the ion-scale. The temporal and spatial scales of Hall fields are exactly the same as those of KAW. The polarity of the Hall electric field (in ±X) and the Hall magnetic field (in ±Y) is also consistent with that of KAW. Similar to KAW, the ratio $|E_x|/|B_y|$ of Hall fields is on the order of Alfven speed (Eastwood et al. 2010; Dai et al. 2017). In addition, the current system of Hall fields are in the xz-plane. The above similarities are expected since KAW and Hall fields are in fact described by the same two-fluid equation in the same regime of temporal and spatial scale.

In the direction parallel to the magnetic field (Z-axis), $B_y$ reverses its sign but $E_x$ remains its sign. This feature is related to the superposition of two KAW mode waves that propagate in the opposite direction and outward from the reconnection region. The implication of the outward propagation of Hall fields are presented in Sect. 2.6. In the perpendicular direction, the Hall fields appears to exist only for one wavelength along the X axis. This is related to the eigenmode (standing mode) structure of KAW in the current layer. The KAW eigenmode solution is described in details in Sect. 2.2.

2.2 The KAW eigenmode structure

The physics underlying the eigenmode solution is from the fact that the reconnection current layer is quite inhomogeneous along the normal direction (x axis). The inhomogeneous scale of the current layer is comparable to the perpendicular scale of the waves. Under this circumstance, both the plane wave solution and the Wentzel–Kramers–Brillouin (WKB) approximation break down (Lysak 2008; Dai 2009). An simplified approach to obtain the equation for KAW eigenmode is to start from the KAW dispersion relation (Lysak and Lotko 1996; Stasiewicz et al. 2000)

$$\begin{aligned} \omega ^2/(k_z ^2V_A^2)=1+k_x^2(\rho _i^2+\rho _a^2), \end{aligned}$$

(1)

where $\rho _i=\sqrt{T_i/m_i\omega ^2_i}$ is the ion gyro-radius, $\omega _i$ is the ion gyro-frequency, $\rho _{a}=\sqrt{T_e/m_i\Omega ^2_i}$ is the ion acoustic gyroradius. From the practice to deal with the Inhomogeneity in the X direction in the mode conversion theory Stix (1992), we could obtain an eigenmode equation by replacing $k_x$ with $-i\partial _x$ in the KAW dispersion relation (1). This approach is also similar to that in obtaining the captured (kinetic) Alfven eigenmode in the homogeneous plasma (Leonovich and Mazur 1989; Fruit et al. 2002). Accordingly, parameters $V_A^2,\rho _i^2$ and $\rho _a^2$ now have a X dependence.

In principle, the KAW eigenmode solution can be obtained from the linearized two-fluid equations (Dai 2009). Readers may skip the technical details and jump to the comparison of the solution with observations following Fig. 3. Notice that the Gaussian units system is applied in Sect. 2.2. The collisionless two-fluid equations are

$$\begin{aligned}{} & {} c\nabla \times {\textbf{B}}=4\pi (\mathbf {J_i+J_e}), \end{aligned}$$

(2)

$$\begin{aligned}{} & {} c\nabla \times {\textbf{E}}=-\partial _t {\textbf{B}}, \end{aligned}$$

(3)

$$\begin{aligned}{} & {} \partial _t(n_sq_s)+\nabla \cdot \mathbf {J_s}=0,\end{aligned}$$

(4)

$$\begin{aligned}{} & {} m_sn_s\partial _t\mathbf {u_s}+m_sn_s(\mathbf {u_s}\cdot \nabla ) \mathbf {u_s}=n_s q_s({\textbf{E}}+\frac{\mathbf {u_s}}{c}\times {\textbf{B}})-\nabla {P}_s, \end{aligned}$$

(5)

s represents the species of ions or electrons. For the moment, Isotropic and isothermal conditions are assumed. The pressure is a scalar $P_s=n_sT_s$. Plasma is quasi neutral so that $n_i\approx n_e$.

We consider a 2D model and apply the approximation of $\partial _y=0$. The Harris sheet (Harris 1962) configuration is used for the reconnection current layer. The background plasma density and magnetic field are $n_s=n_0\textrm{sech}^2(x/a)$ and $B_z=B_o\tanh (-x/a)$. The zero-order current $J_{y}$ is provided by the diamagnetic drifts $u_{s}=2cT_s/q_sB_oa$. a is the thickness scale. To the zero-order, the ${{\textbf {J}}} \times {{\textbf {B}}}$ force is in balance with the pressure gradient force. The equilibrium force balance imposes the relation $n_o(T_e+T_i)=B^2_o/8\pi$ and $u_{i}/T_i=-u_{e}/T_e$.

The two-fluid equations (2, 3, 4, 5) are linearized. We take $\partial _t$ of the x component of (5), eliminating $\partial _t(n_sq_s)$ from (4) and eliminating $\partial _tu_{sy}$ from the y component of (5). The results are

$$\begin{aligned}{} & {} \partial _tE_{x}=4\pi \frac{v_A^2}{c^2}[J_{ix}-\rho _i^2(\partial _{xx} J_{ix}+\partial _{xz} J_{iz})+ \omega _i^{-2}\partial _{tt}J_{ix}\nonumber \\{} & {} +\frac{u_{io}}{\omega _i}(\partial _{x}J_{ix}+\partial _{z}J_{iz})-n_iq_i\frac{E_{y}c}{B_z}]+u_{io}\partial _xE_y,\end{aligned}$$

(6)

$$\begin{aligned}{} & {} J_{ex}=n_eq_e\frac{E_{y}c}{B_z}+\frac{m_ec^2\partial _tE_{x}}{m_i4\pi v_A^2}+\rho _e^2\partial _{xz} J_{ez}-\frac{u_{eo}}{\omega _e}\partial _{z} J_{ez}, \end{aligned}$$

(7)

Eq. (6) are from the ion momentum and Eq. (7) are from the electron momentum. In (7), $\rho _e\partial _x \ll 1$ and $\omega _e^{-1}\partial _t \ll 1$ are assumed.

In the direction parallel to B, the electron pressure gradient dominates the electron inertia term in the KAW (Lysak and Lotko 1996; Stasiewicz et al. 2000). Hence, we neglect the electron inertial term $m_sn_s dt\mathbf {u_e}$ in this equation. Taking $\partial _{t}$ of the Z component of Eq. (5) for electrons, we have

$$\begin{aligned} \partial _tE_z=-(\partial _{zz}J_{ez}+\partial _{zx}J_{ex})T_e/(n_eq^2_e) +u_{eo}\partial _zE_y. \end{aligned}$$

(8)

For the ions in the Z direction, we eliminate $-q_in_iu_{io}B_x/c-\partial _zn_iT_i$ and obtain

$$\begin{aligned} m_in_i\partial _tu_{iz}=q_in_iE_z(1+T_i/T_e). \end{aligned}$$

(9)

We insert (2), (6), and (8) into the $\partial _{t}$ of (3) and then Fourier transform the equation ($\partial _t \sim -i\omega ,\partial _z \sim ik_z$),

$$\begin{aligned} \partial _x\left( \frac{\partial _{x}{\widetilde{B}}_y}{\textrm{sech}^2\,x}\right) +\left( \frac{\omega ^2}{k_z ^2 V_A^2}-\frac{\tanh ^2x}{\textrm{sech} ^2 \,x}\right) \frac{a^2{\widetilde{B}}_y}{\rho _{io}^2+\rho _{ao}^2}=\frac{{\widetilde{S}}}{k_z^2}, \end{aligned}$$

(10)

${\widetilde{S}}(x,\omega ,k_z)$ is the Fourier transform of

$$\begin{aligned} S=\frac{4\pi }{c}\left( \frac{2n_oq_ic}{B_o}\partial _{zx}E_y-n_oq_ia\partial _{zzx}u_{iz}+\partial _{zx}\frac{\partial _x J_{ex}}{\text {sech}^2\,x}-\frac{m_ia^2}{T_i+T_e}\partial _{ttz}J_{ex}\right) . \end{aligned}$$

(11)

In (10), we have neglected $\omega ^2/(\Omega ^2_i\text {sech}^2\,x)$ as compared with $(\omega ^2/k_z ^2 V_A^2-\tanh ^2x/\textrm{sech} ^2 \,x)$ in the limit of low frequency $(\omega ^2/\Omega ^2_i\ll 1)$ and long parallel wavelength $(k^2_zV^2_A/\Omega ^2_i\ll 1)$ (Wygant et al. 2005; Vaivads et al. 2004). Terms of $O(m_e/m_i)$ are also neglected in (10).

Formally, the left-hand side (LHS) of Eq. (10) is the equation of $B_y$ of KAW. Eq. (10) describes the response of KAW eigenmode to the source on the right-hand side (RHS). The fields of KAW eignmode and the source terms are coupled together and shall evolves self-consistently. The response of the sources to the KAW eigenmode are analyzed in the studies (Dai 2009; Dai et al. 2021).

It is tempting to consider the LHS of Eq. (10) as representing the KAW mode, and the RHS of Eq. (10) as representing the coupling to the fast mode ($E_y$, $u_{iz}$ terms). This approach is similar to the analysis of the coupling of transverse mode with fast mode in magnetosphere ULF waves (e.g., Hughes 1994). In the low-$\beta$ and homogeneous plasma, the KAW mode (LHS) decouples from the fast mode (RHS) and the RHS reduces to zero in Eq. (10).

Equation (10) can provide many insights on the structure and evolution of the fields of KAW eigenmode in reconnection. Notice that the source terms ($E_y$, $u_{iz}$ terms) strongly depends on the spatial gradients which are expected to be significant only near the X-line and the outflow channel. In the region away from the X-line, it makes perfect sense to describe the fields of KAW eigenmode using Eq. (10). In the initial phase of reconnection when the source terms are probably small, we may treat source terms as specified perturbations and only consider the KAW eigenmode as a consequence using Eq. (10). As reconnection develops, LHS and RHS may be strongly coupled near the X-line. Then Eq. (10) still formally holds but may be not very useful near the X-line. Because RHS needs to be updated instantaneously to describe the dynamics of the KAW fields in that case.

We set ${\widetilde{B}}_y=\psi \text {sech}\,x$ to transform Eq. (10) to the standard form of a second order differential equation (Morse and Feshbach 1953). Eq. (10) turns into

$$\begin{aligned} \partial _{xx} \psi +[\lambda -1-(R^2+\lambda )\tanh ^2x]\psi ={\widetilde{S}}\textrm{sech}\,x/k_z^2, \nonumber \\ \text {where }\lambda =\frac{\omega ^2R^2}{k_z ^2 V_A^2},R=\frac{a}{\sqrt{\rho _{io}^2+\rho _{ao}^2}}. \end{aligned}$$

(12)

Equation (12) is an inhomogeneous Sturm–Liouville equation. The left-hand side of (12) is a Schrodinger equation with a total energy $E=\lambda -1$ and a potential well $V\tanh ^2x$, $V=R^2+\lambda$. Since $E<V$, the bound-state energy levels $E=V-[\sqrt{V+\frac{1}{4}}-(n+1)]^2$ (see Morse and Feshbach (1953), p.1653) give eigenvalues of $\lambda$

$$\begin{aligned} \lambda _n=(n+1)n+(1+2n)\sqrt{R^2+1}+1. \end{aligned}$$

(13)

The eigenfunctions are

$$\begin{aligned} \psi _n(x)=\frac{F(-n,2\sqrt{V(\lambda _n)+\frac{1}{4}}-n,|b_n+1|,\frac{1}{e^{2x} +1})}{(e^{x}+e^{-x})^{b_n}}, \end{aligned}$$

(14)

where F is the hypergeometric function, $b_n=\sqrt{V(\lambda _n)-E(\lambda _n)}=\sqrt{R^2+1}$. Eigenfunctions are real. $\psi _0(x)$ and $\psi _1(x)$ are

$$\begin{aligned}{} & {} \psi _0(x)=(e^{-x}+e^{x})^{-\sqrt{R^2+1}}, \end{aligned}$$

(15)

$$\begin{aligned}{} & {} \psi _1(x)=(e^{-x}+e^{x})^{-\sqrt{R^2+1}}(e^{2x}-1)/(e^{2x}+1). \end{aligned}$$

(16)

Using the superposition of eigenfunctions (14), we construct the Green’s function for Eq. (12) ( Morse and Feshbach (1953),chapter 7)

$$\begin{aligned}{} & {} G=\sum _n \psi _n^*(x_o)\psi _n(x)/[(\lambda -\lambda _n)\Phi _n^2],\end{aligned}$$

(17)

$$\begin{aligned}{} & {} \Phi _n^2=\int _{-\infty }^{\infty }\psi _n(x)\psi _n^*(x)\textrm{sech}^2\,xdx. \end{aligned}$$

(18)

Using the Green’ function method, we then calculate ${\widetilde{B}}_y$ from equation (12)

$$\begin{aligned} {\widetilde{B}}_y=\textrm{sech}\,x\int _{-\infty }^{\infty }G(x|x_o;\omega ,k_z) \textrm{sech}\,x_o\frac{{\widetilde{S}}(x_o,\omega ,k_z)}{k_z^2}dx_o. \end{aligned}$$

(19)

We replace the Fourier transform with a Laplace transform and solve (19) in the time and space domain. We set $\omega =\omega _r+i \eta , \eta \rightarrow 0^{+},s=\omega /i$, where s is the Laplace transform variable. For simplicity, $B_y|_{t=0}=0,\partial _tB_y|_{t=0}=0$ is the initial condition. We perform the Laplace inversion in time and Fourier inversion in Z for (19). The solution is

$$B_{y} \, = \,\sum\nolimits_{n} {\psi \left( x \right)\text{Sech} \,x\int_{{ - \infty }}^{\infty } {\int_{{ - \infty }}^{\infty } {\int_{{ - 0}}^{t} {\frac{{ - V_{A} \psi _{n}^{ * } \text{sech} \,x_{0} }}{{2\Phi _{n}^{2} \sqrt {\lambda _{n} } R}}} } } \, \times \,H\left[ {\left( {t - t_{o} } \right)V_{A} \sqrt {\lambda _{n} } R^{{ - 1}} - \left| {z - z_{o} } \right|} \right]S\left( {x_{0} ,t_{o} ,z_{o} } \right)dt_{o} dz_{o} dx_{o} .}$$

(20)

H is the step function. $B_y$ is a sum of KAW eigenmodes. Eigenvalue $V_A\sqrt{\lambda _n}R^{-1}$ is the propagation speed of the nth mode. Terms $J_{ix},J_{ez},E_x$ and $E_z$, grouped with $B_y$ are parts of the KAW eigenmode. The $u_{iz},J_{ex}$ and $E_y$ in the source term S represent a coupling to the compressional mode.

Equation (20) has several implications. In symmetric magnetic reconnection, the term S is an odd function of x. This eliminates the generation of even modes. The amplitude factor $1/(\sqrt{\lambda _n}R)$ for the nth mode indicates that the low number modes dominate. With these considerations we compare the n = 1 KAW eigenmode with the observations of Hall fields in Fig. 3. The parameters for the model are $n_o=8cm^{-3},B_o=80nT$ and $a=150km$ from the observation (Mozer et al. 2002). $T_i=5T_e$ is an estimate. In a n = 1 KAW mode $B_y\sim \psi _1(x)\text {sech} x$ and $E_x\sim (V_AR/c\sqrt{\lambda _1})\sinh ^2x [1-(\rho _i^2/a^2)\partial _{xx}+(u_{io}/\omega _i)\partial _x]B_y$. The theoretical result is a good match with observations in the waveform of $B_y$ and $E_x$. The measured amplitude of $B_y$ is taken as an input for the calculated amplitude of $E_x$. The theoretical amplitude of $E_x$ also shows a good agreement with data.

Fig. 3

A comparison between the observations of Hall fields (left) and theoretical model of KAW eigenmode (right) (Dai 2009)

The above comparison with Hall fields is based on the n = 1 KAW eigenmode. In realistic observations, eigenmodes of high n number in principle may exist. The mixture with higher number KAW eigenmodes can account for the complex structure of Hall fields that are occasionally seen in observations and simulations (Ren et al. 2005; Yamada et al. 2006; von der Pahlen and Tsiklauri 2014, 2015; Sang et al. 2019; Tang et al. 2021).

2.3 The Hall electric field in balance with the ion pressure gradient

In the literature, the Hall electric field is usually considered to arise from the ${{\textbf {J}}} \times {{\textbf {B}}}/n_eq$ term in the context of the generalized Ohm’s law (Sonnerup 1979)

$${\mathbf{E}} + {\mathbf{U}} \times {\mathbf{B}} = \frac{{m_{e} \nu _{{ei}} }}{{nq^{2} }}{\mathbf{J}} + \frac{{m_{e} }}{{nq^{2} }}\left[ {\frac{{\partial {\mathbf{J}}}}{{\partial t}} + \nabla \cdot ({\mathbf{J}}U + U{\mathbf{J}} - \frac{{{\mathbf{JJ}}}}{{nq}})} \right] + \frac{1}{{nq}}{\mathbf{J}} \times {\mathbf{B}} - \frac{1}{{nq}}\nabla \cdot \overline{P} _{e} ,$$

(21)

where U is the MHD-fluid bulk velocity, $\nu _{ei}$ is the electron-ion collision frequency. The generalized Ohm’s law is obtained by multiplying the momentum Eq. (5) by the charge of each species and adding them. The first term on the right-hand side of Eq. (21) is the resistivity due to the electron-ion collision. The additional terms on the right-hand side give corrections to the simple Ohm’s law when the small-scale physics is considered.

The argument for the origin of the Hall electric field is as follows: the ${{\textbf {J}}} \times {{\textbf {B}}}/n_eq$ term in Eq. (21) starts to become important at the ion inertial scale, contributing to the Hall electric field. However, the ${{\textbf {J}}} \times {{\textbf {B}}}$ in fact also represents a major force term in the one-fluid MHD momentum equation. In general the ${{\textbf {J}}} \times {{\textbf {B}}}$ force term could be important on the large MHD-scale and the argument for the origin of Hall electric field becomes ambiguous. Physically, the ${{\textbf {J}}} \times {{\textbf {B}}}$ term is equivalent to the ion inertial effect, ion pressure effect and the electron pressure effect as seen clearly in the MHD momentum Eq (22) (Terasawa 1983).

$$\begin{aligned} \rho \frac{{\textbf {dU}}}{dt}+\nabla \cdot (\overline{\texttt {P}}_i+\overline{\texttt {P}}_e)={{\textbf {J}}}\times {{\textbf {B}}}. \end{aligned}$$

(22)

The MHD momentum Eq (22) is the sum of the two-fluid momentum equations multiplied by the mass of each species. The one-fluid MHD momentum equation Eq.(22) together with the general Ohm’s law (21) is nearly equivalent (with some extent of reduction) to the two-fluid momentum Eqs. (5) for two species. The first set of equations is (22–21) and the second set is (5) for two species. The Hall electric field is equivalently described by either set of equations.

Since the Hall electric fields are considered to arise at the ion scale when ${{\textbf {E}}}+{{\textbf {V}}}_i\times {{\textbf {B}}} \ne 0$, we explore the physics of Hall electric field from the two-fluid momentum equation instead of the general Ohm’s law.

$$\begin{aligned} {{\textbf {E}}}+{{\textbf {v}}}_i \times {{\textbf {B}}}=(1/n_iq_i)\nabla \cdot \overline{\texttt {P}}_i+(m_i/q_i)d{{\textbf {v}}}_i/dt. \end{aligned}$$

(23)

The perpendicular component of the non-ideal electric field ${{\textbf {E}}}+{{\textbf {v}}}_i \times {{\textbf {B}}}$ is the Hall electric field at the ion kinetic scale. As seen in Eq. (23), two sources of Hall electric fields are the ion inertial term and the ion pressure gradient.

From the KAW perspective, the Hall electric field is supported by the ion pressure gradient. In the regime of the temporal and spatial scale of KAW, the ion inertial term $(m_i/q_i)d{{\textbf {v}}}_i/dt$ is small and on the order of O($\omega ^2/\Omega _i^2$), where $\Omega _i$ is ion gyro frequency(Stasiewicz et al. 2000).

If the ion inertial term is neglected, Eq. (23) becomes

$$\begin{aligned} {{\textbf {E}}}+{{\textbf {V}}}_i \times {{\textbf {B}}}\approx (1/n_iq_i)\nabla n_iT_i. \end{aligned}$$

(24)

We keep the ${{\textbf {V}}}_i \times {{\textbf {B}}}$ term. The ion flow convection ${{\textbf {V}}}_i \times {{\textbf {B}}}$ may not be neglected near the X-line (Cassak and Shay 2007). We shall show explicitly that the above Eq. (24) of Hall electric field is consistent with KAW dispersion.

To do this, we transform Eq. (24) in the similar way of obtaining KAW dispersion from the linearized momentum equation. Taking the $\partial _t$ of the X component of Eq. (24) and rearranging the terms, we have the following equation(Dai et al. 2017),

$$\begin{aligned} J_{ix}-\rho _i^2 \nabla _{xx}J_{ix}=\frac{\partial _tE_x}{\mu _oV^2_A}+\frac{n_iq_iE_y}{B_z}. \end{aligned}$$

(25)

The second term $\rho _i^2 \nabla _{xx}J_{ix}$ on the left-hand side is the finite gyroradius effect. The origin of this correction is from the ion pressure gradient in the momentum equation.

Above Eq. (25) is consistent with the KAW equation from the kinetic approach (Cheng 1991; Lysak and Lotko 1996; Streltsov et al. 1998),

$$\begin{aligned} {\tilde{J}}_{ix}=-i\omega \epsilon _o\frac{c^2}{V^2_A}\frac{1-e^{-\mu }I_o(\mu )}{\mu }{\tilde{E}}_x, \end{aligned}$$

(26)

where $\mu =k^2_x\rho ^2_i$ and $I_o$ is the modified Bessel function. In the original derivation of KAW, Hasegawa (1976) used a $\mu<<1$ approximation in the long wavelength limit. Instead, we use a Pade approximation $[1-e^{-\mu }I_o(\mu )]/\mu \approx 1/(1+\mu )$ that applies for an arbitrary perpendicular wavelength (Johnson and Cheng 1997; Stasiewicz et al. 2000; Lysak 2008). Applying the Pade approximation, we have the following equation for KAW,

$$\begin{aligned} (1+\rho _i^2k^2_x){\tilde{J}}_{ix}=-i\omega \frac{{\tilde{E}}_x}{\mu _oV^2_A}. \end{aligned}$$

(27)

$-\rho _i^2k^2_x{\tilde{J}}_{ix}$ is the correction due to finite gyroradius. Replacing $ik_x$ with $i\partial _x$, and $-i\omega$ with $\partial _t$, we immediately find that Eq. (27) recovers most of Eq. (25). The $\hbox {E}_y$ term is not a component of KAW. The similar format between Eqs. (27), (25) confirms the following fact: the contribution to the Hall electric field $E_x$ from the ion pressure gradient represents the finite ion gyroradius effect in KAW.

Fig. 4

An overview of THEMIS observations of magnetopause reconnection and Hall electric field on Feb 13, 2013. The Hall electric field is estimated in balance with the ion pressure gradient term (Dai et al. 2015)

Fig. 5

A comparison between the non-ideal Hall electric field ${{\textbf {E}}}- {{\textbf {V}}}_i\times {{\textbf {B}}}$ and the ion pressure gradient term $(1/n_iq_i)\nabla \cdot \texttt {P}_i$ in particle simulations in a the whole domain, b the proximity of X line, c the separatrix region, d and the downstream of separatrix (Huang et al. 2018)

Consistent with the above analysis, observations confirmed that the Hall electric field is mainly supported by the the ion pressure gradient (Burch et al. 2016b; Wang et al. 2016; Dai et al. 2015; Zhang et al. 2016). One example is presented in Fig. 4 showing an observation of magnetopause reconnection from THEMIS-E on Feb 13, 2013 (Dai et al. 2015). The LMN coordinate system from the the minimal variance analysis is N (– 0.78,0.59,0.21) GSM, L=(– 0.07, – 0.42, 0.90) GSM and M completing the right handed coordinate system. In this event, THEMIS spacecraft crosses the reconnection X-line in the north-south direction (Fig. 4a).

Figure 4h indicates that the electric field significantly deviates from the convection electric field $-{{\textbf {v}}_i}\times {\textbf {B}}$. This is evidence of THEMIS-E encountering the ion diffusion region. Within the diffusion region, a Hall electric field E$_N+{{\textbf {v}}_i}\times {\textbf {B}}$ $\sim$7–10 mV/m is found in the normal direction.

Based on observations, we estimate the magnitude of the terms in the ion momentum equation. In the normal direction, (E$+{{\textbf {v}}_i}\times {\textbf {B}})_{N}$ is 7–10 mV/m in the diffusion region. This is close to the pressure gradient $(\partial \texttt {P}_{NN}/\partial N+ \partial \texttt {P}_{LN}/\partial L)/n_iq_i$. The major contribution to the pressure gradient term is $\sim$7.8 mV/m from the $\Delta \texttt {P}_{NN}$. V$_N$ $\sim$– 70km/s, $\Delta$V$_M$ $\sim$130 km/s, and the ion inertial term $(m_i/q_i)$V$_N$ $\Delta$V$_N$/$\Delta$N is less than 0.3 mV/m.

The Hall electric field supported by the ion pressure gradient is also verified in the Particle-in-Cell (PIC) simulation (Huang et al. 2018). Figure 5 shows the comparison of Hall electric field $E_{Hall}$ in the perpendicular direction (Y-axis in this case), the ion convection term $(V_i \times B)_{\bot }$, the ion pressure gradient term $((1/n_iq_i)\nabla \cdot \texttt {P}_i)_{\bot }$ and the ion inertial term $(m_i/q_i)(dV_i/dt)_{\bot }$ in different regions of the reconnection. The comparison indicates that the Hall electric field is mainly in balance with the ion pressure gradient term. The ion convection term and the inertia term are small. This result is consistent with KAW physics and observations.

2.4 The ratio of Hall electric field and Hall magnetic field

Fig. 6

The $<E_{Hall}>/<B_{Hall}>$ as compared with the Alfven speed. The $<>$ represents the mean squire-root power of the field in a specific region (Huang et al. 2018). Region 1 is near the X-line. Region 2 is the downstream of separatrix

Fig. 7

The $<E_{Hall}>/<B_{Hall}>$ as compared with the Alfven speed for simulations runs with different values of a (thickness of the Harris current sheet) (Huang et al. 2018) . Blue, black and red line represent runs with $a=1.0d_i$, $a=0.5d_i$ and $a=0.25d_i$, respectively. $d_i$ is the ion inertial length

For the shear Alfven wave, the ratio of the perpendicular electric field to the perpendicular magnetic field is exact one Alfven speed. For KAW, the ratio $E_x/B_y$ is (Stasiewicz et al. 2000).

$$\begin{aligned} E_x/B_y=\frac{\omega }{k_z}=V_A\sqrt{1+k^2_x\rho ^2_i}. \end{aligned}$$

(28)

For the KAW eigenmode, the $E_{Hall}/B_{Hall}$ is also on the order of the Alfven speed as described in Eq. (12)

$$\begin{aligned} E_{Hall}/B_{Hall}=\frac{\omega }{k_z}=\lambda ^{0.5}V_A/R. \end{aligned}$$

(29)

The $E_{Hall}/B_{Hall}$ for KAW eigenmode and KAW plane waves are quite similar. In the case of KAW eigenmode, the perpendicular scale $1/k_{\bot }$ of the wave is about the thickness of the current layer. Therefore, $R\sim a/\rho _i \sim 1/k_{\bot }\rho _i$ and $E_{Hall}/B_{Hall} \sim V_A\lambda ^{0.5}k_{\bot }\rho _i$. This is close to Eq. (28) when waves are of ion-scale in the perpendicular direction ($k_{\bot }\rho _i \sim 1-10$). This consistence is expected. Because the same physics (the perpendicular ion-scale) is responsible for the increase of $E_{Hall}/B_{Hall}$.

Spacecraft observations conform that the ratio of the Hall fields is about Alfven speed as listed in Table 1. $\Delta E_n$ and $\Delta B_m$ in the table represent the peak values of Hall fields. These observations of Hall fields confirmed the prediction of the KAW physics. This feature is also confirmed in the statistic study of multiple reconnection with Cluster spacecraft (Eastwood et al. 2010).

Table 1 The comparison of the ratio of Hall fields ($E_n/B_m$) with Alfven speed in previous observations (Dai et al. 2017)

PIC simulations also verify the ratio of the Hall fields in collisionless reconnection (Huang et al. 2018). Figure 6 is the temporal evolution of $<E_{Hall} >/< B_{Hall}>$ in reconnection. $<E_{Hall}>$ is the square root of the average power $|E_{Hall}|^2$ in a region. Similarly, $<B_{Hall}>$ is the square root of the average power $|B_{Hall}|^2$ in a region. Because $E_{Hall}$ is not in phase with $B_{Hall}$ near the diffusion region. We need to use the average power in a region to evaluate the ratio. The simulation result of $<E_{Hall} >/< B_{Hall}>$ shown in Fig. 6 is generally a few Alfven speed and consistent with KAW prediction.

According to Eq. (29), $E_{Hall}/B_{Hall}$ is impacted by perpendicular scale of the current layer. A thinner current layer corresponds to smaller perpendicular scales of KAW and a larger ratio $E_{Hall}/B_{Hall}$. In Fig. 6 the simulation run is conducted with $a = 0.5d_i$. Figure 7 shows the comparison of $E_{Hall}/B_{Hall}$ for different thicknesses $a = 0.25d_i,a = 0.5d_i$ and $a = 1.0d_i$. The results show that a larger ratio $E_{Hall}/B_{Hall}$ is associated with a thinner current layer. This is in consistence with the KAW predictions.

2.5 Hall electric field and parallel electric field

Fig. 8

The electrostatic component and electromagnetic component of the Hall electric field in reconnection in the PIC simulations (Lu et al. 2021)

Fig. 9

The electrostatic component and electromagnetic component of the parallel electric field in magnetic reconnection in the PIC simulations Lu et al. (2021)

As described in Sect. 2.1, the perpendicular Hall electric field is a quasi-electrostatic field. The wave vector k of KAW is nearly parallel to the perpendicular Hall electric field. However, it should be clear that the electric field of KAW is not completely electrostatic. The perpendicular electric field, the parallel electric field, and together with the Hall magnetic field indicate an electromagnetic mode.

PIC simulations show that the Hall electric field are mostly electrostatic but with some magnetic induced component (Lu et al. 2021). For the Hall electric field, Fig. 8 shows the composition of its electrostatic component and its electromagnetic component (Lu et al. 2021). The electrostatic component is defined as $E_1=-\nabla \varphi$ and thus $\nabla \times E_1 = 0$. The electromagnetic component is defined as $E_2=-\partial {{\textbf {A}}}/\partial t$ and thus $\nabla \cdot E_2 = 0$. The electrostatic component is found about ten times larger than the induced electromagnetic component. The Hall electric field is dominated by the electrostatic component. But the induced electromagnetic component is finite. The electromagnetic component is due to the time variations of the Hall $B_y$ (Lu et al. 2021).

The parallel electric field associated with the KAW mode is very small and difficult to measure in the space. The existence of a parallel electric field associated with Hall fields is verified in PIC simulations (Lu et al. 2021). The composition of the parallel electric field is examined in Fig. 9. The magnitudes of the electrostatic component and the electromagnetic component are comparable. This is expected because $E_{||}$ is mostly perpendicular to the ‘wave vector’ k of the KAW eigenmode. Hence ${{\textbf {k}}} \times E_{||}$ should be finite, which is more consistent with an induced electromagnetic component. The existence of the parallel electric field associated with KAW eigenmode produces a potential well. The potential well can trap and accelerate electrons in the parallel direction (Egedal et al. 2005, 2012).

2.6 The propagation of Hall fields

Fig. 10

2D overview of the Hall magnetic field $B_y$ and the associated parallel Poynting flux in PIC simulations (Shay et al. 2011)

Fig. 11

The time evolution of the Hall electric field and Poynting flux in the simulations of collisionless magnetic reconnection (Huang et al. 2018). The left column shows the time evolution of Hall electric fields. The middle column shows the time evolution of Poynting flux. The right column shows the time evolution of the wave-number spectrum

One interesting prediction of Hall fields from the KAW physics is the propagation of the fields from the reconnection along the magnetic field. Although the ‘wave-vector’ of KAW is mostly perpendicular to B, the Poynting flux(energy flux) of KAW mode is nearly parallel to B. The complete knowledge of the temporal evolution of the Hall fields during the magnetic reconnection is complicated and remains to be explored. In PIC simulations, however, we see that the Hall fields indeed extend along the magnetic field line and propagate outward from the X-line (Shay et al. 2011; Huang et al. 2018).

Fig. 12

An overview of the THEMIS observations of the Hall field as propagating KAW eigenmode in the near-Earth plasma sheet (Duan et al. 2016). a Electron particle flux; b electron pitch angle distribution; c the perturbations of the electric field, $\delta E_x$ (blue), $\delta E_y$ (green), and $\delta E_z$ (red); d the perturbation magnetic field, $\delta B_y$ (green) and $\delta B_z$ (red); e The local Alfven speed $V_A$ (black), the predicted propagation speed of KAW eigenmode, $V^{*}_A$ (red), and the ratio of $\delta E_z$ to $\delta B_y$, $V_{EB}$ (green); f the Poynting flux, $S_x$ (blue), $S_y$ (green), and $S_z$ (red), g the parallel (blue) and total (pink) Poynting flux

Fig. 13

MMS observations of two events of the propagating Hall fields in the separatrix region at a large distance from magnetotail reconnection (Sergeev et al. 2020). Panels from top to the bottom: a Proton omni-directional energy spectrogram, b the distance of the X-line from a fit of the proton speed; c the convection velocity along the normal to the neutral sheet (green trace) and timing velocities along N; d 1-second averaged GSE $E_y$ and $E_z$ ; e 1-second averaged GSE magnetic field; f plasma beta. Yellow vertical strip marks the interval of intense Hall field $E_z$

Figures 10 and 11 show similar features of the propagation of Hall fields outward from the X-line (Shay et al. 2011; Huang et al. 2018). Figure 10 shows the distribution of the Hall $B_y$ (top panel) and the parallel Poynting flux (bottom panel). The parallel Poynting flux associated with the Hall field is intense and outward along the magnetic field near the separatrix. The origin of these parallel Poynting flux is from the extension of the Hall fields in the diffusion region. Figure 11 shows the temporal evolution of the Hall electric field and parallel Poynting flux. The Hall electric field and the associated Poynting flux first appear near the diffusion region. As reconnection evolves, the Hall fields and the Poynting flux grow and become intense. The Hall fields and the Poynting flux extend outward and along the magnetic field of the separatrix.

The outward propagation of the Hall fields is also reported in THEMIS and MMS observations (Duan et al. 2016; Sergeev et al. 2020; Zhang et al. 2022; Nakamura et al. 2004). Figures 12 and 13 show the observations of Hall-type fields near the plasma sheet boundary layer at a long distance from the expected magnetotail reconnection X-line.

Observations from the THEMIS on Feb 3,2008, are shown in Fig. 12. THMIS-D observes pulses of electric field and magnetic field during the transition from the plasma sheet boundary layer (PSBL) to the plasma sheet center. The pulse is associated with a field-aligned current going toward Earth, as indicated in the electron pitch angle distribution. The major wave components of the pulse are a $E_z$ toward $Z=0$ and a duskward $B_y$. The polarity of these fields is consistent with that of the Hall fields in reconnection as displayed in the cartoon at the top of Fig. 12. The observed ratio $E_z/B_y$ for the pulses is a few Alfven speed. The Poynting flux of the pulse is mostly in the field-aligned direction toward Earth. These features are consistent with KAW eigenmode, suggesting that Hall fields and currents propagate outward as KAW eigenmode from magnetic reconnection.

Figures 13 shows MMS observations of strong Hall-type fields associated with intense FACs in the separatrix region at a long distance (>100 ion inertial length) from the active magnetotail X-line. The distance to the reconnection X-line is inferred from the energy dispersion of ions in Fig. 13a. The MMS spacecraft is located at several Earth radius from ongoing magnetotail X-line. MMS observes intense pulse of electric and magnetic field. A Hall-type electric field is observed in $E_z$. This $E_z$ is associated with variations of $B_y$ in the plasma sheet boundary layer (d1 and d2). The polarity of the $E_z$ and $B_y$ is consistent with that of the Hall field near the X-line. The ratio $E_z/B_y$ are found close to Alfven speed, indicating that these fields are Alfvenic.

2.7 The KAW eigenmode in asymmetric reconnection

In symmetric magnetic reconnection, the Hall magnetic field usually exhibit a quadrupolar pattern (Birn et al. 2001; Zhou et al. 2019). The pattern of Hall fields in asymmetric reconnection is far more complicated. In asymmetric reconnection, a bipolar (Mozer et al. 2008; Tanaka et al. 2008; Pritchett 2008) or quadrupolar (Denton et al. 2016; Zhang et al. 2017; Lavraud et al. 2016; Wang et al. 2017; Peng et al. 2017) Hall magnetic field are observed by THEMIS and MMS.

From the perspective of KAW eigenmode, the quadrupolar pattern is from n = 1 KAW eigenmodes. The asymmetry in the plasma density and magnetic fields breaks the symmetry in the source term for Hall fields in Eqs. (11), (20). In particular, this changes the Alfven speed profile that is important for the structure of KAW eigenmode. As a result, KAW eigenmodes other than the n = 1 mode can occur and cause more complicated patterns in asymmetric reconnection. The structure of Hall magnetic fields is analyzed as follows (Dai 2018).

Fig. 14

A cartoon of the asymmetric reconnection and the profile of the magnetic field, plasma density and the Alfven speed (Dai 2018)

Figure 14 shows the model profile of the magnetic field, plasma density, and the Alfven speed for a dayside magnetopause reconnection. In this asymmetric current layer, the magnetic field and density are modeled as

$$\begin{aligned}{} & {} \frac{B_z}{B_s}\equiv B(x)=\frac{1+C_1}{2}-\frac{1-C_1}{2}\tanh (x/d), \quad C_1=\frac{B_{sp}}{B_s},\end{aligned}$$

(30)

$$\begin{aligned}{} & {} \frac{N}{N_s}\equiv N(x)=1+\frac{1-C_2}{C_1^2-1}-\frac{1-C_2}{C_1^2-1}\left[ \frac{1+C_1}{2}-\frac{1-C_1}{2}\tanh (x/d)\right] ^2, \quad C_2=\frac{N_{sp}}{N_s}. \end{aligned}$$

(31)

$B_s$ and $N_s$ are the field and density in the magnetosheath field, $B_{sp}$ and $N_{sp}$ are the field and density in the magnetosphere, d is the scale of the current layer. The guide field is zero for simplicity. We first use the profile of magnetic field from an asymmetric current layer (Allanson et al. 2017). Then the plasma density is obtained from the force balance.

To obtain the eigenmode equation of KAW in the asymmetric current layer, we start from the dispersion relation for KAW plane waves Eq. (1). Because the inhomogeneity is in the X direction, we replace $k_x$ with $-i\partial _x$ and assign the X dependence of $V_A$ and $\rho$. This is a procedure usually used in the mode conversion calculation (Stix 1992). After some simplifications, the equation for the Hall $B_y$ becomes

$$\begin{aligned} \left( \frac{d^2}{dx^2}+R^2\left( \lambda N(x)-B^2(x) \right) \right) B_y(x,\omega ,k_z)=0, \end{aligned}$$

(32)

R is $d/\rho _s$, $\lambda =\omega ^2/(k_z^2V_{As}^2)$. Eq. (32) is a Schrodinger-type equation and can be written as

$$\begin{aligned} \left( \frac{d^2}{dx^2}+\epsilon -A_1\left( \tanh \left( x\right) +A_2\right) ^2 \right) B_y=0,\nonumber \\ \epsilon =R^2\lambda \frac{C_1^2-C_2}{C_1^2-1}, \quad A_1=\frac{R^2(1-C_1)^2}{4}\left( \frac{\lambda (1-C_2)}{C_1^2-1}+1\right) ,\quad A_2=\frac{C_1+1}{C_1-1}. \end{aligned}$$

(33)

If $C_1=-1$ and $C_2=1$, the current layer becomes symmetric and Eq. (33) returns to the equation in the symmetric current layer. The eigenmode solutions of Eq. (33) are (Morse and Feshbach 1953)

$$\begin{aligned} \psi _n=\frac{e^{-a_nx}}{\left( e^x+e^{-x}\right) ^{b_n}}F\left( -n,2b_n+n+1,\left| a_n+b_n+1\right| ,\frac{e^{-x}}{e^x+e^{-x}}\right) ,\nonumber \\ a_n=\frac{A_1A_2}{\sqrt{A_1+1/4}-(n+1/2)}, b_n=\sqrt{A_1+1/4}-(n+1/2),\epsilon _n=A_1(1+A_2^2)-b_n^2-a_n^2, \end{aligned}$$

(34)

$\psi _n$ gives the X dependence of structure. In particular, $\psi _0$ and $\psi _1$ sfor the asymmetric current layer are

$$\begin{aligned}{} & {} \psi _0\sim \frac{e^{-a_0x}}{\left( e^{-x}+e^{x}\right) ^{-b_0}}, \end{aligned}$$

(35)

$$\begin{aligned}{} & {} \psi _1\sim \frac{-e^{-a_1x}}{\left( e^{-x}+e^{x}\right) ^{-b_1}}\frac{\left( e^{2x}+1-(2+2b_1)/\left| a_1+b_1+1\right| \right) }{e^{2x}+1}. \end{aligned}$$

(36)

Fig. 15

a The profile of the n = 0 KAW eigenmode and the associated bipolar Hall magnetic field. b The profile of the n = 1 KAW eigenmode and the associated quadrupolar Hall magnetic field (Dai 2018)

Fig. 16

The profile of Hall fields $B_y$ showing a mixture of $n=0$ and $n=1$ KAW eigenmodes (Dai 2018). Left: $\psi _0+2\psi _1$. Right: $\psi _0+1.5\psi _1$

KAW eigenmodes are excited near the diffusion region. In the $\pm Z$ direction, outgoing KAW eigenmodes are superposed on each other so that $B_y$ is zero (node) and $E_x$ is maximum (anti-node) at $Z=0$. According to this, we use a pulse $\exp (-z^2/L[t]^2)$ to mimic the Z dependence of Hall electric fields $E_x$. Then $B_y$ ($\sim -\partial _z E_x$) has a Z dependence of $(2z/L^2)\exp (-z^2/L^2)$. L is related to the extending scale of Hall fields in the $\pm Z$.

Applying typical parameters $R=3$, $B_{sp}/B_s=-2$, and $N_{sp}/N_s=0.1$, we compute the profile of Hall $B_y$ as illustrated in Fig. 15. The $n=0$ KAW eigenmodes produces the bipolar $B_y\sim \psi _0(x)(2z/L^2)\exp (-z^2/L^2)$. As a comparison, the $n=1$ KAW eigenmodes makes the quadrupolar $B_y\sim \psi _1(x)(2z/L^2)\exp (-z^2/L^2)$.

In principle, the $n=0$ mode and the $n=1$ mode can occur together. Higher n eigenmodes are also possible to exist (von der Pahlen and Tsiklauri 2014, 2015; Sang et al. 2019; Tang et al. 2021). Under these conditions, the pattern of Hall magnetic fields becomes more complicated. The profile of $\psi _0+2\psi _1$ and $\psi _0+1.5\psi _1$ are illustrated in Fig. 16. The Hall $B_y$ exhibits small-scale quadrants on the high Alfven speed side. This feature has been seen observed in some asymmetric reconnection (Lavraud et al. 2016; Wang et al. 2017).

3 Ion acceleration in the context of KAW eigenmode/Hall fields

Section 2 describes the properties of the KAW eigenmode in magnetic reconnection. In this Sect. 3, we present analysis on how KAW eigenmode (Hall fields) affect ion acceleration and energy conversion in collisionless reconnection (Dai et al. 2021). The magnetic energy are mostly converted to the kinetic energy of the ion bulk in reconnection (Parker 1957; Petschek 1964; Paschmann et al. 1979; Phan et al. 2000).

In the context of collisionless reconnection, energy conversion and the reconnection rate ($\sim 0.1$) is generally considered to be fast. Meanwhile, Hall fields/KAW eigenmode are usually considered as a working definition of collisionless reconnection. It is thus of high interest to explore the link between Hall fields/KAW eigenmode and the fast reconnection rate.

3.1 Theoretical analysis

Fig. 17

Ion motion without (panel a) and with (panel b) Hall fields in collisionless magnetic reconnection (Dai et al. 2021)

The ion motion in a reconnection without Hall fields has been studied in the Speiser orbit (Speiser 1965). In the Speiser orbit, the fields that act on particles is the reconnection electric field and magnetic field of the current layer (Fig. 17a). In addition to these fields, the Hall electric field $E_z$ and Hall magnetic field $B_y$ can act on particles as well In a collisionless reconnection.

Notice that the coordinate in Fig. 17 in this section is different from that in Sect. 2. In this coordinate, the equations for ion particles are

$$\begin{aligned}{} & {} {\mathop {V_x}\limits ^{.}}=V_y\cdot B_z-V_z\cdot B_y, \end{aligned}$$

(37)

$$\begin{aligned}{} & {} {\mathop {V_y}\limits ^{.}}=E_y-V_x\cdot B_z+V_z\cdot B_x, \end{aligned}$$

(38)

$$\begin{aligned}{} & {} {\mathop {V_z}\limits ^{.}}=E_z+V_x\cdot B_y-V_y\cdot B_x. \end{aligned}$$

(39)

The normalization has been done with respect to the magnetic field $B_0$ just outside the current layer, the density $n_0$ at the current layer center, the ion gyro-period $1/\Omega _{i}=m_i/q_iB_0$, the Alfven speed $V_A$, the electric field $B_0V_A$, and the ion inertial length $d_{i}=V_A/\Omega _{i}$.

We first present the qualitative picture of ion motion without solving the equations. In the Speiser orbit, $E_y$ first accelerates ions inside the current layer. Increases in $+V_y$ cause a restoring force $-V_yB_x$ and an oscillation motion in $\pm Z$ within the current layer. In the XY plane, ions also undergo a gyro-motion around $B_z$. When $V_x$ is sufficiently large, these types of motion in Z/XY plane stop and ions leave the current layer.

The acceleration in the Speiser orbit is Fermi acceleration. The acceleration of particles can be thought from the the reflection by a moving magnetic mirror. In the moving frame toward $+X$ at speed $E_y/B_z$, the electric field is zero and the $V_x$ of incoming ions simply reverse the direction. Thus ions with $V_{x-in}$ in the laboratory frame end up with a final velocity $2E_y/B_z-V_{x-in}$ (Fig. 17 left). The acceleration in X depends on the $E_y/B_z$ (the moving speed of the magnetic mirror).

The Hall fields makes modifications on the ion acceleration. Ions are first accelerated by the Hall electric fields ($E_z$) that is much larger than $E_y$. The acceleration induces a $V_z$ that turns into $V_y$ and $V_x$ due to the gyro-motion. After the first crossing of the neutral sheet $Z=0$, $E_z$ becomes a restoring force in Z and ion motion becomes similar to the Speiser orbit.

The Hall electric fields impact the amount of ion acceleration. In contrast to the Speiser-orbit, the Hall electric field now produces an extra boost in the $-V_y$ for the initial velocity. The $|-V_y|$ is roughly $V_A$ due to the energization by $E_z\sim B_0V_A$ over $a\sim V_A/\Omega _i$. In the later stage of the gyro-motion around $B_z$, ions shall reach the point of $V_x=V_{k}=(\sqrt{2}-1)V_A$ toward the X-line and later the point of an enhanced deflection in $+V_y$ as large as $\sqrt{2} V_A$. Ions shall end up with the final outward velocity $2E_y/B_z-(V_{x-in}-|V_{k}|)$. Ion acceleration is enhanced than that for the Speiser orbit.

If its initial velocity $|V_x|$ is large ($>V_A$), ion can quickly leave the diffusion region and Hall fields. Under those conditions, the impact of Hall fields shall be small and ion motion becomes similar to the Speiser orbit. In the inflow region, the core/thermal populations of ions have small initial $|V_x|$. The theoretical estimate mostly applies to these ion populations.

We use test particle calculations to confirm the qualitative analysis. The magnetic and electric fields are $B_x=\tanh (z/a)$, $B_z=0.1 sign(x)$, $a=1.0$, and $E_y=0.1$. We use Eqs. (40)–(41) to mimic the Hall fields and neglect their slow time-variations,

$$\begin{aligned}{} & {} E_z=\exp (-x/L)^2 \varphi (z/a), \end{aligned}$$

(40)

$$\begin{aligned}{} & {} B_y=(1/A)\exp (-x/L)^2 (2x/L) \varphi (z/a), \end{aligned}$$

(41)

$$\begin{aligned}{} & {} \varphi (z/a)=C(e^{-z/a}+e^{z/a})^{-\sqrt{R^2+1}}(1-e^{2z/a})sech(z/a)/(e^{2z/a}+1). \end{aligned}$$

(42)

$\varphi$ is the $n=1$ KAW eigenmode. Figure 18 shows the profiles of the Hall $E_z$ and $B_y$ for the calculation. The parameters are $L=50$, $A=(3+3\sqrt{R^2+1})^{1/2}/R$, $R=a/(\rho _{ion}\sqrt{1+T_e/T_i})=2.0$, $\rho _{ion}=\sqrt{2}$, and $C=15$.

Fig. 18

The Hall fields $E_z$ and $B_y$ for the test particle calculation (Dai et al. 2021). See text for details

For the test particle calculation, the initial position is ($X=6.0$, $Y=0.0$, $Z=3.0$) and the initial velocities are $V_x=0.0$, $V_y=[-0.5,0,0.5]$, and $V_z=[-0.5,0.0,0.5]$. This set up corresponds to a large part (core and thermal) of inflow ions in the velocity space. Because of Liouville’s theorem, the density of ions in the phase space remains unchanged in the ion’s trajectory. Hence our test particle calculations effectively trace a large part of ions in the phase space. In this sense, our test-particle calculations may provide quantitative estimates for the magnitude of the kinetic effects.

Fig. 19

Results of test particle calculations with (red) and without (blue) Hall fields in magnetic reconnection (Dai et al. 2021). High-intensity lines denote ion trajectories with small initial energies and thus a large density in the phase space. See text for details

Figure 19 presents results of the calculations. The Hall electric field deflects ion in $V_x$ before the acceleration. The deflection of $V_x$ before acceleration is as large as $\sim -0.5V_A$ in Fig. 19c, consistent with the estimate ($V_k\sim -0.4V_A$). During the acceleration, there is significant deflection in $+V_y$ due to the Hall fields. The deflection of $V_y$ is found $\sim +1.6V_A$ near $t=30\sim 40$ in Figs. 19c, 19e. After the acceleration, $V_x$ finally reaches $2E_y/B_z-V_k \sim 2.4V_A$ with the presence of Hall fields. By contrast, $V_x$ only reaches $2E_y/B_z=2V_A$ in the Speiser-orbit (Fig. 19d). These test-particle calculations results confirm the kinetic effects as suggested in the qualitative analysis.

Figure 19i, j shows that the ion energization is increased in the presence of Hall fields, consistent with previous studies (Wygant et al. 2005; Nagai et al. 2015; Aunai et al. 2011). The acceleration along the outflow direction X and the velocity spread perpendicular to ${{\textbf {B}}}$ both make contributions to the energization. The Hall electric field can cause ion thermalization in the perpendicular direction (Drake et al. 2009; Liang et al. 2017; Duan et al. 2017).

3.2 The ion kinetic imprint in observations

Using MMS observations, we identify the kinetic imprints of ion acceleration as suggested in the theoretical analysis. A magnetotail reconnection event near (– 24.0, – 0.30, 4.5) Re GSE is shown in Fig. 20. The observation data are from the fluxgate magnetometer, electric field double probes, and the fast plasma investigation onboard MMS spacecraft (Burch et al. 2016a; Russell et al. 2016; Ergun et al. 2016; Lindqvist et al. 2016; Pollock et al. 2016). The parameters of this reconnection are $B_0=10 nT$, $n_0=0.4/cm^3$, $d_{i}=365km$, $V_A=344km/s$, $\Omega _{i}=0.94Hz$, Hall $B_{y}=5.0nT$,Hall $E_{z}=7mv/m$, $E_{z}/B_0=2.0V_A$, $E_{z}/B_{y}\sim 4.0V_A$, $T_i/T_e=5.0$, $T_i=2keV$.

Fig. 20

Magnetotail reconnection observed from MMS on July 3rd, 2017 (Dai et al. 2021). Panels from top to bottom: a B in GSE. b $V_i$. c $E_z$, $-V_e\times B$ and $-V_i\times B$. d $P_{xy}$ from the ion pressure tensor. e The ion differential energy flux. f, i The 2D ($V_x,V_y$) velocity distribution obtained from ions in 60eV–30keV in the range of $-1500km/s<V_z<1500km/s$. j Cartoon of the spacecraft trajectory

The first kinetic imprint is ion deflected by the Hall electric fields before the acceleration. Under the impact of Hall electric fields, ions are deflected in the direction opposite to the outflow before the acceleration. Such ion beams are identified in the 2D velocity distribution during tailward and Earthwards reconnection jets (Fig. 20f–j). The speed of these ion is $\sim 100--200km/s$ and consistent with the theoretical estimate ($\sim 0.4V_A$).

The second kinetic imprint is related to the enhanced deflection in $+V_y$ during the acceleration. Such enhanced deflection corresponds to $t=30 \sim 40$ in Fig. 19c, 19e. The deflection in $+V_y$ is still due to the Hall electric field and causes distorted distributions toward the $+Y$ direction as in Fig. 20f–j. For instance in the earthward ion jet (Fig. 20g), the distorted distribution is mainly in the form of the concentration in the velocity space near $V_x>350km/s$ and $V_y>350km/s$.

On the fluid level, the consequences of these kinetic effects are reflected in the ion pressure tensor $\overline{\texttt {P}}$

$$\begin{aligned} \overline{\texttt {P}}=m_i\int d^3{{\textbf {v}}}({{\textbf {v}}}-\left\langle v\right\rangle )({{\textbf {v}}}-\left\langle v\right\rangle )f({{\textbf {v}}},{{\textbf {x}}},t). \end{aligned}$$

(43)

The distortion in the velocity distribution is approximated as an additional increase near $V_x=(1\sim 2)V_A$ and $V_y=1\sim 1.5V_A$. Because of the symmetry in Eq. (43), the off-diagonal components of the pressure tensor for a symmetric distribution are usually zero. In the case of the distortion in the velocity distribution, the off-diagonal component ($P_{xy}$) becomes non-zero. This is the reflection of the kinetic effect on the fluid level.

In the Earthward flow, $<V_y>\sim 0.1V_A$ and $<V_x>\sim V_A$, and $P_{xy}$ is $\sim (1/4)n_im_iV^2_A$. Our order-of-magnitude estimate $(1/4)n_im_iV^2_A=0.02nPa$ is close to the observations $|P_{xy}|=0.02-0.03 nPa$ (Fig. 20d). In the tailward flow, the term ($v_x-\left\langle v_x\right\rangle$) change its sign, causing a reversal of the sign of $P_{xy}$. This bipolar reversal is confirmed in observations (Fig. 20d).

3.3 The implications for a fast reconnection rate

The reconnection electric field $E_y$ is a measure of the reconnection rate. In classic reconnection models, $E_y$ is a constant for all spatial scales (Parker 1957; Petschek 1964). In realistic magnetic reconnection, the reconnection electric field $E_y$ may behave differently at different scales. One example is recent observations of ‘electron-only’ reconnection that has no responses of $E_y$ at ion-scales and macro-scales.

In the electron diffusion region, the electron-scale $E_y$ is related to the ’breaking’ of the field line. In the ion diffusion region, the ion-scale $E_y$ dominated. If we consider the energy flow in the reconnection, the Poynting flux $E_yB_0$ at the edge of the ion diffusion region is the rate at which magnetic energy comes into the reconnection region. Such incoming energy flux $E_yB_0$ is supported by the rate of flow convection in the macro-scale region. The rate $E_yB_0$ of incoming energy is determined by the ion-scale $E_y$ instead of the electron-scale $E_y$. The ion-scale $E_y$ just outside the ion diffusion region should gradually connect to the macro-scale convection electric field $E_y$.

We examine the ion-scale $E_y$ from the momentum equation of ions

$$\begin{aligned} (E+V_i \times B)_y=\frac{1}{nq_i}(\frac{\partial }{\partial x}P_{xy}+\frac{\partial }{\partial z}P_{zy})+\frac{m_i}{q_i}\frac{dV_i}{dt}|_y. \end{aligned}$$

(44)

Our analysis in Sect. 3.2 indicate that the term $\frac{1}{nq_i} ({\frac{\partial }{\partial x}P_{xy}})$ associated with the reversal of $P_{xy}$ can provide the ion-scale reconnection electric field. This is qualitatively consistent with previous studies (Cai et al. 1994; Cai and Lee 1997; Lyons and Pridmore-Brown 1990). The term $\Delta P_{xy}$ is $\sim \frac{1}{4}n_im_iV^2_a$ and $\Delta X \sim 10d_{i}$. Thus, $\frac{1}{nq_i} ({\frac{\partial }{\partial x}P_{xy}})$ is estimated as $\sim 0.1B_oV_A$, corresponding to a fast reconnection rate $\sim$0.1.

We compare the estimated ion-scale reconnection rate with MMS observations. Observations of magnetotail reconnection (Fig. 20) indicate a $\Delta P_{xy}$ from $=-0.02nPa$ to 0.02nPa across the X-line. $\Delta X$ is estimated as 1800km for this three-minute interval. The term $\frac{1}{nq_i} (\Delta P_{xy}/\Delta x)$ corresponds to an ion-scale $E_y=0.35mV/m$, a reconnection rate $E/(B_0V_A)=0.1$, and an inflow speed $0.1V_A=34km/s$. These values are consistent with the observations (inflow speed $\sim 30km/s$) in Fig. 20b.

4 Concluding remarks and discussion

Short-wavelength KAWs are ubiquitous in nonuniform magnetized plasmas (Chen et al. 2021). One particular form of nonuniform plasmas is a current layer that could be as thin as ion scale (and even electron scale) in magnetic reconnection. In the ion-scale region of reconnection, ions can not follow the magnetic field line but electrons are magnetized, leading to the charge separation and the resulting Hall fields. Similar physics has been invoked in the discovery of KAW as the perpendicular wavelength becomes comparable to the ion scale. Motivated by the similar physics between Hall fields and KAW, we propose a quantitative model of Hall field as KAW eigenmode of the current layer.

In this review, we present recent progresses in theoretical modeling, simulations and observations of analyzing Hall effects of reconnection in terms of KAW eigenmode. KAW mode and Hall fields exhibit the same polarity and scales. Both KAW eigenmode and Hall fields are characterized by a kinetic scale in the perpendicular direction, a much larger scale in the parallel direction, and a timescale much larger than the ion gyro-period. KAW eigenmode and Hall fields for an ion-scale current layer are analyzed in our studies. In principle, the perpendicular scale of KAW mode and the current layer (and associated Hall fields) can extend to the electron-scale as well.

KAW eigenmode model reveals many intrinsic properties of Hall fields. The Hall electric field is mainly supported by the ion pressure gradient at the ion-scale. The origin of this is related to the finite ion gyroradius effect in KAW. The Hall electric field is mainly electrostatic but has a quite small electromagnetic component associated with the time-variation of Hall magnetic fields. The Hall magnetic field is created by the electron field-aligned current. The ratio $E_{Hall}/B_{Hall}$ is a few Alfven speed. Associated with Hall fields, a parallel electric field and the corresponding potential well is established. These predictions of Hall fields and parallel electric field are confirmed by simulations and observations.

KAW eigenmode model provides a comprehensive knowledge of the spatial profile and strength of Hall fields. The KAW eigenmode solution of Hall fields is given and show consistence with observations. In the direction parallel to the magnetic field, the outward propagation of Hall fields as KAW mode is verified in PIC simulations and space observations. In the symmetric reconnection, the $n=1$ KAW eigenmodes produces a quadrupolar Hall magnetic field. In the asymmetry reconnection, the $n=0$ KAW eigenmodes can generate a bipolar Hall magnetic field. The superposition of the n = 0 and n=1 (and higher n number) KAW eigenmodes can explain more complicated patterns of Hall fields as seen in simulations and observations.

We examine how KAW eigenmode (Hall fields) affect ion acceleration and energy conversion in collisionless reconnection. Ions are ballistically accelerated by the Hall electric field and then deflected by the ${{\textbf {V}}}_i \times {{\textbf {B}}}$ force. This causes ion velocity distributions distorted toward the direction of the electric current. Such effect is determined by the strength of the Hall electric field that is specified by the KAW physics. On the fluid-level, the distorted velocity distributions leads to a bipolar reversal of the off-diagonal component in the ion pressure tensor across the X-line. Such kinetic effect supports an ion-scale reconnection electric field $E_y\sim 0.1 V_AB_o$. The ion-scale reconnection electric field $E_y$ is linked to a fast reconnection rate $\sim 0.1$. The underlying physics is as follows. The ion-scale reconnection electric field $E_y$ determines the incoming Poynting flux $E_yB_0$ at the outer edge of the diffusion region. This Poynting flux $E_yB_0$ is the rate at which magnetic energy flows into the reconnection region from the macro-scale region.

Our results suggest a close connection between Hall fields and the fast reconnection rate. Once the KAW eigenmode/Hall fields is set up on the ion-scale, the ion kinetic effects self-consistently support an ion-scale reconnection electric field $E_y$ and the associated fast reconnection rate. The KAW eigenmode/Hall electric field also appears to lead to an enhanced thermalization of ions. The extent of ion thermalization and its portion in the total energy budget of reconnection remains an interesting topic to be explored.