Online monitoring of the center-of-mass energy from real data at BESIII

Abstract

Background

Data Quality Monitoring system (DQM) was developed to monitor data quality at BESIII experiment in real time. The stable center-of-mass energy ($E_\mathrm{cms}$) is essential for the data taking. Online monitoring the $E_\mathrm{cms}$ can help find the beam energy shift in time.

Purpose

The purpose is to monitor the $E_\mathrm{cms}$ in DQM system in real time.

Methods

The $E_\mathrm{cms}$ is measured using Bhabha scattering process in DQM system, due to its large cross section and low background level. The $E_\mathrm{cms}$ is calculated from the invariant mass of $e^{+}e^{-}$, and the correction value from radiation effect and momentum calibration.

Result

The $E_\mathrm{cms}$ calculated with DQM system shows a good consistency with that from offline reconstruction within error. The results are validated with data taken in 2013. The overall systematic uncertainty includes 0.39 MeV/c$^2$ from signal extraction and 2.54 MeV/c$^2$ from calibration and radiation correction.

Conclusions

The $E_\mathrm{cms}$ calculated from Bhabha scattering process is now available on DQM system in real time, which can be used as references for researchers to operate BESIII experiment.

Introduction

BESIII experiment is operating at the Beijing Electron Positron Collider (BEPCII) in the Institute of High Energy Physics (IHEP) of the Chinese Academy of Sciences, Beijing. With the peak luminosity of 1$\times 10^{33}\ \mathrm{cm}^{-2}\mathrm{s}^{-1}$, BESIII experiment has collected many the world’s largest samples of $e^+e^-$ collision data at different energy points in the $\tau$-charm energy region [1].

Fig. 1

$E_\mathrm{cms}$ obtained from dimu process in the DQM system. a Run-by-run, red line is average value of these runs. b Distribution and fitting result for a random run

The BESIII detector is a magnetic spectrometer [2] located at the Beijing Electron Positron Collider (BEPCII) [3]. The cylindrical core of the BESIII detector consists of a helium-based multilayer drift chamber (MDC), a plastic scintillator time-of-flight system (TOF), and a CsI(Tl) electromagnetic calorimeter (EMC), which are all enclosed in a superconducting solenoidal magnet providing a 1.0 T magnetic field. The solenoid is supported by an octagonal flux-return yoke with resistive plate counter muon identifier modules interleaved with steel. The acceptance of charged particles and photons is 93% over $4\pi$ solid angle. The charged-particle momentum resolution at $1~\mathrm{GeV}/$c is $0.5\%$, and the $\mathrm{d}E/\mathrm{d}x$ resolution is $6\%$ for the electrons from Bhabha scattering. The EMC measures photon energies with a resolution of $2.5\%$ ($5\%$) at 1 GeV in the barrel (end cap) region. The time resolution of the TOF barrel part is 68 ps, while that of the end cap part is 110 ps. The end cap TOF system is upgraded in 2015 with multi-gap resistive plate chamber technology, providing a time resolution of 60 ps.

To monitor the data quality with high accuracy in real time, Data Quality Monitoring system (DQM) has been developed [4, 5]. After reconstructing part of real data, which is taken randomly from online data flow, the monitored results of the detector status and data quality will be available.

The stable center-of-mass energy ($E_\mathrm{cms}$) is essential for the data taking. The nominal beam energy given by BEPCII is calculated from the magnetic field and the current intensity, which is affected by multiple time-dependent factors. Therefore, there is usually a difference between real $E_\mathrm{cms}$ and the nominal beam energy, which is needed to be determined. Online measurement of the $E_\mathrm{cms}$ helps to adjust the beam energy to certain value. The Beam Energy Measurement System (BEMS), which was installed in 2008, was designed to measure the beam energy with a relative systematic uncertainty of $2\times 10^{-5}$ based on the Compton back-scattered photons [6]. However, it always takes a few days for the system to initiate before putting into use. Therefore, we need another methods, if it needs to obtain the $E_\mathrm{cms}$ in short time after BESIII detector starting in operation.

In this paper, $E_\mathrm{cms}$ is measured using Bhabha scattering process. The $E_\mathrm{cms}$ is expressed as

$$\begin{aligned} E_\mathrm{cms}= M(e^{+}e^{-}) + \varDelta M_{\mathrm{cor}} \end{aligned}$$

(1)

where $M(e^{+}e^{-})$ is the invariant mass of $e^{+}e^{-}$, and $\varDelta M_{\mathrm{cor}}$ is the mass correction caused by the effects including momentum calibration, multiple scattering, bremsstrahlung, and final state radiation from Bhabha scattering process. In this analysis, $\varDelta M_\mathrm{cor}$ is estimated using simulations of Bhabha process with turning these effects on and off by BABAYAGA 3.5 event generator [7]. The detector geometry, material description and the tracking of the decay particles through the detector including interactions are handled by GEANT4 package [8].

Fig. 2

$E_\mathrm{cms}$ obtained from Bhabha process in the DQM system. a run-by-run, red line is average value of these runs. b Distribution and fitting result for a random run

Fig. 3

Comparison of the statistical uncertainty under different numbers of events from each run. a 5000 events; error: 0.8 MeV/c$^2$. b 20000 events; error: 0.4 MeV/c$^2$. c 50,000 events; error: 0.2 MeV/c$^2$

Measuring $E_\mathrm{cms}$ using dimu and Bhabha processes

The $E_\mathrm{cms}$ is usually measured using dimu process in the offline environment [9] with fully reconstructed data set. The reason of using dimu process rather than Bhabha process in the offline environment is the radiation effect of Bhabha process is more complex. DQM system also provides the $E_\mathrm{cms}$ measurements using dimu process. The $E_\mathrm{cms}$ was obtained from the fitting of the invariant mass of $\mu ^+\mu ^-$, $M(\mu ^{+}\mu ^{-})$ run by run. The period of time of a typical run is about 1 hour in the previous BESIII detector running.

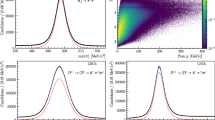
The fitted $E_\mathrm{cms}$ in DQM system for several runs is shown in Fig. 1. The distribution of $M(\mu ^{+}\mu ^{-})$ is fitted with Gaussian function. The average value of these runs is $3872.90\pm 0.19~\mathrm{MeV}/\mathrm{c}^2$. While the statistical uncertainty of each run is about 1–2 MeV/c$^2$, which could not meet the accuracy requirement of online monitoring. Because of the low cross section of dimu process and the partially reconstruction mechanism on DQM [4] [5], only hundreds of events are successfully reconstructed for a typical run, which leads to the high statistical uncertainty of the $E_\mathrm{cms}$ fitting result.

Fig. 4

Comparison of invariant mass of Bhabha and dimu MC events generated at 3.096 GeV. a Bhabha events with all radiation effects turning on. b Bhabha events with all radiation effects turning off. c dimu events with ISR/FSR turning off

To get a more accurate result in the limited time, Bhabha scattering process is another choice. The cross section of Bhabha process is almost hundreds of times larger than that of dimu process, which could obtain much more events in the same time interval, and hence much less statistical uncertainty. Bhabha event candidates are required to two charged tracks reconstructed in MDC with opposite charge. Each charged track is required to pass the interaction point within $\pm 10$ cm in the beam direction and within $\pm 1$ cm in the perpendicular plane. Polar angle of each charged tracks should satisfy $\left| \mathrm{cos}\theta \right| <0.83$ to ensure the good consistency between data and MC. The energy deposited in the EMC of each track is required to be greater than 0.65$\times$$E_{beam}$, where $E_{beam}$ is the beam energy. To select back-to-back tracks in MDC, $\left| \varDelta \theta \right| \le 6^\circ$ and $\left| \varDelta \phi \right| \le 6^\circ$ are required, where $\varDelta \theta$ and $\varDelta \phi$ are the polar angle and azimuthal angle of two tracks.

The background level is about $10^{-5}$ using MC samples of $e^{+}e^{-}\rightarrow (\gamma )\mu ^{+}\mu ^{-}$, $e^{+}e^{-}\rightarrow \gamma \gamma$, and $e^{+}e^{-}\rightarrow q\overline{q}$ processes with the event selection criteria, which is negligibly small.

The result of $M(e^{+}e^{-})$ is shown in Fig. 2. Signal shape is described by the sum of Gaussian and Crystal Ball function [10] with common mean and sigma. Background is described by $1^{st}$ Chebyshev polynomials. The average value of these runs is $3866.30\pm 0.03~\mathrm{MeV}/c^2$, and the statistical uncertainty of each run is about 0.2-0.4 MeV/c$^2$, which is good enough for the online monitoring.

To calculate the $E_\mathrm{cms}$ with flexibility, it is necessary to weigh the time interval between two measurements and the number of events obtained in the interval. The system would collect small number of events in a short time interval, which leads to high statistical uncertainty of the measurement. We checked the statistical uncertainty of each measurement under different number of events. Figure 3 shows the fitting result of each measurement with 5000, 20,000 and 50,000 events, respectively. The corresponding statistical uncertainty is about 0.8 MeV/c$^2$, 0.4 MeV/c$^2$, 0.2 MeV/c$^2$; therefore, 20000 events for each measurement are sufficient. In the current setting of DQM system, this would take about 15 minutes under regular data taking period. Although the statistical uncertainty of low statistical measurement is large, the error of average measurements in a certain time period, e.g., 1 day, is stable. This would allow operators to change the measurement frequency without worrying about losing the measurement accuracy in a long time period.

Radiation correction

The $E_\mathrm{cms}$ in DQM system is measured using Bhabha process. The ISR/FSR effects and momentum calibration contribute to the mass shift of invariant mass using Bhabha process or dimu process respectively. In additional to those effects, the multiple scattering and bremsstrahlung effects also contribute to the measurement of $E_\mathrm{cms}$ since the mass of electron is less than that of muon for Bhabha process. In this analysis, these effects are estimated with MC simulation using BABAYAGA 3.5 [7].

To estimate the radiation effects (including the multiple scattering, bremsstrahlung effect) from Bhabha process, MC samples with radiation effects turning on and off are generated. The $M(e^{+}e^{-})$ with no radiation effects are fitted with Gaussian function, while those with radiation effects are fitted with the sum of Gaussian and Crystal Ball function with common mean and sigma for signal, and $1^{st}$ Chebyshev polynomials for background. The fit results are shown in Fig. 4a, b. The difference between the mean value is taken as $\varDelta M_{\mathrm{Rad}}$ in the calculation of $E_\mathrm{cms}$.

To validate the results of Bhabha events with no radiation effects, dimu events with ISR/FSR turning off under the same $E_\mathrm{cms}$ are also generated, and the $M(\mu ^{+}\mu ^{-})$ is fitted with Gaussian function. The result is shown in Fig. 4c. The difference between the mean value in Fig. 4b, c is less than 0.1 MeV/c$^2$ and within error, which indicates that the method to obtain $\varDelta M_{\mathrm{Rad}}$ from Bhabha events is reasonable.

The dependence of $\varDelta M_{\mathrm{Rad}}$ on the center-of-mass energy is shown in Fig. 5 using the MC samples generated at a series energy points from 2 to 5 GeV. The $\varDelta M_{\mathrm{Rad}}$ are fitted with linear function. The fit result is

$$\begin{aligned} \varDelta M_{\mathrm{Rad}} = (2.689\pm 0.037)*10^{-3}E_\mathrm{cms}/\mathrm{GeV}-(3.394\pm 0.102) \end{aligned}$$

(2)

The resulting $E_\mathrm{cms}$-dependent $\varDelta M_{\mathrm{Rad}}$ will be used to correct the measured $M(e^{+}e^{-})$.

Fig. 5

Difference of the mean value of $M(e^{+}e^{-})$ in MC sample with radiation effect turning on and off versus CMS energy for Bhabha events. Red solid line is the fit result. $\varDelta M_{\mathrm{Rad}} = (2.689\pm 0.037)*10^{-3}E_\mathrm{cms}/\mathrm{GeV}-(3.394\pm 0.102)$

Momentum calibration

To measure the $E_\mathrm{cms}$ more precisely, the momentum of electron needs to be validated. DQM system works in the online environment, and the measurements of momentum of charged tracks are performed with rough MDC calibration constants and with misalignment effect. A fine calibration and alignment study of MDC require an accumulation of events with high statistic which could not be satisfied in the online environment. The calibration constants used in DQM are often obtained from recent data and may not be good enough for the current data. The difference of the $E_\mathrm{cms}$ due to the calibration constants will be treated as systematic uncertainty and will be discussed in chapter 7.

According to the Ref. [9], the muon momentum is validated with $e^{+}e^{-}\rightarrow \gamma _\mathrm{ISR}J/\psi$ and $J/\psi \rightarrow \mu ^{+}\mu ^{-}$. Since muon and electron are both light lepton and have similar momentum in detector, the result of muon momentum validation can be applied on electron. The validation method is introduced below.

To get the momentum calibration correction value for a run interval, e.g., run 47543 to 48170, in which the CMS energy is 4190 MeV, MC sample from these run numbers with a series of input energy is produced. Figure 6 from Ref. [11] shows the difference of the fitting result of $M(\mu ^+ \mu ^-)$ and the input energy. The red line is fitting result: $y=(5.44\times 10^{-4}\pm 3.31\times 10^{-5})x-(0.11\pm 0.12)$(MeV).

On the other hand, the mean value of $M^\mathrm{obs}(\mu ^+\mu ^-)$ for the processes: $e^{+}e^{-}\rightarrow \gamma _\mathrm{ISR}J/\psi$ and $J/\psi \rightarrow \mu ^+\mu ^-\gamma _\mathrm{FSR}$ can be obtained from real data samples. Due to the FSR effect, the measured $M^\mathrm{obs}(\mu ^+\mu ^-)$ is slightly lower than the nominal $J/\psi$ mass. The mass shift $\varDelta M_\mathrm{FSR}$ is estimated by MC simulation from the process $e^{+}e^{-}\rightarrow \gamma _\mathrm{ISR}J/\psi$ with FSR turning on and off. Thus the measured $J/\psi$ mass from real data samples can be calculated as:

$$\begin{aligned} M^\mathrm{obs}(J/\psi )=M^\mathrm{obs}(\mu ^+\mu ^-)+\varDelta M_\mathrm{FSR} \end{aligned}$$

(3)

Afterward, the difference between $M^\mathrm{obs}(J/\psi )$ and the value of $J/\psi$ mass from PDG can be obtained: $\varDelta M=M^\mathrm{obs}(J/\psi )-M^\mathrm{PDG}(J/\psi )$. Then the momentum calibration correction value can be calculated from the function:

$$\begin{aligned} \varDelta M_\mathrm{corr} = (E-3096.92)\times k + \varDelta M(\mathrm{MeV}) \end{aligned}$$

(4)

where k is the slope of the fitting result in Fig. 6, and E is corresponding CMS energy, i.e., 4190 MeV. The measured $J/\psi$ mass in $e^{+}e^{-}\rightarrow \gamma _\mathrm{ISR}J/\psi$ after FSR correction is 3097.83 MeV, and the difference with PDG value is $3097.83-3096.92 = 0.91$ MeV/c$^2$ for run 47543 to 48170 [11]. Hence, the momentum calibration value $\varDelta M_\mathrm{corr}$ is $(4190-3096.92)\times 5.44\times 10^{-4} +0.91= 1.5$ MeV/c$^2$. The final result of $E_\mathrm{cms}$ would be

$$\begin{aligned} E_\mathrm{cms}= M(e^{+}e^{-}) + \varDelta M_{\mathrm{Rad}}-\varDelta M_\mathrm{corr} \end{aligned}$$

(5)

where $M(e^{+}e^{-})$ from offline data is shown in Fig. 7, the fitting result is 4182.71 MeV/c$^2$, and $\varDelta M_{\mathrm{Rad}}$ calculated from Eq. 2 is 7.85 MeV/c$^2$. Therefore, the $E_\mathrm{cms}$ is $4182.71+7.85-1.5=4189.06$ MeV. The result of $E_\mathrm{cms}$ for these runs from dimu process is 4188.8 MeV [12], 4188.96 ± 0.05 ± 0.34 MeV or 4189.07 ± 0.05 ± 0.34 MeV [11], based on different BOSS version [13], which is consistent with the calculation from Bhabha process.

Fig. 6

The distribution of the difference of the output energy and input energy (MC) of the dimu process; red solid line is the average value

Fig. 7

Fitting result of $M(e^+e^-)$ from offline data

To verify the method, MC with different input energy of Bhabha process is generated. The difference of $E_\mathrm{cms}$ calculated from Eq. 5 and the input energy is shown in Fig. 8. The result shows the $E_\mathrm{cms}$ is consistent with input energy within error, that means the method to calculate $E_\mathrm{cms}$ is reliable.

Fig. 8

Difference of $E_\mathrm{cms}$ calculated from Eq. 5 and the input energy; red line is the average value

Fig. 9

Fitting result of the $M(e^{+}e^{-})$ in Bhabha event from data sample a run 33,572 to 33,657 b run 33,659 to 33,719

To ensure the accuracy of the method, cross-check with data is performed. Figure 9 shows the corresponding fitting result of the $M(e^{+}e^{-})$ from data sample taken in 2013. The value of $M(e^{+}e^{-}), M_{\mathrm{Rad}}, and E_\mathrm{cms}$ from dimu process [9] and Bhabha process is listed in Table. 1. The momenta of muon and electron do not need to be corrected. The result indicates that $E_\mathrm{cms}$ from both dimu and Bhabha processes is consistent within error, that means the method to obtain $E_\mathrm{cms}$ from Bhabha events is reasonable and unbiased.

Table 1 Comparison of $M(e^+e^-)$, $M_{\mathrm{Rad}}$ and $E_\mathrm{cms}$ from Bhabha and dimu processes

Algorithm deployment

The algorithm to obtain $E_\mathrm{cms}$ from Bhabha events is deployed on the DQM system. DQM system invokes user-defined histogram-filling algorithm to fill histogram, including the histogram of invariant mass distribution of $e^+e^-$. The histograms are generated during data taking and stored in ROOT file after each run ends [4] [5] [14]. Once a new root file is generated, $E_\mathrm{cms}$ will be calculated and the result will be stored in the DQM databases for further studied. Figure 10 shows the $E_\mathrm{cms}$ in DQM system from several runs. Since the momentum validation cannot be done on DQM system, the correction value is estimated from most recent result or during data taken. Here 2.5 MeV is taken as the correction value of momentum calibration for data obtained in 2018–2019. As shown in Fig. 13, the $E_\mathrm{cms}$ calculated from DQM system and offline environment is around nominal $J/\psi$ mass with 2.5 MeV as momentum correction value.

Systematic uncertainty

The systematic uncertainty of this analysis is contributed from the calculation of radiation correction, the fitting procedure of each measurement and the difference of momentum calibration constants.

The radiation correction of Bhabha event is $E_\mathrm{cms}$ dependent and is calculated from MC samples. The standard deviation of the radiation correction value is given by

$$\begin{aligned} \sigma = \sqrt{\frac{\Sigma (\varDelta M_{\mathrm{Rad}} - \overline{\varDelta M}_{\mathrm{Rad}})^{2}}{N-1}} = 0.16~\mathrm{MeV}/\mathrm{c}^2 \end{aligned}$$

(6)

where the $\varDelta M_{\mathrm{Rad}}$ is the radiation correction value measured from MC simulation in Fig. 5 and $\overline{\varDelta M}_{\mathrm{Rad}}$ is the radiation correction value from fitting in Fig. 5.

The uncertainty from signal extraction procedure is estimated by changing the fitting range and background shape. The uncertainty due to the fitting range is estimated by varying $M(e^{+}e^{-})$ by 20 MeV/c$^2$. The difference of mean value of $M(e^{+}e^{-})$ in $J/\psi$ data is about 0.32 MeV/c$^2$ and is shown in Fig. 11. The uncertainty due to the background shape is estimated by changing the order of Chebyshev polynomials from $1^{st}$ to $2^{nd}$. The difference of mean value of $M(e^{+}e^{-})$ in $J/\psi$ data is about 0.23 MeV/c$^2$ and is shown in Fig. 12.

Fig. 10

$E_\mathrm{cms}$ in Bhabha events from $J/\psi$ data sample in DQM system; the average value is 3096.68 MeV/c$^2$

Fig. 11

$M(e^{+}e^{-})$ mean value difference by varying the fitting mass range from (2.93, 3.2) to (2.95, 3.2) GeV/c$^2$

Fig. 12

$M(e^{+}e^{-})$ mean value difference by changing the background shape from $1^{st}$ to $2^{nd}$ Chebyshev polynomials

The uncertainty due to the calibration constants can be divided into two parts. The first one is the difference of $E_\mathrm{cms}$ between DQM system and the offline environment, which is estimated by comparing the fitting result of the $M(e^{+}e^{-})$ versus run number from $J/\psi$ data sample taken in 2018 and 2019. The difference is about 0.75 MeV/c$^2$, which is shown in Fig. 13. The second one is the difference of the momentum calibration correction value between different data samples. The momentum calibration correction value for the data with $E_\mathrm{cms}$ 4190 to 4280 MeV taken in 2017 is 0.89 to 4.83 MeV [11], and 2.5 MeV is used for $J/\psi$ data taken in 2018–2019. However, from Ref. [9], the momentum calibration does not need to be corrected for the data taken in 2016. The momentum calibration correction value is different even if the $E_\mathrm{cms}$ is closed, the reason of which may be the difference of BOSS version and the background shape [11]. Considering the behavior for different period of data sample, average of minimum and maximum of correction value: $(0+4.83)/2=2.42$ MeV is taken as systematic uncertainty, conservatively.

The systematic uncertainties from signal extraction procedure affect each measurement of the $E_\mathrm{cms}$, while that from the difference of momentum calibration constants and radiation correction only has an effect when the calibration constants or $E_\mathrm{cms}$ changes. For the data obtained at the same calibration constants and $E_\mathrm{cms}$, the systematic uncertainty is only coming from the first term.

Fig. 13

Measured $M(e^{+}e^{-})$ run-by-run from $J/\psi$ data. a From DQM system, average value is 3096.65 MeV/c$^2$. b From offline environment, average value is 3097.40 MeV/c$^2$

Table 2 lists all the systematic uncertainties that contribute to the $E_\mathrm{cms}$ measurement, and the total systematic uncertainty is obtained by adding the individual contributions in quadrature. Because the effects of signal extraction procedure, radiation correction and calibration constants on the measurements are different, the total systematic uncertainty is calculated separately.

Since the value of calibration constants and hence the momentum correction value changes with different time period of data sample, the uncertainty can hardly be estimated clearly and their value is just roughly given in Table 2.

Table 2 Summary of the systematic uncertainty

Summary

The center-of-mass energy can be measured in real time during data taking using Bhabha process from DQM system. The statistical uncertainty is much lower than that used to be done on dimu process, and the overall systematic uncertainty is about 0.39 MeV/c$^2$ from signal extraction and 2.54 MeV/c$^2$ from calibration and radiation correction, which is good enough for monitoring during data taking. The method is validated by dimu process from the data reconstructed in the offline environment. The algorithm has already been deployed on DQM system and achieved satisfied result, which is essential for monitoring the center-of-mass energy in BESIII in realtime.