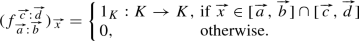Abstract
A recent work by Lesnick and Wright proposed a visualisation of 2D persistence modules by using their restrictions onto lines, giving a family of 1D persistence modules. We give a constructive proof that any 1D persistence module with finite support can be found as a restriction of some indecomposable 2D persistence module with finite support. As consequences of our construction, we are able to exhibit indecomposable 2D persistence modules whose support has holes as well as an indecomposable 2D persistence module containing all 1D persistence modules with finite support as line restrictions. Finally, we also show that any finite-rectangle-decomposable nD persistence module can be found as a restriction of some indecomposable \((n+1)\)D persistence module.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In the theory of persistent homology (Edelsbrunner et al. 2000), 1D persistence modules can be summarized and easily visualized using the so-called persistence diagrams, which led to successful applications of topological data analysis. From a mathematical standpoint, the existence of the persistence diagram is a direct consequence of the fact that, viewed as representations of the underlying quiver \(\mathbb {A}_n\), 1D persistence modules can be uniquely decomposed into indecomposable representations that are intervals (Gabriel 1972). The endpoints of the intervals give the birth and death indices of the topological features.
In the multidimensional case (Carlsson and Zomorodian 2009), multidimensional persistence modules can be studied as representations of an underlying quiver which is a commutative nD grid. The indecomposable representations are no longer intervals and, more devastatingly, cannot be easily listed. More precisely, there is no complete discrete invariant that can describe all indecomposable nD persistence modules when \(n \ge 2\) (Carlsson and Zomorodian 2009). In the representation-theoretic language, the (large enough) commutative grid is of wild representation type.
Lesnick and Wright (2015) proposed an interactive visualisation of 2D persistence modules using restrictions onto lines on the grid. For each line, the restriction is a 1D persistence module and thus can be summarized by a persistence diagram. They took the approach of exploring restrictions onto all possible lines of non-negative slope in order to visualize and obtain insight into the structure of a 2D persistence module. Note that considering the barcodes over all such lines is equivalent to considering the rank invariant (Carlsson and Zomorodian 2009) of the 2D persistence module.
For most of this work, we only consider persistence modules with finite support. For the sake of simplicity, unless stated otherwise, all persistence modules will have finite support. The only exception is the infinite 2D persistence module we build in Sect. 6.
In this work, we look into the possible outcomes of the restriction onto a single line of a 2D persistence module that is indecomposable. It was hoped that, being the building blocks of 2D persistence modules, the 2D indecomposables should have restrictions that are “simple” or coming from a restricted set of possibilities. However, we show that this is not the case.
Our main result is a constructive proof that any 1D persistence module V can be obtained via the restriction onto a line of an indecomposable 2D persistence module (of large enough, but finite, support). We show the following Theorem (see Sect. 2 for precise definitions).
Theorem 1.1
Let \(V \in {{\,\mathrm{rep}\,}}{\vec {A}_{n}}\). Then there exists an indecomposable \(M \in {{\,\mathrm{rep}\,}}\vec {G}_{}\) with finite support such that V is a line restriction of M.
Theorem 1.1 can be seen as another expression of how complicated the indecomposable 2D persistence modules are. Stated another way, the indecomposable 2D persistence modules collectively contain all possible 1D persistence modules via line restrictions. Another, less rigorous, interpretation is that by just looking at one line restriction V of some 2D persistence module M (not necessarily indecomposable), and without any other information about the original 2D persistence module M, we cannot infer much about the decomposition structure of M. More precisely, for each decomposition \( V = \bigoplus _{i=1}^l V_i \) (with \(V_i\) not necessarily indecomposable), it is possible that \( M \cong X \oplus \bigoplus _{i=1}^l M_i \) such that \(M_i\) are indecomposable, \(M_i\) restricts to \(V_i\), and X restricts to 0 on the line. Note that our construction of an indecomposable is not the only choice of such an \(M_i\).
Using our construction for Theorem 1.1, we are able to build several objects of particular interest. First, we are able to exhibit indecomposable 2D persistence modules whose support can have an arbitrary finite number of holes. We believe that their existence was not obvious and that providing a concrete example will help deepen the understanding of 2D persistence modules. We also address the question of what is the smallest number of vertices needed in the support of an indecomposable 2D persistence module with at least one hole. Second, we build a single indecomposable 2D persistence module with infinite support that contains all possible 1D persistence modules with finite support as line restrictions.
Finally, we extend Theorem 1.1 to finite-rectangle-decomposable nD persistence modules. In particular, we show that any finite-rectangle-decomposable nD persistence module V can be obtained via a “hyperplane restriction” of an indecomposable \((n+1)\)D persistence module. The construction directly allows us to build indecomposable \((n+1)\)D persistence modules with an arbitrary finite number of nD holes.
We introduce basic definitions in Sect. 2 and tools in Sect. 3. We then describe our construction of an indecomposable 2D persistence module given V and its properties in Sect. 4. In Sect. 5, we exhibit examples of 2D indecomposables with holey support obtained as a result of our construction. There, we also find the smallest number of vertices needed in the support of an indecomposable 2D persistence module with a hole, via an ad hoc construction. In Sect. 6, we build the indecomposable 2D persistence module with infinite support containing all possible 1D persistence modules with finite support as line restrictions. In Sect. 7 we discuss the extension to finite-rectangle-decomposable nD persistence modules.
2 Background
We use the formalism of both category theory and representation theory, while providing clear intuition as much as possible. For convenience, we mainly use the representation theory of posets, but the representation theory of bound quivers is also used. If needed, we refer the reader to Assem et al. (2006) for more details on the representation theory of bound quivers, and to Mac Lane (2013) for the category theory.
2.1 The poset  and 1D persistence modules
and 1D persistence modules
A poset (a partially ordered set) \((P, \le )\) can be viewed as a category with objects \(i \in P\), and morphisms determined as follows. There is a unique morphism \(i\rightarrow j\) if and only if \(i\le j\). We abuse notation and write \(i\le j\) to also mean this unique morphism. Composition follows from transitivity: if there are morphisms \(i\rightarrow j\) and \(j\rightarrow k\), then \(i\le j\) and \(j \le k\), implying \(i\le k\). Thus, there is a unique morphism \(i \rightarrow k\), which is the composition of the two morphisms. The identity of object \(i\in P\) is clearly the morphism \(i \le i\).
We define [n] to be the set \(\{0,1,\ldots ,n-1\}\). By \(\vec {A}_{n}\), we mean the poset category of \([n] {:}{=}\{0,1,\ldots ,n-1\}\) with the usual order \(\le \). We shall see below that the category \(\vec {A}_{n}\) is intimately related to the quiver

which can be thought of as the Hasse diagram of \(\vec {A}_{n}\).
Let K be a field, which we fix throughout this work. Recall that a K-category is a category where the set of morphisms between any two objects has K-vector space structure, and composition is K-bilinear.
Let P be a poset category and C a K-category. A C-valued representation of P is a functor \(F:P\rightarrow C\). That is, it assigns an object F(i) of C to each \(i\in P\), and to each morphism \(i\rightarrow j\) in P (i.e. denoted by \(i\le j\) in the sequel) a morphism \(F(i\le j) : F(i) \rightarrow F(j)\) in C, satisfying the following properties: \(F(i\le i)\) is the identity on F(i), and \(F(j\le k)F(i\le j) = F(i\le k)\).
A morphism between two C-valued representations of P is nothing but a natural transformation. That is, given \(F: P\rightarrow C\) and \(G:P\rightarrow C\), a morphism \(\eta : F \rightarrow G\) is a family \(\{\eta _i: F(i) \rightarrow G(i)\}_{i\in P}\) of morphisms in C such that

commutes for all \(i\le j\) in P. The set of morphisms from F to G is denoted by \({{\,\mathrm{Hom}\,}}(F,G)\). Morphisms from F to itself are called endomorphisms, and we use the notation \({{\,\mathrm{End}\,}}(F) \doteq {{\,\mathrm{Hom}\,}}(F,F)\). Composition

is the obvious one: \(\nu \eta \) is defined by \((\nu \eta )_i = \nu _i \eta _i\). The category of C-valued representations of P shall be denoted by \(\left[ P,C\right] \).
For the case \(C = {\mathrm {vect}}_K\), the category of finite-dimensional K-vector spaces, we use the notation \({{\,\mathrm{rep}\,}}{P} {:}{=}\left[ P,{\mathrm {vect}}_K\right] \) for the category of \({\mathrm {vect}}_K\)-valued representations, also called K-linear representations. Unless specified otherwise, representation shall mean a K-linear representation. The support of \(V \in {{\,\mathrm{rep}\,}}P\) is the set \(\{i \in P |V(i) \ne 0\}\).
It is known that \({{\,\mathrm{rep}\,}}{P}\) is an additive K-category. The direct sum of two representations V and W is given by \((V\oplus W)(p) = V(p) \oplus W(p)\) for all \(p\in P\). The zero representation is the functor 0 that takes everything in P to zero vector spaces and zero maps. A representation V is said to be indecomposable if \(V \cong W \oplus W'\) implies W or \(W'\) is 0.
For example, a representation V of \(\vec {A}_{n}\) is an assignment of the following data: to each object \(i \in [n]\), a finite-dimensional K-vector space V(i); to each pair \(i\le j\), a K-linear map \(V(i\le j) : V(i) \rightarrow V(j)\) so that the composition
is equal to \(V(i\le k) : V(i) \rightarrow V(k)\) for each \(i\le j \le k\), and \(V(i\le i)\) is the identity for each i.
Thus, \(V \in {{\,\mathrm{rep}\,}}\vec {A}_{n}\) is completely determined by vector spaces V(i) for \(i\in [n]\) and linear maps \(V(i\le i+1)\) for \(i\in [n-1]\). This corresponds to the usual notion of a representation of the quiver \(\mathbf {\mathbb {A}}_n\) given in Diagram (2.1). In fact, \({{\,\mathrm{rep}\,}}\vec {A}_{n} \cong {{\,\mathrm{rep}\,}}\mathbf {\mathbb {A}}_n\), where the latter is the category of finite-dimensional K-linear representations of the quiver \(\mathbf {\mathbb {A}}_n\). We shall freely use this identification. A 1D persistence module is simply a representation of \(\vec {A}_{n}\).
A fundamental result (Krull-Schmidt Theorem) is that every representation in \({{\,\mathrm{rep}\,}}\vec {A}_{n}\) can be uniquely decomposed into a finite direct sum of indecomposable representations, up to isomorphism and permutation of terms. Furthermore, it is known (Gabriel 1972) that any indecomposable representation of \(\vec {A}_{n}\) is isomorphic to an interval representation \(\mathbb {I}[i,j]\) for some \(i\le j \in [n]\). The interval representation\(\mathbb {I}[i,j]\) is defined by:
Combining the above two facts, we get that for each \(V \in {{\,\mathrm{rep}\,}}\vec {A}_{n}\),
uniquely for some positive integers \(m_1,\ldots ,m_N\) and \(b_i \le d_i \in [n]\) for \(i \in \{1,\ldots , N\}\) with all pairs \((b_i,d_i)\) distinct. In other words, the 1D persistence module V is, up to isomorphism, entirely determined by the multiset consisting of pairs \((b_i,d_i)\) with multiplicities \(m_i\) for all \(i\in \{1,\ldots , N\}\). This can be drawn as a multiset of points in \(\mathbb {R}^2\) and is called the persistence diagram of the 1D persistence module V.
In practice, the persistence module is often obtained as the sequence of homology vector spaces and induced homology maps of a sublevel set filtration parametrized over \(\mathbb {R}\). In this case, the underlying poset is \((\mathbb {R},\le )\) instead. However, some mild tameness assumptions on the filtration or persistence module guarantee the existence of a persistence diagram (Chazal et al. 2016; Crawley-Boevey 2015). Moreover, if there are only a finite number of critical points, then we can consider the persistence module as a representation of \(\vec {A}_{n}\).
2.2 Commutative grids and line restrictions
Given \(V \in {{\,\mathrm{rep}\,}}{\vec {A}_{n}}\), we will construct an indecomposable persistence module over an equioriented commutative 2D grid of size \(w \times h\). The size of the grid will depend on V itself, and so may be larger than n. To avoid having to specify sizes in our definition of line restrictions, we use an infinite discrete commutative grid.
First, we extend \(\vec {A}_{n}\) to an infinite line by the inclusion of \(\vec {A}_{n} = (\{0,\ldots ,n-1\},\le )\) in the poset \((\mathbb {Z},\le )\). Thus, \({{\,\mathrm{rep}\,}}\vec {A}_{n}\) is a full subcategory of \({{\,\mathrm{rep}\,}}(\mathbb {Z},\le )\). We use the following definition for the equioriented commutative 2D grids.
Definition 2.1
(Equioriented commutative 2D grids)
-
1.
We define \(\vec {G}_{}\) to be the poset category \((\mathbb {Z}\times \mathbb {Z}, \le )\) with \((a,b) \le (x,y)\) if and only if \(a \le x\) and \(b \le y\).
-
2.
\(\vec {G}_{h,w}\) is the poset category \(([h]\times [w],\le )\), which is the full subcategory of \(\vec {G}_{}\) with set of objects \([h]\times [w]\).
To see why there is a “commutative” in the name, we provide as an example \(\vec {G}_{2,2}\). A representation \(V \in {{\,\mathrm{rep}\,}}(\vec {G}_{2,2})\) is completely determined by the data:

where by functoriality,
That is, a commutativity relation is automatically satisfied.
We call representations of \(\vec {G}_{}\) as 2D persistence modules. If \(V \in {{\,\mathrm{rep}\,}}\vec {G}_{}\) has finite total dimension, then it has finite support, and can be viewed (after translation) as a representation of some finite 2D grid \(\vec {G}_{h,w}\).
Alternatively, \({{\,\mathrm{rep}\,}}\vec {G}_{h,w}\) is isomorphic to the representation category of the \(h\times w\) equioriented 2D grid quiver bound by commutativity relations. See for example, Asashiba et al. (2018a), for precise definitions.
Definition 2.2
(Line) A lineL is a functor
such that if \(i \ne j\), then \(L(i) \ne L(j)\).
Note that the definition above does not correspond exactly with a geometric “line”. For example, the functor L defined on objects \(x\in \mathbb {Z}\) by \(L(x) = (2x,2x)\) is a line. However, it geometrically intersects points on the 2D grid that are not part of its image, for example the point (1, 1). Our result does not rely on this peculiarity.
Given a line L, we get an induced functor between representation categories via composition:
and with effect on morphisms also by composition. That is, if \(\eta :M\rightarrow N\) is a morphism between representations of \(\vec {G}_{}\) (a natural transformation), then \((R_L(\eta ))_i = \eta _{L(i)}\) defines the morphism \(R_L(\eta ) : ML \rightarrow NL\).
Definition 2.3
(Line restriction) Let \(V \in {{\,\mathrm{rep}\,}}\vec {A}_{n} \subset {{\,\mathrm{rep}\,}}\mathbb {Z}\). We say that V is a line restriction of \(M\in {{\,\mathrm{rep}\,}}\vec {G}_{}\) if there is a line L such that \(R_L(M) \cong V\).
3 Tools
3.1 Stacking
To prove Theorem 1.1, for each \(V \in {{\,\mathrm{rep}\,}}\vec {A}_{n}\) we construct an indecomposable 2D persistence module I such that V is a line restriction of I. In order to easily construct 2D persistence modules, we stack together representations of \(\vec {A}_{w}\) (for some longer \(w \ge n\)). This stacking procedure can be theoretically justified by the following lemma.
Lemma 3.1
There is an isomorphism of categories
In words, representations of the commutative grid \(\vec {G}_{h,w}\) can be viewed as \({{\,\mathrm{rep}\,}}\vec {A}_{w}\)-valued representations of a 1D grid (the vertical line \(\vec {A}_{h}\)) by collapsing each row to an object of \({{\,\mathrm{rep}\,}}\vec {A}_{w}\). In this interpretation, the representations of \(\vec {A}_{w}\) are drawn as rows, and h of them are stacked in a line, with a morphism from the ith row to the jth row for \(i\le j \in [h]\).
This can also be seen as “currying” a functor in \({{\,\mathrm{rep}\,}}\vec {G}_{h,w}\). More generally, this is analogous to tensor-hom adjunction in \({\mathrm {vect}}_K\)-enriched functor categories, as in Section 2.3 of Kelly (1982). Note that the poset categories \(\vec {G}_{h,w}\), \(\vec {A}_{w}\), and \(\vec {A}_{h}\) are not \({\mathrm {vect}}_K\)-enriched, but we can consider instead their K-linearizations \(K\vec {G}_{h,w}\), \(K\vec {A}_{w}\), and \(K\vec {A}_{h}\). The analogy follows by considering K-linear functors from the K-linearizations instead of functors from the poset categories and noting that \(K\vec {G}_{h,w}\cong K\vec {A}_{h}\otimes K\vec {A}_{w}\). We provide an elementary proof of Lemma 3.1 in Appendix A.
The stacking lemma is an obvious extension of an idea in the paper Asashiba et al. (2018b), where representations of commutative ladders, which are commutative 2D grids of size \(2\times w\), are viewed as morphisms in \({{\,\mathrm{rep}\,}}\vec {A}_{w}\). This is essentially stacking two representations of \(\vec {A}_{w}\).
Objects M in the category \(\left[ \vec {A}_{h},{{\,\mathrm{rep}\,}}\vec {A}_{w}\right] \) are \({{\,\mathrm{rep}\,}}(\vec {A}_{w})\)-valued representations of \(\vec {A}_{h}\). Thus, each arrow \(i\le j \in \vec {A}_{h}\) is given the data of a morphism \(M(i\le j):M(i) \rightarrow M(j)\) in \({{\,\mathrm{rep}\,}}(\vec {A}_{w})\) since M is \({{\,\mathrm{rep}\,}}(\vec {A}_{w})\)-valued, instead of a morphism between vector spaces as when \({\mathrm {vect}}_K\)-valued. In the next subsection, we study morphisms in \({{\,\mathrm{rep}\,}}(\vec {A}_{w})\) and provide a convenient way to describe them.
3.2 Matrix formalism
Let us quickly review the matrix formalism introduced in the paper Asashiba et al. (2018b), which allows us to write a morphism \(\phi :V\rightarrow W\) in \({{\,\mathrm{rep}\,}}\vec {A}_{w}\) in a matrix form. In this work, we only need to consider V and W equal to a direct sum of the interval representations, and this simplifies the presentation below.
Let \(\phi :V\rightarrow W\) be a morphism in \({{\,\mathrm{rep}\,}}{\vec {A}_{w}}\) with V and W given as below:

Note that the intervals \(\mathbb {I}[b_i,d_i]\) for \(i=1,\ldots ,m\) (respectively \(\mathbb {I}[b'_j,d'_j]\) for \(j=1,\ldots ,m'\)) may contain duplicates. This is not a problem.
Then \(\phi \) can be written in a matrix form \(\varPhi =\left[ \varPhi _{j,i}\right] \) relative to these decompositions, with entries given by \(\varPhi _{j,i} = \pi _j \phi \iota _i\):

where \(\iota _i\) and \(\pi _j\) are the evident inclusions and projections, respectively. Instead of a scalar, each entry \(\varPhi _{j,i}\) in the matrix form is a morphism from \(\mathbb {I}[b_i,d_i]\) to \(\mathbb {I}[b'_j,d'_j]\). The following lemma tells us the possible morphisms between intervals.
Lemma 3.2
(Lemma 1 of Asashiba et al. 2018b) Let \(\mathbb {I}[a,b],\mathbb {I}[c,d]\) be interval representations of \(\vec {A}_{w}\).
-
1.
The dimension of \({{\,\mathrm{Hom}\,}}(\mathbb {I}[a, b], \mathbb {I}[c, d])\) as a K-vector space is either 0 or 1.
-
2.
There exists a canonical basis
 for each nonzero
\({{\,\mathrm{Hom}\,}}(\mathbb {I}[a, b], \mathbb {I}[c, d])\) such that
for each nonzero
\({{\,\mathrm{Hom}\,}}(\mathbb {I}[a, b], \mathbb {I}[c, d])\) such that 
-
3.
In fact,

Going back to our morphism \(\varPhi = \left[ \varPhi _{j,i}\right] \) in matrix form, the entry at (j, i) is given by

for some scalar
\(c_{j,i}\in K\) if the dimension of \({{\,\mathrm{Hom}\,}}(\mathbb {I}[b_i, d_i], \mathbb {I}[b'_j, d'_j])\) is nonzero; otherwise \(\varPhi _{j,i}\) is always 0. As a shorthand, we hide the morphisms
 whenever we display the matrix form of morphisms in \({{\,\mathrm{rep}\,}}\vec {A}_{w}\).
whenever we display the matrix form of morphisms in \({{\,\mathrm{rep}\,}}\vec {A}_{w}\).
3.3 Auslander–Reiten quivers
We give a quick review of Auslander–Reiten quivers, which provide a very convenient framework to visualize our construction. By definition, the vertices of the Auslander–Reiten quiver are the indecomposable representations, and arrows are determined by the irreducible morphisms between indecomposables. See the book Assem et al. (2006), for example, for a more detailed discussion.
For our purposes, we only need to consider the Auslander–Reiten quiver \(\Gamma (\vec {A}_{n})\) of \(\vec {A}_{n}\), which takes on a relatively simple form. It is given by

where \(n' = n-1\) and where we adopt the convention of placing the simple representations (lifespan 0 intervals) \(\mathbb {I}[b,b]\) on a horizontal line, with everything else below.
To visualize our construction, we shall abstractly represent the Auslander–Reiten quiver of \(\vec {A}_{n}\) by a triangle:

Furthermore, we will need to freely extend the length of the underlying poset to some \(w \ge n\). We will thus consider the Auslander–Reiten quiver of \(\vec {A}_{n}\) as being embedded inside that of \(\vec {A}_{w}\), like so:

where the top line keeps track of the simple representations, with \(\mathbb {I}[w-1,w-1]\) at the leftmost and \(\mathbb {I}[0,0]\) at the rightmost.
4 Main construction
Before proving our main result, we introduce the following concept, which is essential in our proof for indecomposability. This is an offshoot of the idea behind the algebraic construction in Buchet and Escolar (2018), where certain configurations of indecomposables were found.
Definition 4.1
(Vertical) A collection of interval representations \(\{\mathbb {I}[b_i,d_i]\}_{i=1}^m\) is said to be vertical if and only if all the pairs \((b_i,d_i)\) are distinct and there exists a constant \(\mu \) such that \(\mu = \frac{b_i+d_i}{2}\) for all \(i \in \{1,\ldots ,m\}\).
If a collection of intervals is vertical, then they are all located along a vertical line on the Auslander–Reiten quiver, as follows:

because of the way we illustrate them. The following (almost trivial) observation about vertical intervals forms an essential part of our construction. Note that the matrix form below is written using the matrix formalism as reviewed in Sect. 3.2.
Lemma 4.2
Let \(W = \bigoplus _{i=1}^m \mathbb {I}[b_i,d_i]\) be a representation of \({\vec {A}_{w}}\) such that \(\{\mathbb {I}[b_i,d_i]\}_{i=1}^m\) is vertical. Then the matrix form of any morphism \(\phi : W\rightarrow W\) is diagonal:
for some scalars \(c_1,c_2,\ldots , c_m \in K\) (recall our shorthand of hiding the morphisms  ).
).
Proof
Since \(\{\mathbb {I}[b_i,d_i]\}_{i=1}^m\) is vertical, there exists \(\mu \) as in the definition and distinct numbers \(h_i\) such that \(b_i = \mu - h_i\) and \(d_i = \mu + h_i\) for all i.
For \(i\ne j\), it follows from part 3 of Lemma 3.2 that
since the inequality \(b_j \le b_i \le d_j \le d_i\) cannot be satisfied. Otherwise, we have
implying \(h_j \ge h_i\) and \(h_j \le h_i\), and so \(h_j = h_i\). This is a contradiction since \(h_i\) and \(h_j\) are supposed to be distinct. Thus, off-diagonal terms are always zero. Terms on the diagonal are some constant \(c_i \in K\) times  , which are identity maps. \(\square \)
, which are identity maps. \(\square \)
We reproduce here our Theorem 1.1 and provide a proof.
Theorem 1.1
Let \(V \in {{\,\mathrm{rep}\,}}{\vec {A}_{n}}\). Then there exists an indecomposable \(M \in {{\,\mathrm{rep}\,}}\vec {G}_{}\) with finite support such that V is a line restriction of M.
Proof
Without loss of generality, we identify \(V = \bigoplus _{i=1}^m \mathbb {I}[b_i,d_i]\). The proof takes the form of a construction process composed of three parts: separate-and-shift, verticalize, and coning.
Separate-and-shift We separate our intervals into distinct death-indices with the extra condition that these indices are large enough so that the next step is possible.
More precisely, we choose m distinct integers \(d'_i\) such that
-
1.
\(d'_i \ge d_i\) for all i and
-
2.
\(\frac{b_j + d'_j}{2} \le d'_i\) for all pairs i and j.
The first condition is clearly possible to satisfy. For the second condition, choose distinct \(d''_i\) satisfying the first, and let \(\ell = \max _i(b_i + d''_i)\) and define \(d'_i {:}{=}d''_i + \ell \). Then
for all pairs i, j, showing that both conditions can be satisfied by m distinct integers \(d_i'\).
We then choose an integer \(w \ge n\) such that \(w-1 \ge d'_i\) for all i. For example, \(w = \max \{n-1,\max \limits _i(d'_i)\} + 1\) will do. We have the inclusion \(\vec {A}_{n}\subset \vec {A}_{w}\), so that we can consider \(V \in {{\,\mathrm{rep}\,}}\vec {A}_{n}\hookrightarrow {{\,\mathrm{rep}\,}}\vec {A}_{w}\) as a representation of \(\vec {A}_{w}\), essentially by padding 0’s from vertices n to \(w-1\). Further constructions will take place in \({{\,\mathrm{rep}\,}}\vec {A}_{w}\).
By construction, there exists a nonzero morphism  for each \(i \in \{1,\ldots ,m\}\), which are in fact surjections. We form the representation \( V' {:}{=}\bigoplus \limits _{i=1}^m \mathbb {I}[b_i, d'_i] \) and the morphism
for each \(i \in \{1,\ldots ,m\}\), which are in fact surjections. We form the representation \( V' {:}{=}\bigoplus \limits _{i=1}^m \mathbb {I}[b_i, d'_i] \) and the morphism

(written in the matrix formalism). The diagonal entries can indeed be nonzero because of the existence of the nonzero morphisms.
The matrix form given in Diagram (4.1) is not the identity matrix and does not represent the identity morphism. The entries are morphisms between intervals, and we are hiding the factors  for simplicity.
for simplicity.
Pictorially, we think of \(V = \bigoplus _{i=1}^m \mathbb {I}[b_i,d_i]\) as a multiset of points on the Auslander–Reiten quiver \(\Gamma (\vec {A}_{n})\) of \(\vec {A}_{n}\), which is considered as a subquiver of \(\Gamma (\vec {A}_{w})\). Separate-and-shift moves each point (treating multiple copies of the same point as different) to a different death-index d. We illustrate this procedure as follows:

where the rightmost point appears with multiplicity 2, and each copy is brought to a different death index.
Verticalize We move our separated-and-shifted intervals into a vertical line by increasing birth indices. The “shift” part (the second condition) of the previous step ensures that the increased birth indices do not go beyond the death indices.
Let \(\mu = \max (\frac{b_i+d'_i}{2})\), the maximum of the midpoints of the intervals \(\mathbb {I}[b_i,d'_i]\). Note that by second condition of the previous step, \(\mu \le d'_i\) for all i. We define \(b'_i {:}{=}2 \mu - d'_i\) for all i, which can be visualized as “pivoting” \(d'_i\) around \(\mu \) to get \(b'_i\). Note that while \(\mu \) may be a half-integer, \(b'_i\) so defined is always an integer.
It follows that
for all pairs i, j. This inequality is very important for our construction, and we will refer again to this fact later.
In particular, we see that \(b'_i \le d'_i\) for all i. Thus, the intervals \(\mathbb {I}[b'_i, d'_i]\) are non-empty and distinct (since \(d'_i\) are), and \(\{\mathbb {I}[b'_i,d'_i]\}_{i=1}^m\) is vertical with common midpoint \(\mu = \frac{b'_i + d'_i}{2}\) as given. Furthermore, Eq. (4.2) says that the common midpoint \(\mu \) shared by all \(\mathbb {I}[b'_i,d'_i]\) serves as a wall separating all birth indices \(b'_i\) and all death indices \(d'_j\).
Since \(b'_i \ge b_i\), there exists a nonzero  for each i, which are in fact inclusions. We form the representation \( \overline{V} {:}{=}\bigoplus \limits _{i=1}^m \mathbb {I}[b'_i, d'_i] \) and the morphism
for each i, which are in fact inclusions. We form the representation \( \overline{V} {:}{=}\bigoplus \limits _{i=1}^m \mathbb {I}[b'_i, d'_i] \) and the morphism

We illustrate this step by the following figure:

Coning There exists
with nonzero morphisms to all \(\mathbb {I}[b'_j,d'_j]\) by using Lemma 3.2 and the fact that \(\max \limits _i(b'_i) \le d_j'\) for all j from Eq. (4.2). We can thus construct the morphism

with nonzero entries.
Constructed object and proof of indecomposability Our construction is summarized in the following picture:

and we obtain \(S\in \left[ \vec {A}_{4},{{\,\mathrm{rep}\,}}\vec {A}_{w}\right] \), a \({{\,\mathrm{rep}\,}}\vec {A}_{w}\)-valued representation of

determined by

where \(S(3){:}{=}V\), \(S(2) {:}{=}V' = \bigoplus _{i=1}^m \mathbb {I}[b_i,d'_i]\) is obtained by separate-and-shift, \(S(1) {:}{=}\overline{V} = \bigoplus _{i=1}^m \mathbb {I}[b'_i,d'_i]\) by verticalization (of \(V'\)), and \(S(0) {:}{=}I_V\) by coning.
Let us show that S is indecomposable. Any \(\phi \in {{\,\mathrm{End}\,}}(S)\) is given by a collection of maps \((\phi _0, \phi _1, \phi _2, \phi _3)\) making the diagram

commutative.
Since the summands of \(\overline{V}\) are vertical, \(\phi _1\) has matrix form
for some scalars \(c_1,c_2,\ldots , c_m \in K\) by Lemma 4.2.
By commutativity of the second and third boxes in Diagram (4.5), the scalars in the matrix forms of \(\phi _2\) and \(\phi _3\) are nonzero only along the diagonal and with scalars along the diagonal given by \(c_1,\ldots , c_m\). This involves some technical details, which we delay to Lemma 4.3, where Eq. (4.2) is essential.
By the commutativity of the first box in Diagram (4.5), we get \(c_1 = c_2 = \ldots = c_m = \phi _0 \in K\). Thus, \({{\,\mathrm{End}\,}}(S) \cong K\) is local and so S is indecomposable.
We have shown that \(S \in \left[ \vec {A}_{4},{{\,\mathrm{rep}\,}}{\vec {A}_{w}}\right] \) is indecomposable. By vertical stacking Lemma 3.1, this can be viewed as an indecomposable representation of the \(4 \times w\) commutative grid \(\vec {G}_{4,w}\). This can be viewed (by padding with zeroes), as an indecomposable representation S of \(\vec {G}_{}\) with finite support.
The original representation V is obtained by line restriction of S to the horizontal line \(L:\mathbb {Z}\rightarrow \mathbb {Z}\times \mathbb {Z}\) that runs along the 4th row. \(\square \)
Finally, let us prove the technical details used to prove the form of the endomorphisms of S.
Lemma 4.3
(Propagation of nonzeroes)
-
1.
Let \(\overline{V} = \bigoplus \limits _{i=1}^m \mathbb {I}[b'_i, d'_i]\) and \(V' = \bigoplus \limits _{i=1}^m \mathbb {I}[b_i, d'_i]\) such that \(b_i \le b'_i \le \min _j(d'_j)\) for all i, and let \(\iota {:}{=} \left[ {\begin{matrix} 1 &{} &{} \\ &{} \ddots &{} \\ &{} &{} 1 \end{matrix}}\right] :\overline{V}\rightarrow V'\) be the morphism given in matrix form with only nonzeros in the diagonal given by the inclusions
 , as above. Suppose that
, as above. Suppose that 
is commutative. Then the matrix form of \(\phi _2\) is \( \left[ {\begin{matrix} c_1 &{} &{} \\ &{} \ddots &{} \\ &{} &{} c_m \end{matrix}}\right] \).
-
2.
Let \(V' = \bigoplus \limits _{i=1}^m \mathbb {I}[b_i, d'_i]\) and \(V = \bigoplus \limits _{i=1}^m \mathbb {I}[b_i, d_i]\) such that \(d'_i \ge d_i\) for all i, and let \(\pi {:}{=} \left[ {\begin{matrix} 1 &{} &{} \\ &{} \ddots &{} \\ &{} &{} 1 \end{matrix}}\right] :V'\rightarrow V\) be the morphism given in matrix form with only nonzeros in the diagonal given by the projections
 , as above. Suppose that
, as above. Suppose that 
is commutative. Then the matrix form of \(\phi _3\) is \( \left[ {\begin{matrix} c_1 &{} &{} \\ &{} \ddots &{} \\ &{} &{} c_m \end{matrix}}\right] \).
Before giving the proof, we give an example where the conclusion of part 1 fails to hold if the condition \(b'_i \le \min _j(d'_j)\) for all i is not satisfied. If \(\overline{V}\) is vertical, then this condition is automatically satisfied, so we construct an example where this is not the case. We let \( V' = \mathbb {I}[1,2] \oplus \mathbb {I}[1,1] \) and \( \overline{V} = \mathbb {I}[2,2] \oplus \mathbb {I}[1,1]. \) The death-indices are fixed at 2 and 1, while \(b_1 = 1 \le 2 = b'_1\) and \(b_2 = 1 \le 1 = b'_2\). Note that \(b'_1 = 2 \not \le 1 = \min _j(d'_j)\). The commutative diagram (4.7) becomes

Note that  is the identity morphism.
is the identity morphism.
The composition \(\iota \phi _1\) is

However, the composition \(\phi _2 \iota \) is

where the lower-left entry is equal to 0 since the composition  . This can be illustrated by the following.
. This can be illustrated by the following.

The birth index 2 has exceeded the smallest death index 1, and so the composition “falls through” and fails to be nonzero.
The commutativity of the diagram implies the equality of Eqs. (4.8) and (4.9), from which we obtain \(a_{11} = c_1\) and \(a_{22} = c_2\), but \(a_{21}\) is not determined. Thus, we cannot conclude that the matrix form of \(\phi _2\) is the same diagonal.
Proof of Lemma 4.3
The matrix formalism hides the morphisms  , and the composition of two nonzero composable
, and the composition of two nonzero composable  can possibly be zero. What is important for this lemma is that the compositions should be nonzero where needed, so that the commutativity relation forces the scalars \(a_{j,i}\) to be zero off-diagonal and the same as \(c_j\) along the diagonal.
can possibly be zero. What is important for this lemma is that the compositions should be nonzero where needed, so that the commutativity relation forces the scalars \(a_{j,i}\) to be zero off-diagonal and the same as \(c_j\) along the diagonal.
-
1.
The composition \(\phi _2 \iota \) is equal to

The entries (j, i) with
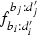 nonzero are given by \( b_j \le b_i \le d'_j \le d'_i \) by Lemma 3.2 (these are the entries where \(a_{j,i}\) are present). For each such entry, the corresponding morphism in the composition \(\phi _2\iota \) is given by
nonzero are given by \( b_j \le b_i \le d'_j \le d'_i \) by Lemma 3.2 (these are the entries where \(a_{j,i}\) are present). For each such entry, the corresponding morphism in the composition \(\phi _2\iota \) is given by 
Using Lemma 3.2 and the fact that \(b'_i \le \min _j(d'_j) \le d'_j\), we see that this composition is nonzero.
Thus, \(\phi _2\iota \) has scalars in its matrix form the same as \(\phi _2\) (nonzeros cannot go to zeros). Equating with the other composition \(\iota \phi _1\) in the commutative diagram, \(a_{j,j} = c_j\) for all j and \(a_{j,i} = 0\) for \(i\ne j\), as required.
-
2.
The composition \(\phi _3 \pi \) is equal to

The entries (j, i) with
 nonzero are given by \( b_j \le b_i \le d_j \le d_i \) by Lemma 3.2. In these entries, the composition
nonzero are given by \( b_j \le b_i \le d_j \le d_i \) by Lemma 3.2. In these entries, the composition 
is also nonzero by Lemma 3.2 and the fact that \(d_i \le d'_j\). Then the conclusion is obtained by a similar argument as above.
\(\square \)
Dual Construction We note that a dual construction is possible. Instead of constructing to the left, we can proceed to the right and obtain

where \(V'' = \bigoplus _{i=1}^m \mathbb {I}[b'_i,d_i]\) is obtained by separate-and-shift choosing smaller (possibly negative) birth-indices that are distinct, and \(\overline{\overline{V}} = \bigoplus _{i=1}^m \mathbb {I}[b'_i,d'_i]\) by verticalization, and \(I'_V\) by coning. Note that in this case, the correct condition to use for separate-and-shift is to have \(b'_i\) all distinct with \(b'_i \le b_i\) for all i and \(b_j' \le \frac{b_i'+d_i}{2}\) for all pairs i, j. Then we use \(\mu {:}{=}\min \left( \frac{b_i'+d_i}{2}\right) \) and \(d_i' {:}{=}2\mu -b_i'\) for verticalization. Coning is given by \(I'_V {:}{=}\mathbb {I}[\min {b_i'},\min {d'_j}]\). Here, we can check that \(b_j' \le d_i' \le d_i\) for all pairs i, j, which allows the 1’s in the matrix form of the morphism to \(I'_V\), and enables the dual version of propagation of nonzeros.
Remark 4.4
Note that the primal and dual constructions can be combined into one, yielding the following object

of \(\left[ \vec {A}_{7},{{\,\mathrm{rep}\,}}\vec {A}_{w}\right] \), where \(V'\) and \(V''\) are obtained from separate-and-shift to the right and left, \(\overline{V}\) and \(\overline{\overline{V}}\) from verticalization, and \(I_V\) and \(I'_V\) from coning. This corresponds to a 2D persistence module by Stacking Lemma 3.1.
We note that the support of the obtained module is contained in a rectangle, with the lower right and upper left corners both supporting one-dimensional vector spaces. Moreover its endomorphism ring is isomorphic to K. In general, we call 2D persistence modules with these properties candy modules as they are wrapped like candies with two handles we can manipulate. These modules will play a central role in the construction of Sect. 6.
5 Consequences on the homology of supports
One consequence of our construction is the easy construction of examples of indecomposable representations of \(\vec {G}_{}\) (indecomposable 2D persistence modules) whose support has a “hole”. We contrast this with interval representations, a restricted class of representations that has been studied before Bjerkevik (2016) and Dey and Xin (2018). By definition, an interval representation associates to each vertex a vector space with dimension at most 1, its internal linear maps are always identity between non-zero vector spaces, and its support satisfies a convexity and connectedness condition. In particular, the support of any interval representation of \(\vec {G}_{m,n}\) always has a distinctive staircase shape (Asashiba et al. 2018a).
5.1 Indecomposables with holes in support
Note that while the technical details of our construction use nonnegative indices, it still works after shifting all indices. Let \(V=\mathbb {I}[-1,-1]\bigoplus \mathbb {I}[1,1]\), whose form is chosen for symmetry. We follow Remark 4.4 and obtain by the primal and dual construction:

corresponding to the 2D persistence module

where all but one zero vector space outside the support are omitted for the sake of clarity. Maps between identical vector spaces are to be understood as the identity maps. Then by the arguments in the proof for Theorem 1.1 and the dual construction, we see that \({{\,\mathrm{End}\,}}(H)\cong K\), and thus H is indecomposable. Moreover its support has a hole as the central vector space is 0.
One way to formally define the notion of the hole in the support is to consider the cubical complex induced by the support of a 2D persistence module V as follows. Recall that the support of V is the set of points \({\mathrm {supp}}(V) = \{x \in \vec {G}_{} |V(x) \ne 0\}\). We then build a cubical complex by adding an edge between x and y whenever \(x,y\in {\mathrm {supp}}(V)\) and x and y are adjacent on the 2D grid. Whenever we have four points \((i,j),(i,j+1),(i+1,j+1),(i+1,j) \in {\mathrm {supp}}(V)\) for some \(i,j\in \mathbb {Z}\), we add a unit square with those corner vertices. This is the clique-cubical complex of \({\mathrm {supp}}(V)\). We then consider holes in the support as being non-trivial classes in the 1-dimensional homology of this cubical complex. We say that the support of a 2D persistence module has n holes if the 1-dimensional homology of the cubical complex built on the support has n linearly independent classes. It is clear that the representation given in Diagram (5.1) has a hole in this sense.
Our construction can then be used to generate indecomposable 2D persistence modules having an arbitrary finite number of holes in its support.
Corollary 5.1
Let \(n \in \{0,1,2,\ldots \}\). There exists an indecomposable 2D persistence module whose support has exactly n holes.
Proof
Let n be as given, and fix \(V=\bigoplus _{i=0}^n \mathbb {I}[2i,2i]\).
Note that \({\mathrm {supp}}V\) has exactly \(n+1\) connected components. Again we define the indecomposable representation

by using the construction in Theorem 1.1 and its dual. By the Stacking Lemma 3.1, H is viewed as a 2D persistence module.
By construction, each representation \(X \in \{V',V'',\overline{V},\overline{\overline{V}},I_V,I'_V\}\) has connected support because all of the intervals composing X have a common index (depending on X) where they are non-zero. Moreover, the right extremities of \(V'\), \(\overline{V}\) and \(I_V\) are aligned, and thus the cubical complex of the support of \(I_V\rightarrow \overline{V}\rightarrow V'\) is contractible. Similarly the left extremities of \(V''\), \(\overline{\overline{V}}\) and \(I'_V\) are also aligned, and the cubical complex of the support of \(V''\rightarrow \overline{\overline{V}}\rightarrow I'_V\) is also contractible.
Finally, the support of V is included in both the support of \(V'\) and \(V''\), ensuring that every neighboring pair of connected components in the support of V can be used to generate a non-trivial 1-homology class in the cubical complex of \({\mathrm {supp}}(H)\). There are n such pairs, and it is clear that H has exactly n holes in its support.
Below, we illustrate the clique cubical complex of the support of H.

Note that this realizes a topological suspension of the support of V. \(\square \)
5.2 A minimal construction
The construction used to prove Theorem 1.1 works for general 1D persistence modules V, but does not consider any size minimality for particular cases of V. For example, the persistence module in Diagram (5.1) is not the smallest example of an indecomposable 2D persistence module whose support has a hole. Indeed, using only the primal construction to obtain the bottom half of Diagram (5.1), and “capping off” the top of V with an interval would have yielded an example with smaller support.
Before discussing a minimal example in Theorem 5.4, let us study a local construction that we use repeatedly for its proof. Consider the family \(\mathcal{P}\) of 2D persistence modules whose support is contained in a small “cross” shape. The small cross shape is the 5 vertices a, b, c, d, e (filled-in circles) and filled-in arrows \(\alpha \), \(\beta \), \(\gamma \), \(\delta \):

where the unfilled circles and grayed-out arrows are not part of the support.
Consider \(M \in \mathcal {P}\). Since the upper-left and lower-right vertices are not part of the support, M associates the zero vector space to those vertices. By commutativity relations, the compositions \(M(\beta )M(\alpha )\) and \(M(\delta )M(\gamma )\) must be zero. These zero relations are denoted by the dashed lines. Thus, we can also treat \(M\in \mathcal {P}\) as a representation of the corresponding bound quiver.
Lemma 5.2
There is no indecomposable \(T \in \mathcal P\) whose support contains both the bottom and right vertices (a and c) or both the left and top vertices (b and d).
We provide a proof in the Appendix.
Remark 5.3
Note that the quiver formed by the filled-in vertices and arrows in Diagram (5.2), together with the relations \(\delta \gamma =0\) and \(\beta \alpha =0\), generates what is known as a string algebra. Lemma 5.2 in fact follows immediately from a known characterization of indecomposable representations of string algebras as the string modules and band modules (Butler and Ringel 1987). \(\square \)
The important consequence of Lemma 5.2 is that given any 2D persistence module M on such a cross shape with zero relations as in Diagram (5.2), bases for its vector spaces can be chosen that allows for a decomposition \(M = M_1 \oplus M_2\) into the direct sum of two representations such that \(M_1(a) = 0\) and \(M_2(c) = 0\), or symmetrically \(M=M'_1 \oplus M'_2\) with \(M'_1(b) = 0\) and \(M'_2(d) = 0\).
Theorem 5.4
The minimal number of vertices in the support of an indecomposable 2D persistence module whose support has a hole is equal to 11. For example, the 2D persistence module

realizes this minimum.
Proof
The support of M contains exactly 11 vertices and has a hole. An elementary computation shows that the endomorphism ring of M is isomorphic to K, and thus M is indecomposable. It is then sufficient to prove that there is no indecomposable 2D persistence module whose support has a hole and contains 10 or less vertices. The existence of a hole requires at least 8 vertices in the support.
8 vertices Suppose that T is an indecomposable 2D persistence module whose support has exactly 8 vertices and has a hole. Then T is of the form:

By commutativity, both \(f_3f_2\) and \(g_3g_2\) are zero maps. We can thus construct the following:

where \(\hat{f_3}\) and \(\hat{g_3}\) are the induced maps on the respective coimages. It is a simple matter to check that \(T\cong T_A\oplus T_B\). Since the support of T has exactly 8 vertices, A and B are nonzero, and so \(T_A\) and \(T_B\) are nonzero. This contradicts the fact that T is indecomposable.
In order to prepare for the remaining cases, let us rephrase this argument using Lemma 5.2 and its proof. First, we view T as a representation of

We then restrict our attention to the “partial crosses” centered at \(x_2\) and \(y_2\), and use a similar argument as in the proof of Lemma 5.2. By choices of bases, we obtain summands where the vector spaces at vertices \(x_1\) and \(x_3\) are not both nonzero, and where the vector spaces at vertices \(y_1\) and \(y_3\) are not both nonzero.
These choices can be done simultaneously for the two partial crosses, as they share no vertices. In general, such a “local” decomposition does not induce a decomposition of a representation as a whole.
However, in this case, we can build the following two subrepresentations \(T_A\) and \(T_B\) of T. For \(T_A\), we take the decomposition summands over the two crosses which are non-zero at vertices \(x_1\) and \(y_1\), and then add the vector space A at vertex a with the linear maps from A to \(X_1\) and A to \(Y_1\). Using Lemma 5.2 ensures that we can simply fix the vector spaces of \(T_A\) at \(x_3\), \(y_3\) and b to be 0, and that the result is indeed a subrepresentation. Note that we obtain the same \(T_A\) as defined previously. Symmetrically, we obtain \(T_B\), and it is a simple matter to show that \(T \cong T_A\oplus T_B\).
9 vertices A support with 9 vertices and containing a hole can only be obtained by adding one vertex somewhere on the outside of Diagram (5.3). Depending on where these vertices are added, an appropriate zero relation needs to be imposed in order to ensure the embeddability in the equioriented commutative 2D grid. For example, with z the additional vertex in the support, the underlying bound quiver becomes

where we still have partial crosses centered at \(x_2\) and \(y_2\). The same argument as the one in the case of 8 vertices, using these two partial crosses, shows that a 2D persistence module with such a support cannot be indecomposable.
Note that the extra vector space at vertex z is handled in two different ways depending on the position of z. If z is part of one of the partial crosses at \(x_2\) or \(y_2\) then it is automatically split in a direct sum of vector spaces, one being part of \(T_A\) and the other part of \(T_B\) by the use of Lemma 5.2.
If z is not part of one of the crosses (for example Diagram (5.4)), then the vector space on its adjacent vertex (\(y_1\) in Diagram (5.4)) is split into a part in \(T_A\) and a part in \(T_B\). By construction, at least one of those must be 0. The vector space at vertex z together with the map connecting it to the rest of the diagram can be added to the subrepresentation with the not necessarily zero part. For example, in Diagram (5.4), the subrepresentation \(T_B\) is 0 at vertex \(y_1\). The vector space and linear map of T associated to z can thus be added to the \(T_A\) obtained in the 8 vertices case while guaranteeing that \(T_A\) is still a subrepresentation.
10 vertices The case with 10 vertices can be obtained in two ways.
First, the hole in Diagram (5.3) can be made wider by adding two vertices (and corresponding arrows) to the support, for example between \(x_3\) and b and between \(y_1\) and \(y_2\). This means that the 2D persistence module will need to encompass two 0 vector spaces in its center. The proof for this case is similar to the one for 8 vertices.
The second case is obtained when we add two vertices (and corresponding arrows) to Diagram (5.3) on the outside. Depending on where these vertices are added, zero relations or commutativity relations need to be imposed in order to ensure the embeddability in the equioriented commutative 2D grid, as we shall see below.
Thus we further subdivide this case. First, in the case that the two new vertices are not adjacent, we only need to deal with new zero relations. For example, both vertices can be attached at corner \(y_2\), as below:

The argument using the partial crosses can be used as before.
A second possibility is that the two new vertices are adjacent, for example:

where we need to impose the commutative relation in the right square.
Even in this case, a variant of the argument in Lemma 5.2 is still feasible. Suppose a 2D persistence module T has Diagram (5.5) as its support. We construct subrepresentations \(T_A\) and \(T_B\). For \(T_A\), its vector spaces at vertices \(x_2\), \(x_1\), a, and \(y_1\) are obtained as before, using the same partial cross argument around vertex \(x_2\).
We set the vector space \(T_A(y_2)\) of \(T_A\) at vertex \(y_2\) as the image of \(T_A(y_1) {:}{=}T(y_1)\) under the linear map of T from \(y_1\) to \(y_2\). Similarly, the vector space \(T_A(y_4)\) is the image of \(T(y_1)\) under the composition of maps from \(y_1\) to \(y_2\) to \(y_4\).
By commutativity and the zero relation, \(T_A(y_4)\) is in the kernel of the map from \(y_4\) to \(y_6\). Thus, \(T_A(y_3)\) and \(T_A(y_6)\) can be set to 0, along with \(T_A(x_3)\) and \(T_A(b)\) as before, while guaranteeing that \(T_A\) is indeed a subrepresentation of T.
Similarly, a subrepresentation \(T_B\) that is 0 on a, \(x_1\), \(y_1\) can be constructed such that \(T\cong T_A\oplus T_B\). As before, we note that \(T_A\) is nonzero at a and \(T_B\) is nonzero at b, showing that T is in fact decomposable.
Finally, it is possible to have adjacent new vertices without inducing a commutative relation either by having an arrow elongating a path such as:

where the arguments from the 9 vertex case apply. Otherwise the new arrow points in the opposite direction of the existing one such as:

This case is a bit more involved. However a careful computation on the subpart induced by vertices \(\{y_1,y_2,y_3,y_5,y_8\}\) leads to a decomposition similar to the one of Lemma 5.2, enabling the same arguments to follow as in the other cases.
In all cases considered, a persistence module with support of the prescribed shape and number of vertices cannot be indecomposable. This shows the claimed result. \(\square \)
6 A representation to contain them all
In Sect. 4, we showed that for every 1D persistence module in \({{\,\mathrm{rep}\,}}\vec {A}_{n}\), we can build an indecomposable 2D persistence module containing it as a line restriction. We can go further and build an indecomposable 2D persistence module with infinite support that contains all 1D persistence modules with finite support as line restrictions.
Recall that the primal and dual construction for Theorem 1.1 starting from a 1D persistence module V results in a 2D candy module (see Remark 4.4) of the form

Given two candy modules A and B, we define the following concatenation operation. Let \(r_A\) be the rightmost vertex in the lowest interval of A. We translate B such that the leftmost vertex of the top interval of B (denoted \(l_B\)) is located below and to the right of \(r_A\):

Note that the vector spaces at both \(r_A\) and \(l_B\) are K. On the vertex x below \(r_A\) (and to the left of \(l_B\)), we associate the vector space K, and put identity maps on the arrows to \(r_A\) and \(l_B\). The concatenation \(A\circ B\) is the 2D persistence module defined as being equal to A and B restricted to their respective supports, K over x, and with identity maps over the arrows from x to \(l_B\) and x to \(r_A\), and zero elsewhere.
Lemma 6.1
Given A and B two candy modules, \(A\circ B\) is a candy module.
Proof
It is easy to see that \(A\circ B\) is a well-defined 2D persistence module, as no commutativity relations are violated by our construction. Indeed the supports of A and B are disjoint, and there are no paths from one to the other. Moreover, the addition of the vector space over x and the two identity maps only create paths from x to the upper row of B and the right column of A.
Next, we check that \(A\circ B\) is indeed a candy module.
Its top left vertex corresponds to the top left vertex of A and is associated to the vector space K, while its bottom right vertex corresponds to the bottom right vertex of B and also supports K.
By the property of candy modules, \({{\,\mathrm{End}\,}}(A)\cong K\cong {{\,\mathrm{End}\,}}(B)\). Let f be an endomorphism of \(A\circ B\). The restriction of f to the support of A, respectively x and B, is defined by a unique scalar \(\alpha \), respectively \(\xi \), \(\beta \). Therefore there exist two non-zero constants \(c_A\) and \(c_B\) such that f restricted at vertex \(r_A\), respectively x and \(l_B\) is the multiplication by the scalar \(c_A\alpha \), respectively \(\xi \) and \(c_B\beta \). The commutativity conditions along the arrows from x to \(r_A\) and from x to \(l_B\) implies that \(c_A\alpha =\xi =c_B\beta \). Note that no other conditions are required for f. Therefore f is completely determined by one scalar \(\xi \), and the endomorphism ring of \(A\circ B\) is isomorphic to K. \(\square \)
Lemma 6.2
The set \(\mathcal {P}\) of isomorphism classes of 1D persistence modules of finite total dimension is a countable set.
Proof
Note that a representative V for a class \([V]\in \mathcal {P}\) can be decomposed as
in a unique canonical way. Indeed the intervals in an indecomposable decomposition can be ordered using the lexicographic order on \(\mathbb {Z}^2\). We thus have a unique representative for each class [V] and denote by S the set of all those representatives.
We define \(S_n\) to be the set of all elements of S whose total dimension is less than n and whose support is contained in \([-n,n]\). Every set \(S_n\) is finite and \(\cup _n S_n = S\). Therefore the set S is countable and is in bijection with the set of all isomorphism classes of 1D persistence modules of finite total dimension.
Note that the sequence \((S_n)_n\) is in fact a filtration of S as \(S_n\subset S_{n+1}\). \(\square \)
Theorem 6.3
There exists an indecomposable 2D persistence module \(M \in {{\,\mathrm{rep}\,}}\vec {G}_{}\) such that any 1D persistence module V of finite total dimension is a line restriction of M.
Proof
As a consequence of Lemma 6.2 the set of all non-zero 1D persistence modules up to isomorphism and translation is a countable set. We can enumerate its elements as a sequence \((L_i)_{i\in \mathbb {N}}\). For each of these \(L_i\), we apply our dual and primal construction to obtain a candy module \(M_i\), as in Remark 4.4. Note that every \(M_i\) has exactly seven rows and that its endomorphism ring is K, see the proof of Theorem 1.1 for details.
We concatenate \(M_0,M_1,\ldots \) to obtain a 2D persistence module M as below:

The proof of Lemma 6.1 naturally extends to the setting of a countable concatenation, and therefore M is a well-defined persistence module with \({{\,\mathrm{End}\,}}(M)\cong K\). Thus M is an indecomposable 2D persistence module.
Note that the line just above the module \(M_0\) is 0 so M also contains the zero 1D persistence module as a line restriction. By construction all non-zero 1D persistence modules with finite total dimension appear as a line restriction to the middle row of the corresponding candy module \(M_i\). Every vertex supports a finite dimensional vector space so M is locally finite. Obviously M has infinite support and vector spaces with arbitrarily high dimension. \(\square \)
7 Rectangle-decomposable nD persistence modules
Denote elements of \(\mathbb {Z}^n\) as n-tuples \(\vec {b} = (b^1,b^2,\ldots ,b^n)\in \mathbb {Z}^n\). We consider the poset \((\mathbb {Z}^n,\le )\), where \(\vec {b} \le \vec {d}\) if and only if \(b^k \le d^k\) for all \(k=1,\ldots ,n\).
Recall that by nD persistence module we mean a functor M in \({{\,\mathrm{rep}\,}}\mathbb {Z}^n = \left[ \mathbb {Z}^n, {\mathrm {vect}}_K\right] \). Throughout this section, persistence module will mean persistence module of finite support: \(\{M(\vec {x}) \ne 0 |\vec {x} \in \mathbb {Z}^n\}\) is a finite set.
Definition 7.1
Let \(\vec {b} \le \vec {d} \in \mathbb {Z}^n\). The finite rectangle from \(\vec {b}\) to \(\vec {d}\), denoted \(\mathbb {I}[\vec {b},\vec {d}]\), is the nD persistence module defined by
The support of \(\mathbb {I}[\vec {b},\vec {d}]\) is exactly the points on the nD grid contained in the rectangle
We denote this set of points on the nD grid by \([\vec {b},\vec {d}]\).
A more general treatment would involve possibly unbounded rectangles (see Bjerkevik 2016 for example). However, we only treat nD persistence modules of finite support, and this finiteness is essential to our proof of Theorem 7.7.
Definition 7.2
An nD persistence module V is said to be finite-rectangle-decomposable if and only if
for some elements \(\vec {b_i} \le \vec {d_i} \in \mathbb {Z}^n\) for \(i=1,\ldots m\).
Note that we assume finite supports, and only discuss finite sums. The finite rectangles \(\mathbb {I}[\vec {b_i}, \vec {d_i}]\) do not need to be distinct.
The following lemma generalizes Lemma 3.2 to finite rectangles.
Lemma 7.3
Let \(\mathbb {I}[\vec {a},\vec {b}],\mathbb {I}[\vec {c},\vec {d}]\) be finite rectangular nD persistence modules.
-
1.
The dimension of \({{\,\mathrm{Hom}\,}}(\mathbb {I}[\vec {a}, \vec {b}], \mathbb {I}[\vec {c}, \vec {d}])\) as a K-vector space is either 0 or 1.
-
2.
There exists a canonical basis
 for each nonzero \({{\,\mathrm{Hom}\,}}(\mathbb {I}[\vec {a}, \vec {b}], \mathbb {I}[\vec {c}, \vec {d}])\) such that
for each nonzero \({{\,\mathrm{Hom}\,}}(\mathbb {I}[\vec {a}, \vec {b}], \mathbb {I}[\vec {c}, \vec {d}])\) such that 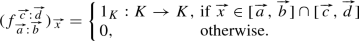
-
3.
In fact,

Proof
Lemma 3.3 and Corollary 3.4 of Bjerkevik (2016). \(\square \)
Thus, for morphisms between finite-rectangle-decomposable nD persistence modules, we have a similar matrix formalism as in the 1D case. As before, we adopt the convention of hiding the morphisms  for simplicity.
for simplicity.
Definition 7.4
(Vertical) A collection of finite rectangles \(\mathcal {I} = \{\mathbb {I}[\vec {b_i},\vec {d_i}]\}_{i=1}^m\) is said to be vertical if and only if all the pairs \((\vec {b_i},\vec {d_i})\) are distinct and there exists a constant \(\vec {\mu }\) such that \(\vec {\mu } = \frac{\vec {b_i}+\vec {d_i}}{2}\) for all i.
In the definition above, the arithmetic operations are performed component-wise. The following is the generalized version of Lemma 4.2.
Lemma 7.5
Let \(W = \bigoplus _{i=1}^m \mathbb {I}[\vec {b_i},\vec {d_i}]\) be finite-rectangle-decomposable nD persistence module whose set of rectangles is vertical. Then the matrix form of any morphism \(\phi : W\rightarrow W\) is diagonal:
for some scalars \(c_1,c_2,\ldots , c_m \in K\).
Proof
Similar to the proof of Lemma 4.2, and using Lemma 7.3. \(\square \)
Definition 7.6
(Hyperplane restriction) Let n be a positive integer.
-
1.
A hyperplaneL is a functor \(L : (\mathbb {Z}^n,\le ) \rightarrow (\mathbb {Z}^{n+1},\le )\) that is injective on objects.
-
2.
Let V be an nD persistence module. We say that V is a hyperplane restriction of the \((n+1)\)D persistence module M if there is a hyperplane L such that \((M\circ L) \cong V\).
Note that in the proof of Theorem 1.1, we used the Auslander–Reiten quiver of \(\vec {A}_{w}\) in order to visualize the movements of the intervals. However, it was not essential to the proof. Above, we have provided generalizations of the essential tools to finite rectangles. Thus, the following theorem can be proved similarly as Theorem 1.1, except we no longer draw the Auslander–Reiten quiver.
Theorem 7.7
Let V be a finite-rectangle-decomposable nD persistence module. Then there exists an indecomposable \((n+1)\)D persistence module M with finite support such that V is a hyperplane restriction of M.
Proof
The proof is similar to the proof of Theorem 1.1. Below is a quick outline.
Without loss of generality, let \(V = \bigoplus _{i=1}^m \mathbb {I}[\vec {b_i},\vec {d_i}]\). We then separate-and-shift to distinct \(\vec {d'_i} \in \mathbb {Z}^n\) such that \(\vec {d'_i} \ge \vec {d_i}\) for all i and \(\frac{\vec {b_j} + \vec {d'_j}}{2} \le \vec {d'_i}\) for all pairs i and j. Take
where the \(\max \) is taken component-wise. This will serve as the shared midpoint for verticalization, by defining \(\vec {b_i'} = 2\vec {\mu } - \vec {d'_i}\). Again, we have
for all pairs i, j. Finally, coning is done with the finite rectangle
We get the object \(S\in \left[ \vec {A}_{4},{{\,\mathrm{rep}\,}}(\mathbb {Z}^n,\le )\right] \), a \({{\,\mathrm{rep}\,}}(\mathbb {Z}^n,\le )\)-valued representation of \(\vec {A}_{4}\):

where \(S(3){:}{=}V\), \(S(2) {:}{=}V' = \bigoplus _{i=1}^m \mathbb {I}[\vec {b_i},\vec {d'_i}]\) is obtained by separate-and-shift, \(S(1) {:}{=}\overline{V} = \bigoplus _{i=1}^m \mathbb {I}[\vec {b'_i},\vec {d'_i}]\) by verticalization (of \(V'\)), and \(S(0) {:}{=}I_V\) by coning. By stacking, S can be viewed as a representation of \((\mathbb {Z}^{n+1},\le )\), id est, an \((n+1)\)D persistence module. Note that the \((n+1)\)D persistence module obtained from S clearly has finite support. The original nD persistence module V is clearly a hyperplane restriction by a natural inclusion \(\mathbb {Z}^n \hookrightarrow \mathbb {Z}^{n+1}\).
It can be shown that \({{\,\mathrm{End}\,}}(S) \cong K\), proving the indecomposability of S. Note that a generalization of Lemma 4.3 (propagation of nonzeros) to finite-rectangle-decomposables is needed, but the proof is similar to that of Lemma 4.3. \(\square \)
Note that, as before, the construction in the proof of the theorem has a dual, which we denote by \( V \rightarrow V'' \rightarrow \overline{\overline{V}} \rightarrow I'_V \). A direct consequence of this extension is the construction of indecomposable \((n+1)\)D persistence modules whose support has an arbitrary number of nD holes. Here, nD holes in the support can be formalized as linearly independent classes of the n-dimensional homology of the clique cubical complex of the support.
Corollary 7.8
For any \(l\in \{0,1,2,\dots \}\), there exists an indecomposable \((n+1)\)D persistence module whose support has exactly lnD holes and no lower dimensional hole.
Proof
The proof is a direct adaptation of the proof of Corollary 5.1.
Clearly, it is possible to build an nD persistence module V that is rectangle decomposable and contains exactly l\((n-1)\)D holes in its support and no lower dimensional hole, for example by building with rectangles the boundaries of lnD hypercubes.
Note that the construction of Theorem 7.7 can be dualized in the same way as the one of Theorem 1.1. As in the proof of Corollary 5.1, we obtain the \((n+1)\)D persistence module H obtained by combining the primal and dual construction with V in the middle. The \((n+1)\)D persistence module H has support with exactly lnD holes and is indecomposable.
To see this, by considering the construction as working in the up and down direction, we can interpret it as stacking nD slices: \(I_V\), \(\bar{V}\), and \(V'\) below V for the primal construction, and \(V''\), \(\overline{\overline{V}}\), and \(I'_V\) above V for the dual construction. Each of those new slices has contractible support, and they are connected along a contractible intersection, so that \(I_V\rightarrow \bar{V}\rightarrow V'\) has contractible support (and similarly for the dual part).
The construction with primal and dual parts modifies the support to become a double cone with apexes \(I_V\) and \(I'_V\), in other words its topological suspension. Such operation transforms each mD hole into an \((m+1)\)D hole for every m, without creating other topological features. In our case this results in the requested topology. \(\square \)
Gluing the constructions in all dimensions using an operation similar to the concatenation of Sect. 6, we obtain the following more interesting result.
Theorem 7.9
Given a positive dimension n and a sequence \((b_i)_{0<i<n}\) of non-negative integers, there exists an indecomposable nD persistence module whose support has \(b_i\) for its Betti number for every \(0<i<n\).
Proof
Using Corollary 7.8, we first build a sequence of indecomposable persistence modules \(T_i\) for \(0<i<n\) that satisfy the condition for exactly the ith Betti number.
More precisely, each \(T_i\) is an indecomposable \((i+1)\)D persistence module whose support has exactly \(b_i\)i-dimensional holes and no other holes. In other words, its Betti numbers are 1 in dimension 0, \(b_i\) in dimension i and 0 otherwise.
By construction, \(T_i\) has two other important properties. First, \({{\,\mathrm{End}\,}}(T_i) \cong K\). Second, the support of \(T_i\) has two extremal vertices, along which we string together these persistence modules. These extremal vertices are minimal and maximal under the following partial order: the usual order for each of the first i coordinates and the opposite order for the last coordinate (along which we stack). In symbols, we define \((x^1,\ldots ,x^i,x^{i+1}) \le (y^1,\ldots ,y^i,y^{i+1})\) if and only if \(x^j \le y^j\) for all \(1\le j \le i\) and \(x^{i+1} \ge y^{i+1}\). For example, \((1,2,2)<(2,3,1)\). Under this order and by construction, the support of \(T_i\) has a minimal element \(l_i\) and a maximal element \(r_i\) and both of them host a one-dimensional vector space. Note that this order is only introduced to simplify the specification of these extremal points. We are not changing the underlying poset of which \(T_i\) is a representation.
We now build an indecomposable persistence module M with the required property inductively. Let \(M_1=T_1\). Clearly, \(M_1\) is an indecomposable 2D persistence module with \({{\,\mathrm{End}\,}}(M)\cong K\) and whose support has Betti numbers \(1, b_1\). Furthermore, \(M_1(r_1) = K\) (a one-dimensional K-vector space), by construction.
Assume that we have built \(M_i\), an indecomposable \((i+1)\)D persistence module with \({{\,\mathrm{End}\,}}(M_i) \cong K\), Betti numbers \(1,b_1,\dots ,b_i\), and with maximal element \(r_i\) in its support where \(M_i(r_i) = K\).
We embed \(M_i\) into the \((i+1)+1 = (i+2)\)-dimensional grid by adding an extra 0 coordinate at the end of all indices, and denote it by \(M_i'\). We translate the \((i+2)\)D persistence module \(T_{i+1}\) in the grid such that the maximal element \(r_i'\) (which is \(r_i\) after embedding) and \(l_{i+1}\) (after this translation) are adjacent on the \((i+2)\)D grid, with the only difference coming from the last coordinate.
The \((i+2)\)D persistence module \(M_{i+1}\) is defined to be equal to \(M'_i\) over its support and equal to the translated \(T_{i+1}\) over its support, with the identity linear map for the arrow from \(M_{i+1}(r'_i) = M'_i(r'_i) = K\) to \(M_{i+1}(l_{i+1}) = T_{i+1}(l_{i+1}) = K\), and zero elsewhere.
First, \(M_{i+1}\) is obtained by assembling the two modules \(M_i'\) and \(T_{i+1}\). To see that this is indeed a \((i+2)\)D persistence module, we check that no nontrivial commutativity condition exists between the two parts as no pair of vertices in the support of \(M'_i\) and \(T_{i+1}\) are comparable except for those on the same slice as \(l_{i+1}\). In other words, no path in the grid, from the support of \(M'_i\) to the support of \(T_{i+1}\), exists that does not go through the newly added arrow.
The support of \(M_{i+1}\) is obtained by linking the support of \(M_i'\) and \(T_{i+1}\) by a single arrow. The Betti numbers of \(M_{i+1}\) are therefore the sum of the Betti numbers of \(M_i'\) and \(T_{i+1}\) for all positive dimensions and the sum minus one for \(\beta _0\). Hence, \(M_{i+1}\) has Betti numbers \(1,b_1,\dots ,b_{i+1}\).
The shifted index \(r_{i+1}\) is maximal for \(M_{i+1}\).
The endomorphism ring of \(M_{i+1}\) is isomorphic to K. Indeed, let f be an endomorphism of \(M_{i+1}\). By hypotheses, f is uniquely defined by two scalar values \(\alpha \) and \(\beta \) corresponding to the parts \(M'_i\) and \(T_{i+1}\). However, we have an extra condition due to the arrow linking the two parts of the module. An elementary computation shows that this condition implies that \(\alpha =c\beta \) for some constant c, and therefore every endomorphism is uniquely defined by one scalar.
By induction \(M=M_n\) satisfies all the desired conditions and therefore is an indecomposable \((n+1)\)D persistence module whose support has Betti numbers \(1,b_1,\dots ,b_n\). \(\square \)
8 Discussion
The construction presented in this paper shows, for any given 1D persistence module with finite support, how to build a 2D indecomposable module containing it as a line restriction. In fact we also built a single 2D indecomposable with infinite support that contains all 1D persistence modules with finite support as line restrictions.
We then showed that our main construction naturally extends to any finite-rectangle-decomposable nD persistence module, showing that each can be found in some indecomposable \((n+1)\)D persistence module as a hyperplane restriction. As a side result, we were also able, given arbitrary numbers \(\beta _l\) for \(1\le l\le n-1\), to build an indecomposable nD persistence module whose cubical complex has Betti number \(\beta _l\) for all dimensions \(1\le l\le n-1\).
Our construction can be extended to persistence modules indexed over \(\mathbb {R}\) that can be decomposed into a finite direct sum of finite intervals. This extension requires a careful handling of the various types of intervals (open, closed and half-open), and separate-and-shift requires an extra enlarging of death indices (the second condition should be a strict inequality).
It is natural to ask whether or not our construction can be made functorial. In particular, suppose that for each \(V \in {{\,\mathrm{rep}\,}}\vec {A}_{n}\), we fix exactly one construction S(V) as in Eq. (4.4) (recall that there are many choices in the construction; fix one choice for each). If we let L be the horizontal line at index 3 (4th row), clearly \(R_L(S(V)) = V\), where V is viewed as an object in \({{\,\mathrm{rep}\,}}\mathbb {Z}\). Indeed, this is what we proved in Theorem 1.1.
Then the question is as follows. For each morphism \(f:V\rightarrow W\), can we give a morphism \(S(f) : S(V) \rightarrow S(W)\) so that \(S:{{\,\mathrm{rep}\,}}\vec {A}_{n}\rightarrow {{\,\mathrm{rep}\,}}G\) becomes a functor? More strictly, is it possible to give the values S(f) so that \(R_L \circ S\) is (or at least isomorphic to) the identity functor? Unfortunately, it seems like our construction cannot be made into a functor in such a nice way.
Our methods relying on the structure of 1D interval (nD finite-rectangle) representations do not extend trivially to general nD persistence modules. We do not yet know whether or not statements similar to our main Theorem 1.1 and Theorem 7.7 can be made for general nD persistence modules, or indeed, for interval-decomposable nD persistence modules with \(n > 1\).
References
Asashiba, H., Buchet, M., Escolar, E.G., Nakashima, K., Yoshiwaki, M.: On interval decomposability of 2d persistence modules. arXiv preprint arXiv:1812.05261 (2018a)
Asashiba, H., Escolar, E.G., Hiraoka, Y., Takeuchi, H.: Matrix method for persistence modules on commutative ladders of finite type. Jpn. J. Ind. Appl. Math. (2018b). https://doi.org/10.1007/s13160-018-0331-y
Assem, I., Skowronski, A., Simson, D.: Elements of the Representation Theory of Associative Algebras: Volume 1: Techniques of Representation Theory, vol. 65. Cambridge University Press, Cambridge (2006)
Bjerkevik, H.B.: Stability of higher-dimensional interval decomposable persistence modules. arXiv preprint arXiv:1609.02086 (2016)
Buchet, M., Escolar, E.G.: Realizations of indecomposable persistence modules of arbitrarily large dimension. In: 34th International Symposium on Computational Geometry (SoCG 2018). Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik (2018)
Butler, M.C., Ringel, C.M.: Auslander-Reiten sequences with few middle terms and applications to string algebras. Commun. Algebra 15(1–2), 145–179 (1987)
Carlsson, G., Zomorodian, A.: The theory of multidimensional persistence. Discrete Comput. Geom. 42(1), 71–93 (2009)
Chazal, F., De Silva, V., Glisse, M., Oudot, S.: The Structure and Stability of Persistence Modules. Springer, Berlin (2016)
Crawley-Boevey, W.: Decomposition of pointwise finite-dimensional persistence modules. J. Algebra Appl. 14(05), 1550066 (2015)
Dey, T.K., Xin, C.: Computing bottleneck distance for 2-d interval decomposable modules. In: 34th International Symposium on Computational Geometry (SoCG 2018). Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik (2018)
Edelsbrunner, H., Letscher, D., Zomorodian, A.: Topological persistence and simplification. In: Proceedings of 41st Annual Symposium on Foundations of Computer Science, 2000. IEEE, pp. 454–463 (2000)
Gabriel, P.: Unzerlegbare darstellungen i. Manuscr. math. 6(1), 71–103 (1972)
Kelly, M.: Basic Concepts of Enriched Category Theory, vol. 64. CUP Archive, Cambridge (1982)
Lesnick, M., Wright, M.: Interactive visualization of 2-d persistence modules. arXiv preprint arXiv:1512.00180 (2015)
Mac Lane, S.: Categories for the Working Mathematician, vol. 5. Springer, Berlin (2013)
Acknowledgements
Open access funding provided by Graz University of Technology. We would like to thank Peter Bubenik for suggesting the extension of our main result to finite-rectangle-decomposable nD persistence modules, and Tomoo Yokoyama for raising the question which we studied in Sect. 6.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Here, we reproduce Lemmas 3.1 and 5.2 and provide their proofs.
Lemma 3.1
There is an isomorphism of categories
Proof
Let us construct an isomorphism
with inverse
Effect of\(\varPhi \)on objects For \(V \in {{\,\mathrm{rep}\,}}\vec {G}_{h,w}\), define the representation \(\varPhi (V): \vec {A}_{h} \rightarrow {{\,\mathrm{rep}\,}}\vec {A}_{w}\) by the following. On \(j\in [h]\), we set
which can be checked to be a functor from \(\vec {A}_{w}\) to \({\mathrm {vect}}_K\), and is thus an object in \({{\,\mathrm{rep}\,}}\vec {A}_{w}\). This is the restriction of V to row j. On \(i\le j\) in [h], we set
which is the collection of maps indexed by [w] with value at \(k\in [w]\):
That each \(\varPhi (V)(i\le j)\) is a morphism (a natural transformation) in \({{\,\mathrm{rep}\,}}\vec {A}_{w}\) follows from the functoriality of V. In detail, we have for each \(k\le \ell \),

commutes since \(\beta \alpha = V((i,k)\le (j,\ell )) = \delta \gamma \).
Finally, it can be checked that \(\varPhi (V)\) itself is a functor \(\varPhi (V): \vec {A}_{h}\rightarrow {{\,\mathrm{rep}\,}}\vec {A}_{w}\), and thus \(\varPhi (V)\) is an object of \(\left[ \vec {A}_{h},{{\,\mathrm{rep}\,}}\vec {A}_{w}\right] \).
Effect of\(\varPhi \)on morphisms For \(f:V\rightarrow W\) a morphism in \({{\,\mathrm{rep}\,}}\vec {G}_{h,w}\), let us construct \(\varPhi (f):\varPhi (V)\rightarrow \varPhi (W)\). This is a collection of maps \(\varPhi (f)_j: \varPhi (V)(j) \rightarrow \varPhi (W)(j)\) for \(j\in [h]\), where \(\varPhi (f)_j\) is given by restriction to the jth row:
This jth row is the collection \(\varPhi (f)_j = \{(\varPhi (f)_j)_i\}_{i\in [w]}\) with
For each j, that \(\varPhi (f)_j\) is a natural transformation follows from naturality of f.
Then we need to check that the collection \(\varPhi (f) = \{\varPhi (f)_j\}\) in fact defines a natural transformation. This also follows from naturality of f.
Functoriality of \(\varPhi \) Next, \(\varPhi \) is clearly a functor: \(\varPhi (1)_j = 1_{(j,-)}\) so that \(\varPhi (1)\) is the identity, and
Effect of\(\varPsi \)on objects In the other direction, let now \(M \in \left[ \vec {A}_{h},{{\,\mathrm{rep}\,}}\vec {A}_{w}\right] \). Let us define \(\varPsi (M) \in {{\,\mathrm{rep}\,}}\vec {G}_{h,w}\). We put \(\varPsi (M)(i,j) = M(i)(j)\) for \((i,j) \in \vec {G}_{h,w}\). For the pairs \((i,j)\le (k,\ell )\),
should be a morphism from M(i)(j) to \(M(k)(\ell )\), which we define to be either composition in

It does not matter which path is taken, as they are equal by naturality of \(M(i\le k): M(i)(-) \rightarrow M(k)(-)\).
Then it can be checked that \(\varPsi (M):\vec {G}_{h,w} \rightarrow {\mathrm {vect}}_K\) is a functor, and thus an object in \({{\,\mathrm{rep}\,}}\vec {G}_{h,w}\).
Effect of\(\varPsi \)on morphisms For \(g:M\rightarrow N\) a morphism in \(\left[ \vec {A}_{h},{{\,\mathrm{rep}\,}}\vec {A}_{w}\right] \), let \(\varPsi (g)_{(i,j)} = (g_i)_j\) for \((i,j) \in \vec {G}_{h,w}\). That \(\varPsi (g):\varPsi (M) \rightarrow \varPsi (N)\) is a morphism can be checked by using naturality of g, as follows. For \((i,j) \le (k,\ell )\) in \(\vec {G}_{h,w}\), consider the diagram

where the composition of the top row is \(\varPsi (M)((i,j)\le (k,\ell ))\) and the bottom row is \(\varPsi (N)((i,j)\le (k,\ell ))\). The commutativity of the left square follows from naturality of \(g_i\) for fixed i, and that of the right square follows from naturality of g and then evaluating at \(\ell \). This shows the commutativity of Diagram (A.1), and thus \(\varPsi (g)\) is indeed a natural transformation.
Functoriality of\(\varPsi \)\(\varPsi (1)\) is clearly the identity, and
Inverse. By the definitions given
and \(\varPsi (\varPhi (V))((i,j)\le (k,\ell ))\) is given by the composition of the top row in

By functoriality of V, we see from the above commutative diagram that
Thus, \(\varPsi \varPhi (V) = V\) as functors.
On morphisms \(f:V\rightarrow W\) in \({{\,\mathrm{rep}\,}}\vec {G}_{h,w}\), we see that
and so \(\varPsi \varPhi (f) = f\). Thus, \(\varPsi \varPhi \) is equal to the identity functor.
In the other direction, it can be checked that \(\varPhi (\varPsi (M)) = M\) for functors \(M\in \left[ \vec {A}_{h},{{\,\mathrm{rep}\,}}\vec {A}_{w}\right] \), and similarly \(\varPhi (\varPsi (f)) = f\) for morphisms f. Thus, \(\varPhi \varPsi \) is also an identity functor. \(\square \)
Lemma 3.2
There is no indecomposable \(T \in \mathcal P\) whose support contains both the bottom and right vertices (a and c) or both the left and top vertices (b and d).
Proof
Write \(T \in \mathcal {P}\) as:

with the relations \(hf=0\) and \(ig=0\) which entails \({{\,\mathrm{Im}\,}}(f)\subset {{\,\mathrm{Ker}\,}}(h)\) and \({{\,\mathrm{Im}\,}}(g)\subset {{\,\mathrm{Ker}\,}}(i)\).
Using the isomorphism theorems, we can decompose A as:
A similar decomposition can be obtained for B due to the symmetry of the structure. Similarly, we can decompose C as:
and symmetrically D. The middle vector space decomposes into 9 summands:

Note that the maps induced by f, g, h and i on these decompositions restricted to one of the summands in its domain has image fully contained in at most one summand of its codomain. Furthermore, every summand in the codomain contains the image of at most one summand of the domain. In other words, this decomposition of the vector spaces induces a direct sum decomposition of T. Note that we did not necessarily compute an indecomposable decomposition of T, as this decomposition already suffices for our purposes.
Finally, inspecting the form of the decomposition gives the claimed result. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Buchet, M., Escolar, E.G. Every 1D persistence module is a restriction of some indecomposable 2D persistence module. J Appl. and Comput. Topology 4, 387–424 (2020). https://doi.org/10.1007/s41468-020-00053-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41468-020-00053-z




 and 1D persistence modules
and 1D persistence modules for each nonzero
for each nonzero


 , as above. Suppose that
, as above. Suppose that 
 , as above. Suppose that
, as above. Suppose that 

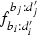 nonzero are given by
nonzero are given by 

 nonzero are given by
nonzero are given by 
 for each nonzero
for each nonzero