Abstract
The robust \(H_\infty\) observer-based control design is addressed here for non-linear Takagi-Sugeno (T-S) fuzzy systems with time-varying delays, subject to uncertainties and external disturbances. This is motivated by the quadruple-tank with time delay control problem. The observer design methodology is based on constructing an appropriate Lyapunov–Krasovskii functional (LKF) for an augmented system formed from the original and the delayed states. The bilinear terms are transferred to the linear matrix inequalities, thanks to a change of variables which can be solved in one step. Furthermore, by employing the \(\mathcal {L}_2\) performance index, the adverse effects of persistent bounded disturbances is largely avoided. The proposed method has the advantage of relating the controller and Lyapunov function to both the original and delayed states. Then, the controller and observer gains are obtained simultaneously by solving these inequalities with off-the-shelf software (Yalmip/MATLAB toolbox). Finally, an application to a simulated quadruple-tank system with time delay is carried out to demonstrate the benefits of the proposed technique, showing a compromise between controller simplicity and robustness that outperforms previous approaches.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Takagi-Sugeno (T-S) systems are a kind of the fuzzy system introduced in Tanaka and Wang (2004) to facilitate the use of fuzzy system tools for some nonlinear systems. Because of the effective representation of a nonlinear system as a set of local linear models that are interpolated by nonlinear functions, T-S fuzzy methods have proved useful in a variety of problems (Ammar et al. 2018; Tuan VLB, and Hajjaji 2018; Chaibi et al. 2019; Naami et al. 2019; Ejegwa 2020; Yang et al. 2020; Saif et al. 2020; Dutta and Doley 2021; Zhang and Huang 2021; Kchaou and Jerbi 2021; Ech-charqy et al. 2020; D’Urso 2017; Najariyan et al. 2017). Stability analysis and controller design can then be handled with this technique (Takagi and Sugeno 1985; Tanaka et al. 1998) for nonlinear systems (Xie et al. (2020)), by an equivalent combination of linear systems. In this context, they have been shown to be useful as universal approximators in (Buckley (1992)) and (Castro (1995)), making possible to extend classical linear model techniques to a wide range of problems, including stabilization, observation, regulation and filtering.
Over the last few decades, many research approaches have studied the observer-based control in the context of disturbances or noises that might create instabilities in nonlinear closed-loop systems (Wang et al. 2021). This control is often obtained under the assumption that the entire state vector can be accessed by output measurement. This is complex in practice when there are disturbances (Wang and Lam (2021)), or when some of the external disturbances to the system are unavailable (Wei and Ma (2021)). In several studies, the problem of constructing observers for systems with noise has been solved by using the \(H_\infty\) filtering approach (Tuan VLB, and Hajjaji 2018; Xie et al. 2019; Naami et al. 2021). Moreover, (He et al. (2021)) developed some important works on stabilisation for T-S fuzzy descriptor systems. Recently, a straightforward method for observer-based \(H_\infty\) control for discrete-time Takagi–Sugeno (T–S) fuzzy systems has been presented (Chang et al. (2015); Zhi (2021)). An observer-based controller as an alternative to direct static state feedback is discussed in (Chang et al. (2016); Mahmoud et al. (2021)). We also point out (Shahbazzadeh et al. (2021)) where dynamic output feedback controller was described for Lipschitz nonlinear systems under input saturation. On the other hand, the \(H_\infty\) observer design for uncertain one-sided Lipschitz systems with time-varying delay (albeit without taking the controller into account) is proposed in (Yan et al. (2020)).
In such context, the presence of parametric uncertainties, make the stabilization of the system more complicated. As a result, attention is being paid to uncertain processes. For example, the authors in (Salehifar et al. (2021)) have been investigated the problem of robust observer-based control for one-sided Lipschitz nonlinear systems subject to parametric uncertainties and external disturbances. Several other articles have addressed the stable stabilization problem of uncertain Takagi–Sugeno (T-S) fuzzy models (Ahammed and Azeem 2019; Dong et al. 2021; Zhu et al. 2021). In (Islam et al. (2020)), the robust controller design for an uncertain fuzzy system with time-varying time-delay was investigated using a fuzzy functional observer. Several results dealing with observer-based controller design method for Lipschitz nonlinear systems with uncertain parameters and disturbances have also been published (Zemouche et al. 2017; Rastegari et al. 2019; Yang et al. 2021; Dinh 2021). Among them we emphasize (Xu et al. (2019)), based on minimizing an index related to the state estimation performance, to optimize the actual value of the uncertainty. Furthermore, using a fuzzy description of the uncertainty bound, the optimal design of the controller is envisaged in (Yang et al. (2021)), using a comprehensive fuzzy performance index that involves the performance and the control cost.
The present work focuses on the design of \(H_\infty\) observer-based controllers for delayed continuous-time Takagi–Sugeno fuzzy systems, in the presence of parameter uncertainties and external disturbances. The research is motivated by a process composed of four interconnected tanks; the model of this process is also used to demonstrate the approach. There are some previous studies on observer-based controllers for fuzzy systems: for instance, in (Tuan VLB et al. (2019)), these controllers were applied to a similar quadruple-tank system; in (Naami et al. (2021)), the robust \(H_\infty\) control problem was studied with parameter uncertainties. However, these previous studies did not take into account the time delay, motivating this work. The main contribution of this paper is then the proposal of a direct approach for designing \(H_\infty\) observer-based controllers for T-S fuzzy systems with uncertainties, external disturbances and time-varying delays. The approach is based on proposing a Lyapunov–Krasovskii functional with time-delay information . Based on it, a controller is proposed based on using both the original state and the time-delay state. Using this approach allows to develop stability conditions expressed as LMIs, so the design conditions are also expressed as LMIs. The solution of these LMIs makes it possible to obtain the observer and controller gains.
The paper is organised as follows. Section 2 describes the mathematical modelling of the fuzzy quadruple-tank systems with time delay, and some previous results. Section 3 presents the main contributions , describing the observer-based controller and the design methodology. Section 4 provides the application to the quadruple-tank system with time delay. Finally, the paper draws some conclusions.
Notation The following standard notation are used in the paper. The superscript \((.)^T\) represent the matrix transpose. \(P > 0\) means that P is a symmetric positive definite matrix, and \(\mathcal {H}_e = \left\{ P + P^T \right\}\). The symbol \(*\) denotes a symmetric block. I denotes the identity matrix with appropriate dimensions.
2 Model description and preliminaries
2.1 Fuzzy quadruple-tank systems
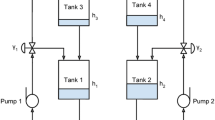
Figure 1 shows the schematic diagram of the quadruple-tank model with disturbances (Johansson and Nunes (1998)). The process is composed of four identical cylindrical tanks numbered 1–4, and a reservoir 5. The two pumps transfer the water from the reservoir to tank-3 and tank-4. The objective is to control the liquid levels in tank-3 and tank-4, by the observation of the dynamic states of tank-1 and tank-2. A delay in the inputs of the system is introduced to make the control problem more challenging (Shah and Patel (2019)). The continuous-time nonlinear system is represented by the following equations:
where \(x_k (t)\) is the liquid level in the tank number k, \(\tilde{A}_{pk}\) is the cross sectional area of tank k, \(\tilde{a}_{pk}\) is the cross-sectional area of the outlet of tank k, g is the gravity constant, \(\eta _j (t) \in \left[ 0,\;1 \right]\) is the valve flow proportion, and \(\vartheta _j (t)\) is the control signal of pump j, with the gain \(\tilde{k}_{\vartheta j}\). The parameters of the process are condensed in Table 1. The measured output signals \(y(t) \in \mathbb {R}^2\), correspond in this study to the levels of tanks 1 and 2. d(t) is the time it takes for the liquid to move to tank-1 from tank-3, tank-2 from tank-4, tank-1 from pump-1, tank-4 from pump-1, tank-2 from pump-2, tank-3 from pump-2, and tank-3 and tank-4. This delay satisfies that:
The nonlinear terms \(\tilde{F}_k (t)=\sqrt{x_k (t)}\) of the level in the tank-k \(\forall k=1,\ldots ,4\), the following sector rules apply:
If\(x_k (t)\) is \(N_1\) Then \(\tilde{F}_k (t)=\tilde{C}_{Fz1}x_k (t)\)
If\(x_k (t)\) is \(N_2\) Then \(\tilde{F}_k (t)=\tilde{C}_{Fz2}x_k (t)\)
with \(N_1\) and \(N_2\) the fuzzy sets.
As a result, the following is the T–S Fuzzy model:
It should be noted that the membership functions (MFs) are
with the following properties:
where
Remark 1
The rules (3) are generalized to calculate only \(\varphi _j (x_1)\), \(j=1,2\), by using the same fuzzy form and nonlinear function characteristics of the model. Thanks to this, the number of membership functions is reduced from 8 to 2. Table 2 details the fuzzy parameters.
Time-varying parameters \(\eta _1 (t)\) and \(\eta _2 (t)\) are:
.
The quadruple-tank system can be expressed by the uncertain T–S Fuzzy model in (3) by:
where \(\mu _{i} (\varphi (t))\) is the grade of membership of \(\varphi (t)\), \(x(t) \in \mathbb {R}^{n}\) is the state vector, \(y(t) \in \mathbb {R}^{p}\) is the output vector, \(u(t) \in \mathbb {R}^{r}\) is the input vector, \(w(t) \in l^{q}_{2}\) is the unknown exogenous disturbance, \(A_i \in \mathbb {R}^{n\times n}\), \(A_{d_i} \in \mathbb {R}^{n\times n}\), \(B_i \in \mathbb {R}^{n\times r}\) and \(C_{i} \in \mathbb {R}^{p \times n}\) \((i=1,\ldots ,m)\), are known constant matrices. Finally, \(\Delta A_{i}(t)\), \(\Delta A_{d_i}(t)\) \(( i=1,\ldots ,m)\) and \(\Delta C(t)\) are unknown matrices that represent model uncertainty.
Throughout the paper, the following assumptions are used:
Assumption 1
The pairs \((A_{i}, B_{i})\), \((A_{i}, C)\), \((A_{d_i}, B_{i})\) and \((A_{d_i}, C)\) \(( i=1,\ldots ,m)\), are stabilisable and detectable, respectively.
Assumption 2
The matrices \(\Delta A_{i}(t)\), \(\Delta A_{d_i}(t)\) \(( i=1,\ldots ,m)\) and \(\Delta C(t)\) are unknown matrices that represent time-varying model uncertainties, as follows:
with
The control scheme can also minimize disturbance attenuation from the pump to tank levels, assuming that the disturbance can be described as follows:
.
Using (1), the following are the nominal constant matrices:
If \(i=1,\ldots ,4\) Then \(j=1\), And \(i=5,\ldots ,m\) Then \(j=2\), with \(m=8\).
The observer-based controller is as follows:
and the following controller is used for the system (8):
where \(L_i \in \mathbb {R}^{n\times p}\), \(K_j \in \mathbb {R}^{x\times n}\) and \(K_{d_j} \in \mathbb {R}^{x\times n}\) \(( i,j=1,\ldots ,m)\) are the observer and the controller gains, respectively, to be calculated, and \(\hat{x}(t) \in \mathbb {R}^{n}\) is the estimation of x(t) provided by the observer.
Let us define \(e(t)=x(t)-\hat{x}(t)\), the dynamics of e(t) which can be obtained as follows:
By using the controller (12), then the system (8) in closed-loop is:
Following this, the augmented system can be written as follows:
2.2 Problem statement
The main objective of the paper is to design a robust observer-based control design in the presence of process delays and disturbances, such that augmented system (15) is asymptotically stable and satisfies that
2.3 Preliminaries
The following lemmas are required to provide the main results in the following section.
Lemma 1
(Lien (2004)) \(\forall \;\sigma\), positive constant, and real matrices M, N, and \(F \in \mathbb {R}\) of appropriate dimensions, such that \(F^{T}(t)F(t) \leqslant I\), the following holds:
Lemma 2
(Chang et al. (2015)) For matrices T, Q, U, and W, with appropriate dimensions, and scalar \(\tilde{\zeta }\) the inequality,
is satisfied if the following condition holds:
Lemma 3
(Dong et al. (2017)) For any constant matrix \(Z = Z^T > 0\) and scalar \(h \ge 0\) such that the following integrations are well defined, then
3 Main results
3.1 Robust observer-based control design
This section aims to investigate the stability problem of system (8) in the presence of uncertainties and disturbances.
Theorem 1
The robust observer-based system (15) is asymptotically stable with \(H_\infty\) performance, for given scalars \(\gamma\), \(\tilde{\zeta }_1\), \(\tilde{\zeta }_2\) and positive scalars \(\sigma _k> 0\) \((k=1,\ldots ,m)\), if there exist symmetric positive-definite matrices \(P_1, P_2, Q_1, Q_2, R_1, R_2 \in \mathbb {R}^{n\times n}\) and unknown matrices \(S_1, S_2 \in \mathbb {R}^{r\times r}\), \(Z_{1j}, Z_{2j} \in \mathbb {R}^{r\times n}\), \(W_{i} \in \mathbb {R}^{n\times p}\), \((i,j=1,\ldots ,m)\) satisfying the following LMIs:
where
and the gains of the controller and observer can be obtained as \(K_j =S_1^{-1} Z_1\), \(K_{d_i} =S_2^{-1} Z_2\) and \(L_i = P_2^{-1} W_i\).
Proof
The following L-K functional is used to demonstrate the result:
The time derivative of V(t) along the trajectory of (15) is the following:
By Lemma 3, it is obtained that
Following that, it is now shown that for any \(w(t) \in L_2 [0, \infty )\) of the T-S system with parametric uncertainty (8), the following condition must be fulfilled:
Under null initial conditions, the Lyapunov function fulfill \(V(0)=0\) and \(V(\infty )\geqslant 0\), which leads to:
To achieve the attenuation level in (16), we must fulfill inequality in the following:
Combining (23) and (26), we have:
After that, Eq. (28) can be rewritten as follows:
Using non-singular matrices \(S_1, S_2\) and defining \(K_j = S_1^{-1} Z_{1j}, K_{d_j} = S_2^{-1} Z_{2j}\) it is possible to show that,
Then, using Eq. (30), inequality (29) is equivalent to:
where \(\Upsilon _1 = \left[ \begin{array}{cccccc} \Upsilon _{11} + T_{11}&{} \Lambda _{12} + T_{12} &{} 0 &{} 0 &{} P \\ * &{} \Upsilon _{22} &{} 0 &{} 0 &{} 0 \\ * &{} * &{} -\frac{1}{\bar{d}} R_1 &{} 0 &{} 0 \\ * &{} * &{} * &{} -\frac{1}{\bar{d}^2} R_2 &{} 0 \\ * &{} * &{} * &{} * &{} - \gamma ^2 I \end{array} \right]\),
\(T_{11} =H_e \left\{ E_{11}\right\}\), \(T_{12} =H_e \left\{ E_{12}\right\}\),
\(E_{11} = \left[ \begin{array}{cc} -B_i Z_1&{} B_i Z_1 \\ 0 &{} 0 \end{array} \right]\), \(E_{12} = \left[ \begin{array}{cc} -B_i Z_2&{} B_i Z_2 \\ 0 &{} 0 \end{array} \right]\),
Using Lemma 2, inequality (31) can be guaranteed by the following condition:
then
Lemma 2 makes possible to verify (33), using the matrix condition of inequality:
where
Taking into account the special structure of \(\Delta A_i (t), \Delta A_{d_i} (t), \Delta C(t)\) and integrating Lemma 3, we obtain
We have the inequality:
for any \(\sigma _{1}> 0\) and \(\sigma _{2} > 0\), such that
Adding (36) to (34) and applying the Schur complement, inequality (20) can be achieved immediately, completing the proof. \(\square\)
Remark 2
The approach introduced in Theorem 1 requires only one step, making it much easier to implement than the two-step LMI method in (Zemouche et al. (2017)), and than the methods based on cone-complementary algorithm linearisation, such as (Tuan VLB, and Hajjaji (2018); Tuan VLB et al. (2019)).
Remark 3
Comparing with earlier works in (Tuan VLB, and Hajjaji (2018); Tuan VLB et al. (2019); Naami et al. (2021)), an observer-based control design methodology for T-S fuzzy systems is proposed: these previous studies use Lyapunov functions related only to the original state, and unrelated to the delayed state. However, in many applications the process delay is a major concern, as it is responsible for the deterioration in the performance. From the above analysis, we can infer that the result presented in this study is more general and practical for real applications.
Remark 4
The following optimisation can be used to find the optimal performance index \(\gamma\):
4 Simulation results and discussions
To compensate for the inherent differences between system states and measurement outputs, an uncertain model is used. The uncertainty matrices for the fuzzy quadruple-tank system (1) are then the following:
for \(i=1,\ldots ,8\), and \(m=8\).
Choosing time-varying delay \(d(t) = 0.66 + 0.5 sin(t)\), \(0 \leqslant d(t) \leqslant 2\) and the parameter constant values are \(\lambda _i \in \left[ 1, 120\right] ,\;i=1,\ldots ,8\), \(m=8\), \(\tilde{\zeta }_1 =0.001\), \(\tilde{\zeta }_2 =0.002\). The simulation starting from the initial conditions \(x(0)=\left[ \begin{array}{ccccccc} 0.34&\,&0.14&\,&0.41&\,&0.31 \end{array} \right] ^T ,\) \(\hat{x}(0)=\left[ \begin{array}{ccccccc} 0.21&\,&0.01&\,&0.22&\,&0.10 \end{array} \right] ^T ,\)
respectively.
Some simulation results are given in Figs. 3 and 4. Figure 3 shows the evolution of the measured levels \((x_1,x_2)\), although Fig. 4 illustrates the evolution of the unmeasured states \((x_3,x_4)\). Despite the existence of model uncertainties and disturbances, the observer estimates adequately the level of the four tanks, as seen in these figures.
Now, by using the YALMIP toolbox (Löfberg (2004)) in Matlab (Higham and Higham (2005)), the LMI (20) in Theorem 1 can be solved, obtaining the following controller gains:
\(K_1 =S_1^{-1}Z_{11} =\left[ \begin{array}{cccc} -2.34 &{} &{} -3.42\\ -7.59 &{} &{} -2.15\\ 1.35 &{} &{} 4.38\\ 3.57 &{} &{} 1.56 \end{array} \right] ^T ,\) \(K_2 =S_1^{-1}Z_{12} =\left[ \begin{array}{cccc} -1.47 &{} &{} -1.52 \\ -2.16 &{} &{} -2.24 \\ 2.15 &{} &{} 4.65 \\ 7.25 &{} &{} 1.25 \end{array} \right] ^T ,\)
\(K_3 =S_1^{-1}Z_{13} =\left[ \begin{array}{cccc} -2.91 &{} &{} -3.03 \\ -1.44 &{} &{} -1.49 \\ 8.85 &{} &{} 8.11 \\ 2.41 &{} &{} 2.52 \end{array} \right] ^T ,\) \(K_4 =S_1^{-1}Z_{14} =\left[ \begin{array}{cccc} -1.98 &{} &{} -2.83 \\ -1.51 &{} &{} -1.48 \\ 7.25 &{} &{} 9.09 \\ 2.34 &{} &{} 2.51 \end{array} \right] ^T ,\)
\(K_5 =S_1^{-1}Z_{15} =\left[ \begin{array}{cccc} 3.98 &{} &{} 4.95\\ 2.50 &{} &{} 2.72 \\ -6.35 &{} &{} -1.25 \\ -3.99 &{} &{} -4.23 \end{array} \right] ^T ,\) \(K_6 =S_1^{-1}Z_{16} =\left[ \begin{array}{cccc} 4.08 &{} &{} 9.90\\ 7.66 &{} &{} 4.46\\ -2.46 &{} &{} -2.97\\ -8.96 &{} &{} -6.86 \end{array} \right] ^T ,\)
\(K_7 =S_1^{-1}Z_{17} =\left[ \begin{array}{cccc} 4.79 &{} &{} 3.25\\ 3.02 &{} &{} 1.22\\ -5.47 &{} &{} -1.24\\ -4.86 &{} &{} -1.74 \end{array} \right] ^T ,\) \(K_8 =S_1^{-1}Z_{18} =\left[ \begin{array}{cccc} 3.15 &{} &{} 7.33 \\ 4.28 &{} &{} 2.42 \\ -3.59 &{} &{} -1.14 \\ -1.19&{} &{} -2.10 \end{array} \right] ^T ,\)
\(K_{d_1} =S_2^{-1}Z_{21} =\left[ \begin{array}{cccc} -5.53 &{} &{} -5.94\\ -2.53 &{} &{} -1.95 \\ 1.39 &{} &{} 1.39 \\ 4.23 &{} &{} 3.30 \end{array} \right] ^T,\) \(K_{d_2} =S_2^{-1}Z_{22} =\left[ \begin{array}{cccc} -5.20 &{} &{} -3.65\\ -2.51 &{} &{} -2.13\\ 1.17 &{} &{} 9.98\\ 4.14 &{} &{} 3.31 \end{array} \right] ^T ,\)
\(K_{d_3} =S_2^{-1}Z_{23} =\left[ \begin{array}{cccc} -5.45 &{} &{} -4.87\\ -2.54 &{} &{} -1.91\\ 1.44 &{} &{} 9.45\\ 4.22 &{} &{} 3.27 \end{array} \right] ^T ,\) \(K_{d_4} =S_2^{-1}Z_{24} =\left[ \begin{array}{cccc} -6.01 &{} &{} -9.16\\ -2.59 &{} &{} -1.91\\ 1.10 &{} &{} 1.63\\ 4.24 &{} &{} 3.28 \end{array} \right] ^T ,\) \(K_{d_5} =S_2^{-1}Z_{25} =\left[ \begin{array}{cccc} 5.77 &{} &{} 1.05\\ 3.20 &{} &{} 3.61 \\ -8.06 &{} &{} -2.17\\ -5.13 &{} &{}-5.66 \end{array} \right] ^T ,\) \(K_{d_6} =S_2^{-1}Z_{26} =\left[ \begin{array}{cccc} 2.44 &{} &{} 2.02\\ 7.16 &{} &{} 6.33\\ -6.45 &{} &{} -4.75\\ -1.11 &{} &{} -9.89 \end{array} \right] ^T ,\)
\(K_{d_7} =S_2^{-1}Z_{27} =\left[ \begin{array}{cccc} 6.86 &{} &{} 1.07\\ 3.79 &{} &{} 2.87\\ -7.41 &{} &{} -2.62\\ -6.14 &{} &{} -4.39 \end{array} \right] ^T ,\) \(K_{d_8} =S_2^{-1}Z_{28} =\left[ \begin{array}{cccc} 2.13 &{} &{} 1.29\\ 1.01 &{} &{} 6.15\\ -4.14 &{} &{} -2.39\\ -1.61 &{} &{} -9.82 \end{array} \right] ^T ,\)
and the observer gains
\(L_1 =P_2 ^{-1}W_{1} =\left[ \begin{array}{ccccccc} -1.24 &{} &{} 2.25 \\ -5.14 &{} &{} 2.14 \\ -1.45 &{} &{} 4.35 \\ -2.23 &{} &{} 1.23 \end{array} \right] ,\) \(L_2 =P_2 ^{-1}W_{2} =\left[ \begin{array}{ccccccc} -1.36 &{} &{} 2.24 \\ -9.34 &{} &{} 1.25 \\ -3.25 &{} &{} 2.97 \\ -2.82 &{} &{} 1.74 \end{array} \right] ,\)
\(L_3 =P_2 ^{-1}W_{3} =\left[ \begin{array}{cccccccc} -2.02 &{} &{} 3.50 \\ -8.86 &{} &{} 1.52 \\ -2.94 &{} &{} 5.23 \\ -1.41 &{} &{} 2.44 \end{array} \right],\) \(L_4 =P_2 ^{-1}W_{4} =\left[ \begin{array}{ccccccc} -2.02 &{} &{} 3.50 \\ -8.85 &{} &{} 1.52 \\ -2.94 &{} &{} 5.23 \\ -1.41 &{} &{} 2.44 \end{array} \right],\)
\(L_5 =P_2 ^{-1}W_{5} =\left[ \begin{array}{ccccccc} 53.41 &{} &{} 66.149 \\ 2.32 &{} &{} 2.88 \\ 80.08 &{} &{} 99.19 \\ 3.71 &{} &{} 4.61 \end{array} \right] ,\) \(L_6 =P_2 ^{-1}W_{6} =\left[ \begin{array}{cccccccc} 19.29 &{} &{} 1.53 \\ 83.62 &{} &{} 6.66 \\ 28.93 &{} &{} 2.29 \\ 1.33 &{} &{} 1.06 \end{array} \right] ,\)
\(L_7 =P_2 ^{-1}W_{7} =\left[ \begin{array}{ccccccccc} 53.64 &{} &{} 65.72 \\ 2.33 &{} &{} 2.86 \\ 80.43 &{} &{} 98.56 \\ 3.73 &{} &{} 4.58 \end{array} \right],\) \(L_8 =P_2 ^{-1}W_{8} =\left[ \begin{array}{cccccccc} 30.42 &{} &{} 2.25 \\ 2.13 &{} &{} 3.14 \\ 32.98 &{} &{} 1.14 \\ 2.63 &{} &{} 3.14 \end{array} \right]\).
The flow distribution rate in the tanks is considered, based on the position of the control valves \(\eta _1(t)\) and \(\eta _2 (t)\), which will be modified according to the following rules:
If \(t_{s}(p) = 0,\ldots ,20\) Then \(\eta _1 (t) +\eta _2 (t) \in \left[ 1, 2 \right] ,\) MP
If \(t_{s}(p) = 20,\ldots ,120\) Then \(\eta _1 (t) +\eta _2 (t) \in \left[ 0, 1 \right] ,\) NMP
If \(t_{s}(p) = 120,\ldots ,220\) Then \(\eta _1 (t) +\eta _2 (t) \in \left[ 1, 2 \right] , \mathbf{MP}\)
If \(t_{s}(p) = 220,\ldots ,300\) Then \(\eta _1 (t) +\eta _2 (t) \in \left[ 0, 1 \right] ,\) NMP
where MP is Minimum Phase setting (Johansson (1997)), and NMP is No-Minimum Phase setting. Using the setting rules, the estimation error of each tank level is presented in Fig. 5. Figure 6 shows the control signals of the observer-based controller designed using the approach in this paper. The results demonstrate the closed-loop stability and the reduction of tracking errors in various situations, including in the presence of parameter uncertainties and perturbations.
5 Conclusions
This paper has proposed a direct approach to design robust observer-based controllers for T-S fuzzy systems with time-varying delays in the presence of parameter uncertainties and admissible external disturbances. Lyapunov-Krasovskii functional have been used to ensure the robust asymptotic stability, making possible to then select both the controller and observer gains in a single step, by solving a set of LMIs. This methodology ensures that the closed-loop system is robust asymptotically stable with a certain performance \(\gamma\). The results reported in this paper are also relevant from the perspective of discrete-time state estimation. The approach was demonstrated using a simulated quadruple tank laboratory process: an observer-based controller was developed, and tested in simulation, to show the effectiveness of the proposed approach. It must be pointed out that the functional used in this article does not include the integral of the derivative, but this issue appears in the application, contributing to non-linear terms that are more complex. This merits further research.
Data availability
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
References
Ahammed AI, Azeem MF (2019) Robust stabilization and control of Takagi-Sugeno fuzzy systems with parameter uncertainties and disturbances via State feedback and output feedback. Int J Fuzzy Syst 21(8):2556–2574
Ammar II, Gassara H, El Hajjaji A, Chaabane M (2018) New polynomial Lyapunov functional approach to observer-based control for polynomial fuzzy systems with time delay. Int J Fuzzy Syst 20(4):1057–1068
Buckley JJ (1992) Universal fuzzy controllers. Automatica 28(6):1245–1248
Castro JL (1995) Fuzzy logic controllers are universal approximators. IEEE Trans Syst Man Cybernet 25(4):629–635
Chaibi R, Hmamed A, Tissir EH, Tadeo F (2019) Control of discrete 2-D Takagi-Sugeno systems via a sum-of-squares approach. J Control AutoElectr Syst 30(2):137–147
Chang XH, Zhang L, Park JH (2015) Robust static output feedback \(H_\infty\) control for uncertain fuzzy systems. Fuzzy Sets Syst 273(15):87–104
Chang XH, Xiong J, Park JH (2016) Fuzzy robust dynamic output feedback control of nonlinear systems with linear fractional parametric uncertainties. Appl Math Comput 291:213–225
Dinh CH (2021) On event triggered robust observer based control problem of one sided Lipschitz time delay systems. Asian Journal of Control
Dong Y, Liu W, Liang S (2017) Nonlinear observer design for one sided Lipschitz systems with time varying delay and uncertainties. Int J Robust Nonlinear Control 27(11):1974–1998
Dong Y, Song Y, Wei G (2021) Membership-function-dependent model predictive control for nonlinear systems in a piecewise-fuzzy framework. Fuzzy Sets and Systems, 0165-0114
D’Urso P (2017) Exploratory multivariate analysis for empirical information affected by uncertainty and modeled in a fuzzy manner: a review. Granular Comput 2(4):225–247
Dutta P, Doley D (2021) Fuzzy decision making for medical diagnosis using arithmetic of generalised parabolic fuzzy numbers. Granular Comput 6(2):377–388
Ech-charqy A, Idrissi S, Ouahi M, Tissir EH, Naami G (2020) Stability Analysis and \(H_\infty\) Performance for Nonlinear Fuzzy Networked Control Systems with Time-Varying Delay. In Embedded Systems and Artificial Intelligence (pp. 43-51). Springer, Singapore
Ejegwa PA (2020) Improved composite relation for Pythagorean fuzzy sets and its application to medical diagnosis. Granular Comput 5(2):277–286
He J, Xu F, Wang X, Liang B (2021) Improvements on stability conditions and control design of Takagi-Sugeno fuzzy descriptor systems. ISA transactions, 0019-0578
Higham DJ, Higham NJ (2005) MATLAB Guide: Sec-ond Edition, SIAM, Philadelphia
Islam SI, Shi P, Lim CC (2020) Robust functional observer for stabilising uncertain fuzzy systems with time-delay. Granular Comput 5(1):55–69
Johansson KH (1997) Relay feedback and multivariable control (Doctoral dissertation, Lund University)
Johansson KH, Nunes JLR (1998) A multivariable laboratory process with an adjustable zero. In Proceedings of the 1998 American Control Conference. ACC (IEEE Cat. No. 98CH36207) (Vol. 4, pp. 2045-2049). IEEE
Kchaou M, Jerbi H (2021) Reliable \(H_\infty\) and Passive Fuzzy Observer-Based Sliding Mode Control for Nonlinear Descriptor Systems Subject to Actuator Failure. International Journal of Fuzzy Systems, 1-16
Lien CH (2004) Robust observer-based control of systems with state perturbations via LMI approach. IEEE Trans Automatic Control 49(8):1365–1370
Löfberg J (2004) YALMIP: A toolbox for modeling and optimization in MATLAB. in Proceedings of the CACSD Conference (Vol. 3)
Mahmoud TA, Abdo MI, Elsheikh EA, Elshenawy LM (2021) Direct adaptive control for nonlinear systems using a TSK fuzzy echo state network based on fractional-order learning algorithm. J Franklin Inst 358(17):9034–9060
Naami G, Ouahi M, Rabhi A, Tadeo F, Tuan VLB (2021, June). \(H_\infty\) Observer-Based Control for Uncertain Takagi-Sugeno Fuzzy Systems with Application to a four-Tank Process. In 2021 29th Mediterranean Conference on Control and Automation (MED) (pp. 633-638). IEEE
Naami G, Ouahi M, Rabhi A, Tuan VLB (2019, April) Existence and design of functional observers for Takagi-Sugeno systems with time delay. In 2019 International Conference on Wireless Technologies, Embedded and Intelligent Systems (WITS) (pp. 1-6). IEEE
Najariyan M, Mazandarani M, John R (2017) Type-2 fuzzy linear systems. Granular Comput 2(3):175–186
Rastegari A, Arefi MM, Asemani MH (2019) Robust \(H_\infty\) sliding mode observer based fault tolerant control for One sided Lipschitz nonlinear systems. Asian J Control 21(1):114–129
Saif AWA, Mudasar M, Mysorewala M, Elshafei M (2020) Observer-based interval type-2 fuzzy logic control for nonlinear networked control systems with delays. Int J Fuzzy Syst 22(2):380–399
Salehifar H, Shahbazzadeh M, Sadati SJ (2021) Observer-Based \(H_\infty\) Control for One-Sided Lipschitz Nonlinear Systems with Uncertain Input Matrix. Circuits, Systems, and Signal Processing, 1-20
Shah DH, Patel DM (2019) Design of sliding mode control for quadruple-tank MIMO process with time delay compensation. J Process Control 76:46–61
Shahbazzadeh M, Salehifar H, Sadati SJ (2021) Optimal dynamic output feedback control of Lipschitz nonlinear systems under input saturation. Journal of Vibration and Control, 10775463211043357
Takagi T, Sugeno M (1985) Fuzzy identifcation of systems and its applications to modeling and control. IEEE Transactions on Systems, Man and Cybernetics, SMC-15(1), 116-132
Tanaka K, Ikeda T, Wang HO (1998) Fuzzy regulators and fuzzy observers: relaxed stability conditions and LMI-based designs. IEEE Trans Fuzzy Syst 6(2):250–265
Tanaka K, Wang HO (2004) Fuzzy control systems design and analysis: a linear matrix inequality approach. John Wiley & Sons
Tuan VLB, El Hajjaji A (2018) Robust Observer-Based Control for TS Fuzzy Models Application to Vehicle Lateral Dynamics. In 2018 26th Mediterranean Conference on Control and Automation (MED) (pp. 1-6). IEEE
Tuan VLB, El Hajjaji A, Naami G (2019) Robust TS-Fuzzy observer-based control for Quadruple-Tank system. In 2019 12th Asian Control Conference (ASCC) (pp. 307-312). IEEE
Wang L, & Lam HK (2021) \(H_\infty\) control for continuous-time Takagi-Sugeno fuzzy model by applying generalized Lyapunov function and introducing outer variables. Automatica, 125, 109409
Wang Y, Li T, Wu Y, Yang X, Chen CP, Long Y, Ning J (2021) \({L_\infty }\) fault estimation and fault-tolerant control for non-linear systems by T-S fuzzy model method with local non-linear models. Int J Fuzzy Syst 23:1714–1727
Wei Z, Ma Y (2021) Robust \(H_\infty\) observer-based sliding mode control for uncertain Takagi-Sugeno fuzzy descriptor systems with unmeasurable premise variables and time-varying delay. Inform Sci 566:239–261
Xie WB, Zheng H, Li MY, Shen MQ (2020) Novel robust observer-controller synthesis method for Takagi-Sugeno systems. Asian Journal of Control
Xie WB, Wang TZ, Zhang J, Wang YL (2019) \(H_\infty\) reduced-order observer-based controller synthesis approach for TS fuzzy systems. J Franklin Inst 356(12):6388–6400
Xu J, Fang H, Zeng F, Chen YH, Guo H (2019) Robust observer design and fuzzy optimization for uncertain dynamic systems. Inte J Fuzzy Syst 21(5):1511–1523
Yan Z, Zhang J, Hu G (2020) A new approach to fuzzy output feedback controller design of continuous-time Takagi–Sugeno fuzzy systems. Int J Fuzzy Syst 22:2223–2235
Yang R, Rotondo D, Puig V (2021) Observer based model reference control of Takagi-Sugeno-Lipschitz systems affected by disturbances using quadratic boundedness. Asian J Control 23(1):42–56
Yang Z, Huang J, Yang D, Zhong Z (2021) Design and Optimization of Robust Path Tracking Control for Autonomous Vehicles with Fuzzy Uncertainty. IEEE Transactions on Fuzzy Systems, 1-1
Yang Y, Lin C, Chen B, Zhao X (2020) \(H_\infty\) observer design for uncertain one-sided Lipschitz nonlinear systems with time-varying delay. Applied Mathematics and Computation, 375, 125066
Zemouche A, Rajamani R, Kheloufi H, Bedouhene F (2017) Robust observer-based stabilization of Lipschitz nonlinear uncertain systems via LMIs-discussions and new design procedure. Int J Robust Nonlinear Control 27(11):1915–1939
Zhang X, Huang W (2021) Robust \(H_ {\infty }\) adaptive output feedback sliding mode control for interval type-2 fuzzy fractional-order systems with actuator faults. Nonlinear Dyn 104(1):537–550
Zhi YL (2021) A variable memory state feedback and its application to robust control of uncertain singular time-delay systems. Neural Computing and Applications, 1-10
Zhu F, Tang Y, Wang Z (2021) Interval-Observer-based fault detection and isolation design for TS fuzzy system based on zonotope analysis. IEEE Transactions on Fuzzy Systems, 1-1
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Naami, G., Ouahi, M., Rabhi, A. et al. Design of robust control for uncertain fuzzy quadruple-tank systems with time-varying delays. Granul. Comput. 7, 951–964 (2022). https://doi.org/10.1007/s41066-021-00306-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41066-021-00306-x