Skip to main content
SpringerLink
Log in

Non-fragile extended dissipative state estimation for delayed discrete-time neural networks: application to quadruple tank process model

  • Original paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

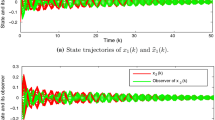
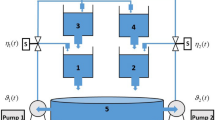
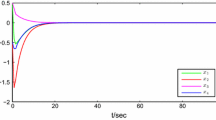
This paper deals with the non-fragile state estimator design to study the robust extended dissipativity criterion for a class of discrete-time neural networks (DNNs) involving uncertainties as well as time-varying delay components. The requisite of the proposed problem is to design a proper state estimator such that the dynamics of the corresponding estimation error is extended dissipative having external disturbance and unpredictable fragility performance. By constructing an appropriate Lyapunov–Krasovskii functional (LKF), the sufficient conditions for the extended dissipativity performance of the error system obtained by means of the proposed DNNs and its estimator which includes the \(H_{\infty }\) performance, \(L_{2}-L_{\infty }\) performance, passivity and dissipativity performance in a unified framework. The established theoretical results are expressed in terms of linear matrix inequalities (LMIs) that can be easily checked by using the standard numerical softwares. In order to analyze the applicability and effectiveness of the proposed theoretical results, numerical examples including a quadruple tank process (QTP) system model have been illustrated with simulation results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Rabunal, J., Dorrado, J.: Artificial Neural Networks in Real-Life Applications. Idea Group Publication, Hershey (2006)

    Book  Google Scholar 

  2. Cichocki, A., Unbehauen, R., Swiniarski, R.W.: Neural Networks for Optimization and Signal Processing, vol. 253. Wiley, New York (1993)

    MATH  Google Scholar 

  3. Wu, Z.G., Park, J.H., Su, H., Chu, J.: Admissibility and dissipativity analysis for discrete-time singular systems with mixed time-varying delays. Appl. Math. Comput. 218(13), 7128–7138 (2012)

    MathSciNet  MATH  Google Scholar 

  4. He, X., Li, C., Shu, Y.: Fold-flip bifurcation analysis on a class of discrete-time neural network. Neural Comput. Appl. 22(2), 375–381 (2013)

    Article  Google Scholar 

  5. He, Y., Liu, G.P., Rees, D., Wu, M.: Stability analysis for neural networks with time-varying interval delay. IEEE Trans. Neural Netw. 18(6), 1850–1854 (2007)

    Article  Google Scholar 

  6. Wu, Z.G., Lam, J., Su, H., Chu, J.: Stability and dissipativity analysis of static neural networks with time delay. IEEE Trans. Neural Netw. Learn. Syst. 23(2), 199–210 (2012)

    Article  Google Scholar 

  7. Wang, Y., Wu, H., Huang, P., Kang, Z.: Adaptive robust control for a class of uncertain stochastic systems with time-varying delays. IEEJ Trans. Electr. Electron. Eng. 13(10), 1461–1467 (2018)

    Article  Google Scholar 

  8. Feng, Z., Lam, J.: Stability and dissipativity analysis of distributed delay cellular neural networks. IEEE Trans. Neural Netw. 22, 976–981 (2011)

    Article  Google Scholar 

  9. Shi, P., Li, F., Wu, L., Lim, C.: Neural network-based passive filtering for delayed neutral-type semi-Markovian jump systems. IEEE Trans. Neural Netw. Learn. Syst. 28(9), 2101–2114 (2016)

    MathSciNet  Google Scholar 

  10. Ahn, C., Shi, P., Agarwal, R., Xu, J.: \(L_{\infty }\)-performance of single and interconnected neural networks with time-varying delay. Inf. Sci. 346, 412–423 (2016)

    Article  MathSciNet  Google Scholar 

  11. Shu, Y., Liu, X.: Improved results on \(H_{\infty }\) state estimation of static neural networks with interval time-varying delay. J. Inequal. Appl. 48(1), 1–16 (2016)

    MathSciNet  Google Scholar 

  12. Manivannan, R., Samidurai, R., Zhu, Q.: Further improved results on stability and dissipativity analysis of static impulsive neural networks with interval time-varying delays. J. Frankl. Inst. 354, 6312–6340 (2017)

    Article  MathSciNet  Google Scholar 

  13. Chen, Y., Zheng, W.X.: Stability and \(L_2\) performance analysis of stochastic delayed neural networks. IEEE Trans. Neural Netw. 22(10), 1662–1668 (2011)

    Article  Google Scholar 

  14. Zhang, B., Zheng, W.X., Xu, S.: Filtering of Markovian jump delay systems based on a new performance index. IEEE Trans. Circuits Syst. I Regul. Pap. 60(5), 1250–1263 (2013)

    Article  MathSciNet  Google Scholar 

  15. Lee, T.H., Park, M.J., Park, J.H., Kwon, O.M., Lee, S.M.: Extended dissipative analysis for neural networks with time-varying delays. IEEE Trans. Neural Netw. Learn. Syst. 25(10), 1936–1941 (2014)

    Article  Google Scholar 

  16. Manivannan, R., Samidurai, R., Cao, R., Alsaedi, J., Alsaadi, E.: Design of extended dissipativity state estimation for generalized neural networks with mixed time-varying delay signals. Inf. Sci. 424, 175–203 (2018)

    Article  MathSciNet  Google Scholar 

  17. Saravanakumar, R., Rajchakit, G., Ali, M.S., Xiang, Z., Joo, Y.H.: Robust extended dissipativity criteria for discrete-time uncertain neural networks with time-varying delays. Neural Comput. Appl. 30(12), 3893–3904 (2018)

    Article  Google Scholar 

  18. Kwon, O.M., Park, M.J., Park, J.H., Lee, S.M., Cha, E.J.: Stability and stabilization for discrete-time systems with time-varying delays via augmented Lyapunov–Krasovskii functional. J. Frankl. Inst. 350(3), 521–540 (2013)

    Article  MathSciNet  Google Scholar 

  19. Zhu, X.L., Yang, G.H.: Jensen inequality approach to stability analysis of discrete-time systems with time-varying delay. In: IEEE Conference on American Control, pp. 1644–1649 (2008)

  20. Jin, L., He, Y., Wu, M.: Improved delay-dependent stability analysis of discrete-time neural networks with time-varying delay. J. Frankl. Inst. 354(4), 1922–1936 (2017)

    Article  MathSciNet  Google Scholar 

  21. Nam, P.T., Pathirana, P.N., Trinh, H.: Discrete Wirtinger-based inequality and its application. J. Frankl. Inst. 352(5), 1893–1905 (2015)

    Article  MathSciNet  Google Scholar 

  22. Feng, Z., Zhang, W.X.: On extended dissipativity of discrete-time neural networks with time delay. IEEE Trans. Neural Netw. Learn. Syst. 26(12), 3293–3300 (2015)

    Article  MathSciNet  Google Scholar 

  23. Park, M.J., Kwon, O.M.: Stability and stabilization of discrete-time T-S Fuzzy systems with time-varying delay via Cauchy–Schwartz-based summation inequality. IEEE Trans. Fuzzy Syst. 25(1), 128–140 (2016)

    Article  Google Scholar 

  24. Hua, M., Tan, H., Fei, J.: State estimation for uncertain discrete-time stochastic neural networks with Markovian jump parameters and time-varying delays. Int. J. Mach. Learn. Cybern. 8(3), 823–835 (2015)

    Article  Google Scholar 

  25. Hu, J., Liang, J., Chen, D., Ji, D., Du, J.: A recursive approach to non-fragile filtering for networked systems with stochastic uncertainties and incomplete measurements. J. Frankl. Inst. 352(5), 1946–1962 (2015)

    Article  MathSciNet  Google Scholar 

  26. Zhang, S., Wang, Z., Ding, D., Dong, H., Alsaadi, F.E., Hayat, T.: Non-fragile \(H_{\infty }\) fuzzy filtering with randomly occurring gain variations and channel fading. IEEE Trans. Fuzzy Syst. 24(3), 505–518 (2015)

    Article  Google Scholar 

  27. Petersen, R.I.: A stabilization algorithm for a class of uncertain linear systems. Syst. Control Lett. 8(4), 351–357 (1987)

    Article  MathSciNet  Google Scholar 

  28. Boyd, S., El-Ghaoui, L., Feron, E., Balakrishnan, V.: Linear Matrix Inequalities in System and Control Theory, vol. 15. SIAM, Philadelphia (1994)

    Book  Google Scholar 

  29. Zhou, J., Lu, J.A., Lu, J.: Pinning adaptive synchronization of a general complex dynamical network. Automatica 44(4), 996–1003 (2008)

    Article  MathSciNet  Google Scholar 

  30. Richards, R.: A review of: controlling multivariable processes by FG SHINSKEY. Int. J. Control 38(3), 713–714 (1983)

    Article  Google Scholar 

  31. Johansson, K.: The quadruple-tank process: a multivariable laboratory process with an adjustable zero. IEEE Trans. Control Syst. Technol. 8(3), 456–465 (2000)

    Article  Google Scholar 

  32. El Haoussi, F., Tissir, E.H., Tadeo, F., Hmamed, A.: Delay-dependent stabilisation of systems with time-delayed state and control: application to a quadruple-tank process. Int. J. Syst. Sci. 42(1), 41–49 (2011)

    Article  MathSciNet  Google Scholar 

  33. Lee, T.H., Park, J.H., Kwon, O.M., Lee, S.M.: Stochastic sampled-data control for state estimation of time-varying delayed neural networks. Neural Netw. 46, 99–108 (2013)

    Article  Google Scholar 

  34. Chen, X., Song, Q., Li, Z., Zhao, Z., Liu, Y.: Stability analysis of continuous-time and discrete-time quaternion-valued neural networks with linear threshold neurons. IEEE Trans. Neural Netw. Learn. Syst. 29(7), 2769–2781 (2017)

    MathSciNet  Google Scholar 

  35. Mohamad, S., Gopalsamy, K.: Exponential stability of continuous-time and discrete-time cellular neural networks with delays. Appl. Math. Comput. 135, 17–38 (2013)

    MathSciNet  MATH  Google Scholar 

  36. Vembarasan, V., Balasubramaniam, P., Chan, C.: Non-fragile state observer design for neural networks with Markovian jumping parameters and time-delays. Nonlinear Anal. Hybrid Syst. 14, 61–73 (2014)

    Article  MathSciNet  Google Scholar 

  37. Ghorbel, H., Souissi, M., Chaabane, M., Tadeo, F.: Robust fault detection for Takagi–Sugeno discrete models: application for a three-tank system. Int. J. Comput. Appl. 44(18), 1–7 (2012)

    Google Scholar 

Download references

Funding

This work was supported by the Department of Atomic Energy (DAE) through the National Board for Higher Mathematics (NBHM) funded by the Government of India (under Grant 02011/16/2019/R & D II/2599).

Author information

Authors and Affiliations

  1. Department of Mathematics, The Gandhigram Rural Institute (Deemed to be University), Gandhigram, Tamil Nadu, 624 302, India

    G. Nagamani, B. Adhira & G. Soundararajan

Authors
  1. G. Nagamani
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. B. Adhira
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. G. Soundararajan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to G. Nagamani.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Nagamani, G., Adhira, B. & Soundararajan, G. Non-fragile extended dissipative state estimation for delayed discrete-time neural networks: application to quadruple tank process model. Nonlinear Dyn 104, 451–466 (2021). https://doi.org/10.1007/s11071-021-06270-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-021-06270-0

Keywords

Search

Navigation