1 Introduction

The concerns on the proper treatment of medical waste and other toxic harmful wastes elements are growing worldwide due to the rapid industrialization and population growth Mato and Kassenga (1997). The significance of reasonable HCWT, specifically in developing countries, cannot be ignored. Adequate improvements need to rescue environmental and human health from serious risks. Healthcare services produce a huge quantity of health care waste (HCW), which results in infections of hospitalized patients, health workers, and living beings, as well as polluting the environment. Recently, an enormous rise in HCW was reported (Windfeld and Brooks 2015; Thakur and Ramesh 2015). As a result, reasonable HCW become a worldwide ecological and community health problem, precisely in rising nations, where HCW is often miscellaneous with municipal corporation solid waste (Debere et al. 2013; Glaize et al. 2019). The World Health Organization (WHO 2021) defines HCW as wastes caused by health care happenings, which has a lot of resources such as used medical tools, syringes, and radioactive materials. According to WHO, near-about 85% of HCW is composed of non-hazardous and 15% hazardous waste, however, the remaining 10% is unsafe which can be infectious, transmittable, and radioactive or chemical waste is 5% of HCW, it can be a risk to the environment and health, if not controlled or disposed of appropriately.

According to (WHO 2018), inappropriate treatment of HCW has injurious effects on the environment and public health. Hinduja and Pandey (2018) evaluated the healthcare waste treatment options and applying combined decision support frameworks. As HCWT methods bestow facilities for the classification of waste produces by health care amenities, the assessment of HCWT technologies can be considered as an intricate MCDM problem. A methodical and severe outlook is needed to effectually address this obligatory matter. Several studies have designated the importance of proper waste treatment technology selection (Lee et al. 2016; Hassan et al. 2018; Liu et al. 2021; Rani et al. 2020a, b, c, d). The analytical hierarchical process (AHP) to calculate five various technologies used for contagious management waste treatment is studied by Voudrias (2016). During this period of the Covid-19 pandemic, the waste treatment especially material waste treatment has increased many folds, and the impact of the Covid-19 outburst on medical waste is appraised by evaluating solid waste production, conformation, and treatment Kalantary et al. (2021). The assessment of the best HCWT alternative has been growing global anxiety. The choice of suitable waste treatment technology is supposed to be a complicated problem, which may be effectually controlled by MCDM approaches. To choose the best HCWT alternative, DEs require to ponder some inconsistent criteria. Thereby, a competent and exact HCWT assessment process is needed to discuss the problem.

Zadeh (1965) developed the fundamental of fuzzy set (FS). In this rating, fuzzy sets can be proper to carry the best results for real-world queries. The fuzzy set is based on membership degree which lies between 0 and 1. In a real-life scenario, membership value and a non-membership value are not always zero or one but lies somewhere between. It is worth saying that every aspect is not always black or white but has some grey-level values. This approach of fuzzy sets has various applications in many fields of engineering, life sciences, social sciences, management, etc. There have been many applications of fuzzy sets, Turksen (1986) have presented IVFSs (abbreviations are given Table 1) for the assessment of collective concepts based on normal forms, and has solved some complex problems associated with fuzzy set theory. Chen et al. (1997) and Chen and Hsiao (2000) presented a new technique for dealing with bidirectional approximate reasoning for rule-based systems on IVFSs, and expanding this work to bidirectional approximations based on IVFSs. Chen et al. (2012) introduced a method for handling the interpolation interval based on type-2 Gaussian fuzzy sets. Further, the intuitionistic fuzzy set introduced by Atanassov (1986) generalized the notion of FS to IFSs that contain both \(\mu\)-membership value (MV) and \(\vartheta\)-non-membership value (N-MV). Subsequently, many researchers have thought to this extent, and it has wide applications of IFSs (see Rani et al. 2019a, b; Rani and Jain 2019; Mishra et al. 2019a, b).

Table 1 Abbreviations used in the present paper
Full size table

Garg and Rani (2021) presented intuitionistic fuzzy sets MULTIMOORA method-based new aggregation operators for solid waste management techniques. Meanwhile, Ye (2010) introduced two effective measures of IF-entropy. Wei et al. (2012) introduced an entropy measure on trigonometric function for IFSs. Ali (2018) discussed the distance measure of H-max for IFS and its find results for intuitionistic t-norm. Szmidt and Kacprzyk (2001) introduce entropy measures for IFSs. Chang et al. (2019) introduced a consolidated model with emergency plan selection for IF-MCDM.

Later on, various drawbacks of IFSs have been seen, as the sum of the MV and N-MV is greater than 1, \(\left(0.7+0.6>1\right).\) To overcome the drawback of the IFS, Yager (2013a) introduced the basic theory of Pythagorean fuzzy set (PFS). This perception has a wider range than the IFS as the domain of PFS’s membership value is wider as compared to the IFS’s membership values. In a Pythagorean fuzzy set, MV and N-MV satisfy the condition \({\mu }^{2}+{\vartheta }^{2}\le 1.\) It is a controlling device to express ambiguous ideas. It provides greater flexibility in dealing with the real-life decision making as compared to other fuzzy models. Yager (2013a, b) and Yager and Abbasov (2013) studied the basic concepts related to PFS and explained the relationship between complex numbers and PFNs. Thereafter, a set of various types of Pythagorean fuzzy aggregation operators are also proposed, such as PFWAO. Thereafter, Zhang and Xu (2014) introduce the basic mathematical operations for PFNs. In the meantime, they also presented the elementary operative law properties based on PFNs. Peng andand score function for PFNs. Thereafter, Peng and Yang (2015) presented operations, subtraction, and division and discussed their properties based on PFNs. Peng and Yang (2016) and Peng et al. (2017) introduced two new operators applied them to solve the Pythagorean fuzzy Choquet integral-average-geometric (PF-CI-A-G) operator and discussed the relationship and presented a superiority and interiority ranking technique based on MAGDM with Pythagorean fuzzy numbers. Ma and Xu (2016) proposed a score and accuracy function for Pythagorean fuzzy numbers. Peng et al. (2020) generated novel PF-score functions and applied them to COCOSO and CRITIC methods. Wang et al. (2021) established some interactive Hamacher power aggregation operators on PFNs weighted average and geometric aggregation operators. Some authors introduced PF-operators (Zeng et al. 2016; Rahman et al. 2019; Rong et al. 2020). Thereafter, Zhang et al. (2019) presented a new similarity measure on PFS. Zhou and Mo (2020) introduced the Dempster–Shafer indication theory on PFS. Rani et al. (2020a, b, c, d) proposed TOPSIS technique under Pythagorean fuzzy sets. The PFS theory has involved the interest of numerous researchers, and an idea has been implemented in many application fields. For some applications on PFS, see Wei (2018), Rani et al. (2020a, b, c, d), Ejegwa and Awolola (2021), and Ejegwa (2021).

The COPRAS technique developed by Zavadskas et al. (1994) is one of the powerful methods for ranking the alternatives over a set of qualitative and quantitative criteria. This approach compares each alternative and calculates their priorities based on criteria weights. The principal profits of the COPRAS technique are (i) it has effortless and comprehensible calculation steps; (ii) it ponders the ratio of an ideal and worst solution together; (iii) compared to other MCDM methods, it offers the outcomes in a short period. Recently, the COPRAS method has been applied in various uncertain environments. Vahdani and Mousavi (2014) established an innovative interval-valued COPRAS method for solving MCDM problems. Bekar et al. (2016) established a decision support system based on the COPRAS technique with grey numbers for evaluating the MCDM problems. Zheng et al. (2018) presented a complex proportional assessment technique to solve the chronic obstructive pulmonary disease problem. Mishra et al. (2019a, b) studied an integrated hesitant fuzzy COPRAS method for service quality evaluation problems under the hesitant fuzzy sets (HFS) context. Further, Thao and Smarandache (2019) expanded the basic conception of fuzzy entropy for PFS and developed measures using the COPRAS technique for PFS. Mishra et al. (2020) presented the Shapley function and information measures based COPRAS model for the hazardous waste recycling facility selection problem on IVIFSs. In a study, Rani et al. (2020a, b, c, d) designed a decision support system by unifying the COPRAS technique on PFS and applied it to calculate the pharmacological therapies for type-2 diabetes patients. Some scholars have currently proposed the COPRAS method in various areas of MCDM (see Lu et al. 2021; Krishankumar et al. 2021; Jain and Chand 2021). This method effectively establishes the interrelationship between criteria and allows decision experts to capture the ambiguity involved in decisions of many inconsistent criteria. The abbreviations used in the article are mentioned in Table 1.

Based on the literature survey, it has been proven that PFS has greater functioning competence than IFSs to deal with ambiguity in decision-making problem real cases. Hence, this article expanded the conventional COPRAS technique corresponding to proposed entropy measure and score function within PFS. This technique is very simple and easy to understand. The application of the classical COPRAS technique has focused on a wider range of problems. However, many MCDM methodologies have been proposed beneath the PFS environment; there have been no studies on PFS using the COPRAS method with the use of structure to evaluate and prefer the required HCWT alternatives. To tackle this issue, the COPRAS method is presented in this article that can be used to discuss the implicit hesitancy and ambiguity concerned with DEs opinion. This article can be summarized as follows:

  1. (1)

    A new entropy measure on PFSs is proposed and compared with existing ones.

  2. (2)

    Defined a multi-criterion decision-making problem using COPRAS technique

  3. (3)

    Calculate the decision experts’ weights in PFS, and evaluating the score values by improved score function formula in PFS.

  4. (4)

    To compute the criteria weights on the basis of the proposed entropy and score function on PFSs.

  5. (5)

    Presented an empirical case study for deciding an HCWT alternative on PFS to manifest the applicability of the delivered COPRAS technique.

  6. (6)

    Finally, comparative analysis of the proposed method with the existing techniques is presented to verify the validity and reasonability of the established PF-COPRAS method.

The framework of the study is organized in the following sections: in Sect. 2, we have discussed the basic concept of the Pythagorean fuzzy set. In Sect. 3, the entropy measure on Pythagorean fuzzy sets is proposed and studied its validity. Further the comparison of the proposed entropy measure with existing entropies is discussed. In Sect. 4, we derived the weights and the best alternative is selected using PF-COPRAS algorithm. In Sect. 5, a real-life application of healthcare waste treatment is selected, and assessed using the proposed entropy and PF-COPRAS technique. In Sect. 6, we discuss the results and conclusions.

2 Preliminaries

Here, we present the basic concepts of IFS and PFS.

Definition 2.1

(Atanassov 1986) Let \(T\) be a finite universal set. An IFS \(I\subset T\) is mathematically defined as:

$$I = \left\{ {\left\langle { t_{i} , \mu_{I} \left( {t_{i} } \right), \vartheta_{I} \left( {t_{i} } \right)} \right\rangle | t_{i} \in T} \right\},$$
(1)

where \({\mu }_{I}\left({t}_{i}\right) :T\to \left[\mathrm{0,1}\right]\) and \({\vartheta }_{I}\left({t}_{i}\right) :T\to \left[\mathrm{0,1}\right]\) are the membership values and non-membership values of the element\({t}_{i}\in T\), and satisfies the condition:

$$0 \le \mu_{I} \left( {t_{i} } \right) + \vartheta_{I} \left( {t_{i} } \right) \le 1.$$
(2)

Furthermore, for all \({t}_{i}\in T,\) the indeterminacy degree is defined as

$$\pi_{I} \left( {t_{i} } \right) = 1 - \mu_{I} \left( {t_{i} } \right) - \vartheta_{I} \left( {t_{i} } \right).$$
(3)

For an IFS \(I\, \mathrm{on}\, T\), the pair \(\left({\mu }_{I}\left({t}_{i}\right), {\vartheta }_{I}\left({t}_{i}\right)\right)\) is referred to as an IFN.

Definition 2.2

(Yager 2013a) In mathematical form, a Pythagorean fuzzy set B on T is given by:

$$B = \left\{ {\left\langle {t_{i} , \mu_{B} \left( {t_{i} } \right), \vartheta_{B} \left( {t_{i} } \right)} \right\rangle |t_{i} \in T} \right\},$$
(4)

where \({\mu }_{B}\left({t}_{i}\right) :T\to [\mathrm{0,1}]\) denotes the membership value and \({\vartheta }_{B}\left({t}_{i}\right) :T\to \left[\mathrm{0,1}\right]\) denotes the non-membership value of the element \({t}_{i}\in T\) and satisfying the following condition:

$$0 \le \mu_{B}^{2} \left( {t_{i} } \right) + \vartheta_{B}^{2} \left( {t_{i} } \right) \le 1.$$
(5)

For all \({t}_{i}\in T\) to B, \({\pi }_{B}\left({t}_{i}\right)=\sqrt{1-{\mu }_{B}^{2}\left({t}_{i}\right)-{\vartheta }_{B}^{2}\left({t}_{i}\right)}\) denotes the hesitance or indeterminacy degree of the Pythagorean fuzzy set. For accessibility, Zhang and Xu (2014) named the pair \(\left({\mu }_{B}\left({t}_{i}\right), {\vartheta }_{B}\left({t}_{i}\right)\right)\) as the Pythagorean fuzzy number, and denote it by \(\beta =\left({\mu }_{\beta }, {\vartheta }_{\beta }\right)\).

Definition 2.3

(Yager 2013a, b; Yager and Abbasov 2013) Let \(\beta =\left({\mu }_{\beta }, {\vartheta }_{\beta }\right), {\beta }_{1}=\left({\mu }_{{\beta }_{1}}, {\vartheta }_{{\beta }_{1}}\right)\) and \({\beta }_{2}=\left({\mu }_{{\beta }_{2}}, {\vartheta }_{{\beta }_{2}}\right)\) be the PFNs. Then, some operating laws on Pythagorean fuzzy numbers are presented as:

  1. (i)

    \(\beta^{c} = \left( { \vartheta_{\beta } , \mu_{\beta } } \right).\)

  2. (ii)

    \(\beta_{1} \oplus \beta_{2} = \left( {\sqrt {\mu_{{\beta_{1} }}^{2} + \mu_{{\beta_{2} }}^{2} - \mu_{{\beta_{1} }}^{2} \mu_{{\beta_{2} }}^{2} } ,\vartheta_{{\beta_{1} }} \vartheta_{{\beta_{2} }} } \right).\)

  3. (iii)

    \(\beta_{1} \otimes \beta_{2} = \left( {\mu_{{\beta_{1} }} \mu_{{\beta_{2} }} , \sqrt {\vartheta_{{\beta_{1} }}^{2} + \vartheta_{{\beta_{2} }}^{2} - \vartheta_{{\beta_{1} }}^{2} \vartheta_{{\beta_{2} }}^{2} } } \right).\)

  4. (iv)

    \(\lambda \beta = \left( {\sqrt {1 - \left( {1 - \mu_{\beta }^{2} } \right)^{\lambda } } ,\left( {\vartheta_{\beta } } \right)^{\lambda } } \right), \lambda > 0.\)

  5. (v)

    \(\beta^{\lambda } = \left( {\left( {\mu_{\beta } } \right)^{\lambda } , \sqrt {1 - \left( {1 - \vartheta_{\beta }^{2} } \right)^{\lambda } } } \right), \lambda > 0.\)

Definition 2.4

(Zhang and Xu 2014) For a PFN \(\beta =\left({\mu }_{\beta }, {\vartheta }_{\beta }\right)\), the score function and accuracy function are presented as follows:

$${\mathcal{S}}\left( \beta \right) = \left( {\mu_{\beta } } \right)^{2} - \left( {\vartheta_{\beta } } \right)^{2} ,$$
(6)
$$\hbar \left( \beta \right) = \left( {\mu_{\beta } } \right)^{2} + \left( {\vartheta_{\beta } } \right)^{2} ,$$
(7)

\(\mathrm{where }\,\mathcal{S}\left(\beta \right)\in \left[-1, 1\right]\) and \(\hbar\left(\beta \right)\in \left[0, 1\right]\).

Definition 2.5

(Zhang and Xu 2014) For a PFN \(\beta =\left({\mu }_{\beta }, {\vartheta }_{\beta }\right)\), the normalized score and ambiguity functions are as follows:

$${\mathcal{S}}^{*} \left( \beta \right) = \frac{1}{2}\left( {{\mathcal{S}}\left( \beta \right) + 1} \right), \hbar^{^\circ } \left( \beta \right) = 1 - \hbar \left( \beta \right),$$
(8)

and, Peng and Li (2019) improve a new score function

$${\mathcal{S}}^{*} \left( \beta \right) = \frac{{2\left( {\mu_{{\beta_{j} }} } \right)^{2} + \left( {1 - \left( {\vartheta_{{\beta_{j} }} } \right)^{2} } \right) + \left( {\left( {\mu_{{\beta_{j} }} } \right)^{2} } \right)^{2} }}{4}.$$
(9)

such that \({\mathcal{S}}^{*}\left(\beta \right), {\hbar}^{^\circ }\left(\beta \right)\in \left[\mathrm{0,1}\right].\)  

Definition 2.6

(Peng et al. 2017) Let \(B, C\in PFSs\left(T\right).\) An entropy measure G \(:PFS\left(T\right)\to \left[\mathrm{0,1}\right]\) for PFS is a real-valued mapping that satisfies the following properties:

(P1) \(0 \le G\left( B \right) \le 1.\)

(P2) \(G\left( B \right) = 0\, {\text{iff }}\,B\,{\text{ is a crisp set}}.\)  

(P3) \(G\left( B \right) = 1\, {\text{if and only if }}\mu_{B} \left( {t_{i} } \right) = \vartheta_{B} \left( {t_{i} } \right),\) for all \(t_{i} \in T\)

(P4) \(G\left( B \right) = G\left( {B^{c} } \right)\), where \(B^{c}\) is the compliment of \(B\).

(P5) For each, \(t_{i} \in T, G\left( B \right) \le G\left( C \right){\text{ if }}B < { }C,\)

i.e., \(\mu_{B} \left( {t_{i} } \right) \le \mu_{C} \left( {t_{i} } \right) \le \vartheta_{C} \left( {t_{i} } \right) \le \vartheta_{B} \left( {t_{i} } \right)\)

or \(\vartheta_{B} \left( {t_{i} } \right) \le \vartheta_{C} \left( {t_{i} } \right) \le \mu_{C} \left( {t_{i} } \right) \le \mu_{B} \left( {t_{i} } \right).\)

3 Proposed Pythagorean fuzzy entropy measure

In FS theory, entropy is a quantitative calculation of uncertainty. Initially, De Luca and Termini (1972) studied the fundamental properties of fuzzy entropy measure based on Shannon probability entropy. Later on, Szmidt and Kacprzyk (2001) expanded the entropy measure for IFS. Since the appearance of PFS, Peng et al. (2017) studied some entropy, distance, similarity, and inclusion measure for PFS and utilized it for pattern recognition, clustering analysis, and medical diagnosis. Further, Yang and Hussain (2018) offered some probabilistic and non-probabilistic types of entropy measures for PFS and their application in MCDM problems. In a study, Xue et al. (2018) suggested entropy measure-based Pythagorean fuzzy linear programming technique for multidimensional analysis of preference (PF-LINMAP) approach for railway project investment problem. Guleria and Bajaj (2018) proposed Pythagorean fuzzy (R, S)-norm information measure and its application in DM problem. In the recent past, Biswas and Sarkar (2019) developed a novel entropy distance measure on PFS and then, entropy has been used to evaluate criterion weights by the proposed TOPSIS method. Several studies have been focused their attention on the development and application of entropy measures (Rani et al. 2020a, b, c, d; Xu et al. 2020) with the increasing scope and efficiency of Pythagorean fuzzy entropy, here in this section, we have proposed an entropy measure on PFS.

Corresponding to the Wei et al. (2012) entropy measure on intuitionistic fuzzy entropy, we have proposed the following Pythagorean fuzzy entropy measure:

$$G\left( B \right) = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left[ {\left\{ {\sqrt 2 {\text{Cos}}\left( {\pi \left( {\frac{{\mu_{B}^{2} \left( {t_{i} } \right) - \vartheta_{B}^{2} \left( {t_{i} } \right)}}{4}} \right)} \right) - 1} \right\}\frac{1}{\sqrt 2 - 1}} \right] ,$$
(10)

where \(B\in PFS\left(T\right) , T=\left\{{t}_{1}, {t}_{2}, {t}_{3},\dots , {t}_{n}\right\}.\)

Theorem 1

The function \(G\left(B\right)\) as defined above is a valid entropy measure on PFS(T).

Proof

According to Definition (2.6), to prove the validity of the theorem, it must satisfy axioms (P1–P5):

(P1). Since in PFS theory, \({0\le \mu }_{B}^{2}\left(t\right)+{\vartheta }_{B}^{2}\left(t\right)\le 1,\) hence, it is clear that \(0\le G(B)\le 1.\)

(P2). When B is a crisp set, i.e., \({\mu }_{B}\left({t}_{i}\right)=1, {\vartheta }_{B}\left({t}_{i}\right)=0\; \mathrm{or}\;{\mu}_{B}\left({t}_{i}\right)=0, { \vartheta }_{B}\left({t}_{i}\right)=1,\) then from Eq. (10), we get \(G\left(B\right)=0.\)

$${\text{Conversely}},{\text{ if}}\,\,G\left( B \right) = 0,\,{\text{ie}}{.,}\, G\left( B \right) = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left[ {\left\{ {\sqrt 2 Cos\left( {\pi \left( {\frac{{\mu_{B}^{2} \left( {t_{i} } \right) - \vartheta_{B}^{2} \left( {t_{i} } \right)}}{4}} \right)} \right) - 1} \right\}\frac{1}{\sqrt 2 - 1}} \right] = 0,$$
(11)

then for all \(t_{i} \in T\), we have \(\begin{gathered} \left\{ {\sqrt 2 {\text{Cos}} \left( {\pi \left( {\frac{{\mu_{B}^{2} \left( {t_{i} } \right) - \vartheta_{B}^{2} \left( {t_{i} } \right)}}{4}} \right)} \right) - 1} \right\}\frac{1}{\sqrt 2 - 1} = 0, \hfill \\ {\text{Cos}} \left( {\pi \left( {\frac{{\mu_{B}^{2} \left( {t_{i} } \right) - \vartheta_{B}^{2} \left( {t_{i} } \right)}}{4}} \right)} \right) = \frac{1}{\sqrt 2 }. \hfill \\ \end{gathered}\)

It implies \({\mu }_{B}^{2}\left({t}_{i}\right)-{\vartheta }_{B}^{2}\left({t}_{i}\right)=1,\) then we have \({\mu }_{B}\left({t}_{i}\right)=1,\) \({\vartheta }_{B}\left({t}_{i}\right)=0 \mathrm{or }{\mu }_{B}\left({t}_{i}\right)=0, { \vartheta }_{B}\left({t}_{i}\right)=1\). Thus, \(B\) is a crisp set.

(P3). Let \({\mu }_{B}\left({t}_{i}\right)= {\vartheta }_{B}\left({t}_{i}\right), \forall {t}_{i}\in T\), from Eq. (10), we have \(G\left(B\right)=1.\)

Conversely, assume that \(G\left(B\right)=1\), then \(\forall {t}_{i}\in T,\) we have

$$\begin{gathered} \left\{ {\sqrt 2 {\text{Cos}} \left( {\pi \left( {\frac{{\mu_{B}^{2} \left( {t_{i} } \right) - \vartheta_{B}^{2} \left( {t_{i} } \right)}}{4}} \right)} \right) - 1} \right\}\frac{1}{\sqrt 2 - 1} = 1, \hfill \\ {\text{Cos}} \left( {\pi \left( {\frac{{\mu_{B}^{2} \left( {t_{i} } \right) - \vartheta_{B}^{2} \left( {t_{i} } \right)}}{4}} \right)} \right) = 1. \hfill \\ \end{gathered}$$

It implies \({\mu }_{B}^{2}\left({t}_{i}\right)-{\vartheta }_{B}^{2}\left({t}_{i}\right)=0,\) then we can obtain \({\mu }_{B}\left({t}_{i}\right)= {\vartheta }_{B}\left({t}_{i}\right), \forall { t}_{i}\in T\).

(P4). \({B}^{c}\) is the complementary set of \(B\) is equal to\(\left\{\left({t}_{i} ,{\vartheta }_{B}\left({t}_{i}\right), {\mu }_{B}\left({t}_{i}\right)\right)|{t}_{i}\in T\right\}\). Now, it is clear from Eq. (10) that

$$\begin{gathered} G\left( {B^{c} } \right) = \frac{1}{n} \hfill \\ \mathop \sum \limits_{i = 1}^{n} \left[ {\left\{ {\sqrt 2 Cos\left( {\pi \left( {\frac{{\vartheta_{B}^{2} \left( {t_{i} } \right) - \mu_{B}^{2} \left( {t_{i} } \right)}}{4}} \right)} \right) - 1} \right\}\frac{1}{\sqrt 2 - 1}} \right] \hfill \\ = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left[ {\left\{ {\sqrt 2 Cos\left( {\pi \left( {\frac{{\mu_{B}^{2} \left( {t_{i} } \right) - \vartheta_{B}^{2} \left( {t_{i} } \right)}}{4}} \right)} \right) - 1} \right\}\frac{1}{\sqrt 2 - 1}} \right] \hfill \\ = G\left( B \right) \hfill \\ \end{gathered}$$

i.e., \(G\left( {B^{c} } \right) = G\left( {\text{B}} \right).\)

(P5). Let \(x,y\in [\mathrm{0,1}]\) and

$$f\left( {x,y} \right) = \left\{ {\sqrt 2 Cos\left( {\pi \left( {\frac{{x^{2} - y^{2} }}{4}} \right)} \right) - 1} \right\}\frac{1}{\sqrt 2 - 1}.$$
(12)

Now, from Eq. (12), we shall prove that \(f\left(x,y\right)\) is increasing for \(x\) and decreasing to \(y\).

For this, we can partially differentiate the function \(f\left(x,y\right)\) to \(x\) and \(y\), given as

$$\frac{{\partial f\left( {x,y} \right)}}{\partial x} = \frac{\pi x}{{\sqrt 2 \left( {\sqrt 2 - 1} \right)}} {\text{Sin}} \left( {\pi \left( {\frac{{y^{2} - x^{2} }}{4}} \right)} \right).$$
(13)
$$\frac{{\partial f\left( {x,y} \right)}}{\partial y} = \frac{ - \pi x}{{\sqrt 2 \left( {\sqrt 2 - 1} \right)}} {\text{Sin}} \left( {\pi \left( {\frac{{y^{2} - x^{2} }}{4}} \right)} \right).$$
(14)

When \(x\le y\), we obtain \(\frac{\partial f\left(x,y\right)}{\partial x}\ge 0\) and \(\frac{\partial f\left(x,y\right)}{\partial y}\le 0,\) it means that the function \(f\left(x,y\right)\) is increasing concerning \(x\) and decreasing concerning \(y\), therefore, if \(B\le C\), then Eq. (12), we have

$$\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} f\left( {\mu_{B} \left( {t_{i} } \right),\vartheta_{B} \left( {t_{i} } \right)} \right) \le \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} f\left( {\mu_{C} \left( {t_{i} } \right),\vartheta_{C} \left( {t_{i} } \right)} \right).$$
(15)

i.e., \(G\left( B \right) \le G\left( C \right)\).

3.1 Comparison of the proposed entropy with the existing entropies

Here, we compare the proposed entropy measure \(G\left(B\right)\) with the existing Pythagorean fuzzy entropy measures:

(Xue et al. 2018)

$$G_{X} \left( B \right) = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left[ {1 - \left( {\mu_{B}^{2} \left( {t_{i} } \right) + \vartheta_{B}^{2} \left( {t_{i} } \right)} \right)\left| {\mu_{B}^{2} \left( {t_{i} } \right) - \vartheta_{B}^{2} \left( {t_{i} } \right)} \right|} \right].$$
(16)

(Yang and Hussain 2018)

$$G_{Y} \left( B \right) = 1 - \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {\mu_{B}^{2} \left( {t_{i} } \right) - \vartheta_{B}^{2} \left( {t_{i} } \right)} \right)^{2} .}$$
(17)

(Thao and Smarandache 2019)

$$G_{T} \left( B \right) = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left[ {1 - \left| {\mu_{B}^{2} \left( {t_{i} } \right) - \frac{1}{3}} \right| - \left| {\vartheta_{B}^{2} \left( {t_{i} } \right) - \frac{1}{3}} \right|} \right].$$
(18)

(Rani et al. 2019a, b)

$$\begin{gathered} G_{R} \left( B \right) = \frac{1}{{n\left( {\sqrt e - 1} \right)}} \hfill \\ \mathop \sum \limits_{i = 1}^{n} \left[ {\begin{array}{*{20}c} {\left( {\frac{{\mu_{B}^{2} \left( {t_{i} } \right) + 1 - \vartheta_{B}^{2} \left( {t_{i} } \right)}}{2}} \right)e^{{\left( {\frac{{\vartheta_{B}^{2} \left( {t_{i} } \right) + 1 - \mu_{B}^{2} \left( {t_{i} } \right)}}{2}} \right)}} } \\ { + \left( {\frac{{\vartheta_{B}^{2} \left( {t_{i} } \right) + 1 - \mu_{B}^{2} \left( {t_{i} } \right)}}{2}} \right)e^{{\left( {\frac{{\mu_{B}^{2} \left( {t_{i} } \right) + 1 - \vartheta_{B}^{2} \left( {t_{i} } \right)}}{2}} \right)}} - 1} \\ \end{array} } \right]. \hfill \\ \end{gathered}$$
(19)

Let \(B\in PFS(T)\) be defined as:

$$B = \left\{ {\left( {t , \left( {\mu_{B} \left( t \right), \vartheta_{B} \left( t \right)} \right)} \right)|t \in T} \right\}.$$

We have characterized the following linguistic terms:

B1/2 as ‘More or less Large’,

B as ‘Large’,

B2 as ‘Quite Large’,

B3 as ‘Very Large’,

B4 as ‘Very Very Large’.

$$B = \left\{ {\begin{array}{*{20}c} {\left( {6, 0.25, 0.8} \right), \left( {7, 0.4, 0.7} \right), \left( {8, 0.5, 0.7} \right), } \\ {\left( {9, 0.9, 0.3} \right), \left( {10, 1, 0.5} \right) } \\ \end{array} } \right\}$$

From Table 2, it is clear that for \({B}^\frac{1}{2}\succ B\succ {B}^{2}\succ {B}^{3}\succ {B}^{4}\), the various Pythagorean fuzzy entropy measures satisfy the same trend, i.e.,

$$G(B^{\frac{1}{2}} )\, \succ\, G\left( B \right)\, \succ\, G(B^{2} )\, \succ\, G\left( {B^{3} } \right)\, \succ\, G(B^{4} ).$$
(20)
Table 2 Comparison of the degree of fuzziness of different entropy measures
Full size table

Hence, from the above Table 2, it can be concluded that the proposed entropy measure is in harmonization with the already existing entropy measures.

4 Pythagorean fuzzy COPRAS technique

In this section, we discussed the PF-COPRAS technique to rank the various alternatives in an MCDM problem. The proposed COPRAS technique is modified by utilizing the proposed entropy measure on PFS and score function to calculate the criterion weight. A step-by-step explanation algorithm of the multi-criteria decision-making PF-COPRAS technique is given as follows:

Step 1: Let \(\mathcal{L}=\left\{{\mathcal{L}}_{1}, {\mathcal{L}}_{2},\dots , {\mathcal{L}}_{m}\right\}\) denote a series of alternatives, \(\mathcal{Q}=\left\{{\mathcal{Q}}_{1}, {\mathcal{Q}}_{2},\dots , {\mathcal{Q}}_{n}\right\}\) denotes a series of criteria. A collection of experts \(E=\left\{{E}_{1},{ E}_{2}, \dots {E}_{l}\right\}\) represents their ideas on each alternative \({\mathcal{L}}_{i}\) for each attribute \({\mathcal{Q}}_{j}\) of linguistic terms (LTs). Let \({\mathbb{Z}}=\left({z}_{ij}^{(k)}\right), i=1\left(1\right)m,\, j=1(1)n\) be a linguistic DM recommended by experts, where \({z}_{ij}^{(k)}\) denotes the appraisal of an alternative \({\mathcal{L}}_{i}\) regarding criterion \({\mathcal{Q}}_{j}\) in the forms of LTs for \({k}^{th}\) DE.

Step 2: Evaluate an initial decision experts (DEs) weight. Let the DEs be measured as LTs that are converted in PFNs. For the assessment of the kth DEs weight, let \({E}_{k}=\left[{\mu }_{k},{\vartheta }_{k},{\pi }_{k}\right]\) be a PFNs:

$$\lambda_{k} = \frac{{\mu_{k}^{2} \left( {2 - \mu_{k }^{2} - \vartheta_{k}^{2} } \right)}}{{\mathop \sum \nolimits_{k = 1}^{\ell } \mu_{k}^{2} \left( {2 - \mu_{k}^{2} - \vartheta_{k}^{2} } \right)}},$$
(21)

where \(\sum_{k=1}^{\mathcal{l}}{\lambda }_{k}=1\).

Step 3: Calculate the aggregation PF-decision matrix (APF-DM) corresponding to weights expert opinions on the criteria that are aggregated using a Pythagorean fuzzy weighted average operator to assess the weighting of each criterion. Let \({\mathbb{N}}={\left({\eta }_{ij}\right)}_{m\times n}\) be the PF-decision matrix by Yager (2013b), where

$$\eta_{ij} = \left( {\sqrt {1 - \mathop \prod \limits_{k = 1}^{\ell } \left( {1 - \mu_{k}^{2} } \right)^{{\lambda_{k} }} } , \mathop \prod \limits_{k = 1}^{\ell } \left( {\vartheta_{k} } \right)^{{\lambda_{k} }} } \right)$$
(22)

Step 4: Calculate the weight \(\varpi ={\left({\varpi }_{1}, {\varpi }_{2}, \dots ,{\varpi }_{n}\right)}^{\mathrm{T}}\) for each criterion computed by formula (23) based on Pythagorean fuzzy environment and the obtained formula is given as

$$\varpi_{j} = \frac{{\mathop \sum \nolimits_{i = 1}^{m} \left[ {\mathop \sum \nolimits_{j = 1}^{n} E\left( {\eta_{ij} } \right) + {\mathcal{S}}^{*} \left( {\eta_{ij} } \right)} \right]}}{{\mathop \sum \nolimits_{j = 1}^{n} \left( {\mathop \sum \nolimits_{i = 1}^{m} \left[ {\mathop \sum \nolimits_{j = 1}^{n} E\left( {\eta_{ij} } \right) + {\mathcal{S}}^{*} \left( {\eta_{ij} } \right)} \right]} \right)}}.$$
(23)

Step 5: Sum the values of benefit-type criteria \({\sigma }_{i}\) and cost-type criteria \({\varphi }_{i}\) where \(i=1(1)m\) and calculate the value of \({\sigma }_{i}\) and \({\varphi }_{i}\) as follows:

$$\sigma_{i} = \mathop {\mathop \oplus \limits_{j = 1} }\limits^{l} \varpi_{j} \eta_{ij} , ({\text{for benefit-type}}).$$
(24)
$$\varphi_{i} = \mathop {\mathop \oplus \limits_{j = l + 1} }\limits^{n} \varpi_{j} \eta_{ij} ,({\text{for cost-type}}).$$
(25)

Step 6: Calculate of the relative weight (\(\rho_{i}\)) to each alternative as follows:

$$\rho_{i} = {\mathcal{S}}^{*} (\sigma_{i} ) + \frac{{\mathop \sum \nolimits_{i = 1}^{m} {\mathcal{S}}^{*} (\varphi_{i} ) }}{{{\mathcal{S}}^{*} (\varphi_{i} ) \mathop \sum \nolimits_{i = 1}^{m} \frac{1}{{ {\mathcal{S}}^{*} (\varphi_{i} )}} }},$$
(26)

where \({\mathcal{S}}^{*} (\sigma_{i} )\) and \({\mathcal{S}}^{*} (\varphi_{i} )\) are the score values of \(\sigma_{i}\) and \(\varphi_{i}\), respectively.

Step 7: Evaluate priority values of the alternatives; the priority value of the alternatives is evaluated, compatible with the relative weights of the alternatives. The higher relative degree of the alternative is ranked as a better priority, and thus, is the best alternative:

$$P^{*} = \mathop {\max }\limits_{i} \left( {\rho_{i} } \right),\, i = 1, 2, \ldots ,m.$$
(27)

Step 8: Compute the utility degree. Evaluate the order of importance \(\gamma_{i}\) of the optimum range 0–100% defined by

$$\gamma_{i} = \frac{{\rho_{i} }}{{\max (\rho_{i} )}} \times 100\% ,$$
(28)

where \({\rho }_{i}\) and \(\mathrm{max}{(\rho }_{i})\) are the relative weights computed using Eq. (26). The proposed COPRAS technique allows assessing the direct and proportional dependency of the degree of importance and the utility degree of the alternative in criteria set and weights (Fig. 1).

Fig. 1
figure 1

Flowchart of the PF-COPRAS method

Full size image

5 Application in healthcare waste treatment

In India, due to the regulations on Biomedical Waste Management and Handling Rules (1998), the healthcare waste management treatment is receiving much attention. The existing condition is studied based on various aspects such as extents and types of different waste, the ways of their handling, treatment, and disposal methods in some health care components. At numerous places, authorities are failing to set up appropriate systems due to the non-availability of suitable technologies, inadequate financial resources, and lack of vocational training on waste management. With the increasing perils associated with this HCWT and shortcomings in the existing method, it becomes very important to identify the best technique of management of these biomedical wastes. It is required to propose a waste-management scheme for the healthcare establishment, which has suitable technologies, institutional facilities, operational schemes, economic management, and preparation of suitable staff training programs. In this regard, we have proposed an MCDM technique for estimating and selecting HCWT alternatives using the COPRAS technique. We have evaluated, the criteria weights by utilizing the above-proposed Pythagorean fuzzy entropy and score function and decides the order of preferences of the HCWT alternatives based on the proposed method.

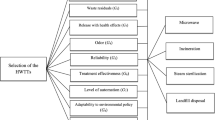
The various alternatives associated with the HCWT are as given as follows.

5.1 Steam sterilization

It is obtained by exposing the substances to be inactivated with saturated steam beneath the pressure. Increases the functionality of warmth to kill microorganisms with the aid of using decreasing time and temperature which had to denature the proteins in microorganisms.

5.2 Microwave disinfection

It is a procedure that sterilizes the waste with humid warmth and steam created with the aid of using microwave energy. It is a microwave medical waste treatment to destroy solids and other pathogenic organisms including bacteria, all liquids, peaked needles, and surgical equipment, as ensured by microwave approved biological indicators. Microwaves with a frequency of about 2450 MHz and a wavelength of 12.24 nm destroy most of the microorganisms.

5.3 Plasma pyrolysis

It is a revolutionary technology for transforming excessive calorific plastic waste into precious syngas via thermal plasma.

5.4 Chemical disinfection

It is a chemical process that is introduced to inactivate the pathogens present. This remedy system makes use of a chemical with NaOCl (Sodium Hypochlorite) as a disinfectant. Chemical disinfection is best suited for the treatment of liquid waste inclusive of blood, needles, and other sharp-edged things, urine, or hospital sewage, infectious glassware, which are first treated. However, solid wastes as well as microbiological cultures, body fluids, etc. can be disinfected with chemicals.

5.5 Incineration

It is an excessive warmth remedy technology used to convert waste substances into non-combustible residues and gases. Diverse factors, several of that rely upon local conditions, inhibit and reduce waste production. Although, this technique is extremely effective in eliminating all types of waste items, it produces large amount of poisonous gases which are perilous to public health; hence, employ or recycle waste as far as possible.

The above-defined alternatives are discussed based on the following criterion: Cost \(({\mathcal{Q}}_{1})\), Disposal cost \(({\mathcal{Q}}_{2})\), Energy consumption \({(\mathcal{Q}}_{3}),\) Treatment effectiveness \({(\mathcal{Q}}_{4}),\) Level of automation \({(\mathcal{Q}}_{5}),\) Need for skilled operators (\({\mathcal{Q}}_{6})\), Public acceptance \({(\mathcal{Q}}_{7})\), and the Land requirement (\({\mathcal{Q}}_{8})\).

To identify the best HCWT alternative, a team of four discussion experts of different areas is constituted. The ordered structure to select the HCW treatment method is given in Fig. 2. The procedural explanation for the execution of the PF-COPRAS method is described in detail as follows.

Fig. 2
figure 2

Structure to select HCWT method

Full size image

The linguistic terms for the relative performance rating of criteria are presented in Table 3. In Tables 4 and 5, the weight of each decision expert is computed using Eq. (21). The DEs have offered their opinion for the assessment of chosen alternatives on each criterion under the PFNs and are given in Tables 6 and 7 displayed.

Table 3 LT values for rating the expert’s performance
Full size table
Table 4 The evaluation of expert’s weights for LTs
Full size table
Table 5 Linguistic terms for the performance ratings of alternative
Full size table
Table 6 LTs calculation of performance of HCWT
Full size table
Table 7 Aggregated PF-decision matrix for HCWT
Full size table

APF-DM is based on the priorities of DEs, see Eq. (22). In Table 7, applying Eq. (9), the generalized improved score values are calculated. Then, we calculate the weights of the criteria by Eqs. (9), (10), and (23). The measurement of criteria’s weights is as follows:

$${\varpi }_{j}={\left(\begin{array}{c}0.1241, 0.1129, 0.1245, 0.1217,\\ 0.1330, 0.1247, 0.1344, 0.1246 \end{array}\right)}^{\mathrm{T}}.$$

Finally, using the PF-COPRAS technique on the evaluated weight’s, in Table 8, the preference order of each alternative is as \({\mathcal{L}}_{1}\,\succ\, {\mathcal{L}}_{2}\,{\succ\, \mathcal{L}}_{5}\,\succ\, {\mathcal{L}}_{3}\,\succ\, {\mathcal{L}}_{4}\)

Table 8 Ranking order of PF-COPRAS for HCWT alternative selection
Full size table

5.6 Result and discussion

Health care has become a very popular problem in today’s environment. It is very important to remove it and dispose of it properly. For disposing of the waste, many alternatives are available. It is our core responsibility to choose the best alternative. To obtain the best alternative, here, in this paper, we have developed a special technique as discussed above. The empirical results of the proposed technique give some vital insights concerning assessment criteria and the main alternative for the HCWT in India. As can be seen in Table 8, on the basis of waste residuals and their environmental impacts, the effectiveness of treatment \({\mathcal{L}}_{1}\) is the foremost significant. We found that among the existing options, \({\mathcal{L}}_{1}\) is the best available alternatives. Considering the results of this paper, the problem of waste health care treatment problem can be solved to a greater extent. It must not be ignored when selecting the best treatment technology for waste material. We also analyzed the performances of HCWT alternatives for the evaluation of every criterion. The ranking of the HCWT alternatives is displayed in Table 8. It may be seen that steam sterilization (\({\mathcal{L}}_{1}\)) ranked first concerning all the criteria, therefore, it is selected as the best HCWT alternative satisfying all the evaluation criteria.

5.7 Comparative study

Here, a comparison was done on the results achieved from the PF-COPRAS method with interval 2-tuple LVs based, distance measure based, integrated approach based on DEMATEL, IF-AHP technique, and integrated SWARA-ARAS methodology. In Table 9, our technique is compared with the predetermined techniques, and it can be concluded that the method developed by us is the best method. The method developed by us is in coordination with the predetermined method. The best alternative with respect to all the methodologies is same that is \({\mathcal{L}}_{1}\), which validates our method and prove that our method is in synchronization with the previous techniques. The comparative discussion displays the best alternative as \({\mathcal{L}}_{1}\) by PF-COPRAS technique which shows high conformity with these existing techniques. Next, if we draw our attention to the ranking order, then we will see that it is very spectacular.

Table 9 Comparison of ranking with various methods
Full size table

The last option from our method is chemical disinfection \({\mathcal{L}}_{4}\), which is really expensive and not suitable for the environment. We are all well aware of the consequences of this alternative. Hence, we can summarize the significance of the results of the proposed technique as follows: In the existing techniques, to tackle the ambiguity connected with MCDM problems, all the major aspects, i.e., the assessments of criteria, alternative over the criteria, and importance degrees of DEs are measured in the form of PFNs. While, in the developed approach, criteria weights are evaluated by the proposed entropy and improved score function-based formula, which indicates weights of higher accuracy and optimality.

  • The methods PF-SWARA-ARAS (Rani et al. 2020a, b, c, d) and PF-TOPSIS (Zhang and Xu 2014) and the proposed PF-COPRAS are presented in the references of PFS, in contrast to Hinduja and Pandey (2018) IFS while Lu et al. (2016) I2TLVs are used.

  • By the proposed PF-COPRAS technique, we have calculated criteria weights based on entropy and score function and experts’ opinions, leaving no room to ambiguity, while Zhang and Xu (2014) and Lu et al. (2016) process has been assumed. It specifies that for MCDM problems with large number of criteria or alternatives, the PF-COPRAS model may increase the operating capacity by some quantity and has better operability.

  • Zhang and Xu (2014) and Lu et al. (2016) TOPSIS procedures have used arithmetic operators to aggregate data, because we have done using arithmetic and geometric operators. In addition, the PF-COPRAS structure makes the computation process easy, and thus, the precision and consistency of the results are high.

  • PF-COPRAS outperforms PF-SWARA-ARAS in phrases of proficiency and effectiveness. In addition, PF-COPRAS is stronger and stable than PF-SWARA-ARAS (Rani et al. 2020a, b, c, d) in phrases of parameter weight variation.

  • The decision delivered by PF-COPRAS is more accomplished and less biased than the PF-TOPSIS (Zhang and Xu 2014) decisions.

6 Conclusion

The main objective of the present article is to propose an MCDM technique on PFS. In this regard, we first proposed a new entropy measure on PFS and discussed the validity of the proposed measure. The propose entropy measure on PFS is compared with the existing entropy measures on PFS. Then, the study of MCDM method is for estimating and selecting the best alternative using the COPRAS technique. In this, we have evaluated the criteria weights by utilizing the above-proposed Pythagorean fuzzy entropy and score function and decided the order of preferences of the alternatives based on the proposed method. In recent years, the selection of appropriate HCWT techniques has important anxiety in the management of HCW and is receiving more attention from researchers and industrialists. Selecting the optimum technology for HCWT using the MCDM problem is a complex and challenging task in developing countries for local government and non-government bodies. PFS plays a more resilient and efficient tool to handle such problems. Hence, we applied the proposed PF-COPRAS technique of solving the MCDM problem to obtain the best alternative in a HCWT technique. Further, the discussion of comparative study of the proposed techniques with the existing techniques is presented. Based on a comparison with existing techniques, it is worth stating that the PF-COPRAS technique delivers an ingenious computation with precise and efficient results for the outgrowth of MCDM problems with PF-information.

Hence, it is worth stating that the present article would help in the valuation of HCWT over the financial, social, methodological, and environmental aspects. The vital advancement of the HCWT policy needs effective manpower, including the proper education of health care employees and waste collecting workers. In addition, the patients and their attenders would likewise be well informed regarding the benefits of utilizing proper HCWT. Last but not the least, technological innovations, government policies, and their executions can also be utilized for better HCWT. In addition, we will enlarge the work by harmonizing objective and subjective knowledge concerning the weight of the criterion. Furthermore, we will also advise various MCDM such as COVID-19 precautionary measures, sustainable web-based applications, biomass crop selection, and so on to be evaluated by applying COCOSO, FUCOM, and MARCOS methods.