An integrated decision-making COPRAS approach to probabilistic hesitant fuzzy set information

Abstract

The paper aims to present an integrated approach to solve the decision-making problem under the probabilistic hesitant fuzzy information (PHFI) features, which is an extension of the hesitant fuzzy set. The considered PHFI not only allows multiple opinions, but also associates occurrence probability to each opinion, which increases the reliability of the information. Motivated by these features of PHFI, an approach is presented to solve the decision problem with partial known information about the attribute and expert weights. In addition, an algorithm for finding some missing values in the preference information is presented and stated their properties. Afterward, the Hamy mean operator has been used to aggregate the different collective information into a single one. Also, we presented a COPRAS method to the PHFI for ranking the given alternatives. The presented algorithm has been demonstrated through a case study of cloud vendor selection and its validity has been revealed by comparing the approach results with the several existing algorithm results.

Introduction

Hesitant fuzzy set (HFS) [1] is a promising extension to the classical fuzzy set that promotes multi-criteria decision-making (MCDM) with effective uncertainty management. Though the fuzzy sets and orthopairs have wide practical usage [2,3,4,5], HFS was generic and more flexible. Rodriguez et al. [6] made a detailed review on HFS and different approaches under HFS for MCDM. From the review, it is clear that the (i) HFS is a flexible preference structure with the ability to mitigate subjective randomness; (ii) also, HFS eases the experts’ preference elicitation behavior; and (iii) occurrence probability of each element is ignored. Driven by the claims made in the systematic review, Zhou and Xu [7] put forward a generalized structure called probabilistic hesitant fuzzy information (PHFI) that associates occurrence probability to each element. By doing so, the confidence of each element is obtained that acts as potential information for MCDM.

Let us consider an example of a beauty contest, where the judges/experts rate models (candidates) based on their walk & posture. For this, experts associate multiple membership grades to each model along with the respective confidence values, such as ${\rm Mod}_{1}=\left(\begin{array}{c}0.6|0.35\\ 0.45|0.40\end{array}\right)$, ${\rm Mod}_{1}=\left(\begin{array}{c}0.65|0.30\\ 0.5|0.50\end{array}\right)$, and ${\rm Mod}_{1}=\left(\begin{array}{c}0.7|0.45\\ 0.55|0.35\end{array}\right)$. Another example deals with rating IQ levels of school students, in which a teacher gives rating as ${Stu}_{1}=\left(\begin{array}{c}0.7|0.35\\ 0.6|0.50\end{array}\right)$, and ${Stu}_{2}=\left(\begin{array}{c}0.8|0.40\\ 0.5|0.60\end{array}\right)$. According to the PHFI structure, it is seen that expert can not only give multiple membership grades or preference grades, but also associate confidence value to each grade. This flexible style and generalization along with the structural strength that allows association of occurrence probability with each grade is the main advantage of PHFI that is lacking in other HFS variants [8,9,10,11]. For ease of understanding the semantics, ${1}=\left(\begin{array}{c}0.65|0.30\\ 0.5|0.50\end{array}\right)$ infers that an expert rates ${\rm Mod}_{1}$ as 50% or 65% preferable with occurrence probability (confidence) of 50% and 30%, respectively. Driven by the flexibility of PHFI, many researchers applied the information for MCDM. Zhou and Xu [12] extended value at risk concept to PHFI and evaluated stocks in China. Zhou and Xu [13] also proposed a new uncertain PHFI structure for stock assessment with the help of integrated decision model. Gao et al. [14] solved emergency decision situation that involves uncertainty and dynamism with the help of dynamic referencing approach under PHFI context by developing a novel expectation measure to cope with the evolutionary and dynamic factors. Zhou and Xu [15] further determined consistency and repaired inconsistent PHFI-based relations iteratively based on judgment principle and expected consistency index. Also optimization model is formulated for probability calculation of preference relations with PHFI and used the framework for research candidate selection. Wang and Li [16] introduced correlation measures to PHFI and assessed commodities for investment. Li et al. [17] selected research candidate based on outranking methods under PHFI environment by extending PROMETHEE and QUALIFLEX approaches. Ding et al. [18] made an interactive decision framework by developing new axiomatic distance measure that is used in the formulation of PHFI-based mathematical model. Positive and negative ideal solutions are determined with PHFI and the model is used for solving project selection under virtual reality domain. Zhang et al. [19] provided an improvement of PHFI structure and presented some properties along with their proofs. Some aggregation operators are proposed for this improved structure and its continuous domain variants are also presented and industrial safety in automobile sector is evaluated. Wu et al. [20] made an integrated model with GM (1, 1) to predict information for decision process. Later, distance measure with hesitation degree is put forward along with mathematical model for weight estimation and risk in coal mines are evaluated using TOPSIS method with PHFI for making emergency decision.

Hao et al. [21] proposed a variant of PHFI called probabilistic dual hesitant fuzzy set (PDHFS) that considers both degree of membership and non-membership in multiple grades and put forward a new framework with aggregation operator and entropy measure for risk evaluation in the Artic zone. Tian et al. [22] evaluated funding of venture capitals in the form of sequential investment based on a consensus model by developing a decision index system with Prospect consensus model under PHFI structure. Li and Wang [23] developed prioritized operators under arithmetic and geometric contexts for aggregation and ranking of faculties for a Chinese university in the management department. They also discussed the fundamental properties nad the relationship between arithmetic/geometric operators. Bashir et al. [24] integrated preference relations to PHFI and designed algorithms of consistency measures and consensus reaching that was used them for group decision-making. Recently, Song et al. [25] created a clustering algorithm based on two correlation measures that helps in understanding the relationship between PHFI and validated the usefulness through synthetic/real time experiments. Garg & Kaur [26] developed new correlation measures and weighted variants by introducing new informational energy and covariance measures under PDHFS context that was utilized for personnel selection. Li et al. [27] integrated a framework with dominance degree and best–worst method for investor assessment by presenting a new density function that supported the construction of dominance matrix, which was in turn used in the formulation of best–worst approach. He and Xu [28] proposed reference ideal based distance and ranking methods by identifying the relationship between ideal values and PHFI that were further used in the assessment of water saving projects. Garg and Kaur [29] also extended Maclaurin mean operator to PDHFS for gesture understanding in brain hemorrhage situations. Farhadinia et al. [30] proposed new correlation measures along with its theoretical base and evaluated strategies. Liu et al. [31] developed an integrated approach with PHFI using entropy measure and regret theory for venture capital investment assessment. Li et al. [32] put forward an ORESTE-based approach with PHFI by making use of new distance measure for choosing apt research topic. Farhadinia and Herrera-Viedma [33] fine-tuned the PHFI and developed theoretical base for the same by introducing operational laws and evaluating safety of industries in automobile sector. Li et al. [34] made a consensus model with PHFI by introducing normalized PHFI for candidate selection and evaluation. Lin et al. [35] measured consistency and repaired inconsistent preferences with newly proposed algorithms under PHFI context and adopted the model for decisions on investment projects. Jin et al. [36] developed a new consistency check and adjustment measure for preference relations with PHFI and used DEA approach for logistics selection. Guo et al. [37] developed a Choquet integral-based TODIM approach with PHFI for rational selection of sites of CO₂ storage.

The literature review helped in identification of potential research challenges that could be mitigated by novel contributions whose intuitions are inspired from the literatures and cognition. As there is limited amount of time and domain knowledge, experts may not be comfortable with preference elicitation for each alternative over a specific criterion. This causes missing values in the preference matrices that must be methodically imputed before further processing. Binning methods [38] from data mining provided the intuition for imputation. Similarly, weights of experts and criteria must be calculated to avoid subjective bias and inaccuracies in MCDM. Works from Kao [39] and Koksalmis and Kabak [40] provides intuition for methodical weight calculation of criteria and experts, respectively. Besides, the partial information can be effectively utilized by formulating mathematical models that depict the partial weight information as inequality constraints. Moreover, inter dependencies among experts need to be rationally captured for proper aggregation of preferences, which offered intuition for proposing HM operator [41] to aggregate PHFI. Finally, COPRAS [42] is a popular and powerful ranking method that actively considers the nature of criteria by handling preferences from different angles along with consideration to direct and proportional alternatives’ relationship [43].

Based on the review conducted above, certain research challenges are encountered. Firstly, extant decision models with PHFI do not consider missing values during MCDM. But, these are common phenomenon owing to the implicit hesitation/pressure that experts face during MCDM. Secondly, when partial information about the importance of experts and criteria are available, it becomes a critical challenge to use the information effectively, which is lacking in extant PHFI-based models. Further, inter dependencies among experts are not captured rationally in the extant models during aggregation of PHFI. Finally, ranking of alternatives from different angles with apt consideration to nature of criteria is lacking in the extant PHFI-based models.

Driven by these research challenges, some novel contributions are put forward to mitigate the challenges and they are:

• 1. Hesitation/confusion is common in practical MCDM and so missing values occur in preference matrices and they can be effectively imputed by proposing weighted averaging technique. The rationale behind weighted average approach is that it helps in retaining the PHFI structure of the imputed value and also grants flexibility to the experts to express their personal opinion on each alternative.

• 2. Due to dilemma, partial information on the importance of each criterion and experts are possible, which can be utilized efficiently by proposing mathematical models. Unlike the direct elicitation of weights, methodical calculation reduces subjective biases and inaccuracies, which are driven by the claims from Kao [39] and Koksalmis & Kabak [40].

• 3. Experts participating in MCDM tend to reflect some inter dependencies in their views/opinions that can be rationally captured by extending Hamy mean (HM) operator to PHFI. The intuition behind using the operator is that it is generic in nature and also considers both the weights and risk appetite values of experts that aids in rational aggregation of information.

• 4. Finally, popular COPRAS (complex proportional assessment) method is extended to PHFI for ranking alternatives by properly considering the nature of criteria and offering decision from different angles based on the complex proportional factors. Zheng et al. [43] rightly pointed out these features that motivated our research focus in this direction.

The rest of the paper is constructed in the following fashion. Basic concepts are of HFS and PHFI are reviewed in “Preliminaries”. Core contribution of this paper is presented in “Novel decision model with PHFEs”, where the procedure for each method is provided step wise. A numerical example is presented in “Numerical example” to aid in demonstrating the usefulness of the framework. Results are compared with extant models in “Comparative investigation—proposed vs. other models” to discuss the merits and limitations of the work. Finally, concluding remarks with future research scope is provided in “Conclusion and future directions”.

Preliminaries

It is essential to note some basics of HFEs and PHFEs before presenting the proposed methodologies.

Definition 1

[1]: Consider $T$ as a fixed set, an HFS on $T$ is a function $h$ which yields a subset with values in the range 0 to 1. Mathematically,

$$\overline{T }=\left\{\left(t,{h}_{\overline{T }}\left(t\right)\right)|t\in T\right\}$$

(1)

where ${h}_{\overline{T }}\left(t\right)$ has values in the range 0 to 1 and they represent the membership grade of $t\in T$.

Definition 2

[7]: $T$ is as before, an PHFS on $T$ is a pair and it is given by,

$${T}_{p}=\left\{\left(t,{h}_{{T}_{p}}\left({\gamma }_{i}|{p}_{i}\right)\right)|t\in T\right\}$$

(2)

where ${h}_{{T}_{p}}\left({\gamma }_{i}|{p}_{i}\right)$ is a pair with membership grade and occurrence probability associated with the grade for $z$ on the set ${T}_{p}$, $0\le {\gamma }_{i}\le 1$, $0\le {p}_{i}\le 1$ and $\sum_{i}{p}_{i}\le 1$.

Note 1 Sum of occurrence probability is less than or equal to unity due to the idea of partial ignorance. By normalization, sum is brought to unity. Let ${{h}_{{T}_{p}}\left({\gamma }_{i}|{p}_{i}\right)=h}_{i}=\left({\gamma }_{i}^{k}|{p}_{i}^{k}\right)$ be a probabilistic hesitant fuzzy element (PHFE) with $k= {1,2},\dots ,\#{h}_{i}$ and such PHFE constitutes a PHFS.

Definition 3

[7]: Consider two PHFEs ${h}_{1}$ and ${h}_{2}$ as in Note 1. Some arithmetic operations are,

$${h}_{\mathrm{c}}\oplus{h}_{\mathrm{d}}={ \cup }_{c= {1,2},\dots \#{h}_{c}, d= {1,2},\dots ,\#{h}_{d}}\left\{{\gamma }_{c}+{\gamma }_{d}-{\gamma }_{c}{\gamma }_{d}|{p}_{c}{p}_{d}\right\}$$

(3)

$${h}_{c} {h}_{d}={\cup }_{\mathrm{c}={1,2},\dots \#{h}_{c},d={1,2},\dots ,\#{h}_{d}}\left\{{\gamma }_{c}{\gamma }_{d}|{p}_{c}{p}_{d}\right\}$$

(4)

$${h}_{c}^{\lambda }={\cup }_{\mathrm{c}={1,2},\dots \#{h}_{c}}\left\{{\left({\gamma }_{c}\right)}^{\lambda }|{p}_{c}\right\} \lambda \ge 0$$

(5)

$${h}_{d}^{cc} = {\cup }_{d={1,2},\dots \#{h}_{d}}\left\{\left(1-{\gamma }_{d}\right)|{p}_{d}\right\}$$

(6)

$$\lambda {h}_{c}={\cup }_{\mathrm{c}={1,2},\dots \#{h}_{c}}\left\{1-{\left(1-{\gamma }_{c}\right)}^{\lambda }|{p}_{c}\right\} \lambda \ge 0$$

(7)

Equations (3–7) show the addition, multiplication, power operation, complement, and scalar multiplication, respectively. Some interesting properties of these operations can be found in [7].

Novel decision model with PHFEs

This is the core section that proposes new methods under PHFS context that are integrated to form a decision model for MCDM.

Imputation of non-available entries

This section focuses on presenting a new and elegant approach for imputing values that are missing in the preference matrices. In the process of MCDM, experts provide their preferences that are formulated into a matrix called the preference/decision matrix. This matrix represents the choice/opinion that an expert makes on an alternative based on a criterion. Due to hesitation, confusion, and pressure, experts may not be able to provide all values in the matrices. This causes missing values that must be imputed methodically to avoid inaccuracies in MCDM.

Previous studies on PHFS have clearly ignored the missing values and assumed that the matrices are complete, which is not possible in practical cases. Driven by the assumption and to alleviate the issue, in this section, missing (non-available) values are considered and they are imputed methodically using Eq. (8).

$${h}_{\mathrm{miss}}=\left\{\begin{array}{c}\left({\oplus}_{i=1}^{mm}\left(1-{\left(1-{\gamma }_{ij}^{k}\right)}^{{\zeta }_{i}^{l}}\right)|{\oplus}_{i=1}^{mm}\left(1-{\left(1-{p}_{ij}^{k}\right)}^{{\zeta }_{i}^{l}}\right)\right) ; Scheme A\\ \left({\oplus}_{l=1}^{qq}\left(1-{\left(1-{\gamma }_{ij}^{k}\right)}^{{\zeta }_{i}^{l}}\right)|{\oplus}_{i=1}^{qq}\left(1-{\left(1-{p}_{ij}^{k}\right)}^{{\zeta }_{i}^{l}}\right)\right) ; Otherwise\end{array}\right.$$

(8)

where $mm$ denotes the number of alternatives with PHFEs, ${\zeta }_{i}^{l}$ is the normalized relative importance of the ${i}^{{\rm th}}$ alternative (values available) for the ${l}^{\rm th}$ expert, and $qq$ denotes the number of experts with PHFEs in a specific $\left(i,j\right)$ position.

$\mathrm{Scheme} A$ – The equation is applied when at least two alternatives are present for a particular criterion.

$\mathrm{Otherwise}$ – The equation is applied when the values for the entire criterion is missing from a particular expert. When there is one element per criterion, repeat the element to all other non-available rows.

It must be noted that the values for ${\zeta }_{i}^{l}$ are in the unit interval that depicts the relative importance of the ${i}^{\rm th}$ alternative by the ${l}^{\rm th}$ expert. These are personal opinions on each alternative by the experts, which is potential information in determining the missing values as it influences the preference information from an expert. We generally get this vector from experts and normalize the same before applying the weights to Eq. (8). Experts are given equal importance during imputation process.

Theorem 1

The values that are imputed by Eq. (8) are PHFEs.

Proof

From Definition 2, it is evident that the PHFEs have two components viz., the HFE and the probability associated with the HFE. It is well known that these values are in the unit interval and the $\sum_{k}{p}_{ij}^{k}\le 1$. Equation (8) adopts the base formulation of scalar multiplication of PHFEs with idea of addition of PHFEs. Hence, from Eq. (8), it is obvious that the resultant value is an PHFE.

Some typical merits of the imputation method are (i) it is simple and straightforward; (ii) it considers relative importance of each alternative by obtaining personal opinions from experts; and (iii) it does not force the experts to confine their relative importance values to the constraint of sum equals to unity, which thereby promotes flexibility and allows experts to share their opinions effectively.

Mathematical model for expert weight estimation

This section focuses on presenting a new mathematical model for determining the weight vector of experts based on the partial weight information provided the officials who constitute the expert panel. It must be noted that weights are either calculated with fully unknown information or partially known information. The former situation is applicable when the information is unavailable or not presentable. But, when partial information is provided, it is important to use the information effectively for weight calculation. As mentioned earlier, Koksalmis & Kabak [40] strongly argued on the importance of methodical weight calculation of experts, which eventually reduces bias and inaccuracies.

Driven by the claim, in this section, an optimization model is put forward that considers the available partial information as useful component and formulates them as inequality constraints. So, a constrained optimization model is proposed, which is solved using MATLAB® optimization toolbox.

Model 1:

$$\mathrm{Min }Z=\sum_{l=1}^{q}{\eta }_{l}\sum_{i=1}^{m}\sum_{j=1}^{n}\left(d\left({h}_{ij},{h}_{j}^{+}\right)-d\left({h}_{ij},{h}_{j}^{-}\right)\right)$$

Subject to

$${0\le \eta }_{l}\le 1; \sum_{l=1}^{q}{\eta }_{l}=1$$

In Model 1, ${h}_{j}^{+}$ is the positive ideal solution (PIS) of the ${j}^{\rm th}$ criterion, ${h}_{j}^{-}$ is the negative ideal solution (NIS) of the ${j}{\rm th}$ criterion, and $d(a1,b1)$ is the distance between any two PHFEs $a1$ and $b1$.

$${h}_{j}^{+}={\rm max}_{j\in BT}\left(\sum_{k}{\gamma }_{ij}^{k}.{p}_{ij}^{k}\right) or {\rm min}_{j\in CT}\left(\sum_{k}{\gamma }_{ij}^{k}.{p}_{ij}^{k}\right)$$

(9)

$${h}_{j}^{-}={\rm min}_{j\in BT}\left(\sum_{k}{\gamma }_{ij}^{k}.{p}_{ij}^{k}\right) or {\rm max}_{j\in CT}\left(\sum_{k}{\gamma }_{ij}^{k}.{p}_{ij}^{k}\right)$$

(10)

where $BT$ is the benefit type criterion and $CT$ is the cost type criterion.

Readers must note that Eqs. (9, 10) yields a single-valued entity for each criterion. But, we need to consider the PHFE that corresponds to the respective single-valued entity. Hence, Eqs. (9, 10) yields a vector each of order $1\times n$ that contains PHFEs.

$$d\left(a1,b1\right)=\sqrt{\sum_{k=1}^{\#h}{\left({\gamma }_{ij}^{k(a1)}.{p}_{ij}^{k(a1)}-{\gamma }_{ij}^{k\left(b1\right)}.{p}_{ij}^{k(b1)}\right)}^{2}}$$

(11)

Equation (11) is applied to formulate the objective function in Model 1. Some advantages of the proposed expert weight calculation model are (i) it is methodical and adheres to the argument of Koksalmis and Kabak [40]; (ii) it makes efficient use of the partial information for rational weight calculation.

Mathematical model for criteria weight determination

This section focuses on a new mathematical model for criteria weight calculation with PHFEs. Inspired by the claim from Kao [39], in this section, a methodical approach is presented. The mathematical model adopts Euclidean distance norm for formulating the objective function. Commonly, criteria weights are determined either using partial information or under fully unknown information context. Popular methods under the latter part are entropy methods [44], step-wise weight assessment ratio analysis [45], and analytical hierarchy process [46]. But, these methods lack the ability to utilize partial information on each criterion for weight determination.

To alleviate the issue, a new category of weight calculation with partial information is put forward. Mathematical models are proposed to properly consider the partial information during weight calculation. Driven by the claim, in this section, a new model is put forward that makes use of the partial information as inequality constraints. A constrained optimization model is developed that is solved using the optimization toolbox of MATLAB®.

Model 2:

$$\mathrm{Min }Z=\sum_{j=1}^{n}{cwt}_{j}\sum_{l-1}^{q}\left(d\left({h}_{lj},{h}_{j}^{+}\right)-d\left({h}_{lj},{h}_{j}^{-}\right)\right)$$

Subject to

$${0\le cwt}_{j}\le 1; \sum_{j=1}^{n}{cwt}_{j}=1$$

Equations (9–11) are used for calculating the PIS, NIS, and distance measure. Some advantages of Model 2 are (i) it is simple and straightforward; (ii) it accepts partial information as inequality constraints for better determination of weights; and (iii) weights of criteria are determined by considering the nature of criteria that promotes rational weight calculation.

PHFS-based Hamy mean operator

This section focuses on a new extension to the Hamy mean (HM) operator under PHFS context for aggregation of PHFI. HM operator [41] is a popular aggregation operator that is a generalized version of different arithmetic and geometric mean operators along with its weighted variants. It must be noted that the HM operator adheres to monotonicity, idempotency and bounded properties as per the base formulation of weighted HM. Thus, the operator is said to be Schnur convex in nature and considers risk appetite factor in the context of group decision-making. HM operator yields arithmetic mean and geometric mean operators as special cases, when $g=1$ in Eq. (12), the operator transforms to arithmetic mean and when $g=q$, the operator proposed in Eq. (12) transforms to geometric mean. In general, operators defined in [7] under PHFI context are special cases of the operator proposed in this section. Apart from the advantage of generalization, the HM operator also considered risk appetite values of experts along with the relative importance, which intuitively aided in rational aggregation of information. Specifically, it is observed that as value of $g=1$, the experts attitude is towards risk aversion compared to when $g=q$.

Recently researchers explored HM operator under different fuzzy structures such as orthopair fuzzy sets [47,48,49,50] with their variants [51,52,53], HFSs [54] with its variants [55] and used the same for decision-making. Inspired by the flexibility and generic nature of HM operator, motivation is gained and in this section, a new extension is put forward.

Definition 4

Aggregation of PHFI using $\mathrm{{\rm PHFWHM}}$ operator is a mapping from ${H}^{l}\to H$ and is given by,

$${\mathrm{{\rm PHFWHM}}}^{g}\left({h}_{1},{h}_{2},\dots ,{h}_{q}\right)=\left(\begin{array}{c}{\left(1-\prod_{l=1}^{q}{\left(1-\prod_{ll=1}^{g}{\left({\gamma }_{ij}^{k}\right)}^{\left(\frac{\left(\begin{array}{c}q\\ g\end{array}\right)}{g}\right)}\right)}^{{\eta }_{l}}\right)}^{\frac{1}{\sum_{ll}\left(\frac{\left(\begin{array}{c}q\\ g\end{array}\right)}{g}\right)}}|\\ {\left(1-\prod_{l=1}^{q}{\left(1-\prod_{ll=1}^{g}{\left({p}_{ij}^{k}\right)}^{\left(\frac{\left(\begin{array}{c}q\\ g\end{array}\right)}{g}\right)}\right)}^{{\eta }_{l}}\right)}^{\frac{1}{\sum_{ll}\left(\frac{\left(\begin{array}{c}q\\ g\end{array}\right)}{g}\right)}}\end{array}\right)$$

(12)

where $g$ is a risk appetite parameter that can take values ${1,2},\dots ,q$, ${\eta }_{l}$ is the weight of the ${l}{\rm th}$ expert, and $\left(\begin{array}{c}q\\ g\end{array}\right)=\frac{q!}{g!\left(q-g\right)!}$. The weights of experts used in Eq. (12) are calculated by solving Model 1 proposed in “Mathematical model for expert weight estimation”. Let us discuss some properties of ${\rm PHFWHM}$ operator.

Theorem 2

The proposed $\mathrm{{PHFWHM}}$ operator satisfies the idempotent, commutative, monotonicity, and bounded properties.

(Idempotent)—For all ${h}_{l}=h$ where $l={1,2},\dots ,q$; ${\mathrm{{PHFWHM}}}^{g}\left({h}_{1},{h}_{2},\dots ,{h}_{q}\right)=h$.

(Commutative)—For any permutation of ${h}_{l}$; ${\mathrm{{PHFWHM}}}^{g}\left({h}_{1},{h}_{2},\dots ,{h}_{q}\right)={\mathrm{{ PHFWHM}}}^{g}\left({h}_{1}^{*},{h}_{2}^{*},\dots ,{h}_{q}^{*}\right)$.

(Bounded) – If ${h}^{\rm min}={\rm min}_{l}\left({h}_{l}\right)$ and ${h}^{\rm max}={\rm max}_{l}\left({h}_{l}\right)$ for all $l={1,2},\dots ,q$; then ${h}^{\rm min}\le {{\rm PHFWHM}}^{g}\left({h}_{1},{h}_{2},\dots ,{h}_{q}\right)\le {h}^{\rm max}$.

(Monotonicity) – Let ${h}_{l}^{{^{\prime\prime}}}$ be a new set of PHFEs such that ${h}_{l}^{{^{\prime\prime}}}\le {h}_{l}$ for all $l={1,2},\dots ,q$. Then, ${{\rm PHFWHM}}^{g}\left({h}_{1},{h}_{2},\dots ,{h}_{q}\right)\ge {{\rm PHFWHM}}^{g}\left({h}_{1}^{{^{\prime\prime}}},{h}_{2}^{{^{\prime\prime}}},\dots ,{h}_{q}^{{^{\prime\prime}}}\right)$.

Proof

(Idempotent).

$${{\rm PHFWHM}}^{g}\left({h}_{1},{h}_{2},\dots ,{h}_{q}\right)=\left(\begin{array}{c}{\left(1-\prod_{l=1}^{q}{\left(1-\prod_{ll=1}^{g}{\left({\gamma }_{ij}^{k}\right)}^{\left(\frac{\left(\begin{array}{c}q\\ g\end{array}\right)}{g}\right)}\right)}^{{\eta }_{l}}\right)}^{\frac{1}{\sum_{ll}\left(\frac{\left(\begin{array}{c}q\\ g\end{array}\right)}{g}\right)}}|\\ {\left(1-\prod_{l=1}^{q}{\left(1-\prod_{ll=1}^{g}{\left({p}_{ij}^{k}\right)}^{\left(\frac{\left(\begin{array}{c}q\\ g\end{array}\right)}{g}\right)}\right)}^{{\eta }_{l}}\right)}^{\frac{1}{\sum_{ll}\left(\frac{\left(\begin{array}{c}q\\ g\end{array}\right)}{g}\right)}}\end{array}\right)$$

Since PHFEs are equal;

$$=\left(\begin{array}{c}{\left(1-\prod_{l=1}^{q}{\left(1-\prod_{ll=1}^{g}{\left({\gamma }_{ij}^{k}\right)}^{\left(\frac{\left(\begin{array}{c}q\\ g\end{array}\right)}{g}\right)}\right)}^{{\eta }_{1}+{\eta }_{2}+\dots {\eta }_{l}}\right)}^{\frac{1}{\sum_{ll}\left(\frac{\left(\begin{array}{c}q\\ g\end{array}\right)}{g}\right)}}|\\ {\left(1-\prod_{l=1}^{q}{\left(1-\prod_{ll=1}^{g}{\left({p}_{ij}^{k}\right)}^{\left(\frac{\left(\begin{array}{c}q\\ g\end{array}\right)}{g}\right)}\right)}^{{\eta }_{1+{\eta }_{2}+\dots {\eta }_{l}}}\right)}^{\frac{1}{\sum_{ll}\left(\frac{\left(\begin{array}{c}q\\ g\end{array}\right)}{g}\right)}}\end{array}\right)$$

As experts’ weights add up to unity, we obtain

$$=\left({\left(\prod_{ll=1}^{g}{\left({\gamma }_{ij}^{k}\right)}^{\left(\frac{\left(\begin{array}{c}q\\ g\end{array}\right)}{g}\right)}\right)}^{\frac{1}{\sum_{ll}\left(\frac{\left(\begin{array}{c}q\\ g\end{array}\right)}{g}\right)}}|{\left(\prod_{ll=1}^{g}{\left({p}_{ij}^{k}\right)}^{\left(\frac{\left(\begin{array}{c}q\\ g\end{array}\right)}{g}\right)}\right)}^{\frac{1}{\sum_{ll}\left(\frac{\left(\begin{array}{c}q\\ g\end{array}\right)}{g}\right)}}\right)=\left({\gamma }_{ij}^{k}|{p}_{ij}^{k}\right)=h$$

(Monotonicity)

Let ${h}^{{{\prime}}{{\prime}}}$ be an aggregated PHFE that is obtained by aggregating ${h}_{l}^{{{\prime\prime}}}$ for all $l={1,2},\dots .,q$. Similarly, $h$ is an aggregated PHFE obtained from the aggregation of ${h}_{l}$ for all $l={1,2},\dots .,q$. Measures such as score and deviation are adopted from [7] and it is observed that $s\left({h}_{l}\right)\ge s\left({h}_{l}^{{{\prime\prime}}}\right)$ and if $s\left({h}_{l}\right)=s\left({h}_{l}^{{{\prime\prime}}}\right)$, $d\left({h}_{l}\right)\le d\left({h}_{l}^{{{\prime\prime}}}\right)$ as ${h}_{l}\ge {h}_{l}^{{{\prime\prime}}}$ for all $l={1,2},\dots ,q$. Extending the idea further, we get, $s\left(h\right)\ge s\left({h}^{{{\prime\prime}}}\right)$ and when $s\left(h\right)=s\left({h}^{{{\prime\prime}}}\right)$, $d\left(h\right)\le d\left({h}^{{{\prime\prime}}}\right)$. Thus, ${\mathrm{{\rm PHFWHM}}}^{g}\left({h}_{1},{h}_{2},\dots ,{h}_{q}\right)\ge {\mathrm{{\rm PHFWHM}}}^{g}\left({h}_{1}^{{{\prime\prime}}},{h}_{2}^{{{\prime\prime}}},\dots ,{h}_{q}^{{{\prime\prime}}}\right)$

(Commutative)

Since ${h}_{l}^{*}$ is any permutation of ${h}_{l}$ for all $l={1,2},\dots ,q$; ${{\rm PHFWHM}}^{g}\left({h}_{1}^{*},{h}_{2}^{*},\dots ,{h}_{q}^{*}\right)=\left(\begin{array}{c}{\left(1-\prod_{l=1}^{q}{\left(1-\prod_{ll=1}^{g}{\left({\gamma }_{ij}^{*k}\right)}^{\left(\frac{\left(\begin{array}{c}q\\ g\end{array}\right)}{g}\right)}\right)}^{{\eta }_{l}}\right)}^{\frac{1}{\sum_{ll}\left(\frac{\left(\begin{array}{c}q\\ g\end{array}\right)}{g}\right)}}|\\ {\left(1-\prod_{l=1}^{q}{\left(1-\prod_{ll=1}^{g}{\left({p}_{ij}^{*k}\right)}^{\left(\frac{\left(\begin{array}{c}q\\ g\end{array}\right)}{g}\right)}\right)}^{{\eta }_{l}}\right)}^{\frac{1}{\sum_{ll}\left(\frac{\left(\begin{array}{c}q\\ g\end{array}\right)}{g}\right)}}\end{array}\right)=\left(\begin{array}{c}{\left(1-\prod_{l=1}^{q}{\left(1-\prod_{ll=1}^{g}{\left({\gamma }_{ij}^{k}\right)}^{\left(\frac{\left(\begin{array}{c}q\\ g\end{array}\right)}{g}\right)}\right)}^{{\eta }_{l}}\right)}^{\frac{1}{\sum_{ll}\left(\frac{\left(\begin{array}{c}q\\ g\end{array}\right)}{g}\right)}}|\\ {\left(1-\prod_{l=1}^{q}{\left(1-\prod_{ll=1}^{g}{\left({p}_{ij}^{k}\right)}^{\left(\frac{\left(\begin{array}{c}q\\ g\end{array}\right)}{g}\right)}\right)}^{{\eta }_{l}}\right)}^{\frac{1}{\sum_{ll}\left(\frac{\left(\begin{array}{c}q\\ g\end{array}\right)}{g}\right)}}\end{array}\right)={{\rm PHFWHM}}^{g}\left({h}_{1},{h}_{2},\dots ,{h}_{q}\right)$

(Bounded)

From idempotent property, it is clear that ${h}^{\rm min}={{\rm PHFWHM}}^{g}\left({h}^{\rm min},{h}^{\rm min},\dots ,{h}^{\rm min}\right)$ and ${h}^{\rm max}={{\rm PHFWHM}}^{g}\left({h}^{\rm max},{h}^{\rm max},\dots ,{h}^{\rm max}\right)$. Let $h={{\rm PHFWHM}}^{g}\left({h}_{1},{h}_{2},\dots ,{h}_{q}\right)$ be an aggregated PHFE. From monotonicity property, ${{\rm PHFWHM}}^{g}\left({h}^{\rm min},{h}^{\rm min},\dots ,{h}^{\rm min}\right)\le h$ and ${{\rm PHFWHM}}^{g}\left({h}^{\rm max},{h}^{\rm max},\dots ,{h}^{\rm max}\right)\ge h$. Thus,${h}^{\rm min}\le {{\rm PHFWHM}}^{g}\left({h}_{1},{h}_{2},\dots ,{h}_{q}\right)\le {h}^{\rm max}$

Theorem 3

When PHFEs are aggregated using ${\rm PHFWHM}$ operator, the resultant value is also an PHFE.

Proof

From Theorem 2, it is evident that the ${\rm PHFWHM}$ operator satisfies bounded property. By extending the property further to a general scenario, we get, ${(h}^{\rm min}=0)\le \left(\begin{array}{c}{\left(1-\prod_{l=1}^{q}{\left(1-\prod_{ll=1}^{g}{\left({\gamma }_{ij}^{k}\right)}^{\left(\frac{\left(\begin{array}{c}q\\ g\end{array}\right)}{g}\right)}\right)}^{{\eta }_{l}}\right)}^{\frac{1}{\sum_{ll}\left(\frac{\left(\begin{array}{c}q\\ g\end{array}\right)}{g}\right)}}|\\ {\left(1-\prod_{l=1}^{q}{\left(1-\prod_{ll=1}^{g}{\left({p}_{ij}^{k}\right)}^{\left(\frac{\left(\begin{array}{c}q\\ g\end{array}\right)}{g}\right)}\right)}^{{\eta }_{l}}\right)}^{\frac{1}{\sum_{ll}\left(\frac{\left(\begin{array}{c}q\\ g\end{array}\right)}{g}\right)}}\end{array}\right)\le {(h}^{\rm max}=1)$. Thus, ${(h}^{\rm min}=0)\le {{\rm PHFWHM}}^{g}\left({h}_{1},{h}_{2},\dots ,{h}_{q}\right)\le {(h}^{\rm max}=1)$. Further, it must be noted that $\sum_{k}{p}_{ij}^{k}\le 1$ for the aggregated value as the inputs hold this inequality. This clearly shows that the aggregated value is also an PHFE.

New extension to COPRAS method

This section focuses on presenting a new extension to the popular COPRAS method under PHFS context. The genesis for COPRAS method was made in [56] that led to increasing usage of COPRAS in MCDM. Zavadskas et al. [42] selected dwelling equipment for the project using COPRAS method. Zavadskas et al. [57] assessed contractors with an integrated gray-COPRAS approach under uncertain context. Gorabe et al. [58] made a methodical selection of industrial robots using COPRAS approach. Yazdani et al. [59] developed an integrated model with QFD and COPRAS for assessment of green suppliers. Zheng et al. [43] assessed the severity of the pulmonary disease by adopting COPRAS to hesitant linguistic preferences. Vahdani et al. [60] evaluated robots under interval valued fuzzy context with COPRAS approach. Mousavi et al. [61] analyzed the efficacy of COPRAS approach for auxiliary tool selection by comparison with other MCDM methods. Chatterjee et al. [62, 63] performed methodical selection of materials by adopting COPRAS method. Valipour et al. [64] assessed risk in excavation projects in Iran by adopting SWARA-COPRAS combination under uncertain situations. Nguyen et al. [65] presented AHP with COPRAS under fuzzy context for machine tool selection. Ayrim et al. [66] selected cargo company based on new stochastic COPRAS approach. Mardani et al. [67] reviewed different utility functions/methods to better understand the efficacy of COPRAS method in comparison to other methods. Recently, Roy et al. [68] evaluated hotels-based on web data by extending COPRAS to rough numbers. Ramadass et al. [69] evaluated cloud vendors for an organization using COPRAS method under linguistic preference context. Krishankumar et al. [70] put forward a new framework with COPRAS under double hierarchy linguistic information for green supplier selection. Rani et al. [71] made an assessment of suppliers based on sustainable factors using SWARA-COPRAS combination under HFS.

Based on the literature review made above, it is clear that COPRAS is an interesting and flexible approach for MCDM. Moreover, Zheng et al. [43] rightly pointed out the superiority of COPRAS method as (i) simple and straightforward approach; (ii) considers the nature of criteria for better ranking of alternatives; (iii) offers ranking from different angles based on the calculation of complex proportional factors; and (iv) final ranking of alternatives is influenced by strategy values that associates degree of importance to the types of criteria. Driven by these advantages of COPRAS approach, a step-wise procedure for ranking alternatives with PHFI is given below.

Step 1: Collect the weight vector of the criteria and the aggregated matrix by applying the proposed methods from “Mathematical model for criteria weight determination” and “PHFS-based Hamy mean operator”, respectively.

Step 2: Identify the benefit and cost types of the criteria and apply Eqs. (13, 14) to determine the COPRAS parameters.

$${R1}_{i}^{k}={\oplus}_{j=1}^{B}\left(1-{\left(1-{\gamma }_{ij}^{k}\right)}^{{cwt}_{j}}|1-{\left(1-{\gamma }_{ij}^{k}\right)}^{{cwt}_{j}}\right)$$

(13)

$${R2}_{i}^{k}={\oplus}_{j=B+1}^{C}\left(1-{\left(1-{\gamma }_{ij}^{k}\right)}^{{cwt}_{j}}|1-{\left(1-{\gamma }_{ij}^{k}\right)}^{{cwt}_{j}}\right)$$

(14)

where $B$ denotes number of criteria in the benefit type and $C$ denotes the number of criteria in the cost type.

Step 3: Calculate the net ranking values of alternatives using Eq. (15) that forms a vector of order $1\times m$. Apply arithmetic mean instance wise to determine the average values ${R1}_{i}$ and ${R2}_{i}$.

$${R3}_{i}=\xi {R1}_{i}+\left(1-\xi \right)\left(\frac{{\sum }_{i=1}^{m}{R2}_{i}}{{R2}_{i}\left(\frac{1}{{\sum }_{i=1}^{m}{R2}_{i}}\right)}\right)$$

(15)

where $\xi$ is the strategy value in the unit interval, ${R1}_{i}=\sum_{k}{R1}_{i}^{k}$, and ${R2}_{i}=\sum_{k}{R2}_{i}^{k}$.

Step 4: Arrange ${R3}_{i}$ values in the descending order to obtain the ranking order of the alternatives.

The explanation for the proposed algorithm is provided below to clarify the working of COPRAS method. Initially, an aggregated matrix of order $m\times n$ is considered as input along with a weight vector of order $1\times n$. Equations (13, 14) are used to calculate ${R1}_{i}^{k}$ and ${R2}_{i}^{k}$, respectively. These are vectors of order $1\times m$ and are determined for all instances. The ${R1}_{i}^{k}$ is associated with the benefit type criteria and ${R2}_{i}^{k}$ is associated with the cost type criteria. It must be noted that $n=B+C$ and final rank value of each alternative is determined using Eq. (15), which yields ${R3}_{i}$. This is also a vector of order $1\times m$ that is calculated based on the linear combination of ${R1}_{i}$ and ${R2}_{i}$. The strategy value $\xi$ is used to alter influence and attitude mode during ranking. When the strategy value follows $0\le \xi <0.50$ condition, cost type criteria are given preference over benefit type. Similarly, when strategy value follows $0.50<\xi \le 1$ condition, benefit type is preferred over cost type. Finally, when strategy value is equal to 0.50, there is neutral preference over criteria.

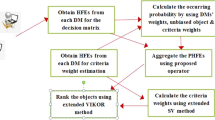
Based on the flowchart depicted in Fig. 1, it is clear that the proposed framework under PHFS context obtains data from experts. Initially, matrices are formed based on the opinions from experts on each alternative over each criterion. Later, experts share their opinions on each criterion. Missing values are imputed methodically and the filled matrices are used for expert weight assessment. Further, criteria weight matrix is utilized for criteria weight calculation. PHFS information from experts is aggregated with the help of the expert weight vector and finally, the aggregated matrix along with the criteria weight vector are used for ranking alternatives. This working flow is carefully adopted in the next section for demonstrating the usefulness of the framework.

Fig. 1

Flowchart of the proposed research framework

Numerical example

This section exemplifies the usefulness of the proposed framework by demonstrating CV selection example for a startup company. A startup company A2P Soft (name modified) in Chennai is an active company that delivers software products to food industries for creating, managing, and analyzing data from the diverse set of customers. A2P Soft provided the food industries with support in data analytics to help them gain profit and achieve global market. Due to the data intensive nature and data-driven strategy adopted by A2P Soft, it is essential for the startup to invest more money for data storage. Since the company is a startup and focuses mainly on software product delivery to other food industries, their core investment is on technological advancement and software developers.

With the view of cutting cost in terms with data storage, the startup company plans to store data in cloud by utilizing the maximum power of cloud computing. As mentioned earlier, due to the massive data-driven strategy adopted by A2P Soft, large volumes of data needs to be stored and process synchronously for offering effective decisions to food industries. The head of the company decides to adopt group decision-making for selecting an appropriate cloud vendor (CV) for the process. Due to large number of potential alternatives (CVs) in the market, a rational selection with supportive mathematical grounds is essential. To achieve the goal, the head of the startup company constitutes a panel of three experts viz., senior software architect, audit manager, and software developer who aid in the decision-making process. Let us refer the three experts as ${D}_{1}$, ${D}_{2}$, and ${D}_{3}$, respectively. These experts analyzed the cloud vendors from cloud rating websites such as best cloud and cloud hosting review. Further, they analyzed the SLAs (service level agreements) of CVs and made emails and phone calls to understand their services and billing patterns. Based on the initial scrutiny, the experts selected 11 CVs (from Cloud Armor repository) who were pre-screened for their suitability to the task being considered. From Delphi approach, six CVs were shortlisted for the decision-making process. We refer the CVs as ${A}_{1}$, ${A}_{2}$, ${A}_{3}$, ${A}_{4}$, ${A}_{5}$, and ${A}_{6}$ (names are kept anonymous for ethical reasons). These vendors are rated based on seven functional criteria. Experts analyzed the literatures [72, 73] to make an initial selection of the criteria that were further revised based on the scorecard-based voting principle and a set of seven criteria referred as assurance, availability, security, agility, scalability, total cost and response time were finalized. We denote them as ${B}_{1}$ to ${B}_{7}$. Among the seven criteria, last two are cost type and the rest are benefit type.

Experts plan to adopt PHFS information for rating CVs based on these criteria. Steps for apt selection of CVs are given below.

Step 1: Provide three decision matrices of order $6\times 7$ where we consider six CVs rated based on seven criteria. Due to hesitation/pressure, some entries are missing, which are methodically imputed based on the procedure proposed in “Imputation of non-available entries”.

Table 1 gives the data from each expert that rates each CV based on the functional criteria mentioned above. It must be noted that due to hesitation/confusion, some entries are missing (that is, experts are unable to provide data). Based on the literature review on PHFS-based MCDM, it is clear that the data matrices are assumed to be filled, which is not practical due to the implicit hesitation/confusion. In this research model, we consider missing entries and impute the values methodically. A lookup table provided below shows the entries that are imputed by adopting the procedure described in “Imputation of non-available entries”.

Table 1 Data matrix with PHFI from experts

It must be noted that the lookup table offers values in the following order, that is, (a, b, c, d) denotes the expert’s number, CV’s number, criteria’s number, and instance’s number.

Step 2: Provide a criteria evaluation matrix of order $3\times 7$ where there are three DMs offering their opinion on each criterion. Table 2 is used as input for weight calculation of criteria (Table 3).

Table 2 Criteria weight determination matrix with PHFI

Table 3 Ideal solution-criteria

Table 4 Ideal solution-DMs

Table 2 is also obtained as an input to determine the weights of the criteria. This matrix utilizes PHFS information. Each expert shares his/her opinions on each criterion. Equations (9, 10) are used for calculating the PIS and NIS values, which are vectors of order $1\times 7$. It must be noted that these are also PHFS information. By applying Eq. (11), an objective function is obtained that is solved using the optimization toolbox of MATLAB® based on certain constraints. The objective function is determined as $0.18{cwt}_{1}+0.24{cwt}_{2}+0.64{cwt}_{3}-0.54{cwt}_{4}+0.69{cwt}_{5}+0.88{cwt}_{6}+0.61{cwt}_{7}$ and the constraints are presented as ${cwt}_{1}+{cwt}_{2}+{cwt}_{3}\le 0.50$; ${cwt}_{4}+{cwt}_{5}+{cwt}_{6}+{cwt}_{7}\le 0.50$; ${cwt}_{2}+{cwt}_{3}+{cwt}_{4}\le 0.70$; ${cwt}_{5}+{cwt}_{6}+{cwt}_{7}\le 0.30$; $0.35\le {cwt}_{2}+{cwt}_{4}\le 0.40$; and ${cwt}_{3}+{cwt}_{6}+{cwt}_{7}\le 0.5$. Thus the solutions are given by 0.1, 0.2, 0.2, 0.2, 0.1, 0.1, 0.1, which are considered as the weights of the criteria.

Step 3: Calculate the weights of DMs using the data in Table 4 and procedure proposed in “Mathematical model for criteria weight determination”.

By applying Eqs. (9–11), the PIS and NIS values for each expert are determined, which are vectors of order $1\times 7$. Using the distance norm, a vector of order $1\times 3$ is obtained that is considered as the objective function. It is solved using MATLAB® based on the constraints. Objective function is presented as ${3.74\eta }_{1}+4.93{\eta }_{2}+0.61{\eta }_{3}$ and the constraints are given as ${\eta }_{1}+{\eta }_{2}\le 0.70$; ${\eta }_{1}+{\eta }_{3}\le 0.60$; and ${\eta }_{2}+{\eta }_{3}\le 0.70$. By solving the model, we get the experts’ weights as 0.30, 0.40, and 0.30, respectively.

Step 4: Aggregate the matrices from Table 1 to form Table 5 using the operator proposed in “PHFS-based Hamy mean operator”. A single matrix of order $6\times 7$ is obtained with six cloud vendors rated based on seven criteria.

Table 5 Aggregated PHFI from experts

Table 5 presents the aggregated PHFS information that takes data from Table 1 and the methodically determined experts’ weights from Step 3. This aggregated value is used for ranking CVs. Operator proposed in Eq. (12) is applied to aggregate preferences from each expert with a risk appetite value of $g=2$.

Step 5: Calculate the parameters of COPRAS method that forms three vectors of order $1\times 6$. Ranking order is determined based on the vector values in the last column that is a derivate from the values provided in ${R1}_{i}^{k}$ and ${R2}_{i}^{k}$.

Note: The first two columns depict values for two instances in the HFE followed by occurrence probability fashion as the data has two instances.

Equations presented in “New extension to COPRAS method” are adopted to calculate the parameter values of COPRAS method and it is shown in Table 6. ${R3}_{i}$ is the ranking vector that is used for forming the ranking order of CVs. Based on this vector, a suitable CV is chosen for A2P Soft. The ranking order is given by.

Table 6 Parameters of COPRAS approach with PHFI

${A}_{2}\succ {A}_{4}\succ {A}_{1}\succ {A}_{5}\succ {A}_{3}\succ {A}_{6}$ and the suitable CV for A2P Soft is ${A}_{2}$.

Comparative investigation—proposed vs. other models

This section demonstrates the comparative investigation of the proposed model with other extant models under PHFS. For this purpose, extant models such as Li and Wang [23], Li et al. [27], Liu et al. [31], and Guo et al. [37] are compared with the proposed work. All these models actively use PHFI. Table 7 summarizes the advantages of the proposed work over other extant models, which are further detailed below for clarity. Following this, sensitivity analysis of criteria weights are performed to understand the effects of change of weight values in the ranking order. Through this analysis, robustness of the proposed work is realized. Finally, consistency of the proposed work is also measured using Spearman correlation [74].

Table 7 Summarized discussion of different decision models with PHFI

Based on Table 7, a detailed description on the advantages of the proposed work is presented below:

• 1. PHFI is a flexible preference style that not only takes advantage of the HFS, but also associates occurrence probability as confidence level to each element.

• 2. Due to hesitation/confusion in MCDM, missing values are common and extant models do not consider the missing entries. Proposed work not only considers missing entries, but also puts forward a novel procedure to impute the missing entries systematically. The core strength of the procedure is that it is simple, intuitive/interpretable, and also yields values that are PHFS in nature.

• 3. Weights of both criteria and experts are methodically determined to mitigate subjective biases and inaccuracies. Further, partial information provided to the system are rationally utilized for weight calculation, unlike the extant models.

• 4. Preferences are aggregated using a generalized operator called the Hamy mean that can easily interpret other arithmetic/geometric operators as special cases. Furthermore, the weights of experts that are needed for aggregation are calculated and not directly obtained extant models) to avoid biases.

• 5. As stated by Zheng et al. [43], COPRAS method is (i) simple and straightforward; (ii) determines rank from different angles, and (iii) considers the nature of criteria during rank calculation. This inspired authors to extend COPRAS method to PHFI.

• 6. Sensitivity analysis is conducted to realize the effects of change of criteria weights on the ranking order. Figure 1 is shown below that contains rank values of different sets of criteria weights. Since there are seven criteria, seven sets are formed by applying right shift operation. From the figure, it is clear that the proposed work is robust and the final ranking order is given by ${A}_{2}\succ {A}_{4}\succcurlyeq {A}_{1}\succ {A}_{5}\succ {A}_{3}\succ {A}_{6}$.

• 7. Rank values of the proposed work are compared with the extant models by applying the Spearman correlation to determine the consistency of the proposed work. Figure 2 depicts the correlation values and confidence factors that are determined based on the and the values are given as ((1,1); (0.6, 0.79); (0.49, 0.68); (0.1,0.2); (0.49, 0.68)). Clearly the proposed work is moderately consistent with the extant models. Due to the ability of COPRAS to consider the nature of criteria, fairly unique ranking order is obtained with proper understanding of each criterion.

Fig. 2

Sensitivity analysis of PHFS-COPRAS with varying criteria weights (X axis – 1 to 7 refers to seven sets of weights obtained from shift operation)

Conclusion and future directions

This paper puts forward a new decision model with PHFI by integrating different methods for achieving rational decisions with minimum human intervention and subjective biases. Unlike the extant models under PHFS, the proposed model considers missing entries and imputes the same methodically without loss of generality. Furthermore, weights of both criteria and experts are calculated by properly utilizing the partial information. Also, the preferences are sensibly aggregated and cloud vendors are rationally prioritized. Table 7 describes the theoretical strengths/innovations of the proposed work. Further, sensitivity analysis reveals that the proposed work is robust even after adequate alterations are made to the criteria weights. Besides, the consistency factor is also moderate with a fairly unique ranking order with ${A}_{2}$ being the most viable cloud vendor based on the majority wins principle. These are merits from the statistical perception that can be observed from Figs. 2 and  3, respectively.

Fig. 3

Consistency analysis using Spearman correlation (X axis: 1 denotes proposed vs. method [15]; 2 denotes proposed vs. method [19]; 3 denotes proposed vs. [23]; and 4 denotes proposed vs. method [29])

Certain shortcomings of the proposed work are (i) occurrence probabilities are not methodically determined; and (ii) consistency of imputed matrices are not checked and repaired. Certain managerial implications that can be inferred are (i) the proposed model is a ready-to-use tool, which could act in a bidirectional manner to help both cloud users (customers) and CVs; (ii) the model carefully mitigates biases by reducing human intervention through systematic calculation of parameter values; (iii) uncertainty is managed effectively by utilizing the flexibility of HFE and associating probabilities as confidence values; and (iv) finally, it must be noted that experts need training to properly use the tool for practical decision-making and to extend the scope of the tool to other MCDM applications.

As future research directions, shortcomings of the model are planned to be addressed. Also, plans are made to adopt the framework for real case studies with primary data from empirical experimentation and more generalized operators for calculation. Further, machine learning techniques can be integrated with the framework for decision-making with large volumes of data. Finally, the proposed work could be improved with other theoretical concepts such as hyperbolic functions [75, 76] for solving problems in business and health sectors.

Appendix

Table A1 is presented below that provides the list of abbreviations along with the expansions.

Table A1 List of abbreviations with expansions