Introduction

Metallic sandwich panels are extensively used in various infrastructure, such as bridges, marine, offshore, protective structures and transportation systems. They are especially effective when subjected to extreme dynamic loads due to their inherent energy dissipation capacity. Sandwich panels can be constructed with various core configurations. In recent years, innovative structural configurations for core elements have been proposed in order to change certain structural properties or improve overall response under specific circumstances including I-core [1,2,3], corrugated-core [4,5,6], Y-core [7, 8], tube-core [9, 10], honeycomb core [11, 12] and auxetic core [13]. Aforesaid configuration can also be used in foam-filled [6, 14] or multilayers forms [15, 16].

Many researchers have focused on the dynamic response of sandwich structures under blast loads particularly in the recent decades. These studies can be categorized as experimental [5, 17], numerical [1, 8, 18] and analytical [19, 20] studies. In the most of published numerical studies, commercial nonlinear FEA packages are used, namely Abaqus [1, 18], NASTRAN [21], LS-DYNA [2, 22] and AUTODYN [4, 6].

Depend on the goals of the study and level of simplification, numerical blast simulations are performed either by triangular equivalent load [23,24,25] or by ConWep function [1, 18, 26], or by modeling the explosive as a material [2, 6, 27]. When explosive is modeled as material, Jones–Wilkins–Lee (JWL) equation of state is mainly adopted. The Arbitrary Lagrangian–Eulerian method (ALE) was frequently used in the numerical analysis of blast loaded sandwich panels.

Some researchers have also considered complicated or multi-hazards scenarios including underwater explosion [28, 29], effects of extreme temperatures on blast response [30, 31], combined shock and projectile impact [32], combined blast and fragment loading [2], multiple blasts [18, 33] and dynamic response under buried explosives [34].

Outperformance of metallic sandwich panels compared with monolithic plates has been frequently reported. According to the current literature, sandwich structures perform better under blast loads in term of energy dissipation, deflection and damage in comparison to solid plates with same density and material [1, 2, 18, 28, 33]. Although large number of steel I-core sandwich panels were designed and constructed, the effects of adopted details on the structural response are not always well-understood and there is still room for further studies.

Energy absorption in blast loaded structures is one of the most important parameters that determine their overall dynamics, therefore, current study seeks to numerically investigate the validity of soft core hypothesis by using drilled I-core, instead of conventional intact web elements. This simple, straightforward and economical novel configuration, i.e., drilling the I-core element, potentially allows more plastic deformation and less midpoint displacements. To this end, drilled holes were considered in the I-core elements of conventional I-core panels and the potential impact of this innovative modification on structural response was studied by finite element analysis. Several parameters that can affect structural response under blast loads, are considered and comprehensively discussed. Most notably, the influence of asymmetrical blast loading and boundary conditions are deeply discussed, that usually are not taken into account in the current literature. Obtained results provide comprehensive insight into the dynamic response of steel drilled I-core sandwich panels under air blast loading.

Methodology

Details of FE modeling, blast loading and analysis techniques are provided in this section.

Geometry of panels

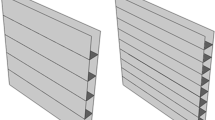
The dimensions of numerical model are \(1500\times 1500~\mathrm{mm}^2\). The overall assembly of model structure is shown in Fig. 1. Thickness of cover plates and I-core are 6 mm and 1 mm, respectively. The core plates of sandwich structures were assumed drilled. The size of the drilled hole is 10 mm. Geometry of drilled core is shown in Fig. 1b.

Fig. 1
figure 1

Geometry of the panel; a general assembly of numerical model and b details of core elements

Full size image

Material property

An elastic-plastic material model was used in numerical modeling. While for extreme loading on structures, more advanced material models accounting for material damage, e.g., Johnson–Cook or different ductile damage models are preferred, the selected model is suitable for the scope of the current study, as illustrated in the “Appendix 1”. It should be noted that the main purpose of the current study is to investigate the dynamic response of the novel proposed configuration, and compare it to alternative solutions. To this aim, adopted models are sufficient. The elastic part is defined by Young’s modulus and Poisson’s ratio. The plastic part is defined as the true stress versus plastic strain. The material behaves as elastic material up to the yield stress and after this stage; it goes into the hardening stage until reaching the ultimate stress [35]. The yield stress of all panels is 300 MPa, Young’s modulus is 210 GPa and Poisson’s ratio is 0.3. The plastic part is defined using the curve shown in Fig. 2. In the case of high-rate loading such as blast and high-speed impact, strain-rate dependency is important. Therefore, strain-rate are included by adjusting the dynamic yield stress according to Eq. 1, i.e., Cowper-Symonds equation [36]:

$$\begin{aligned} {\frac{\sigma _{yd}}{\sigma _y}=1+\left( \frac{\dot{\varepsilon }}{c}\right) ^{\frac{1}{q}}}. \end{aligned}$$
(1)

where \(\sigma _{yd}\) and \(\sigma _y\) are dynamic and static yield stresses, respectively. c and q are experimentally defined material constants and \({\dot{\varepsilon }}\) is the strain rate. On the basis of this equation, static and dynamic yield stress ratio is related to the deformation speed. In the numerical study, three sets of values for c and q were adopted: (1) \(c=40\) s\(^{-1}\) and \(q=5\); (2) \(c=240\) s\(^{-1}\) and \(q=4.74\); (3) \(c=6844\) s\(^{-1}\) and \(q=3.91\) [24, 37].

Fig. 2
figure 2

Plastic Property of steel material

Full size image

Boundary conditions

In a real construction, based on the configurations of the construction site, topology of the structure and application of the panels, different boundary conditions are applied to the panels. However, usually this situation is ignored in the literature and perfectly clamped boundary conditions is preferred. To study the boundary effects, different boundary conditions are adopted in the numerical modeling. Figure 3 shows these boundary conditions. These boundary conditions are applied to both cover plates except for BC1 in which two state were considered; BC1-1 where perfectly fix boundary conditions were applied to both cover plates and BC1-2 where these conditions were applied only to back plate. The connections of the cover plates with the core material are guaranteed via the “tie” command from Abaqus library.

Fig. 3
figure 3

Adopted boundary conditions for numerical studies

Full size image

Blast loading

The threat of a conventional bomb can be defined by two basic parameters; explosive charge weight and standoff distance. As shown in Fig. 4, blast pressure time-history is divided into a positive phase and a negative phase. In the positive phase, maximum over-pressure, \(P_s^+\), is developed promptly and decreases to ambient pressure, \(P_0\), in the time \(T^+\). For the negative phase, the maximum negative pressure, \(P_s^-\), has lower amplitude and longer duration (\(T^-\)) than the positive phase. Therefore, in the numerical study of blast loaded structures using just the positive phase is recommended. The pressure time-history in Fig. 4 can be approximated by the exponential Equation (Eq. 2) [38]:

$$\begin{aligned} P(t)=P^+_s\left( 1-\frac{t}{T^+}\right) e^\frac{-bt}{T^+}. \end{aligned}$$
(2)

where P(t) is overpressure at time t, \(P_s^+\) is maximum over pressure and b is experimental constant.

Abaqus/Explicit provides the ConWep model which can be utilized for air blast loading on structures. The ConWep model uses the scaled distance based on the distance of the target surfaces from the source of the explosion and the amount of the explosive charge based on equivalent weight of Trinitrotoluene (TNT). In ConWep, the total pressure on a surface due to the blast wave is a function of the incident pressure, the reflected pressure and the angle of incidence. The total pressure is defined as Eq. 3 [35]:

$$\begin{aligned} P(t)&=P_{\mathrm{incident}}\left( t\right) \left[ 1+\cos \left( \theta \right) -2\cos ^2\left( \theta \right) \right] \nonumber \\&\quad +P_{\mathrm{reflect}}\left( t\right) \cos ^2(\theta ) \end{aligned}$$
(3)

where P(t) is total pressure, \(P_{\mathrm{incident}}\left( t\right)\) and \(P_{\mathrm{reflect}}\left( t\right)\) are incident pressure and reflected pressure, respectively, and \(\theta\) is angle between the normal of the loading surface and the vector that points from the surface to the blast source.

In this study, 1, 2 and 3 kg TNT are adopted as explosive charges in the numerical analysis. The standoff distance is 500 mm for all models and charges. In order to study the influences of asymmetrical blast loading, in addition to symmetrical blast loads, four sets of asymmetrical blast scenarios are also considered. The positions of hypocenter are shown in Fig. 5. The blast sources in these cases are also 500 mm above the selected points. The ConWep model produces time-dependent non-uniform distribution of blast pressure on the target surface. Figure 6, as an example, shows blast pressure distribution over time for symmetrical blast when 1 kg explosive charge is applied.

Fig. 4
figure 4

Typical blast pressure time-history. ConWep pressure time history is shown in the inset

Full size image
Fig. 5
figure 5

Asymmetrical blast loading scenarios

Full size image
Fig. 6
figure 6

Blast pressure distribution over time for symmetrical blast under 1 kg TNT

Full size image

Finite elements modeling and numerical analysis approach

Abaqus/Explicit solver was adopted for finite element analyses. The fourth nodded doubly curved shell element, S4R, was used to model both cover plates and core’s elements. This element is a 4-node general-purpose shell, quadrilateral, stress/displacement shell element with reduced integration and a large-strain formulation [35]. While using reduced integration, S4R is very robust element and suitable for a wide range of applications and have successfully used in structures under extreme loading conditions as reported in [13, 18, 39]. Hourglass control was employed even though there is no evidence that hourglassing is a considerable issue in such analyses. The effects of damping are not considered in this study because damping has little importance in controlling the maximum response of common structures subjected to blast loads as discussed by [23]. The influence of mesh size has been studied and the size is sufficiently fine to ensure the accuracy of developed FE model. More details are provided in the “Appendix 1”.

Results and discussion

Unless otherwise specified in relevant sections, all results are obtained based on perfect clamped boundary conditions (BC1-1) and symmetrical loading on drilled I-core model.

Dynamic response under blast loading scenarios

Figure 7 shows the midpoint displacement time-histories of sandwich panels’ front face and back face under three explosive charges including 1, 2 and 3 kg TNT. As expected, front faces have more deflections than back plates due to energy dissipation in the core elements. The differences between displacements of two face plates increase as explosive charge increases. When 1 kg TNT is applied, midpoint node vibrated and reached a peak deflection of 31 mm for front face and 26 mm for back face (see Fig. 7). In this case, the difference between deflections of front face and back face is not considerable, because explosive charge is not strong enough to use complete plastic dissipation capacity of such a panel. For 3 kg TNT, midpoint node vibrated and reached a peak deflection of 76 mm for front face and 30 mm for back face. In this case, the differences between deflection of front face and back face is quite considerable.

Fig. 7
figure 7

Time-history of midpoint displacement under different explosive charges

Full size image

The performance of blast loaded sandwich panels is a function of blast intensity and therefore, design of the panels is extremely dependent to the expected threat. Figure 8 shows deformed cross sections of blast loaded sandwich panels under 3 kg explosive charge. It is evident that the deflections of the midpoint of the back faces do not change considerably for all applied charges, because only for the largest explosive charge, i.e., 3 kg TNT, almost complete densification of the middle web elements is occurred.

Fig. 8
figure 8

Displacement contour and deformed cross section of drilled I-core sandwich panel under 3 kg explosive charge

Full size image

Comparison of the total work and the total plastic dissipation of the models shows that most of the work done by the blast loads is dissipated by plastic deformation. With the increase in explosive charge weight, this effect is intensified. Figure 9 shows a comparison of total work and plastic energy time-history for 2 kg explosive charge. Same results also observed for other charges. Figure 10 compares plastic dissipation in core and face plates; for 1 kg explosive charge, most of the energy dissipation occurred in I-core. In this case, face plates remain almost elastic. For 2 kg TNT, energy dissipation in I-core and cover plates are almost equal, that means face plates start to inelastic deformation. For largest blast load (i.e., 3 kg TNT), plastic dissipation in face plates meaningfully exceeds the energy dissipation in I-core, because in this case cover plates start to plastic deformation.

Fig. 9
figure 9

Total work and plastic dissipation energy time-history (2 kg TNT)

Full size image
Fig. 10
figure 10

Energy dissipation in cover plates and I-core under different explosive charges

Full size image

Comparison with equivalent structures

To evaluate the influence of drilled I-core on dynamic response of sandwich panel, a solid plate and also a sandwich panel without holes in the web elements (conventional I-core sandwich panel) subjected to the same blast scenarios were modeled and analyzed. The results were compared with those of proposed drilled I-core configuration. It should be noticed that these sandwich structures are completely similar in weight, material and boundary conditions and the only difference is in core element; while conventional panel has intact core elements, the proposed innovative panel utilized with drilled core elements.

Figure 11 shows the midpoint displacements of the equivalent structures under 1 kg explosive charge. The benefits of a sandwich structures over a solid plate to withstand blast loads are clearly evident by the lower back face displacement. At low impulse levels (i.e., 1 kg TNT), the maximum displacements of the drilled sandwich panel are about 83 percent of the solid plate and the maximum midpoint displacements of two panels, with or without drilled I-core, are almost equal. On the other hand, at high explosive charge (i.e., 3 kg TNT) the maximum displacements of the drilled sandwich panels is about 80 percent of the conventional I-core panel and 57 percent of the equivalent solid plate. In addition to maximum deflection, drilled I-core panel obviously shows a better performance in free vibration phase in the term of deflection. As presented in Fig. 12, the benefits of such structure are particularly important at high impulse loads. Therefore, the panels should be designed according to possible blast loads to achieve its maximum benefits. It could be concluded that the weakening the core elements by drilling, improve plastic dissipation capacity. This improvement could also be due to altering the folding patterns and yield lines of core elements during blast loading. In Table 1, maximum midpoint displacements of these numerical specimens are presented.

Fig. 11
figure 11

Time-history of midpoint displacement under 1 kg TNT

Full size image
Fig. 12
figure 12

Time-history of midpoint displacement under 3 kg TNT

Full size image
Table 1 Maximum midpoint deflection (mm) under blast loading
Full size table

Asymmetrical blast scenarios

To study the effects of asymmetrical blast loads, numerical models were analyzed under 2 kg explosive charge with the four asymmetrical blast scenarios as presented in Fig. 5. The standoff distances also considered 500 mm directly above the selected points. Figure 13 shows displacement time-history for asymmetrical Case 4 under 2 kg explosive charge.

According to results, for all front faces, maximum displacements in hypocenter exceed the displacement in the center of the cover plate due to localized nature of blast loads and subsequently more applied pressure to hypocenter. On the other hand, for the back face plates, the deflection in the center is more than hypocenter, because, plastic deformation in the core elements dissipates most of the blast energy, and therefore, back faces’ responses is much smoother. This phenomenon is partially function of the distance from clamped boundary conditions; the center of the plate has the maximum distance from the clamped boundary conditions and therefore its response is smoother. Asymmetrical blast loads not only change the overall response of panels as discussed above, but also affect the stress distribution pattern. Figure 14 shows deformed shape and displacement distribution at time associated with the maximum displacement in the front plate when subjected to asymmetrical blast loads (Case 4). As presented in this figure, deflection concentrated in the hypocenter of blast loads and nearby core elements. The results of asymmetrical blast analyses are summarized in Table 2

Fig. 13
figure 13

Displacement time-history for asymmetrically blast loaded sandwich panel (Case 4, 2 kg TNT)

Full size image
Fig. 14
figure 14

Displacement contour for asymmetrical load Case 4

Full size image
Table 2 Maximum midpoint deflection (mm) under 2 kg TNT asymmetrical blast loading scenario
Full size table

Influence of boundary conditions

In this study, five different boundary conditions were adopted for the numerical analyses. These boundary conditions applied to both cover plates except for BC 1 (see the section related to boundary conditions). According to the results, the boundary conditions of cover plates have a major influence on the dynamic response of sandwich panels under air blast loading. Free edges increase midpoint displacement meaningfully. Table 3 summarizes these numerical results.

Table 3 Maximum deflection (mm) for different boundary conditions under 2 kg TNT
Full size table

Figures 15 and 16 show the displacement time-history of center of the panel and also middle of free edges for BC4 and BC5. As presented in Fig. 15, while for front plates, displacement of center is always larger than the displacement in center of the free edges, for the back plate displacement of free edges can exceed the center. If clamped boundary conditions apply only on one cover plate (BC 1-2), complete densification of the web elements occurs. In this case, increasing the thickness of core elements can be useful. Figure 17 shows the time-history of midpoint displacements of the model with 1.5 mm thick core elements. With the increase in the core’s thickness, complete densification does not occur in the web of the panel.

Fig. 15
figure 15

Displacement time-history under 2 kg TNT (BC 4)

Full size image
Fig. 16
figure 16

Displacement time-history under 2 kg TNT (BC 5)

Full size image
Fig. 17
figure 17

Model with strengthened core subjected to 2 kg explosive charge (BC 1-2)

Full size image

Strain rate dependency

Current results (see Fig. 18) show that when rate dependency is included in numerical modeling of blast loaded sandwich panels, a stiffer response is achieved and less deflection is recorded. The rate of decrease in midpoint deflections depends mainly on the charge weight and results are sensitive to the values of adopted material constants. Therefore, precise data would be required for design purposes. Time-histories of the midpoint displacements of the model 1 under 1, 2 and 3 kg explosive charges have shown in Fig. 18.

Fig. 18
figure 18

Influence of strain rate on panels’ dynamic response when subjected to different explosive charges

Full size image

Conclusion

A novel configuration, i.e., drilled I-core elements, is suggested for the steel sandwich panels under blast scenarios. The nonlinear dynamic response of an innovative steel I-core sandwich panel with drilled core under blast loading scenarios is numerically investigated. Several parameters such as different boundary conditions and asymmetrical loading that can affect structural dynamics under blast loads were considered. Obtained results are compared with available experimental data to verify the developed finite element model and good agreement is achieved (see “Appendix 1”). The results confirm that this slight and economical modification in the conventional I-core sandwich panel leads to major performance improvement under blast loads. The main results of this study can be summarized as follows:

Proposed model with drilled I-core allows more plastic deformation, energy absorption and less midpoint deflection than equivalent structures, i.e., conventional I-core sandwich panel and solid plate with same weight and material. The dynamic response of the sandwich panel is drastically dependent on explosive weight. The differences between deflection of the front face and the back face are dependent on blast intensity; while for lowest blast load this differences are negligible, for the largest this differences are quite considerable. Performance of blast loaded sandwich panels is a function of blast intensity and therefore, design of panel should be performed according to specific expected blast risk on the target infrastructures to achieve maximum energy absorption capacity.

In asymmetrical loading, for all front faces, maximum displacements in hypocenter exceed the displacement in the center of the cover plates due to localized nature of blast loads. On the other hand, for the back face plates, the deflection in the center is more than hypocenter, because plastic deformation in core element dissipates most of the blast energy. Therefore, back faces’ responses are always smoother.

Boundary conditions have a significant influence on the dynamic response of sandwich panels under blast loading. Freedom of the edges increases the midpoint displacement. While for front plates, the displacement of the center is always larger than the center of the free edges, for the back plates deflection of free edges may exceed the center. Therefore, in the design and construction of infrastructures using sandwich panels with free edges, such a phenomenon should be carefully considered.

This study reports a comprehensive numerical study of blast response of the steel I-core sandwich panels. Indeed, there is still room for improvement. Size, pattern and distribution of the holes on the I-core elements affect the structural response and energy dissipation capacity of the sandwich panel. Focusing on this issue in the future researches is recommended.