Global Dynamics of a Two-Strain Disease Model with Amplification, Nonlinear Incidence and Treatment

Abstract

In recent years, antibiotic resistance to the most effective treatments has emerged and spread. This has led to a decline in the efficacy of antibiotics used to treat patients, with drug-resistant strain experiencing much higher failure rates and serious side effects. In this study, we considered two-strains (e.g., drug-susceptible and drug-resistant) susceptible-infected-recovery disease model with amplification, nonlinear incidence and treatment. We assumed amplification develops mainly through the choice of naturally happening mutations in the presence of inappropriate treatment. We performed a rigorous analytical analysis of the model properties and solutions to predict late-time behavior of the disease dynamics and find that the model contains four equilibrium points: disease-free equilibrium, monoexistence endemic equilibrium 1 concerning drug-susceptible strain, monoexistence endemic equilibrium 2 concerning drug-resistant strain and coexistence equilibrium regarding to drug-susceptible as well as drug-resistant strains. Two basic reproduction numbers ${R}_{0\mathrm{s}}$ and $R_{{0{\text{m}}}}$ are found, and we have presented that if both are less than one $({\text{i}}.{\text{e}}.\max \left[ {R_{{0{\text{s}}}} ,{ }R_{{0{\text{m}}}} } \right] < 1)$, the disease fade-out, and if both greater than one $({\text{i}}.{\text{e}}.\max \left[ {R_{{0{\text{s}}}} ,{ }R_{{0{\text{m}}}} } \right] > 1)$ the epidemic situation occurs. Moreover, epidemics occur regarding to any strain when the basic reproduction number remains above the value 1 and disease fade-out with regard to any strain when the basic reproduction number remains below the value 1. In all equilibrium points, the global stability analysis was determined with the help of appropriate Lyapunov functions. In addition, we also found that the drug-resistant strain prevalence increases when the drug-susceptible strain is treated due to the poor-quality treatment (i.e., amplification). We also performed the sensitivity analysis through evaluation of Partial Rank Correlation Coefficients (PRCC) to identify the most important model parameters and found that transmission rate of both strains had the maximum influence on disease outbreak. To support those analytical results, numerical simulations of the model were performed using ODE45 MATLAB routine.

1 Introduction

Many infectious diseases including dengue fever, tuberculosis, HIV, other sexually transmitted diseases are engendered by more than one strain due to inappropriate treatment (Bhunu 2009; Jabbari et al. 2016; Kooi et al. 2014; Lin et al. 2003). Pathogen mutation is a common phenomenon in disease transmission and outcomes in the presence of multiple variants. Therefore, one of the major challenges in preventing or controlling the spread of infectious diseases is to deal with the genetic variations of pathogens.

Mathematical models can provide a significant insight to understand the transmission dynamics of the infectious diseases and imitate a prevention strategy which keeps a vital role to mitigate the spread of the disease. Several mathematical models providing dynamic analysis of the multi-strain interactions have been proposed by considering different aspects (Ackleh and Allen 2003; Cai et al. 2007, 2012; Feng et al. 2002; Li et al. 2004; Lin et al. 2003). The epidemic models also demonstrated that any strain will defeat to the other strains automatically when the basic reproduction number is remarkably high (Bremermann 1989). The basic reproduction number represented the number of secondary individuals who became infected through a single contaminated individual introduced into the totally susceptible population. So, the number of infected cases increases and the disease becomes spread-out in the community when the basic reproduction number is greater than one. However, if the basic reproduction number is less than one, the disease becomes die-out from the community and the number of newly infective cases moves to zero (Childs et al. 2015). Recent studies (Davies 2001; Dodd et al. 2016; McBryde et al. 2017a, b; Mistry et al. 2012; Stengel 2008) have demonstrated that in disease transmission, drug-resistant strains can possess higher virulence compared to the drug-susceptible strain. As a result, the infected individuals with a drug-resistant strain belong to the highest mortality rate, e.g., tuberculosis and HIV.

In mathematical models, incidence rate plays a key role to spread the diseases outbreak. In epidemiology perspective, the incidence rate is generally known as the number of infected individuals per unit time. Incidence rate can be described in various ways. First of all, the bilinear incidence rate is based on the mass action (Anderson and May 1992; Kermack and McKendrick 1927) ($\beta SI$, where the infection rate is $\beta$ as well as $S$ and $I$ represent the susceptible and infected individuals, respectively). In large-scale population for the bilinear incidence rate, if the number of susceptible cases increases, the number of infected cases also increases, which is not realistic. Secondly, saturated incidence rate $\frac{\alpha SI}{{\left( {1 + \beta S} \right)}}$ was introduced by (Anderson and May 1978a, b). The effect of saturated factor $\beta$ stems from epidemical control. Thirdly, nonlinear incidence rate was introduced by (Li et al. 2009). In the case of nonlinear incidence rate, the effective interactions between infective and susceptible individuals may saturate with a significant level due to overflowing of infective individuals. There were some studies, demonstrated nonlinear incidence rate individually which are known as Beddington–DeAngelis-type incidence rate $\left( {\frac{\alpha SI}{{1 + \beta S + \gamma I}}} \right)$ (Beddington 1975; DeAngelis et al. 1975). Later, there were some studies utilized the incidence rate to delineate epidemiological models (Elaiw and Azoz 2013; Huang et al. 2011; Kaddar 2009).

Several studies have been conducted to simulate the model properties with fractional-order derivatives (Al-Smadi et al. 2020a, b; Al-Smadi et al. 2021; Al-Smadi 2021; Arqub and Shawagfeh 2019; Djennadi et al. 2020, 2021). For example, Djennadi et al. (2021) studied the Tikhonov regularization method in the sense of fractional-order derivative for reformulation of the stable solution and compared between the exact and regularized solutions under the a-priori and the a-posteriori parameter choice rules (Djennadi et al. 2021). A fractional-order derivative with a nonlocal and nonsingular kernel is proposed for heat equation and obtained solution for the inverse problem using the eigen functions expansion method (Djennadi et al. 2020). Al-Smadi et al. (2021) examined the numerical and graphical representation using the Atangana–Baleanu–Caputo (ABC) fractional-order derivative and displayed the impact of the ABC fractional derivative (Al-Smadi et al. 2021). A new approach is proposed to perform the analytical and numerical simulations for the time-fractional partial differential equations. This study examined various numerical examples including linear and nonlinear terms and interpreted the n-term of the exact solutions (Arqub and Shawagfeh 2019). Al-Smadi et al. (2020a, b) studied the fractional Kundu–Eckhaus and massive Thirring models to simulate nonlinear PDEs in the concept of fractional derivative and acquired the approximate solution of that nonlinear system (Al-Smadi et al. 2020a).

In epidemiological field, intervention programs including treatment, vaccination initiate a significant impact to prevent the spread of disease. Treatment is an efficacious appliance to expunge diseases. Many authors (Cohen et al. 2009; Kuddus et al. 2021a, b; Kuddus et al. 2020) have discussed the consequences of treatment considering various type of treatment functions. Normally, in a classical model, treatment rate is assumed to be commensurate with the number of infected cases. Zhang and Liu (2008) demonstrated the better treatment rate in terms of continuous differentiable function which reaches at its highest value. The removal rate is designated by the expression $\frac{rI}{{{ }1 + \beta I}}$, where r represents the rate of remedy from the disease which is positive constant, and $\beta$ identifies the consequences of delay in treatment which is also a non-negative constant.

However, the rising threat of drug-resistant strain presents a major challenge in the world, predominantly in low- and middle-income countries. Once drug-resistant strains have arisen in a population, amplification of these strains may also contribute to the disease burden. Current studies (Dodd et al. 2016; Kuddus et al. 2020; McBryde et al. 2017a, b) have demonstrated that drug-resistant strains can in some cases contain higher virulence to convey disease than drug-susceptible strains, and those individuals infected with a drug-resistant strain have the maximum death rate. To examine the threat posed by drug-resistant strain, we present a two-strain disease model with associated infectious compartments and use it to investigate the emergence and spread of drug-resistant strain through amplification. Here, we incorporated Beddington–DeAngelis-type incidence rate and the saturated treatment rate, and with a competing mechanism between the drug-susceptible and drug-resistant strains. The global stability of the disease-free equilibrium, monoexistence equilibrium with respect to drug-susceptible or drug-resistant strain is investigated through suitable Lyapunov functions, and coexistence endemic equilibrium with respect to both strains performs through numerical analysis. Sensitivity analysis also performed to identify the most important parameter for the disease outbreak.

The rest of the paper is constructed as follows: In Sect. 2 we exhibit the two-strain SIR model Beddington–DeAngelis-type incidence rate and the saturated treatment rate, and validate the positivity and boundedness of solutions as well as the existence of the equilibria. Global stability analysis of all of the equilibrium point is demonstrated in Sect. 3. Sensitivity of the model parameter is presented in Sect. 4. To buttress the analytical solution of the proposed two-strain model, numerical simulations are demonstrated in Sect. 5. In the end, an incisive discussion about our findings is described and delivered a concluding remark.

2 Model Formulation and Assertion

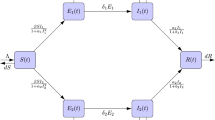
We presented a two-strain SIR model for drug-susceptible and drug-resistant strains with amplification, nonlinear incidence and treatment among the following mutually exclusive compartments: $S\left( t \right)$-susceptible individuals (those who are free from disease but infected in any time); $I_{{\text{s}}} \left( t \right)$-infected individuals (who are infected and have entered the active cases) associated with the drug-susceptible strain; $I_{{\text{m}}} \left( t \right)$-infected individuals (who are infected and infectious) associated with the drug-resistant strain, and $R\left( t \right)$-recovered individuals, who were previously infected and were successfully treated and have immunity against both strains. Thus, the total number of the populations is:

$$N\left( t \right) = S\left( t \right) + I_{{\text{s}}} \left( t \right) + I_{{\text{m}}} \left( t \right) + R\left( t \right).$$

(1)

At the progresses, the infected persons with the drug-susceptible and drug-resistant strain lose infectivity and shift to the recovered compartment (R) owing to their health immunity or by treatment. These recovered individuals are able to protect them against the infectious microbes and that is why they are not being infected again with the disease (Fig. 1). According to our consideration, the model is constructed with the following differential equations:

$$\dot{S} = {\Lambda } - \mu S - \frac{{\beta_{{\text{s}}} I_{{\text{s}}} S}}{{1 + \beta_{1} S + \gamma_{1} I_{{\text{s}}} }} - \frac{{\beta_{{\text{m}}} I_{{\text{m}}} S}}{{1 + \beta_{2} S + \gamma_{2} I_{{\text{m}}} }},$$

(2)

$$\dot{I}_{{\text{s}}} = \frac{{\beta_{{\text{s}}} I_{{\text{s}}} S}}{{1 + \beta_{1} S + \gamma_{1} I_{{\text{s}}} }} - \frac{{\tau_{{\text{s}}} I_{{\text{s}}} }}{{1 + \delta_{1} {\text{I}}_{{\text{s}}} }} - \left( {\omega_{{\text{s}}} + \phi_{{\text{s}}} + \mu } \right)I_{{\text{s}}} ,$$

(3)

$$\dot{I}_{{\text{m}}} = \rho \omega_{{\text{s}}} I_{{\text{s}}} + \frac{{\beta_{{\text{m}}} I_{{\text{m}}} S}}{{1 + \beta_{2} S + \gamma_{2} I_{{\text{m}}} }} - \frac{{\tau_{{\text{m}}} I_{{\text{m}}} }}{{1 + \delta_{2} I_{{\text{m}}} }} - \left( {\omega_{{\text{m}}} + \phi_{{\text{m}}} + \mu } \right)I_{{\text{m}}} ,$$

(4)

$$\dot{R} = \left( {1 - \rho } \right)\omega_{{\text{s}}} I_{{\text{s}}} + \omega_{{\text{m}}} I_{{\text{m}}} + \frac{{\tau_{{\text{s}}} I_{{\text{s}}} }}{{1 + \delta_{1} I_{{\text{s}}} }} + \frac{{\tau_{{\text{m}}} I_{{\text{m}}} }}{{1 + \delta_{2} I_{{\text{m}}} }} - \mu R{.}$$

(5)

where $S\left( 0 \right) > 0,\,\,I_{{\text{s}}} \left( 0 \right) \ge 0,\,\,I_{{\text{m}}} \left( 0 \right) \ge 0,\,\,R\left( 0 \right) \ge 0.$

Fig. 1

Flow chart of two-strain mathematical model

Let the total inflow into the susceptible individuals be a constant rate $\Lambda$ and the natural death rate $\mu$ is included in every compartment. Let $\phi_{{\text{s}}}$ and $\phi_{{\text{m}}}$ are the disease-related death rate for the drug-susceptible and drug-resistant strains, respectively. $\rho$ be the proportion of amplification due to inappropriate or incorrect treatment. Amplification develops mainly through the choice of naturally happening mutations in the presence of inappropriate treatment. When preliminary resistance has established, acquisition of resistance to supplementary drugs more likely treatment with usual regimens may be suboptimal (Trauer et al. 2014). In model (2–5), we choose the incidence rates as Beddington DeAngelis type:

$$f_{1} \left( {S,{ }I_{{\text{s}}} } \right) = \frac{{\beta_{{\text{s}}} I_{{\text{s}}} S}}{{1 + \beta_{1} S + \gamma_{1} I_{{\text{s}}} }},$$

(6)

$$f_{2} \left( {S,I_{{\text{m}}} } \right) = \frac{{\beta_{{\text{m}}} I_{{\text{m}}} S}}{{1 + \beta_{2} S + \gamma_{2} I_{{\text{m}}} }}.$$

(7)

Here, $\beta_{{\text{s}}}$ and $\beta_{{\text{m}}}$ are transmission rate for the drug-susceptible and drug-resistant strains, respectively. $\beta_{1}$ and $\beta_{2}$ are the preventive measure according to the drug-susceptible individuals and drug-resistant individuals. Further, $\gamma_{1}$ and $\gamma_{2}$ are other measure of inhibition effect like treatment for the drug-susceptible and drug-resistant infective strains.

In this paper, it is fascinating to declare that the following three different incidence rate can be obtained from the proposed incidence rate.

• (1) If we consider $\beta_{1} = \beta_{2} = 0$ and $\gamma_{1} = \gamma_{2} = 0$ then $f_{1} \left( {S,{ }I_{{\text{s}}} } \right) = \beta_{{\text{s}}} S{ }I_{{\text{s}}}$ and $f_{2} \left( {S,I_{{\text{m}}} } \right) = \beta_{{\text{m}}} SI_{{\text{m}}}$ which are bilinear incidence rates (Anderson and May 1978a, b; Bailey 1975; Hethcote 2000; Shulgin et al. 1998; Zhonghua and Yaohong 2010).

• (2) If we consider $\gamma_{1} = \gamma_{2} = 0,$ then $f\left( {S,{ }I_{{\text{s}}} } \right) = \frac{{\beta_{{\text{s}}} S{ }I_{{\text{s}}} }}{{1 + \beta_{1} S}}$ and $f\left( {S,{ }I_{{\text{m}}} } \right) = \frac{{\beta_{{\text{m}}} S{ }I_{{\text{m}}} }}{{1 + \beta_{2} S}},$ which are saturated incidence rates to the saturation factors $\beta_{1}$ and $\beta_{2}$ owing to the preventive measure to prevent the transmission of the epidemic disease (Capasso and Serio 1978; Korobeinikov and Maini 2005; Xu and Ma 2009).

• (3) If we consider $\beta_{1} = \beta_{2} = 0,$ then $f\left( {S,{ }I_{{\text{s}}} } \right) = \frac{{\beta_{{\text{s}}} S{ }I_{{\text{s}}} }}{{1 + \gamma_{1} I_{{\text{s}}} }}$ and $f\left( {S,{ }I_{{\text{m}}} } \right) = \frac{{\beta_{{\text{m}}} { }S{ }I_{{\text{m}}} }}{{1 + \gamma_{2} I_{{\text{m}}} }},$ which are saturated incidence rates according to the infected individuals. In this instance, the interaction of susceptible individuals with the infected individuals may saturate at extreme infection risk due to crowding of infective individuals or due to nonappearance of protection equipment taken by susceptible individuals (Li et al. 2009; Meng et al. 2010; Zhang et al. 2008). Furthermore, the contact between susceptible individuals and drug-resistant infected individuals may spread infection at significant level due to the inappropriate or poorly administrated treatment.

The terms $h\left( {I_{{\text{s}}} } \right) = \frac{{\tau_{{\text{s}}} I_{{\text{s}}} }}{{1 + \delta_{1} I_{{\text{s}}} }}$ and $h\left( {I_{{\text{m}}} } \right) = \frac{{\tau_{{\text{m}}} I_{{\text{m}}} }}{{1 + \delta_{2} I_{{\text{m}}} }}$ in system (2–5) represent the treatment terms, where $\tau_{{\text{s}}}$ and $\tau_{{\text{m}}}$ are positive constant, whereas the resource limitation is taking into account with a constant rate $\delta_{1}$ and $\delta_{2}$ (Zhonghua and Yaohong 2010; Zhou and Fan 2012).

From proposed two-strain model (2–5) we can indicate that recovered individuals, R, have no effect on $S,{ }I_{{\text{s}}} ,$ and $I_{{\text{m}}}$; for that reason, we can only concentrate on following reduced system (8–10) if we desire to demonstrate the disease incidence and prevalence dynamics. The reduced system is:

$$\dot{S} = \Lambda - \mu S - \frac{{\beta_{{\text{s}}} I_{{\text{s}}} S}}{{1 + \beta_{1} S + \gamma_{1} I_{{\text{s}}} }} - \frac{{\beta_{{\text{m}}} I_{{\text{m}}} S}}{{1 + \beta_{2} S + \gamma_{2} I_{{\text{m}}} }},$$

(8)

$$\dot{I}_{{\text{s}}} = \frac{{\beta_{{\text{s}}} I_{{\text{s}}} {\text{S}}}}{{1 + \beta_{1} S + \gamma_{1} I_{{\text{s}}} }} - \frac{{\tau_{{\text{s}}} I_{{\text{s}}} }}{{1 + \delta_{1} I_{{\text{s}}} }} - \left( {\omega_{{\text{s}}} + \phi_{{\text{s}}} + \mu } \right){ }I_{{\text{s}}} ,$$

(9)

$$\dot{I}_{{\text{m}}} = \rho \omega_{{\text{s}}} I_{{\text{s}}} + \frac{{\beta_{{\text{m}}} I_{{\text{m}}} S}}{{1 + \beta_{2} S + \gamma_{2} I_{{\text{m}}} }} - \frac{{\tau_{{\text{m}}} I_{{\text{m}}} }}{{1 + \delta_{2} I_{{\text{m}}} }} - \left( {\omega_{{\text{m}}} + \phi_{{\text{m}}} + \mu } \right){ }I_{{\text{m}}} .$$

(10)

where $S\left( 0 \right) > 0,{ }I_{{\text{s}}} \left( 0 \right) \ge 0,{ }I_{{\text{m}}} \left( 0 \right) \ge 0.$

2.1 Positivity Analysis

For the system above from (8) to (10), we observe a region of attraction which is described details with the help of Lemma 1.

Lemma 1

The set ${\Omega } = \left\{ {\left( {S,{ }I_{{\text{s}}} ,{ }I_{{\text{m}}} } \right){ } \in { }R_{ + }^{3} { }:0 < S + I_{{\text{s}}} + I_{{\text{m}}} \le \frac{\Lambda }{\mu }} \right\}$ is a positively invariant region of system (8–10).

Proof

Let, $N = S + I_{{\text{s}}} + I_{{\text{m}}} ,\,{\text{then}}\,\dot{N} = \dot{S} + \dot{I}_{{\text{s}}} + \dot{I}_{{\text{m}}} ,$

$$\begin{aligned} & \dot{N} = {\Lambda } - \mu N - \frac{{\tau_{{\text{s}}} I_{{\text{s}}} }}{{1 + \delta_{1} I_{{\text{s}}} }} - \frac{{\tau_{{\text{m}}} I_{{\text{m}}} }}{{1 + \delta_{2} I_{{\text{m}}} }} - \left( {\omega_{{\text{s}}} + \phi_{{\text{s}}} - \rho \omega_{{\text{s}}} } \right)I_{{\text{s}}} - \left( {\omega_{{\text{m}}} + \phi_{{\text{m}}} } \right)I_{{\text{m}}} ,\,{\text{then}} \\ & N\left( t \right) \le N\left( 0 \right)e^{ - \mu t} + \frac{{\Lambda }}{\mu }{ }\left( {1 - e^{\mu t} } \right). \\ \end{aligned}$$

$$\square$$

Thus, $\mathop {\lim }\nolimits_{t \to \infty } \sup N\left( t \right) \le \frac{\Lambda }{\mu }$. Furthermore, if $N > \frac{\Lambda }{\mu }$ then $\dot{N} < 0$. This reveals that the solutions of system (8–10) point toward ${\Omega }$. Hence, ${\Omega }$ is positively invariant and the solutions are bounded with the non-negative conditions.

We determined the biological feasible solution set. Above Lemma 1 convinced that all solutions of model (8–10) are non-negative and bounded in the feasible set. Thus, the model is biologically meaningful.

2.2 Existence of Equilibria

The existence of endemic equilibrium ${ }E_{1} \left( {S_{{\text{m}}}^{*} ,{ }0,{ }I_{{\text{m}}}^{*} } \right)$, equating Eq. (10) to zero, we get

$$\frac{{\beta_{{\text{m}}} I_{{\text{m}}}^{*} S_{{\text{m}}}^{*} }}{{1 + \beta_{2} S_{{\text{m}}}^{*} + \gamma_{2} I_{{\text{m}}}^{*} }} = \frac{{\tau_{{\text{m}}} I_{{\text{m}}}^{*} }}{{1 + \delta_{2} I_{{\text{m}}}^{*} }} + \chi_{{\text{m}}} I_{{\text{m}}}^{*} ,$$

(11)

After simplify above Eq. (11), we have $S_{{\text{m}}}^{*}$ in respect of $I_{{\text{m}}}^{*}$ as follows:

$$S_{{\text{m}}}^{*} = \frac{{\left( {1 + \gamma_{2} I_{{\text{m}}}^{*} } \right)\left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} + \chi_{{\text{m}}} \delta_{2} I_{{\text{m}}}^{*} } \right)}}{{\beta_{{\text{m}}} - \beta_{2} \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right) + \left( {\beta_{{\text{m}}} - \beta_{2} \chi_{{\text{m}}} } \right)\delta_{2} I_{{\text{m}}}^{*} }},$$

(12)

$S_{{\text{m}}}^{*}$ is positive if,

$$\beta_{{\text{m}}} > { }\beta_{2} \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right).$$

(13)

Now equating Eq. (8) to zero and solving we obtain the following quadratic equation in $S_{{\text{m}}}^{*} ,$

$${\Lambda } - \mu S_{{\text{m}}}^{*} - \frac{{\beta_{{\text{m}}} I_{{\text{m}}}^{*} S_{{\text{m}}}^{*} }}{{1 + \beta_{2} S^{*} + \gamma_{2} I_{{\text{m}}}^{*} }} = 0,$$

After simplify we get the following equation

$$\mu \beta_{2} S_{{\text{m}}}^{{{*}2}} + \left[ {\mu - \Lambda \beta_{2} + \left( {\mu \gamma_{2} + \beta_{{\text{m}}} } \right)I_{{\text{m}}}^{*} } \right]S_{{\text{m}}}^{*} - \Lambda \left( {1 + \gamma_{2} I_{{\text{m}}}^{*} } \right) = 0.$$

(14)

Now substituting the value of $S_{{\text{m}}}^{*}$ from Eq. (12) into Eq. (14), we get the following cubic equation in ${\text{ I}}_{{\text{m}}}^{*} .$

$$\mu \beta_{2} \frac{{\left( {1 + \gamma_{2} I_{{\text{m}}}^{*} } \right)^{2} \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} + \chi_{{\text{m}}} \delta_{2} I_{{\text{m}}}^{*} } \right)^{2} }}{{\left( {q + p\delta_{2} I_{{\text{m}}}^{*} } \right)^{2} }} + \left( {m + {\text{l }}I_{{\text{m}}}^{*} } \right)\frac{{\left( {1 + \gamma_{2} I_{{\text{m}}}^{*} } \right)\left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} + \chi_{{\text{m}}} \delta_{2} I_{{\text{m}}}^{*} } \right)}}{{\left( {q + p\delta_{2} I_{{\text{m}}}^{*} } \right)}} - \Lambda \left( {1 + \gamma_{2} I_{{\text{m}}}^{*} } \right) = 0,$$

where $p = \beta_{{\text{m}}} - \beta_{2} \chi_{{\text{m}}} ,{ }q = \beta_{{\text{m}}} - \beta_{2} \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right),{ }m = \mu - \Lambda \beta_{2} ,{\text{ l}} = \mu \gamma_{2} + \beta_{{\text{m}}} ,$

$$\begin{aligned} & \mu \beta_{2} \left( {1 + \gamma_{2} I_{{\text{m}}}^{*} } \right)^{2} \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} + \chi_{{\text{m}}} \delta_{2} I_{{\text{m}}}^{*} } \right)^{2} + \left( {m + {\text{l }}I_{{\text{m}}}^{*} } \right)\left( {1 + \gamma_{2} I_{{\text{m}}}^{*} } \right)\left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} + \chi_{{\text{m}}} \delta_{2} I_{{\text{m}}}^{*} } \right)\left( {q + p\delta_{2} I_{{\text{m}}}^{*} } \right){ } \\ & \quad - \Lambda \left( {1 + \gamma_{2} I_{{\text{m}}}^{*} } \right)\left( {q + p\delta_{2} I_{{\text{m}}}^{*} } \right)^{2} = 0, \\ & \Rightarrow \mu \beta_{2} \left( {1 + \gamma_{2} I_{{\text{m}}}^{*} } \right)\left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} + \chi_{{\text{m}}} \delta_{2} I_{{\text{m}}}^{*} } \right)^{2} + \left( {m + {\text{l }}I_{{\text{m}}}^{*} } \right)\left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} + \chi_{{\text{m}}} \delta_{2} I_{{\text{m}}}^{*} } \right)\left( {q + p\delta_{2} I_{{\text{m}}}^{*} } \right) \\ & \quad - \Lambda \left( {q + p\delta_{2} I_{{\text{m}}}^{*} } \right)^{2} = 0, \\ \end{aligned}$$

(15)

After simplify we get the following cubic equation in terms of $I_{{\text{m}}}^{*}$

$$\begin{aligned} & \left( {\mu \beta_{2} \gamma_{2} \chi_{{\text{m}}}^{2} \delta_{2}^{2} + p \delta_{2}^{2} { }\chi_{{\text{m}}} { }l} \right)I_{{\text{m}}}^{{{*}3}} \\ & \quad + \left[ {\mu \beta_{2} \chi_{{\text{m}}}^{2} \delta_{2}^{2} + 2{ }\chi_{{\text{m}}} \mu \beta_{2} \gamma_{2} \delta_{2} { }\left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right) + \chi_{{\text{m}}} l \delta_{2} { }q + \delta_{2} p\left\{ {\left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)l + m\chi_{{\text{m}}} \delta_{2} - \Lambda { }p{ }\delta_{2} } \right\}} \right]I_{{\text{m}}}^{{{*}2}} \\ & \quad + \left[ {2 \mu \delta_{2} \chi_{{\text{m}}} \beta_{2} \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right) + \mu \beta_{2} \gamma_{2} \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)^{2} + m \delta_{2} p\left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right) + q\{ \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)l + \chi_{{\text{m}}} m \delta_{2} - 2\Lambda p{\updelta }_{2} \} } \right]I_{{\text{m}}}^{*} \\ & \quad + \mu \beta_{2} \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)^{2} + m \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)q - \Lambda q^{2} = 0, \\ \end{aligned}$$

The above equation will be in the following form,

$$A_{1} I_{{\text{m}}}^{{{*}3}} + A_{2} I_{{\text{m}}}^{{{*}2}} + A_{3} I_{{\text{m}}}^{*} + A_{4} = 0.$$

(16)

where

$$\begin{aligned} A_{1} & = \mu \beta_{2} \gamma_{2} \chi_{{\text{m}}}^{2} \delta_{2}^{2} + p{ }\delta_{2}^{2} { }\chi_{{\text{m}}} { }l{,} \\ A_{2} & = \mu \beta_{2} \chi_{{\text{m}}}^{2} \delta_{2}^{2} + 2{ }\chi_{{\text{m}}} \mu \beta_{2} \gamma_{2} \delta_{2} { }\left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right) + \chi_{{\text{m}}} l{ }\delta_{2} { }q + \delta_{2} p\left\{ {\left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)l + m\chi_{{\text{m}}} \delta_{2} - \Lambda p{ }\delta_{2} } \right\}, \\ A_{3} & = 2{ }\mu \delta_{2} \chi_{{\text{m}}} \beta_{2} \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right) + \mu \beta_{2} \gamma_{2} \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)^{2} + m \delta_{2} { }p\left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right) + q\left\{ {\left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)l + \chi_{{\text{m}}} { }m \delta_{2} - 2\Lambda p\delta_{2} } \right\}, \\ A_{4} & = \mu \beta_{2} \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)^{2} + m \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)q - \Lambda q^{2} , \\ \end{aligned}$$

and

$$p = \beta_{{\text{m}}} - \beta_{2} \chi_{{\text{m}}} , q = \beta_{{\text{m}}} - \beta_{2} \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right), m = \mu - \Lambda \beta_{2} , l = \mu \gamma_{2} + \beta_{{\text{m}}} .$$

It can be declared that $p, q > 0$ with condition (13). Now employing the Descartes’ rule of sign technique, cubic Eq. (16) can have unique positive real root $I_{{\text{m}}}^{*}$ if satisfying the following conditions:

• 1. $A_{2} > 0,{ }A_{3} > 0\,\,{\text{and}}\,\,A_{4} < 0,$

• 2. $A_{2} > 0,{ }A_{3} < 0\,\,{\text{and}}\,\,A_{4} < 0,$

• 3. $A_{2} < 0,{ }A_{3} < 0\,\,{\text{and}}\,\,A_{4} < 0,$

We consider first two cases from which we have the following inequalities.

$$\begin{aligned} & \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)l + m \chi_{{\text{m}}} \delta_{2} - \Lambda p \delta_{2} > 0, \\ & \Rightarrow \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)l + m \chi_{{\text{m}}} \delta_{2} > \Lambda p \delta_{2} , \\ & \Rightarrow \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)l + \chi_{{\text{m}}} \delta_{2} \left( {\mu - \Lambda \beta_{2} } \right) > \Lambda \delta_{2} \left( {\beta_{{\text{m}}} - \beta_{2} \chi_{{\text{m}}} } \right), \\ & \Rightarrow \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)l + \chi_{{\text{m}}} \delta_{2} \mu - \chi_{{\text{m}}} \delta_{2} \Lambda \beta_{2} > \Lambda \beta_{{\text{m}}} \delta_{2} - \Lambda \delta_{2} \beta_{2} \chi_{{\text{m}}} , \\ & \Rightarrow \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)l + \chi_{{\text{m}}} \delta_{2} \mu > \Lambda \beta_{{\text{m}}} \delta_{2} , \\ \end{aligned}$$

(17)

and

$$\begin{aligned} & A_{4} < 0, \\ & \Rightarrow \mu \beta_{2} \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)^{2} + m \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)q - {\Lambda }q^{2} < 0. \\ \end{aligned}$$

Now putting the value of $q$ and $m$ then we get,

$$\begin{aligned} & \Rightarrow \mu \beta_{2} \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)^{2} + \left( {\mu - {\Lambda }\beta_{2} } \right)\left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)\left\{ {\beta_{{\text{m}}} - \beta_{2} \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)} \right\} - {\Lambda }\left\{ {\beta_{{\text{m}}} - \beta_{2} \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)} \right\}^{2} < 0,{ } \\ & \Rightarrow { }\mu \beta_{2} \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)^{2} + \left( {\mu - \Lambda { }\beta_{2} } \right)\left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)\left\{ {\beta_{{\text{m}}} - \beta_{2} \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)} \right\} - \Lambda \left\{ {\beta_{{\text{m}}}^{2} - 2{ }\beta_{{\text{m}}} \beta_{2} \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)} \right. \\ & \quad + \left. {\beta_{2}^{2} { }\left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)^{2} } \right\} < 0, \\ & \Rightarrow { }\mu \beta_{2} \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)^{2} + \left( {\mu - \Lambda { }\beta_{2} } \right)\left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)\left\{ {\beta_{{\text{m}}} - \beta_{2} \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)} \right\} - \Lambda \beta_{{\text{m}}}^{2} + 2{ }\Lambda { }\beta_{{\text{m}}} \beta_{2} \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right) \\ & \quad - \Lambda { }\beta_{2}^{2} { }\left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)^{2} < 0, \\ & \Rightarrow \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)\left[ {\mu \beta_{2} \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right) + \mu \beta_{{\text{m}}} - \mu \beta_{2} \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right) - \Lambda { }\beta_{2} \beta_{{\text{m}}} + \Lambda \beta_{2}^{2} \left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right) + 2\Lambda \beta_{{\text{m}}} \beta_{2} - \Lambda \beta_{2}^{2} { }\left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)} \right] \\ & < \Lambda { }\beta_{{\text{m}}}^{2} , \\ & \Rightarrow \mu \beta_{{\text{m}}} + \Lambda \beta_{{\text{m}}} \beta_{2} < \frac{{\Lambda { }\beta_{{\text{m}}}^{2} }}{{\left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)}}, \\ & \Rightarrow \beta_{{\text{m}}} \left( {\mu + \Lambda \beta_{2} } \right) < \frac{{\Lambda { }\beta_{{\text{m}}}^{2} }}{{\left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)}}, \\ & \Rightarrow 1 < \frac{{\Lambda { }\beta_{{\text{m}}} }}{{\left( {\chi_{{\text{m}}} + \tau_{{\text{m}}} } \right)\left( {\mu + \Lambda \beta_{2} } \right)}}, \\ & \Rightarrow 1 < R_{{0{\text{m}}}} , \\ & \Rightarrow R_{{0{\text{m}}}} > 1. \\ \end{aligned}$$

(18)

After finding the value of ${ }I_{{\text{m}}}^{*}$, we can evaluate the value of $S_{{\text{m}}}^{*}$ using Eq. (12). This indicates that there exists a unique endemic equilibrium point $E_{1} \left( {S_{{\text{m}}}^{*} ,{ }0,I_{{\text{m}}}^{*} } \right)$ if inequalities (13), (17) and (18) are satisfied.

The existence of endemic equilibrium $E_{2} { }\left( {S_{{\text{s}}}^{*} ,{ }I_{{\text{s}}}^{*} ,{ }0} \right)$. Equating Eq. (9) to zero, we get

$$\begin{aligned} & \frac{{\beta_{{\text{s}}} I_{{\text{s}}}^{*} S^{*} }}{{1 + \beta_{1} S^{*} + \gamma_{1} I_{{\text{s}}}^{*} }} - \frac{{\tau_{{\text{s}}} I_{{\text{s}}}^{*} }}{{1 + \delta_{1} I_{{\text{s}}}^{*} }} - \left( {\omega_{{\text{s}}} + \phi_{{\text{s}}} + \mu } \right){ }I_{{\text{s}}}^{*} = 0, \\ & \Rightarrow \frac{{\beta_{{\text{s}}} I_{{\text{s}}}^{*} S^{*} }}{{1 + \beta_{1} S^{*} + \gamma_{1} I_{{\text{s}}}^{*} }} = \frac{{\tau_{{\text{s}}} I_{{\text{s}}}^{*} }}{{1 + \delta_{1} I_{{\text{s}}}^{*} }} + \left( {\omega_{{\text{s}}} + \phi_{{\text{s}}} + \mu } \right){ }I_{{\text{s}}}^{*} , \\ & {\text{i}}.{\text{e}}.,\frac{{\beta_{{\text{s}}} { }I_{{\text{s}}}^{*} { }S_{{\text{s}}}^{*} }}{{1 + \beta_{1} S_{{\text{s}}}^{*} + \gamma_{1} I_{{\text{s}}}^{*} }} = { }\frac{{\tau_{{\text{s}}} { }I_{{\text{s}}}^{*} }}{{1 + \delta_{1} I_{{\text{s}}}^{*} }} + { }\chi_{{\text{s}}} I_{{\text{s}}}^{*} . \\ \end{aligned}$$

(19)

where ${ }\chi_{{\text{s}}} = \left( {\omega_{{\text{s}}} + \phi_{{\text{s}}} + \mu } \right).$

After simplifying above Eq. (18), we have $S_{{\text{s}}}^{*}$ with regard to $I_{{\text{s}}}^{*}$ as follows

$$S_{{\text{s}}}^{*} = \frac{{\left( {1 + \gamma_{1} I_{{\text{s}}}^{*} } \right)\left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} + \chi_{{\text{s}}} \delta_{1} I_{{\text{s}}}^{*} } \right)}}{{\beta_{{\text{s}}} - \beta_{1} \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right) + \left( {\beta_{{\text{s}}} - \beta_{1} \chi_{{\text{s}}} } \right)\delta_{1} I_{{\text{s}}}^{*} }},$$

(20)

$S_{{\text{s}}}^{*}$ is positive if,

$$\beta_{{\text{s}}} > \beta_{1} \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right).$$

(21)

Now equating Eq. (8) to zero and solving, we get the following quadratic equation in $S_{{\text{s}}}^{*}$,

$${\Lambda } - \mu { }S_{{\text{s}}}^{*} - \frac{{\beta_{{\text{s}}} I_{{\text{s}}}^{*} S_{{\text{s}}}^{*} }}{{1 + \beta_{1} S_{{\text{s}}}^{*} + \gamma_{1} I_{{\text{s}}}^{*} }} = 0,$$

After simplifying we get the following equation in the following form,

$$\mu \beta_{1} S_{{\text{s}}}^{{{*}2}} + \left[ {\mu - \Lambda \beta_{1} + \left( {\mu \gamma_{1} + \beta_{{\text{s}}} } \right)I_{{\text{s}}}^{*} } \right]S_{{\text{s}}}^{*} - \Lambda { }\left( {1 + \gamma_{1} I_{{\text{s}}}^{*} } \right) = 0.$$

(22)

Now substituting the value of $S_{{\text{s}}}^{*}$ from Eq. (19) into Eq. (21), we get the following cubic equation in $I_{{\text{s}}}^{*} .$

$$\mu \beta_{1} { }\frac{{\left( {1 + \gamma_{1} I_{{\text{s}}}^{*} } \right)^{2} { }\left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} + \chi_{{\text{s}}} \delta_{1} I_{{\text{s}}}^{*} } \right)^{2} }}{{\left( {{\text{q}}_{1} + p_{1} \delta_{1} I_{{\text{s}}}^{*} } \right)^{2} }} + \left( {m_{1} + {\text{l}}_{1} I_{{\text{s}}}^{*} } \right)\frac{{\left( {1 + \gamma_{1} I_{{\text{s}}}^{*} } \right)\left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} + \chi_{{\text{s}}} \delta_{1} I_{{\text{s}}}^{*} } \right)}}{{\left( {q_{1} + p_{1} \delta_{1} I_{{\text{s}}}^{*} } \right)}} = 0,$$

where $p_{1} = \beta_{{\text{s}}} - \beta_{1} \chi_{{\text{s}}} ,{ }q_{1} = \beta_{{\text{s}}} - \beta_{1} \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right),{ }m_{1} = \mu - \Lambda \beta_{1} ,{ }l_{1} = {\upmu }\gamma_{1} + \beta_{{\text{s}}} ,$

$$\begin{aligned} & \Rightarrow { }\mu \beta_{1} \left( {1 + \gamma_{1} I_{{\text{s}}}^{*} } \right)^{2} { }\left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} + \chi_{{\text{s}}} \delta_{1} I_{{\text{s}}}^{*} } \right)^{2} + \left( {m_{1} + l_{1} I_{{\text{s}}}^{*} } \right){ }\left( {{1} + \gamma_{1} I_{{\text{s}}}^{*} } \right)\left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} + \chi_{{\text{s}}} \delta_{1} I_{{\text{s}}}^{*} } \right)\left( {q_{1} + p_{1} \delta_{1} I_{{\text{s}}}^{*} } \right) \\ & \quad - \Lambda \left( {1 + \gamma_{1} I_{{\text{s}}}^{*} } \right)\left( {q_{1} + p_{1} \delta_{1} I_{{\text{s}}}^{*} } \right)^{2} = 0, \\ & \Rightarrow { }\mu \beta_{1} \left( {1 + \gamma_{1} I_{{\text{s}}}^{*} } \right){ }\left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} + \chi_{{\text{s}}} \delta_{1} I_{{\text{s}}}^{*} } \right)^{2} + \left( {m_{1} + l_{1} I_{{\text{s}}}^{*} } \right){ }\left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} + \chi_{{\text{s}}} \delta_{1} I_{{\text{s}}}^{*} } \right)\left( {q_{1} + p_{1} \delta_{1} I_{{\text{s}}}^{*} } \right) \\ & \quad - \Lambda \left( {q_{1} + p_{1} \delta_{1} I_{{\text{s}}}^{*} } \right)^{2} = 0, \\ \end{aligned}$$

(23)

After simplifying Eq. (22), we get the following form,

$$\begin{aligned} & (\mu \beta_{1} \gamma_{1} \chi_{{\text{s}}}^{2} \delta_{1}^{2} + l_{1} \chi_{{\text{s}}} \delta_{1}^{2} p_{1} )I_{{\text{s}}}^{{{*}3}} \\ & \quad + \left[ {\mu \beta_{1} \chi_{{\text{s}}}^{2} \delta_{1}^{2} + 2{ }\mu \beta_{1} \gamma_{1} \delta_{1} \chi_{{\text{s}}} \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right) + l_{1} \chi_{{\text{s}}} \delta_{1} q_{1} + \delta_{1} p_{1} \left\{ {\left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right)l_{1} + m_{1} \chi_{{\text{s}}} \delta_{1} - \Lambda p_{1} \delta_{1} } \right\}} \right]I_{{\text{s}}}^{{{*}2}} \\ & \quad + \left[ {2{ }\mu \beta_{1} \chi_{{\text{s}}} \delta_{1} \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right) + \mu \beta_{1} \gamma_{1} \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right)^{2} + m_{1} \delta_{1} p_{1} \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right) + q_{1} \left\{ {\left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right)l_{1} + m_{1} \chi_{{\text{s}}} \delta_{1} - 2\Lambda p_{1} \delta_{1} } \right\}} \right]I_{{\text{s}}}^{*} \\ & \quad + \mu \beta_{1} \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right)^{2} + m_{1} q_{1} \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right) - \Lambda q_{1}^{2} = 0, \\ \end{aligned}$$

The above equation will be in the following form,

$$K_{1} I_{{\text{s}}}^{{{*}3}} + K_{2} I_{{\text{s}}}^{{{*}2}} + K_{3} I_{{\text{s}}}^{*} + K_{4} = 0.$$

(24)

where

$$\begin{aligned} & K_{1} = \mu \beta_{1} \gamma_{1} \chi_{{\text{s}}}^{2} \delta_{1}^{2} + l_{1} \chi_{{\text{s}}} \delta_{1}^{2} p_{1} , \\ & K_{2} = \mu \beta_{1} \chi_{{\text{s}}}^{2} \delta_{1}^{2} + 2{ }\mu \beta_{1} \gamma_{1} \delta_{1} \chi_{{\text{s}}} \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right) + l_{1} \chi_{{\text{s}}} \delta_{1} q_{1} + \delta_{1} p_{1} \left\{ {\left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right)l_{1} + m_{1} \chi_{{\text{s}}} \delta_{1} - {\Lambda }p_{1} \delta_{1} } \right\}, \\ & K_{3} = 2{ }\mu \beta_{1} \chi_{{\text{s}}} \delta_{1} \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right) + \mu \beta_{1} \gamma_{1} \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right)^{2} + m_{1} \delta_{1} p_{1} \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right) + q_{1} \left\{ {\left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right)l_{1} + m_{1} \chi_{{\text{s}}} \delta_{1} - 2{\Lambda }p_{1} \delta_{1} } \right\}, \\ & K_{4} = \mu \beta_{1} \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right)^{2} + m_{1} q_{1} \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right) - {\Lambda }q_{1}^{2} , \\ \end{aligned}$$

and

$$p_{1} = \beta_{{\text{s}}} - \beta_{1} \chi_{{\text{s}}} ,{ }q_{1} = \beta_{{\text{s}}} - \beta_{1} \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right),{ }m_{1} = \mu - \Lambda \beta_{1} ,{ }l_{1} = \mu \gamma_{1} + \beta_{{\text{s}}} .$$

It can be declared that $p_{1} ,q_{1} > 0$ with condition (21). Now, employing the Descartes rule of sign technique, cubic Eq. (24) can have unique positive real root $I_{{\text{s}}}^{*}$ if satisfying any one of the following conditions.

• (a) ${ }K_{2} > 0,{ }K_{3} > 0\,\,{\text{and}}\,\,K_{4} < 0,$

• (b) $K_{2} > 0,{ }K_{3} < 0\,\,{\text{and}}\,\,K_{4} < 0,$

• (c) $K_{2} < 0,{ }K_{3} < 0\,\,{\text{and}}\,\,K_{4} < 0.$

We consider first two cases from which we have the following inequalities,

$$\begin{aligned} & \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right)l_{1} + m_{1} \chi_{{\text{s}}} \delta_{1} - \Lambda p_{1} \delta_{1} > 0, \\ & \Rightarrow \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right)l_{1} + m_{1} \chi_{{\text{s}}} \delta_{1} > \Lambda p_{1} \delta_{1} , \\ & \Rightarrow \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right)l_{1} + \left( {\mu - \Lambda \beta_{1} } \right)\chi_{{\text{s}}} \delta_{1} > \Lambda \delta_{1} \left( {\beta_{{\text{s}}} - \beta_{1} \chi_{{\text{s}}} } \right), \\ & \Rightarrow \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right)l_{1} + \mu \chi_{{\text{s}}} \delta_{1} - \Lambda \beta_{1} \chi_{{\text{s}}} \delta_{1} > \Lambda \delta_{1} \beta_{{\text{s}}} - {\Lambda }\delta_{1} \beta_{1} \chi_{{\text{s}}} , \\ & \Rightarrow \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right)l_{1} + \mu { }\chi_{{\text{s}}} \delta_{1} > \Lambda \delta_{1} \beta_{{\text{s}}} , \\ \end{aligned}$$

(25)

and

$$\begin{aligned} & K_{4} < 0, \\ & \Rightarrow \mu \beta_{1} \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right)^{2} + m_{1} q_{1} \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right) - \Lambda q_{1}^{2} < 0, \\ & q_{1} = \beta_{{\text{s}}} - \beta_{1} \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right){\text{ and }}m_{1} = \mu - \Lambda \beta_{1} , \\ & \Rightarrow \mu \beta_{1} \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right)^{2} + \left( {\mu - {\Lambda }\beta_{1} } \right){ }\left\{ {\beta_{{\text{s}}} - \beta_{1} \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right)} \right\}\left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right) - \Lambda \left\{ {\beta_{{\text{s}}} - \beta_{1} \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right)} \right\}^{2} < 0, \\ & \Rightarrow \mu \beta_{1} \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right)^{2} + \left( {\mu - {\Lambda }\beta_{1} } \right){ }\left\{ {\beta_{{\text{s}}} - \beta_{1} \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right)} \right\}\left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right) \\ & \quad - {\Lambda }\left\{ {\beta_{{\text{s}}}^{2} - 2{ }\beta_{1} \beta_{{\text{s}}} { }\left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right) + \beta_{1}^{2} { }\left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right)^{2} } \right\} < 0, \\ & \Rightarrow \mu \beta_{1} \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right)^{2} + \left( {\mu - {\Lambda }\beta_{1} } \right) \left\{ {\beta_{{\text{s}}} - \beta_{1} \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right)} \right\}\left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right) - \Lambda \beta_{{\text{s}}}^{2} + 2 \Lambda \beta_{1} \beta_{{\text{s}}} \left( {\chi_{s} + \tau_{{\text{s}}} } \right) \\ & - \Lambda \beta_{1}^{2} { }\left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right)^{2} < 0, \\ & \Rightarrow \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right)[{ }\mu \beta_{1} \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right) + \mu \beta_{{\text{s}}} - \mu \beta_{1} \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right) - {\Lambda }\beta_{1} \beta_{{\text{s}}} + {\Lambda }\beta_{1}^{2} \left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right) + 2{\Lambda }\beta_{1} \beta_{{\text{s}}} \\ & \quad - \Lambda \beta_{1}^{2} { }\left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right)] < {\Lambda }\beta_{{\text{s}}}^{2} , \\ & \Rightarrow {\upmu }\beta_{{\text{s}}} + \Lambda \beta_{1} \beta_{{\text{s}}} < \frac{{{\Lambda }\beta_{{\text{s}}}^{2} }}{{\left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right)}}, \\ & \Rightarrow \left( {\mu + \Lambda \beta_{1} } \right)\beta_{{\text{s}}} < \frac{{{\Lambda }\beta_{{\text{s}}}^{2} }}{{\left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right)}}, \\ & \Rightarrow 1 < \frac{{{\Lambda }\beta_{{\text{s}}} }}{{\left( {\chi_{{\text{s}}} + \tau_{{\text{s}}} } \right)\left( {\mu + {\Lambda }\beta_{1} } \right)}}, \\ & \Rightarrow 1 < R_{{0{\text{s}}}} , \\ & \Rightarrow R_{{0{\text{s}}}} > 1. \\ \end{aligned}$$

(26)

After having the value of ${I}_{\mathrm{s}}^{*},$ we can evaluate the value of ${S}_{\mathrm{s}}^{*}$ using Eq. (20). This indicates that there exists a unique endemic equilibrium point $E_{2} \left( {S_{{\text{s}}}^{*} ,{ }I_{{\text{s}}}^{*} ,{ }0} \right)$ if inequalities (21), (25) and (26) are satisfied.

2.3 Analysis of Equilibrium Points and Their Stability

We analyze proposed model (8–10) and get four equilibrium points as: (1) the disease-free equilibrium (DFE) $E_{0} \left( {S_{0} ,{ }I_{{{\text{s}}0}} , I_{{{\text{m}}0}} } \right),$ i.e., there is no disease infection, (2) the disease endemic equilibrium 1 $E_{1} \left( {S^{*} ,{ }0,{ }I_{{\text{m}}}^{*} } \right),$ i.e., drug-susceptible strain comes to an end, but drug-resistant strain persists in the community, (3) the disease endemic equilibrium 2 $E_{2} \left( {S^{*} ,{ }I_{{\text{s}}}^{*} ,{ }0} \right),$ i.e., drug-resistant strain comes to an end, but drug-susceptible strain persists in the community and (4) the coexistence equilibrium $E_{2} \left( {S^{*} ,{ } I_{{\text{s}}}^{*} ,{ } I_{{\text{m}}}^{*} } \right),$ i.e., both drug-susceptible and drug-resistant strains keep continue to spread in the community. We can conclude from the analytical evidence of system (8–10) that the disease-free equilibrium $E_{0}$ is a trivial equilibrium point which is given as follows:

$$E_{0} (S_{0} ,{ }I_{{{\text{s}}0}} ,{ }I_{{{\text{m}}0}} = E_{0} \left( {\frac{{\Lambda }}{\mu },{ }0,{ }0} \right).$$

We determine the basic reproduction number utilizing the next generation matrix method (Diekmann et al. 2010). We define the matrix $\dot{x} = \left( {T + {\Sigma }} \right)x$ using the same notation expressed in (Diekmann et al. 2010), where $x = \left( {I_{{\text{s}}} ,{ }I_{{\text{m}}} } \right)^{^{\prime}}$, the matrix T corresponding to transmission (the rate of being infected of susceptible individuals who move into the infected compartments $I_{{\text{s}}}$ and $I_{{\text{m}}}$) and the matrix ${\Sigma }$ represents the corresponding transitions among the compartments.

Regarding the subsystem $I_{{\text{s}}}$ and $I_{{\text{m}}}$ we have the transmission and transition matrices are given by

$$T = \left( {\begin{array}{*{20}l} {\frac{{\beta_{{\text{s}}} S_{0} }}{{1 + \beta_{1} S_{0} }}} \hfill & 0 \hfill \\ 0 \hfill & {\frac{{\beta_{{\text{m}}} S_{0} }}{{1 + \beta_{2} S_{0} }}} \hfill \\ \end{array} } \right)\,\,{\text{and}}\,\,{\Sigma } = \left( {\begin{array}{*{20}l} { - \left( {\mu + \tau_{{\text{s}}} + \phi_{{\text{s}}} + \omega_{{\text{s}}} } \right)} \hfill & 0 \hfill \\ {\rho \omega_{{\text{s}}} } \hfill & { - \left( {\mu + \tau_{{\text{m}}} + \phi_{{\text{m}}} + \omega_{{\text{m}}} } \right)} \hfill \\ \end{array} } \right) = { }\left( {\begin{array}{*{20}l} { - \chi_{{\text{s}}} } \hfill & 0 \hfill \\ {\rho \omega_{{\text{s}}} } \hfill & { - \chi_{{\text{m}}} } \hfill \\ \end{array} } \right).$$

Now the next generation matrix, $K_{L} = T\left( { - {\Sigma }^{ - 1} } \right)$

$$= { }\left( {\begin{array}{*{20}l} {\frac{{\beta_{{\text{s}}} S_{0} }}{{1 + \chi_{{\text{s}}} \left( {1 + \beta_{1} S_{0} } \right)}}} \hfill & 0 \hfill \\ {\frac{{\rho \omega_{{\text{s}}} \beta_{{\text{s}}} S_{0} }}{{\chi_{{\text{s}}} \chi_{{\text{m}}} \left( {1 + \beta_{2} S_{0} } \right)}}} \hfill & {\frac{{\beta_{{\text{m}}} S_{0} }}{{1 + \chi_{{\text{m}}} \left( {1 + \beta_{2} S_{0} } \right)}}} \hfill \\ \end{array} } \right).$$

The characteristic equation is $\left| {K_{L} - \lambda { }I} \right| = { }\left| {\begin{array}{*{20}l} {\frac{{\beta_{{\text{s}}} S_{0} }}{{\chi_{{\text{s}}} \left( {{1} + \beta_{1} S_{0} } \right)}} - \lambda } \hfill & 0 \hfill \\ {\frac{{\rho \omega_{{\text{s}}} S_{0} \beta_{{\text{s}}} }}{{\chi_{{\text{s}}} \chi_{{\text{m}}} \left( {1 + \beta_{2} S_{0} } \right)}}} \hfill & {\frac{{\beta_{{\text{m}}} S_{0} }}{{\chi_{{\text{m}}} \left( {1 + \beta_{2} S_{0} } \right)}} - \lambda } \hfill \\ \end{array} } \right| = 0,$

$$\left( {\frac{{\beta_{{\text{s}}} S_{0} }}{{\chi_{{\text{s}}} \left( {1 + \beta_{1} S_{0} } \right)}} - \lambda } \right)\left( {\frac{{\beta_{{\text{m}}} S_{0} }}{{\chi_{{\text{m}}} \left( {1 + \beta_{2} S_{0} } \right)}} - \lambda } \right) = 0,$$

i.e., $\lambda_{1} = \frac{{\beta_{{\text{s}}} S_{0} }}{{\chi_{{\text{s}}} \left( {1 + \beta_{1} S_{0} } \right)}}$ and $\lambda_{2} = \frac{{\beta_{{\text{m}}} S_{0} }}{{\chi_{{\text{m}}} \left( {1 + \beta_{2} S_{0} } \right)}}$.

Hence, the basic reproduction numbers for drug-susceptible and drug-resistant quantities are

$$R_{{0{\text{s}}}} = \frac{{\beta_{{\text{s}}} S_{0} }}{{\chi_{{\text{s}}} \left( {1 + \beta_{1} S_{0} } \right)}} = { }\frac{{\beta_{{\text{s}}} { }\Lambda { }}}{{\chi_{{\text{s}}} \left( {\mu + \beta_{1} \Lambda } \right)}},$$

$$R_{{0{\text{m}}}} = \frac{{\beta_{{\text{m}}} S_{0} }}{{\chi_{{\text{m}}} \left( {1 + \beta_{2} S_{0} } \right)}} = \frac{{\beta_{{\text{m}}} \Lambda { }}}{{\chi_{{\text{m}}} \left( {\mu + \beta_{2} \Lambda { }} \right)}}.$$

Figure 2 shows the correlation between the model outputs $R_{{0{\text{s}}}}$ and $R_{{0{\text{m}}}}$ for the existence and stability of the four equilibrium points. The purple shaded region indicates the disease-free equilibrium point $E_{0}$ which is bounded by $\max \left[ {R_{01} ,{ }R_{02} } \right] < 1.$ The red shaded area illustrates the drug-resistant strain equilibrium point $\left( {E_{1} } \right)$ where ${ }R_{{0{\text{m}}}} > {\text{max}}\left[ {R_{{0{\text{s}}}} ,{ }1} \right].$ Conversely, drug-susceptible endemic equilibrium point $E_{2}$ is green shaded region where $R_{{0{\text{s}}}} > {\text{max}}\left[ {R_{{0{\text{m}}}} ,{ }1} \right]$. Finally, the yellow region indicates the coexistence equilibrium ${ }E^{*}$ where ${ }\max \left[ {R_{01} ,{ }R_{02} } \right] > 1.$

Fig. 2

Correlation between the model outputs basic reproduction numbers $R_{{0{\text{s}}}}$ and $R_{{0{\text{m}}}}$ corresponding to the four equilibrium points

3 Global Stability Analysis

In this section, we discuss the global stability analysis of our proposed model. We operate the method of Lyapunov function to perform the global stability analysis of each of the equilibrium point. A Lyapunov function is a scalar function founded on phase space to perform a stability analysis of the equilibrium points of a system. The benefit of this function is that without an actual solution, we can perform whether a system is stable or unstable. In addition, the global stability analyses of mathematical models can recognize areas in the parameter space where the numerous asymptotic states are stable or unstable, thus permitting us to forecast the long-term behavior of the dynamical system.

3.1 Disease-Free Equilibrium

Theorem 1

The disease-free equilibrium $E_{0}$ is globally asymptotically stable if $\rho = 0$ and $\max \left[ {R_{{0{\text{s}}}} ,{ }R_{{0{\text{m}}}} } \right] < 1.$

Proof

Consider the appropriate Lyapunov function (V), which is defined as:

$$V = \left( {S - S_{0} \ln S} \right) + I_{{\text{s}}} + I_{{\text{m}}} + C{,}$$

where $C = - S_{0} + S_{0} \ln S_{0} .$

$$\begin{aligned} & \dot{V} = \left( {1 - \frac{{S_{0} }}{S}} \right)\dot{S} + \dot{I}_{{\text{s}}} + \dot{I}_{{\text{m}}} , \\ & \quad = { }\left( {1 - \frac{{S_{0} }}{S}} \right)\left( {{\Lambda } - \mu S - \frac{{\beta_{{\text{s}}} I_{{\text{s}}} S}}{{1 + \beta_{1} S + \gamma_{1} I_{{\text{s}}} }} - \frac{{\beta_{{\text{m}}} I_{{\text{m}}} S}}{{1 + \beta_{2} S + \gamma_{2} I_{{\text{m}}} }}} \right) + \frac{{\beta_{{\text{s}}} I_{{\text{s}}} S}}{{1 + \beta_{1} S + \gamma_{1} I_{{\text{s}}} }} - \frac{{\tau_{{\text{s}}} I_{{\text{s}}} }}{{1 + \delta_{1} I_{{\text{s}}} }} - \left( {\omega_{{\text{s}}} + \phi_{{\text{s}}} + \mu } \right)I_{{\text{s}}} \\ & \quad \quad + \frac{{\beta_{{\text{m}}} I_{{\text{m}}} S}}{{1 + \beta_{2} S + \gamma_{2} I_{{\text{m}}} }} - \frac{{\tau_{{\text{m}}} I_{{\text{m}}} }}{{1 + \delta_{2} I_{{\text{m}}} }} - \left( {\omega_{{\text{m}}} + \phi_{{\text{m}}} + \mu } \right){ }I_{{\text{m}}} , \\ & \quad = \mu S_{0} - \frac{{\mu S_{0}^{2} }}{S} - \mu S + \mu S_{0} - \frac{{\beta_{{\text{s}}} I_{{\text{s}}} S}}{{1 + \beta_{1} S + \gamma_{1} I_{{\text{s}}} }} + \frac{{\beta_{{\text{s}}} I_{{\text{s}}} S_{0} }}{{1 + \beta_{1} S + \gamma_{1} I_{{\text{s}}} }} - \frac{{\beta_{{\text{m}}} I_{{\text{m}}} S}}{{1 + \beta_{2} S + \gamma_{2} I_{{\text{m}}} }} + \frac{{\beta_{{\text{m}}} I_{{\text{m}}} S_{0} }}{{1 + \beta_{2} S + \gamma_{2} I_{{\text{m}}} }} \\ & \quad \quad + \frac{{\beta_{{\text{s}}} I_{{\text{s}}} S}}{{1 + \beta_{1} S + \gamma_{1} I_{{\text{s}}} }} - \frac{{\tau_{{\text{s}}} I_{{\text{s}}} }}{{1 + \delta_{1} I_{{\text{s}}} }} - \left( {\omega_{{\text{s}}} + \phi_{{\text{s}}} + \mu } \right)I_{{\text{s}}} + \frac{{\beta_{{\text{m}}} I_{{\text{m}}} S}}{{1 + \beta_{2} S + \gamma_{2} I_{{\text{m}}} }} - \frac{{\tau_{{\text{m}}} I_{{\text{m}}} }}{{1 + \delta_{2} I_{{\text{m}}} }} - \left( {\omega_{{\text{m}}} + \phi_{{\text{m}}} + \mu } \right){ }I_{{\text{m}}} , \\ & \quad = 2\mu S_{0} - \mu S - \frac{{\mu S_{0}^{2} }}{S} + \frac{{\beta_{{\text{s}}} I_{{\text{s}}} S_{0} }}{{1 + \beta_{1} S + \gamma_{1} I_{{\text{s}}} }} + \frac{{\beta_{{\text{m}}} I_{{\text{m}}} S_{0} }}{{1 + \beta_{2} S + \gamma_{2} I_{{\text{m}}} }} - \frac{{\tau_{{\text{s}}} I_{{\text{s}}} }}{{1 + \delta_{1} I_{{\text{s}}} }} - \left( {\omega_{{\text{s}}} + \phi_{{\text{s}}} + \mu } \right)I_{{\text{s}}} - \frac{{\tau_{{\text{m}}} I_{{\text{m}}} }}{{1 + \delta_{2} I_{{\text{m}}} }} \\ & \quad \quad - \left( {\omega_{{\text{m}}} + \phi_{{\text{m}}} + \mu } \right) I_{{\text{m}}} , \\ & \quad = \mu S_{0} \left( {2 - \frac{S}{{S_{0} }} - \frac{{S_{0} }}{S}} \right) + \frac{{\beta_{{\text{s}}} I_{{\text{s}}} S_{0} }}{{1 + \beta_{1} S + \gamma_{1} I_{{\text{s}}} }} - \chi_{{\text{s}}} I_{{\text{s}}} + \frac{{\beta_{{\text{m}}} I_{{\text{m}}} S_{0} }}{{1 + \beta_{2} S + \gamma_{2} I_{{\text{m}}} }} - \chi_{{\text{m}}} I_{{\text{m}}} - \frac{{\tau_{{\text{s}}} I_{{\text{s}}} }}{{1 + \delta_{1} I_{{\text{s}}} }} - \frac{{\tau_{{\text{m}}} I_{{\text{m}}} }}{{1 + \delta_{2} I_{{\text{m}}} }}. \\ \end{aligned}$$

where $\chi_{{\text{s}}} = \omega_{{\text{s}}} + \phi_{{\text{s}}} + \mu$ and $\chi_{{\text{m}}} = \omega_{{\text{m}}} + \phi_{{\text{m}}} + \mu .$

$$\begin{gathered} = \mu S_{0} \left( {2 - \frac{S}{{S_{{0}} }} - \frac{{S_{{0}} }}{S}} \right) - \chi_{{\text{s}}} \left( {1 - \frac{{\beta_{{\text{s}}} S_{{0}} }}{{\left( {1 + \beta_{1} S_{0} } \right)\chi_{{\text{s}}} }}} \right) I_{{\text{s}}} - \chi_{{\text{m}}} \left( {1 - \frac{{\beta_{{\text{m}}} S_{0} }}{{\left( {1 + \beta_{2} S_{0} } \right)\chi_{{\text{m}}} }}} \right) I_{{\text{m}}} - \frac{{\tau_{{\text{s}}} I_{{\text{s}}} }}{{1 + \delta_{1} I_{{\text{s}}} }} - \frac{{\tau_{{\text{m}}} I_{{\text{m}}} }}{{1 + \delta_{2} I_{{\text{m}}} }}, \hfill \\ \dot{V}_{0} \le \mu S_{0} \left( {2 - \frac{S}{{S_{0} }} - \frac{{S_{0} }}{S}} \right) - \chi_{{\text{s}}} \left( {1 - R_{{{\text{0s}}}} } \right) I_{{\text{s}}} - \chi_{{\text{m}}} \left( {1 - R_{{{\text{0m}}}} } \right) I_{m} - \frac{{\tau_{{\text{s}}} I_{{\text{s}}} }}{{1 + \delta_{1} I_{{\text{s}}} }} - \frac{{\tau_{{\text{m}}} I_{{\text{m}}} }}{{1 + \delta_{2} I_{{\text{m}}} }}, \hfill \\ \end{gathered}$$

$$\square$$

Since the arithmetic mean is greater than or equal to the geometric mean, so it becomes as:

$$\frac{S}{{S_{0} }} + \frac{{S_{0} }}{S} \ge 2.$$

Therefore, we have $\dot{V}_{0} \le 0$ for $\max \left[ {R_{{0{\text{s}}}} ,{ }R_{{0{\text{m}}}} } \right] < 1.$ Hence, it follows from Lyapunov stability that $E_{0}$ is globally asymptotically stable.

3.2 Monoexistence Endemic Equilibrium 1

Theorem 2

The strain1 endemic equilibrium 1, $E_{1}$ is globally asymptotically stable if $R_{{0{\text{m}}}} > {\text{max}}\left[ {R_{{0{\text{s}}}} ,{ }1} \right].$

Proof

Consider the suitable Lyapunov function (V₁) as follows:

$${\text{V}}_{1} \left( {\text{t}} \right) = \frac{1}{{{\upbeta }_{{\text{m}}} {\text{f}}\left( {{\text{I}}_{{\text{m}}}^{*} } \right)}}{\text{ V}}_{{\text{s}}} \left( {\text{t}} \right) + \frac{{{\text{I}}_{{\text{m}}}^{*} }}{{{\upbeta }_{{\text{m}}} {\text{S}}_{{\text{m}}}^{*} {\text{f}}\left( {{\text{I}}_{{\text{m}}}^{*} ,{\text{ S}}_{{\text{m}}}^{*} } \right)}}{\text{ V}}_{{\text{m}}} \left( {\text{t}} \right).$$

(27)

$$\begin{aligned} & V_{{\text{s}}} \left( t \right) = \frac{S}{{S_{{\text{m}}}^{*} }} - 1 - \ln \left( {\frac{S}{{S_{{\text{m}}}^{*} }}} \right), \\ & \dot{V}_{{\text{s}}} \left( t \right) = \frac{1}{{S_{{\text{m}}}^{*} }} \left( {1 - \frac{{S_{{\text{m}}}^{*} }}{S}} \right)\frac{{{\text{d}}s}}{{{\text{d}}t}}, \\ & \quad \quad = { }\frac{1}{{S_{{\text{m}}}^{*} }}{ }\left( {1 - \frac{{S_{{\text{m}}}^{*} }}{S}} \right)\left( {{\Lambda } - \mu S - \frac{{\beta_{{\text{m}}} I_{{\text{m}}} S}}{{\left( {1 + \beta_{2} S + \gamma_{2} I_{{\text{m}}} } \right)}}} \right), \\ & \quad \quad = { }\frac{1}{{S_{{\text{m}}}^{*} }}{ }\left( {1 - \frac{{S_{{\text{m}}}^{*} }}{S}} \right)\left( {\mu S_{{\text{m}}}^{*} + \frac{{\beta_{{\text{m}}} I_{{\text{m}}}^{*} S_{{\text{m}}}^{*} }}{{\left( {1 + \beta_{2} S_{{\text{m}}}^{*} + \gamma_{2} I_{{\text{m}}}^{*} } \right)}} - \mu S - \frac{{\beta_{{\text{m}}} I_{{\text{m}}} S}}{{\left( {1 + \beta_{2} S + \gamma_{2} I_{{\text{m}}} } \right)}}} \right), \\ & \quad \quad = \frac{1}{{S_{{\text{m}}}^{*} }} \left( {1 - \frac{{S_{{\text{m}}}^{*} }}{S}} \right)\left[ {\mu \left( {S_{{\text{m}}}^{*} - S} \right) + \beta_{{\text{m}}} S_{{\text{m}}}^{*} f\left( {S_{{\text{m}}}^{*} , I_{{\text{m}}}^{*} } \right) - \beta_{{\text{m}}} Sf\left( {S, I_{{\text{m}}} } \right)} \right], \\ & \quad \quad = - \frac{{\left( {S - S_{{\text{m}}}^{*} } \right)^{2} }}{{S_{{\text{m}}}^{*} S}} + \beta_{{\text{m}}} f\left( {S_{{\text{m}}}^{*} , I_{{\text{m}}}^{*} } \right)\left( {1 - \frac{{S_{{\text{m}}}^{*} }}{S}} \right)\left[ {1 - \frac{{Sf\left( {S, I_{{\text{m}}} } \right)}}{{S_{{\text{m}}}^{*} f\left( {S_{{\text{m}}}^{*} , I_{{\text{m}}}^{*} } \right)}}} \right], \\ & \quad \quad = - \frac{{\left( {S - S_{{\text{m}}}^{*} } \right)^{2} }}{{S_{{\text{m}}}^{*} S}} + \beta_{{\text{m}}} f\left( {S_{{\text{m}}}^{*} , I_{{\text{m}}}^{*} } \right)\left( {1 - \frac{1}{x}} \right)\left( {1 - xF\left( z \right)} \right), \\ \end{aligned}$$

where $x = \frac{S}{{S_{{\text{m}}}^{*} }}, z = \frac{{I_{{\text{m}}} }}{{I_{{\text{m}}}^{*} }}, {\text{and}} F\left( z \right) = \frac{{f\left( {S, I_{{\text{m}}} } \right)}}{{f\left( {S_{{\text{m}}}^{*} , I_{{\text{m}}}^{*} } \right)}}.$

$$\dot{V}_{{\text{s}}} \left( t \right) = - \frac{{\left( {S - S_{{\text{m}}}^{*} } \right)^{2} }}{{S_{{\text{m}}}^{*} S}} + \beta_{{\text{m}}} f\left( {S_{{\text{m}}}^{*} , I_{{\text{m}}}^{*} } \right)\left( {1 - xF\left( z \right) - \frac{1}{x} + F\left( z \right)} \right).$$

(28)

Again

$$\begin{aligned} & V_{{\text{m}}} \left( t \right) = \frac{{I_{{\text{m}}} }}{{I_{{\text{m}}}^{*} }} - 1 - \ln \left( {\frac{{I_{{\text{m}}} }}{{I_{{\text{m}}}^{*} }}} \right), \\ & \dot{V}_{{\text{m}}} \left( t \right) = \frac{1}{{I_{{\text{m}}}^{*} }}\left( {1 - \frac{{I_{{\text{m}}}^{*} }}{{I_{{\text{m}}} }}} \right)\frac{{{\text{d}}I_{m} }}{{{\text{d}}t}}, \\ & \quad \quad = \frac{1}{{I_{{\text{m}}}^{*} }}\left( {1 - \frac{{I_{{\text{m}}}^{*} }}{{I_{{\text{m}}} }}} \right)\left( {\frac{{\beta_{{\text{m}}} I_{{\text{m}}} S}}{{\left( {1 + \beta_{2} S + \gamma_{2} I_{{\text{m}}} } \right)}} - \frac{{\tau_{{\text{m}}} I_{{\text{m}}} }}{{\left( {1 + \delta_{2} I_{{\text{m}}} } \right)}} - \chi_{{\text{m}}} I_{{\text{m}}} } \right) & , \\ & \quad \quad = \frac{1}{{I_{{\text{m}}}^{*} }}\left( {1 - \frac{{I_{{\text{m}}}^{*} }}{{I_{{\text{m}}} }}} \right)\left[ {\beta_{{\text{m}}} S f\left( {S,I_{{\text{m}}} } \right) - \left( {\frac{{\tau_{{\text{m}}} }}{{1 + \delta_{2} I_{{\text{m}}} }} + \chi_{{\text{m}}} } \right)I_{{\text{m}}}^{*} \frac{{I_{{\text{m}}} }}{{I_{{\text{m}}}^{*} }}} \right], \\ & \quad \quad = \frac{1}{{I_{{\text{m}}}^{*} }}\left( {1 - \frac{{I_{{\text{m}}}^{*} }}{{I_{{\text{m}}} }}} \right)\left[ {\beta_{{\text{m}}} S_{{\text{m}}}^{*} f\left( {S_{{\text{m}}}^{*} ,I_{{\text{m}}}^{*} } \right) \frac{{S f\left( {S,I_{{\text{m}}} } \right)}}{{S_{{\text{m}}}^{*} f\left( {S_{{\text{m}}}^{*} , I_{{\text{m}}}^{*} } \right)}} - \beta_{{\text{m}}} S_{{\text{m}}}^{*} f\left( {S_{m}^{*} , I_{{\text{m}}}^{*} } \right)\frac{{I_{{\text{m}}} }}{{I_{{\text{m}}}^{*} }}} \right], \\ & \quad \quad = \frac{1}{{I_{{\text{m}}}^{*} }}\left( {1 - \frac{1}{z}} \right)\beta_{{\text{m}}} S_{{\text{m}}}^{*} f\left( {S_{{\text{m}}}^{*} ,I_{{\text{m}}}^{*} } \right)\left[ {x F\left( z \right) - z} \right], \\ \end{aligned}$$

where $x = \frac{S}{{S_{{\text{m}}}^{*} }}, z = \frac{{I_{{\text{m}}} }}{{I_{{\text{m}}}^{*} }}, {\text{and}} F\left( z \right) = \frac{{f\left( {S, I_{{\text{m}}} } \right)}}{{f\left( {S_{{\text{m}}}^{*} , I_{{\text{m}}}^{*} } \right)}}.$

$$\dot{V}_{{\text{m}}} \left( t \right) = \frac{1}{{I_{{\text{m}}}^{*} }}\beta_{{\text{m}}} S_{{\text{m}}}^{*} f\left( {S_{{\text{m}}}^{*} ,I_{{\text{m}}}^{*} } \right)\left( {xF\left( z \right) - z - \frac{xF\left( z \right)}{z} + 1} \right).$$

(29)

From (27),

$$\begin{aligned} \dot{V}_{1} \left( t \right) & = - \frac{{\left( {S - S_{{\text{m}}}^{*} } \right)^{2} }}{{\beta_{{\text{m}}} f\left( {S_{{\text{m}}}^{*} , I_{{\text{m}}}^{*} } \right)S_{{\text{m}}}^{*} S}} + 1 - xF\left( z \right) - \frac{1}{x} + F\left( z \right) + xF\left( z \right) - z - \frac{xF\left( z \right)}{z} + 1, \\ \dot{V}_{1} \left( t \right) & = - \frac{{\left( {S - S_{{\text{m}}}^{*} } \right)^{2} }}{{\beta_{{\text{m}}} f\left( {S_{{\text{m}}}^{*} , I_{{\text{m}}}^{*} } \right)S_{{\text{m}}}^{*} S}} + \left\{ {1 - \frac{1}{x} + \ln \left( \frac{1}{x} \right)} \right\} + \left\{ {1 - \frac{xF\left( z \right)}{z} + \ln \left( {\frac{xF\left( z \right)}{z}} \right)} \right\} + F\left( z \right) - \ln \left( \frac{1}{x} \right) \\ & \quad - \ln \left( {\frac{xF\left( z \right)}{z}} \right) - z, \\ \dot{V}_{1} \left( t \right) & = - \frac{{\left( {S - S_{{\text{m}}}^{*} } \right)^{2} }}{{\beta_{{\text{m}}} f\left( {S_{{\text{m}}}^{*} , I_{{\text{m}}}^{*} } \right)S_{{\text{m}}}^{*} S}} - g\left( \frac{1}{x} \right) - g\left( {\frac{xF\left( z \right)}{z}} \right) + F\left( z \right) - \ln \left( \frac{1}{x} \right) - \ln \left( {\frac{xF\left( z \right)}{z}} \right) - z. \\ \end{aligned}$$

$$\square$$

It is easy to prove that $F\left( z \right) - z - \ln \left( \frac{1}{x} \right) - \ln \left( {\frac{xF\left( z \right)}{z}} \right) \le 0$ only for the values, $x = z = 1.$ Combining with the fact $g \ge 0$ only for the argument is 1, we observe that $\dot{V}_{1} \left( t \right) \le 0.$ We recognize that $\dot{V}_{1} \left( t \right)$ becomes zero only for the condition, $x = z = 1$. In particular, those conditions necessitate for any solution of $S\left( t \right) = S_{{\text{m}}}^{*} \left( t \right),$ and $I_{{\text{m}}} \left( t \right) = I_{{\text{m}}}^{*} \left( t \right)$ for all $t$. Thus, we observe that all solutions limit to the monoexistence endemic equilibrium 1. Hence, we conclude that $E_{{1}} \left( {S_{{\text{m}}}^{*} , 0, I_{{\text{m}}}^{*} } \right)$ is globally asymptotically stable.

3.3 Monoexistence Endemic Equilibrium 2

Theorem 3

The strain 2 endemic equilibrium 2, $E_{2}$, is globally asymptotically stable if $R_{{{\text{0s}}}} > \max \left[ {R_{{{\text{0m}}}} , 1} \right].$

Proof

Consider the following Lyapunov function,

$$V_{{2}} \left( t \right) = \frac{1}{{\beta_{{\text{s}}} f\left( {S_{s}^{*} , I_{{\text{s}}}^{*} } \right)}}V_{{\text{s}}} \left( t \right) + \frac{{I_{{{\text{s2}}}}^{*} }}{{\beta_{{\text{s}}} S_{{\text{s}}}^{*} f\left( {S_{{\text{s}}}^{*} , I_{{\text{s}}}^{*} } \right)}} V_{{{\text{is}}}} \left( t \right).$$

(30)

Now

$$\begin{aligned} V_{{\text{s}}} \left( t \right) & = g\left( {\frac{S}{{S_{{\text{s}}}^{*} }}} \right) = \frac{S}{{S_{{\text{s}}}^{*} }} - 1 + \ln \left( {\frac{S}{{S_{{\text{s}}}^{*} }}} \right), \\ \frac{{{\text{d}}V_{{\text{s}}} }}{{{\text{d}}t}} & = \frac{1}{{S_{{\text{s}}}^{*} }} \left( {1 - \frac{{S_{{\text{s}}}^{*} }}{S}} \right)\frac{{{\text{d}}s}}{{{\text{d}}t}}, \\ & = \frac{1}{{S_{{\text{s}}}^{*} }} \left( {1 - \frac{{S_{{\text{s}}}^{*} }}{S}} \right)\left( {\mu S_{{\text{s}}}^{*} + \frac{{\beta_{{\text{s}}} I_{{\text{s}}}^{*} S_{{\text{s}}}^{*} }}{{\left( {1 + \beta_{1} S_{{\text{s}}}^{*} + \gamma_{1} I_{{\text{s}}}^{*} } \right)}} - \mu S - \frac{{\beta_{{\text{s}}} I_{{\text{s}}} S}}{{\left( {1 + \beta_{1} S + \gamma_{1} I_{{\text{s}}} } \right)}}} \right), \\ & = \frac{1}{{S_{{\text{s}}}^{*} }} \left( {1 - \frac{{S_{{\text{s}}}^{*} }}{S}} \right)\left( {\mu \left( {S_{{\text{s}}}^{*} - S} \right) + \beta_{{\text{s}}} S_{{\text{s}}}^{*} f\left( {S_{{\text{s}}}^{*} ,I_{{\text{s}}}^{*} } \right) - \beta_{{\text{s}}} S f\left( {S,I_{{\text{s}}} } \right)} \right), \\ & = - \frac{{\left( {S - S_{{\text{s}}}^{*} } \right)^{2} }}{{S_{{\text{s}}}^{*} S}} + \beta_{{\text{s}}} f\left( {S_{{\text{s}}}^{*} ,I_{{\text{s}}}^{*} } \right)\left( {1 - \frac{{S_{{\text{s}}}^{*} }}{S}} \right)\left( {1 - \frac{{S f\left( {S,I_{{\text{s}}} } \right)}}{{S_{{\text{s}}}^{*} f\left( {S_{s}^{*} ,I_{{\text{s}}}^{*} } \right)}}} \right), \\ & = - \frac{{\left( {S - S_{{\text{s}}}^{*} } \right)^{2} }}{{S_{{\text{s}}}^{*} S}} + \beta_{{\text{s}}} f\left( {S_{{\text{s}}}^{*} ,I_{{\text{s}}}^{*} } \right)\left( {1 - \frac{1}{x}} \right)\left( {1 - xF\left( y \right)} \right), \\ \end{aligned}$$

where $x = \frac{S}{{S_{{\text{s}}}^{*} }}, y = \frac{{I_{{\text{s}}} }}{{I_{{\text{s}}}^{*} }}, {\text{and}} F\left( z \right) = \frac{{f\left( {S, I_{{\text{s}}} } \right)}}{{f\left( {S_{{\text{s}}}^{*} , I_{{\text{s}}}^{*} } \right)}}.$

$$\dot{V}_{{\text{s}}} = - \frac{{\left( {S - S_{{\text{s}}}^{*} } \right)^{2} }}{{S_{{\text{s}}}^{*} S}} + \beta_{{\text{s}}} f\left( {S_{{\text{s}}}^{*} ,I_{{\text{s}}}^{*} } \right)\left( {1 - xF\left( y \right) - \frac{1}{x} + F\left( y \right)} \right).$$

(31)

Again

$$\begin{aligned} V_{{{\text{is}}}} & = g\left( {\frac{{I_{{\text{s}}} }}{{I_{{\text{s}}}^{*} }}} \right) = \frac{{I_{{\text{s}}} }}{{I_{{\text{s}}}^{*} }} - 1 + \ln \left( {\frac{{I_{{\text{s}}} }}{{I_{{\text{s}}}^{*} }}} \right), \\ \frac{{{\text{d}}V_{is} }}{{{\text{d}}t}} & = \frac{1}{{I_{{\text{s}}}^{*} }}\left( {1 - \frac{{I_{{\text{s}}}^{*} }}{{I_{{\text{s}}} }}} \right)\frac{{{\text{d}}I_{{\text{s}}} }}{{{\text{d}}t}}, \\ & = \frac{1}{{I_{{\text{s}}}^{*} }}\left( {1 - \frac{{I_{{\text{s}}}^{*} }}{{I_{{\text{s}}} }}} \right)\left( {\frac{{\beta_{{\text{s}}} I_{{\text{s}}} S}}{{\left( {1 + \beta_{1} S + \gamma_{1} I_{{\text{s}}} } \right)}} - \frac{{\tau_{{\text{s}}} I_{{\text{s}}} }}{{\left( {1 + \delta_{1} I_{{\text{s}}} } \right)}} - \chi_{{\text{s}}} I_{{\text{s}}} } \right), \\ & = \frac{1}{{I_{{\text{s}}}^{*} }}\left( {1 - \frac{{I_{{\text{s}}}^{*} }}{{I_{{\text{s}}} }}} \right)\left[ {\beta_{{\text{s}}} S f\left( {S,I_{{\text{s}}} } \right) - I_{{\text{s}}}^{*} \left( {\frac{{\tau_{{\text{s}}} }}{{\left( {1 + \delta_{1} I_{{\text{s}}} } \right)}} + \chi_{s} } \right)\frac{{I_{{\text{s}}} }}{{I_{{\text{s}}}^{*} }}} \right], \\ & = \frac{1}{{I_{{\text{s}}}^{*} }}\left( {1 - \frac{{I_{{\text{s}}}^{*} }}{{I_{{\text{s}}} }}} \right) \left[ {\beta_{{\text{s}}} S_{{\text{s}}}^{*} f\left( {S_{{\text{s}}}^{*} ,I_{{\text{s}}}^{*} } \right)\frac{{Sf\left( {S,I_{{\text{s}}} } \right)}}{{S_{{\text{s}}}^{*} f\left( {S_{{\text{s}}}^{*} ,I_{{\text{s}}}^{*} } \right)}} - \frac{{\beta_{{\text{s}}} I_{{\text{s}}}^{*} S_{{\text{s}}}^{*} }}{{\left( {1 + \beta_{1} S_{{\text{s}}}^{*} + \gamma_{1} I_{{\text{s}}}^{*} } \right)}}\frac{{I_{{\text{s}}} }}{{I_{{\text{s}}}^{*} }}} \right], \\ & = \frac{1}{{I_{{\text{s}}}^{*} }}\left( {1 - \frac{{I_{{\text{s}}}^{*} }}{{I_{{\text{s}}} }}} \right) \left[ {\beta_{{\text{s}}} S_{{\text{s}}}^{*} f\left( {S_{{\text{s}}}^{*} ,I_{{\text{s}}}^{*} } \right)\frac{{Sf\left( {S,I_{{\text{s}}} } \right)}}{{S_{{\text{s}}}^{*} f\left( {S_{{\text{s}}}^{*} ,I_{{\text{s}}}^{*} } \right)}} - \beta_{{\text{s}}} S_{{\text{s}}}^{*} f\left( {S_{s}^{*} ,I_{s}^{*} } \right)\frac{{I_{{\text{s}}} }}{{I_{{\text{s}}}^{*} }}} \right], \\ & = \frac{1}{{I_{{\text{s}}}^{*} }}\left( {1 - \frac{1}{y}} \right)\beta_{{\text{s}}} S_{{\text{s}}}^{*} f\left( {S_{{\text{s}}}^{*} , I_{{\text{s}}}^{*} } \right)\left( {xF\left( y \right) - y} \right), \\ \end{aligned}$$

where $x = \frac{S}{{S_{{\text{s}}}^{*} }}, y = \frac{{I_{{\text{s}}} }}{{I_{{\text{s}}}^{*} }}, {\text{and}} F\left( z \right) = \frac{{f\left( {S, I_{{\text{s}}} } \right)}}{{f\left( {S_{{\text{s}}}^{*} , I_{{\text{s}}}^{*} } \right)}}.$

$$\begin{aligned} & = \frac{1}{{I_{{\text{s}}}^{*} }}\beta_{{\text{s}}} S_{{\text{s}}}^{*} f\left( {S_{{\text{s}}}^{*} , I_{{\text{s}}}^{*} } \right)\left( {1 - \frac{1}{y}} \right) \left( {xF\left( y \right) - y} \right), \\ & = \frac{1}{{I_{{\text{s}}}^{*} }}\beta_{{\text{s}}} S_{{\text{s}}}^{*} f\left( {S_{{\text{s}}}^{*} , I_{{\text{s}}}^{*} } \right)\left( {xF\left( y \right) - y - \frac{xF\left( y \right)}{y} + 1} \right). \\ \end{aligned}$$

(32)

Putting Eqs. (31) and (32) in (30), we get

$$\begin{aligned} \frac{{{\text{d}}V_{2} \left( t \right)}}{{{\text{d}}t}} & = - \frac{{\left( {S - S_{2}^{*} } \right)^{2} }}{{\beta_{{\text{s}}} f\left( {S_{{\text{s}}}^{*} ,I_{{\text{s}}}^{*} } \right)S S_{{\text{s}}}^{*} }} + 1 - xF\left( y \right) - \frac{1}{x} + F\left( y \right) + xF\left( y \right) - y - \frac{xF\left( y \right)}{y} + 1, \\ & = - \frac{{\left( {S - S_{2}^{*} } \right)^{2} }}{{\beta_{{\text{s}}} f\left( {S_{{\text{s}}}^{*} ,I_{{\text{s}}}^{*} } \right)S S_{{\text{s}}}^{*} }} + \left( {1 - \frac{1}{x} + \ln \left( \frac{1}{x} \right)} \right) + \left( {1 - \frac{xF\left( y \right)}{y} + \ln \left( {\frac{xF\left( y \right)}{y}} \right)} \right) + F\left( y \right) - y - \ln \left( \frac{1}{x} \right) \\ & \quad - \ln \left( {\frac{xF\left( y \right)}{y}} \right), \\ \frac{{{\text{d}}V_{2} \left( t \right)}}{{{\text{d}}t}} & = - \frac{{\left( {S - S_{2}^{*} } \right)^{2} }}{{\beta_{{\text{s}}} f\left( {S_{{\text{s}}}^{*} ,I_{{\text{s}}}^{*} } \right)S S_{{\text{s}}}^{*} }} - g\left( \frac{1}{x} \right) - g\left( {\frac{xF\left( y \right)}{y}} \right) + F\left( y \right) - y - \ln \left( \frac{1}{x} \right) - \ln \left( {\frac{xF\left( y \right)}{y}} \right). \\ \end{aligned}$$

$$\square$$

It is simple to show that $F\left( y \right) - y - \ln \left( \frac{1}{x} \right) - \ln \left( {\frac{xF\left( y \right)}{y}} \right) \le 0$ only for the values, $x = y = 1$. Combining with the fact $g \ge 0$ only for the argument is 1, we observe that $\frac{{{\text{d}}V_{2} }}{{{\text{d}}t}} \le 0$. We recognize that $\frac{{{\text{d}}V_{2} }}{{{\text{d}}t}}$ becomes zero only for the condition, $x = y = 1$. In particular, those conditions necessitate for any solution $S\left( t \right) = S_{{\text{s}}}^{*} \left( t \right)$ and $I_{{\text{s}}} \left( t \right) = I_{{\text{s}}}^{*} \left( t \right)$ for all $t$. Thus, we observe that all solutions limit to the monoexistence endemic equilibrium 2. Hence, we concluded that $E_{{2}} \left( {S_{{\text{s}}}^{*} , I_{{\text{s}}}^{*} , 0} \right)$ is globally asymptotically stable.

In addition, we observed that if $R_{{{\text{0s}}}} > \max \left[ {R_{{{\text{0m}}}} , 1} \right],$ then both the drug-susceptible and drug-resistant strains persist in the population. Figure 3 shows that the drug-susceptible strain is not essentially the most prevalent at equilibrium even if it has the highest basic reproduction number. This is a result of the circumstance that the drug-susceptible strain persists purely on direct transmission, whereas the drug-resistant strain prevalence is driven by a combination of direct transmission and amplification. These outcomes describe in part the increase in drug-resistant strain prevalence when the drug-susceptible strain is treated, which is similar to the previous study (Kuddus et al. 2021a, b).

Fig. 3

Impact of amplification $\left( \rho \right)$ on drug-susceptible and drug-resistant strains when $R_{{0{\text{s}}}} > {\text{max}}\left[ {R_{{0{\text{m}}}} ,{ }1} \right]$

4 Sensitivity Analysis

In this section, we performed sensitivity analysis which is very important to identify the significance of the model parameter to prevent the control of drug-susceptible and drug-resistant strains. In this analysis, we implemented the PRCC to identify the effect of specific parameter on the model outcome according to the variation of those value. The Latin Hypercube Sampling (LHS) procedure is taken to evaluate the PRCC values for several input parameters. A total of 100,000 simulations are executed, and a uniform distribution is allocated to every model parameter. Here, we consider the model outputs are the basic reproduction numbers, namely $R_{{0{\text{s}}}}$ and $R_{{0{\text{m}}}}$. The PRCC values remain between the ranges −1 and + 1. Positive PRCC value for the model parameters reveals a favorable response to the outcome; however, negative value for the model parameters represents a deleterious correlation of the model outcomes. The enormous (smaller) value of the absolute PRCC value demonstrates more (less) significant interdependence between the parameter and the model outcome.

Figures 4, 5 represent the correlation between the model outputs ${ }R_{{0{\text{s}}}} , R_{{0{\text{m}}}}$ corresponding to the model parameters $\beta_{{\text{s}}} ,{ }\beta_{{\text{m}}} ,{ }\omega_{{\text{s}}} ,{ }\omega_{{\text{m}}} ,{ }\phi_{{\text{s}}},{ }\tau_{{\text{s}}},{ }\tau_{{\text{m}}},{ }\beta_{{\text{1}}},{ }\beta_{{\text{2}}}$ and $\phi_{{\text{m}}}$. The transmission rate $\beta_{{\text{s}}}$ and $\beta_{{\text{m}}}$ has highest positive PRCC values, which reveals that β_s and β_m are most significant parameter to increase the basic reproduction numbers $R_{{0{\text{s}}}}$ and $R_{{0{\text{m}}}}$, respectively. In contrast, the parameters $\omega_{{\text{s}}},{ }\tau_{{\text{s}}},{ }\beta_{{\text{1}}}$, and $\phi_{{\text{s}}} { }$ as well as $\omega_{{\text{m}}},{ }\tau_{{\text{m}}},{ }\beta_{{\text{2}}}$ and $\phi_{{\text{m}}}$ have negative PRCC values, which infers that increasing these parameters value will decrease $R_{{0{\text{s}}}}$ and $R_{{0{\text{m}}}}$ and the disease will be going to eradicate from the society.

Fig. 4

PRCC values representing the sensitivities of the model output $R_{{0{\text{s}}}}$ with regard to the estimated parameters ${ }\beta_{{\text{s}}}$, $\omega_{{\text{s}}},{ }\tau_{{\text{s}}},{ }\beta_{{\text{1}}}$, and $\phi_{{\text{s}}}$

Fig. 5

PRCC values representing the sensitivities of the model output $R_{{0{\text{m}}}}$ with regard to the estimated parameters ${ }\beta_{{\text{m}}}$, $\omega_{{\text{m}}},{ }\tau_{{\text{m}}},{ }\beta_{{\text{2}}}$, and $\phi_{{\text{m}}}$

5 Numerical Simulations

In this section, we conducted numerical simulations of our proposed two-strain disease model with the help of MATLAB routine (ode45 solver) to support the analytical result. The ode45 solver is very useful for solving ordinary differential equations with several initial condition. It associates approaches of orders four and five to evaluate error and regulate step size. ODE45 is so precise to deliver appropriate results than the other numerical methods. According to the analytical result, we found four equilibrium points such as: a disease-free equilibrium $\left( {E_{0} } \right)$; a monoexistent endemic equilibrium 1 $\left( {E_{1} } \right)$; a monoexistent endemic equilibrium 2 $\left( {E_{2} } \right)$ and coexistent endemic equilibrium $\left( {{\text{E}}_{3} } \right)$. Using the basic reproduction numbers for drug-susceptible $\left( {R_{{0{\text{s}}}} } \right)$ and drug-resistant strain $\left( {R_{{0{\text{m}}}} } \right)$ found using the next generation matrix technique, we investigated the impact of their relative magnitude on the infected population of both drug-susceptible and drug-resistant strains. Figures 6, 7, 8 and 9 represent in which conditions the drug-susceptible and drug-resistant strains will be fade-outs or persist in the population, thus allow us to predict the long-term behavior of the disease dynamics.

Fig. 6

Disease-free equilibrium: $\left[ {R_{{0{\text{s}}}} ,\;R_{{0{\text{m}}}} } \right] < 1$. In this case both drug-susceptible prevalence and drug-resistant prevalence dies-out

Fig. 7

Disease endemic equilibrium 1: $R_{{0{\text{m}}}} > {\text{max}}\left[ {R_{{0{\text{s}}}} ,{ }1} \right]$. In this case drug-resistant prevalence spreads in the population but drug-susceptible dies-out

Fig. 8

Disease endemic equilibrium 2: $R_{{0{\text{s}}}} > {\text{max}}\left[ {R_{{0{\text{m}}}} ,{ }1} \right]$. In this case drug-susceptible prevalence spreads in the population, but drug-resistant prevalence dies-out

Fig. 9

Co-existent endemic equilibrium: $\max \left[ {R_{{0{\text{s}}}} ,{ }R_{{0{\text{m}}}} } \right] > 1$. In this case both of the drug-susceptible and drug-resistant prevalence spreads in the population

Here, we used different initial conditions to demonstrate the system of trajectories in all equilibrium points. From Fig. 6 we observe that both of the disease strains are dies-out when the basic reproduction numbers are less than one (i.e., $\max \left[ {R_{{0{\text{s}}}} ,{ }R_{{0{\text{m}}}} } \right] < 1$). From Fig. 7 we discover that the drug-susceptible strain dies-out, whereas the drug-resistant strain persists in the population when ${ }R_{{0{\text{m}}}} > {\text{max}}\left[ {R_{{0{\text{s}}}} ,{ }1} \right]$. Figure 8 depicts that if $R_{{0{\text{s}}}} > {\text{max}}\left[ {R_{{0{\text{m}}}} ,{ }1} \right]$ hold, then the drug-susceptible strain transmits into the population, whereas the drug-resistant strain dies-out from the population. Finally, from Fig. 9 we observe that both drug-susceptible and drug-resistant strains spread-out in the population if $\max \left[ {R_{{0{\text{s}}}} , R_{{0{\text{m}}}} } \right] > 1$. Therefore, we need to reduce the period of infectiousness down until $\max \left[ {R_{{0{\text{s}}}} ,{ }R_{{0{\text{m}}}} } \right] < 1$ for controlling drug-susceptible and drug-resistant strains. This information can hopefully advise Ministry of Health for the programmatic management of treatment regimens.

6 Conclusion

In this study, we proposed a two-strain SIR epidemic model and mathematically inspected the nonlinear incidence and treatment. We executed a series of analytical and numerical simulations of our model and obtained four equilibrium points such as: a disease-free equilibrium $\left( {E_{0} } \right)$; a monoexistent endemic equilibrium 1 $\left( {E_{1} } \right)$; a monoexistent endemic equilibrium 2 $\left( {E_{2} } \right)$ and coexistent endemic equilibrium $\left( {E_{3} } \right)$. We performed the existence of all equilibria. The stability analysis also performed for the disease-free equilibrium $\left( {E_{0} } \right)$, monoexistent endemic equilibrium 1 $\left( {E_{1} } \right)$ and monoexistent endemic equilibrium 2 $\left( {E_{2} } \right)$ of the system and showed that they are globally asymptotically stable. We determined the basic reproduction numbers $R_{{0{\text{s}}}}$ and $R_{{0{\text{m}}}}$ for the drug-susceptible and drug- resistant strains. From this determination, we observed that the disease will eradicate from the society if the basic reproduction numbers are less than one; otherwise, the disease persists in the population.

We also investigated that drug-susceptible strain persists mainly on direct transmission, whereas the drug-resistant strain is driven by a combination of direct transmission and amplification. These outcomes describe in part the increase in drug-resistant strain prevalence when the drug-susceptible strain is treated, which is similar to the previous study (Haq et al. 2022; Kuddus et al. 2021a, b; Meehan et al. 2018). Therefore, rapid identification of drug-resistant strain, rapid diagnosis and prompt commencement of treatment and successful completion of treatment are the most effective ways of eliminating drug-resistant strain. The information that we generate from this model about amplification and transmission will either challenge or support the recommendation that exposure to drug-resistant patients and person to person transmission is the major mode of acquiring drug-resistant strain. If most is transmitted and not acquired, this recommends that efforts to improve present treatment of drug-susceptible patients—aimed at enhancing adherence to therapy and dropping acquired resistance—will not significantly decrease the epidemic of drug-resistant strain.

In addition, a sensitivity analysis is carried out to identify the most significance model parameter for the controlling of the disease outbreak. We found that transmission rates $\beta_{{\text{s}}}$ and $\beta_{{\text{m}}}$ are the most important parameters. We also performed the correlation between two basic reproduction numbers, namely $R_{0s}$ and $R_{0m}$, and displayed their consequences. Finally, numerical simulations are conducted to support the analytical outcomes of the model and displayed the system trajectories at each equilibrium point.

The existence and global stability of the transmission dynamics of infectious diseases models with treatment and vaccination were considered in previous modeling studies using different types of methods (e.g., fractional-order, Atangana–Baleanu–Caputo Operator) (Gholami et al. 2022; Naik et al. 2020; Naim et al. 2022). Previous studies showed that if the basic reproduction number is less than one, then the disease fade-out using Routh-Hurwitz stability criterion. If the basic reproduction number is greater than one, then the disease persists in the population. Finally previous studies also showed the impact of treatment and vaccination on the dynamics of COVID-19 (Allegretti et al. 2021; Joshi et al. 2023; Yavuz et al. 2021, 2022).

In this study, we measured a two-strain disease model with related infectious compartments and use it to examine the emergence and spread of drug-resistant strain through amplification. Here, we integrated Beddington–DeAngelis-type incidence rate and the saturated treatment rate, and with a competing mechanism between the drug-susceptible and drug-resistant strains. Here we found that if the basic reproduction numbers of drug-susceptible strain and drug-resistant strain are less than one, then the disease is die-out from the community. If the basic reproduction number of drug-resistant strain is greater than one, but that of the drug-susceptible strain is less than one, then only drug-resistant strain persists. Finally, the drug-susceptible and drug-resistant strains persist in the population if the drug-susceptible strain basic reproduction number is greater than one and the drug-resistant strain’s basic reproduction number bigger than threshold, owing to the amplification pathway to achieve co-existence.