1 Introduction

High-level radioactive waste (HLW) stored in a deep rock mass can be effectively isolated from human living environments through engineering and geological barriers of a deep geological repository (Hietala 2021; Wang 2014; Wang et al. 2019). The deep granite has long been believed to be the ideal geological barrier of the deep geological repository for HLW because of its high strength, excellent integrity, and reduced permeability (Chopra et al. 2015; Soler et al. 2015; Souley et al. 2001; Young et al. 2020). In China, the first underground research laboratory (URL) as the research platform for the deep geological repository for HLW is being built in a deep granite rock mass in the Beishan area of Gansu Province in Northwest China (Wang et al. 2018). Therefore, the deep granite’s damaged characteristics and mechanical properties under loading significantly influence the URL’s structure safety and its disposal function for HLW.

The rock mass is made up of the rock blocks and structural surfaces, including joints and fissures. The evolution characteristic of the cracks and defects inside the rock are crucial in the rock mass stability under the loading and unloading process (Wang et al. 2020). The crack development of granite under loading testing can be divided into the following four stages (Fig. 1): crack closure (I), elastic deformation (II), stable crack propagation (III), and crack unsteady growth (IV) stages (Cai et al. 2004; Martin and Chandler 1994). Crack stress thresholds denote the stress limits of different crack development stages of rock and include crack closure stress (σcc), initiation stress (σci), damage stress (σcd) and peak stress (σf). Currently, the crack volumetric strain model as the primary technique, and AE parameters and strain energy methods have been used in the rock to obtain these crack stress thresholds(Ghasemi et al. 2020; Wu et al. 2021; Zhao and Cai 2010). Rock volumetric strain under loading can be calculated using the motoring axial and radial strain. Based on the crack of the volumetric strain model, the volumetric strain also equals the sum of the volumetric strain of elastic deformation of rock under loading and the volumetric strain of the crack’s development. Based on this idea, σcd can be derived from the inflection point of the rock volumetric strain curve, and σcc and σci are obtained from the beginning and end point of the horizontal development stage of the crack’s volumetric strain curve, respectively, as shown in Fig. 1.

Fig. 1
figure 1

The crack’s development stages of granite under loading testing (Martin and Chandler 1994)

Full size image

The released elastic waves inside the rock loading are generally called acoustic emission (AE) and can be continuously monitored with the help of an AE monitoring device. A series of AE information, such as AE characteristic parameters, AE spatial locations, AE time series, and AE spectral characteristics, can accurately reflect the cracks and damage development status inside the tested rock (Lei et al. 2000; Ishida et al. 2017; Ruck et al. 2017). Therefore, rock crack damage characteristics based on AE monitoring have become a hot topic in the rock engineering field. The AE hit count, AE accumulative count and AE amplitude of crack damage development of rock were determined using an AE monitoring device, which was performed by several researchers in laboratory and field tests to study the correlation between AE parameters and damage variables (Gong et al. 2017; Moradian et al. 2016; Huang and Li 2014). The strain energy evolution can best analyze the rock damage development based on the energy theory. Several researchers have recently constructed a set of constitutive models and energy strength criteria based on energy theory (Chen et al. 2017; Deng et al. 2016; Li et al. 2017; Tarasov and Stacey 2017; Zhang et al. 2018, 2019b). In order to study the strain energy evolution mechanism of rock damage, several experts subjected to soft and hard rock have conducted various loading and unloading tests (Li et al. 2019; Zhalehjoo et al. 2018; Zhu et al. 2016; Zhang et al. 2019a). They discovered that the strain energy absorbed inside the rock, strain energy corresponding to the rock failure point and dissipated strain energy of rock during loading all increase linearly with the confining pressure levels rising. The failure angle of rock during triaxial compression tests increases in proportion to the absorbed strain energy. The dissipated strain energy rises when confining pressure is unloaded throughout different loading path experiments, showing a nonlinear connection with time and radial strain.

In recent years, various testing methods have extensively investigated rock damage characteristics. While there have been few studies on the damage characteristics of Beishan deep granite based on the AE method and energy theory. Therefore, conventional triaxial compression tests for the Beishan deep granite specimens used in five confining pressure settings were carried out in this study. The AE monitoring technology was used in the rock loading process in the testing. The mechanical properties, AE characteristics and energy evolution of Beishan deep granite during triaxial loading were investigated, and the AE parameters and strain energy evolutions under various damage stages of the rock loading were analysed. This research can provide helpful information that may inform the construction of the Beishan URL.

2 Methodology

2.1 Specimen preparation

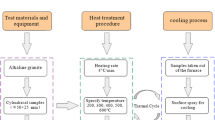
China’s first URL of deep geological disposal for HLW is being built in the Beishan region in Northwest China. The main structure of the Beishan URL includes three vertical shafts, a sloping ramp and two layers of research chambers, as shown in Fig. 2a. The deep granite cores used in this study were obtained from the BS33 exploration borehole near the construction site of the Beishan URL, and the sampling depth ranges from 540 to 560 m. X-ray diffraction testing results show that the material matrix of the Beishan deep granite core is composed of 17% quartz, 60% plagioclase, 15% alkaline feldspar, 5% biotite, 2% sodium feldspar, and 1% myrmekite. According to the ISRM suggesting method (Zheng et al. 2010), the Beishan deep granite cores were turned into cylinder specimens of φ50 × 100 mm, as shown in Fig. 2b. The natural density of the specimens ranges from 2.612 to 2.713 g/cm3, and the average water content of the specimens is approximately 0.68%.

Fig. 2
figure 2

The Beishan URL’s structure and deep granite specimens: a Beishan URL structure; b Beishan deep granite specimens

Full size image

2.2 Testing apparatus and testing procedures

The conventional triaxial compression testing for the Beishan deep granite specimens in this study was conducted through an MTS815 loading system (Fig. 3a). The maximum axial loading and confining pressure of 4600 kN and 140 MPa can be provided from the MTS815 loading system (Sun et al. 2020). Before the testing started, a series of linear variable differential transformers with 1 m accuracy were installed inside the confining pressure chamber to monitor the axial and radial strains of the rock loading process, as shown in Fig. 3b. In this test, a PCI-2 AE monitoring device automatically tracked the AE signals throughout the rock loading process. The AE sensors were symmetrically mounted outside the confining pressure chamber, as shown in Fig. 3c, and the AE amplitude threshold and AE sampling frequency under the rock loading tests were set at 40 dB and 300 kHz to minimize the inaccuracy as much as possible.

Past in situ hydraulic fracturing tests of the Beishan URL shown that the rock mass’s maximum horizontal in situ stress is within 25 MPa at a depth of 600 m. Therefore, the triaxial compression tests in this study were conducted with confining pressure settings of 0.5, 5, 10, 15, and 25 MPa, and three granite specimens were repeatedly tested under the same confining pressure condition. During the whole compression testing, different types of loading rate control methods are used to make the rock stable failure. First, the hydrostatic pressure loading at a rate of 5 MPa/min is used to simultaneously load the axial and radial stresses until the confining pressure reaches the designed value. Then, the axial loading rate was 30 kN/min to the peak strength of the rock. Finally, the axial displacement rate remained constant at 0.02 mm/min until the rock completely failed.

Fig. 3
figure 3

MTS815 loading system and PCI-2 monitoring device: a MTS815 loading system; b LVDTs; c AE sensors

Full size image

3 Experimental results

3.1 Deformation and crack damage characteristics of specimens

Figure 4 displays the relationship curves between the stress and strain of the specimens under this test. In Fig. 4, σ1 represents axial stress, σ3 represents confining pressure, and ε1, ε3, εv and εcv represent axial, radial, volumetric, and crack volumetric strains, respectively. As seen in Fig. 4, there is a wide change range of deformation properties between the specimens subjected to various confining pressure levels. When the confining pressures are 0.5, 5, 10, 15 and 25 MPa, the peak stresses of the specimens are 225.74, 229.18 and 287.01, 373.37, and 382.48 MPa, the axial peak strains of the specimens are 0.281%, 0.331%, 0.403%, 0.663%, and 0.520%, and the radial peak strains of the specimens are − 0.143%, − 0.197%, − 0.414%, − 0.379%, and − 0.315% (Table 1). The peak stress and strain in the axial and radial direction rise with increasing confining pressure. In the prepeak stress‒strain stage, the deviatoric stress rises roughly linearly with increasing axial strain, but in the postpeak stress‒strain stage, the deviatoric stress falls sharply. The Beishan deep granite specimens show elastic–brittle failure characteristics under various confining pressure conditions.

Fig. 4
figure 4

The relationship curves of stress and strain of the specimen under various confining pressure levels: a σ3 = 0.5; b 5; c 10; d 5; e 25 MPa

Full size image

The elastic modulus E and Poisson’s ratio λ of the deep granite specimens were determined and are listed in Table 1. When the confining pressure levels rise, the E and λ of the rock increase at decreasing rates, and the E and λ are approximately constant for confining pressures over 15 MPa. In addition, the peak strains in both the axial and radial directions progressively increase with increasing confining pressure and tend to remain constant when the confining pressure level reaches 15 MPa. The primary causes of these patterns are that initial cracks and flaws inside the rock have lower closure degrees when the hydrostatic pressure is low and higher closure degrees when the confining pressure is high. Both E and λ increase with the relative compactness of the rock. With confining pressures over 15 MPa, however, the compactness of the rock does not improve noticeably with increasing pressure, and the deformation characteristics of the rock tend to remain constant.

To determine the crack stress thresholds for various damage stages of granite, Martin and Chandler (1994) analysed the rock progressive failure process and established the crack volumetric strain model. The εv, εcv, εev and ε1 of the Beishan deep granite specimens at varying confining pressures were measured using the crack volumetric strain model, and their respective relationship curves are given in Fig. 4. The prepeak phases of the stress‒strain curve for the Beishan deep granite includes the following four stages:

  1. (I)

    During the first stage, known as the “Crack closure stage,“ initial fractures and internal faults inside the rock gradually close, resulting in crack volumetric strain εcv decreasing nonlinearly with increasing axial strain. At this stage, the relationship between the stress and strain of the Beishan deep granite under various confining pressures is somewhat varied because of the varying microcrack numbers and shapes inside the rock.

  2. (II)

    In the second stage, the “Elastic deformation stage, " all initial cracks and imperfections inside the rock have closed, and the rock may be treated as if it were a linearly elastic material. A higher axial strain does not significantly alter the crack volumetric stain εcv. The rock exhibits an almost linear relationship between deviatoric stress and both axial and radial strain. The crack closure stress σcc is the deviatoric stress that begins at the point where the horizontal line of the crack volumetric stain εcv begins.

  3. (III)

    As the axial strain grows, the rock undergoes stable crack propagation stage, during which new cracks originate and grow inside the rock. It can be shown that the crack initiation stress σci is located at the endpoint of the horizontal growth stage of the crack volumetric strain εcv. The crack damage stress σcd is located at the maximum volumetric strain εv.

  4. (IV)

    In the unsteady crack growth stage, the crack propagation and coalescence of fractures inside the rock occur at a high rate, and the crack volumetric strain εcv rises at an even higher rate. The crack damage stress σcd is the border point from stable crack expansion to unstable crack expansion. It is commonly considered that the long-term strength of the rock at the stress exceeds the peak stress σf, and a macro fracture is formed in the rock.

Table 1 shows the crack stress thresholds and their stress ratios (σcc/σf, σci/σf and σcd/σf) for the specimens from the Beishan area under varying confining pressures. The confining pressure has little influence on the stress ratios, but it is strongly connected to the crack stress thresholds. The Beishan deep granite has a σcd/σf of 74–89% over a range of confining pressures. Martin and Chandler (1994) found that the average ratio of σcd/σf of Lac du Bonnet granite is 80%. Because of their unique internal structures, minerals, and formation conditions, Beishan granite and Lac du Bonnet granite have distinct crack damage characteristics.

The crack stress thresholds of the specimens rise linearly with increasing confining pressure, but the growth rates in individual thresholds differ noticeably, as shown in Fig. 5a. With increasing confinement pressure, the peak stressσf rises faster than the crack closure stress σcc. Furthermore, the various thresholds are similar under lower confining pressures and diverge with increasing pressure. As shown in Fig. 5b, with increasing confining pressure, the stress ratio of the Beishan granite exhibits almost no change.

Fig. 5
figure 5

The crack stress thresholds, stress ratio, and confining pressure connection curves: a Crack stress threshold; b Stress ratios

Full size image
Table 1 The deformation parameters and crack stress thresholds
Full size table

3.2 Strength parameters of specimens

Rock compressive strength is an essential geotechnical metric for many engineering uses (Wang and Wan 2019). Rock mechanics and engineering rely heavily on the Mohr‒Coulomb (M–C) and Hoek‒Brown (H–B) failure criteria. Rock fracture occurs when the shear force reaches its maximum value at the shear face, as stated by the M–C criterion. The maximum shear force is determined by the shear face cohesion and internal frictional force. Therefore, this is how the linear M–C criteria are stated in the σ1–σ3 coordinate system (Su et al. 2003):

$$\sigma _{1} = \frac{{1 + \sin \varphi }}{{1 - \sin \varphi }}\sigma _{3} + \frac{{2c \cdot \cos \varphi }}{{1 - \sin \varphi }}$$
(1)

where c is the rock’s cohesiveness, and φ is the rock’s internal friction angle.

The H–B criterion was established and improved through indoor and field tests. In the σ1–σ3 coordinate system, the nonlinear H–B criterion is written as follows:

$$\sigma _{1} = \sigma _{3} + \sigma _{c} \left( {m_{i} \frac{{\sigma _{3} }}{{\sigma _{c} }} + s} \right)^{a}$$
(2)

where σc represents the uniaxial compressive strength and mi, s, and a represent the other rock strength parameters. When mi is large, the rock is robust. In intact rock, s and a are 1 and 0.5, respectively.

Equations (1) and (2) were used to fit the relationship between σf and σ3. In Fig. 6, the M–C and H–B criteria both have excellent fitting correlation coefficients (R2 = 0.891 and 0.896, respectively), demonstrating their ability to reflect the triaxial compressive strength of Beishan deep granite more accurately. The strength parameters are c = 34.01 MPa, φ = 1.56° and σc = 193.91 MPa and mi=26.38. As shown in Fig. 7, H–B fitting curves at varying confining pressure intervals were collected to study the effect of confining pressure on the parameter mi of the H–B criterion. For instance, the fitting curve of mi = 25.71 (0~15 MPa) means that the strength parameter mi obtained for confining pressures of 0~5 MPa is 25.71. As shown in Fig. 7, as the confined pressure interval becomes small, the parameter mi also decreases. The parameter mi has a fluctuation range of 25.71 to 26.38 (in σ3 ≥ 15 MPa), and it is insensitive to variations in the high confining pressure interval. For low confining pressure (in σ315 MPa), however, the parameter mi clearly falls, with a range of 21.66 to 22.60.

Fig. 6
figure 6

Fitting curves of the M–C and H–B criteria

Full size image
Fig. 7
figure 7

Effect of confining pressure intervals on the H–B parameter mi of Beishan deep granite

Full size image

The studied Beishan granite specimens all failed macroscopically as single-sided shear fractures, as seen in Fig. 8. The rock failure mechanism at lower confining pressures is greatly influenced by tensile fractures, as shown by the immediate region of the fracture surface being noticeably rough and the fracture surface exhibiting several bends before further propagation. The fracture angles steadily decrease, and the fracture surfaces tend to flatten with increasing confining pressure.

Fig. 8
figure 8

Failure mode of the specimens under varying confining pressures

Full size image

4 Discussion

4.1 Acoustic emission characteristics

The development of crack damage due to rock underloading may be accurately reflected by the spatial position of AE events during the whole testing procedure. Because the AE spatial location results of the Beishan deep granite specimens with varying confining pressure settings were similar, the development of the AE spatial location of specimen BS3–1 during the testing process was analysed. The evolution of the AE spatial location was divided into six segments with a stress increment of 0.2σf, as shown in Fig. 9. In the 0~0.4σf segment, the original defects and initial microcracks inside the rock are gradually closed under loading, and the AE events are evenly distributed inside the rock. Rock deformation roughly reaches the elastic deformation stage in the 0.4~0.6σf segment as stress increases. At this stage, new fractures are not forming inside the rock, and only a few AE events are being generated by the friction of the closed microcracks. When stresses exceed 0.6σf, existing cracks expand, and new ones form over time. The AE events increase significantly in the 0.6~0.8σf segment. Inside the 0.8~1.0σf section, AE events within the rock grow dramatically as the stress continues to rise, and the AE events cluster together within the rock. Despite the formation of a macroscopic fracture surface after the stress has reached its maximum, the rock retains some of its original bearing capacity. The AE events in the 1.0~0.8 σf range are caused by the frictional sliding of the fracture surfaces.

Fig. 9
figure 9

The spatial location of AE events: σ3  = 10 MPa

Full size image

Figure 10 shows how the AE hit count changes as crack damage progresses through its various phases. During the crack closure stage, the initial fractures inside the rock are progressively closed. The pace at which the AE hit count is low at this point is because fewer AE events are being created. During the elastic deformation stage of the rock, the slipping of the microcrack surface produces a lower AE hit count. When the pressure is increased, the rock enters the stable crack propagation stage, during which internal fissures begin to form and spread. AE event occurrences occur, and the AE hot count gradually rises but stays relatively low at this stage. Rapid fracture propagation, an exponential rise in the AE hit count, and an emergence time of approximately 1.5103/s characterize the unsteady crack growth stage. It is common for the AE hit count to have a high-frequency component after the peak. The confining pressure significantly impacts the variance in the AE hit count under varying stages of crack damage. There is a correlation between the confining pressure and the time spent in each stage of crack damage, and the AE hit count oscillates more erratically as the pressure grows.

Fig. 10
figure 10figure 10

The curves of axial stress, AE hit count and time under various confining pressure levels: a σ3  = 0.5; b 5; c 10; d 5; e 25 MPa

Full size image

The curves between the AE accumulative count and the testing time of the specimens are shown in Fig. 11. The high-frequency section of the AE hit count typically coincides with the increase in the AE accumulative count. The changes in the AE accumulative count of specimens under varying confining pressure conditions are similar in each crack damage stage. Six distinct phases were identified in the AE accumulation curves: the initial stable, the first fast growth, the gentle growth, the second rapid growth, and the stable phases.

Fig. 11
figure 11figure 11

The curves of axial stress, AE energy accumulative count and time of the specimens under various confining pressure levels: a σ3  = 0.5; b 5; c 10; d 5; e 25 MPa

Full size image

The initial stable phase mainly coincides with the crack closure, elastic deformation and stable crack propagation stages of the crack damage process, and the AE accumulative count is low. The first rapid growth phase corresponds to the unsteady crack growth stage, and the cracks inside the rock rapidly propagate, intersect, and penetrate with increasing loading. The AE accumulative count is relatively high at this phase. When the peak stress occurs, the rock strength is composed of the biting force and friction force of the shear fracture surface. Therefore, specimens still exhibit stable crack expansion, causing the AE accumulative count to increase. When the internal cracks accumulate to a certain extent, the unstable propagation and penetration of cracks occur again, and the AE accumulative count rapidly increases for the second time. After the rock reaches its residual strength, the AE accumulative count tends to be stable.

4.2 Analysis of strain energy

When rocks are deformed, energy is often added, stored, dissipated, and eventually released. During the experiment, the rock absorbs strain energy from the testing equipment, which is then transformed into elastic strain energy and stored inside the rock. This stored energy is progressively lost as cracks emerge in the rock. This is an examination of the strain energy development of cracks in deep granite from Beishan. As seen in Fig. 12, the rock’s strain energy has three components: total energy U, elastic energy Ue and dissipated energy Ud.

Fig. 12
figure 12

Relationship between Ue and Ud under the triaxial compression tests

Full size image

U in these tests can be calculated using Eq. (3). Ue and Ud can be calculated using Eqs. (4) and (5), respectively.

$$U = \int_{0}^{{_{{\varepsilon _{1} }} }} \sigma _{1} d\varepsilon _{1} {\text{ + 2}}\int_{0}^{{_{{\varepsilon _{3} }} }} \sigma _{3} d\varepsilon _{3}$$
(3)
$$U_{d} = U{\text{ - }}U_{e}$$
(4)
$$\sigma _{1} = \sigma _{3} + \sigma _{c} \left( {m_{i} \frac{{\sigma _{3} }}{{\sigma _{c} }} + s} \right)^{a}$$
(5)

The strain energy and axial strain of specimens at varying confining pressures are shown graphically in Fig. 13. In the prepeak phase, as shown in Fig. 13, U, Ue and Ud all rise. Ue increases faster than Ud during the prepeak period, suggesting a critical function for Ue. Because Ud measures the amount of rock damage, it rises gradually as axial stress rises. As stress approaches its peak value, fissures in the rock expand and penetrate more profoundly, and the rates of rise in U and Ud accelerate. After the peak, Ue is gradually reduced after being released, while Ud shows a dramatic rise. The following is a description of the strain energy development of this Beishan granite based on the crack damage process in this rock material.

  1. 1.

    Crack closure and elastic deformation stage: cracks are closed, and elastic strain energy stored unit strain rises, both of which are indicative of a rising Ue rate. The values of U and Ue keep rising, and some Ud is produced as well.

  2. 2.

    Stable crack propagation stage: fissures in the rock propagate steadily, and the rock’s strength progressively rises. U and Ue slowly increase, and Ud gradually increases.

  3. 3.

    Crack unsteady growth stage: fissures in the rock grow fast, cross one another, and eventually combine. As U rises, Ue rises at a slower and slower pace until it reaches its peak, where it can no longer grow because of the energy storage limit. Ud rapidly increases in this stage.

  4. 4.

    Postpeak failure stage: After the peak stress is reached, the rock develops macroscopic fracture surfaces, although it still has some bearing capacity. From the upper limit on energy storage, Ue drops while Ud increases in discrete steps.

Fig. 13
figure 13figure 13

Strain energy of Beishan deep granite specimens under various confining pressure levels: a σ3  = 0.5 MPa; b 5 MPa; c 10 MPa; d 15 MPa; e 25 MPa

Full size image

The Ue and Ud curves of the Beishan deep granite are classified and plotted in Fig. 14. Gradually raising the confining pressure causes the slopes of the elastic strain energy curve and the residual elastic strain energy of the specimens to rise. As the confining pressure rises, more energy is stored per unit of elastic strain because the rock becomes more compact and unyielding. Higher confining pressure is beneficial to storing higher residual elastic strain energy. The Ud is negligible before an axial strain of 0.002. The Ud of the rock under a lower confining pressure first increases rapidly as the axial strain increases. Figure 14b shows that as the confining pressure is increased, the slope of the dissipated strain energy curve in the prepeak stage drops, whereas the slope in the postpeak stage rises. The characteristic values of Ue and Ud corresponding to crack stress thresholds are defined as Ueci, Uecd, Uef and Udci, Udcd, and Udf. Table 2 demonstrates that the characteristic values of strain energy vary among the specimens. There is an initial rapid rise in the characteristic value of the elastic strain energy when the confining pressure is increased, followed by a slower growth rate. The characteristic value of dissipated strain energy slowly increases with increasing confining pressure and then abruptly leaps. The jump point is also within the range of 10 to 15 MPa. Rock compaction is improved at more significant confining pressures, and more strain energy is stored in the prepeak phase. At confining pressures beyond 15 MPa, however, the rock compaction growth rate steadily declines.

Table 2 The characteristic value of strain energy of the specimens
Full size table
Fig. 14
figure 14

Relationship curves between various strain energies and axial strains a Ue; b Ud

Full size image

During the crack damage process of Beishan deep granite, Ue/U and Ud/U constantly transform. Figure 15 shows that the evolutions of Ue/U and Ud/U have strong regularity during crack damage. In the prepeak stress‒strain curve stage, U is mainly converted into Ue, and the value of Ue/U is larger than that of Ud/U. In the postpeak stress‒strain stage, Ue stored in the rock is rapidly released, and Ud increases sharply, which causes Ue/U to decrease and Ud/U to increase. Specifically, when the rock is in the crack compaction phase, the initial fissures in the rock are closed, and the energy absorbed is converted to Ue and Ud. Ue and Ud are small, but the strain energy ratio changes considerably. Ud/U first decreases and then increases, while Ud/U first increases and then decreases in this stage. During the elastic deformation stage of rock, the original cracks in the rock have been compacted. Ue constantly increases in the rock. Ue/U is much greater than Ud/U in this stage, and Ue plays a dominant role. Ue/U begins to increase, but Ud/U begins to decrease in this stage. When rock is in the stable crack expansion stage, cracks in the rock gradually initiate and propagate, and Ud increases gradually in specimens. Ue/U gradually decreases, and Ud/U slowly increases. When the rock is in the unstable crack expansion stage, many new cracks considerably propagate at this stage, and the rate of increase in Ue continuously decreases. The increasing increment of Ue is lower than Ud. Then, the Ue/U of the rock dramatically decreases, whereas Ud/U rapidly increases. In the postpeak stage, Ue rapidly releases, and Ue/U rapidly decreases; Ud rapidly increases, and Ud/U rapidly increases. The maximum value of Ue/U grows, whereas the maximum value of Ud/U falls steadily with increasing confining pressure.

Fig. 15
figure 15

Relationship between the energy ratio and axial strain: σ3 = 0.5 MPa

Full size image

5 Conclusion

This study used Beishan deep granite for the triaxial compression and AE tests with various confining pressure settings. Analysis of AE characteristics and strain energy evolution of the rock at various damage stages revealed some interesting trends. These findings were as follows:

  1. 1.

    As the initial confining pressure increases, the elastic modulus and Poisson’s ratio increase, but the growth rates gradually decline. Meanwhile, the duration time of each crack damage stage gradually extends, and the crack stress thresholds of the specimens increase with increasing confining pressure levels, but the ratios of the stress thresholds remain relatively constant. In this test, the parameters φ and c of the M–C criterion are 51.56° and 34.01 MPa, respectively, and the strength parameters σc and mi of the H–B criterion are 193.91 MPa and 26.38, respectively. In the tests, the parameter mi is not sensitive to changes at high confining pressure levels (σ3 ≥ 15 MPa), but the parameter mi obviously decreases at low confining pressure levels (σ3 < 15 MPa).

  2. 2.

    The AE hit count and AE accumulative count under various damage stages of the rock are both affected by the confining pressure levels. With a higher confining pressure, the AE hit count varies more dramatically. The AE hit count reaches a maximum shortly after the peak stress at high confining pressure conditions. In the rock loading tests, a high-frequency segment of the AE hit count usually accompanies a jump in the AE accumulative count.

  3. 3.

    In the prepeak stress‒strain stage, the U, Ue, and Ud curves continue to increase with increasing axial strain, and the rate of increase in Ue is significantly higher than that in Ud. U is mainly converted into Ue in the prepeak stage, and Ue/U is larger than Ud/U. However, Ue is rapidly dissipated in the postpeak stage, and Ud increases sharply, which causes Ue/U to decrease and Ud/U to increase. As the confining pressure rises, the maximum of Ue/U increases gradually, but the maximum of Ud/U decreases gradually. In addition, when the confining pressure is lower, Ud/U is greater than Ue/U after the peak stress.