1 Introduction

Surface mines primarily use drilling and blasting, which is an effective and relatively inexpensive method to excavate the hard rock mass. The geometry of surface mine bench blasting has a significant influence on drilling and blasting efficiency and cost, as well as various subsequent activities, like loading and hauling, and finally crushing (Bowa 2015). As a consequence, if the blast design is not optimal, the bench blast might also cause undesirable impacts, such as fly rock, blast vibrations, air blast, backbreak, noise, etc. (Jimeno et al.1995).

The main influencing factors of blasting are rock mass properties, explosive properties, and blast geometry. For rock fragmentation, blast hole diameter is one of the most important blast geometry parameters, since it determines the burden, spacing, stemming length, and other blast design parameters (Sazid and Singh 2015; Ghiasi et al. 2016; Ozdemir and Kumral 2019). Eloranta (1994), pointed out that increasing blast hole diameter will increase fragment size and reduce drilling and blasting costs in surface mines. Dhekne et al. (2020) indicated that when site mixed emulsion (SME) is used in large-diameter blast holes, fewer boulders are produced than when the same explosive is used in small-diameter blast holes.

A study by Pradhan (2007) found that the in-hole VoD of commercial explosives increases with increasing diameter until a value of optimum diameter is reached. A similar conclusion has been made by Furtney et al. (2009). Nonetheless, Dhekne et al. (2016) concluded in their study that an increase in the in-hole VoD due to an increase in hole diameter will not result in the generation of oversized boulders because the increase was not significant for both SME and ammonium nitrate and fuel oil (ANFO) blasts.

Prasad et al. (2017) investigated the influence of blast geometry on rock fragmentation and concluded that mean fragment and maximum fragment sizes increase with increasing stemming length to burden ratio. It was also found that the mean fragment and the maximum fragment sizes decrease with the increase in powder factor (m3/kg). Furthermore, the extra spacing and burden produce weak fractures between charges and significant toe issues.

However, the mechanics of rock fragmentation under large-diameter blast hole blasting have not yet been completely researched particularly, the detonation process, the application of explosion energy distribution characteristics, and the mechanism for forming enormous boulders and toes. As a result, the drilling and blasting strategy must be optimized to decrease production costs and boost productivity.

Another consequence of inappropriate blasting is back break, which has been investigated in several studies (Ghiasi et al. 2016; Khandelwal and Monjezi 2013; Monjezi et al. 2012, 2010; Sharma et al. 2022). In blast patterns, backbreak can be defined as rocks broken beyond the limits of the back row of holes. It can lead to rock falls, mine wall instability, improper fragmentation, and consequently increase the cost of the mining operation.

Konya (2003) indicated that back break increases when the burden and/or stemming increase. Gate et al. (2005) found that the primary cause of the backbreak is insufficient delay timing and/or increasing number of rows in a blast round. Monjezi and Dehghani, (2008) applied the artificial neural network (ANN) and concluded that the most important parameters of the backbreak phenomenon are the ratio of stemming to the burden, the ratio of last row charge to the total charge, powder factor, the total charge per delay and the number of rows in a blasting round.

Optimal blasting is always accompanied by optimal fragmentation with less backbreak and blast vibrations. Blast vibrations transfer a part of the explosive energy to the ground and generate elastic waves. The disturbance ensued and spreads inside the rock mass in the form of stress waves and source energy is transferred in the form of energy flux (Srbulov 2010). This transferred energy induces vibrations inside the rock mass and on the ground surface. High-intensity surface waves cause vibrations in monuments and structures located in the vicinity of the mines. When wave frequency is in the range of the natural frequency of the structure, it will result in more damage due to the resonance phenomenon (Attewell 2013).

Blair and Jiang (1995) indicated that the vibrations in the far field always increase with the explosive charge length. In the near-field, however, vibration increases with charge length until a critical threshold is reached. Once the critical value is achieved, vibration is no longer affected by the charge length. Afrasiabian et al. (2020) found that the stemming length and blast hole diameter has a significant effect on the reduction in surface blast vibrations.

Although numerous pieces of research have emphasized the impact of blast design parameters on blasting results, the exact behavior of these factors is still undetermined. A Taguchi design is a set of approaches created by Dr. Genichi Taguchi that take the inherent unpredictability of materials and production processes into consideration during the design stage. This approach was widely used by several US and European companies after the 1980s. A Taguchi design has the advantage of allowing multiple factors to be analyzed simultaneously. To increase manufacturing yield and product dependability, nominal design points that are not susceptible to fluctuations in production and user circumstances are desired. Taguchi design, in contrast to the design of experiments (DOE), only conducts balanced (orthogonal) test combinations, making it even more efficient than fractional factorial design (Zhang et al. 2007). Therefore, in this study, Taguchi analysis has been performed for sensitivity analysis of blast design parameters to optimize the blasting outcomes. Consequently, a total of 32 experiments were designed using blast geometry parameters such as burden, spacing, row numbers, stemming, and blast hole diameters, as well as explosive and detonation properties such as explosive velocity, explosive density, row-to-row delay, and hole-to-hole delay. Afterward, each parameter was examined concerning rock damage, backbreak, and peak particle velocity (PPV).

2 Design experiment

Processes generally depend on a few or several independent factors. A full factorial or fractional factorial approach can be used to estimate the independent effects of the different variables on the process behavior. When the number of factors is low, full factorial sampling is considered to be more practical. In cases where a process is dependent on several factors, the Taguchi method is mainly used as a robust experimental design technique. By identifying the most influential factors, a subsequent full factorial design can be performed with only a few most important ones. This method has been used to optimize the number of experiments in a wide variety of scientific disciplines (Türkmen et al. 2008; Singaravelu et al. 2009; Zolfaghari et al. 2011; Sadeghi et al. 2012; Asadizadeh et al. 2019). It is based on a two-step methodology developed by Dr. Taguchi (Taguchi 1987): (1) select an orthogonal array (OA) to determine the experimental requirements, and (2) calculate the signal-to-noise ratio (S/N) and analyze the test results using analysis of variance (Wasantha and Ranjith 2014). In designing, the first step is to determine how many 'factors' and 'levels' are needed. A level does not always have to be a numerical value, and linguistic terms can be used to appropriately assign levels to discontinuous factors. The results of the experiments, as determined by an OA matrix, are then used to calculate the S/N ratio. As a performance characteristic, S/N represents the scatter around a target value. S/N has a three-fold calculation method, which allows it to be applied to a wide range of applications. Using Eqs. 1, and 2, it can be derived that larger is better and smaller is better, respectively, while Eq. 3 can be used to determine the scatter around a nominal value.

$$\frac{S}{N} = - 10\log \left( {\frac{1}{n} \sum \limits_{i = 1}^{n} \frac{1}{{Y_{i}^{2} }}} \right)$$
(1)
$$\frac{S}{N} = - 10\log \left( {\frac{1}{n} \sum \limits_{i = 1}^{n} Y_{i}^{2} } \right)$$
(2)
$$\frac{S}{N} = - 10\log \left( {\frac{1}{n} \sum \limits_{i = 1}^{n} \left( {Y_{i} - Y_{0} } \right)^{2} } \right)$$
(3)

Yi is the performance value of the ith experiment, Y0 is a nominal value specified by the user and n is the number of repetitions for an experimental combination. In this study, the Taguchi method has been used to design the blast tests. In Table 1, nine factors were considered, including burden, spacing, stemming, hole-to-hole delay, row-to-row delay, hole diameter, row number, and explosive density with four levels of each, and explosive velocity with two levels. These parameters represent the most critical blast geometry parameters and explosive properties that can influence the blasting outcomes. A total of 32 different experiments have been proposed to analyze the impact of blast design parameters using the Taguchi method, which is listed in Table 2. It should be noted that in all the models, the explosive diameter is equal to the hole diameter. Table 3 shows the charge column weight for each of the 32 models.

Table 1 The parameters used to investigate the blasting results
Full size table
Table 2 A total of 32 tests were designed using the Taguchi method
Full size table
Table 3 The charge weight per hole in 32 models
Full size table

To simulate bench blasting, coupled Particle Blast Method (PBM) and Finite Element Method (FEM) has been applied. The PBM method has been used to simulate the explosion, whereas FEM has been implemented to simulate the rock mass behavior. The PBM model has been developed to simulate the interaction of structure, air, and explosives. This model can simulate how the gas behaves at very high temperatures in addition to thermally non-equilibrium behavior. The PBM model contains a co-volume effect to better depict gas behavior at high pressures. A spherical form is considered for particles to efficiently interact with one another (Teng and Wang 2014). According to Eq. 4, the PBM can be calculated by calculating the amount of energy released when a pressurized bubble ruptures.

$$E_{b} = \frac{4}{3}\pi r_{b}^{3} \left( {p_{b} e_{b} - p_{0} e_{0} } \right)$$
(4)

where \({e}_{b}\) is the energy in the bubble, rb is the radius of the bubble (assuming it’s a sphere), \({p}_{b}\) is the density of the pressurized air in the bubble, \({e}_{b}\) is the energy of the bubble, \({p}_{0}\) is the density of the air in the surrounding vicinity and \({e}_{0}\) is the energy of air (Mohotti et al. 2022).

3 Numerical verification

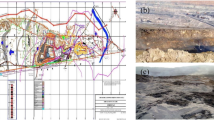
The PPV results from the Delijan copper mine have been used to calibrate the numerical model. The mine is located in Iran, about 10 km from Delijan city. In this case, the depth of the pit is 1510 m and the height of each bench is 10 m. Blast no.HN1 is chosen to compare with the numerical method. During this blast, there are 21 blast holes with a diameter of 5 inches and 3 rows of blast holes (Fig. 1). The burden of blast holes is 3 m along with a 4 m of spacing. However, the burden of the first blast row has been considered 1 m to increase the effect of the free surface. A total of 79 kg of ANFO and 2 kg of cartridge emulsion are used in each blast hole, with a row-to-row delay of 42 ms. A numerical model in size of 214 m × 30 m × 13 m has been generated as presented in Fig. 2. Each blast hole has divided into three parts including Stemming, ANFO, and cartridge emulsion. The material of the rock mass, stemming and explosive are listed in Table 4. The PPV is measured at distances 95 m, 135 m and 185 m away from the blast face. A comparison of PPV values obtained from Delijan copper mine and the numerical method is presented in Table 5. As can be seen, the trend of the numerical results is similar to the measured values, although in most cases the numerical method overestimates the PPV value. Especially, the difference between the two methods increases with increasing distance from the blasting face. This may be the result of fractures and faults in the field that cause waves to be dampened.

Fig. 1
figure 1

Blast no. HN1 in Delijan copper mine

Full size image
Fig. 2
figure 2

a Numerical model of blast no. HN1, b explosive length in the blast hole

Full size image
Table 4 The rock mass and explosive properties of the Delijan copper mine
Full size table
Table 5 A comparison of the field-measured PPV with numerical results
Full size table

4 Numerical simulation

To investigate the influence of the blast design parameters on blast outcomes, A total of 32 models with dimensions of 43 m × 55 m × 14 m have been generated using LS DYNA software. A sub-drilling of 60 cm has been considered for each blast hole. A view of the bench model is presented in Fig. 3. The number of elements is 719219 with a mesh size of 3 cm × 3 cm × 3 cm. In the bench model, the top and front are considered free surfaces since non-reflecting boundaries are applied to the other boundaries.

Fig. 3
figure 3

The bench model and boundary condition

Full size image

The rock mass has been modeled using the Riedel–Hiermaier–Thoma (RHT) model, an advanced plasticity model in LS-DYNA. A list of rock mass properties can be found in Table 6. In the RHT model, the shear and pressure parts are coupled in which the pressure is described by the Mie-Gruneisen form with a polynomial Hugoniot curve and a p-α compaction relation. When hardening states reach the ultimate strength of the rock on the failure surface, the damage is accumulated during further inelastic loading controlled by plastic strain. To this end, the plastic strain at failure is given as (Borrvall and Riedel 2011):

$$\varepsilon_{p}^{f} = \left\{ {\begin{array}{*{20}l} {D_{1} \left[ {p^{*} - \left( {1 - D} \right)p_{t}^{*} } \right]^{{D_{2} }} } \hfill & {p^{*} \ge \left( {1 - D} \right)p_{t}^{*} + \left( { \frac{{\varepsilon_{p}^{m} }}{{D_{1} }}} \right)^{{1/D_{2} }} } \hfill \\ {\varepsilon_{p}^{m} } \hfill & {p^{*} < \left( {1 - D} \right)p_{t}^{*} + \left( { \frac{{\varepsilon_{p}^{m} }}{{D_{1} }}} \right)^{{1/D_{2} }} } \hfill \\ \end{array} } \right.$$
(5)

where D1 and D2 are the damage parameters, p∗ is the shear strength, \(p_{t}^{*}\) is the failure cut-off pressure. The damage is accumulated with plastic strain according to (Borrvall and Riedel 2011):

$$D = \int\limits_{{\varepsilon_{p}^{h} }}^{{\varepsilon_{p} }} {\frac{{d\varepsilon_{p} }}{{\varepsilon_{p}^{f} }}}$$
(6)

where \(\varepsilon_{p}^{h}\) is the strain hardening, and the resulting damaged surface is given as (Borrvall and Riedel 2011):

$$\sigma_{d} \left( {p^{*} ;s;\varepsilon_{p} } \right) = \left\{ {\begin{array}{*{20}l} {\sigma_{y} \left( {p^{*} ;s;\varepsilon_{p} ;1} \right)\left( {1 - D} \right) + Df_{c} \sigma_{r}^{*} \left( {p^{*} } \right)} \hfill & {p^{*} \ge 0} \hfill \\ {\sigma_{y} \left( {p^{*} ;s;\varepsilon_{p} ;1} \right)\left( {1 - D - \frac{{p^{*} }}{{p_{t}^{*} }}} \right)} \hfill & {\left( {1 - D} \right)p_{t}^{*} \le p^{*} < 0} \hfill \\ \end{array} } \right.$$
(7)

where

Table 6 Input parameters of RHT model for rock mass
Full size table
$${\sigma }_{r}^{*}\left({p}^{*}\right)={A}_{f}{\left({p}^{*}\right)}^{{n}_{f}}$$
(8)

In which, Af and nf are residual surface parameters, s is the deviatoric stress and fc is the compressive strength. The rock mass has been modeled as the lagrangian part and stemming as the Eulerian part, as well as explosive as particle blast. A sensitivity analysis of 32 models has been conducted to assess how blast design parameters influence rock damage, backbreak, and blast vibrations.

4.1 Effect of blast design parameters on vibration

Due to the blast, a wave motion propagates outward from the blast, like ripples spread outward from a stone dropped into a water pond (Dowding 2006). Ground vibrations are not only problematic for nearby dwellings, but they also negatively affect the integrity of surrounding structures within the close vicinity of the mine area. Ground vibrations and associated damage are generally assessed by PPV (Khandelwal and Singh 2009).

The PPV was calculated for each model in intervals of 2, 5, 8, 10 and 12 m from the last blast row as well as the PPVglobal, and the results are listed in Table 7. The PPVglobal of the bench model is determined by calculating the average velocity of the bench part elements, which represents the overall vibration of the entire bench model. It can be seen that except for distances of 2 and 8 m, where models 4 and 17 have higher PPV, in other cases, the PPV of model 31 is greater than the other models.

Table 7 The results of the calculated PPV
Full size table

A sensitivity analysis has been performed using the Taguchi method to evaluate the influence of blast design parameters on PPV and the results are shown in Fig. 4. A smaller signal-to-noise (S/N) ratio was selected as the optimal case to reduce the PPV, and as the S/N ratio decreased, PPV increased. Furthermore, the delta of the S/N ratio is calculated based on the difference between the maximum and minimum value of the S/N ratio recorded for each of the nine parameters. A higher delta value for a parameter indicates that it has a greater impact on PPV.

Fig. 4
figure 4figure 4figure 4figure 4

Effect of the blast design parameters on PPV

Full size image

PPV was most influenced by hole diameter, and the delta value for hole diameter in all cases was at least twice that for the other factors. The hole diameter, burden, and the number of blast rows had the most effect on PPV2. However, as the distance from the blast increased, the hole diameter had the most dominant effect on the PPV. Also, the effect of all the other parameters was approximately equal. Moreover, the impact of the burden and spacing has been almost reduced as the distance from the blast face increases, while the effect of explosive detonation velocity increases. Accordingly, burden and spacing have only impacted PPV2 and PPVglobal, whereas, at other distances from the blast face, their influence was similar to that of the other factors. When hole diameter increases, explosives release more energy, while burden and spacing cause wave interfaces. As the distance from the blast face increases, the effect of the released energy on PPV becomes more critical due to wave damping.

The PPV-charge graph is shown in Fig. 5. Models 1 and 20 have the lowest hole charge, while models 14 and 31 have the highest hole charge weight. As can be seen, higher charges do not necessarily result in higher PPV. Additionally, the diameter of the blast hole, the row-to-row delay, and the blast shape also play significant roles. Compared to rectangular blasts, square blasts cause more wave interference and have higher PPV.

Fig. 5
figure 5figure 5

The Charge-PPV relationship

Full size image

4.2 Effect of blast design parameters on backbreak

In this study, the backbreak was calculated based on the length of the rocks broken beyond the last row of blast holes. Figure 6 shows the calculated back break for each of the 32 models. The maximum back break was seen in models 6, 14 and 27. In order to evaluate the effect of design parameters on backbreak, a sensitivity analysis of the results has been performed and the outcomes of which are shown in Fig. 7. A smaller S/N ratio is considered optimal to reduce the back break. The value of the delta has been determined similarly, as it was calculated for the PPV, and a larger delta value for a parameter implies that it has a stronger influence on the back break.

Fig. 6
figure 6

The calculated back break for each model

Full size image
Fig. 7
figure 7

Effect of the blast design parameters on back break

Full size image

It is evident that all the parameters have delta values of more than one which indicates that all the factors have a significant effect on backbreak. However, as can be seen, blast row number, hole diameter, and stemming have a greater impact than the other parameters. While detonation velocity has the smallest influence on backbreak. Furthermore, explosive density had much greater effects than burden and spacing, as explosive density increased, backbreak increased. In addition, row to row delay was more significant than the hole-to-hole delay, burden, and spacing. Therefore, it can be inferred that the three key factors controlling backbreak are hole diameter, powder factor, and explosion wave interference.

4.3 Effect of blast design parameters on rock damage

To assess the rock mass damage, a cumulative percent elements-damage graph for each of the models is presented in Fig. 8. On the horizontal axis, a value of one indicates maximum element damage, and zero indicates no damage. In addition, the vertical axis represents the cumulative percentage of elements with damage values equal to or less than those corresponding to the horizontal axis. As can be seen, model 31 has more than 77% of the elements with a damage value greater than 0.8, and models 4 and 9 have close to 76%. Therefore, the rock mass has been damaged with most of these models. Also, the least damage is related to models 20, 23, and 30. The damage contours of these six models have been shown in Fig. 9. It should be noted that the charge weight per hole of all three models 4, 9 and 31 is more than 180 kg, while models 20, 23 and 30 have less than 110 kg charge per hole. Also, model 20 has the lowest charge weight among all the 32 models. Therefore, the impact of the charge weight on the damage is critical, although other parameters also affected the rock mass damage.

Fig. 8
figure 8figure 8

Cumulative percentage of elements associated with damage

Full size image
Fig. 9
figure 9figure 9

Damage contour of the rock mass

Full size image

A sensitivity analysis has been performed to investigate the impact of design parameters on rock damage. In order to increase the rock damage, a larger S/N ratio is selected as the optimal case. As shown in Fig. 10, the delta value for hole diameter, burden, and spacing is significantly greater than the other parameters, which demonstrates that these three factors have the greatest influence on rock damage. So, the blast geometry is more significant than the explosive type for rock damage. Furthermore, the influence of other factors was very similar, although explosive density had a practically very marginal effect.

Fig. 10
figure 10

Effect of the blast design parameters on rock damage

Full size image

5 Discussion

The outcome of blasting is affected by many parameters. When a process is dependent on multiple factors, the Taguchi method is primarily used as a robust experimental design method. As a result of the sensitivity analysis, it was found that the hole diameter has the greatest influence on back break, rock damage, and PPV. However, the number of blast rows has a slightly greater impact on the backbreak than the hole diameter. Therefore, the hole diameter is the most important parameter that affects blasting results. Therefore, it is critical to control the blast hole diameter in order to achieve a prosperous blasting outcome.

PPV is also affected significantly by the hole diameter compared to the other parameters. In large diameter holes, the energy released by explosives is greater than the small diameter holes and due to that, a higher PPV occurred. As a result, PPV is affected primarily by hole diameter and charge weight. Although the results showed that increases in charge do not necessarily increase the PPV but the other design parameters also affect it. Consequently, charge weight increases can be offset by an increase in rock crushing, and ground vibration can be reduced by changing other blasting design parameters. When a blast is located near residential areas or cities, this can be extremely important.

When the burden is reduced, the blast wave interface is increased, resulting in an increase in PPV. However, according to the results, the burden impact is almost reduced by increasing the distance from the blast, while the explosive detonation velocity is raised.

The influence of design parameters on backbreak is more complicated, and all parameters are crucial. However, the impact of blast row numbers and hole diameter is greater than the other parameters. It should be noted that the explosive density has a very high effect and is much more effective than the burden and spacing. The powder factor increases due to the increase in explosive density without changing any other factors, which also increases backbreak. Furthermore, because the influence of explosive velocity is smaller than the effect of burden and spacing, it can be concluded that the effect of the powder factor on backbreak is greater than that of the geometric parameters of blast and explosive type.

On the other hand, geometric blast parameters, such as hole diameter, burden, and spacing play a significant role in rock damage, whereas the impact of other parameters is much less. Additionally, explosive properties have a much lower effect than the blast geometry on rock damage. Therefore, the damage and crushing of rock can be increased without changing the explosive type by optimizing the geometric properties of the blast. Nonetheless, it is important to note that in this study, the rock type has been considered the same in all the models and further study will be necessary for weaker rock masses.

An optimal explosion should be accompanied by the most rock damage, the least backbreak, and PPV. As a result, model-9 is the most appropriate among the 32 models. However, as far as PPV is concerned, model-9 has a PPV close to the average of the other models. In model 6, 9 spacing to burden ratio is 1.6, and the stemming is half a meter smaller than the burden with three rows of low detonation velocity and high-density explosives are considered. The weakest performance is associated with Model 5, in which low density and low detonation velocity explosive was used. In addition, there were only two rows with small diameter holes. Here a spacing-to-burden ratio is 1.2 for a minimum amount of stemming. Therefore, using high-density explosives, large diameter holes, appropriate spacing-to-burden ratios, and a stemming-to-burden ratio of 1 or close to 1 can significantly improve the blasting results.

Several parameters affect open-pit blasting that are interdependent. In this case, the Taguchi method, in which a number of factors are examined simultaneously, is more suitable than a full factorial analysis. However, in this study, the fracture and joint effects were not investigated and should be examined in future studies. Moreover, no consideration was given to rock mass properties, and all results are associated with hard rock masses. So, further studies will need to be conducted on other types of rock masses to evaluate blast design parameters.

6 Conclusion

A sensitivity analysis was performed on blast geometric parameters and explosive properties in this study to investigate the effect of blast design parameters on blast outcomes. Based on the results, it was found that hole diameter is the most influential parameter of blast design, which strongly affects backbreak, rock damage, and PPV.

In addition, blast geometric parameters have a greater effect on rock damage and PPV than explosive properties. However, as the distance from the blast face increases, the explosive detonation velocity has an increasing effect on the PPV. In addition, it was observed that an increase in charge weight does not necessarily increase the PPV but the other design parameters also affect it. Thus, increasing charge weight can increase rock crushing, while modifying other blasting parameters can reduce ground vibrations. When a blast is located near residential areas or cities, this can be extremely important to reduce PPV.

The effects of the blast design parameters on backbreak are more complicated. In this case, all the geometric parameters of the blast, along with the explosive properties, have a significant impact. Particularly, explosive density has a greater impact on the backbreak than the burden or spacing. However, the effect of explosive properties on rock damage is much less than that of the geometric parameters. To increase the rock mass damage, it is more important to choose the geometric parameters carefully and only by optimizing the geometric parameters can rock crushing be improved without changing the explosive type. Nevertheless, backbreak requires identifying the explosive properties correctly, including its density.

In this study, the rock property has been kept constant during all the experiments, so its effect can be considered in future studies. The PPV is also calculated in the near field, and to evaluate the blast design parameters, the PPV can also be calculated far-field. However, in this study, PPV was calculated at transverse distances ranging from 2 to 12 m from the blast face to account for the effect of increasing distance on the results.