K-stable Fano threefolds of rank 2 and degree 30

Abstract

We find all K-stable smooth Fano threefolds in the family No. 2.22.

Let X be a smooth Fano threefold. Then X belongs to one of the 105 families, which are labeled as No. 1.1, No. 1.2, $\ldots$, No. 9.1, No. 10.1. See [2], for the description of these families. If X is a general member of the family No. $\mathscr {N}$, then [2, Main Theorem] gives

$$\begin{aligned} X\ \text {is K-polystable} \iff \mathscr {N}\not \in \left\{ \begin{aligned}&\ 2.23, 2.26, 2.28, 2.30, 2.31, 2.33, 2.35, 2.36, \\&\ 3.14, 3.16, 3.18,3.21, 3.22, 3.23, \\&\ 3.24, 3.26, 3.28, 3.29, 3.30, 3.31, \\&\ 4.5, 4.8, 4.9, 4.10, 4.11, 4.12,\\&\ 5.2 \end{aligned} \right\} . \end{aligned}$$

The goal of this note is to find all K-polystable smooth Fano threefolds in the family No. 2.22. This family contains both K-polystable and non-K-polystable smooth Fano threefolds, and a conjectural characterization of all K-polystable members has been given in [2, Section 7.4]. We will confirm this conjecture—this will complete the description of all K-polystable smooth Fano threefolds of Picard rank 2 and degree 30 started in [2].

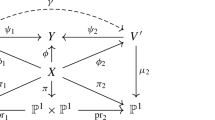
Starting from now, we suppose that X is a smooth Fano threefold in the family No. 2.22. Then X can be described both as the blow-up of ${\mathbb {P}}^3$ along a smooth twisted quartic curve, and the blow-up of $V_5$, the unique smooth threefold No. 1.15, along an irreducible conic. More precisely, there are a smooth twisted quartic curve , a smooth conic $C\subset V_5$, and a commutative diagram

where $\pi$ is the blow-up of ${\mathbb {P}}^3$ along $C_4$, $\phi$ is the blow-up of $V_5$ along C, and $\psi$ is given by the linear system of cubic surfaces containing $C_4$. Here, $V_5$ is embedded in ${\mathbb {P}}^6$ as described in [2, Section 5.10]. All smooth Fano threefolds in the family No. 2.22 can be obtained in this way.

The curve $C_4$ is contained in a unique smooth quadric surface , and $\phi$ contracts the proper transform of this surface. Note that

Choosing appropriate coordinates on , we may assume that Q is given by $x_0x_3=x_1x_2$, where $[x_0\,{:}\, x_1\,{:}\, x_2\,{:}\, x_3]$ are coordinates on . Fix the isomorphism given by

$$\begin{aligned} ([u\,{:}\,v],[x\,{:}\,y])\mapsto [xu\,{:}\,xv\,{:}\,yu\,{:}\,yv], \end{aligned}$$

where $([u\,{:}\,v],[x\,{:}\,y])$ are coordinates in . Swapping $[u\,{:}\,v]$ and $[x\,{:}\,y]$ if necessary, we may assume that $C_4$ is a divisor of degree (1, 3) in Q, so that $C_4$ is given in Q by

$$\begin{aligned} uf_3(x,y)=vg_3(x,y) \end{aligned}$$

for some non-zero cubic homogeneous polynomials $f_3(x,y)$ and $g_3(x,y)$.

Let $\sigma :C_4\rightarrow {\mathbb {P}}^1$ be the map given by the projection $([u\,{:}\,v],[x\,{:}\,y])\mapsto [u\,{:}\,v]$. Then $\sigma$ is a triple cover, which is ramified over at least two points. After an appropriate change of coordinates $[u\,{:}\,v]$, we may assume that $\sigma$ is ramified over $[1\,{:}\,0]$ and $[0\,{:}\,1]$. Then both $f_3$ and $g_3$ have multiple zeros in . Changing coordinates $[x\,{:}\,y]$, we may assume that these zeros are $[0\,{:}\,1]$ and $[1\,{:}\,0]$, respectively. Keeping in mind that the curve $C_4$ is smooth, we see that $C_4$ is given by

$$\begin{aligned} u(x^3+ax^2y)=v(y^3+by^2x) \end{aligned}$$

for some complex numbers a and b, after a suitable scaling of the coordinates. If $a=b=0$, then the curve $C_4$ is given by , which gives . In this case, the threefold X is known to be K-polystable [2, Section 4.4].

FormalPara Example

Suppose that $ab=0$, but $a\ne 0$ or $b\ne 0$. We can scale the coordinates further and swap them if necessary, and assume that the curve $C_4$ is given by

$$\begin{aligned} ux^3=v(y^3+y^2x). \end{aligned}$$

In this case, the threefold X is not K-polystable [2, Section 7.4].

A conjecture in [2, Section 7.4] says that the non-K-polystable Fano threefold described in this example is the unique non-K-polystable smooth Fano threefold in the family No. 2.22. Let us show that this is indeed the case. To do this, we may assume that $a\ne 0$ and $b\ne 0$. Then, scaling the coordinates, we may assume that $C_4$ is given by

for some non-zero complex number $\lambda$. Since the curve $C_4$ is smooth, we must have $\lambda \ne \pm 1$. Moreover, if $\lambda =\pm 3$, then we can change the coordinates on Q in such a way that $C_4$ would be given by $ux^3=v(y^3+y^2x)$, so that X is not K-polystable in this case.

We know from [2] that X is K-stable if $C_4$ is given by ($\bigstar$) with $\lambda$ general. In particular, we know from [2, Section 4.4] that the threefold X is K-stable when $\lambda =\pm \sqrt{3}$. Our main result is the following theorem.

FormalPara Theorem

Suppose that $C_4$ is given in ($\bigstar$) with $\lambda \not \in \{0,\pm 1,\pm 3\}$. Then X is K-stable.

Let us prove this theorem. We suppose that $C_4$ is given by ($\bigstar$) with $\lambda \not \in \{0,\pm 1,\pm 3\}$. Then the triple cover $\sigma :C_4\rightarrow {\mathbb {P}}^1$ is ramified in four distinct points $P_1$, $P_2$, $P_3$, $P_4$, which implies that is a finite group, since

Without loss of generality, we may assume that

$$\begin{aligned} P_1&=([1\,{:}\,0],[0\,{:}\,1])=[0\,{:}\,1\,{:}\,0\,{:}\,0],\\ P_2&=([0\,{:}\,1],[1\,{:}\,0])=[0\,{:}\,0\,{:}\,1\,{:}\,0], \end{aligned}$$

where we use both the coordinates on and ${\mathbb {P}}^3$ simultaneously.

Observe that the group contains an involution $\tau$ that is given by

$$\begin{aligned} ([u\,{:}\,v],[x\,{:}\,y])\mapsto ([v\,{:}\,u],[y\,{:}\,x]). \end{aligned}$$

Let us identify using the isomorphism fixed above. Then $\tau$ is given by $[x_0\,{:}\,x_1\,{:}\,x_2\,{:}\,x_3]\mapsto [x_3\,{:}\,x_2\,{:}\,x_1\,{:}\,x_0]$. Note that $\tau$ swaps $P_1$ and $P_2$, and the $\tau$-fixed points in $C_4$ are $([1\,{:}\,1],[1\,{:}\,1])$ and , which are not ramification points of the triple cover $\sigma$. This shows that $\tau$ swaps the points $P_3$ and $P_4$. In fact, the group is larger than its subgroup $\langle \tau \rangle \cong \varvec{\mu }_2$. Indeed, one can change coordinates $([u\,{:}\,v],[x\,{:}\,y])$ on Q so that

$$\begin{aligned} P_1&=([1\,{:}\,0],[0\,{:}\,1]),\\ P_4&=([0\,{:}\,1],[1\,{:}\,0]), \end{aligned}$$

and the curve $C_4$ is given by

$$\begin{aligned} u(x^3+\lambda ^\prime x^2y)=v(y^3+\lambda ^\prime y^2x) \end{aligned}$$

for some complex number . This gives an involution such that $\iota (P_1)=P_4$ and $\iota (P_2)=P_3$. Let G be the subgroup . Then $G\cong \varvec{\mu }_2^2$. Note that the group can be larger for some . For instance, if $\lambda =\pm \sqrt{3}$, then , c.f. [2, Example 4.4.6].

The G-action on $C_4$ is faithful, so that the curve $C_4$ does not contain G-fixed points. Hence, the quadric Q does not contain G-fixed points, since otherwise Q would contain a G-invariant curve of degree (1, 0), which would intersect $C_4$ by a G-fixed point. So, in particular, we see that ${\mathbb {P}}^3$ contains finitely many G-fixed points. Since the G-action on ${\mathbb {P}}^3$ is given by 4-dimensional linear representation of the group G, we conclude this representation splits as a sum of four distinct one-dimensional representations, which implies that the space ${\mathbb {P}}^3$ contains exactly four G-fixed points. Denote these points by $O_1$, $O_2$, $O_3$, $O_4$. These four points are not co-planar. For every $1\leqslant i<j\leqslant 4$, let $L_{ij}$ be the line in ${\mathbb {P}}^3$ that passes through $O_i$ and $O_j$. Then the lines $L_{12}$, $L_{13}$, $L_{14}$, $L_{23}$, $L_{24}$, $L_{34}$ are G-invariant, and they are the only G-invariant lines in . For each $1\leqslant i\leqslant 4$, let $\Pi _i$ be the plane in ${\mathbb {P}}^3$ determined by the three points . Then the four planes $\Pi _1$, $\Pi _2$, $\Pi _3$, $\Pi _4$ are the only G-invariant planes in .

FormalPara Remark

Each plane $\Pi _i$ intersects $C_4$ at four distinct points. Indeed, if $|\Pi _i\,{\cap }\, C_4|<4$, then $\Pi _i\cap C_4$ is a G-orbit of length 2, and $\Pi _i$ is tangent to $C_4$ at both the points of this orbit. Therefore, without loss of generality, we may assume that the intersection $\Pi _i\cap C_4$ is just the fixed locus of the involution $\tau$. Then , so that $\Pi _i\vert _{Q}$ is a smooth conic that is given by

$$\begin{aligned} a(vx-uy)=b(ux-vy) \end{aligned}$$

for some . But the conic $\Pi _i\vert _{Q}$ cannot tangent $C_4$ at the points $([1\,{:}\,1],[1\,{:}\,1])$ and , so that $|\Pi _i\,{\cap }\, C_4|=4$.

The curve $C_4$ contains exactly three G-orbits of length 2, and these G-orbits are just the fixed loci of the involutions $\tau$, $\iota$, described earlier. Let L, $L^\prime$ and $L^{\prime \prime }$ be the three lines in ${\mathbb {P}}^3$ such that and are the fixed loci of the involutions $\tau$, $\iota$ and , respectively. Then L, $L^\prime$ and $L^{\prime \prime }$ are G-invariant lines, so that they are three lines among $L_{12}$, $L_{13}$, $L_{14}$, $L_{23}$, $L_{24}$, $L_{34}$. In fact, it easily follows from Remark that the lines L, , $L^{\prime \prime }$ meet at one point. Therefore, we may assume that $L\cap L^{\prime }\cap L^{\prime \prime }=O_4$ and $L=L_{14}$, $L^{\prime }=L_{24}$, $L^{\prime \prime }=L_{34}$. Then

$$\begin{aligned} \Pi _1\cap C_4&=(L^{\prime }\cap C_4)\cup (L^{\prime \prime }\cap C_4), \\ \Pi _2\cap C_4&=(L\cap C_4)\cup (L^{\prime \prime }\cap C_4), \\ \Pi _3\cap C_4&=(L\cap C_4)\cup (L^{\prime }\cap C_4). \end{aligned}$$

On the other hand, the intersection $\Pi _4\cap C_4$ is a G-orbit of length 4.

Since $C_4$ is G-invariant, the action of the group G lifts to the threefold X, so that we also identify G with a subgroup of the group . Let E be the $\pi$-exceptional surface, let $\widetilde{Q}$ be the proper transform of the quadric Q on the threefold X, let $H_1$, $H_2$, $H_3$ and $H_4$ be the proper transforms on X of the G-invariant planes $\Pi _1$, $\Pi _2$, $\Pi _3$ and $\Pi _4$, respectively, and let H be the proper transform on X of a general hyperplane in . Then

$$\begin{aligned} {}-K_X\sim 2\widetilde{Q}+E\sim \widetilde{Q}+2H_1\sim \widetilde{Q}+2H_2\sim \widetilde{Q}+2H_3\sim \widetilde{Q}+2H_4\sim 4H-E, \end{aligned}$$

and the surfaces E, $\widetilde{Q}$, $H_1$, $H_2$, $H_3$, $H_4$ are G-invariant. Observe that , and $H_1$, $H_2$, $H_3$, $H_4$ are smooth del Pezzo surfaces of degree 5.

FormalPara Claim

Let S be a possibly reducible G-invariant surface in X such that $-K_X\sim _{\mathbb {Q}}\mu S+\Delta$, where $\Delta$ is an effective $\mathbb {Q}$-divisor, and $\mu$ is a positive rational number such that $\mu >{4}/{3}$. Then S is one of the surfaces $\widetilde{Q}$, $H_1$, $H_2$, $H_3$, $H_4$.

FormalPara Proof

This follows from the fact that the cone is generated by E and $\widetilde{Q}$.$\square$

Suppose X is not K-stable. Since is finite, the threefold X is not K-polystable. Then, by [3, Corollary 4.14], there is a G-invariant prime divisor F over X with $\beta (F)\leqslant 0$, see [2, Section 1.2] for the precise definition of $\beta (F)$. Let us seek for a contradiction.

Let Z be the center of F on X. Then Z is not a surface by [2, Theorem 3.7.1], so that Z is either a G-invariant irreducible curve or a G-fixed point. In the latter case, the point $\pi (Z)$ must be one of the G-fixed points $O_1$, $O_2$, $O_3$, $O_4$, so that the point Z is not contained in $\widetilde{Q}\cup E$. Let us use the Abban–Zhuang theory [1] to show that Z does not lie on $\widetilde{Q}\cup E$ in the former case.

FormalPara Lemma

The center Z cannot be contained in $\widetilde{Q}\cup E$.

FormalPara Proof

We suppose that $Z\subset \widetilde{Q}\cup E$. Then Z is an irreducible G-invariant curve, because neither $\widetilde{Q}$ nor E contains G-fixed points. Let us use notations introduced in [2, Section 1.7]. Namely, we fix $u\in \mathbb {R}_{\geqslant 0}$. Then

$$\begin{aligned} {}-K_X-u\widetilde{Q}\sim _{\mathbb {R}} (4-2u)H+(u-1)E\sim _{\mathbb {R}} (1-u)\widetilde{Q}+2H, \end{aligned}$$

so that ${}-K_X-u\widetilde{Q}$ is nef for $0\leqslant u\leqslant 1$, and not pseudo-effective for $u>2$. Thus, we have

$$\begin{aligned} P({}-K_X-u\widetilde{Q})= {\left\{ \begin{array}{ll} \,{}-K_X-u\widetilde{Q} &{} \text {if}\;\;0\leqslant u\leqslant 1, \\ \,(4-2u)H &{} \text {if}\;\; 1\leqslant u\leqslant 2, \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} N({}-K_X-u\widetilde{Q})= {\left\{ \begin{array}{ll} \,0 &{} \text {if}\;\;0\leqslant u\leqslant 1, \\ \,(u-1)E &{} \text {if}\;\; 1\leqslant u\leqslant 2. \end{array}\right. } \end{aligned}$$

If $Z\subset \widetilde{Q}$, then [2, Corollary 1.7.26] gives

where

and

$$\begin{aligned} S\bigl (W^{\widetilde{Q}}_{\bullet ,\bullet };Z\bigr )&= \frac{3}{(-K_X)^3}\Biggl \{\,\mathop {\int }\limits _0^2\bigl (P(-K_X-u\widetilde{Q})^{2}\cdot \widetilde{Q}\bigr )\cdot \mathrm {ord}_{Z}\bigl (N(-K_X-u\widetilde{Q})\vert _{\widetilde{Q}}\bigr )\,du\\&\qquad \qquad \qquad \qquad \qquad +\mathop {\int }\limits _0^2\mathop {\int }\limits _0^\infty \mathrm {vol}\bigl (P(-K_X-u\widetilde{Q})\vert _{\widetilde{Q}}-vZ\bigr )\,dvdu\Biggr \}. \end{aligned}$$

Therefore, we conclude that $S(W_{\bullet ,\bullet }^{\widetilde{Q}};Z)\geqslant 1$, because $S_X(\widetilde{Q})<1$, see [2, Theorem 3.7.1]. Similarly, if $Z\subset E$, then we get $S(W_{\bullet ,\bullet }^{E};Z)\geqslant 1$.

Fix an isomorphism such that $E\vert _{\widetilde{Q}}$ is a divisor in $\widetilde{Q}$ of degree (1, 3). For , let $\mathcal {O}_{\widetilde{Q}}(a,b)$ be the class of a divisor of degree (a, b) in . Then

$$\begin{aligned} P(-K_X-u\widetilde{Q})\vert _{\widetilde{Q}}\sim _{\mathbb {R}} {\left\{ \begin{array}{ll} \,\mathscr {O}_{\widetilde{Q}}(3-u,u+1) &{} \text {if}\;\; 0\leqslant u\leqslant 1, \\ \,\mathscr {O}_{\widetilde{Q}}(4-2u,4-2u) &{} \text {if}\;\; 1\leqslant u\leqslant 2. \end{array}\right. } \end{aligned}$$

Therefore, if $Z=E\cap \widetilde{Q}$, then

To estimate $S(W_{\bullet ,\bullet }^{\widetilde{Q}};Z)$ in the case when $Z\subset \widetilde{Q}$ and $Z\ne E\cap \widetilde{Q}$, observe that $|Z-\Delta |\ne \varnothing$, where $\Delta$ is the diagonal curve in $\widetilde{Q}$. Indeed, this follows from the fact that $\widetilde{Q}$ contains neither G-invariant curves of degree (0, 1) nor G-invariant curves of degree (1, 0), which in turns easily follows from the fact that the curve $C_4\cong {\mathbb {P}}^1$ does not have G-fixed points. Thus, if $Z\subset \widetilde{Q}$ and $Z\ne E\cap \widetilde{Q}$, then

Therefore, $Z\not \subset \widetilde{Q}$, and hence $Z\subset E$ and $Z\ne \widetilde{Q}\cap E$.

One has $E\cong \mathbb {F}_n$ for some integer $n\geqslant 0$. It follows from the argument as in the proof of [2, Lemma 4.4.16] that n is either 0 or 2. Indeed, let $\mathbf {s}$ be the section of the projection $E\rightarrow C_4$ such that $\mathbf {s}^2=-n$, and let $\mathbf {l}$ be its fiber. Then $-E\vert _{E}\sim \mathbf {s}+k\mathbf {l}$ for some integer k. But

$$\begin{aligned} {}-n+2k=E^3={}-\mathrm {c}_1(\mathscr {N}_{C_4/{\mathbb {P}}^3})={}-14, \end{aligned}$$

so that $k=({n-14})/{2}$. Then

which implies that $\widetilde{Q}\vert _{E}\not \sim \mathbf {s}$. Moreover, we know that $\widetilde{Q}\vert _{E}$ is a smooth irreducible curve, since the quadric surface Q is smooth. Thus, since $\widetilde{Q}\vert _{E}\ne \mathbf {s}$, we have

so that $n=0$ or $n=2$. Now, let us show that $S(W_{\bullet ,\bullet }^{E};Z)<1$ in both cases.

For $u\geqslant 0$,

$$\begin{aligned} {}-K_X-uE\sim 2\widetilde{Q}+(1-u)E, \end{aligned}$$

so that ${}-K_X-uE$ is pseudo-effective if and only if $u\leqslant 1$, and it is nef if and only if $u\leqslant {1}/{3}$. Furthermore, if ${1}/{3}\leqslant u\leqslant 1$, then

$$\begin{aligned} P({}-K_X-uE)=(2-2u)(3H-E) \end{aligned}$$

and $N({}-K_X-uE)=(3u-1)\widetilde{Q}$. Thus, if $n=0$, we have

Similarly, if $n=2$, then

Recall that $Z\ne \widetilde{Q}\cap E$. Moreover, we have $Z\not \sim \mathbf {l}$, since $\pi (Z)$ is not one of the G-fixed points $O_1$, $O_2$, $O_3$, $O_4$. Thus, using [2, Corollary 1.7.26], we get

because the divisor $|Z-\mathbf {s}|\ne \varnothing$.

Consequently, if $n=0$, then

Similarly, if $n=2$, then

In both cases, we have $S(W_{\bullet ,\bullet }^{E};Z)<1$, which is a contradiction.$\square$

Now, we prove our main technical result using the Abban–Zhuang theory, see also [2, Section 1.7].

FormalPara Proposition

The center Z is not contained in $H_1\cup H_2\cup H_3\cup H_4$.

FormalPara Proof

We first suppose that $Z\subset H_1\cup H_2\cup H_3$. Without loss of generality, we may assume that $Z\subset H_1$. Then $\pi (Z)\subset \Pi _1$. Therefore, we see that one of the following two subcases are possible:

• either $\pi (Z)$ is one of the G-fixed points $O_2$, $O_3$, $O_4$, or

• Z is a G-invariant irreducible curve in $H_1$.

We will deal with these subcases separately. In both subcases, we let $S=H_1$ for simplicity. Recall that S is a smooth del Pezzo surface of degree 5, the surface S is G-invariant, and the action of the group G on the surface S is faithful. Note also that $Z\not \subset \widetilde{Q}$ by Lemma.

Let us use notations introduced in [2, Section 1.7]. Take $u\in \mathbb {R}_{\geqslant 0}$. Then

$$\begin{aligned} {}-K_X-uS\sim _{\mathbb {R}} (4-u)H-E\sim _{\mathbb {R}} \widetilde{Q}+(2-u)H\sim _{\mathbb {R}} (u-1)\widetilde{Q}+(2-u)(3H-E). \end{aligned}$$

Let $P(u)=P({}-K_X-uS)$ and $N(u)=N({}-K_X-uS)$. Then

$$\begin{aligned} P(u)= {\left\{ \begin{array}{ll} \,{}-K_X-uS &{} \text {if}\;\;0\leqslant u\leqslant 1, \\ \,(2-u)(3H-E) &{} \text {if}\;\; 1\leqslant u\leqslant 2, \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} N(u)= {\left\{ \begin{array}{ll} \,0 &{} \text {if}\;\; 0\leqslant u\leqslant 1, \\ \,(u-1)\widetilde{Q} &{} \text {if}\;\; 1\leqslant u\leqslant 2. \end{array}\right. } \end{aligned}$$

Note that $S_X(S)<1$, see [2, Theorem 3.7.1]. In fact, one can compute $S_X(S)={17}/{30}$.

Let $\varphi :S\rightarrow \Pi _1$ be the birational morphism induced by $\pi$. Then $\varphi$ is a G-equivariant blow-up of the four intersection points $\Pi _1\cap C_4$. Let $\ell$ be the proper transform on S of a general line in $\Pi _1$, and let $e_1$, $e_2$, $e_3$, $e_4$ be $\varphi$-exceptional curves, and let $\ell _{ij}$ be the proper transform on the surface S of the line in $\Pi _1$ that passes through $\varphi (e_i)$ and $\varphi (e_j)$, where $1\leqslant i<j\leqslant 4$. Then the cone is generated by the curves $e_1$, $e_2$, $e_3$, $e_4$, $\ell _{12}$, $\ell _{13}$, $\ell _{14}$, $\ell _{23}$, $\ell _{24}$, $\ell _{34}$. Recall also that

$$\begin{aligned} \Pi _1\cap C_4=(L_{24}\,{\cap }\, C_4)\cup (L_{34}\,{\cap }\, C_4). \end{aligned}$$

Therefore, we may assume that $L_{24}\cap C_4=\varphi (e_1)\cup \varphi (e_2)$ and $L_{34}\cap C_4=\varphi (e_3)\cup \varphi (e_4)$, so that we have $\varphi (\ell _{12})=L_{24}$ and $\varphi (\ell _{34})=L_{34}$.

Observe that, the group $\mathrm {Pic}^G(S)$ is generated by the divisor classes $\ell$, $e_1+e_2$, $e_3+e_4$, because both $L_{24}\cap C_4$ and $L_{34}\cap C_4$ are G-orbits of length 2. Therefore, if Z is a curve, then $\varphi (Z)$ is a curve of degree $d\geqslant 1$, so that

$$\begin{aligned} Z\sim d\ell -m_{12}(e_1+e_2)-m_{34}(e_3+e_4) \end{aligned}$$

for some non-negative integers $m_{12}$ and $m_{34}$, which gives

and

Moreover, if $Z\ne \ell _{12}$ and $Z\ne \ell _{34}$, then and . Hence, if Z is a curve, then $|Z-\ell _{12}|\ne \varnothing$ or $|Z-\ell _{34}|\ne \varnothing$.

On the other hand, if Z is a curve, then [2, Corollary 1.7.26] gives

where

$$\begin{aligned} S\bigl (W^S_{\bullet ,\bullet };Z\bigr )=\frac{3}{(-K_X)^3}\mathop {\int }\limits _0^2\mathop {\int }\limits _0^\infty \mathrm {vol}(P(u)\vert _{S}-vZ)\,dvdu, \end{aligned}$$

because $Z\not \subset \widetilde{Q}$. Moreover, if $S(W^S_{\bullet ,\bullet };Z)=1$, then [2, Corollary 1.7.26] gives

which is absurd. Thus, if Z is a curve, then $S(W^S_{\bullet ,\bullet };Z)>1$, which gives

because $|Z-\ell _{12}|\ne \varnothing$ or $|Z-\ell _{34}|\ne \varnothing$. Note also that

Hence, if Z is a curve, then the second statement in [2, Corollary 1.7.26] gives

Let us compute $S(W_{\bullet ,\bullet }^S;\ell _{12})$. For $0\leqslant u\leqslant 1$ and $v\geqslant 0$, we have

Therefore, if $0\leqslant v\leqslant 1$, then this divisor is nef, and its volume is $u^2+2uv-v^2-8u-4v+12$. Similarly, if $1\leqslant v\leqslant 2-u$, then its Zariski decomposition is

so that its volume is $u^2+2uv+v^2-8u-8v+14$. Likewise, if $2-u\leqslant v\leqslant 3-u$, then the Zariski decomposition of the divisor $P(u)\vert _{S}-v\ell _{12}$ is

so that its volume is $2(3-u-v)^2$. If $v>3-u$, then $P(u)\vert _{S}-v\ell _{12}$ is not pseudo-effective, so that the volume of this divisor is zero. Thus, we have

Similarly, if $1\leqslant u\leqslant 2$, then

If $0\leqslant v\leqslant 2-u$, this divisor is nef, and its volume is $5u^2+2uv-v^2-20u-4v+20$. Likewise, if $2-u\leqslant v\leqslant 4-2u$, then its Zariski decomposition is

$$\begin{aligned} P(u)\vert _{S}-v\ell _{12}\sim _{\mathbb {R}}\underbrace{(4-2u-v)(2\ell -e_3-e_4)}_{\text {positive part}}+ \underbrace{(v-2+u)(e_1+e_2+\ell _{34})}_{\text {negative part}}, \end{aligned}$$

and its volume is . If $v>4-2u$, this divisor is not pseudo-effective, so that

Therefore, we see that

which implies, in particular, that Z is not a curve.

Hence, we see that $\pi (Z)$ is one of the points $O_2$, $O_3$, $O_4$. Without loss of generality, we may assume that either $\pi (Z)=O_2$ or $\pi (Z)=O_4$, so that $Z\in \ell _{12}$ in both subcases. Now, using [2, Theorem 1.7.30], we see that

where $S(W_{\bullet , \bullet ,\bullet }^{S,\ell _{12}};Z)$ is defined in [2, Section 1.7]. In fact, [2, Theorem 1.7.30] implies the strict inequality $S(W_{\bullet , \bullet ,\bullet }^{S,\ell _{12}};Z)<1$, because $S_X(S)<1$. Let us compute $S(W_{\bullet , \bullet ,\bullet }^{S,\ell _{12}};Z)$.

For $0\leqslant u\leqslant 2$ and $v\geqslant 0$, let P(u, v) be the positive part of the Zariski decomposition of the divisor $P(u)\vert _{S}-v\ell _{12}$, and let N(u, v) be its negative part.

If $0\leqslant u\leqslant 1$, then

and

Similarly, if $1\leqslant u\leqslant 2$, then

and

$$\begin{aligned} N(u,v)={\left\{ \begin{array}{ll} \,0 &{} \text {if}\;\;\ 0\leqslant v\leqslant 2-u, \\ \,(v-2+u)(e_1+e_2+\ell _{34}) &{} \text {if}\;\; 2-u\leqslant v\leqslant 4-2u. \end{array}\right. } \end{aligned}$$

Recall from [2, Theorem 1.7.30] that

for

where $N^\prime _S(u)$ is the part of the divisor $N(u)\vert _{S}$ whose support does not contain $\ell _{12}$, so that $N^\prime _S(u)=N(u)\vert _{S}$ in our case, which implies that $\mathrm {ord}_{Z}(N^\prime _{S}(u)\vert _{\ell _{12}})=0$ for $0\leqslant u\leqslant 2$, because $Z\not \in \widetilde{Q}$. Thus, if $\pi (Z)=O_2$, then $Z\not \in \ell _{34}\cup e_1\cup e_2$, which gives $F_Z(W_{\bullet ,\bullet }^{S,\ell _{12}})=0$. On the other hand, if $\pi (Z)=O_4$, then $Z=\ell _{12}\cap \ell _{34}$ and $Z\not \in e_1\cup e_2$, so that

Therefore, we see that

However, as we already mentioned, one has $S(W_{\bullet ,\bullet }^{S,\ell _{12}};Z)<1$ by [2, Theorem 1.7.30]. The obtained contradiction concludes that $Z\subset H_4$.

Since $Z\not \subset H_1\cup H_2\cup H_3$, the center Z must be a G-invariant curve on $H_4$. Moreover, $\pi (Z)$ cannot be one of the lines determined by the points $O_1$, $O_2$, $O_3$ on $\Pi _4$. This implies that $\pi (Z)$ is a curve of degree $d\geqslant 2$ on $\Pi _4$.

We keep the same notations as in the beginning of the proof, i.e., put $S=H_4$ and let $\varphi :S\rightarrow \Pi _1$ be birational morphism induced by $\pi$. As before, $\varphi$ is a G-equivariant blow-up of the four intersection points $\Pi _4\cap C_4$ which consist of a G- orbit of length 4. We also denote by $\ell$ the proper transform on S of a general line in $\Pi _4$ and by $e_1$, $e_2$, $e_3$, $e_4$ the four $\varphi$-exceptional curves. In addition, denote by $\mathscr {C}$ the proper transform of a general conic passing through the four points $\Pi _4\cap C_4$.

Since the group $\mathrm {Pic}^G(S)$ is generated by the divisor classes $\ell$, $e_1+e_2+e_3+e_4$, we have

$$\begin{aligned} Z\sim d\ell -m(e_1+e_2+e_3+e_4). \end{aligned}$$

where m is a non-negative integer. By taking intersection with the proper transforms of the lines on $\Pi _4$ passing through $\varphi (e_i)$, $\varphi (e_j)$, we obtain $d\geqslant 2m$. Since $d\geqslant 2$, this implies that $|Z-\mathscr {C}|\ne \varnothing$. Note that $\mathscr {C}\not \subset \widetilde{Q}$. By the same argument as before, we obtain

where P(u) is the positive part of $-K_X-uS$ as before. Let us compute $S(W^S_{\bullet ,\bullet };\mathscr {C})$.

Similarly to the notations used earlier in the proof, we denote by P(u, v) the positive part of the Zariski decomposition of the divisor $P(u)\vert _{S}-v\mathscr {C}$ for $0\leqslant u\leqslant 2$ and $v\geqslant 0$, and we denote by N(u, v) its negative part. If $0\leqslant u\leqslant 1$, then

and

$$\begin{aligned} N(u,v)={\left\{ \begin{array}{ll} \,0 &{} \text {if}\;\; 0\leqslant v\leqslant 1, \\ \,(v-1)(e_1+e_2+e_3+e_4) &{} \text {if}\;\; 1\leqslant v\leqslant \frac{4-u}{2}. \end{array}\right. } \end{aligned}$$

Similarly, if $1\leqslant u\leqslant 2$, then

and

$$\begin{aligned} N(u,v)={\left\{ \begin{array}{ll} \,0 &{} \text {if}\;\; 0\leqslant v\leqslant 2-u, \\ \,(v+u-2)(e_1+e_2+e_3+e_4) &{} \text {if}\;\; 2-u\leqslant v\leqslant \frac{6-3u}{2}. \end{array}\right. } \end{aligned}$$

This gives

which is a contradiction. This completes the proof of the proposition.$\square$

FormalPara Corollary

Both Z and $\pi (Z)$ are irreducible curves, and $\pi (Z)$ is not entirely contained in $\Pi _1\cup \Pi _2\cup \Pi _3\cup \Pi _4\cup Q$.

Using [2, Lemma 1.4.4], we see that $\alpha _{G,Z}(X)<{3}/{4}$. Now, using [2, Lemma 1.4.1], we see that there are a G-invariant effective $\mathbb {Q}$-divisor D on the threefold X and a positive rational number $\mu <{3}/{4}$ such that $D\sim _{\mathbb {Q}}-K_X$ and Z is contained in the locus . Moreover, it follows from Claim that $\mathrm {Nklt}(X,\mu D)$ does not contain G-irreducible surfaces except maybe for $\widetilde{Q}$, $H_1$, $H_2$, $H_3$, $H_4$. Now, applying [2, Corollary A.1.13] to , we see that $\pi (Z)$ must be a G-invariant line in . But this is impossible by Corollary, since all G-invariant lines in ${\mathbb {P}}^3$ are contained in $\Pi _1\cup \Pi _2\cup \Pi _3\cup \Pi _4$.

The obtained contradiction completes the proof of our Theorem.