Unexpected surfaces singular on lines in ${\mathbb {P}}^{3}$

Abstract

We study linear systems of surfaces in ${\mathbb {P}}^3$ singular along general lines. Our purpose is to identify and classify special systems of such surfaces, i.e., those non-empty systems where the conditions imposed by the multiple lines are not independent. We prove the existence of four surfaces arising as (projective) linear systems with a single reduced member. Till now no such examples have been known. These are unexpected surfaces in the sense of recent work of Cook II, Harbourne, Migliore, and Nagel. It is an open problem if our list is complete, i.e., if it contains all reduced and irreducible unexpected surfaces based on lines in ${\mathbb {P}}^3$. As an application we find Waldschmidt constants of six general lines in ${\mathbb {P}}^3$ and an upper bound for this invariant for seven general lines.

1 Introduction

The study of linear systems of hypersurfaces in complex projective spaces with assigned base points of given multiplicity is a classical and central problem in algebraic geometry; see, e.g. [2, 12, 21, 28].

In the last few years this problem has been generalized to linear systems of hypersurfaces with assigned base loci consisting of linear subspaces of higher dimension [16, 19]. Conjectures such as [19, Conjecture 5.5] and [16, Conjectures A, B and C] suggest that the asymptotic behavior of such linear systems in the case of linear subspaces of higher dimension is similar to the case of points. In particular, after fixing sufficiently many sufficiently general linear subspaces, it is expected that the conditions imposed on forms by vanishing along these subspaces will be independent. (For efficiency we slightly abuse terminology by saying that r homogeneous linear equations in a vector space of dimension s are independent if the subspace of solutions has dimension either $s-r$ or 0.) On the other hand, it is interesting and important to understand special linear systems, i.e., non-empty systems for which the imposed conditions are dependent, or, equivalently, non-empty linear systems whose dimension is greater than expected from a naive conditions count.

In the classical setup of assigned base points in the case of generic points in ${\mathbb {P}}^2$, the well-known Segre–Harbourne–Gimigliano–Hirschowitz Conjecture (SHGH for short) [18, 22, 27, 34] provides a complete (yet still conjectural) explanation of all special linear systems of plane curves; see [10] for a nice survey and [11] for an account on recent progress. In the case of ${\mathbb {P}}^3$, there is an analogous conjecture due to Laface and Ugaglia [29, 30]. In addition, there is a very nice partial result due to Brambilla et al. [6] valid for points in projective spaces of arbitrary dimension. Special linear systems in ${\mathbb {P}}^n$ are also discussed in [5].

Moving from points to lines, we know, by the result of [26] that general reduced lines in ${\mathbb {P}}^n\!$, $n\hbox {\,\,\char 062\,\,}3$, impose independent conditions on linear systems. Systems with such lines and one multiple line were investigated by [1, 3].

Recently a new path of research has been opened in [13, 23], where the authors introduce the notion of unexpected hypersurfaces; see also [36] for interesting connections with Lefschetz Properties and hypo-osculating varieties as well as [4] for the role of singular loci. The idea is to study non-complete linear systems arising by imposing a base locus which might be, and typically is, based on a non-generic configuration of points, and studying postulation of an additional generic base point. If the number of conditions imposed is less than expected (i.e., the system is special as defined above) then we say that there are unexpected hypersurfaces. More generally, given a degree $d>0$ and a scheme $Z\subset {\mathbb {P}}^n$, let ${\mathcal {L}}_d(Z)$ be the vector space of forms of degree d on ${\mathbb {P}}^n$ vanishing on Z. Given a scheme $L=\bigcup m_iL_i$ of general linear spaces $L_i$ with specified multiplicities $m_i$, we can ask if the system ${\mathcal {L}}_d(L\cup Z)$ has dimension greater than 0 and codimension in ${\mathcal {L}}_d(Z)$ less than is expected (i.e., less than $\sum _i (\dim {\mathcal {L}}_d(\varnothing ) - \dim {\mathcal {L}}_d(L))$). When this is the case one refers to the hypersurfaces defined by forms in ${\mathcal {L}}_d(L\cup Z)$ as being unexpected with respect to Z. When $Z=\varnothing$ and ${\mathcal {L}}_d(L)$ is unexpected with respect to Z, it is traditional to say that ${\mathcal {L}}_d(L)$ is special. We will refer to hypersurfaces defined by elements of special systems as being, simply, unexpected.

The main aim of the present paper is to explain the reasons for the existence of some unexpected surfaces in ${\mathbb {P}}^3$ (in the particular case that $L_i$ are lines and $Z=\varnothing$). These surfaces are single, reduced and irreducible members of certain linear systems with negative virtual dimension, so these systems should be empty, and we prove that the systems consist of one element. Till now there have been no such examples. The existence (and uniqueness) of three out of four considered surfaces (cases (A), (B), (D) of Theorem 3.3) is explained by means of some birational transformations of ${\mathbb {P}}^3$.

The most involved part of the paper (Sect. 5) is the proof of the existence and uniqueness of the remaining surface (case (C) of Theorem 3.3). We also prove that, rather surprisingly, this unexpected surface is of general type.

This is in contrast, for example, to the case of unexpected curves C in ${\mathbb {P}}^2$, where L consists of general non-reduced points and Z is 0-dimensional (or empty). In all known cases at least one of the component curves of C is rational. (A construction in the proof of [23, Theorem 2.15] shows that given a curve $C\subset {\mathbb {P}}^2$ unexpected for a 0-dimensional scheme Z, one can, for any curve A, make $C\cup A$ unexpected for a scheme $Z'\!\supseteq Z$ by taking $Z'$ to be the scheme theoretic union of Z with sufficiently many points of A. However, the unexpectedness of $C\cup A$ with respect to $Z'$ is due to the unexpectedness of C with respect to Z, which in turn always (at least so far) seems to depend on the unexpectedness of a rational component of C with respect to some subset of Z.) Thus, having an unexpected hypersurface of general type is a new geometric phenomenon.

It is not known so far if the discussed four surfaces are the only examples of such unique, reduced and unexpected surfaces, singular along lines in ${\mathbb {P}}^3$.

The paper is organized as follows. In the next section we establish notation. Our main result is Theorem 3.3 presented in Sect. 3. The rest of the paper is in a sense devoted to its proof. In Sect. 4 we prove cases (A), (B) and (D) of Theorem 3.3. The reader familiar with birational transformations may skip some parts of this section and go directly to Sect. 4.4. The hardest case (C) is proved in Sect. 5. In particular we prove that the unexpected surface appearing in this case is of general type. Finally, in Sect. 6 we apply our results towards Waldschmidt constants of ideals of general lines in ${\mathbb {P}}^3$.

2 Notation and basic properties

In our context of imposed base lines, we will use the same notation customarily used for linear systems with imposed base points. This has the advantage of working with familiar notation but with no danger of confusion since we clearly flag appearances of assigned base points.

Thus, ${\mathcal {L}}={\mathcal {L}}_d(m_1,\dots ,m_s)$ denotes the linear system of surfaces of degree d in ${\mathbb {P}}^3$ passing through s general lines (hence the lines are in particular disjoint) with assigned multiplicities $m_1,\dots ,m_s$. If $d<m_i$ for some i, then clearly ${\mathcal {L}}_d(m_1,\dots ,m_s)=\varnothing$, so we will always assume that $d\hbox {\,\,\char 062\,\,}\max (m_1,\ldots ,m_s)$. As is customary, if the multiplicities are repeated, then we abbreviate the notation in a natural way. For example ${\mathcal {L}}_d(m^{\times s})$ denotes a linear system of surfaces of degree d with s lines of the same multiplicity m.

Let $c_{m,d}$ be the number of conditions which vanishing to order m along a line in ${\mathbb {P}}^3$ imposes on forms of degree $d\hbox {\,\,\char 062\,\,}m$. This number is well known and is worked out in [16, Lemma A.2 (c)]:

$$\begin{aligned} c_{m,d}=\sum _{i=0}^{m-1}\,(d+1-i)(i+1)=\frac{1}{6}\,m(m+1)(3d+5-2m). \end{aligned}$$

For the convenience of the reader we provide explicit formulas for a few initial values of m:

$$\begin{aligned} c_{1,d}=d+1,\;\; c_{2,d}=3d+1,\;\; c_{3,d}=6d-2,\;\; c_{4,d}=10d{-}10,\;\; c_{5,d}=15d{-}25. \end{aligned}$$

The virtual dimension of ${\mathcal {L}}$ is therefore

$$\begin{aligned} \mathrm{dim_{vir}}({\mathcal {L}})=\left( {\begin{array}{c}d+3\\ 3\end{array}}\right) -\frac{1}{6}\sum _{i=1}^{s}\,m_i(m_i+1)(3d+5-2m_i). \end{aligned}$$

(1)

Note that we use here affine dimension; i.e., the dimension of the vector space of forms defining the surfaces in the linear system. As usual, the expected dimension of ${\mathcal {L}}$ is

$$\begin{aligned} \mathrm{dim_{exp}}({\mathcal {L}})=\max \{\mathrm{dim_{vir}}({\mathcal {L}}),0\}. \end{aligned}$$

Note that when the actual dimension of ${\mathcal {L}}$ is larger than the expected dimension, then ${\mathcal {L}}$ is special and the hypersurfaces defined by elements of ${\mathcal {L}}$ are unexpected. In this note we are primarily interested in certain special systems.

3 Reasons for speciality

The conditions imposed by general lines with multiplicity 1 are always independent. In other words, linear systems of the type

$$\begin{aligned} {\mathcal {L}}_d(1^{\times s}) \end{aligned}$$

are always non-special. While general assigned base points of multiplicity 1 trivially impose independent conditions, in the case of base lines of multiplicity 1 this is a non-trivial result due to Hartshorne and Hirschowitz [26].

Thus as with points it requires lines of higher multiplicities in order to get a special system. There are two easy ways to construct such special linear systems. We discuss them in the following two examples.

Example 3.1

(Multiples of non-special systems) Let ${\mathcal {L}}={\mathcal {L}}_2(1,1,1)$. Then, by the Hartshorne and Hirschowitz result, ${\mathcal {L}}$ is non-special with $\dim ({\mathcal {L}})=1$, so the (projective) linear system ${\mathcal {L}}$ contains a unique quadric Q. On the other hand, for ${\mathcal {M}}=2{\mathcal {L}}={\mathcal {L}}_4(2^{\times 3})$ we have

$$\begin{aligned} \mathrm{dim_{vir}}({\mathcal {M}})=-4, \;\;\text{ hence } \;\;\mathrm{dim_{exp}}({\mathcal {M}})=0 \end{aligned}$$

but of course $\dim ({\mathcal {M}})\hbox {\,\,\char 062\,\,}1$ since 2Q is in ${\mathcal {M}}$, and it is not hard to verify that $\dim ({\mathcal {M}})=1$ so 2Q is the only member of the projectivisation of ${\mathcal {M}}$. In fact, all linear systems ${\mathcal {L}}_{2m}(m^{\times 3})$ with $m\hbox {\,\,\char 062\,\,}2$ are special of affine dimension 1.

Another instance of this is given by the linear system ${\mathcal {L}}_{3}(1^{\times 4})$ of cubics containing four general lines. By considering quadrics through three of the four lines with a plane containing the fourth we see that ${\mathcal {L}}_{3}(1^{\times 4})$ is non-empty.

Since ${\mathcal {L}}_{3m}(m^{\times 4})$ has negative virtual dimension if (and only if) $m\hbox {\,\,\char 062\,\,}8$, yet is a multiple of the non-empty system ${\mathcal {L}}_{3}(1^{\times 4})$, it is non-empty and hence special for $m\hbox {\,\,\char 062\,\,}8$. Note for four general lines that there are two lines which meet each of the four transversally. Thus both of these transversal lines are in the base locus of ${\mathcal {L}}_{3}(1^{\times 4})$, and by considering quadrics through three of the four lines with a plane containing the fourth, it is not hard to see that the base locus is precisely the two transversals (see [15, Example 3.4.3]). Since the base locus of ${\mathcal {L}}_{3}(1^{\times 4})$ has no divisorial components, the general member of ${\mathcal {L}}_{3m}(m^{\times 4})$ is reduced. In particular, these give special linear systems whose general members are reduced. This is in contrast to ${\mathcal {L}}_{2m}(m^{\times 3})$, and to the assertion of the SHGH Conjecture for special linear systems of curves in the plane (which says that every special system has a multiple curve in its base locus).

Instead of taking multiples of a fixed system, one may add some distinct systems.

Example 3.2

(Unions of non-special systems) Let ${\mathcal {L}}={\mathcal {L}}_8(3^{\times 4})$. Then

$$\begin{aligned} \mathrm{dim_{vir}}({\mathcal {L}})=-19, \;\;\text{ hence }\;\; \mathrm{dim_{exp}}({\mathcal {L}})=0 \end{aligned}$$

but this system is non-empty, as it contains the element consisting of the union of four quadrics (hence it is reduced), each of which vanishes along three of the four given general lines. By [26], such quadrics are unique but not unexpected. However, the union of all four quadrics is unexpected. Moreover, it can easily be checked that this union is the only octic vanishing triply on the four general lines.

In contrast to the previous examples, it is possible for a special system to be reduced, irreducible and of affine dimension one. An extensive computer search using Singular [14] exhibited four such special linear systems, listed in Theorem 3.3. Since in each case the projectivisation of the system contains a unique, irreducible member, the speciality cannot be explained along the lines of Examples 3.1 and 3.2. We will see in Sect. 6 how the existence of systems (B) and (C) is related to some important asymptotic invariants of homogeneous ideals.

Theorem 3.3

The following systems are special of (affine) dimension 1:

• (A) ${\mathcal {L}}_{10}(3^{\times 4}\!,1^{\times 5})$;

• (B) ${\mathcal {L}}_{12}(4,3^{\times 5})$;

• (C) ${\mathcal {L}}_{12}(3^{\times 6}\!,2)$;

• (D) ${\mathcal {L}}_{20}(6^{\times 5}\!,1)$.

Thus there is a single surface of the given degree vanishing to given order along the given number of general lines.

The systems above are special as long as they are effective. Note that the Singular computation which led to the systems in Theorem 3.3 works with random rather than general lines, and so it gives strong evidence, but not proof, of the effectivity of the given systems. This theorem is proved in Sect. 4.4 and in Sect. 5.

Remark 3.4

In cases (A), (B) and (D) of Theorem 3.3 the unexpected surfaces are rational. However in case (C) the unexpected surface is of general type by Corollary 5.4. This is quite surprising in view of the special effect varieties program proposed by Bocci [5].

4 Cremona transformations of ${\mathbb {P}}^3$

Cremona transformations have long played a prominent role in the study of special linear systems in the plane. It turns out that this is also a useful approach in our situation. We recall here two birational transformations of ${\mathbb {P}}^3$ which best suit our needs. We provide some background for non-experts.

4.1 A cubo-cubic transformation

First, there is the cubo-cubic transformation ${\mathcal {C}}:{\mathbb {P}}^3\!\dashrightarrow {\mathbb {P}}^3$ induced by the linear system of cubics vanishing to order 1 along four general lines, for which both the image and inverse image of a general plane is a cubic surface (hence the name cubo-cubic). This compares to the more familiar plane quadratic Cremona transformation induced by the linear system of conics vanishing to order 1 at three general points (which by analogy is called a quadro-quadric transformation).

Fig. 1

The cubo-cubic transformation

As mentioned in Example 3.1, the base locus of the linear system of cubic surfaces vanishing on four general lines consists of six lines: the four general lines, and two additional lines which are transversal to the first four; i.e., both tranversal lines intersect each of the four general lines (see [15, Example 3.4.3]).

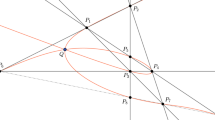
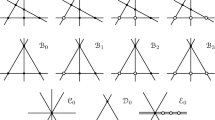
Let $\pi :X\rightarrow {\mathbb {P}}^3$ be the morphism obtained by first blowing up ${\mathbb {P}}^3$ along each of four general lines $l_1,\ldots ,l_4$ (whose exceptional divisors we denote by $E_1,\ldots ,E_4$) and then blowing up the two transversal lines $t_1,t_2$ (whose exceptional divisors we denote by $T_1$ and $T_2$). One can show that $\pi$ resolves the indeterminacy of ${\mathcal {C}}$, giving a morphism ${\mathcal {C}}_0$, as shown in Fig. 1.

Denote by H the pullback via $\pi$ to X of a plane in ${\mathbb {P}}^3$. By ${\mathbb {E}}$ we denote $E_1+\dots +E_4$ and by ${\mathbb {T}}$ we denote $T_1+T_2$. Thus ${\mathcal {C}}_0$ is induced by the linear system of sections of $3H-{\mathbb {E}}-{\mathbb {T}}$. By $H'$ we denote the pullback of a plane via ${\mathcal {C}}_0$, so $H'\!=3H-{\mathbb {E}}-{\mathbb {T}}$.

The intersection product on X is determined by

$$\begin{aligned} H^3 =1,\quad H E_i^2=H T_j^2=E_iT_j^2=-1\quad \text{ and } \quad -E_i^3 =T_j^3=2 \end{aligned}$$

(2)

with all other monomial triple intersections being 0. As $H^3\!=1$ and $H^2E_i=H^2T_i=0$ are clear, we briefly explain the other intersections. Note that the blowup of a line in ${\mathbb {P}}^3$ is isomorphic to ${\mathbb {P}}^1{\times }{\mathbb {P}}^1$, thus sections of $H-E_i$ are disjoint so $H(H-E_i)^2\!=0$. Expanding this shows that $HE_i^2=-1$. Similarly expanding $(H-E_i)^3=0$ we get $E_i^3=-2$.

Computing $T_j^3$ is more subtle. Consider $(H-T_1)^2T_1$. We will show that this intersection equals 4, then expanding, we get that $T_1^3=2$.

Each element of $|H-T_1|$ is the proper transform of a plane $h\subset {\mathbb {P}}^3$ containing $t_1$. The proper transform of h is the blowup of h in the four points $p_1,\ldots , p_4$ where the lines $l_i$ meet h. So if A, B are different elements of $|H-T_1|$, then the restrictions $A\xrightarrow {\scriptscriptstyle \pi } a$, $B\xrightarrow {\scriptscriptstyle \pi } b$ of $\pi$ to A and B are the blowups of $p_1,\ldots , p_4$ on the planes a and b. Thus, $A\cap B=e_{p_1}\!\cup \cdots \cup e_{p_4}$, where $e_{p_i}$ is the exceptional curve given by the blowup of $p_i$. Since $\#(e_{p_i}\!\cap T_1)=1$ and the intersection is transversal, we get $(H-T_1)^2T_1=4$.

Fig. 2

A factorization of the morphism ${{\mathcal {C}}}_2'$ as blowups of the $l_i'$ and the $t_i'$

The morphism ${\mathcal {C}}_0:X\rightarrow {\mathbb {P}}^3$ factorizes into an isomorphism of X followed by a sequence of blowups of ${\mathbb {P}}^3$, as we now explain. There are four quadrics, say $q_1,\ldots ,q_4$, where $q_1$ is the unique quadric which passes through the lines $l_2,l_3,l_4$, $q_2$ is the unique quadric which passes through $l_1,l_3,l_4$, etc. The proper transform by $\pi$ of $q_i$ is $Q_i$. The divisor class of $Q_i$ is $2H- {\mathbb {E}}+E_i-{\mathbb {T}}$. The image of $Q_i$ under ${\mathcal {C}}_0$ is a line in ${\mathbb {P}}^3$, call it $l_i'$ (as the restriction of $3H-{\mathbb {E}}-{\mathbb {T}}$ to $Q_i$ is a (1, 0) class). The images of $T_1$ and $T_2$ are lines $t_1',t_2'$ transversal to $l_1',\ldots ,l_4'$. We note that $\pi (T_i)$ is a projection along one ruling of $T_i={\mathbb {P}}^1{\times }{\mathbb {P}}^1$ and ${\mathcal {C}}_0(T_i)$ is a projection along the other ruling. In Fig. 2, let $\pi _1':X_1'\rightarrow {\mathbb {P}}^3$ be the blowup of the lines $l_i'$ and let $\pi _2':X_2'\rightarrow X_1'$ be the blowup of the proper transforms of the lines $t_i'$. By the universal property of blowups, ${{\mathcal {C}}}_0$ lifts to ${{\mathcal {C}}}_1$, and then ${{\mathcal {C}}}_1$ lifts to ${{\mathcal {C}}}_2$.

We claim ${{\mathcal {C}}}_2$ is an isomorphism. Because $H^2H'\!=3$, the inverse of ${\mathcal {C}}$ is defined by a four-dimensional family of cubic surfaces. Since the fibers over $l_i', t_j'$ are positive dimensional, the inverse ${\mathcal {C}}'$ of ${\mathcal {C}}$ is not defined on these six lines, so the base locus of ${\mathcal {C}}'$ contains these six lines, and, as for ${{\mathcal {C}}}$, this is the whole base locus and a morphism ${\mathcal {C}}_0':X_2'\rightarrow {\mathbb {P}}^3$ resolving the indeterminacies of ${{\mathcal {C}}}'$ is obtained by blowing them up, $l_1',\ldots ,l_4'$ first, and then $t_1', t_2'$. Arguing as before, ${\mathcal {C}}_0'$ lifts to a morphism ${{\mathcal {C}}}_2'$, and since ${{\mathcal {C}}}$ and ${{\mathcal {C}}}'$ are inverse birational maps, we see that ${{\mathcal {C}}}_2$ and ${{\mathcal {C}}}_2'$ are inverse morphisms.

The following transformation rules:

$$\begin{aligned} \begin{aligned} H'&\mapsto 3H -{\mathbb {E}}-{\mathbb {T}},\\ E_i'&\mapsto 2H -{\mathbb {E}}+E_i-{\mathbb {T}}, \\ T_i'&\mapsto T_i \end{aligned} \end{aligned}$$

(3)

define a linear transformation $\Gamma _{{\mathcal {C}}}:\mathrm{Cl}(X_2')\rightarrow \mathrm{Cl}(X)$ on the divisor class group of $X_2'$ (i.e., the free ${\mathbb {Z}}$-module generated by $H'\!, E_1',\ldots ,E_4',T_1',T_2'$). This transformation preserves all triple products and its matrix is its own inverse. This is the map on the divisor class groups induced by pullback by the birational map ${\mathcal {C}}$ in Fig. 2.

Remark 4.1

The divisors $T_i$ play a role in defining ${\mathcal {C}}$ but, as explained below in Remark 4.3, we will obtain special systems by applying $\Gamma _{{\mathcal {C}}}$ to divisor classes in which the $T_i$ do not occur as summands.

4.2 Todd transformation

There is another interesting transformation ${\mathcal {T}}:{\mathbb {P}}^3\!\dashrightarrow {\mathbb {P}}^3$ which seems to go back to Todd [38, Introduction]. It is given by the linear system of surfaces of degree 19 vanishing to order 5 along six general lines $l_1,\ldots ,l_6$ in ${\mathbb {P}}^3$. We now summarize Todd’s results. The special (symmetric) case of the transformation is studied by Cheltsov and Shramov [8, 9].

The geometry of this Cremona map can be analyzed similarly to the cubo-cubic case. The base locus of the linear system of surfaces of degree 19 vanishing to order 5 along six general lines consists of the six lines, the 30 transversal lines which are determined by subsets of four out of the six lines, and, as explained in [40] the six twisted cubics that have the six lines as chords. For a modern treatment of the existence of such twisted cubics see [7, Proposition 3.1].

We explain the action of ${\mathcal {T}}$ decomposing it into more elementary birational transformations, quite in the spirit of the Sarkisov program. To this end let $L_1,\ldots ,L_6$ be six general lines in ${\mathbb {P}}^3$. Let ${\mathcal {C}}_L$ be the cubo-cubic transformation determined by the first four lines and let $M_1,\ldots ,M_4$ be the four skew lines in the base locus of the inverse transformation ${\mathcal {C}}_M={\mathcal {C}}_L$. Let furthermore $\Gamma _5, \Gamma _6$ be the images of the lines $L_5, L_6$ under ${\mathcal {C}}_L$. These are twisted cubics which have $M_1,\ldots ,M_4$ as chords (i.e., each $\Gamma _i$ intersects $M_j$ in two points for $i=5,6$ and $j=1,\ldots ,4$). Let ${\mathbb {G}}=M_1+\cdots +M_4+\Gamma _5+\Gamma _6$. Then ${\mathbb {G}}$ is a curve of degree 10 and arithmetic genus 11. The last assertion can be easily checked computing the Hilbert polynomial of ${\mathbb {G}}$. Quartic surfaces vanishing along ${\mathbb {G}}$ are images under ${\mathcal {C}}_L$ of quartics vanishing along ${\mathbb {L}}=L_1+\cdots +L_6$. Hence

$$\begin{aligned} \dim (I({\mathbb {G}}))_4=\dim (I({\mathbb {L}}))_4=5, \end{aligned}$$

where the last equality follows from [26, Theoreme 0.1].

The minimal free resolution of ${\mathbb {G}}$ is

$$\begin{aligned} 0\leftarrow I({\mathbb {G}})\leftarrow R^5(-4)\leftarrow R^4(-5)\leftarrow 0, \end{aligned}$$

so ${\mathbb {G}}$ is arithmetically Cohen–Macaulay (its codimension equals the length of the resolution, see e.g. [33]).

Its ideal $I({\mathbb {G}})$ gives a $5{\times }4$ Hilbert–Burch matrix L. Here $R={\mathbb {C}}[x_0,\ldots ,x_3]$ is the coordinate ring of ${\mathbb {P}}^3\!\supset {\mathbb {G}}$.

Let $z_0,\ldots ,z_4$ be coordinates in ${\mathbb {P}}^4$ and evaluate $[z_0,\ldots ,z_4]{\cdot }L$. This gives a vector $[v_0,\ldots , v_3]$, whose entries have degree 1 both in variables $x_0,\ldots ,x_3$ and $z_0,\ldots ,z_4$. Thus there exists a $4{\times }4$ matrix M such that $[x_0,\ldots ,x_3]{\cdot }M=[v_0,\ldots ,v_3]$.

Let $g_0,\ldots ,g_4$ be degree 4 generators of $(I({\mathbb {G}}))$ and let $z_i=g_i(x_0,\ldots ,x_3)$ for $i=0,\ldots ,4$ be the rational map $\alpha :{\mathbb {P}}^3\!\dashrightarrow {\mathbb {P}}^4$. The closure of the image of $\alpha$ is a quartic threefold $Q\subset {\mathbb {P}}^4$. This threefold has 36 nodes, 16 of which correspond to the singularities of ${\mathbb {G}}$ and 20 are images of quartisecants of ${\mathbb {G}}$, see [37, p. 325]. There are three types of such quartisecants:

• two lines transversal to $M_1,\ldots ,M_4$;

• six common chords of $\Gamma _1$ and $\Gamma _2$ which are different from $M_1,\ldots ,M_4$ (for the existence of 10 common chords to two twisted cubics, see e.g. [7, Section 3]);

• 12 lines intersecting $M_i, M_j$ and $\Gamma _5, \Gamma _6$ for $1\hbox {\,\,\char 054\,\,}i<j\hbox {\,\,\char 054\,\,}4$ (these lines are images of transversals to $L_i, L_j, L_5, L_6$ under ${\mathcal {C}}_L$).

Since Q is determinantal, the mapping $\alpha '$, inverse to $\alpha$, is given in the following way:

• delete a row of M,

• take all $3{\times }3$ minors of the resulting $4{\times }3$ matrix.

These four minors, up to a linear change of coordinates, define $\alpha '$.

Transposing M and performing the same construction, we obtain another map, $\beta ':Q\rightarrow {\mathbb {P}}^3$. Composing $\beta '{\circ }\alpha$ we obtain a new rational map, which we call the Roth transformation and denote by $\gamma _{11}$. This map is defined by the linear systems of surfaces of degree 11 vanishing to order at least 3 along ${\mathbb {G}}$. The map is discussed by Todd, see [38] and also [32]. We have the diagram shown in Fig. 3.

Fig. 3

The Roth transformation

By construction $\gamma _{11}$ is a birational transformation. It is self-inverse (i.e., the inverse map is given by hypersurfaces of degree 11 passing triply through an analogous curve ${\mathbb {G}}'$) and satisfies the following transformation rules:

$$\begin{aligned} \begin{aligned} H'&\mapsto 11H -3(E_1+\cdots +E_4+C_5+C_6),\\ E_i'&\mapsto 4H -(E_1+\cdots +E_4+C_5+C_6)-E_i, \\ C_i'&\mapsto 12H-3(E_1+\cdots +E_4+C_5+C_6)-C_i. \end{aligned} \end{aligned}$$

(4)

where $E_i$ the are exceptional divisors of the blowup in $L_i$, $i=1,\dots ,4$, and $C_i$ the exceptional divisors of the blowup in $\Gamma _i$, $i=5,6$.

The passage to the transformation ${\mathcal {T}}$ is now easy. We have the diagram shown in Fig. 4.

Fig. 4

The Todd transformation

where $C_{M'}$ is defined by cubics through four lines from ${\mathbb {G}}'$.

Thus, ${\mathcal {T}}$ is given by hypersurfaces of degree 19 passing 5 times through six lines. Let $\pi :X\rightarrow {\mathbb {P}}^3$ be the composition of the blowing up of the source ${\mathbb {P}}^3$ in the set of base lines, followed by the blowing up in the additional 30 lines and then the six cubics (which are in the base locus of ${\mathcal {T}}$). We denote the exceptional divisors by $E_1,\ldots ,E_6$, $T_1,\ldots ,T_{30}$, $G_1,\ldots ,G_6$. Then ${\mathcal {T}}$ induces a birational morphism ${\mathcal {T}}_0:X\rightarrow {\mathbb {P}}^3$ determined by the linear system $19H-5(E_1+\cdots +E_6)-(T_1+\cdots +T_{30})-3(G_1+\cdots +G_6)$. We have the commutative diagram shown in Fig. 5.

Fig. 5

A resolution of the transformation ${\mathcal {T}}$

Similarly to (2), and using the same notation, the intersection product on X satisfies

$$\begin{aligned} H^3 =1,\;\; H E_i^2=-1\;\; \text{ and }\;\; E_i^3 =-2 \end{aligned}$$

(5)

with all other monomial triple intersections of $E_i$ and H being 0.

Composing (3) and (4) we get the following transformations rules for ${\mathcal {T}}$:

$$\begin{aligned} \begin{aligned} E_i'&\mapsto 12H -3(E_1+\cdots + E_6) -E_i,\\ H'&\mapsto 19H -5(E_1+\cdots + E_6) , \end{aligned} \end{aligned}$$

(6)

which preserve triple products (5) and which is self-inverse.

4.3 Limits of fat disjoint lines

The Cremona transformations above will be used to show non-emptiness of the systems in Theorem 3.3. To show uniqueness of each surface, we shall rely on semicontinuity proving uniqueness in some particular position of the lines. In some cases the chosen special position involves some of the lines becoming coplanar—so they intersect; in that case the limit linear system acquires a higher multiplicity at the point of intersection of these lines:

Lemma 4.2

Let l be a fixed line and let $r_t, t\in \Delta \subset {\mathbb {C}}$, be an analytic family of lines in ${\mathbb {P}}^3$ where $\Delta$ is a disk around 0, such that l and $r_t$ are skew for $t\ne 0$ and the lines l and $r_0$ intersect at a point p. Let m, n be positive integers. If $F\in {\mathbb {C}}[[t]][X,Y,Z,W]$ is the equation of an analytic family of surfaces, such that for every $t\in \Delta {\setminus }0$, $F_t$ has multiplicity at least m (respectively n) along l (respectively $r_t$), then $F_0$ has multiplicity at least m (respectively n) along l (respectively $r_0$), and multiplicity at least $m+n$ at p.

Proof

Without loss of generality we may assume that l is the line $X=Y=0$ and $r_t$ is $Y-tW=Z=0$, so $p=[0{:}0{:}0{:}1]$. The only claim that needs proof is the multiplicity at p, which is a local issue, so we will work in the regular local ring $R={\mathbb {C}}[[t]][x,y,z]_p$, where $x=X/W$, $y=Y/W$, $z=Z/W$ and the lines are given by the ideals $I_l=(x,y)$ and $I_{r_t}=(y-t,z)$. Then it is easy to see that $R/I_l^m$ and $R/I_{r_t}^n$ are Cohen–Macaulay modules, and $\dim R/I_l^m+\dim R/I_{r_t}^n=4=\dim R$. Hence by [35, V.B.6, Corollary after Theorem 4] one has ${\text {Tor}}^R_1(R/I_l^m, R/I_{r_t}^n)=0$. Therefore, tensoring the exact sequence $0\rightarrow I_l^m\rightarrow R\rightarrow R/I_l^m\rightarrow 0$ with $R/I_{r_t}^n$ we obtain the exact sequence

$$\begin{aligned} 0 \rightarrow I_l^m/(I_l^m{\cdot }I_{r_t}^n) \rightarrow R/I_{r_t}^n \rightarrow R/(I_l^m+I_{r_t}^n)\rightarrow 0. \end{aligned}$$

Then injectivity of the first map gives

$$\begin{aligned} I_l^m\cap I_{r_t}^n=I_l^m{\cdot }I_{r_t}^n \end{aligned}$$

in R. Any F as in the claim of course belongs to $I_l^m\cap I_{r_t}^n$, and it follows that it belongs to $I_l^m{\cdot }I_{r_t}^n$. In particular, $F_0\in I_l^m{\cdot }I_{r_0}^n$ has multiplicity at least $m+n$ at p. $\square$

4.4 First part of the proof of main theorem

We are now in position to prove part of Theorem 3.3.

Proof of Theorem 3.3, part I

We see immediately from (6) that the duodecic vanishing to order 3 along five general lines and to order 4 along the sixth line is the image under ${\mathcal {T}}_0$ of the exceptional divisor $E_i$ of $\pi$. In particular it is a unique and irreducible member of the (projective) linear system in Theorem 3.3 (B). Moreover surfaces of this kind are rational. We will show in Sect. 6 that these surfaces allow us to extend the list of known Waldschmidt constants of configurations of general lines in ${\mathbb {P}}^3$ obtained in [16, Proposition B.2.1].

The Todd transformation explains also the linear system in Theorem 3.3 (D). Indeed, it is easy to check with the rules stated in (6) that the system $20H-6{\mathbb {E}}+5E_6$, with ${\mathbb {E}}=E_1+\dots +E_6$ here, is the image under $\Gamma _{{\mathcal {T}}}$ of the system $8H-{\mathbb {E}}-5E_6$, which is non-empty by (1). To check that $8H-{\mathbb {E}}-5E_6$ has (projectively) a single element let $\Pi \subset X$ be the strict transform of a general plane through $\ell _6$, and consider the residual exact sequence

$$\begin{aligned} 0\rightarrow {\mathcal {O}}_X(7H-{\mathbb {E}}-4E_6)\rightarrow {\mathcal {O}}_X(8H-{\mathbb {E}}-5E_6)\rightarrow {\mathcal {O}}_\Pi ((8H-{\mathbb {E}}-5E_6)|_\Pi ) \rightarrow 0. \end{aligned}$$

Since the system restricted to the plane $\Pi$ is the planar system of curves of degree 2 with five general base points, which consists of the unique conic through the five points, it will be enough to show that $7H-{\mathbb {E}}-4E_6$ is empty. Specialize the lines so that for $i=1,\dots ,4$, $l_i$ and $l_{i+1}$ intersect at a point $P_i$. By Lemma 4.2, the limit of $7H-{\mathbb {E}}-4E_6$ consists of surfaces which have multiplicity 2 at the points $P_i$. Call $\Pi _i$ the strict transform of the plane $P_i\vee l_6$ and $\Pi _i'$ the strict transform of the plane $l_i\vee l_{i+1}$ (where for projective subspaces $A,B\subset \mathbb {P}^n$, $A\vee B$ denotes the span of A and B).

The restriction of the specialized system to $\Pi _i$ consists of septics containing $5l_6$, double at $P_i$ and with three further points, which are not aligned if the lines are general with the given restrictions; so this system is empty, which means that the four planes $\Pi _i$ are fixed components of the specialized system. The residual consists of cubic surfaces passing through the six (special) lines. It is not hard to see that the restriction of this residual to the planes $\Pi _1'$ and $\Pi _4'$ is non-effective, so these are also fixed components. What remains is the system ${\mathcal {L}}_1(1^{\times 2})$, obviously empty. By semicontinuity, $7H-{\mathbb {E}}-4E_6$ is also empty for lines in general position.

Finally, the linear system in Theorem 3.3 (A) is explained by the means of the cubo-cubic transformation ${\widetilde{{\mathcal {C}}}}$ based at the first four fat lines. To this end we show that already the linear system $10H-3{\mathbb {E}}$, with ${\mathbb {E}}=E_1+\cdots +E_4$, is special. Indeed, we have $\mathrm{dim_{exp}}(10H-3{\mathbb {E}})=54$ but the actual dimension is 56 since this system is the image of the system $6H-{\mathbb {E}}$, which has the expected dimension 56 and is non-special by the aforementioned result of Hartshorne and Hirschowitz. Then, vanishing along an additional line imposes at most 11 conditions, so that the system $10H-3{\mathbb {E}}-E_5-\dots -E_9$ has dimension at least 1. To show that it is exactly 1, we exhibit again a specialization for which the dimension is 1. Denote, $Q_i$ for each $i\in \{1,2,3,4\}$ the unique quadric containing all lines $l_j$ with $j\in \{1,2,3,4\}$, $j\ne i$. Let $\{P_1^1,P_2^1\}=Q_1\cap l_5$, $\{P_1^2,P_2^2\}=Q_2\cap l_5$, and $\{P_1^3,P_2^3\}$ two points in $Q_3$. Specialize the four last lines so that

$$\begin{aligned} l_6&=P_1^1 {\vee }P_1^3,&l_7=P_2^1 {\vee }P_1^3,\\ l_8&=P_1^2 {\vee }P_2^3,&l_9=P_2^2 {\vee }P_2^3. \end{aligned}$$

By Lemma 4.2, the limit system has multiplicity 2 at each point $P_i^j$. If the points $P_i^3$ are general, the restriction of the limit system to $Q_i\cong {\mathbb {P}}^1{\times }{\mathbb {P}}^1$ consists of curves of bidegree (10, 10) containing three triple sections $l_i^3$, $i=2,3,4$, of type (3, 0) with two triple points at $l_1\cap Q_1$, which by Bézout forces the sections of type (0, 1) through these two points to split twice each; the residual are curves of bidegree (1, 6), with two double points $P_1^1$, $P_2^2$ and passing through eight additional general simple points; this is known to be empty, see [31]. The same analysis applied to $Q_2, Q_3$ shows that the three quadrics $Q_1, Q_2, Q_3$ are fixed components of the system. The residual system consists of surfaces of degree 4 passing with multiplicity 1 through all lines except $l_4$; it is not hard to see that the only such surface splits as $Q_4 + (P_1^1\vee P_2^1 \vee P_1^3)+(P_1^2\vee P_2^2 \vee P_2^3)$.

The remaining case (C) is the most interesting and it is dealt with in Sect. 5. $\square$

Remark 4.3

Note that in the proof above we obtained special systems by applying cubo-cubic or Todd transformations to particular divisors. Similarly, by applying them to $aH-(E_1+\dots +E_4)$ or to $aH-(E_1+\dots +E_6)$ respectively, we obtain systems $(3a-8)H-(a-3)(E_1+\dots +E_4)$ and $(19a-72)H-(5a-19)(E_1+\dots +E_6)$. For a big enough the resulting systems have smaller expected dimensions than their actual dimensions, thus producing many examples of unexpected surfaces.

5 The linear system ${\mathcal {L}}_{12}(3^{\times 6}\!,2)$

This section is devoted to the system (C) in Theorem 3.3.

For the system ${\mathcal {L}}={\mathcal {L}}_{12}(3^{\times 6}\!,2)$ we have

$$\begin{aligned} \mathrm{dim_{vir}}({\mathcal {L}})=-2,\;\; \text{ hence } \;\;\mathrm{dim_{exp}}({\mathcal {L}})=0. \end{aligned}$$

We will now show that nevertheless the projectivisation of this system is non-empty and contains a single irreducible element (and no other elements). We do not see how to show the speciality of this system using birational transformations of the ambient space, so we take a different approach.

Proof of Theorem 3.3, part II

Let $l_1,\ldots ,l_7$ be general lines in ${\mathbb {P}}^3$ and let $f:X\rightarrow {\mathbb {P}}^3$ be the blowup of ${\mathbb {P}}^3$ along the first six lines with exceptional divisors $E_1,\dots ,E_6$, respectively. As usual we write ${\mathbb {E}}$ for the union of the exceptional divisors $E_1,\dots ,E_6$ and denote by H the pullback of the hyperplane bundle to X. Then $K_X=-4H+{\mathbb {E}}$. We study the morphism defined by the anti-canonical system

$$\begin{aligned} M=-K_X=4H-{\mathbb {E}}. \end{aligned}$$

The divisors in this system correspond to quartics in ${\mathbb {P}}^3$ vanishing along the first six lines. By the aforementioned result of Hartshorne and Hirschowitz we have

$$\begin{aligned} h^0(X,M)=5, \end{aligned}$$

hence M defines a rational map

$$\begin{aligned} \varphi _M:X\rightarrow {\mathbb {P}}^4\!. \end{aligned}$$

The map is a morphism; one sees this by looking at reducible quartics containing the six lines (namely, products of two quadrics, each containing three of the six lines), and concluding that a base point on the blowup of one of the six lines implies that there would be a transversal to all six general lines. Note that $\varphi _M$ contracts lines transversal to any four of the six given lines (there are $2\left( {\begin{array}{c}6\\ 4\end{array}}\right) =30$ such contracted lines). By [39] (or by computer calculations) the image

$$\begin{aligned} Y =\varphi _M(X) \end{aligned}$$

is a quartic hypersurface, and $\varphi _M$ is generically $1\,{:}\,1$.

5.1 Existence

Let now $C\subset {\mathbb {P}}^4$ be the image of the seventh line under $\varphi _M$. Then C is a rational normal curve of degree 4. It is well known that its secant (chordal) variety is a determinantal threefold T of degree 3 in ${\mathbb {P}}^4$, singular along C, see for example [24, Proposition 9.7].

Note that $T\cap Y$ is an element in ${\mathcal {O}}_{{\mathbb {P}}^4}(3)|_{Y}$, so it pulls back to a surface D of degree 12 in ${\mathbb {P}}^3$, which vanishes to order 3 along the first six lines.

Moreover, since T is singular along C and $C\subset T\cap Y$ we conclude that D is singular along $L_7$. Hence D has vanishing orders along the lines $l_i$ with $i=1,\ldots ,7$ corresponding exactly to those required for part (C) of Theorem 3.3. Thus the existence of duodecics D vanishing to order 3 along six general lines and singular along the seventh line is established.

5.2 Uniqueness

To show that the surface is unique we apply semicontinuouity, proving it in the particular case when the lines $l_1, \dots , l_5$ are chosen to be disjoint lines in a general cubic surface, and $l_6, l_7$ are general.

A general cubic $\Sigma$ in $\mathbb P^3$ can be understood as the blowup $\sigma :\Sigma \rightarrow {\mathbb {P}}^2$ of $\mathbb P^2$ at six general points, $A_1,\ldots ,A_6$, embedded by the system ${\mathcal {O}}_{\mathbb {P}^2}(3){\otimes }I_{A_1}{\otimes }\cdots {\otimes }I_{A_6}$. The pullback of ${\mathcal {O}}_{\mathbb {P}^2}(1)$ on the cubic surface is denoted by h. The 27 lines on $\Sigma$ are identified as the six exceptional divisors $a_1, \dots , a_6$, the $\left( {\begin{array}{c}6\\ 2\end{array}}\right) =15$ lines through pairs of points, and the six conics through five out of six points. We choose $l_1, \dots , l_5$ to be five of these latter lines.

Denote by $\pi :W\rightarrow \mathbb P^3$ the blowup of the seven lines, $l_1,\dots , l_7$, (in this particular position) with exceptional divisors $E_1,\dots , E_7$. Let $S\subset W$ (respectively $N\subset W$) be the proper transform of the cubic (respectively of any duodecic D vanishing to order 3 along our chosen $l_1,\dots ,l_6$ and singular along $l_7$). In S the divisor $E_i|_S$ has class $2h-\mathbb {a}+a_i$ for $i=1,\dots ,5$ (where as usual $\mathbb {a}=a_1+\dots +a_6$). S is the blowup $\pi :S\rightarrow \Sigma$ of the cubic at six additional points, $F_1, F_2, F_3, G_1, G_2, G_3$, namely its intersection points with $l_6$ and $l_7$. Denote the exceptional curves of this blowup by $f_1,f_2,f_3,g_1,g_2,g_3$ respectively, and set $\mathbb {f}=f_1+f_2+f_3$, $\mathbb {g}=g_1+g_2+g_3$. The fact that these points $S\cap (l_6\cup l_7)$ lie on two lines translates to

$$\begin{aligned} h^0(S,{\mathcal {O}}_{S} (3h-\mathbb {a}-\mathbb {f}))= h^0(S,{\mathcal {O}}_{S} (3h-\mathbb {a}-\mathbb {g}))=2, \end{aligned}$$

(7)

as the system $3h-\mathbb {a}-\mathbb {f}$ on S corresponds to ${\mathcal {O}}_{{\mathbb {P}}^2}(3)$ in ${\mathbb {P}}^2$ passing through six points $A_1,\dots ,A_6$ and through three more points on an intersection of two cubics—corresponding to the sections of $\Sigma$ by two planes giving $l_6$. Thus, the system is a system on ${\mathbb {P}}^2$ of curves of degree 3 passing through nine points and having two different members—hence it is a pencil. The argument for $3h-\mathbb {a}-\mathbb {g}$ is the same.

Remark 5.1

We claim that for a general choice of the lines $l_6, l_7$, no three of the image points of $F_1, F_2, F_3, G_1, G_2, G_3$ in ${\mathbb {P}}^2$ are collinear. To prove this, first observe that $F_1, F_2$ (respectively $G_1, G_2$) can be chosen arbitrarily, and then $F_3$ (respectively $G_3$) is determined as the third intersection of $l_6=F_1\vee F_2$ (respectively $l_7=G_1\vee G_2$) with the cubic surface $\Sigma$. So we can assume that the image points of $F_1, F_2$ (respectively $G_1, G_2$) in ${\mathbb {P}}^2$ are not aligned with any $A_i$. This already implies that the images of $F_1, F_2, F_3$ (or equivalently $G_1, G_2, G_3$) are not collinear, because if they were, by (7) there would be at least one section of ${\mathcal {O}}_S(3h-\mathbb {a}-\mathbb {f})$ vanishing on the line containing them, and then the six points $A_1, \dots , A_6$ would belong to a conic, which contradicts their being general points. Now fix a choice of $F_1, F_2, F_3$ and let $t\subset \Sigma$ be the pullback of the triangle through their images in ${\mathbb {P}}^2$. Consider the rational map

$$\begin{aligned} \tau :\Sigma \times \Sigma&\dashrightarrow \Sigma \\ (G_1,G_2)&\mapsto G_3 \end{aligned}$$

which is clearly dominant. If U is the open subset of $\Sigma {\times }\Sigma$ where $\tau$ is defined, then choosing $(G_1,G_2)\in U{\setminus }((t{\times }\Sigma ) \cup (\Sigma {\times }t) \cup \tau ^{-1}(t))$ guarantees that the images of $F_i, F_j, G_k$ in ${\mathbb {P}}^2$ are not aligned. By symmetry, a general choice of $l_6$ and $l_7$ will give that the images of $G_i, G_j, F_k$ are not aligned either.

Now consider the residual exact sequence

$$\begin{aligned} 0 \rightarrow {\mathcal {O}}_{W}(N-S)\rightarrow {\mathcal {O}}_{W}(N) \rightarrow {\mathcal {O}}_S(N|_S) \rightarrow 0. \end{aligned}$$

We need to see that the global sections of the sheaf in the middle have dimension (at most) 1; we do so by proving that the global sections of the two other sheaves have dimensions 0 and 1 respectively.

The restriction of the class of the duodecic to S is

$$\begin{aligned} N|_S&=12H|_S-3{\mathbb {E}}|_S+E_7|_S\\&= 12(3h-\mathbb {a})-3\sum _{i=1}^5\,(2h-\mathbb {a}+a_i)-3\mathbb {f} -2\mathbb {g}\\&= 6h+3a_6-3\mathbb {f}-2\mathbb {g}. \end{aligned}$$

Thus $a_6$ (which as a line in ${\mathbb {P}}^3$ is the unique common transversal to $l_1,\dots ,l_5$) is a fixed component of the restricted system $N|_S$. After subtraction of this fixed part the residual corresponds to the planar system ${\mathcal {O}}_{\mathbb {P}^2}(6){\otimes }I_{F_1}^3{\otimes } I_{F_2}^3{\otimes }I_{F_3}^3{\otimes }I_{G_1}^2{\otimes }I_{G_2}^2{\otimes }I_{G_3}^2$ (by a slight abuse of notation we identify the points $F_1,F_2, F_3, G_1, G_2, G_3$ with their images under $\sigma$ in $\mathbb {P}^2$). Any sextic in this system splits by the Bézout theorem into the sum of three conics: $C_i$ through $F_1, F_2, F_3, G_j, G_k$ for $i=1,2,3$ and j, k such that $\{i,j,k\}=\{1,2,3\}.$ Note that these conics are irreducible by Remark 5.1. Thus, the dimension of this system is 1 and consequently $h^0(S,{\mathcal {O}}_S(N|_S))=1$. It remains to see that $h^0(W,{\mathcal {O}}_W(N-S))=0$, which we prove in Proposition 5.2 below.$\square$

Proposition 5.2

Let $l_1, \dots , l_5\subset {\mathbb {P}}^3$ be disjoint lines in a general cubic surface, and $l_6, l_7$ general lines in ${\mathbb {P}}^3$. Let $W\rightarrow {\mathbb {P}}^3$ be the blowup of the seven lines, and denote $E_i$ the exceptional divisors, with ${\mathbb {E}}=E_1+\dots +E_7$. Then $H^0({\mathcal {O}}_W(9H-2{\mathbb {E}}-E_6))=0$.

Proof

By the projection formula (see [25, II.5.1]) we have

$$\begin{aligned} H^0(W, {\mathcal {O}}_W(9H-2{\mathbb {E}}-E_6))=H^0( {\mathbb {P}}^3\!, {\mathcal {O}}_{{\mathbb {P}}^3}(9) {\otimes }I_{l_1}^2 {\otimes }\cdots {\otimes }I_{l_5}^2{\otimes }I_{l_6}^3 {\otimes }I_{l_7}^2). \end{aligned}$$

We specialize further $l_7$ to $l_7'$, which is the line on $\Sigma$, the proper transform of the line $A_1\vee A_2$ in ${\mathbb {P}}^2$. This line intersects $l_1$ and $l_2$ and no other line $l_i$. Let $P_1=l_1\cap l_7'$ and $P_2=l_2\cap l_7'$.

By semicontinuity and Lemma 4.2, it will be enough to show that there is no surface T of degree 9 in $\mathbb {P}^3$ which is singular along all seven lines, has multiplicity 3 along $l_6$, and multiplicity 4 at $P_1$ and $P_2$. The restriction of such a surface to $\Sigma$ would be, in the notations as above,

$$\begin{aligned} T|_{\Sigma }&=9(3h-\mathbb {a})-2\sum _{i=1}^5\, (2h-\mathbb {a}+a_i)-2(h-a_1-a_2)-3\mathbb {f}\\&= 5h+a_1+a_2-(a_3+a_4+a_5)+a_6-3\mathbb {f}. \end{aligned}$$

After taking out the fixed components $a_1+a_2+a_6$ we are left with the planar system ${\mathcal {O}}_{{\mathbb {P}}^2}(5){\otimes }I_{F_1}^3{\otimes }I_{F_2}^3{\otimes }I_{F_3}^3{\otimes }I_{A_1}{\otimes }I_{A_2}{\otimes }I_{A_3}$, which by Remark 5.1 is non-effective. Therefore $\Sigma$ must be a component of T.

Let $U=T-\Sigma$, which would be a surface of degree 6 passing through all seven lines, with multiplicity 3 along $l_6$, and multiplicity 3 at $P_1$ and $P_2$. Let $\Pi _1, \Pi _2$ be the two planes $\Pi _i=l_6\vee P_i$, $i=1,2$. The restriction $U|_{\Pi _i}$ is a plane curve of degree 6 containing $l_6$ as a triple component, and vanishing at $P_i$ to order 3 and vanishing in four additional points, which are intersection points $\Pi _i\cap l_j$ for $j\ne 6$ and such that $P_i\notin l_j$. Since such a curve does not exist, $\Pi _1$ and $\Pi _2$ must be components of U.

Let $V=U-\Pi _1-\Pi _2$ be a surface of degree 4 passing through all seven lines, and singular at $P_1$ and $P_2$. A similar computation as above shows that $V|_{\Sigma }$ is a system of divisors $h+a_1+a_2+a_6$ passing through $F_1,F_2,F_3$, which is non-effective, so $\Sigma$ is again a component of V. But $V-\Sigma$ would then be a plane containing $l_6$, $P_1$, and $P_2$, which is clearly impossible, and we are done. $\square$

Lemma 5.3

Let $l_1, \dots , l_7\subset {\mathbb {P}}^3$ be general lines in ${\mathbb {P}}^3$, let $W\rightarrow {\mathbb {P}}^3$ be the blowup of the seven lines, and denote $N \subset W$ the pullback of the unique surface in ${\mathcal {L}}_{12}(3^{\times 6}\!,2)$. Then N is smooth.

Proof

By semicontinuity of multiplicities it is enough to check smoothness for a particular choice of lines. We do this computationally, see [42]. $\square$

Corollary 5.4

Let D be the unique surface in ${\mathcal {L}}_{12}(3^{\times 6}\!,2)$, and $N\subset W$ its smooth model. Then D is a surface of general type, with $p_g=6$, $q=0$, and $K_N^2=8$.

Proof

Denote $\pi _6:X\rightarrow {\mathbb {P}}^3$ the blowup of the first six lines, and $\tau :W\rightarrow X$ the blowup of $l_7$. By Lemma 5.3, N is the strict transform of D in W,  and by adjunction the canonical class of N is given as $K_N=(K_W+N)|_N$. Since $h^0({\mathcal {O}}_W(K_W))=h^1({\mathcal {O}}_W(K_W))=0$, $p_g(N)=h^0({\mathcal {O}}_W(K_W+N))$. This can be computed, with the help of the map $\varphi _M$ introduced in the proof of the existence of D, see Sect. 5.1. Indeed, $K_W+N=-4H+{\mathbb {E}}+12H-3{\mathbb {E}}+E_7=-2K_W+E_7=\pi ^*(2M)-E_7,$ so

$$\begin{aligned} p_g(N)&=h^0(W,{\mathcal {O}}_W(\pi ^*(2M)-E_7)= h^0(X,{\mathcal {O}}_X(2M){\otimes }{\mathcal {I}}_{L_7})\\&= h^0(Y,{\mathcal {O}}_{Y}(2){\otimes }{\mathcal {I}}_{C}), \end{aligned}$$

where as before $Y=\varphi _M(X)$ is a quartic threefold in ${\mathbb {P}}^4$, and ${\mathcal {I}}_C$ is the ideal sheaf of the quartic curve $C=\varphi _M(L_7)$. Now the residual exact sequence

$$\begin{aligned} 0\rightarrow {\mathcal {O}}_{{\mathbb {P}}^4}(-2)\rightarrow {\mathcal {O}}_{{\mathbb {P}}^4}(2) \rightarrow {\mathcal {O}}_{Y}(2)\rightarrow 0 \end{aligned}$$

gives

$$\begin{aligned} p_g(N)=h^0({\mathbb {P}}^4\!,{\mathcal {O}}_{{\mathbb {P}}^4}(2){\otimes } {\mathcal {I}}_C)=\dim _{\mathbb {C}}(I_C)_2, \end{aligned}$$

where $I_C$ is the homogeneous ideal of C in the coordinate ring of ${\mathbb {P}}^4$, and $(I_C)_2$ is the degree 2 piece. The ideal of a rational normal quartic curve is well known: it is generated by six independent quadrics [24, Examples 1.14 and 9.3]. So $p_g(N)=6$. The selfintersection of the canonical divisor is computed as the intersection number of three divisor classes on W, which by (5) is

$$\begin{aligned} K_N^2=(K_W+N)^2{\cdot }N =(8H-2{\mathbb {E}}+E_7)^2{\cdot }(12H-3{\mathbb {E}}+E_7)=8. \end{aligned}$$

So we have $p_g(N)>0$, $K_N^2>0$, and hence N is a surface of general type. On the other hand, the exact sequence

$$\begin{aligned} 0 \rightarrow {\mathcal {O}}_W(2K_W+N) \rightarrow {\mathcal {O}}_W(2K_W+2N) \rightarrow {\mathcal {O}}_N(2K_N)\rightarrow 0 \end{aligned}$$

tells us that $\chi (N,{\mathcal {O}}_N(2K_N))=\chi (W,{\mathcal {O}}_W(2K_W+2N))-\chi (W,{\mathcal {O}}_W(2K_W+N))$, and these two Euler characteristics can be computed as virtual dimensions with (1):

$$\begin{aligned} \chi (W,{\mathcal {O}}_W(2K_W+2N))&=\chi (W,{\mathcal {O}}_W(16H-4{\mathbb {E}}+2E_7))\\&=\dim _{\mathrm {vir}}({\mathcal {L}}_{16}(4^{\times 6}\!,2))=20\\ \chi (W,{\mathcal {O}}_W(2K_W+N))&=\chi (W,{\mathcal {O}}_W(4H-{\mathbb {E}}+E_7))= \dim _{\mathrm {vir}}({\mathcal {L}}_{4}(1^{\times 6}))=5. \end{aligned}$$

Therefore, by Riemann–Roch we have

$$\begin{aligned} 15=\chi (N,{\mathcal {O}}_N(2K_N))=\frac{1}{2}\,((2K_N)^2-2K_N{\cdot }K_N)+1-q+p_g=8+1-q+6, \end{aligned}$$

so the irregularity vanishes, and $\chi ({\mathcal {O}}_N)=7$. $\square$

6 Waldschmidt constants

The rest of this note is devoted to asymptotic invariants of the homogeneous ideal $I=I(Z_s)$ of s reduced general lines in ${\mathbb {P}}^3$. Recall that $I=\bigoplus (I)_d$ and that the initial degree of I is defined as the number

$$\begin{aligned} \alpha (I)=\min \{d\,{:}\,(I)_d\ne 0\}. \end{aligned}$$

The m-th symbolic power in this situation is

$$\begin{aligned} I^{(m)}=\bigcap I(L_i)^m\!. \end{aligned}$$

The asymptotic counterpart of $\alpha (I)$ is the Waldschmidt constant of I, defined as

$$\begin{aligned} \widehat{\alpha }(I)=\inf {\frac{\alpha (I^{(m)})}{m}}= \lim \limits _{m\rightarrow \infty }\frac{\alpha (I^{(m)})}{m}. \end{aligned}$$

These constants were first studied by Waldschmidt [41] for ideals defining finite sets of points in ${\mathbb {P}}^n$. They are very hard to compute in general. For ideals of general lines in ${\mathbb {P}}^3$, Waldschmidt constants were studied in [16, 17, 20] and computed for up to five lines; see [20, Corollary 1.1] for up to four lines or [16, Proposition B.2.1]. In this section we extend these results to six lines. We expect that the value of the Waldschmidt constant for seven lines is determined by the duodecics of type (C) in Theorem 3.3 and that Waldschmidt constants of a greater number of lines in ${\mathbb {P}}^3$ are governed by [19, Conjecture 5.5] (see [16, Conjecture A] for a generalization).

Proposition 6.1

Let $Z_6$ be the union of six general lines in ${\mathbb {P}}^3$. Then

$$\begin{aligned} \widehat{\alpha }(I)=\frac{72}{19} \end{aligned}$$

for $I=I(Z_6)$.

Proof

Let I be the homogeneous ideal of the union of six general lines $L_1,\ldots ,L_6$. By Theorem 3.3 (type (B)) for each $i=1,\ldots ,6$, there exists a duodecic $D_i$ vanishing along $L_j$, $j\ne i$, to order 3 and along $L_i$ to order 4. Then the symmetrized divisor $D=\sum _{i=1}^6 D_i$ has degree 72 and vanishing order 19 along all lines. Hence

$$\begin{aligned} \widehat{\alpha }(I)\hbox {\,\,\char 054\,\,}\frac{72}{19}. \end{aligned}$$

In order to see the reverse inequality, it suffices to show that $h^0({\mathcal {O}}_{{\mathbb {P}}^3}(d){\otimes }I^{(m)})=0$, whenever $\frac{d}{m}<\frac{72}{19}$. In fact, it suffices to show that

$$\begin{aligned} h^0({\mathcal {O}}_{{\mathbb {P}}^3}(72m-1){\otimes }I^{(19m)})=0 \end{aligned}$$

for all $m\hbox {\,\,\char 062\,\,}1$. Here the Todd transformation again comes into the picture. We check easily, that the Todd transformation of the system $(72m-1)H-19m{\mathbb {E}}$ (in the notation from Sect. 4) is $-19H+m{\mathbb {E}}$ which is obviously non-effective. $\square$

The reader might find it convenient to have an overview of known Waldschmidt constants for $s\hbox {\,\,\char 054\,\,}6$ general lines in ${\mathbb {P}}^3$ as well as the expected value for $s\hbox {\,\,\char 062\,\,}7$.

s	1	2	3	4	5	6
$\widehat{\alpha }(I_s)$	1	2	2	$\frac{8}{3}$	$\frac{10}{3}$	$\frac{72}{19}$

For $s=7$ we expect that $\widehat{\alpha }(I_7)=21/5$ and for $s\hbox {\,\,\char 062\,\,}8$ we conjecture:

Conjecture 6.2

$$\begin{aligned} \widehat{\alpha }(I_s) = \tau _0, \end{aligned}$$

where $\tau _0$ is the largest real root of the polynomial

$$\begin{aligned} \tau ^3-3s\tau +2s. \end{aligned}$$

This is inspired by the conjectures given in [16, 19], but it is stronger, because it is specific about the values of s for which it is conjectured to hold.