On the unique unexpected quartic in ${\mathbb {P}}^2$

Abstract

The computation of the dimension of linear systems of plane curves through a bunch of given multiple points is one of the most classic issues in algebraic geometry. In general, it is still an open problem to understand when the points fail to impose independent conditions. Despite many partial results, a complete solution is not known, even if the fixed points are in general position. The answer in the case of general points in the projective plane is predicted by the famous Segre–Harbourne–Gimigliano–Hirschowitz conjecture. When we consider fixed points in special position, even more interesting situations may occur. Recently, Di Gennaro, Ilardi and Vallès discovered a special configuration Z of nine points with a remarkable property: A general triple point always fails to impose independent conditions on the ideal of Z in degree four. The peculiar structure and properties of this kind of unexpected curves were studied by Cook II, Harbourne, Migliore and Nagel. By using both explicit geometric constructions and more abstract algebraic arguments, we classify low-degree unexpected curves. In particular, we prove that the aforementioned configuration Z is the unique one giving rise to an unexpected quartic.

1 Introduction

One of the central problems in algebraic geometry is the study of linear systems of hypersurfaces of ${\mathbb {P}}^n$ with imposed singularities, namely divisors containing a set of given points $P_1,\dots ,P_r$ with multiplicities $m_1,\dots ,m_r$. Interpolation theory addresses the problem of computing the dimension of such systems. It is actually an open problem to understand when the points fail to impose independent conditions—naively counting parameters does not always give the correct result.

Let us start with the basic definitions in the projective plane. We work over the field of complex numbers ${\mathbb {C}}$.

Definition 1.1

Given $P_1,\dots ,P_r\in {\mathbb {P}}^2$ and their ideals $I_1,\dots , I_r\subset {\mathbb {C}}[x,y,z]$, we define the fat point subscheme of ${\mathbb {P}}^2$ supported at $P_1,\dots ,P_r$ with multiplicities $m_1,\dots , m_r$ to be the scheme $X=m_1P_1+\ldots +m_rP_r$ associated with the ideal

$$\begin{aligned} I(X)=I_1^{m_1}\cap \ldots \cap I_r^{m_r}. \end{aligned}$$

We will indicate by $I(X)_d$ the homogeneous component of degree d of I(X). The vector space $I(X)_d$ is the linear system of curves of degree d in ${\mathbb {P}}^2$ containing X, that is, having multiplicity at least $m_i$ at $P_i$ for all $i\in \{1,\ldots , r\}$.

The virtual dimension of such a system is

$$\begin{aligned} \mathrm{vdim\,}I(X)_d=\left( {\begin{array}{c}d+2\\ 2\end{array}}\right) -\sum _{i=1}^r{m_i+1\atopwithdelims ()2}, \end{aligned}$$

(1)

while its expected dimension is

$$\begin{aligned} \mathrm{expdim\,}I(X)_d = \max \left\{ \mathrm{vdim\,}I(X)_d, 0\right\} . \end{aligned}$$

(2)

In general, $\dim I(X)_d\ge \mathrm{expdim\,}I(X)_d$. If either the conditions given by X are independent or $\dim I(X)_d=0$, then $\dim I(X)_d= \mathrm{expdim\,}I(X)_d$ and the system is called nonspecial. Otherwise, it is called special.

Classifying the special linear systems is a very hard task, even if the base points are in general position. A conjectural answer comes from the celebrated Segre–Harbourne–Gimigliano–Hirschowitz conjecture (see [8, 9, 12, 13]).

Conjecture 1.2

(SHGH Conjecture) Let $X=m_1P_1+\ldots +m_rP_r$ be a fat point scheme. Assume that $P_1,\dots ,P_r$ are in general position. If the linear system $I(X)_d$ is special, then its general element is non-reduced, namely the linear system has a multiple fixed component.

Mathematicians have been working on interpolation problems for over a century. A nice survey of the known results and the techniques applied to get them is [3].

In [4], Cook II, Harbourne, Migliore and Nagel focused on a subtler problem about special linear systems of plane curves. Namely, they drop the hypothesis of generality of some of the points, and they propose a classification problem analogous to the SHGH conjecture (see [4, Problem 1.4]), although this problem seems too difficult to be solved in full generality. In the same spirit, we focus on a simplified version, and we consider degree d curves containing a general point of multiplicity $d-1$ and a bunch of (not necessarily general) simple points.

Definition 1.3

Let $d\in {\mathbb {N}}$. We say that a finite set of distinct points $Z\subset {\mathbb {P}}^2$ admits an unexpected curve of degree d if

$$\begin{aligned} \dim I(Z+(d-1)P)_d>\max \left\{ \dim I(Z)_d -{d\atopwithdelims ()2}, 0\right\} \end{aligned}$$

(3)

for a general $P\in {\mathbb {P}}^2$.

We want to stress that in the definition of an unexpected curve we do not take into account the number of conditions that Z imposes on curves of degree d. Compare inequality (3) with Eq. (2).

Recently, unexpected curves and hypersurfaces have been intensively studied. In the paper [6], Di Marca, Malara and Oneto present a way to produce families of unexpected curves using supersolvable arrangements of lines. In [2], Bauer, Malara, Szemberg and Szpond consider the existence of special linear systems in ${\mathbb {P}}^3$ and exhibit there a quartic surface with unexpected postulation properties. In [11], Harbourne, Migliore, Nagel and Teitler construct new examples both in the projective plane and in higher-dimensional projective spaces. Moreover, they introduce two new methods for constructing unexpected hypersurfaces.

One of the purposes of this paper is to classify all unexpected plane curves in low degrees. By [4, Theorem 1.2] and [4, Corollary 6.8], unexpected conics cannot exist. For $d=3$, we recover the following result of Akesseh [1].

Theorem 1.4

No set of points $Z\subset {\mathbb {P}}^2$ admits an unexpected cubic over ${\mathbb {C}}$.

Things become more complicated for $d=4$. In this case, there exists a configuration of nine points in ${\mathbb {P}}^2$ which admits an unexpected quartic. It was observed by Di Gennaro, Ilardi and Vallès in [5, Proposition 7.3] and is discussed in [4, Example 6.14] and by Harbourne in [10, Example 4.1.10].

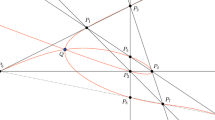
Example 1.5

(An unexpected quartic) Let $Z_1,Z_2,Z_3,Z_4\in {\mathbb {P}}^2$ be four general points. The lines joining any two of them determine three intersection points $Z_5,Z_6,Z_7$. Take a line through any two of the points $Z_5$, $Z_6$ and $Z_7$ (in Fig. 1, through $Z_6$ and $Z_7$). Call $Z_8$ and $Z_9$ the two intersection points with the previous lines and define $Z=\{Z_1,\dots ,Z_9\}$.

Note that the construction of the points $Z_8$ and $Z_9$ depends on the choice of two points among $Z_5$, $Z_6$ and $Z_7$. Nevertheless, the three possible choices provide three projectively equivalent configurations of nine points. For instance, choosing the pair $(Z_5,Z_7)$ is the same as choosing $(Z_6,Z_7)$ and then considering the projective linear transformation swapping $Z_1$ and $Z_4$ and fixing $Z_2$ and $Z_3$. Therefore, we conclude that the configuration Z is unique up to projective equivalence.

Fig. 1

A configuration of nine points in ${\mathbb {P}}^2$ admitting an unexpected quartic

In this paper, we analyze the geometry of this configuration and prove the following result.

Theorem 1.6

Up to projective equivalence, the configuration of points $Z\subset {\mathbb {P}}^2$ in Example 1.5 is the only one which admits an unexpected curve of degree four.

Our paper is organized as follows. In Sect. 2, we use plane geometry arguments and Bézout’s theorem to prove Theorem 1.4. Moreover, we describe in detail the configuration of nine points of Example 1.5 and give a geometric proof of the existence of an unexpected quartic. Then, we turn our attention to all possible configurations admitting an unexpected quartic. In Sect. 3, we prove some tight necessary conditions on a set Z with this property, and we achieve the results with a degeneration technique. Finally, in Sect. 4 we show how these necessary conditions lead to a unique configuration of points. Here, the stability of vector bundles turns out to be a powerful tool to prove Theorem 1.6.

2 Unexpected cubics and quartics in ${\mathbb {P}}^2$

Let us fix the notation. Given two points $A,B\in {\mathbb {P}}^2$, we denote by AB the line joining them. We call a line simple if it contains only two points of Z. For $k\ge 3$, we say that a line is k-rich if it contains exactly k points of Z.

A standard tool to prove that a linear system is empty is to degenerate some of the points to a special position. If the degenerated linear system is empty, then the original one is empty as well.

As shown in [4, Corollary 5.5], the most interesting case is $|Z|=2d+1$. We will repeatedly use the following simple but useful result.

Proposition 2.1

Let d be a positive integer. Let Z be a set of $2d+1$ distinct points, and $P\in {\mathbb {P}}^2$ a general point. If there are a d-rich line $L_Q$ and a simple line $L_R$ such that $L_Q\cap L_R\notin Z$, then $I(Z+(d-1)P)_d=0$.

Proof

Assume by contradiction that $I(Z+(d-1)P)_d\ne 0$. Consider $\{Q_1,\ldots ,Q_d\}=Z\cap L_Q$, $\{R_1,R_2\}=Z\cap L_R$ and $\{S_1,\ldots ,S_{d-1}\}=Z\setminus (L_Q\cup L_R)$. Let C be the degree d curve defined by a nonzero element of $I(Z+(d-1)P)_d$.

We specialize the $(d-1)$-ple point P to a general point on $L_R$. By Bézout’s theorem, $L_R$ and $L_Q$ are irreducible components of C. We are left with a degree $d-2$ curve $C'$ passing through $d-1$ simple points and a $(d-2)$-ple point P. Again by Bézout’s theorem, for all $i\in \{1,\ldots ,d-1\}$ the line joining $S_i$ and P is an irreducible component of $C'$. Hence, $C'$ is a curve of degree $d-2$ having $d-1$ lines as components, which is impossible. $\square$

We now consider the problem of existence of unexpected cubics and we show that they cannot appear if the ground field is ${\mathbb {C}}$.

Proof of Theorem 1.4

Consider a set of points $Z\subset {\mathbb {P}}^2$. If $|Z|<7$, then any unexpected cubic is reducible by [4, Corollary 5.5]. By [4, Theorem 5.9], this implies that some subset of Z admits an unexpected conic, but this is impossible.

Assume now that $|Z|\ge 7$. Let W be any subset of seven points of Z. Observe that $I(W+2P)_3$ contains $I(Z+2P)_3$ for every $P\in {\mathbb {P}}^2$, and hence $\dim I(W+2P)_3\ge \dim I(Z+2P)_3$. Moreover, if Z admits an unexpected cubic, then there exists a subset of seven points of Z admitting an unexpected cubic: Indeed, any seven smooth points of an irreducible plane cubic impose independent conditions on the system of plane cubics. For this reason, in order to conclude it is enough to prove that no subset Z of seven points admits an unexpected cubic over ${\mathbb {C}}$. Therefore, for the rest of the proof we assume that $|Z|=7$.

If an unexpected cubic exists, then [4, Theorem 1.2] implies that Z contains no subset of four or more collinear points. On the other hand, [4, Corollary 6.8] shows that the points of Z cannot be in linearly general position. Suppose then that L is a 3-rich line and consider $\{Z_1,Z_2,Z_3\}=Z\cap L$. Let $Z_4$ and $Z_5$ be two points of $Z\setminus L$. By Proposition 2.1, $Z_4Z_5$ must meet L at a point of Z, and we assume that $Z_3=L\cap Z_4Z_5$. Since there cannot be four collinear points, we have that $Z\setminus (L\cup Z_1Z_2)=\{Z_6,Z_7\}$. Again by Proposition 2.1, the lines $Z_4Z_6$ and $Z_5Z_6$ meet L at a point of Z. Up to relabeling, the only possibility is that $Z_1\in Z_4Z_6$ and that $Z_2\in Z_5Z_6$. A similar argument is used to show that $Z_2\in Z_4Z_7$ and that $Z_1\in Z_5Z_7$. Hence, up to projective equivalence, Z is the configuration described in Fig. 2.

Fig. 2

The considered configuration of seven points

It is easy to check that in this case it is not possible that $Z_3\in Z_6Z_7$ over ${\mathbb {C}}$. Hence, the line $Z_6Z_7$ is simple and L is a 3-rich line, and therefore Z does not admit an unexpected cubic by Proposition 2.1. $\square$

Actually, a stronger version of Theorem 1.4 holds. In [1], Akesseh proves that unexpected cubics exist only if the characteristic of the ground field is 2.

Now, we turn our attention to the case $d=4$. The proof of existence of the unexpected quartic in Example 1.5 presented in [4] uses splitting types. Here, we give a new, simpler proof.

Proposition 2.2

The configuration Z of nine points of Example 1.5 admits an unexpected curve of degree four.

Proof

Let $P=[a,b,c]$ be a general point. Up to projective equivalence, we can assume that

$$\begin{aligned} Z_1=[-1,0,1],\ Z_2=[0,-1,1],\ Z_3=[1,0,1],\ Z_4=[0,1,1]. \end{aligned}$$

By construction, the remaining points have coordinates

$$\begin{aligned} Z_5=[0,0,1],\ Z_6=[1,-1,0],\ Z_7=[1,1,0],\ Z_8=[0,1,0],\ Z_9=[1,0,0]. \end{aligned}$$

Let $L_1$ be the linear form defining the line $Z_1Z_3$, let $L_2$ define $Z_2Z_4$, and let $L_3$ define the line $Z_6Z_7$. Furthermore, for every j define $M_j$ to be the linear form defining the line $PZ_j$.

By using reducible quartics, it is easy to see that $I(Z+2P)_4$ is nonspecial. One can check that

$$\begin{aligned} G_1=L_1L_2M_6M_7,\ G_2=L_1L_3M_2M_4,\ G_3=L_2L_3M_1M_3 \end{aligned}$$

are linearly independent and thus form a basis of $I(Z+2P)_4$. Since each $G_i$ is singular at P, we have $G_i(P)=(G_i)_x(P)=(G_i)_y(P)=0$ for every i. The existence of an unexpected quartic is equivalent to the fact that the three additional conditions that the triple point P imposes on $G_1$, $G_2$, $G_3$ (given by the three second-order partials in x and y) are linearly dependent. This means that

$$\begin{aligned} \det \left( \begin{array}{ccc} (G_1)_{xx} &{} (G_2)_{xx} &{} (G_3)_{xx} \\ (G_1)_{xy} &{} (G_2)_{xy} &{} (G_3)_{xy} \\ (G_1)_{yy} &{} (G_2)_{yy} &{} (G_3)_{yy} \end{array}\right) (P)=0. \end{aligned}$$

This condition can be directly checked by exploiting the facts that $G_1$, $G_2$, $G_3$ are completely reducible with pairwise common factors and that $M_j(P)=0$ for every j. $\square$

3 Geometric conditions on unexpected quartics

We now focus on the proof of Theorem 1.6. As [4, Corollary 5.5] suggests, the most significant case is $|Z|=9$. Hence, throughout this section Z will indicate a set of nine points, and $P\in {\mathbb {P}}^2$ a general point. If an unexpected quartic exists, then [4, Theorem 1.2] shows that Z does not contain any subset of five or more collinear points. On the other hand, by [4, Corollary 6.8], the points of Z cannot be in linearly general position. In this section, we aim to provide further necessary conditions for the sets Z giving rise to unexpected quartics.

For instance, the presence of a 4-rich line imposes a precise behavior on the configuration. The next propositions show how such a line has to intersect the other lines.

Proposition 3.1

If there are two 4-rich lines $L_Q,L_R$ such that $L_Q\cap L_R\notin Z$, then $I(Z+3P)_4=0$.

Fig. 3

Two 4-rich lines not intersecting in Z

Proof

Assume by contradiction that $I(Z+3P)_4\ne 0$. By hypothesis, there exists a unique point $S\in Z\setminus (L_R\cup L_Q)$. Set $Z\cap L_R=\{R_1,R_2,R_3,R_4\}$. By Proposition 2.1, for any $i\in \{1,2,3,4\}$ the lines $SR_i$ and $L_Q$ meet at a point of Z, say $Q_i$ (see Fig. 3). Up to projective equivalence, we assume that

$$\begin{aligned} S=[0,0,1],\quad R_1=[1,0,0],\quad R_2=[0,1,0],\quad Q_3=[1,1,1]. \end{aligned}$$

This choice of coordinates implies that $L_R$ is the line $z=0$ and that $R_3=[1,1,0]$. Since $Q_4\notin L_R$, $Q_4=[a,b,1]$ for some parameters a and b. Therefore, $L_Q$ is the line $(1-b)x+(a-1)y+(b-a)z=0$, $Q_1=[a-b,0,1-b]$ with $a\ne b$ and $b\ne 1$, $Q_2=[0,a-b,a-1]$ with $a\ne 1$ and finally $R_4=[a,b,0]$ with $a\ne 0$ and $b\ne 0$.

Now, let D be the quartic defined by a nonzero element of $I(Z+3P)_4$. We consider three different specializations of P that put constraints on a and b and we show that there is no choice of a and b that satisfies all the constraints simultaneously.

First of all, observe that the lines $R_1Q_2$ and $R_2Q_1$ are simple. If we specialize P to the point $R_1Q_2\cap R_2Q_1=[(1-a)(a-b),(1-b)(b-a),(1-a)(1-b)]$, then D contains $R_1Q_2$, $R_2Q_1$ and the singular conic $R_3Q_3\cup R_4Q_4$. Moreover, since D has multiplicity 3 at P, P must be on either $R_3Q_3$ or $R_4Q_4$, in which case $b=2-a$ or $1/a+1/b=2$, respectively.

Similarly as before, the lines $R_1Q_3$ and $R_3Q_1$ are simple. If we specialize P to the point $R_1Q_3\cap R_3Q_1=[2b-a-1,b-1,b-1]$, then D contains $R_1Q_3$, $R_3Q_1$ and the singular conic $R_2Q_2\cup R_4Q_4$. The conclusion now is that P must be on either $R_2Q_2$ or $R_4Q_4$. The first case yields the condition $a=2b-1$, whereas the second one gives the condition $b=1/2$.

On the one hand, if we assume that $a=2b-1$, then the only one compatible constraint between the two provided by the first specialization of P is $1/a+1/b=2$. This gives the only one possible solution $(a,b)=(-1/2,1/4)$. On the other hand, if we assume that $b=1/2$, from the first specialization of P we must have that $b=2-a$. Then, another solution is $(a,b)=(3/2,1/2)$.

Finally, we observe that the lines $R_1Q_4$ and $R_4Q_1$ are simple as well. If we specialize P to the point $R_1Q_4\cap R_4Q_1=[ab-2a+b,b(b-1),b-1]$, then D contains $R_1Q_4$, $R_4Q_1$ and the singular conic $R_2Q_2\cup R_3Q_3$. The conclusion now is that P must be on either $R_2Q_2$ or $R_3Q_3$. Since $R_2Q_2$ and $R_3Q_3$ are the lines $x=0$ and $x-y=0$, respectively, we reach a contradiction either if $(a,b)=(-1/2,1/4)$ or $(a,b)=(3/2,1/2)$. $\square$

The previous result is important because it imposes a tight restriction on the set Z admitting an unexpected quartic. Indeed, there is only one Z having more than one 4-rich line.

Proposition 3.2

Assume that $I(Z+3P)_4\ne 0$. If there are two 4-rich lines $L_Q$, $L_R$, then the configuration of the points of Z is the one described in Example 1.5.

Proof

By Proposition 3.1, the 4-rich lines $L_Q$ and $L_R$ meet at a point of Z. Then, we can suppose that $L_R\cap Z=\{R_1,R_2,R_3,B\}$ and that $L_Q\cap Z=\{Q_1,Q_2,Q_3,B\}$. Let $\{S_1,S_2\}=Z \setminus (L_R \cup L_Q)$ and $L_S$ be the line containing $S_1$ and $S_2$. By Proposition 2.1, $L_S$ meets $L_Q$ and $L_R$ at a point of Z.

Assume by contradiction that $B\in L_S$. Let $L_{ij}$ be the line joining $S_i$ and $R_j$ for $i\in \{1,2\}$ and $j\in \{1,2,3\}$. By Proposition 2.1, each line $L_{ij}$ meets $L_Q$ at a point of Z. We show that the two cubics $C_1=L_{11}\cup L_{12}\cup L_{13}$ and $C_2=L_{21}\cup L_{22}\cup L_{23}$ never coincide when restricted to the line $L_Q$. This implies that one of the $L_{ij}$ meets $L_Q$ outside Z, hence contradicting Lemma 2.1. Assume that $B=[1,0,0]$ and that the equations of $L_Q$, $L_R$ and $L_S$ are, respectively, $z=0$, $y=0$ and $y-z=0$. In particular, $S_i=[s_i,1,1]$ and $R_j=[r_j,0,1]$ for some parameters $s_i$ and $r_j$ for $i\in \{1,2\}$ and $j\in \{1,2,3\}$. With these assumptions, we obtain that $L_{ij}$ is defined by the linear form $l_{ij}=x+(r_j-s_i)y-r_jz=0$ for all i and j. With a bit of work, one can see that $l_{11}l_{12}l_{13}$ and $l_{21}l_{22}l_{23}$ have the same roots on $L_Q$ if and only if $s_1=s_2$, and the latter condition is impossible since $S_1\ne S_2$.

The above argument implies that $B\notin L_S$. Up to relabeling, we assume that $Q_2\in L_S$ and $R_2 \in L_S$. Let $M_1$ be the line containing $R_1$ and $S_2$, and let $M_3$ be the line containing $R_3$ and $S_2$. By Proposition 2.1, $M_1$ and $M_3$ meet $L_Q$ at a point of Z, and up to relabeling we assume that $Q_1\in M_1$ and that $Q_3\in M_3$. Now consider the line $N_1$ joining $S_1$ and $R_1$ and the line $N_3$ joining $S_1$ and $R_3$. Again by Proposition 2.1, $N_1$ and $N_3$ meet $L_Q$ at a point of Z. In particular, $Q_i\notin N_i$ for $i\in \{1,3\}$ because $S_1 \ne S_2$. Moreover, $Q_2\notin N_i$ because $R_2\ne R_i$ for $i\in \{1,3\}$. Therefore, the only possibility is that $Q_3 \in N_1$ and that $Q_1 \in N_3$. Hence, the obtained configuration is projectively equivalent to the one described in Example 1.5. $\square$

The following property of 4-rich lines is a further step toward the proof of uniqueness.

Proposition 3.3

Assume that there is exactly one 4-rich line $L_R$. If there is a 3-rich line $L_Q$ such that $L_Q\cap L_R\notin Z$, then $I(Z+3P)_4=0$.

Proof

Assume by contradiction that $I(Z+3P)_4\ne 0$. Suppose that $L_R\cap Z=\{R_1,R_2,R_3,R_4\}$ and that $L_Q\cap Z=\{Q_1,Q_2,Q_3\}$. By hypothesis, there are only two points $S_1$, $S_2$ in $Z \setminus (L_R\cup L_Q)$. Moreover, by Proposition 2.1, $L_S=S_1S_2$ must meet either $L_R$ or $L_Q$ at a point of Z.

Suppose that $L_S$ meets $L_R$ at a point of Z. If, in turn, $L_S$ meets $L_Q$ at a point of Z, then a 4-rich line distinct from $L_R$ appears, which is not allowed by hypothesis. Hence, $L_S\cap L_Q\cap Z=\emptyset$ and we assume that $R_4\in L_S$. By Proposition 2.1, the line $Q_iS_1$ meets $L_R$ at a point of Z for $i\in \{1,2,3\}$. Moreover, $Q_iS_1\cap L_R\ne Q_jS_1\cap L_R$ for $i\ne j$ and $Q_iS_1\cap L_R$ is distinct from $R_4$ for $i\in \{1,2,3\}$. Therefore, we may assume that $Q_iS_1$ contains $R_i$ for all $i\in \{1,2,3\}$. Similarly, the line $Q_iS_2$ meets $L_R$ at a point of Z distinct from $R_4$ for $i\in \{1,2,3\}$. Suppose that $R_3\in Q_1S_2$. (The proof is similar if we consider $R_2\in Q_1S_2$.) Consequently, $R_1\in Q_2S_2$ and $R_2\in Q_3S_2$. Up to projective equivalence, we assume that

$$\begin{aligned} R_1=[0,0,1],\quad R_2=[0,1,0],\quad Q_3=[1,0,0],\quad S_1=[1,1,1]. \end{aligned}$$

This choice of coordinates implies that $L_R$ and $Q_3S_1$ are the lines $x=0$ and $y-z=0$, respectively. Besides that, $R_3=[0,1,1]$. Since $S_2\in R_2Q_3$ and $R_2Q_3$ has equation $z=0$, $S_2=[1,a,0]$ for some $a\ne 0$. After little computation, one verifies that $Q_2=[1,a,1]$, $Q_1=[1,1,1-a]$, $R_4=[0,1-a,1]$ for some $a\notin \{0,1\}$, and that $L_Q$ has equation $y-az=0$. Since $Q_1\in L_Q$ as well, we get the relation $a^2-a+1=0$. Now let D be the quartic defined by a nonzero element of $I(Z+3P)_4$. Observe that the lines $R_2Q_1$ and $R_4Q_2$ are simple. If we specialize P to the point $R_2Q_1 \cap R_4Q_2=[1,a^2,1-a]$, then D contains $R_2Q_1$, $R_4Q_2$ and the singular conic $R_1S_2\cup R_3Q_3$. Since D has multiplicity 3 at P, P must be on either $R_1S_2$ or $R_3Q_3$. On the one hand, if P is on the line $R_1S_2$ of equation $y-ax=0$, then necessarily $a\in \{0,1\}$, a contradiction. On the other hand, if P lies on the line $R_3Q_3$ of equation $y-z=0$, then necessarily $a^2+a-1=0$. This relation, combined with the relation $a^2-a+1=0$ obtained before, implies that $a=1$, again a contradiction.

Now suppose that $L_S$ meets $L_Q$ at a point of Z. In particular, suppose that $L_S$ contains the point $Q_3$. By Proposition 2.1, the lines $Q_1S_1$ and $Q_1S_2$ are not simple; hence, up to labeling we assume that $Q_1S_1\cap L_R=R_1$ and $Q_1S_2\cap L_R=R_2$. Regarding the lines $Q_2S_1$ and $Q_2S_2$, we have three cases to consider (Fig. 4):

Fig. 4

The cases (1), (2) and (3) of Proposition 3.3

• (1) $Q_2S_1 \cap L_R=R_3$ and $Q_2S_2 \cap L_R=R_4$. Observe that the lines $Q_1R_3$, $Q_1R_4$ and $Q_2R_2$ are simple. Let $X_1=Q_1R_3\cap Q_2R_2$ and $X_2=Q_1R_4\cap Q_2R_2$. On the one hand, we can specialize P to $X_1$. In order for D to exist, we need a conic having $L_R$ and $L_S$ as components. Noting that $X_1\notin L_R$, we have that $X_1\in L_S$. On the other hand, we can specialize P to $X_2$. In order for D to exist, we need a conic having $L_R$ and $L_S$ as components and, similarly as before, $X_2\in L_S$. Hence, $Q_2R_2$ and $L_S$ should coincide, a contradiction.

• (2) $Q_2S_1 \cap L_R=R_2$ and $Q_2S_2 \cap L_R=R_3$. Note that the lines $Q_1R_3$, $Q_1R_4$ and $Q_2R_1$ are simple. Now repeat the argument from case (1).

• (3) $Q_2S_1 \cap L_R=R_2$ and $Q_2S_2 \cap L_R=R_1$. Up to projective equivalence, we assume that

  $$\begin{aligned} R_1=[1,0,0],\quad R_2=[0,1,0],\quad S_1=[0,0,1],\quad S_2=[1,1,1]. \end{aligned}$$

  This choice of coordinates implies that $L_R$ and $L_S$ are the lines $z=0$ and $x-y=0$, respectively. Moreover, we obtain that $Q_1=[1,0,1]$, $Q_2=[0,1,1]$. Therefore, $L_Q$ is the line $x+y-z=0$ and $Q_3=[1,1,2]$. Now, we assume that $R_3=[1,a,0]$ and $R_4=[1,b,0]$ for some parameters a and b such that $a\ne 0$, $b\ne 0$ and $a\ne b$. Moreover, we exclude the case $\{a,b\}=\{-1,1\}$, which is not allowed by hypothesis and in particular coincides with the configuration of Example 1.5. Let D be the quartic defined by a nonzero element of $I(Z+3P)_4$. We follow the same argument used in Proposition 3.1. First of all, observe that, with the given constraints on the parameters a and b, the lines $R_3S_1$, $R_3Q_2$, $R_3Q_3$ and $R_4S_2$ are simple.

  If we specialize P to the point $Y_1=R_3S_1\cap R_4S_2=[b-1,a(b-1),b-a]$, then D contains $R_3S_1$, $R_4S_2$ and the singular conic $L_Q\cup L_R$. Moreover, $Y_1$ must be on either $L_R$ or $L_Q$, in which case $a=b$ (impossible by our assumption) or $ab=1$, respectively. Hence, we can rewrite $R_4=[a,1,0]$.

  If we specialize P to the point $Y_2=R_3Q_2\cap R_4S_2=[1,1+a-a^2,1-a^2]$, then D contains $R_3Q_2$, $R_4S_2$ and the singular conic $Q_3R_2\cup Q_1R_1$. The conclusion now is that $Y_2$ must belong either to $Q_3R_2:2x-z=0$ or to $Q_1R_1:y=0$. The first case yields the condition $a^2+1=0$, whereas the second one gives the condition $a^2-a-1=0$.

  Finally, if we specialize P to the point $Y_3=R_3Q_3\cap R_4S_2=[a+2,2a+1,2(a+1)]$, then D contains $R_3Q_3$, $R_4S_2$ and the singular conic $Q_1R_1\cup Q_2R_2$. Hence, $Y_3$ must be on either $Q_1R_1:y=0$ or $Q_2R_2:x=0$, so either $a=-1/2$ or $a=-2$. Since neither $a=-1/2$ nor $a=-2$ is a root of either of the polynomials $a^2+1$ or $a^2-a-1$, we have that the initial constraints on a and b prevent the configuration from admitting an unexpected quartic.

$\square$

Proposition 3.4

If Z admits exactly one 4-rich line L, then $I(Z+3P)_4=0$.

Proof

Suppose there is a 4-rich line L, with $L \cap Z=\{Z_1,Z_2,Z_3,Z_4\}$. Let $R = \{R_1,\ldots ,R_5\}$ denote the remaining five points of Z. First of all, by Propositions 3.2 and 3.3, if three of the points of R are collinear, then $I(Z+3P)_4=0$. For $i\in \{1,\ldots ,5\}$, let $L_i$ be the line containing $Z_1$ and $R_i$. Since |R| is odd and none of the lines $L_i$ can contain more than two points of R, one of the lines $L_i$ must contain exactly one of the points of R. So say $L_1$ contains only $R_1$. For $j\in \{2,\ldots ,5\}$, define $M_j$ to be the line $R_1R_k$. By Proposition 2.1, the line $M_2$ intersects L in $\{Z_1,Z_2,Z_3,Z_4\}$. Hence, up to relabelings we may assume that $M_2\cap L=Z_2$. Now, the point $R_3$ cannot belong to the line $M_2$ by hypothesis, so $M_2\ne M_3$ and we may assume that $M_3\cap L=Z_3$. By the same argument we obtain that $M_2,M_3,M_4$ are distinct lines and $M_4\cap L=Z_4$. Then, the line $M_5$ contains two points of R and $M_5\cap L\cap Z=\emptyset$. Proposition 2.1 implies that $I(Z+3P)_4=0$. $\square$

Corollary 3.5

The configuration of Example 1.5 is the only configuration of nine points in ${\mathbb {P}}^2$ containing a 4-rich line which admits an unexpected quartic.

Corollary 3.5 will be the first step in the proof of Theorem 1.6. In the next section, we will show that if a configuration Z of nine points admits an unexpected quartic, then Z has a 4-rich line.

4 Unexpected curves and stability conditions

Let $Z\subset {\mathbb {P}}^2$ be a finite set of points. For us, the stability (respectively, the semistability) of Z is the stability (respectively, the semistability) of its dual line arrangement ${\mathcal {A}}_Z$. The latter is defined in [4, Section 6] in terms of the derivation bundle of ${\mathcal {A}}_Z$, but what we actually need are the following properties. The first one follows from [4, Proposition 6.4].

Lemma 4.1

If $Z\subset {\mathbb {P}}^2$ is semistable or stable, then Z admits no unexpected curve.

The next results are proven in [4, Lemma 6.5] and [4, Proposition 6.7].

Lemma 4.2

Let $Z\subset {\mathbb {P}}^2$ be a set of points and $P\in Z$. Consider $Z'=Z\setminus \{P\}$ and the line arrangement ${\mathcal {A}}=\{PQ\mid Q\in Z'\}$. We define the set $Z''\subset {\mathbb {P}}^2$ to be the dual of ${\mathcal {A}}$. Then,

• (1) if |Z| is odd, $Z'$ is stable and $|Z''| > \frac{|Z|+1}{2}$, then Z is stable,

• (2) if |Z| is odd and $Z'$ is stable, then Z is semistable,

• (3) if |Z| is even, $Z'$ is semistable and $|Z''| > \frac{|Z|}{2}$, then Z is stable,

• (4) if |Z| is even and $Z'$ is stable, then Z is stable.

Lemma 4.3

If $Z\subset {\mathbb {P}}^2$ is a set of at least four points in linearly general position, then Z is stable.

There are some configurations of points which will be useful for us.

Definition 4.4

For $n\ge 3$, the factors of the polynomial

$$\begin{aligned} (x^n - y^n)(x^n - z^n)(y^n - z^n)\in {\mathbb {C}}[x,y,z] \end{aligned}$$

define the Fermat arrangement of 3n lines in ${\mathbb {P}}^2$. Its dual is a configuration of 3n points in ${\mathbb {P}}^2$, called the dual Fermat configuration and denoted by $F_n$.

Since we are dealing with sets of nine points in the plane, for us the most interesting Fermat configuration is $F_3$, shown in Fig. 5.

Fig. 5

The dual Fermat configuration $F_3$ and its corresponding twelve 3-rich lines. The first eight 3-rich lines are depicted on the left picture. The remaining four 3-rich lines are obtained regarding the open circles as representing collinear points, and likewise the dotted circles as representing collinear points

As pointed out in [10, Section 1.1], $F_3$ has the peculiar feature to admit no simple lines and no k-rich lines for any $k\ge 4$. For our purpose, we need to know whether there are other configurations of nine points with similar properties. Our next task is to prove that $F_3$ is the only one, thereby solving [10, Open problem 1.1.6] for sets of nine points.

Lemma 4.5

Let $Y\subset {\mathbb {P}}^2$ be a set of nine points. Assume that every line that meets Y at at least two points contains exactly three points of Y. Then,

• (1) every point of Y is contained in exactly four 3-rich lines,

• (2) Y admits twelve 3-rich lines,

• (3) for every 3-rich line M, there are two other 3-rich lines $M',M''$ such that $M\cap M'\notin Y$ and $M\cap M''\notin Y$.

Proof

• (1) Let $P\in Y$. By hypothesis, for every $Q\in Y\setminus \{P\}$, the line PQ is 3-rich, so there exists a unique $Q'\in T\setminus \{P,Q\}$ such that $Y\cap PQ=\{P,Q,Q'\}$. In this way, the eight points of $Y\setminus \{P\}$ are partitioned in four pairs. Each pair defines a 3-rich line containing P.

• (2) By hypothesis, each pair of points of Y defines a 3-rich line. In this way, every such line is counted $\left( {\begin{array}{c}3\\ 2\end{array}}\right)$ times, so the number of 3-rich lines is $\left( {\begin{array}{c}9\\ 2\end{array}}\right) \cdot \frac{1}{3}=12$.

• (3) Let M be a 3-rich line and let $P\in M\cap Y$. As in part (1), the remaining eight points of Y are partitioned into four pairs $(Q_1,Q_1'),\dots ,(Q_4,Q_4')$ is such a way that $P\in Q_iQ_i'$ for every $i\in \{1,\dots ,4\}$. We may assume $M=Q_1Q_1'$. Another 3-rich line meeting M at a point of Y is defined by the choice of a point among $\{P,Q_1,Q_1'\}$ and an index among $\{2,3,4\}$, so there are nine of them. Now, the statement follows from part (2).

$\square$

Corollary 4.6

$F_3$ is the only configuration of nine points in ${\mathbb {P}}^2$ with no k-rich lines for every $k\ge 4$ and no simple lines.

Proof

Let Y be such a configuration, and let $P_1\in Y$. By Lemma  4.5(1), the point $P_1$ is contained in exactly four 3-rich lines, call them $P_2P_3$, $P_4P_5$, $P_6P_7$ and $P_8P_9$ (see Figure 5 (middle)). By Lemma 4.5(3), there is a 3-rich line meeting $P_2P_3$ outside Y. Up to relabeling, we may assume that this line is $P_4P_6$ and that $P_4P_6\cap Y=\{P_4,P_6,P_8\}$. By Lemma 4.5(1), the point $P_4$ is contained in exactly four 3-rich lines. Two of them are $P_4P_5$ and $P_4P_6$. Since Y does not admit 4-rich lines, the remaining two 3-rich lines through $P_4$ must be $P_iP_j$ and $P_kP_l$ with $\{i,j,k,l\}=\{2,3,7,9\}$ and $\{i,j\}\ne \{2,3\}$. Without loss of generality, we can therefore suppose that $P_4\in P_2P_7\cap P_3P_9$. In a similar fashion, one may verify that $P_3\in P_1P_2\cap P_4P_9\cap P_5P_6\cap P_7P_8$. In the same way, $P_2\in P_6P_9\cap P_5P_8$ and $P_7\in P_5P_9$. Thus $Y=F_3$. $\square$

Now that we have a better understanding of the dual Fermat configuration, we can state our result on semistability of sets of nine points.

Proposition 4.7

If $Z\subset {\mathbb {P}}^2$ is a set of nine points containing no k-rich lines for $k \ge 4$, then either $Z=F_3$ or Z is semistable.

Proof

Our idea is to reduce the problem to the study of smaller subsets of Z. Assume that Z is not $F_3$. By Corollary 4.6, Z admits a simple line L. Assume $L\cap Z=\{Z_8,Z_9\}$. By Lemma 4.2(2), in order to conclude it is enough to show that there exists a stable subset of Z with eight points. Since there are no 4-rich lines, the set $\{Z_jZ_9\mid j\in \{1,\ldots ,8\}\}$ has at least five distinct elements $L,L_1,\ldots ,L_4$. Up to relabeling, we can assume $Z_1\in L_1,\ldots ,Z_4\in L_4$. Let $A\in \{Z_5,Z_6,Z_7\}$ and set $W_8=Z\setminus \{A\}$. All we need to do is to prove that $W_8$ is stable. In order to do that, we want to apply Lemma 4.2(3). Define $W_7=W_8\setminus \{Z_9\}$. We will prove that $W_7$ is semistable. In turn, by Lemma 4.2(2) it is enough to check that there exists a stable subset $W_6\subset W_7$ with six elements.

We indicate by S the configuration of six points in ${\mathbb {P}}^2$ given by the intersection points of four general lines. Now, we want to show that $W_7$ contains at least a subset $W_6$ of six elements which is different from the configuration S. Consider one of the subsets of six points of $W_7$. If it is not S, then we are done. If it is S, then the seventh point of $W_7$ does not lie on any of the four 3-rich lines of S, because our hypothesis guarantees that Z has no k-rich lines for $k\ge 4$. Therefore, if we replace one of the points of S with the seventh one, the resulting subset of $W_7$ is not S. Call this subset $W_6$.

Since $W_6$ is not S, there exists a subset $W_5\subset W_6$ of five elements with at most one 3-rich line. By Lemma 4.2(4), it is enough to prove that $W_5$ is stable. If $W_5$ has no 3-rich lines, then it is stable by Lemma 4.3. Otherwise, $W_5$ has exactly one 3-rich line. Up to projective equivalence, we assume that $W_5=\{B_1,B_2,B_3,B_4,B_5\}$, where

$$\begin{aligned} B_1=[1,0,0],\quad B_2=[0,1,0],\quad B_3=[0,0,1],\quad B_4=[1,1,1],\quad B_5=[1,a,0] \end{aligned}$$

for some parameter a. Using the following Macaulay2 lines [7] one can verify that also in this case $W_5$ is stable.

In this way, we check that the splitting type (see [4, Section 1] for a definition) of $W_5$ is (2, 2); hence, $W_5$ is stable. $\square$

The last result of this section is an important step toward the proof of Theorem 1.6.

Lemma 4.8

Up to projective equivalence, the only configuration of nine points $Z\subset {\mathbb {P}}^2$ admitting an unexpected quartic is the one presented in Example 1.5.

Proof

If Z has a 4-rich line, then we conclude by Corollary 3.5. Assume then that Z admits no 4-rich lines. Since the configuration $F_3$ does not admit an unexpected curve by [4, Section 6], Proposition 4.7 and Lemma 4.1 imply that Z does not admit an unexpected quartic. $\square$

Remark 4.9

It is interesting to point out that if $n\ge 5$, then the configuration $F_n$ admits unexpected curves of degrees $n+2,\ldots ,2n-3$ by [4, Proposition 6.12].

As a consequence, we can now complete the proof of our main result.

Proof of Theorem 1.6

Thanks to Lemma 4.8, we know that the thesis holds if $|Z|=9$. If $|Z|<9$, then the unexpected curve is reducible by [4, Corollary 5.5]. By [4, Theorem 5.9], this implies that some subset of Z admits an unexpected cubic, and this contradicts Theorem 1.4.

Assume now that $|Z|>9$. Let W be any subset of nine points of Z. Observe $I(W+3P)_4$ contains $I(Z+3P)_4$ for every $P\in {\mathbb {P}}^2$; hence, $\dim I(W+3P)_4\ge \dim I(Z+3P)_4$. The latter equals 1 by [4, Corollary 5.5]. Since $I(W+3P)_4$ is expected to be empty, W admits an unexpected quartic too, so $\dim I(W+3P)_4=1$ for the same reason. It follows that $I(V+3P)_4=I(Z+3P)_4$ for every $V\subset Z$ such that $9\le |V|\le |Z|$. In particular, we consider a set of 10 points. This V enjoys a peculiar property: If we remove any point from it, we get a subset W admitting an unexpected quartic. By Lemma 4.8, this means that every time we remove a point from V, we get a configuration equivalent to Example 1.5. Such configuration has three 4-rich lines. In order to preserve this property, if we remove $Z_9$ (see Fig. 1), the tenth point of V should lie in the intersection of two 3-rich lines, and this is not possible. $\square$

We conclude by pointing out that there is a connection between existence and uniqueness of unexpected curves and de Jonquières transformations.

Example 4.10

Let P be a general point, and let $Z=\{Z_1, \dots ,Z_9\}\subset {\mathbb {P}}^2$ be a set of nine points, not containing five collinear points. Let $\varphi$ be the degree four de Jonquières transformation with centers P and $Z_1,\dots ,Z_6$. In other words, $\varphi :{\mathbb {P}}^2\dashrightarrow {\mathbb {P}}^2$ is the birational map associated with the linear system of quartic plane curves containing $Z_1,\dots ,Z_6$ and having multiplicity three at P. Let

be the resolution of indeterminacy of $\varphi$. If Z admits an unexpected quartic D, then $\Phi (D)$ has degree $4\cdot 4-3^2-6=1$. Therefore, the points $\Phi (Z_7)$, $\Phi (Z_8)$, $\Phi (Z_9)$ are collinear.

This phenomenon occurs every time that the linear system associated with such a de Jonquières-type transformation has no fixed components. However, this is not always the case.

Example 4.11

Consider the Fermat configuration $F_{60}$ and a general point $P\in {\mathbb {P}}^2$. By Remark 4.9, there is an unexpected curve $C\in I(F_{60}+21P)_{22}$. Such C is irreducible by [4, Lemma 5.1]. By Bézout’s theorem, C is an irreducible component of $I(F_{60}+30P)_{31}$, so $I(F_{60}+30P)_{31}\cong I(9P)_{9}$ has dimension ten. In this case, the rational map $\varphi$ associated with the linear system of degree 31 curves containing $F_{60}$ and having multiplicity 30 at P is not a birational transformation of ${\mathbb {P}}^2$, but rather is a rational map $\varphi :{\mathbb {P}}^2\dashrightarrow {\mathbb {P}}^9$.