Modeling the Effects of Grain and Porosity Structure on Copper Spall Response

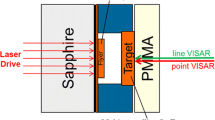
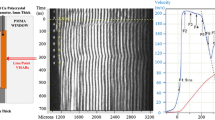
Abstract

Ongoing efforts to characterize the incipient spallation of copper have increased the experimental fidelity at which the material’s microstructure is measured. Various imaging techniques have allowed for 3D characterization of the structure of inclusions, porosity, and crystallographic grains. This work employs a combined crystal mechanics and porosity model that, for the first time, addresses the influence of three different types of spatial distributions of second phase particles, relative to features in both experimentally-measured and synthetically-generated microstructures. With these features, the model can probe the sensitivity of copper spall response to both grain and porosity structures. The sensitivity of the model to various nucleation and porosity growth parameters is also shown. These sensitivity studies illustrate where increased experimental accuracy can most readily affect modeling results. Likewise, the model’s fidelity captures many of the key features measured experimentally and is a step toward a model capable of predicting and improving the spall resistance in many materials.

Appendices

Appendix 1

Kinematics

The material kinematics are based on a multiplicative decomposition of the deformation gradient

$$\begin{aligned} \pmb {\text {F}} = \pmb {\text {V}} \cdot \pmb {\text {R}} \cdot \pmb {\text {F}}_p \cdot \pmb {\text {F}}_d, \end{aligned}$$

(8)

where $\pmb {\text {R}}$ is the lattice rotation, and $\pmb {\text {V}}$ is the thermoelastic lattice stretch. The plastic deformation gradient due to dislocation slip is described by $\pmb {\text {F}}_p$, and $\pmb {\text {F}}_d$ captures the volume change from porosity (i.e., damage). This multiplicative decomposition results in several intermediate configurations ${\bar{{\mathscr {B}}}}$, $\hat{{\mathscr {B}}}$, $\tilde{{\mathscr {B}}}$ (similar to those in [47]) between a reference configuration ${\mathscr {B}}_o$ and current (deformed) configuration ${\mathscr {B}}$ as is illustrated in Fig. 16.

Fig. 16

The kinematics of the multiplicative decomposition of the deformation gradient

The velocity gradient is decomposed into a symmetric ($\pmb {\text {D}}$) and skew-symmetric ($\pmb {\text {W}}$) part as

$$\begin{aligned} \pmb {\text {L}} = \text {sym}(\pmb {\text {L}}) + \text {skew}(\pmb {\text {L}})= \pmb {\text {D}}+ \pmb {\text {W}}. \end{aligned}$$

(9)

The velocity gradient is

$$\begin{aligned} \pmb {\text {L}} = \dot{\pmb {\text {F}}} \cdot \pmb {\text {F}}^{-1}. \end{aligned}$$

(10)

Combining Eqs. 8 and 10 gives

$$\begin{aligned} \pmb {\text {L}} = \dot{\pmb {\text {V}}}\cdot \pmb {\text {V}}^{-1} + \pmb {\text {V}}\cdot \left[ \pmb {\text {W}}_R + \pmb {\text {R}} \cdot \left( \hat{\pmb {\text {L}}}_p + \pmb {\text {F}}_p \cdot {\bar{\pmb {\text {L}}}}_d \cdot \pmb {\text {F}}_p^{-1} \right) \cdot \pmb {\text {R}}^{T} \right] \cdot \pmb {\text {V}}^{-1}, \end{aligned}$$

(11)

where $\hat{\pmb {\text {L}}}_p \equiv \dot{\pmb {\text {F}}}_p\cdot \pmb {\text {F}}_p^{-1}$ and ${\bar{\pmb {\text {L}}}}_p \equiv \dot{\pmb {\text {F}}}_d\cdot \pmb {\text {F}}_d^{-1}$ represent deformation from slip and porosity growth respectively and $\pmb {\text {W}}_R \equiv \dot{\pmb {\text {R}}}\cdot \pmb {\text {R}}^T$ accounts for rigid rotation.

Dislocation Slip Kinematics

The decomposition of $\hat{\pmb {\text {L}}}_p$ into symmetric ($\hat{\pmb {\text {D}}}_p$) and skew-symmetric ($\hat{\pmb {\text {W}}}_p$) parts gives

$$\begin{aligned} \hat{\pmb {\text {L}}}_p = \text {sym}(\hat{\pmb {\text {L}}}_p) + \text {skew}(\hat{\pmb {\text {L}}}_p)= \hat{\pmb {\text {D}}} _p+ \hat{\pmb {\text {W}}}_p. \end{aligned}$$

(12)

The governing equations for the material response concerning slip are then

$$\begin{aligned} \pmb {\text {R}}^T \cdot \pmb {\text {D}}^\prime \cdot \pmb {\text {R}}= \frac{1}{a} \dot{\tilde{\pmb {\text {V}}}}^\prime + \hat{\pmb {\text {D}}} _p, \end{aligned}$$

(13)

$$\begin{aligned} \pmb {\text {R}}^T \cdot \pmb {\text {W}}\cdot \pmb {\text {R}}= \pmb {\text {R}}^T \cdot \pmb {\text {W}}_R \cdot \pmb {\text {R}} + \hat{\pmb {\text {W}}} _p - \frac{1}{2a^2} \left( \dot{\tilde{\pmb {\text {V}}}}^\prime \cdot \tilde{\pmb {\text {V}}}^\prime - \tilde{\pmb {\text {V}}}^\prime \cdot \dot{\tilde{\pmb {\text {V}}}}^\prime \right) , \end{aligned}$$

(14)

where $(\bullet )^\prime$ denotes the deviator and $\tilde{\pmb {\text {V}}} \equiv \pmb {\text {R}}^T\cdot \pmb {\text {V}}\cdot \pmb {\text {R}}$. These equations are similar to those in [63, 64], where more details on their derivation are given.

Following the assumptions of [49], $\hat{\pmb {\text {D}}} _p$ and $\hat{\pmb {\text {W}}}_p$ are determined from

$$\begin{aligned} \hat{\pmb {\text {L}}}_p= {\dot{\pmb {\text {F}}}}_p \cdot \pmb {\text {F}}_p^{-1}= \sum _{\alpha =1}^{N} {\dot{\gamma }}^{\alpha } \; \hat{\pmb {\text {s}}} ^{\alpha } \otimes \hat{\pmb {\text {m}}} ^{\alpha } , \end{aligned}$$

(15)

where N is the number of slip systems, ${\dot{\gamma }}$ is the shear slip rate, $\hat{\pmb {\text {s}}}^{\alpha }$ is the slip direction, and $\hat{\pmb {\text {m}}}^{\alpha }$ is the slip plane normal, all for a slip system $\alpha$. In Eqs. 13 and 14 it is assumed that that the deviatoric part of the elastic strain is small (a reasonable assumption for metal alloys) such that the elastic stretch can be written as

$$\begin{aligned} \pmb {\text {V}} \equiv a \left( \pmb {\text {I}} + \pmb {\epsilon }^* \right) , \end{aligned}$$

(16)

where $\pmb {\text {I}}$ is the identity tensor, $\pmb {\epsilon }^*$ is defined as a deviatoric tensor, and a is a variable related to volume change. Equations 13 and 14 are solved for fundamental degrees-of-freedom $\pmb {\epsilon }^*$, $\pmb {\text {W}}_\mathrm {R}$ where $\pmb {\text {D}}$ and $\pmb {\text {W}}$ are known from the finite element method.

Porosity Kinematics

Porosity evolution is assumed to account for volume change only and is governed by the Cocks–Ashby porosity kinetics in Eq. 3. Porosity evolution is connected to the crystal mechanics via the trace of Equation 11. Since $\pmb {\text {F}}_p$ and $\pmb {\text {W}}_R$ do not contribute to volume change this gives

$$\begin{aligned} \mathrm {tr} \left( \pmb {\text {D}}\right) = \mathrm {tr} \left( {\dot{\pmb {\text {V}}}}\cdot \pmb {\text {V}}^{-1} \right) + \mathrm {tr} \left( {\dot{\pmb {\text {F}}}_d}\cdot \pmb {\text {F}}_d^{-1} \right) , \end{aligned}$$

(17)

which for simplicity (in implementation) is written as

$$\begin{aligned} \mathrm {tr} \left( \pmb {\text {D}}\right) = \mathrm {tr} \left( \pmb {\text {D}}_V\right) + \mathrm {tr} \left( {\bar{\pmb {\text {D}}}}_d\right) , \end{aligned}$$

(18)

where $\pmb {\text {D}}_V = {\dot{\pmb {\text {V}}}}\cdot \pmb {\text {V}}^{-1}$ and ${\bar{\pmb {\text {D}}}}_d$ is the symmetric part of ${\bar{\pmb {\text {L}}}}_d$. Using the assumption in [65], the deformation due to porosity change is $\pmb {\text {F}}_d = \varPhi \pmb {\text {I}}$. Applying the definition $J_d = \mathrm {det} (\pmb {\text {F}}_d)$ then gives $\varPhi = J_d^{1/3}$ and $\pmb {\text {F}}_d = J_d^{1/3}\pmb {\text {I}}$. Differentiating gives

$$\begin{aligned} \dot{\pmb {\text {F}}}_d = \frac{1}{3}J_d^{-2/3}\dot{J}_d \pmb {\text {I}}, \end{aligned}$$

(19)

resulting in

$$\begin{aligned} \bar{\pmb {\text {D}}}_d = \text {sym} (\dot{\pmb {\text {F}}_d}\cdot \pmb {\text {F}}_d^{-1}) = \frac{1}{3} \frac{{\dot{J}}_d}{J_d} \pmb {\text {I}}. \end{aligned}$$

(20)

Thus, $\text {tr}({\bar{\pmb {\text {D}}}}_d) = {\dot{J}}_d/J_d$ and rearranging shows that this an ordinary differential equation (ODE) of the form

$$\begin{aligned} {\dot{J}}_d = \mathrm {tr}({\bar{\pmb {\text {D}}}}_d) J_d. \end{aligned}$$

(21)

Similarly, applying the definition $J_V = \mathrm {det} (\pmb {\text {V}})$ and the approximation that $\mathrm {det} (\pmb {\text {V}}) = a^3$, results in $\pmb {\text {V}} = J_V^{1/3}(\pmb {\text {I}} + \pmb {\epsilon }^*)$. Differentiating then gives

$$\begin{aligned} \dot{\pmb {\text {V}}} = \frac{1}{3}J_V^{-2/3}{\dot{J}}_V (\pmb {\text {I}} + \pmb {\epsilon }^*). \end{aligned}$$

(22)

Using the Cayley-Hamilton theorem for the inverse of a $3 \times 3$ matrix and neglecting higher-order term gives $\pmb {\text {V}}^{-1} = \frac{1}{a} \left( \pmb {\text {I}} - \pmb {\epsilon }^*\right)$ and

$$\begin{aligned} \pmb {\text {D}}_V = {\dot{\pmb {\text {V}}}} \cdot \pmb {\text {V}}^{-1} = \frac{1}{3} \frac{\dot{J}_V}{J_V}\pmb {\text {I}}. \end{aligned}$$

(23)

Following the same logic used to arrive at Eq. 21 gives

$$\begin{aligned} {\dot{J}}_V = \mathrm {tr}(\pmb {\text {D}}_V) J_V. \end{aligned}$$

(24)

Solving the ODEs in 21 and 24 numerically gives

$$\begin{aligned} J_d= & {} \exp \left( \text {tr}({\bar{\pmb {\text {D}}}}_d) \varDelta t\right) J_d^o, \end{aligned}$$

(25)

$$\begin{aligned} J_V= & {} \exp \left( \text {tr}(\pmb {\text {D}}_V) \varDelta t\right) J_V^o. \end{aligned}$$

(26)

Where $J_d$ and $J_V$ are at the current step and $J_d^o$ and $J_V^o$ are at the previous step and $\varDelta t$ is the current time increment. In implementing porosity evolution, $\text {tr}({\bar{\pmb {\text {D}}}}_d)$ is considered as unknown (i.e., degree-of-freedom). The value of $\text {tr}\left( \pmb {\text {D}}_V \right)$ is then determined from Eq. 17 and $J_V$ is used to determine stress, while $J_d$ is used to determine the porosity. Following the derivation by Bammann and Aifantis [51] and accounting for nucleated porosity ($f_n$) gives

$$\begin{aligned} J_d = \frac{1 - f_o}{1 - (f - f_n)}, \end{aligned}$$

(27)

where f is the total porosity and $f_o$ is the initial porosity (which in this work is always zero). The porosity is then calculated from Eq. 27. The pressure and porosity are used to evaluate Eq. 3. Using Eq. 18, the pressure (based on $J_V$) and porosity (based on $J_d$) are determined from $\mathrm {tr} \left( {\bar{\pmb {\text {D}}}}_d\right)$ which is iterated upon until Eq. 3 is satisfied.

Slip Kinetics

As discussed in [66], thermally activated glide and dislocation drag are competing mechanisms of slip where the controlling mechanism is strain-rate dependent. Due to the heterogeneity of the microstructure simulated in this work, a range of local strain-rates occur and thus both thermally activated and dislocation drag slip kinetics are modeled. To account for both mechanisms, it is assumed that the time needed for dislocation motion is the sum of the time spent overcoming thermal barriers and the time spent gliding between barriers respectively. Since the slip-rate of a given slip system is inversely proportional to the time a dislocation spends overcoming or moving between various barriers, the total slip-rate is assumed to follow the form

$$\begin{aligned} {\dot{\gamma }}^{\alpha } = \left( \frac{1}{\dot{\gamma }_T^\alpha } + \frac{1}{ \dot{\gamma }_d^\alpha } \right) ^{-1}, \end{aligned}$$

(28)

where ${\dot{\gamma }}_T^\alpha$ accounts for dislocations overcoming barriers by thermal activation and ${\dot{\gamma }}_d^\alpha$ accounts for the dislocation glide motion before encountering the nearest forest dislocations (i.e., dislocation drag). This drag term (similar to [43, 67,68,69,70]) is given by

$$\begin{aligned} {\dot{\gamma }}_d^\alpha = \left\{ \begin{array}{cl} \left( {\dot{\gamma }}_{do} h \right) \left( 1 - \exp \left( -\frac{(\tau ^{\alpha } - g^{*\alpha })}{D_d^*} \right) \right) &{} {\text{for}} \quad \tau ^\alpha> g^{*\alpha } \\ 0 &{} {\text{for}} \quad \tau ^\alpha \le g^{*\alpha } \end{array}, \right. \end{aligned}$$

(29)

where $D_d$ is the drag stress, ${\dot{\gamma }}_{do}$ is a reference slip-rate between obstacles, and $g^\alpha$ is the strength of slip system $\alpha$, and star superscripts denoted degraded strength values. The variable h is the current dislocation density normalized by a reference dislocation density: $1\, {\upmu \text{m}}^{-2}$. The initial value of normalized dislocation density is denoted by $h_o$. The thermally activated term [43, 66] is given by

$$\begin{aligned} {\dot{\gamma }}_T^\alpha = \frac{{\dot{\gamma }}_{To}}{\sqrt{h}} \left[ \exp \left( -\frac{\varDelta G^\alpha (\tau ^\alpha )}{kT}\right) - \exp \left( -\frac{\varDelta G^\alpha (-\tau ^\alpha )}{kT}\right) \right] , \end{aligned}$$

(30)

where k is the Boltzmann constant, T is the temperature, ${\dot{\gamma }}_{To}$ is a reference thermal activation slip-rate. The free energy $\varDelta G$ is given by

$$\begin{aligned} \varDelta G^\alpha (\tau ^\alpha ) = {\mathcal {G}}_o b^3 \mu ^{\alpha } \left[ 1 - \left( \frac{(\tau ^\alpha - \tau _a^*)}{g^{*\alpha }}\right) ^{p} \right] ^{q} \;\;\text{ for} \quad \tau ^\alpha \le g^{*\alpha }+ \tau _a^* , \end{aligned}$$

(31)

where ${\mathcal {G}}_o$ is a normalized activation energy, b is the magnitude of the Burgers vector, $\mu ^{\alpha }$ is the shear modulus resolved onto the slip system, and p and q are constant parameters. The slip system strength caused by dislocations is given by

$$\begin{aligned} g^\alpha = s \sqrt{h}, \end{aligned}$$

(32)

where s is constant and the slip system strength is assumed to be the same for all systems. For dislocation density evolution, a Kocks–Mecking [71, 72] type hardening model is used

$$\begin{aligned} {\dot{h}} = ( k_1\sqrt{h} - k_2 h ){\dot{\gamma }} \;\;\text{ where }\;\; k_2= \left( k_{2o}\frac{{\dot{\gamma }}_{k0}}{\dot{\gamma }}\right) ^{1/c} . \end{aligned}$$

(33)

The first term accounts for dislocation multiplication and the second term accounts for dislocation sinks by annihilation and is a function of shearing rate and strain-rate sensitivity, c. The parameter $k_1$, $k_2$, $k_{2o}$, and ${\dot{\gamma }}_{ko}$ are material dependent. The normalized dislocation density h is the final fundamental degrees-of-freedom for the system.

Equation of State

The model uses a Grüneisen equation of state in the form employed in [73]

$$\begin{aligned} p = \frac{\rho _o C^2 {\mathscr {U}} \left[ 1 + \left( 1 - \varGamma _o/2\right) {\mathscr {U}} - A {\mathscr {U}}^2/2\right] }{\left[ 1 - (S-1){\mathscr {U}} \right] ^2} + \left( \varGamma _o + A {\mathscr {U}}\right) E , \end{aligned}$$

(34)

where $\rho$ and $\rho _o$ are current and initial density, respectively C is the bulk wave speed, $\varGamma _o$ is the Grüneisen parameter, A is a volume correction term, E is internal energy, and

$$\begin{aligned} {\mathscr {U}} = \frac{\rho }{\rho _o} - 1 = J_V^{-1} - 1 . \end{aligned}$$

(35)

The temperature is calculated using

$$\begin{aligned} T = \frac{E -E_c}{\rho C_v} , \end{aligned}$$

(36)

where $C_v$ is the heat capacity at a constant volume and $E_c$ represents the cold energy [74]. No heat transfer is modeled.

Stress and Material Degradation

The deviatoric Kirchhoff stress is determined using

$$\begin{aligned} \pmb {\tau }^\prime = \pmb {\mathscr {L}}: \text {ln}(\pmb {\text {V}}^\prime ) , \end{aligned}$$

(37)

where $\pmb {\mathscr {L}}$ is a fourth-order tensor representing a constant crystallographic elastic moduli. For this work $\pmb {\mathscr {L}}$ is characterized by three elastic constants $C_{11}$, $C_{12}$, and $C_{33}$ that describe $\pmb {\mathscr {L}}$ in Voigt notation (see [34]).

The equivalent stress (which is based on the deviator of the Kirchhoff stress, $\pmb {\tau }$) is given by $\tau _{eq} = \sqrt{\frac{3}{2}\pmb {\tau }^\prime :\pmb {\tau }^\prime }$. The Cauchy stress $\pmb {\sigma }$ is given by

$$\begin{aligned} \pmb {\sigma }=\frac{\pmb {\tau }}{ J_V J_d} . \end{aligned}$$

(38)

The degraded matrix material equivalent strength $\tau _{eq}^*$ is given by

$$\begin{aligned} \tau ^*_{eq} = w \cdot \tau _{eq}, \end{aligned}$$

(39)

where w is a degradation function given by $w=1 - \text {tanh}(c_2f)$. All associated crystal slip system strengths are likewise degraded by w and are denoted with stars (e.g., $g^{*\alpha }$, $D_r^*$, $\tau _a^*$, etc.). The degradation function phenomenologically represents a smooth transition from full load carrying capability at zero porosity to a very low loading carrying capability (the value of which is determined by $c_2$) at high porosity without the implementation complexity of a micromechanics-based degradation function as in [75].

Implementation

The materials model presented here respectively solves Eqs. 13, 14, 3, 33 for degrees-of-freedom $\pmb {\epsilon }^*$, $\pmb {\text {W}}_\mathrm {R}$ , $\text {tr}({\bar{\pmb {\text {D}}}}_d)$, and h. Equation 13 is solved using a dogleg trust region method. The crystal mechanics and porosity equations are solved in a staggered manner holding $J_V$ constant (i.e., at its beginning of time step value) during the solution for Eqs. 13, 14 and holding $\pmb {\epsilon }^*$, $\pmb {\text {W}}_\mathrm {R}$ constant during the solution of Eq. 3.

Appendix 2

The parameters used in each simulation are shown in Table 2 in Appendix 2. The parameters associated with thermal activation ${\mathcal {G}}_o$, b, p and q are set to the values determined by Follansbee and Kocks [66] for their mechanical threshold stress model of 99.99$\%$ copper. Arsenlis et al.’s [67] values of resolved shear modulus $\mu$ and drag stress $D_r$ for unalloyed copper are also used. The initial temperature is 300 K and the elastic constants $C_{11}$, $C_{12}$, and $C_{44}$ values were reported in Casals et al.’s [76] study of single crystal copper. The 12 face-centered cubic $\langle 1{\bar{1}}0 \rangle$/$\left\{ 111\right\}$ slip systems are also used [77]. The equation of state parameter S, $\varGamma _o$, and A values are taken from Benson et al. [73].

Table 2 Parameters for copper simulations

The strength ($\tau _a$, s), kinetics (${\dot{\gamma }}_{To}$, ${\dot{\gamma }}_{do}$), and hardening ($k_1$, $k_{2o}$, ${\dot{\gamma }}_{ko}$, c, $h_o$) parameters are all calibrated to the quasi-static stress–strain response reported by Fensin et al. [5].

The value of the degradation parameter $c_2$ is estimated as 20. In each simulation the material is considered fully degraded when the degradation function in Eq. 39 is $w = 0.001$. Using $c_2 = 20$ and solving the degradation function expression for porosity gives a failure porosity of $f_{fail} \approx 0.2$. This value lies between the coalescence and failure porosity used by Tvergaard and Needleman [78] of 0.15 and 0.25 respectively and is considered (by the authors) to be an adequate estimate for the purposes of this work.

The unitless value of strain-rate sensitivity exponent n is chosen as 10. At room temperature, n values for copper are generally higher than 10 (see [66, 79, 80]) and a function of strain-rate. Lower strain-rates tend to result in a rate insensitive responses (i.e., high n) and higher strain-rates result in a rate dependent responses (i.e., low n) [66]. For this work, the heterogeneity of the system leads to a spectrum of local strain-rates. Since the region of interest (where spalling occurs) has the highest strain-rates, a low value of n (such as 10) is more appropriate for these regions. While this may introduce inaccuracies for regions away from the spall plane, these inaccuracies (as they pertain to the porosity kinetics in Eq. 3) are alleviated partially through the calibration of the porosity kinetics parameter $c_1$. The Cocks–Ashby [48] porosity kinetics expression, was originally derived for material creep, where they considered values of n ranging from 1 to 9; therefore, the chosen value of 10 is similar to the values where Cocks–Ashby’s assumptions are considered valid.