A Computational Analysis of Interfacing Converters with Advanced Control Methodologies for Microgrid Application

Abstract

Power electronics converter and inverter systems for microgrid operations are always stochastic. When the system is operating in grid-tied mode, the attached load is not constant, so the current which drawn from the DC grid also varies leads to a voltage drop and that causes steady-state error in between the actual and desired output voltage in microgrid. DC-DC bidirectional converters are widely used in microgrid application that facilitates bidirectional energy convertion which having boost mode operation in one direction and bucking mode in other operation. The Interfacing converter is controlled by using the Maximum Power Point Tracking (MPPT) control technique for obtaining maximum power during different atmospheric conditions. In this work, a Model Predictive Control (MPC) strategy is proposed which having an improved cost function, single prediction horizon, and an observer to keep tracking the output voltage. Here, MPC is proposed for cumulative control in between the DC grid side converters and AC grid side inverter, and for improving the power quality and reliability of the utility grid. Both continuous time and discrete time domain models are formed for the whole system for applying different control strategies. Along with MPC, the system has been controlled by using other controllers like as PI controller, Sliding Mode Controller (SMC). Luenberger observer is used to check the DC grid voltage when disturbances are implemented. Here, all the computational results are compared for justifying and validate a better controlling method for microgrid application. These kind of work is first time reported in this manuscript.

Introduction

Utilization of green energy sources has been carried out an excellent alternative of electrical power inspite of fossile fuels based power station for last three decades. As the renewable energy sources are dependent on environmental factors, there should be more than one distributed sources implemented for the sake of reliability, which leads to a path towards designing of nanogrids and microgrids. Microgrids generally constitutes more than one of type of distributed power sources, hybrid storage systems, interfacing converters for each of the distributed energy sources and inverter for converting DC to AC power. For the sake of simplicity, here only solar power has been taken with DC-DC interfacing converter and battery storage with inverter for the conversion of DC to AC power, which is connected to the utility grid for back-up. Generally, DC-DC Bi-directional converters have great significance as a charge controller in case of DC power storage as they allow the power flow in both the directions so that the power source can both store and dissipate the charge [1, 2]. So interfacing and Bi-directional converters have several usages in case of an electric hybrid vehicle, energy storage facilities and grid integration [3]. Since this topology holds some nonlinearities, continuous and discontinuous modes of operations, Bi-directional operation, and a non-minimum phase system behavior for a wide range of operating conditions there are various control strategies proposed to have control of the output voltage [4,5,6,7,8,9]. A simple three-legged inverter is chosen for the DC to AC conversion for simplicity sake. A boost converter for Photovoltaic Energy Conversion System (PVEC) is chosen where Incremental Conductance (INC) is applied for maximum power output. The overall parameters are included in  Tables 1, 2, 3.

Table 1 Parameter details of PI Controlled Microgrid

Table 2 Parameter details of Sliding Mode Controlled Microgrid

Table 3 Parameter details of Model Predictive Controlled Microgrid

In this work, different control architectures like Propotional Integral (PI) controller, Model Predictive Control (MPC), Sliding Mode Controller (SMC) are implemented to the proposed system. By using PI controller the system gave a sluggish response in case of transients and regulation operations of the converters. Thus SMC and MPC are implemented for better response of the overall system. Prior researchers are already reported some sudies on advanced control applications (like SMC, MPC etc.) on microgrid. Wang et al. discussed about advanced control strategies of a hybrid energy storage system for the grid integration of wind power generations [10]. Ghosh et al reported some work on designing of SMC for buck and boost converter [11, 12]. Design of robust higher order sliding mode control strategy for hybrid microgrids were discussed by Cucuzzella et al. and Baghaee et al. [13, 14]. Mohammadi et al also reported some works on power management strategy in multi-terminal VSC-HVDC system, adaptive neural observer-based nonsingular terminal sliding mode controller & intelligent controller design for a class of nonlinear systems, bidirectional power charging control strategy for plug-in hybrid EVs for MT-HVDC grids [15,16,17,18,19,20,21,22]. In proposed work, the constant switching SMC is described in which the switching losses are reduced as compared to the primitive SMC by maintaining a constant switching frequency. They should be working in good condition without compromising their efficiency and capacity, but the disadvantage of this control is that it required several iterations to choose a proper cost function in the time of fast transients and so the smoothing time was high which might bring instability into the system. The system is modeled by taking a single state variable as a sliding point with cascaded two loop control strategy was implemented for steady-state error reduction. But the disadvantage of this model is the sliding manifest required the same work as PI controller to tune its state variable integrator part. The feedback control law is not a continuous function of time. Instead, it can vary from one time structure to another based on the original position in the state space model. Hence, sliding mode control is a structure variable control method. Due to a continuous change in system time structure, the operating frequency varies, which forces the system to slide near the sliding surface, causing a “chattering effect”.

Model predictive control of the interfacing converter for microgrid system is all about predicting the system variables for the next instant considering the present instant values and extrapolating them. An optimization function is chosen for calculating the errors, and the optimization function has to go through all the possible switching combinations and has to accept that one producing least error in next instant. Thus the predictive control can be achieved. Yaramasu et al. discussed about the Model predictive control of wind energy conversion systems [23]. Experimental validation of a robust continuous nonlinear model predictive control based grid-interlinked photovoltaic inverter was reported by Errouissi et al. [24]. Cheng et al. designed model predictive control for DC–DC boost converters with reduced-prediction horizon and constant switching frequency [25]. Model predictive control of power converters for robust and fast operation of ac microgrids was analysed by Dragičević [26]. Sajadian et al., Panda et al., and Ouammi et al. also reported about MPC application in islanded and grid-connected condition of microgrid [27,28,29]. Despite many developments in MPC, some problems are still exist. New theoretical methods have proven that MPC is better than many other control strategies with an intermediate computational complexity [24,25,26,27,28,29]. The non-linear dynamics were approximated as a piecewise linear model [30], and then the MPC is applied. In the case of the inverter, a look-up table is created for reference concerning various switching states, and then the one with more suitable switching state is applied to the inverter. The cost function used was optimized using Euler-Lagrange one dimensional optimization algorithm [31,32,33]. In the case of the DC-DC converter [34,35,36,37,38,39,40], an observer is implemented to keep track of the output voltage. In this work, a low ripple control strategy is designed where a single step prediction horizon is used with a dynamically modifying inductor current reference intended for keeping track of the output voltage.

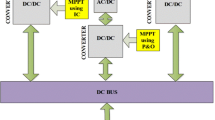
The schematic presented in Fig. 1 is the test system, which consists of a Photo Voltaic Energy Conversion System (PVEC) for distributed power generation. It converts solar energy into electrical energy and supplies to the DC grid with the help of a DC-DC interfacing converter. The interfacing converter helps in regulate the voltage up to the DC grid voltage so that the grid voltage would be constant. This interfacing converter operates though a conventional MPPT algorithm, namely Incremental Conductance Method (INC) for MPPT. A Battery Storage System (BSS) unit is taken for the reliability of the system, which either intakes the extra power or dissipates the shortage amount of energy according to the requirement. So the BSS is interfaced with the DC grid with the help of a charge controller which allows power flow in both the directions namely Bi-directional Converter. The Bi-directional Converter will charge when there is excess power in DC grid, and so the power will flow from DC-grid to BSS whereas it will discharge when there is a shortage of power in the DC grid and at that time power will flow from BSS to the grid. A Voltage Source Inverter (VSI) further connects the DC grid to the utility grid and local AC loads. So VSI will take DC power input and give AC power output to the load or the utility grid in case of excess power conditions. The AC load connected in our test system are non-linear, unbalanced load to observe how our control system takes care of the power factor as well as to follow the cumulative control of DC and AC grid in the time of load demand.

Fig. 1

Schematic of the proposed test system

This novelty of this research work includes the cumulative control of DC and AC grid subjected to different stochastic behavior of the grid as the whole microgrid is considered in the test system. Four different types of control strategies have been applied to the test system and compared the results of all the control strategies for the whole microgrid. This paper also proposes a continuous current set MPC with a single prediction horizon with one controlled ON state of switch followed by an OFF state and then a forced ON state of the switch. The second on time in each interval was forcefully made same as the OFF time to reduce the ripple in case of load changes and to reduce the overshoot. It also helped in giving quicker dynamics than other strategies. An inductor current reference is calculated which will change dynamically. An observer is implemented as the outer loop of this two-loop control strategy, which will monitor the output voltage by providing dynamic input to the inductor current reference. The computational analysis is exercised to give the required output. The basic objective of this proposed work is to find out the best suitable control architecture for micrigrid applications. A Model Predictive Control (MPC) strategy is proposed which having an improved cost function, single prediction horizon, and an observer to keep tracking the output voltage in this work. Here, MPC is proposed for cumulative control in between the DC grid side converters and AC grid side inverter. Along with MPC, the system has been controlled by using other controllers like as PI controller, Sliding Mode Controller (SMC). Here, all the computational results are compared for justifying and validate a better controlling method for microgrid application. These kind of work is first time reported in this manuscript.

The paper is ordered as follows. In section II, the converter and inverter modeling is given in a continuous time domain model, and in part III, all these models are converted into the discrete time domain. System modeling and control using the PI controller and SMC are given in section IV and V, respectively. In section VI, cost function formation and observer modeling for single prediction horizon based MPC was proposed followed by the MPC strategy and block diagrams in section VII. Section VIII briefly describes the multiple prediction horizon MPC and its cost function formulation. All the parameters and consideration are given in the next section, i.e. section IX. The following section holds the simulation results in section X, and then the comparison of results of all four controllers are given in section XI. After that, the conclusion was given in section XII, and the reference section follows it.

Continuous Time Domain Model of the Hybrid System

The modeling approach presented in this paper divides the whole system into two major subgroups which are given as the modeling of inverter and modeling of both the DC-DC converter. The DC-DC converter modeling is different from the state space averaging or small signal modeling approach. The DC-DC converter control output is only to the switch, which indicates an ON or an OFF. So the model is simplified by taking the multiplication of control output with the input variables or state variables. So overall, the multiplication of control output controls the appearance of a multiplied variable at that particular state or time.

Modeling of the inverter is quite different from the DC-DC converter. Here only output phase voltage is modified into the stationary reference frame, and the grid voltages are also modified to stationary reference frame for applying KVL in the inverter loop. The schematic diagrams of  interfacing converters are illustrated in Fig. 2 and Fig. 3 respectively.

Fig. 2

Schematic of the Bi-directional Converter

Fig. 3

Schematic of the Interfacing Converter (Boost Converter)

DC-DC Converter Modelling

Let us consider the inductor current (i_L) and the capacitor voltage (v_c) as the state variables then the state space representation of the Bi-directional Converter is given in [8].

$$ {V}_{in}-{S}_1{v}_c-{R}_L{i}_L-L\frac{d{i}_L}{dt}=0 $$

(1)

Where L is the inductor present in the Bi-directional Converter and V_in is the voltage input provided on the input side, and S₁ is the switch 1 switching state value of switch defined as,

$$ {S}_1=\left\{\begin{array}{c}1\kern0.50em if\ switch\ is\ on\\ {}0\ \ if\ switch\ is\ off\end{array}\right. $$

(2)

By applying KCL at the junction we have,

$$ {S}_1{i}_L-\frac{V_c}{R_{DC}}-C\frac{d{v}_c}{dt}=0 $$

(3)

Where C is the standard capacitor on the DC grid side and v_c is the voltage across the common capacitor, now by taking the derivatives out from the above equations, we can define the state equations as [15, 16],

$$ \left\{\begin{array}{l}\frac{d{i}_L}{dt}=-\frac{R_L{i}_L}{L}-\frac{S_1}{L}\ {v}_c+\frac{1}{L}\ {V}_{in}=0\\ {}\frac{d{v}_c}{dt}=-\frac{S_1}{C}\ {i}_L-\frac{1}{C\ {R}_{DC}}{V}_c=0\end{array}\right. $$

(4)

Modeling of Solar PV Interfacing Converter

We have used a DC-DC boost converter for interfacing the solar PV system to the DC grid. Let us consider the inductor current (i_L) and the capacitor voltage (v_c) as the state variables then the state space representation of the interfacing Converter is given by,

$$ {V}_{PV}-S{v}_c-{R}_L{i}_L-L\frac{d{i}_L}{dt}=0 $$

(5)

Where L is the inductor present in the DC-DC boost converter and V_PV is the voltage input produced by the solar PV system on the input side of distributed generation, and S is the switch switching state of the switch given as

$$ S=\left\{\begin{array}{c}1\kern0.50em if\ switch\ is\ on\\ {}0\ \ if\ switch\ is\ off\end{array}\right. $$

(6)

By applying KCL at the junction we have,

$$ S{i}_L-\frac{V_c}{R_{DC}}-C\frac{d{v}_c}{dt}=0 $$

(7)

Where C is the common capacitor on the DC grid side and v_c is the voltage across the common capacitor, now by taking the derivatives out from the above equations, we can define the state equations as,

$$ \left\{\begin{array}{l}\frac{d{i}_L}{dt}=-\frac{R_L{i}_L}{L}-\frac{S}{L}\ {v}_c+\frac{1}{L}\ {V}_{PV}=0\\ {}\frac{d{v}_c}{dt}=-\frac{S}{C}\ {i}_L-\frac{1}{C\ {R}_{DC}}{V}_c=0\end{array}\right. $$

(8)

Voltage Source Inverter Modelling

The KVL equation written along a single phase of inverter considering the voltage on grid side of Fig. 4 as ‘E’ and output voltage from inverter side is taken as ‘V’ is given as

$$ V-E=L\frac{di}{dt}+ Ri $$

(9)

Fig. 4

Schematic of the Inverter circuit

The ‘ON time’ of the upper leg and lower leg switches are complement to each other for avoiding the case of short-circuiting. There are eight possible switching states given by the space vector modulation technique in Fig. 5. By removing the two zero vectors, we have six working vectors.

Fig. 5

The orientation of Space Vectors in Space Vector Modulation (SVM)

Now for the voltage output of the inverter (V), we have to find out the stationary reference frame components of each of the space vectors. The voltage vectors for the switching states are defined as, ${\overline{V}}_i=\frac{2}{3}{V}_{dc}{e}^{j\ast \theta }, where\theta =i\times \frac{\pi }{3},i=0,1,2,3,4,5.$where $\theta =i\times \frac{\varPi }{3},i=0,1,2,3,4,5.$.

Discrete Time Domain Model of the Hybrid System

Model Predictive Controller is a digital controller as it predicts it’s variables in steps and so it’s necessary to consider the step size in the design, and for that, the whole model is converted into the discrete time domain. The time step T_s is 10e-5 in the given model. The computational time required for a state feedback path to complete involves a delay of single time step which needs to be accommodated otherwise this much delay time is sufficient to give a chattering effect if not taken into account. But in the proposed control strategy, we have two ON periods in a single time step which shows another advantage to us in reducing the chattering. In a discrete time domain model, we have different values of all the parameters in different time instants. Using the current and previous values, we are predicting the following values of those parameters by extrapolating those with an extrapolation principle. Now by finding those future values, we can lure the system to operate smoothly in a pre-designed way.

DC-DC Converter Modelling

The modeling of the DC-DC Bi-directional converter in the discrete time domain is written as

$$ \left\{\begin{array}{l}{v}_C\left(n+1\right)=\left(1-\frac{T_s}{C{R}_{DC}}\right){v}_C(n)-\left(\frac{T_s{S}_1}{C}\right){i}_L\\ {}{i}_L\left(n+1\right)=\left(1-\frac{T_S{R}_L}{L}\right){i}_L(n)-\frac{S_1{T}_S}{L}{v}_C(n)+\frac{1}{L}{V}_{in}(n)\end{array}\right. $$

(10)

Modeling of Solar PV Interfacing Converter

The modeling of the interfacing converter in discrete time domain is presented as,

$$ \left\{\begin{array}{l}{v}_C\left(n+1\right)=\left(1-\frac{T_s}{C{R}_{DC}}\right){v}_C(n)-\left(\frac{T_sS}{C}\right){i}_L\\ {}{i}_L\left(n+1\right)=\left(1-\frac{T_S{R}_L}{L}\right){i}_L(n)-\frac{S{T}_S}{L}{v}_C(n)+\frac{1}{L}{V}_{PV}(n)\end{array}\right. $$

(11)

Voltage Source Inverter Modelling

The discretization formula can be written as $\dot{X}=\frac{X\left(n+1\right)-X(n)}{T_s}$ where X(n + 1) is the next time sample, X(n) is the present sample, and T_s is the sampling time given by,

$$ E=V-L\frac{di}{dt}+ Ri $$

$$ \Rightarrow E\left(n+1\right)=V(n)-L\left(\frac{i\left(n+1\right)-i(n)}{T_s}\right)- Ri(n) $$

(12)

For controlling the inverter currents, we need the equation in terms of the next current sample, which can be deduced by rearranging Eq. (12),

$$ i\left(n+1\right)=\left(1-\frac{R{T}_s}{L}\right)i(n)+\frac{T_s}{L}\left(V\left(n+1\right)-E\left(n+1\right)\right) $$

(13)

Where V(n + 1) is the voltage for the next instant, which needs to be found out by choosing a proper switching state by applying MPC and optimizing the cost function values.

System Modelling Using the Primitive Proportional Integral (PI) Controller

There are two types of PI controller in use for controlling the voltages, namely manual tuning and Ziegler Nichols tuning method. With the manual tuning method, the loop is automated, and the integral actions of the controller are removed by setting K_I to very high at first. Then, the proportional gain of the controller K_P is increased until the loop oscillates with the amplitude remaining constant. After that, the proportional gain K_P should be set to approximately half of that value for obtaining a decay response. Then the integral gain K_I is adjusted until the offset is corrected in sufficient time for the loop operation and there is no steady state error after any regulation operation. But this process is time taking so if we can model the converter and operate in loop shaping technique, then we can get a faster and better response.

Modeling and Transfer Function of bi-Directional Converter

If we try to find out the relation between the input and output voltage of Bi-directional converter for boost operation, then we know that it will follow the below relation [8],

$$ \frac{V_0}{V_{in}}=\frac{1}{1-D} $$

(14)

When the lower leg switch is going to be turned OFF the KVL equation will be,

$$ {V}_{in}=L\frac{d{i}_L}{dt} $$

(15)

Using Laplace transformation,

$$ {V}_{in}(s)=L\times s\times {I}_L(s) $$

(16)

Similarly, the output voltage relation at the same time can be given as,

$$ {V}_0(s)={I}_L(s)\times {R}_{DC} $$

(17)

From Eq. (17) the input-output transfer function can be given as,

$$ \frac{V_o(s)}{V_{in}(s)}=\frac{R}{Ls} $$

(18)

Transfer Function of Closed Loop System

Now to serve the real purpose of the DC-DC converter, it needs to maintain the output voltage at a constant value irrespective of load regulation and line regulation. For that, a feedback loop is given to the system. So when we use a PI controller in the system, then the input-output transfer function considering the effect PI controller is given by [27],

$$ {V}_0=\left(\frac{R}{L\times s}\right)\times \left[{V}_{in}+\left({K}_P+\frac{K_I}{s}\right)\times e\right] $$

(19)

Taking V_ref = 0,

$$ {\displaystyle \begin{array}{l}{V}_0+\left[\left(\frac{R}{L\times s}\right)\times \left({K}_P+\frac{K_I}{s}\right)\times \left(\frac{1}{1-D}\right)\times {V}_0\right]={V}_{in}\times \left(\frac{R}{L\times s}\right)\\ {}\frac{V_0}{V_{in}}=\frac{\raisebox{1ex}{$R$}\!\left/ \!\raisebox{-1ex}{$L\times s$}\right.}{\left[1+\left(\frac{R}{L\times s}\right)\times \left({K}_P+\frac{K_I}{s}\right)\times \left(\frac{1}{1-D}\right)\right]}\end{array}} $$

(20)

The above equation gives the relation for input and output voltage in closed-loop control.

Modeling of the System Using Sliding Mode Controller (SMC)

In control systems, sliding mode control, or SMC is a nonlinear control method that changes the dynamics of a nonlinear system by application of a discontinuous control signal that drives the system to “slide” along a cross-section of the system’s behavior. Sliding mode controller provides stability and maintains consistency performance. The chosen surface is termed as a sliding surface, which further provides law for switching. The gain of the feedback path is unity for the sliding surface below the plant trajectory and has a different gain for the sliding surface above the plant trajectory. Standard controls such as regulation, stabilization, and tracking can be observed by adequately choosing a sliding window. Ideally, SMC can operate at infinite, varying, and oscillating switching frequencies so that the controlled variables can track the desired path. But in practice, the switching losses, inductor and transformer core losses, electromagnetic interference issues reduces its operating region, and so basically it can be used within a specific switching frequency.

Modelling of the System

Let’s consider the voltage error be X, the rate of change of voltage error be Y and integral of it be Z. Under Continuous conduction mode (CCM) it can be expressed as

$$ \left.\begin{array}{l}X=\left({V}_{ref}-\beta {V}_0\right)\\ {}Y=\dot{X}=\frac{\beta }{C}\left[\frac{V_0}{R_L}-\int \frac{S_1{V}_{in}-{V}_0}{R_L} dt\right]\\ {}Z=\int Xdt\end{array}\right\} $$

(21)

$$ {X}_{DC- DC}=\left[\begin{array}{c}\left({V}_{ref}-\beta {V}_0\right)\\ {}\frac{\beta }{C}\left[\frac{V_0}{R_L}-\int \frac{S_1{V}_{in}-{V}_0}{R_L} dt\right]\\ {}\int \left({V}_{ref}-\beta {V}_0\right)\Big) dt\end{array}\right] $$

(22)

$$ {\dot{X}}_{DC- DC}=A{X}_{DC- DC}+B{S}_1 $$

Where,

$$ A=\left[\begin{array}{ccc}0& 1& 0\\ {}0& \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${R}_LC$}\right.& 0\\ {}1& 0& 0\end{array}\right] $$

(23)

$$ B=\left[\begin{array}{c}0\\ {}\frac{\beta {V}_0}{LC}-\frac{\beta {V}_{in}}{LC}\\ {}0\end{array}\right] $$

(24)

Controller Design

For this system if we want to implement the general sliding mode control (SMC) then, we have to adopt the switching law as.

S₁ = 1 when S > 0.

S₁ = 0 when S < 0,

$$ {S}_1=\frac{1}{2\left(1+\mathit{\operatorname{sign}}(S)\right)} $$

(25)

Where S₁ is the switching state or control input which needs to be controlled and S is the instantaneous state vector path or the sliding surface defined as,

$$ S={\alpha}_1{X}_1+{\alpha}_2{X}_2+{\alpha}_3{X}_3 $$

(26)

(With) J^T = [α₁ α₂ α₃]

Where α_1, α₂ and α₃ are representing the control parameters termed as sliding coefficients of the sliding surface.

To find out the sliding mode operating conditions, the equations should satisfy the requirement mentioned below,

$$ \underset{S\to 0}{\lim }S.\dot{S}<0 $$

The above raises the following terms as given in

$$ \left\{\begin{array}{l}{\dot{S}}_{S\to {0}^{+}}={J}^TA{X}_{DC- DC}+{J}^TB{S}_{1_{S\to {0}^{+}}}<0\\ {}{\dot{S}}_{S\to {0}^{-}}={J}^TA{X}_{DC- DC}+{J}^TB{S}_{1_{S\to {0}^{-}}}>0\end{array}\right. $$

(27)

A sliding surface can be obtained by equating the state trajectory to zero, i.e., S = 0. Finally, the equivalent control function can be mapped on the duty ratio d as follows

$$ 0<d=\frac{V_{ctrl}}{V_{ramp}}<1 $$

(28)

The expression between the control signal V_ctrl and the ramp signal V_ramp are written below

$$ {\displaystyle \begin{array}{l}{V}_{ctrl}={S}_{eq}=-\beta L\left[\left(\frac{\alpha_1}{\alpha_2}\right)-\left(\frac{1}{R_LC}\right)\right]{i}_C+ LC\left(\frac{\alpha_3}{\alpha_2}\right)\left({V}_{ref}-{V}_0\right)+\beta \left({V}_0-{V}_{in}\right)\\ {}{V}_{ctrl}=-{k}_{p1}{i}_c+{k}_{p2}\left({V}_{ref}-\beta {V}_0\right)+\beta \left({V}_0-{V}_{in}\right)\end{array}} $$

(29)

Where,

$$ {\displaystyle \begin{array}{l}{k}_{p1}=\beta L\left[\left(\frac{\alpha_1}{\alpha_2}\right)-\left(\frac{1}{R_LC}\right)\right]\&{k}_{p2}= LC\left(\frac{\alpha_3}{\alpha_2}\right)\\ {}{V}_{ramp}=\beta \left({V}_0-{V}_{in}\right)\end{array}} $$

(30)

By applying the controlled voltage equation, the sliding mode control of the boost converter can be obtained.

Selection of Sliding co-Efficient

Using Ackermann’s formula for static controllers the sliding coefficients can be chosen according to the desired dynamics. In this way, the stability aspect can also be fulfilled. By making S = 0, it will result in a linear second order equation whose parameters can be easily chosen. If we take the settling time as T_s = 5τ (1% criteria) where τ is a natural time constant which can be found out from the circuit and ζ is the damping constant then we can tune the sliding coefficients as follows

$$ {\displaystyle \begin{array}{l}\frac{\alpha_1}{\alpha_2}=\frac{10}{T_S}\\ {}\frac{\alpha_3}{\alpha_2}=\frac{25}{\zeta^2{T_s}^2}\end{array}} $$

(31)

Where ζ can be calculated from the following relation,

$$ \zeta =\sqrt{\frac{{\left[\ln \left(\frac{M_P}{100}\right)\right]}^2}{\varPi^2+{\left[\ln \left(\frac{M_P}{100}\right)\right]}^2}} $$

(32)

Where M_P is the maximum peak overshoot can be decided by the user. The β value can be determined as

$$ \beta =\frac{V_{ref}}{V_{desired}}. $$

(33)

Proposed Cost Function and Observer Implementation for Single Prediction Horizon Based Model Predictive Controller

Cost Function

It is considered that the output voltage remains constant during the switch ON time, then the incremental current expressions can be written as

$$ {g}_1=\frac{V_{in}}{L} $$

(34)

$$ {g}_2=\frac{V_{in}-{V}_C(n)}{L} $$

(35)

$$ {g}_3=\frac{V_{in}}{L} $$

(36)

Let us take the initial inductor current i_L(n) = i_L0, within a sampling time period T_s. Now this time period is divided into three parts, one ON time (t₁) followed by an OFF time (t₂) and again an ON time (t₃). Here t₃ is forcefully made equal to t₂ because it would help in keeping the inductor current level constant so that a faster dynamics can be achieved. The inductor current at any point can be expressed as

$$ {i}_L\left(n+1\right)={i}_{L0}+{g}_1{i}_{L1}+{g}_2{i}_{L2}+{g}_3{i}_{L3} $$

(37)

Then the error tracking cost function is standardized as,

$$ G(n)={\left({i}_L\left(n+1\right)-{i}_{Lref}\left(n+1\right)\right)}^2 $$

(38)

Where i_Lref is the reference current that needs to be designed for each power converter. In the case of the VSI, the reference current can be taken as taking the fractionalized grid voltage to avoid phase mismatch between current and voltage. Now the line currents are transformed into stationary reference frame and termed as inductor current reference for voltage source inverter (VSI). In case of DC-DC Bi-directional converter, the reference current is found out by solving the power balance equation for iLref and adding a dynamically modifying term from the observer to have a better current control loop.

$$ {V}_o={v^{\ast}}_C\left(n+1\right) $$

(39)

From the power balance equation, we have,

$$ {V}_{in}{i}_L-{i_L}^2{R}_L=\frac{{V_o}^2}{R_{DC}} $$

(40)

By rearranging the above equation

$$ {i_L}^2{R}_L-{V}_{in}{i}_L+\frac{{V_o}^2}{R_{DC}}=0 $$

By solving the above quadratic equation of inductor current, we can get the dynamic inductor reference current which is

$$ {i}_{Lref}=\frac{V_{in}}{2{R}_L}-\sqrt{{\left(\frac{V_{in}}{2{R}_L}\right)}^2-\frac{{\left({V}_o\right)}^2}{R_{DC}{R}_L}} $$

(41)

Now we can replace V_o as V^∗_C(n + 1)

$$ {i}_{Lref}=\frac{V_{in}}{2{R}_L}-\sqrt{{\left(\frac{V_{in}}{2{R}_L}\right)}^2-\frac{{V^{\ast}}_C{\left(n+1\right)}^2}{R_{DC}{R}_L}} $$

(42)

Now G(n) can be written as,

$$ {\displaystyle \begin{array}{c}G(n)={\left({i}_{Lref}\left(n+1\right)-{i}_{L1}\right)}^2+{\left({i}_{Lref}\left(n+1\right)-{i}_{L2}\right)}^2+{\left({i}_{Lref}\left(n+1\right)-{i}_{L3}\right)}^2\\ {}={\left(e\left(n+1\right)-{g}_1{t}_1\right)}^2+{\left(e\left(n+1\right)-{g}_1{t}_1-{g}_2{t}_2\right)}^2\\ {}+{\left(e\left(n+1\right)-{g}_1{t}_1-{g}_2{t}_2-{g}_3{t}_3\right)}^2\\ {}={\left(e\left(n+1\right)-{g}_1{t}_1\right)}^2+{\left(e\left(n+1\right)-{g}_1{t}_1-0.5{g}_2\left({T}_s-{t}_1\right)\right)}^2\\ {}+{\left(e\left(n+1\right)-{g}_1{t}_1-0.5{g}_2\left({T}_s-{t}_1\right)-0.5{g}_3\left({T}_s-{t}_1\right)\right)}^2\end{array}} $$

(43)

Where e(n + 1) = i_Lref(n + 1)-i_L(n + 1) is the current tracking error found out by the difference between the reference inductor current and the measured inductor current at that time period. Now the ON time period t₁ can be optimized by performing the derivative of the cost function i.e.

$$ \frac{dG(n)}{d{t}_1}=0 $$

(44)

Then optimized time t₁, t_2, and t₃ can be expressed as,

$$ {t}_1=\frac{\left(8{g}_1-2{g}_2\right)e+\left(3{g}_1^2+2{g}_2^2-2{g}_1{g}_2\right){T}_s}{9{g}_1^2-6{g}_1{g}_2+2{g}_2^2} $$

(45)

$$ {t}_2={t}_3=\frac{T_s-{t}_1}{2} $$

(46)

Design of Disturbance Observer (Luenberger Observer) for the DC-DC Converter

With the time-varying load or time-varying input in the output side, the control fails to control the output voltage to the desired value as it starts giving a steady state error. As the load changes with time, the current drawn from the DC grid will also change, which leads to a voltage drop if there is no observer to have a check. So an observer is introduced (Luenberger Observer) in the control system, which will have a check on the output voltage and remove the steady-state error.

Luenberger observer helps in compensating the steady state error voltage by making a copy of the whole system and adding a compensatory term to it. That compensatory term could be tuned as per the requirement as per the stability of the system. The stability of the system was found out by Hurwitz’s criteria, and from that, those tunable values could be calculated. Now our system can be represented as

$$ {\displaystyle \begin{array}{c}X\left(n+1\right)= AX(n)+ Bu(n)+ Ev\\ {}Y(n)= CX(n)\end{array}} $$

(47)

A disturbance D(n) is added to the original state of DC-DC converter which is given by,

$$ {\displaystyle \begin{array}{c}{X}^{\prime}\left(n+1\right)={A}^{\prime }{X}^{\prime }(n)+{B}^{\prime }u(n)+{E}^{\prime }{v}^{\prime}\\ {}{Y}^{\prime }(n)={X}^{\prime }(n)+{D}^{\prime }(n)\end{array}} $$

(48)

The capped symbols represent the duplicate system. If we consider our assumed system is the same as original, then we need to add a compensatory term to the duplicate system and tune it properly so that it will achieve the characteristics of original system. Now the system equation looks like,

$$ {\displaystyle \begin{array}{c}\hat{X}\left(n+1\right)={A}^{\prime}\hat{X}(n)+{B}^{\prime }u(n)+{E}^{\prime }{v}^{\prime }+{L}_1\left(Y(n)-\hat{Y}(n)\right)\\ {}\hat{D}\left(n+1\right)=\hat{D}(n)+{L}_2\left(Y(n)-\hat{Y}(n)\right)\end{array}} $$

(49)

Where $\hat{X}(n)={\left[{\hat{i}}_L(n)\ {\hat{v}}_C(n)\right]}^T,\hat{D}(n)={\left[ dI(n)\ dV(n)\right]}^T$ and L₁ and L₂ are two 2 × 2 dimension constant matrices that have to be tuned as per requirement and stability of the error matrix coefficients. So to make the duplicate output Y^′(n)in eq. (48) equals to the original system output Y(n), in eq. (47) The balancing terms are used, and it is appropriately tuned to get original like characteristics.

Now in eq. (49) by replacing $\hat{Y}\left(n+1\right)=\hat{X}(n)+\hat{D}(n)\ \mathrm{and}\ Y(n)={Y}^{\prime }(n)={X}^{\prime }(n)+{D}^{\prime }(n)$we will get the equation as follows,

$$ \left[\begin{array}{c}\hat{X}\left(n+1\right)\\ {}\hat{D}\left(n+1\right)\end{array}\right]=\left[\begin{array}{cc}{A}^{\prime }-{L}_1& -{L}_1\\ {}-{L}_2& {I}_{2\times 2}-{L}_2\end{array}\right]\left[\begin{array}{c}\hat{X}(n)\\ {}\hat{D}(n)\end{array}\right]+\left[\begin{array}{c}\hat{B}\\ {}{0}_{2\times 2}\end{array}\right]u(n)+\left[\begin{array}{cc}{L}_1& {L}_1\\ {}{L}_2& {L}_2\end{array}\right]\left[\begin{array}{c}{X}^{\prime }(n)\\ {}{D}^{\prime }(n)\end{array}\right]+\left[\begin{array}{c}{I}_{2\times 2}\\ {}{0}_{2\times 2}\end{array}\right]{E}^{\prime }{v}^{\prime } $$

(50)

Replacing the original state variable equations in the above equation, we have,

$$ {\displaystyle \begin{array}{c}\left[\begin{array}{c}{\hat{i}}_L\left(n+1\right)\\ {}{\hat{v}}_C\left(n+1\right)\\ {}\hat{d}I\left(n+1\right)\\ {}\hat{d}V\left(n+1\right)\end{array}\right]=\left[\begin{array}{cccc}1-{L}_1-\frac{T_S{R}_L}{L}& 0& -{L}_1& 0\\ {}0& 1-L1-\frac{T_S}{R_{dc}.C}& 0& -{L}_1\\ {}-{L}_2& 0& 1-{L}_2& 0\\ {}0& -{L}_2& 0& 1-{L}_2\end{array}\right]\left[\begin{array}{c}{i}_L\left(n+1\right)\\ {}{v}_C\left(n+1\right)\\ {} dI\left(n+1\right)\\ {} dV\left(n+1\right)\end{array}\right]\\ {}+\left[\begin{array}{c}\frac{-{T}_S}{L}\\ {}\frac{T_S}{C}\\ {}0\\ {}0\end{array}\right]{S}_1+\left[\begin{array}{cccc}{L}_1& 0& {L}_1& 0\\ {}0& {L}_1& 0& {L}_1\\ {}{L}_2& 0& {L}_2& {L}_2\\ {}0& {L}_2& 0& {L}_2\end{array}\right]\left[\begin{array}{c}{i}_L^{\prime }(n)\\ {}{v}_C^{\prime }(n)\\ {}{d}^{\prime }I(n)\\ {}{d}^{\prime }V(n)\end{array}\right]+\left[\begin{array}{c}\frac{T_s}{L}\times {V}_{in}\\ {}0\\ {}0\\ {}0\end{array}\right]\end{array}} $$

(51)

Now the observer error is defined as,

$$ e(n)={\left[{X}^{\prime }(n)\ {D}^{\prime }(n)\right]}^T-{\left[\hat{X}(n)\ \hat{D}(n)\right]}^T $$

(52)

Then using Eq. (48) and Eq. (49) we can form the error matrix as follows,

$$ e\left(n+1\right)=\left[\begin{array}{cccc}1-{L}_1-\frac{T_S{R}_{DC}}{L}& 0& -{L}_1& 0\\ {}0& 1-L1-\frac{T_S}{R_{DC}{C}_I}& 0& -{L}_1\\ {}-{L}_2& 0& 1-{L}_2& 0\\ {}0& -{L}_2& 0& 1-{L}_2\end{array}\right]e(n) $$

(53)

To get a stable and converging MPC, the error matrix should also be stable, and the stability of the error matrix can be found out by checking if the modulus of eigenvectors is less than 1. So the system will be converging if the error coefficient matrix is stable if the modulus of eigenvalues is less than 1. The feedforward reference current term speeds up the transients while the observer tries to reduce the steady-state error. The dynamically modified current is given by,

$$ {i}_L^{\ast}\left(n+1\right)=\frac{V_{in}}{2{R}_L}-\sqrt{{\left(\frac{V_{in}}{2{R}_L}\right)}^2-\frac{{\left({v}_C^{\ast}\left(n+1\right)-\hat{d}v\left(n+1\right)\right)}^2}{R_L{R}_{DC}}}-\hat{d}I\left(n+1\right) $$

(54)

For faster transients, a voltage term $k\left({v}_C^{\ast}\left(n+1\right)-{v}_C(n)\right)$ can be added to the current equation.

Description of Model Predictive Control Algorithm

MPC control algorithm cost function plays a vital role as it has to be optimized. For the VSI, we have taken a cost function which will determine the difference between the predicted variable and set a variable and applies the switching states from a look-up table to optimize it. In the case of the DC-DC converter, the reference value is found from the observer as it is dynamically modified according to parameter variation. Now, as optimization is to be done, the predicted value will tend to be equal to the reference value in finite time. Then the algorithm initiates with massive value to the cost function and starts taking switching states for optimization. The algorithm iterates all the switching states to finds the optimum value of membership function and the switching state for optimum value and locks them down as control input for the next instant. The described control strategies of PI controller, SMC and inductor current wave form are illustrated in Fig. 6, Fig. 7, & Fig. 8 respectively. 

Fig. 6

Control strategy of PI Controller

Fig. 7

Schematic for SMC of Bi-directional Converter

Fig. 8

Inductor current change during a time period

In case of the DC-DC converter if the output load changes i.e. if it increases then it will be in need of extra current so there will be a voltage drop in our output which is undesired. That extra current has to be supplied from the input and so we need to modify the current reference value dynamically to get a constant output voltage. This iterative process will continue till all the switching combinations are verified and so the number of switching states will very as the number of switches vary. The number of switches in case of the three level converter is higher than the normal inverter. So there we need can choose only the required switching states instead of verifying all the switching combinations. The cost function also can be optimized by adding some fractions of voltage difference so that there won’t be any fear of losing the track or diverging of the voltage. Now the control algorithm flow chart is given in Fig. 9b.

Fig. 9

a Proposed Control Scheme for the System b Flow chart of the control algorithm

Design of Multi Prediction Horizon Model Predictive Controller (MPC) for the Microgrid

The discrete time domain model of the system given in section III is now taken into consideration. The MPC applied in this control has considered seven prediction horizon. The cost function is the error in inductor current, which needs to be optimized with the help of the control algorithm given in Fig. 9b. The current reference is already given in Eq. 42. At time step k, the current error average over the whole prediction interval NT_s is given by,

$$ {i}_{L, err}(k)=\frac{1}{N{T}_s}\underset{k{T}_s}{\overset{\left(k+N\right){T}_s}{\int }}\mid {i}_{L, err}\left(t|k\right)\mid dt $$

(55)

Where N is the prediction horizon, and T_s is the sampling time step. Now if we consider the current slope does not change between sampling instants, then the error function can be given as,

$$ {i}_{L, err}(k)=\frac{1}{N}\sum \limits_{t=k}^{k+N-1}\mid {\overline{i}}_{L, err}\left(t|k\right)\mid $$

(56)

Where${\overline{i}}_{L, err}\left(t|k\right)=\left({i}_{L, err}\left(t|k\right)+{i}_{L, err}\Big(t+1|k\Big)\right)/2$.

Now if we prepare the objective function, it is given by the following equation,

$$ {J}_{avg}(k)=\sum \limits_{t=k}^{k+N-1}\frac{1}{N}\mid {\overline{i}}_{L, err}\left(t|k\right)+\lambda \mid \varDelta S\left(t|k\right)\mid $$

(57)

The second term is the compensatory term, which finds the difference between two consecutive states. This term is added to decrease the switching frequency in case of excessive switching.

Parameter Details and Considerations

Simulation Results and Discussions of Proposed MPC

The DC-DC converter modelled using R_L = 0.1 Ω, L = 10 mH, C = 8000 μF, V_DC = 100 V, V_in = 48 V and L₁ = 0.03, L₂ = 0.5 values are chosen. Total 1024 iterations required for converging our problem. Now considering the L₁ and L₂ values if we want to find out the stability of observer then first we have to find out the Eigenvalues of the system and check whether the Eigenvalues are less than one or not according to Hurwitz stability criterion. Now Eigenvalues for A-LC can be found by solving | A-LC-λI | = 0.

$$ \left[\begin{array}{cc}1-{L}_1-0.01-\lambda & 0\\ {}0& 1-1.25\ast {10}^{-6}-{L}_2-\lambda \end{array}\right]=0 $$

(58)

The determinant turns out to be (0.96-λ) (0.5-λ) = 0, by solving this, Eigenvalues are given as λ = 0.5, 0.96. According to the stability criterion, both values should be less than one, which is satisfied, and so our system is observable and controllable.

Observation of DC-DC Converter Output Voltage and Inverter Current Subjected to Different Conditions

Start-up

The DC-DC converter current, voltage, and inverter output current need to be observed at the startup when the initial transients are present.

A Step Change in Current

The step change in reference current occurs at the time of 0.5 s, and at that time, we have observed the DC and AC grid characteristics and discussed in the following results.

Load Regulation

The DC load is increased at time 1.5 s with the help of a circuit breaker so there should be a drop in output voltage, but due to our controller the output voltage remains constant and the input current increases to fulfill the required load demand.

Line Regulation

The input battery voltage is changed at 2 s, and then the output voltage of the DC grid was observed.

Observation at Initial Transient Conditions

Voltage Source Inverter

The current in all three phases have some transients initially which after 30 ms dies down and tracks the path of reference current nicely. We want our output current from the inverter to be in the same phase as the grid voltage, so we have taken the reference current for inverter as a scaled version of the grid voltage. From the observations of Fig. 10, and Fig. 11a, b, c, we can see that the actual current follows the reference current after 30 ms.

Fig. 10

a Simulation results of Current in phase ‘A,’ b Simulation results of Current in phase ‘B,’ c Simulation results of Current in phase ‘C,’ d Simulation results of DC output voltage, e Simulation results showing DC grid output current, f Simulation results showing DC output current

Fig. 11

Initial transient responses of currents of all 3 phases along with the DC-DC converter output voltage, current and inductor current; a Simulation results of Current in phase ‘A,’ b Simulation results of Current in phase ‘B,’ .c Simulation results of Current in phase ‘C,’ d Simulation results of DC output voltage, e Simulation results showing DC grid output current, f Simulation results showing DC output current

DC-DC Converter

V₀reaches its reference value, i.e. 100 V around after 30 ms (Fig. 11d) when the initial transients die down. Similarly, the DC grid output current and DC load current increases. The increment in inductor current and the output current is shown in Fig. 11e, and Fig. 11f respectively.

Observation at a Step Change in Current

Voltage Source Inverter

The reference current step is changed from +5 A to −4 A at time 0.5 Seconds. So there are some disturbances can be seen in all three phase currents are illustrated in Fig. 12a, b, c and then after 3 ms, they follow the reference currents. To compensate the current, the DC input current also changes which can be seen in Fig. 10.e.

Fig. 12

Step-up responses of currents of all 3 phases along with the DC-DC converter output voltage, current and inductor current; a Simulation results of Current in phase ‘A,’ .b Simulation results of Current in phase ‘B’ Current, c Simulation results of Current in phase ‘C,’ .d Simulation results of DC output voltage, e Simulation results showing DC grid output current, f Simulation results showing DC output current

DC-DC Converter

The DC load current step change occurs at 1.5 s, i.e. we have doubled the output current by reducing the DC resistance to half. So there should be a voltage drop on, but our control strategy keeps the output voltage ripple free as shown in the simulation result in Fig. 12d which is a quite exciting property in case of the small scale rapid varying loads.

Observation of Line Regulation

The DC input voltage of the battery is changed from 48 to 60 at time equals to 2 s, and then the control is observed. We can see the control action as the voltage remains constant at the desired value.

Comparison of Results of Four Different Controllers

Here four types of the controller have been applied to control the DC voltage output for the DC grid, and those are namely Proportional Integral Controller (PI Controller), Sliding Mode Controller (SMC), Model Predictive Controller (MPC) with Seven Prediction Horizon and Proposed Model Predictive Controller (MPC) with single prediction horizon. Those four controllers are used for cumulative control of the effects on the AC grid side as well as DC grid side. The results are compared below and are given in Fig. 13.

Fig. 13

DC line regulation responses of DC-DC converter output voltage, current, and current using MPC; a. Simulation results of DC grid voltage, b. Simulation results of battery input voltage, c. Simulation results showing DC grid output current, d. Simulation results showing DC output current

Overall Response of Controllers Subjected to Different Stochastic Conditions

Figure 14 gives the comparison results of all four type controllers with subjected to different conditions. The Vdc_MPC_1 is shown by the red color, which is the control of our proposed controller, and Vdc_MPC_2 is the output using MPC with multiple prediction horizon shown by blue color. The initial transients were observed at the starting conditions after that at 0.5 s, there is an AC load current step change occurs which was given in Fig. 12(a, b, c). At time 1.5 Seconds the DC load current was doubled so that the nature of controllers at the time of voltage drop could be observed and at last in time 2 s, the line regulation is tested where the input voltage is increased and for that the controllers are observed. So from Fig. 14, we can observe all our controllers are controlling the DC voltage in all the stochastic conditions but some there are variations in the settling time, amount of transients present and steady-state error, etc.

Fig. 14

Overall Response of DC grid Voltage for 3 s

Observation at Initial Transient Conditions

As we can see from Fig. 15 that the fastest of the controllers is the SMC as it settles down within 25 ms whereas the slowest one is the primitive PI controller which able to control the voltage after 0.35 s. The Vdc_MPC_1 is shown by the red color, which is the control of our proposed controller, and Vdc_MPC_2 is the output using MPC with multiple prediction horizon shown by blue color. Now we can observe that our proposed controller has a lower settling time of about 5 ms than the multi prediction horizon MPC. As the desired voltage is 100 V the proposed MPC gives zero steady-state error whereas the MPC with multiple prediction horizon gives a steady state error of 0.5 Volt (0.5%) and the though the SMC provides faster response, due to chattering effect the average voltage increases up to 5 V (5%) which is less desirable.

Fig. 15

Observation of Controllers at initial transient Conditions

Observation at AC Load Variation Conditions

There is a current-step change forced at 0.5 s we can see in Fig. 16 (iLoad_grid), and so the output changes at time 0.5 s from +5 to −4 A. So there are some disturbances at first then all the phase currents follow the reference currents. So now the battery will supply the current requirements and thus the output current from DC grid will rise and due to that DC grid voltage will fall, but as we can see with the help of our controllers, we can control it. The PI controller takes the highest time, i.e. 0.3 s for controlling and the SMC voltage rises a bit but as we can see there is almost no variation (0.1 Volts or 1%) drop occurs in case of MPC.

Fig. 16

Observation of Controllers at AC load variation Conditions

Observation at DC Load Variation Conditions

In Fig. 17 (idc) we can see that DC load current was doubled and so the grid voltages should fall below the desired voltage level, i.e. 100 V, but the controllers could make it constant to the desired value after their respective control times. The PI controller takes 0.35 s whereas other controllers required less time. The voltage of SMC rises a bit, and the controlled voltage of MPC remains almost constant (Fig. 18).

Fig. 17

Observation of Controllers at DC load variation Conditions

Fig. 18

Observation of Controllers at Line regulation

Observation at Line Regulation Conditions

At time 2 s the input battery voltage is increased from 48 to 60 V and the control of four controllers observed. The voltage output of the PI controller first increases and then settles down in 0.25 s. The average voltage of the SMC rises a bit, but the output voltage of the MPC remains almost constant (0.2% variation) except for the MPC with multiple prediction horizon has a steady state error of 0.5%. The observation od line regualation is reported in Fig. 18.

Conclusion

The basic objective to find out the suitable control architecture for micrigrid applications has been satisfied from these computational studies. In this work, the response of MPC has been compared with other controllers like as PI controller, Sliding Mode Controller (SMC). By observing these three controllers that the MPC with single prediction horizon and double switch ON step is the best suitable for the above-described grid as it takes less time as for its transient reduction and the ripple during the load and line regulation is almost negligible (0.2%) which is best for the DC grids.

Whereas if MPC results are compared with SMC, it can be observed that only the initial transient in case of SMC goes down faster approximately 1 ms than in the MPC but due to its chattering effect the average DC grid voltage increases which is not a desirable condition. The load and line regulation in case of SMC is excellent as the ripple in this is also less, or it can be said that it is same as of MPC. But there is not any chattering effect in MPC. So, MPC is best suited. The response of the PI controller is sluggish, and it’s not comparable to the other two controllers the line regulation, load regulation, and the initial transient takes about 0.4 s to reach up to desirable value, and the DC grid output current which is fed to the inverter is also full of very high ripples which can damage the circuit. Seeing the above arguments, the conclusion can be drawn that MPC is more suitable than the other control schemes.

This work has proposed a robust and straightforward MPC strategy for integral control of various parts of a microgrid such as DC-DC Bi-directional converters integrated with the AC grid through a Voltage Source Inverter (VSI) and integration of solar PV system to DC grid. Here an optimized cost function is used, and a single prediction horizon is used for the controller and due to which the computational efficiency of the controller is drastically reduced, unlike multiple prediction horizon MPC. A dynamic inductor current reference was designed with the help of the observer, which helped in keeping track of the output voltage at a particular level. In this work for the controlling the inverter output currents, a scaled grid voltage is taken as the inverter current reference, and the controller kept track of the reference and thus helped in making the grid voltage and current in the same phase. The double ON time in a single time step made the output voltage ripple free as first ON time kept track of voltage while second ON time kept track of the inductor current. For future work, the effect of second ON time in the time step can be incorporated with the voltage equations so that the controller can take more load and still be ripple free and the inverter used can be multilevel to have more control of currents and voltages. These kind of work is first time reported in this manuscript.