Approximate Solutions for Dark and Singular Optical Solitons of Chen-Lee-Liu Model by Adomian-based Methods

Abstract

The current manuscript investigates by proposing new numerical schemes based on the Adomian's technique for the resolution of the dark and singular solutions of the Chen-Lee-Liu (CLL) equation. More precisely, the schemes are derived from the Wazwaz's modification of the Adomian's method and the improved Adomian's method for treating complex-valued evolution equations. The CLL model is applicable to a variety of applications including photonic and optical crystal fibers. The schemes which are implemented via the help of the Maple software have many salient advantages as contained in the comparative analysis. Finally, we depict certain results graphically together with some supportive tables, in addition to some comprehensive remarks.

Introduction

Complex evolution equations are important models that play vital roles in the field of nonlinear sciences including the fluid dynamics, optic fibers, plasma physics, pulse in biological chains, quantum mechanics and so on [1,2,3,4,5]. A notable equation that surfaces from the Derivative Nonlinear Schrödinger's Equation (DNLSE) and utilized for studying soliton propagation through optical fibers is the famous Chen-Lee-Liu (CLL) equation [6] with vast applicability to a variety of applications, including photonic and optical crystal fibers. More recently, there has been an increasing amount of literature on the dark and singular solitons in optical and photonic crystal fibers [7,8,9,10,11]. The literature has attracted a great deal of attention due to their attractive characteristics and wide-ranging applications. Dark solitons are robust complex objects that have better stability (constant amplitude) against different disturbances compared to the bright solitons that are characterized by fiber loss, Raman effects, the mutual interaction between the adjacent pulses and the overlay of noise emitted by optical amplifiers, see [2] among others. More so, there are many various analytical and computational methods in the literature to address the class of Nonlinear Schrodinger Equations (NLSE) including among others [12,13,14,15,16,17,18,19,20,21,22,23] and the references therewith. Nevertheless, with regards to the CLL equation, very few computational techniques are available to numerically treat the model via the application of the standard Adomian's method and its modifications with particular types of soliton solutions [24,25,26,27,28,29]. Other similar numerical-based considerations to treat both the integer and non-integer order evolution equations and other broader forms of differential equations models are available in [30,31,32,33,34,35,36,37,38,39,40] and the references therein.

However, the aim of this paper is to numerically study the CLL equation amidst the presence of dispersion and steepening terms via the applications of the Adomian Decomposition Method (ADM) and Improved Adomian Decomposition Method (IADM) [21,22,23]. Two types of optical soliton solutions comprising the dark and singular solitons are sought for as benchmark exact solitons for the validation of the proposed schemes. Illustrative examples cases to exhibit the applicability and effectiveness of the schemes will be examined.

Thus, the dimensionless form of the CLL model in optical fibers is expressed as follows:

$$i{q}_{t}+a{q}_{xx}+ib{\left|q\right|}^{2}{q}_{x}=0,$$

(1.1)

where $q=q(x,t)$ is the complex-wave profile in spatial $x$ and temporal $t$, variables; $a$ and $b$ are real constants. Physically, the parameter $a$ is group velocity dispersion, while the parameter $b$ denotes the self-steepening phenomena in the context of optical fiber [14]. It is also worth noting here that when $a=b=1$ in Eq. (1.1), the CLL equation recasts to the Regular CLL (RCLL) equation [6]. Furthermore, the newly constructed dark and singular solitary wave solutions [7, 8] of Eq. (1.1) using the ansatz method will be used as benchmark exact solutions for numerical comparisons. Also, the manuscript follows the organization: Sect. 2 and Sect. 3 recall some exact dark and singular solitons, correspondingly. The outline of the methodologies is given in Sect. 4. Discussions of the results acquired are presented in Sect. 5; while Sect. 6 gives the conclusion.

Dark Optical Soliton Solutions

• The first type of dark solution of Eq. (1.1) for $\delta >0$ and $\sigma <0$ is given by [7]:

$$q\left(x,t\right)=R\sqrt{1-\mathrm{sech}[G\left(x-vt\right)]}{e}^{i[-kx+\omega t+\theta \left(x-vt\right)]},$$

(2.2)

coupled to the initial condition

$$q\left(x,0\right)=R\sqrt{1-\mathrm{sech}(Gx)}{e}^{i\left[-kx\right]},$$

with $R$ and $G$ as parameters given by some relations defined as

$$ R = \sqrt { - \frac{8\delta }{{5\sigma }}} , \quad G = \sqrt {\frac{4\delta }{5}} , $$

of which given the constants $a,b,k,v$ and $\omega$,$\delta =\frac{{v}^{2}}{4{a}^{2}}+\frac{vk-\omega }{a} \mathrm{and} \sigma =-\frac{bv}{2{a}^{2}}.$

• The second type of dark solution of Eq. (1.1) from [7] for $\gamma > 0$ and $\sigma < 0$ is given by:

$$ q\left( {x,t} \right) = \frac{{B {\text{tanh}}\left[ {r\left( {x - vt} \right)} \right]}}{{\sqrt {3 + {\text{tanh}}^{2} \left[ {r\left( {x - vt} \right)} \right]} }} e^{{i\left[ { - kx + \omega t + \theta \left( {x - vt} \right)} \right]}} , $$

(2.3)

coupled to the initial condition

$$ q\left( {x,0} \right) = \frac{{B {\text{tanh}}\left( {rx} \right)}}{{\sqrt {3 + {\text{tanh}}^{2} \left( {rx} \right)} }}e^{{i\left[ { - kx} \right]}} , $$

where $B$ and $r$ are related by some relations defined as

$$ B = \sqrt { - \frac{\sigma }{ \gamma }} , r = \sqrt {\frac{{\sigma^{2} }}{16 \gamma }} , \gamma = \frac{{3\sigma^{2} }}{16 \delta }, $$

of which given the constants $a,b,k,v$ and $\omega$, $\delta = \frac{{v^{2} }}{{4a^{2} }} + \frac{vk - \omega }{a} {\text{and }} \sigma = - \frac{bv}{{2a^{2} }}.$

• The third type of dark (gray) solution of Eq. (1.1) from [7] for $\delta < 0$ and $\sigma > 0$ is given by:

$$ q\left( {x,t} \right) = \frac{{n\cosh \left[ {\mu \left( {x - vt} \right)} \right]}}{{\sqrt { \in + cosh^{2} \left[ {\mu \left( {x - vt} \right)} \right]} }}e^{{i\left[ { - kx + \omega t + \theta \left( {x - vt} \right)} \right]}} , $$

(2.4)

with the initial condition

$$ q\left( {x,0} \right) = \frac{{n\cosh \left( {\mu x} \right)}}{{\sqrt { \in + cosh^{2} \left( {\mu x} \right)} }}e^{{i\left[ { - kx} \right]}} , $$

where $n, \in ,v,k$ and $\mu$ are arbitrary constants.

Singular Optical Soliton Solutions

• The first type of singular solution of Eq. (1.1) to be considered is expressed as [8]:

$$ q\left( {x,t} \right) = A\sqrt {1 + \coth [r\left( {x - vt} \right)]} e^{{i\left[ { - kx + \omega t + \theta \left( {x - vt} \right)} \right]}} , $$

(3.1)

coupled to the initial condition

$$ q\left( {x,0} \right) = A\sqrt {1 + \coth (r x)} e^{{i\left[ { - kx} \right]}} , $$

with $A$ and $r$ as parameters defined as follows

$$ A = \sqrt { - \frac{2 \delta }{\sigma }} ,\quad r = \sqrt { - \delta } , $$

of which given the constants $a,b,k,v$ and $\omega$, $\delta = \frac{{v^{2} }}{{4a^{2} }} + \frac{vk - \omega }{a} {\text{and}} \sigma = - \frac{bv}{{2a^{2} }}$ for all $\delta < 0$ and $\sigma > 0,$ provided that $\gamma = \frac{{3 \sigma^{2} }}{16\delta }$.

• The second type of singular solution of Eq. (1.1) to be considered is defined as [12]:

$$ q\left( {x,t} \right) = \frac{M}{{\sqrt {1 + {\text{R sinh}}[\mu \left( {x - vt} \right)]} }}e^{{i\left[ { - kx + \omega t + \theta \left( {x - vt} \right)} \right]}} , $$

(3.2)

coupled to the initial condition

$$ q\left( {x,0} \right) = \frac{M}{{\sqrt {1 + {\text{R sinh}}(\mu x)} }}e^{{i\left[ { - kx} \right]}} , $$

where $M,\mu$ and $r$ are real parameters given by the expressions

$$ M = \sqrt { - \frac{4 \delta }{\sigma }} , \quad \mu = \sqrt { - 4\delta } ,\quad R = \sqrt {\frac{16 \delta \gamma }{{3\sigma^{2} }} - 1} , $$

of which given the constants $a,b,k,v$ and $\omega$, $\delta = \frac{{v^{2} }}{{4a^{2} }} + \frac{vk - \omega }{a} {\text{and}} \sigma = - \frac{bv}{{2a^{2} }},$ for all $\delta < 0$ and $\sigma > 0,$ provided that $\gamma > \left| {\frac{{3 \sigma^{2} }}{16\delta }} \right|.$

• The third type of singular solution of Eq. (1.1) to be considered is expressed as [8]:

$$ q\left( {x,t} \right) = \frac{{P {\text{csch}}\left[ {Q\left( {x - vt} \right)} \right]}}{{\sqrt {1 - {\text{R }}\coth^{2} [Q\left( {x - vt} \right)]} }}e^{{i\left[ { - kx + \omega t + \theta \left( {x - vt} \right)} \right]}} , $$

(3.3)

coupled to the initial condition

$$ q\left( {x,0} \right) = \frac{{P {\text{csch}}\left( {Q x} \right)}}{{\sqrt {1 - {\text{R }}\coth^{2} (Q x)} }}e^{{i\left[ { - kx} \right]}} , $$

with $P,Q$ and $R$ parameters given by the following relations

$$ P = \sqrt {\frac{{2\delta \left( {1 + R} \right)}}{\sigma }} , \quad Q = \sqrt { - \delta } , \quad \gamma = \frac{{3\sigma^{2} R}}{{4\delta \left( {1 + R} \right)^{2} }}, $$

of which given the constants $a,b,k,v$ and $\omega$, $\delta = \frac{{v^{2} }}{{4a^{2} }} + \frac{vk - \omega }{a} {\text{and}} \sigma = - \frac{bv}{{2a^{2} }},$ for all $\delta < 0$, all $\sigma \left\langle {0, \gamma } \right\rangle 0$ and $R < - 1.$

• The fourth type of singular solution of Eq. (1.1) to be considered is found as [8]:

$$ q\left( {x,t} \right) = \sqrt {\frac{Z}{{m + \sinh^{2} \left[ {n\left( {x - vt} \right)} \right]}}} e^{{i\left[ { - kx + \omega t + \theta \left( {x - vt} \right)} \right]}} , $$

(3.4)

coupled to the initial condition

$$ q\left( {x,0} \right) = \sqrt {\frac{Z}{{m + \sinh^{2} \left( {n x} \right)}}} e^{{i\left[ { - kx} \right]}} , $$

where $Z$ and $n$ are real parameters given by the expressions

$$ Z = \sqrt { - \frac{{2\delta \left( {2m - 1} \right)}}{\sigma }} , n = \sqrt { - \delta } , m = \frac{1}{2} \left( {1 + \left[ {1 - \frac{16\delta \gamma }{{3\sigma^{2} }}} \right]^{{ - \frac{1}{2}}} } \right), $$

of which given the constants $a,b,k,v$ and $\omega$, $\delta = \frac{{v^{2} }}{{4a^{2} }} + \frac{vk - \omega }{a} {\text{and}} \sigma = - \frac{bv}{{2a^{2} }},$ for all $\delta < 0$ and $\gamma < \left| {\frac{{3\sigma^{2} }}{16\delta }} \right|$.

Numerical Methods

Adomian Decomposition Method

Here, a consideration of the modification of ADM proposed by Wazwaz [22, 25, 30] is made. Making use of the operator notation by assuming $L_{t} = \frac{\partial }{\partial t}$, and its analogous inverse operator $L_{t}^{ - 1} = \mathop \smallint \limits_{0}^{t} \left( . \right)dt$, Eq. (1.1) is expressed as

$$ q = q\left( {x,0} \right) + aiL^{ - 1} q_{xx} - bL^{ - 1} A, $$

(4.1)

where $A$ in the above equation is the nonlinear term originally given by

$$ A = \left| q \right|^{2} q_{x} , $$

(4.2)

Therefore, the decomposition method represents the given solution in Eq. (4.1) by an infinite series given as

$$ q\left( {x,t} \right) = \mathop \sum \limits_{n = 0}^{\infty } q_{n} \left( {x,t} \right), $$

(4.3)

and decomposes the nonlinear term $A$

$$ A = \mathop \sum \limits_{n = 0}^{\infty } A_{n} , $$

(4.4)

with $A_{n} ^{\prime}s$ denoting the Adomian’s polynomials explicitly defined by the given formula

$$ A_{n} = \frac{1}{n!}\frac{{d^{n} }}{{d\lambda^{n} }}N\left( {\mathop \sum \limits_{j = 0}^{\infty } \left( {\lambda^{j} q_{j} \left( {x,t} \right)} \right)} \right)_{\lambda = 0} , \quad n = 0,1,2, \ldots $$

(4.5)

Now, on substituting Eq. (4.3) and Eq. (4.4) into Eq. (4.1) yields the following

$$ q = \mathop \sum \limits_{n = 0}^{\infty } q_{n} \left( {x,t} \right) = q\left( {x,0} \right) + aiL^{ - 1} \mathop \sum \limits_{n = 0}^{\infty } q_{{n_{xx} }} \left( {x,t} \right) - bL^{ - 1} \mathop \sum \limits_{n = 0}^{\infty } A_{n} , $$

(4.6)

which consequently reveals the recursive solution scheme as follows

$$ \begin{aligned} q_{0} \left( {x,t} \right) & = q\left( {x,0} \right) \\ q_{k + 1} \left( {x,t} \right) & = aiL^{ - 1} \left( {{ }q_{{k_{xx} }} \left( {x,t} \right)} \right) - bL^{ - 1} A_{k} ,\quad k \ge 0. \\ \end{aligned} $$

(4.7)

Improved Adomian Decomposition Method

The IADM [20, 21, 24, 26] was mainly proposed to transform complex-valued equations into systems of real-valued equations for onward treatment using the ADM. Thus, to transform the complex-valued equation of Eq. (1.1) form to a real system, the method goes by splitting the imaginary and real components of the complex profile $q\left( {x,t} \right)$ as follows

$$ q\left( {x,t} \right) = q_{1} + iq_{2} , $$

(4.8)

where $q_{1} {\text{and }} q_{2}$ are real-valued functions. Therefore, making use of Eq. (4.8) into Eq. (1.1), the following system of real-valued equations is obtained

$$ \begin{gathered} q_{1t} + aq_{2xx} + b\left( {q_{1}^{2} + q_{2}^{2} } \right)q_{1x} = 0, \hfill \\ q_{2t} - aq_{1xx} + b\left( {q_{1}^{2} + q_{2}^{2} } \right)q_{2x} = 0, \hfill \\ \end{gathered} $$

(4.9)

where $q_{1} \left( {x,0} \right) = \left[ {q\left( {x,0} \right)} \right]_{R }$ and $q_{2} \left( {x,0} \right) = \left[ {q\left( {x,0} \right)} \right]_{I} ,$ with $R$ denoting the real component and $I$ represents the imaginary component.

Furthermore, the solutions in the above equation $q_{1} {\text{and }} q_{2}$ are decomposed using the following infinite sums

$$ q_{i} \left( {x,t} \right) = \mathop \sum \limits_{n = 0}^{\infty } q_{in} \left( {x,t} \right), i = 1,2, \ldots $$

(4.10)

where the components $q_{1n} , q_{2n} , \left( {n \ge 0} \right)$ are to be determined recursively.

The nonlinear terms in Eq. (4.9) are represented by the following

$$ \begin{aligned} A_{1} & = \left( {q_{1}^{2} + q_{2}^{2} } \right)q_{1x} , \\ A_{2} & = \left( {q_{1}^{2} + q_{2}^{2} } \right)q_{2x} . \\ \end{aligned} $$

(4.11)

Applying the inverse operator $L_{t}^{ - 1} = \mathop \smallint \limits_{0}^{t} \left( . \right)dt$ into Eq. (4.9) together with the application of Eq. (4.11) yields

$$ \begin{aligned} q_{1} \left( {x,t} \right) & = q_{1} \left( {x,0} \right) - aq_{2xx} - b L^{ - 1} A_{1} , \\ q_{2} \left( {x,t} \right) & = q_{2} \left( {x,0} \right) + aq_{1xx} - b L^{ - 1} A_{2} . \\ \end{aligned} $$

(4.12)

Substituting the solution form from Eq. (4.10) into Eq. (4.12), we get

$$ \begin{aligned} q_{1,0} \left( {x,t} \right) & = q_{1} \left( {x,0} \right), \\ q_{2,0} \left( {x,t} \right) & = q_{2} \left( {x,0} \right), \\ q_{1,k + 1} \left( {x,t} \right) & = - L^{ - 1} a\left( { q_{2,k} \left( {x,t} \right)} \right)_{xx} - b L^{ - 1} A_{1,m} , k \ge 0, \\ q_{2,k + 1} \left( {x,t} \right) & = L^{ - 1} a\left( { q_{1,k} \left( {x,t} \right)} \right)_{xx} - b L^{ - 1} A_{2,m} , \quad k \ge 0, \\ \end{aligned} $$

(4.13)

where $A_{1m} , {\text{and}} A_{2m}$ are the Adomian's polynomials belonging to the nonlinear terms $A_{1} {\text{and}} A_{2}$ given in Eq. (4.11). These polynomials are to be computed recursively from Eq. (4.5). Finally, the overall recurrent scheme for the model is obtained by the components in Eq. (4.13) via Eq. (4.4).

Numerical Results

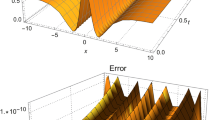
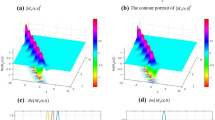
This section presents the obtained numerical results using the said two methods and deduces comparatively the relationship between the schemes. Taking into consideration various dark and singular optical soliton solutions given in Sects. 2 and 3, we utilize the recurrent schemes determined in Sect. 4 to simulate the solutions for the CLL model. In doing so, we make use of the Maple software to exhibit the resultant depictions in Figs. 1, 2, 3, 4, 5, 6 and report the error analysis in Tables 1, 2, 3, 4. Figures 1 and 2 compare the two results between the exact and approximate solutions of the model using the dark (first and second types) and gray (third type) solitons via the use of the ADM and IADM, correspondingly; additionally, Figs. 3, 4, 5, 6 graphically illustrate the comparison of results between the exact and approximate solutions of the model using singular (first, second, third and forth types) solitons via the two methods, correspondingly. Furthermore, looking at the revealed minimal error discrepancies, it is remarked here that the method due to IADM is more efficient than the ADM with regards to these types of solutions considered as benchmarks; this also is in conformity with most related numerical literatures on the ADM and IADM.

Table 1 The error for the first and second dark solitons when $b = 10$ and $t = 0.5$

Table 2 The error for the gray soliton when $B = 0.00001$ and $t = 0.5$

Fig. 1

Comparison between the exact and approximation solutions with ADM for the dark and gray solitons

Fig. 2

Comparison between the exact and approximation solutions with IADM for the dark and gray solitons

Table 3 The error for the singular soliton with ADM when $t = 0.5$

Fig. 3

Comparison between the exact and approximation solutions with ADM for the singular solitons

Fig. 4

Comparison between the exact and approximation solutions with ADM for the singular solitons

Table 4 The error for the singular soliton with IADM when $t = 0.5$

Fig. 5

Comparison between the exact and approximation solutions with IADM for the singular solitons

Fig. 6

Comparison between the exact and approximation solutions with IADM for the singular solitons

Conclusions

The purpose of the current investigation was to derive two numerical recursive schemes based the decomposition methods to investigate the optical CLL model amidst the presence of dispersion and steepening terms. The results for the exact and numerical solutions of the CLL model are evaluated to exhibit the correctness and effectiveness of the devised methods. In order to achieve this, we hunted for certain exact dark and singular solitons of the model to ascertain a computational relative analysis. The choice of dark solitons is indeed in favour of their stability against disturbances compared to the bright solitons; while and singular soliton solution for their discontinuous derivatives. We simulated the results on the Maple software. Both the two schemes revealed quite interesting results and demonstrated high-level of accuracy. Through Tables 1, 2, 3, 4 and Figs. 1, 2, 3, 4, 5, 6, it can be observed that the IADM possessed higher accuracy with minimal error than the ADM; however, this is also is in conformity with most related literatures on the ADM and IADM. The reported figures indeed spoke for themselves with regards to accuracy of the methods. In all, the contribution of this study is to confirm the exactness, from a numerical perspective, of the exact solutions available for the CLL model. In addition, similar investigations may be conducted with other types of solutions or by considering different complex evolution equations.