An EOQ Model for Time Dependent Backlogging Over Idle Time: A Step Order Fuzzy Approach

Abstract

The present article deals with a backorder Economic Order Quantity (EOQ) model for natural leisure/closing time system where the demand rate depends upon the total shortage period and the seasonal effect. A cost minimization problem is developed by trading off setup cost, inventory cost, cost for idle time and shortage cost. The intuitionistic step order fuzzy number for optimization has been developed, assuming all parameters as fuzzy numbers. Ranking is done by employing score function, accuracy value on the centre of gravity and Euclidean distance function over the objective function. Finally numerical examples are considered to justify the model.

Introduction

It is common to all enterprises that the inventory models determine optimal order quantity, shortage quantity and the duration of the opening and closing time of the shop/industry/inventory itself. In inventory literature, several research articles have been published along these directions except the use of natural opening or closing time duration in each day. Among those, some noteworthy works [1–6] are mentioned here. De [7] used first the concept of natural idle time. In this article, he developed a model measuring an error on customers’ demand on spot for without backorder model under intuitionistic fuzzy environment. In the early stage of the invention of Step Order Fuzzy (SOF), Zadeh [8] used the concept of linguistic variable in fuzzy set. A book on module of SOF was developed by Kosinski [9]. Fortin et al. [10] studied an article over gradual numbers in fuzzy systems. A defuzzification method for ordered fuzzy numbers was analyzed by Kosinski and Wilezynska-Sztyma [11]. Also, Kosinski and Wegrzyn-Wolska [12] developed a neural network under defuzzification functional approximation method using step fuzzy numbers. On the other hand, several extensions in fuzzy concept as well as methodology of defuzzifications were discussed extensively. In intuitionistic fuzzy environment, Chakraborty et al. [13] considered a model for manufacturing inventory with shortages using Pareto-optimality method. Scoring of fuzzy numbers was nicely introduced by Chen et al. [14]. Recently, [15] and [16] published two novel articles of backlogging EOQ model using score functions and interpolating by pass to Pareto optimality over intuitionistic fuzzy technique respectively. The centroid in different approach was developed by [17, 18] and [19]. A numerous research articles over the ranking of fuzzy numbers were developed by Adamo [20], Chen and Lu [21] and Fortemps and Roubens [22]. A fast method for ranking fuzzy numbers was studied by Buckley and Chanas [23]. Jain [24, 25], Kerre [26], and Nakamura [27] studied a lot over the fuzzy decision making process. In general fuzzy system, Mabuchi [28] studied the index value where the index itself was $\alpha$-cut dependent. Tran and Duckstein [29] investigated fuzzy numbers extensively, comparing among different types of fuzzy numbers. Recently, De and Sana [30] introduced fuzzy promotional effect on customers’ demand in more realistic and concrete way in a fuzzy backorder EOQ model.

In the present article, we investigate a backorder EOQ model for natural idle time in which the demand rate in shortage time decreases exponentially with backorder time. Moreover, the demand rate may vary for season to season. The commodities like vegetables, fruits, woollen shawl, rain coats/ umbrella etc. are fall into this category. For this reason, we are to incorporate fuzzy environment in which the membership value may vary with domain set of the demand rate. Moreover, introducing a varying membership grade, we have had a step-up and step-down fuzzy numbers as well. Based on the center of gravity of the fuzzy objective function, the Ranking index and Euclidean Distance method under the score values and accuracy values of the minimization problem for both the cases of strong and weak fuzzy numbers are used in the model. Finally, a decision is made using the ranking values.

Assumptions and Notations

The following notations and assumptions are used to develop the model.

Assumptions

• 1. A day splits into two parts—one is inventory run time duration and other is closing time duration. In practice, it is observed that shops/enterprises are closed and opened at fixed times which may vary with location of enterprise. For instance, the closing and opening times of the enterprises are 8:00 p.m. to 8:00 a.m. respectively. Here, the duration (8:00 p.m. to 8:00 a.m.) is an unavoidable pause time.

• 2. Replenishments are instantaneous.

• 3. The time horizon is infinite (days).

• 4. The sum of opening and closing time period is unity.

• 5. Shortages are allowed.

• 6. Demand rate per unit time is constant for stock inventory and it decreases exponentially for stock- out period viz. $d^{{\prime }}=de^{-\lambda (m+1)}$, where $m$ is an positive integer, $0\le \lambda \le 1$ and $d(>0)$ is demand per unit time during inventory period. This is a realistic assumption, as the demand rate decreases gradually with the shortage period.

• 7. Holding cost and shortage cost are uniform over the cycle time.

• 8. Average natural idle time (leisure/pause) cost is constant per unit idle time.

• 9. Stock inventory period is (n + 1) days and backlogging period is $(m+1)$ days.

• 10. The security charge, telephone charge, transportation cost (if any) etc. beyond the working hours of inventory run time may be treated as cost for the idle time.

Notation

• (i) $q$ : The order quantity per cycle

• (ii) $t_1$: Duration of opening time (day)

• (iii) $t_2$: Duration of closing /natural idle time (day)

• (iv) $d$ : Demand rate per unit time in ($i-1, t_1$), $i =1,2,3,{\ldots },n+1$.

• (v) $c_1$: Inventory holding cost($) per unit quantity per day.

• (vi) $c_2$: shortage cost($) per unit quantity per day.

• (vii) $c_3$: Set up cost($) per cycle.

• (viii) $i_c$: Average natural idle time cost($) per unit idle time.

• (ix) $(n+m+1)$: The number of days per cycle, $n$ and $m$ are positive integers and $n>m$.

• (x) $T$: Cycle length (days).

• (xi) $t$: Time horizon (days).

• (xii) $z$: Average cost of the system per cycle ($).

Crisp Model Formulation

The inventory starts at the beginning of the opening time duration $t_1$ and meets the demand quantity $d$ per unit time. Then, it remains steady up to the closing time period $t_2$. Again, it starts from the next day opening time and hence it continues up to $(n+1)$ days. After that shortage continue up to $(m+1)$ days (see Fig. 1). Now, the objective function can be developed as follows:

Fig. 1

Backorder EOQ model

The inventory holding cost (HC) can be stated as

$$\begin{aligned} HC&= c_1 \left[ \frac{1}{2}\left( {2q-dt_1 } \right) t_1 +\frac{1}{2}\left( {2q-3dt_1 } \right) t_1 +\frac{1}{2}\left( {2q-5dt_1 } \right) t_1\right. \nonumber \\&\quad \left. +\cdots \left( {n+1} \right) times\frac{1}{2}\left( {2q-ndt_1 } \right) t_1 \right] \nonumber \\&\quad +c_1 \left[ {\left( {q-dt_1 } \right) t_1 +\left( {q-2dt_1 } \right) t_1 +\left( {q-3dt_1 } \right) t_1 +\cdots ntimes} \right] \nonumber \\&= \frac{1}{2}\left( {n+1} \right) dc_1 t_1 (n+t_1 ) \end{aligned}$$

(1)

where

$$\begin{aligned} q=\left( {n+1} \right) dt_1 \end{aligned}$$

(2)

and

$$\begin{aligned} t_1 +t_2 =1 \end{aligned}$$

(3)

The shortage cost (SC) is given by

$$\begin{aligned} SC&= c_2 \left[ \frac{1}{2}d^{{\prime }}t_1 +\frac{1}{2}t_1 \left( {d^{{\prime }}t_1 +2d^{{\prime }}t_1 } \right) +\frac{1}{2}t_1 \left( {2d^{{\prime }}t_1 +3d^{{\prime }}t_1 } \right) +\frac{1}{2}t_1 \left( {3d^{{\prime }}t_1 +4d^{{\prime }}t_1 } \right) \right. \nonumber \\&\quad \left. +\left. {\cdots +\frac{1}{2}t_1 \left( {md^{{\prime }}t_1 +(m+1)d^{{\prime }}t_1 } \right) } \right] \right. \nonumber \\&= \frac{1}{2}d^{{\prime }}c_2 t_1^2 (m+1)^{2}\nonumber \\&= \frac{1}{2}c_2 t_1^2 (m+1)^{2}de^{-\lambda (m+1)} \end{aligned}$$

(4)

using

$$\begin{aligned} d^{{\prime }}=de^{-\lambda (m+1)} \end{aligned}$$

(5)

The idle time cost (IC) is given by

$$\begin{aligned} IC&= i_c \left\{ {\left( {n+1} \right) t_2 +(m+1)t_2 } \right\} \nonumber \\&= i_c (m+n+2)t_2 \nonumber \\&= i_c (m+n+2)(1-t_1 ) \end{aligned}$$

(6)

The cycle time,

$$\begin{aligned} T&= \left( {m+n+2} \right) (t_1 +t_2 ) \nonumber \\&= (m+n+2) \end{aligned}$$

(7)

Using equations (1), (4) and (5) the total average cost of the system by trading off holding cost, shortage cost, idle time cost and setup cost per cycle is given by

$$\begin{aligned} Z&= \left[ \textit{Holding Cost} + \textit{Shortage Cost} + \textit{Idle Time Cost} + \textit{Setup cost}\right] \times \textit{number of cycle} \nonumber \\&= \left[ {HC+SC+IC+c_3 } \right] \frac{1}{T} \nonumber \\&= \frac{1}{m+n+2}\left[ \frac{1}{2}\left( {n+1} \right) dc_1 t_1 \left( {n+t_1 } \right) +\frac{1}{2}c_2 dt_1^2 (m+1)^{2}e^{-\lambda (m+1)}\right. \nonumber \\&\qquad \qquad \qquad +\left. i_c \left( {m+n+2} \right) \left( {1-t_1 } \right) +c_3 \right] \end{aligned}$$

(8)

Now, our objective is to minimize the objective function $(Z)$ stated as follows:

$$\begin{aligned} \textit{Minimize Z}&= \frac{1}{m+n+2}\left[ \frac{1}{2}\left( {n+1} \right) dc_1 t_1 \left( {n+t_1 } \right) +\frac{1}{2}c_2 dt_1^2 (m+1)^{2}e^{-\lambda (m+1)}\right. \nonumber \\&\quad +\left. i_c \left( {m+n+2} \right) \left( {1-t_1 } \right) +c_3 \right] \end{aligned}$$

(9)

subject to the conditions

$$\begin{aligned} q=\left( {n+1} \right) dt_1 ; \quad t_1 +t_2 =1; \quad n\ge 0 \quad \hbox {and}\quad m\ge 0. \end{aligned}$$

Special cases If we take $t_2 \rightarrow 0$ then $i_c =0$. Consequently, the equation (9) reduces to

$$\begin{aligned} z=\left[ {\frac{c_1 q}{2}+\frac{c_3 d}{q}} \right] \end{aligned}$$

(10)

which is the classical EOQ model without backorder.

Preliminaries

Step Order Fuzzy Numbers

It is worthwhile to point out that a class of order fuzzy number (OFNs) represents the whole class of convex fuzzy numbers that possess continuous membership functions. To include all OFN (with discontinuous membership function) some generalization of function $f$ and $g$ is needed, developed by Kosinski [31] from function of bounded variation (BV). Then, all convex fuzzy numbers are contained in this new space $\mathcal{R}_{BV} \supset \mathcal{R}$ of OFN. Then, operations are defined by $\mathcal{R}_{BV}$ in the similar way. The norm, however, will change into the norm of the Cartesian product of the space of function of bounded variation. All convex fuzzy numbers are contained in the new space $\mathcal{R}_{BV}$ of OFN. Notice that functions of BV (Lojasiewicz [32]) are continuous except for a countable numbers of points.

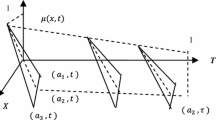
Important consequence of this generalization is the possibility of introducing a sub-space of OFN, composed of pair of step function. If we fix a natural number $K$ and split [0,1) into (K $-$ 1) sub-intervals $[a_i ,a_{i+1} )$ i.e. $\bigcup _{i=1}^{K-1} [a_i ,a_{i+1} )=[0,1)$, where $0=a_1 <a_2 <\cdots <a_K =1$ and define a step function $f$ of resolution $K$ by putting $u_i$ on each sub-interval $[a_i ,a_{i+1} )$, then each such function $f$is identified with a $K$-dimensional vectors $f\sim u=(u_1 ,u_2 \ldots ,u_K )$, the K-th value of $u_K$ corresponds to $s=1$, i.e., $f(1)=u_K$. Taking a pair of such functions, we have an order fuzzy number from $\mathcal{R}_{BV}$. Graphical representations of SOF are shown in Figs. 2, 3, and 4 in which the horizontal and vertical axes represent demand rate and the membership grade value respectively.

Fig. 2

Step up fuzzy number

Fig. 3

Step down fuzzy number

Fig. 4

Step function fuzzy number

Definition 1

By a step order fuzzy number $A$ of resolution $K$ we mean an order pair ($f, g$) of functions such that $\left\{ {f,g:[0,1]\rightarrow {\mathbb {R}}} \right\}$ are $K$-step function.

We use $\mathcal{R}_K$ for denotation the set of elements satisfying Definition 1. The example of a step order fuzzy number and its membership function are shown in Fig. 1. The set $\mathcal{R}_K \subset \mathcal{R}_{BV}$ has been extensively elaborated by Gruszczynska and Krajewska [33]. We can identify $\mathcal{R}_K$ with the Cartesian product of ${\mathbb {R}}^{K}\times {\mathbb {R}}^{K}$ since each $K$-step function is represented by its $K$ values. It is obvious that each elements of the space $\mathcal{R}_K$ may be regarded as an approximation of elements from $\mathcal{R}_{BV}$. By increasing the number $K$of steps, we have the better approximation. The norm of $\mathcal{R}_K$ is assumed to be the Euclidean one of ${\mathbb {R}}^{2K}$ which provides us an inner product structure for our disposal.

Lattice Structure on ${\mathcal{R}_K}$

Let the set $\mathcal{R}_K$ of step ordered fuzzy numbers with operations $\vee$ and $\wedge$ such that, for

$$\begin{aligned}&A=(f_A ,g_A )\, \hbox {and}\, B=(f_B ,g_B ), A\vee B=(\sup \left\{ {f_A ,f_B } \right\} ,\sup \left\{ {g_A ,g_B } \right\} ),\\&A\wedge B=\inf \left\{ {f_A ,f_B } \right\} ,\inf \left\{ {g_A ,g_B } \right\} ). \end{aligned}$$

In the article (Kacprzak and Kosinski [34]), the algebra $(\mathcal{R}_K ,\vee ,\wedge )$ defines a lattice structure and it is proved in the following theorem.

Theorem 1

The algebra $({{\mathcal {R}}}_{\text {K}} ,{\vee } ,{\wedge } )$ is a lattice.

Let $\mathcal{B}$ be the set of two binary values: $\{0,1\}$ and let us introduce the particular subset ${\mathcal {N}}$ of $\mathcal{R}_K$ where $\mathcal{N}=\{A=\left( {\underline{u},\underline{v}} \right) \in \mathcal{R}_K :\underline{u} \in \mathcal{B}^{K}, \underline{v} \in \mathcal{B}^{K}\}$. It means such that each component of the vector $\underline{u}$ as well as $\underline{v}$ have value 1 and 0. It is easy to observe that all subsets of $\mathcal {N}$ have both a join and a meet in $\mathcal {N}$. In fact, for pair of numbers form the set {0,1} we can determine max and min and it is always constituted by 0 or 1. Therefore, $\mathcal {N}$ creates a complete lattice. In such a lattice, we can distinguish the greatest element $\underline{1}$ represents by (1,1,...,1) and the least element $\underline{0}$ represent by (0,0,...,0).

Theorem 2

The algebra ($\mathcal{N}, \vee , \wedge$) is a complete lattice.

We say that two elements A and B are compliments of each other if and only if $\hbox {A}\vee \hbox {B}=\underline{1}$ and $\hbox {A}\wedge \hbox {B}=\underline{0}$. The complement of a number is marked with $A^{c}$ and is defined as follows:

Definition 2

Let $A \in \mathcal{N}$ be a step order fuzzy number represented by a binary vector $(a_1 ,a_2 {\ldots }a_{2K} )$. By the complement of $A$, we understand

$A^{c}=\left( {1-a_1 ,1-a_2 ,\ldots ,1-a_{2K} } \right)$. A bounded lattice for which every element has a complement which is called a complemented lattice. Moreover, the structure of step order fuzzy numbers {$\mathcal{N}\vee , \wedge$} forms a complete and complemented lattice in which complements are unique. In fact it is a Boolean algebra. In the example with $K =2$ a set of universe is created by vectors $\mathcal{N}=\left\{ {\left( {a_1 ,a_2 ,a_3 ,a_4 } \right) \in {\mathbb {R}}^{4}:a_i \in \left\{ {0,1} \right\} ,for\, i=1,2,3,4} \right\}$. The complements of elements are $(0,1,0,0)^{c}=\left( {1,0,1,1} \right) ,(1,0,0,1)^{c}=(0,1,1,0)$ etc. Now, we can rewrite the definition of the complements in terms of a new mapping.

Definition 3

For any $A \in \mathcal{N}$, we define its negation as $\mathcal{N}\left( A \right) =\left( 1-a_1 ,1-a_2 ,\ldots ,1\right.$ $\left. -a_{2K} \right) ,$ if $A=(a_1 ,a_2 {\ldots }a_{2K} )$. It is obvious, from Definition 1 and 2, that the negation of given number A is its complement. Moreover, the operator $\mathcal{N}$ is a strong negation, because it is involutive, i.e. $\mathcal{N}\, (\mathcal{N}(A))=A$ for any $A \in \mathcal{N}$. One can refer [35] to define the strong negation N in terms of the standard strong negation $\mathcal{N}_I$ on the unit interval $I = [0, 1]$ defined by $\mathcal{N}_I \left( x \right) \!=\!1-x,x\!\in \! I$, namely $\left( {\left( {a_1 ,a_2 \ldots ,a_{2K} } \right) } \right) =(\mathcal{N}_I \left( {a_1 } \right) ,\mathcal{N}_I \left( {a_2 } \right) ,\ldots ,\mathcal{N}_I \left( {a_{2K} } \right) )$. In the classical Zadeh’s [8] fuzzy logic, the definition of a fuzzy implication on an abstract lattice $\mathcal{L}=(L,\le _L)$ is based on the notation from the fuzzy set theory introduced in [35].

Implication of SOF in Inventory Systems

Generally, the features of SOF of an element appear whenever we can able to characterize it into clustered several subintervals. Also, the most vital factor of inventory model lies in its demand rate. Thus clustering is possible when the demand rate has exclusively sensitive on several seasons in a year. The commodities like medicine, umbrella, woollen shawl, rain coat, special types of vegetable etc. fall under this considerations. In each subinterval the membership values of fuzzy number is constant and are of step up and step down in nature which are to be determined by the decision maker. That is, within several interval values of demand rate, how much amount of membership grade will be added to the fuzzy information so that the total average inventory cost be minimum. Thus for any seasonal product, it is quite natural to incorporate SOF under consideration.

4-Tuples SOF

Let us define SOF for cost vector $\tilde{A}=\langle {a_1 ,a_2 ,a_3 ,a_4} \rangle$ and for demand rate and other parameters as $\tilde{B}=\langle {b_1 ,b_2 ,b_3 ,b_4} \rangle$ respectively and they can be expressed in Tables 1 and 2 respectively as follows:

Table 1 SOF for cost vector

Table 2 SOF for demand rate and other

Now, the member and non-membership functions for $\tilde{A}$ may be stated as follows:

$$\begin{aligned} \upmu (x)=\left\{ {{\begin{array}{lll} \mu _1 &{} for&{} a_1 \le x\le a_2 \\ \mu _2 &{}for&{} a_2 \le x\le a_3 \\ \mu _3 &{}for&{} a_3 \le x\le a_4 \\ \end{array} }} \right. \end{aligned}$$

(11)

and

$$\begin{aligned} \upgamma (x)=\left\{ {{\begin{array}{lll} (1-\mu _1 )w_1 &{}for&{}a_1 \le x\le a_2 \\ (1-\mu _2 )w_2 &{}for&{}a_2 \le x\le a_3 \\ (1-\mu _3 )w_3 &{}for&{}a_3 \le x\le a_4 \\ \end{array} }} \right. \end{aligned}$$

(12)

where $w_1 ,w_2 ,w_3 <1$ and they are called weights iff

$$\begin{aligned} w_1 +w_2 +w_3 =1. \end{aligned}$$

(13)

The schematic diagram of membership and non membership function of SOF are shown in Figs. 5 and 6 respectively.

Fig. 5

Membership function of SOF

Fig. 6

Non-membership function of SOF

Basic Arithmetic Operations on Ordered SOF

Let $A= \left\langle a_1 ,a_2 ,a_3 ,a_4\right\rangle \hbox { and } B= \left\langle b_1 ,b_2 ,b_3 ,b_4\right\rangle$ are two ordered SOF, then for usual Arithmetic operations $\left\{ {+,-,\times ,\div } \right\}$, namely addition, subtraction, multiplication between $A$ and $B$ are given below:

• (i) $A+B=\langle a_1 +b_1 ,a_2 +b_2 ,a_3 +b_3 ,a_4 +b_4 \rangle ,$

• (ii) $A-B=\langle a_1 -b_5 ,a_2 -b_4 ,a_3 -b_3 ,a_4 -b_2\rangle$

• (iii) $\hbox {A} \times B=\langle \hbox {Min}(a_{\mathrm{i}} b_{\mathrm{j}} ),\hbox {Max}(a_{\mathrm{i}} b_{\mathrm{j}} )\rangle \, \forall i,j=1,2,3,4$

• (iv) $A/B=\langle \hbox {Min}(a_{\mathrm{i}} /b_{\mathrm{j}} ),\hbox {Max}(a_{\mathrm{i}} /b_{\mathrm{j}} )\rangle \, \hbox {for} \, b_j \ne 0,\forall i,j=1,2,3,4$

• (v) $\delta A=\langle \delta a_1 ,\delta a_2 ,\delta a_3 ,\delta a_4\rangle \, \hbox {if} \updelta \ge 0 \; \hbox {and} \; \updelta \mathrm{A}=\langle \delta a_4 ,\delta a_3 ,\delta a_2 ,\delta a_1\rangle \; \hbox {if} \; \updelta <0.$

Centroid of SOF

From the perspectives of geometry, if a closed region $R$ formed by a variable point ($x, y$) where $y$ is a function of $x$, then the centroid of the enclosed region is defined by $\left( \overline{x_0} ,\overline{y_0}\right)$ and is defined by

$$\begin{aligned} \overline{x_0} =\frac{\int \int _R xdxdy}{ \int \int _R dxdy} \end{aligned}$$

(14)

and

$$\begin{aligned} \overline{y_0 } =\frac{\int \int _R ydxdy}{\int \int _R dxdy} \end{aligned}$$

(15)

Now, using (7) and (8) we get,

$$\begin{aligned} \overline{x_0 }&= \frac{\left( {\int \int _{R_1 } +\int \int _{R_2 } +\int \int _{R_3} +\int \int _{R_4 }\cdots } \right) xdxdy}{\left( { \int \int _{R_1 } +\int \int _{R_2 } +\int \int _{R_3 } +\int \int _{R_4 }\cdots } \right) dxdy} \nonumber \\&= \frac{\frac{\mu _1 }{2}\left( {c_2^2 -c_1^2 } \right) +\frac{\mu _2 }{2}\left( {c_3^2 -c_2^2 } \right) +\frac{\mu _3 }{2}\left( {c_4^2 -c_3^2 } \right) }{\mu _1 \left( {c_2 -c_1 } \right) +\mu _2 \left( {c_3 -c_2 } \right) +\mu _3 \left( {c_4 -c_3 } \right) } \end{aligned}$$

(16)

and

$$\begin{aligned} \overline{y_0 }&= \frac{\left( {\int \int _{R_1 } +\int \int _{R_2 } +\int \int _{R_3} +\int \int _{R_4 }\cdots } \right) ydxdy}{\left( { \int \int _{R_1 } +\int \int _{R_2 } +\int \int _{R_3 } +\int \int _{R_4 }\cdots } \right) dxdy} \nonumber \\&= \frac{\frac{\mu _1^2 }{2}\left( {c_2 -c_1 } \right) +\frac{\mu _2^2 }{2}\left( {c_3 -c_2 } \right) +\frac{\mu _1^2 }{2}\left( {c_4 -c_3 } \right) }{\mu _1 \left( {c_2 -c_1 } \right) +\mu _2 \left( {c_3 -c_2 } \right) +\mu _3 \left( {c_4 -c_3 } \right) } \end{aligned}$$

(17)

Ranking Index

According to the article proposed by Chen [36], the ranking index value of a given element is given by

$$\begin{aligned} I\left( x \right) =\sqrt{\left( {\overline{x_0 } } \right) ^{2}+\left( {\overline{y_0 } } \right) ^{2}} \end{aligned}$$

(18)

Maximum index value gives the value of strong fuzzy number, otherwise it is a weak fuzzy number.

Euclidean Distance

Let $\delta _{max} =Max\left\{ {x,x\in Domain\left( {A_1 ,A_2, \ldots {A_{n-1}} ,A_n } \right) } \right\}$ where $A_i^{\prime }$ are fuzzy sets for $i=1,2,\ldots n$ . The distance between the two points $\left( {\overline{x_0 } ,\overline{y_0 } } \right)$ and $\left( {\delta _{max} ,0} \right)$ is called Euclidean Distance and is defined by

$$\begin{aligned} d\left( x \right) =\sqrt{\left( {\overline{x_0 } -\delta _{max} } \right) ^{2}+\left( {\overline{y_0 } } \right) ^{2}} \end{aligned}$$

(19)

Now, minimizing the distance, we get the higher index value, which is generated from strong fuzzy number (degree of membership $>$0.5) otherwise it is a weak fuzzy number.

Fuzzy Mathematical Model

In reality, we know every parametric value portending to any inventory system have a characteristic of flexibility. That is why, in our model, the cost component vectors, demand rate and time fraction of the exponential demand rate are fuzzified occasionally. Therefore, the fuzzy mathematical problem can be stated as

$$\begin{aligned} Minimize\, {\tilde{z}}&= \frac{\left( {n+1} \right) (n+t_1 )t_1 }{2(m+n+2)}\tilde{d}\widetilde{c_1 }\!+\!\frac{(m+1)^{2}t_1^2 e^{-\tilde{\lambda }(m+1)}}{2(m+n+2)}\tilde{d}\widetilde{c_2 }+\left( {1-t_1 } \right) \widetilde{i_c }\!+\!\frac{\widetilde{c_3}}{m+n+2}\nonumber \\\end{aligned}$$

(20)

$$\begin{aligned}&= f_1 \widetilde{A_1 }+f_2 \widetilde{A_2 }+f_3 \widetilde{A_3 }+f_4 \widetilde{A_4 } \end{aligned}$$

(21)

where

$$\begin{aligned} \left[ {{\begin{array}{l} {f_1 =\frac{\left( {n+1} \right) (n+t_1 )t_1 }{2(m+n+2)}} \\ {f_2 =\frac{(m+1)^{2}t_1^2 }{2(m+n+2)}} \\ {{\begin{array}{l} {f_3 =(1-t_1 )} \\ {f_4 =\frac{1}{m+n+2}} \\ \end{array} }} \\ \end{array} }} \right. \end{aligned}$$

(22)

and

$$\begin{aligned} \left[ {{\begin{array}{l} {\widetilde{A_1 }=\tilde{d}\widetilde{c_1 }} \\ {\widetilde{A_2 }=\tilde{d}\widetilde{c_2 }e^{-\tilde{\lambda }(m+1)}} \\ {{\begin{array}{l} {\widetilde{A_3 }=\widetilde{i_c }} \\ {\widetilde{A_4 }=\widetilde{c_3 }} \\ \end{array} }} \\ \end{array} }} \right. \end{aligned}$$

(23)

Considering all the parameters as SOF, we have

$$\begin{aligned} \left[ {{\begin{array}{l} {\widetilde{A_1 }={\langle }d_1 c_{11} ,d_2 c_{12} ,d_3 c_{14} c_{14}{\rangle }} \\ {\widetilde{A_2 }={\langle }d_1 c_{21} e^{-\lambda _1 (m+1)},d_2 c_{22} e^{-\lambda _{2(m+1)} },d_3 c_{23} e^{-\lambda _3 (m+1)},d_4 c_{24} e^{-\lambda _4 (m+1)}{\rangle }} \\ {{\begin{array}{l} {\widetilde{A_3 }={\langle }i_{c1} ,i_{c2} ,i_{c3} ,i_{c4}{\rangle }} \\ {\widetilde{A_4 }={\langle }c_{31} ,c_{32} ,c_{33} ,c_{34}{\rangle }} \\ \end{array} }} \\ \end{array} }} \right. \end{aligned}$$

(24)

And, the SOF of the fuzzy objective function is

$$\begin{aligned} \tilde{z}={\langle }z_1 ,z_2 ,z_3 ,z_4 {\rangle } \end{aligned}$$

(25)

where

$$\begin{aligned} \left[ {{\begin{array}{l} {z_1 =\frac{\left( {n+1} \right) (n+t_1 )t_1 }{2(m+n+2)}d_1 c_{11} +\frac{(m+1)^{2}t_1^2 e^{-\lambda _1 (m+1)}}{2(m+n+2)}d_1 c_{21} +\left( {1-t_1 } \right) i_1 +\frac{c_{31} }{(m+n+2)}} \\ {z_2 =\frac{\left( {n+1} \right) (n+t_1 )t_1 }{2(m+n+2)}d_2 c_{12} +\frac{(m+1)^{2}t_1^2 e^{-\lambda _2 (m+1)}}{2(m+n+2)}d_1 c_{22} +\left( {1-t_1 } \right) i_2 +\frac{c_{32} }{(m+n+2)}} \\ {{\begin{array}{l} {z_3 =\frac{\left( {n+1} \right) (n+t_1 )t_1 }{2(m+n+2)}d_3 c_{13} +\frac{(m+1)^{2}t_1^2 e^{-\lambda _3 (m+1)}}{2(m+n+2)}d_1 c_{23} +\left( {1-t_1 } \right) i_3 +\frac{c_{33} }{(m+n+2)}} \\ {z_4 =\frac{\left( {n+1} \right) (n+t_1 )t_1 }{2(m+n+2)}d_1 c_{14} +\frac{(m+1)^{2}t_1^2 e^{-\lambda _4 (m+1)}}{2(m+n+2)}d_1 c_{24} +\left( {1-t_1 } \right) i_4 +\frac{c_{34} }{(m+n+2)}} \\ \end{array} }} \\ \end{array} }} \right. \end{aligned}$$

(26)

The centroid of $\tilde{z}$ is given by $(\overline{x_0 } ,\overline{y_0 } )$ where

$$\begin{aligned} \overline{x_0 } =\frac{\frac{\mu _1 }{2}\left( {z_2^2 -z_1^2 } \right) +\frac{\mu _2 }{2}\left( {z_3^2 -z_2^2 } \right) +\frac{\mu _3 }{2}\left( {z_4^2 -z_3^2 } \right) }{\mu _1 \left( {z_2 -z_1 } \right) +\mu _2 \left( {z_3 -z_2 } \right) +\mu _3 \left( {z_4 -z_3 }\right) } \end{aligned}$$

(27)

and

$$\begin{aligned} \overline{y_0 } =\frac{\frac{\mu _1^2 }{2}\left( {z_2 -z_1 } \right) +\frac{\mu _2^2 }{2}\left( {z_3 -z_2 } \right) +\frac{\mu _1^2 }{2}\left( {z_4 -z_3 } \right) }{\mu _1 \left( {z_2 -z_1 } \right) +\mu _2 \left( {z_3 -z_2 } \right) +\mu _3 \left( {z_4 -z_3 } \right) } \end{aligned}$$

(28)

We may rewrite the problem is as follows:

$$\begin{aligned} \hbox {Minimize} \, I\left( x \right) =\sqrt{\left( {\overline{x_0 } } \right) ^{2}+\left( {\overline{y_0 } } \right) ^{2}} \end{aligned}$$

(29)

and

$$\begin{aligned} \hbox {Minimize} \, d\left( x \right) =\sqrt{\left( {\overline{x_0 } -\delta _{max} } \right) ^{2}+\left( {\overline{y_0 } } \right) ^{2}} \end{aligned}$$

(30)

Cases of Optimality

Now, we shall study the cases where the cost component vectors and the demand parameters are of step up/down fuzzy numbers. For different seasons, we have assumed that the cost vectors and demand vectors follow the same membership grade values. We consider the cases of three seasons such as Summer, Rainy and Winter which are as follows:

Where we put $\gamma _1 =(1-\mu _1 )w_1$, $\gamma _2 =(1-\mu _2 )w_2$, $\gamma _3 =(1-\mu _3 )w_3$, $\hbox {and} \;w_1 ,w_2 ,w_3 <1$ (Table 3).

Table 3 Assumptions on SOF

Numerical Example-1

Let us consider the holding cost $c_1 =\$ 1.5$, the shortage cost $c_2 =\$ 1.2$, set up cost $c_3 =\$ 150$, idle time cost $i_c =\$ 4.5$, demand rate $d=150$ units and time exponent multiplier $\lambda =0.5$. Then, the optimal solution of the crisp optimal is

$$\begin{aligned} (q^{*}=225.0,s^{*}=55.182,t_1^*=t_2^*=0.5,n^{*}=2,m^{*}=1,z^{*}=\$ 123.25). \end{aligned}$$

Numerical Example-2

Let us assume SOF values of the different parameters $\lambda =(0.4, 0.6, 0.8, 0.9), c_1 =(1.2, 1.4, 1.6, 1.8),c_3 = (80, 100, 150, 160),c_2 = (0.9,1,1.3,1.4), d =(130, 140, 150, 160), i_c =(3.5,4.5,5,5.5)$ and $w_1 =w_2 =w_3 =\frac{1}{3}.$ The solutions of the three models for strong and weak fuzzy cases are provided in Table 4.

Table 4 Optimal solution under SOF

Now, considering only the expected values of the optimal solutions for strong and weak fuzzy numbers, we have the Table 5.

Table 5 General feasible solutions of the models

Moreover, we need to justify our result by the accuracy test, developed by Chen [36] and rank them accordingly. We shall do this only for case-II, as Table 5 shows model-II is optimum.

From Table 6, we see that the minimum membership grade for SOF in model-II provides optimum result under the considerations of standard score and accuracy function as well. Also, in Table 5, the optimality occurs when the demand rate is weak fuzzy number. The step down fuzzy number generates the minimum inventory cost due to seasonal variations (summer, rainy, winter). The required optimal solution is: the minimum average cost is $z^{*}=\$ 104.69, \hbox {the optimal order quantity}$ is $q^{*}=210.83,$ the optimum shortage quantity is $s^{*}=38.35,$ the optimal opening and closing time are 12 h each, the inventory run time is 3 days and the shortage period is 2 days only. Also, from Table 5, the optimality occurs when the demand rate is considered as weak fuzzy number.

Table 6 Various $I$(z) values for model-II

Conclusion

The present article develops a realistic EOQ model incorporating opening time and closing time of the inventory system. During stock out situation, demands of the customers follow an exponentially decaying with total time of shortage period. The basic insight lies in the consideration of SOF for several parameters of the model itself. In SOF model, the several membership grade values are considered but which one will give the minimum cost is the managerial part of an inventory system as a whole. However, introducing SOF in the intuitionistic fuzzy model, we have had a scope to utilize the laws of lattice algebra. Because, the negation or complementation of SOF numbers have been illustrated properly by max-min operators of a lattice. The larger step will give the stronger fuzzy number, but in our study, we have assumed only three steps; if it is possible to develop a model for 12 steps (the value of the parameter whose value can vary monthly in a year and perform 12 non-intersecting intervals) then the model under SOF would be viewed in real life problems. Moreover, in our study, we have shown that the step down fuzzy number provides the minimum inventory cost under weak fuzzy environment. The application of intuitionistic SOF in such EOQ model is quite new compared to the existing inventory literature. The present article may be extended in future in the light of $\alpha$-levels set of both member and non-membership functions of SOF, Hamming distance method and several Aggregation Operators methods.