Abstract
We prove global in time well-posedness for perturbations of the 2D stochastic Navier–Stokes equations
driven by additive space-time white noise \( \xi \), with perturbation \( \zeta \) in the Hölder–Besov space \(\mathcal {C}^{-2 + 3\kappa } \), periodic boundary conditions and initial condition \( u_{0} \in \mathcal {C}^{-1 + \kappa } \) for any \( \kappa >0 \). The proof relies on an energy estimate which in turn builds on a dynamic high-low frequency decomposition and tools from paracontrolled calculus. Our argument uses that the solution to the linear equation is a \( \log \)–correlated field, yielding a double exponential growth bound on the solution. Notably, our method does not rely on any explicit knowledge of the invariant measure to the SPDE, hence the perturbation \( \zeta \) is not restricted to the Cameron–Martin space of the noise, and the initial condition may be anticipative. Finally, we introduce a notion of weak solution that leads to well-posedness for all initial data \( u_{0}\) in \( L^{2} \), the critical space of initial conditions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The aim of this article is to study the global in time well-posedness of the 2D stochastic Navier-Stokes (SNS) equations
for \( (t, x) \in [0, \infty ) \times \textbf{T}^{2} \), with \( \textbf{T}^{2} \) the 2D torus and where \(\xi = (\xi _{i})_{i=1,2}\) is a two-dimensional space-time white noise, namely a Gaussian generalised random field which formally has the covariance
The symbol \( \zeta \) denotes a perturbation belonging to \( \mathcal {C}^{-2 + \kappa } \) (on parabolic space-time) and \( \Pi _{\times } \) is the projection on mean-free functions \( \Pi _{\times } f = f - \int _{\textbf{T}^{2} } f(x) \mathrm {\,d}x \) (introduced merely for simplicity, as the zero mode decouples from all others). Our main result shows that there exists a null set \(\mathcal {N}\) such that for all realisations of the noise \( \xi \) outside \(\mathcal {N}\), any initial condition \( u_{0} \in L^{2} \cup \mathcal {C}^{-1 + \kappa } \) and any perturbation \( \zeta \in C([0, \infty ]; \mathcal {C}^{-2 + \kappa }) \), for arbitrary \( \kappa > 0 \), there exists a unique solution to (1.1) for all times. For initial data in \( L^{2} \), this result requires the introduction of a suitable notion of weak solution, while for initial data in \( \mathcal {C}^{-1 + \kappa } \) we consider mild solutions in the sense of Da Prato and Debussche.
Indeed, in a by now classical work, Da Prato and Debussche [8] establish the local well-posedness of (1.1) (a similar approach was taken earlier by Bourgain [3] in a related context), a first step in the development of solution theories for singular SPDEs. Both the study of local and global solutions to singular SPDEs has seen enormous progress in recent years. In particular, with respect to global in time well-posedness we can highlight at least three different lines of research. On the one hand, a number of equations, including (1.1) with \( \zeta = 0 \) but also Burgers’ equation and SQG equations, admit an explicit invariant measure, in our case the Gaussian field
with \( P_{t} \) the heat semigroup and \( \textbf{P} \) the Leray projection. Explicit knowledge of the invariant measure \(\mu \) allows, under rather weak technical assumptions, to deduce global well-posedness for the equation for \(\mu \)-almost all initial data [8], a result that can be strengthened to all initial data, almost surely (with the null set possibly depending on the initial condition), if the law of the solution satisfies the strong Feller property, see for example [16, Theorem 4.10] or [26]. Approaches building on explicit knowledge of the invariant measure appear to fail in our setting though since, as soon as \( \zeta \not \in L^{2}_{\textrm{loc}}([0, \infty ) \times \textbf{T}^{2} ) \), the Cameron–Martin space of the noise, the law of the solution has no obvious link to the law of X.
Second, and very relevant to our setting are a number of recent works by Hofmanovà, Zhu and Zhu [17,18,19,20]. There, the authors establish global in time existence of invariant solutions to equations such as the 3D Navier–Stokes equations with space time white noise or the SQG equations within certain parameter ranges. These results build on the equations being super-critical and on convex integration tools that allow to construct infinitely many solutions at once.
Finally, the results closest to this work both in their methods and in their motivation concern equations linked to stochastic quantisation. For models such as \( \Phi ^{4}_{d} \) or (Euclidean) Yang–Mills, one aims to give meaning to a probability measure on a space of distributions given by some formal expression. The idea then is to consider the corresponding Langevin process (noisy gradient flow), which is typically a singular stochastic PDE. If one can give a meaning to and then prove well-posedness and unique ergodicity for that SPDE, the desired measure can then be defined as its (unique) invariant measure. In the case of the \( \Phi ^{4} \) models in any subcritical regime, global well-posedness has been established
[7, 9, 10, 23], making use of the strongly coercive effect of the nonlinearity. In the case of Yang–Mills however, while local well-posedness has recently been established [4,5,6], global in time well-posedness remains as challenging as it is interesting. Morally the Yang–Mills nonlinearity should behave similarly to the Navier–Stokes nonlinearity, providing at least heuristically an energy estimate and not a negative drift as is the case for the \( \Phi ^{4}_{d} \) model.
In view of these considerations, establishing global well-posedness for equations such as Equation (1.1) is particularly interesting. Arguably, the drawback of our approach is that the exact regularity of \( \xi \) plays a role, and we are not able to rule out finite time explosion if one consider an even slightly more irregular noise. On the other hand we provide a pathwise argument for global well posedness: in particular, no finite time explosion holds for every realisation of the noise outside a null set, uniformly over all initial conditions and perturbations. In addition and to the best of our knowledge for the first time, we establish well-posedness of the equation also for \( L^{2} \) initial data. Of course, the choice of the initial condition is intuitively a local rather then a global question, and indeed we expect this part of our result to extend to a broader class of equations. The link between global well-posedness and well-posedness for critical initial data is that both rely on an energy estimate and some kind of weak formulation of the equation.
The technique used in the present work is to introduce a dynamical high-low frequency decomposition, which splits the solution into an irregular, but small, component and a more regular, but arbitrarily large component. This is in spirit similar to the approach taken by Gallagher and Planchon [12] to establish well-posedness of the deterministic Navier–Stokes equations with critical initial data and integrability index \( p >2 \) where the energy of the initial condition is allowed to be infinite. In our setting, even for smooth initial data, the \( L^{2} \) norm of the solution is infinite at any positive time: this motivates our division of scales, so that our efforts concentrate towards establishing an energy estimate for the large scale component of the solution. In the literature on singular SPDEs, similar decompositions have appeared in the study of \( \Phi ^{4}_{d} \) models by Mourrat and Weber [23] and in particular also by Gubinelli and Hofmanovà [9], where the authors introduce a time-independent paracontrolled structure similar to ours, in order to obtain global well-posedness in space. As a matter of fact, an argument with a somewhat similar flavour already appears in Nelson’s original construction of the \(\Phi ^4_2\) measure [24] (see [15, Chapter 9] for a modern account).
Ultimately, to establish the lack of finite time blow-up, we rely on a careful study of a certain quadratic form linked to a singular operator. The latter requires a finite, but solution-dependent, logarithmic renormalisation, leading us to the following (very heuristic) bound:
for an appropriate norm \( \Vert \cdot \Vert \). Hence we obtain a quantitative estimate with double-exponential growth of the type
where the quantity \( c_t > 0 \) depends on the noise up to time t, so in particular the growth estimate is more than double exponential.
Let us conclude with a final remark. The original local well-posedness result by Da Prato and Debussche did not require any tools from singular SPDEs (paracontrolled calculus [11], regularity structures [14], etc). However, both our well-posedness result for critical initial conditions and our global in time well-posedness result build on the deeper understanding of the fine structure of the solution provided by these tools. In this instance, we will use paracontrolled calculus for our analysis.
1.1 Notations
We let \(\textbf{N}= \{0, 1,2,3,\dots \}\), \( \textbf{N}_{+} = \textbf{N}\setminus \{ 0 \}\), and \( \textbf{Z}_{*} = \textbf{Z}\setminus \{ 0 \} \). Given a function said to depend on ‘space’ and ‘time’, we will always assume that the spatial variable takes values in the 2-dimensional torus \( \textbf{T}^2 =\textbf{R}^2 /\textbf{Z}^2\). Given \(d \in \textbf{N}_+\) and a vector \(v \in \textbf{R}^{d}\) we write |v| for its Euclidean norm. We identify \(\textbf{M}^d\), the space of \(d \times d\) square matrices with \(\textbf{R}^d \otimes \textbf{R}^d\) in the usual way, and we set \(u \mathbin {\otimes _{\!s}}v = \frac{1}{2}(u\otimes v + v\otimes u )\) Given two topological spaces X, Y we write \(C(X;Y)\) for the space of continuous functions from \(X\) to \(Y\). For any \(k, d \in \textbf{N}\) if \(O \subseteq \textbf{R}^d\) we write \(C^{k}(\textbf{T}^{2} ; O)\) for the space of k times differentiable maps \(\varphi :\textbf{T}^{2} \rightarrow O\) (the derivatives being continuous). The gradient \(\nabla \) and divergence \({\text {div}}\) are defined as usual and, for \(\varphi \in C^1 (\textbf{T}^2 ; \textbf{M}^2)\) we set
while, for \(\varphi \in C^1 (\textbf{T}^2 ; \textbf{R}^2)\) we define \(\nabla \varphi , \nabla _{\!{\text {sym}}}\varphi \in C(\textbf{T}^{2}; \textbf{M}^{2})\) by
When its arguments are functions taking values in a Hilbert space, \(\langle \cdot ,\cdot \rangle \) denotes the corresponding \(L^2\)-scalar product. Finally, the function spaces that we will need throughout the paper are described in Section A. Let us merely note that we write \( \Vert \varphi \Vert = \Vert \varphi \Vert _{L^{2}}\) for the \( L^{2} \) norm of a function \( \varphi \).
1.1.1 Conventions
When the domain and target space of a function are clear from context, we will omit them from our notations, writing for instance simply \(C^{k}\) or \(L^p\). Given a set \( \mathcal {X}\) and two functions \( f, g :\mathcal {X}\rightarrow \textbf{R}\), we write
if there exists a constant \( C> 0 \) such that \( f(x) \leqslant C g(x) \) for all \( x \in \mathcal {X}\) (similarly \( f > rsim g \) or \( f \simeq g\), the latter if both inequalities hold). In order to lighten the notation and reduce the number of letters used to denote constants, we will allow the exact value of generic constants \( C( \vartheta ) \) depending on some parameter \( \vartheta \) from a parameter set \( \Theta \), to change from line to line.
2 Main results
Throughout this work the following assumptions are in force.
Assumption 2.1
We fix a (small enough) constant \( \kappa > 0 \).
-
1.
(Noise) Let \((\Omega , \mathcal {F}, \mathbb {P})\) be a probability space supporting a space-time white noise \(\xi :\Omega \rightarrow (\mathcal {S}^{\prime }(\textbf{R}\times \textbf{T}))^{2}\), namely a random variable such that the \(\xi _{i}(\varphi )\) are jointly centered Gaussian for \(i=1,2\) and \(\varphi \in \mathcal {S}(\textbf{R}\times \textbf{T}^{2})\), with covariance
$$\begin{aligned} \mathbb {E}\big [ \xi _{i}(\varphi ) \xi _{j}(\varphi ^{\prime }) \big ] = 1_{\{i=j\}} \int _{\textbf{R}\times \textbf{T}^{2}} \varphi (t, x) \varphi ^{\prime }(t, x) \mathrm {\,d}t \mathrm {\,d}x. \end{aligned}$$ -
2.
(Perturbation) One has \( \zeta \in \mathcal {C}_{\textrm{parab}}^{-2+3\kappa } (\textbf{R}\times \textbf{T}^2; \textbf{R}^2)\).
-
3.
(Initial condition) One has \( u_{0} \in \mathcal {C}^{-1 + \kappa } \cup L^{2} \) with \( {\text {div}}(u_{0}) = 0 \) and \( \Pi _{\times } u_{0} = 0 \).
Here the space \(\mathcal {C}^{-2+3\kappa }_{\textrm{parab}}(\textbf{R}\times \textbf{T}^2; \textbf{R}^2)\) denotes the parabolically scaled Hölder–Besov space of space-time distributions as in [14, Definition 3.7] with \(\mathfrak {s} = (2,1)\). This space satisfies that if \(\zeta \in \mathcal {C}^{-2+3\kappa }_{\textrm{parab}}\), then also \((t,x) \mapsto \zeta (t,x) 1_{[0,\infty )} (t) \in \mathcal {C}^{-2+3\kappa }_{\textrm{parab}}\) and the convolution with the heat kernel \(\int _0^t P_{t-s} \Pi _{\times } \zeta \mathrm {\,d}s \in C([0, \infty ); \mathcal {C}^{2 \kappa })\). We loose a \(\kappa \) in spatial regularity (which we think of as small) in order to obtain continuity in time. The factor 2 in front of \( \kappa \) is simply for later convenience. Here and in the rest of the work \(\mathcal {C}^\alpha \), for \(\alpha \in \textbf{R}\), refers to the spatial Hölder–Besov space \(\mathcal {C}^\alpha (\textbf{T}^2;\textbf{R}^2)\) as defined in Appendix A.
Remark 2.1
Assumption 2.1 allows for perturbations \( \zeta \) that do not lie in the Cameron–Martin space \( L^{2}_{\textrm{loc}}([0, \infty ) \times \textbf{T}^{2}) \) of the noise \( \xi \): in particular for such \( \zeta \), the law of the solution is not absolutely continuous to the solution to the 2D SNS equations with space-time white noise, for which global existence for non-anticipative initial conditions is already understood. Our assumption allows, for instance, \( \zeta \) to be a realisation of a noise that is white in time but smoother than \( \xi \) in space. In addition \( \zeta \) could depend on the realisation \( \omega \in \Omega \) of the noise \( \xi \), since our argument is completely pathwise.
Remark 2.2
For \( u_{0} \in \mathcal {C}^{-1 + \kappa }\) we will prove the existence of global mild solutions. For \( u_{0} \in L^{2} \) we will introduce a suitable notion of weak solution and prove global well-posedness for such solutions.
To simplify the study of (1.1) it is convenient to project onto the space of divergence-free functions, thus removing the pressure from the equation. For \(k = (k_1, k_2) \in \textbf{Z}^2\) write \( k^{\perp } = (k_2, - k_1)\) and define the Leray projection in terms of Fourier coefficients by:
where \( v \cdot w\) denotes the scalar product in \(\textbf{R}^{2} \). Applying \(\textbf{P}\) to (1.1), we obtain
since by assumption \({\text {div}}(u_0) = 0\). Due to the irregularity of the noise, the solution u to (2.1) does not lie in \(L^2\), so the non-linearity \( \textbf{P} (u \cdot \nabla u) = \textbf{P} {\text {div}}(u^{\otimes 2}) \) is a priori ill-defined. The key insight of [8] (following earlier works such as [3]) was to consider the solution to (2.1) as a perturbation of the solution X to the linear equation:
Note that contrary to a setting common in the SPDE literature we do not choose \( X_{0} \) so that the process \( t \mapsto X_{t} \) is stationary. Instead, our choice of zero initial condition will be convenient later on to deal with initial data in \( L^{2}\). Gaussian computations guarantee that (2.2) admits a unique solution \( X \in C ([0, \infty ) ; \mathcal {C}^{- \kappa }) \) for any \( \kappa > 0 \), implying that X is barely not a function (these calculations are by now classical, but see also Lemma 6.2 for similar bounds). Setting \(u = X + v\), v should at least formally solve
Indeed the term \({\text {div}}(X^{\otimes 2}) \) is defined in \(C( [0, \infty ) ; \mathcal {C}^{- 1-\kappa }) \) for any \( \kappa > 0 \) as a field in the second Wiener chaos (despite the product being a-priori ill-posed, since X has negative regularity), and parabolic regularity estimates guarantee that one can find, at least for smooth initial conditions, a solution v to (2.3) satisfying \( v \in C ( (0, \infty ); \mathcal {C}^{2\kappa } ) \), for \( \kappa > 0 \) small, as is captured by the following result.
Theorem 2.3
(Da Prato, Debussche [8]) There exists a null set \( \mathcal {N}\subseteq \Omega \) such that for any \( \omega \not \in \mathcal {N}\) and \(\kappa > 0 \) the following holds. For any \( u_{0} \in \mathcal {C}^{-1 + \kappa } \) there exists a \(T^{{\text {fin}}}(\omega , u_{0} ) \in (0, \infty ]\) and a unique maximal mild solution \(v(\omega )\) to (2.3) on \( [0, T^{{\text {fin}}} (\omega , u_{0})) \), with \( v (\omega , 0, \cdot ) = u_{0}(\cdot )\).
The meaning of mild solutions is kept vague: we refer the reader to Proposition 3.2 and its (sketch of) proof. With the solution being maximal we understand that if there exists another \( \overline{v}(\omega )\) on an interval \([0, \overline{T}(\omega ))\) that solves (2.3) with the same initial condition \( u_{0}\), then
We say that the maximal solution is global for given \( \omega \) and \( u_{0} \), if \( T^{{\text {fin}}} (\omega , u_{0}) = \infty \).
Remark 2.4
By Sobolev embedding in dimension \( d =2 \) (see (A.1)), \( H^{\kappa } \subseteq \mathcal {C}^{-1 + \kappa } \), so that mild solutions can deal with any initial condition with slightly better regularity than the critical space \( L^{2} \).
Our main result concerns the existence of global solutions for an arbitrary initial condition, almost surely.
Theorem 2.5
(Global solutions) There exists a null set \( \mathcal {N}^{\prime } \subseteq \Omega \) such that
for all \(\omega \not \in \mathcal {N}^{\prime }, \kappa >0\) and \(u_{0} \in \mathcal {C}^{- 1 + \kappa }, \zeta \) satisfying Assumption 2.1.
The null set \( \mathcal {N}^{\prime } \) is the one appearing in Lemma 3.1. Theorem 2.5 is proven at the very end of Section 5. Next we consider initial condition \( u_{0} \in L^{2} \). Note that in this case Theorem 2.3 does not guarantee even local in time well-posedness.
Theorem 2.6
(Global high-low weak solutions) For the same null set \( \mathcal {N}^{\prime } \subseteq \Omega \) as in Theorem 2.5 the following holds. For every \( \omega \not \in \mathcal {N}^{\prime }, \kappa >0 \) and \( u_{0} \in L^{2}, \zeta \) satisfying Assumption 2.1 there exists a unique, global high-low weak solution to (2.3), with initial condition \( u_{0}\), in the sense of Definition 7.1.
This result follows from Lemma 7.3 (existence) and Lemma 7.4 (uniqueness). The crux of the argument for both results lies in an energy estimate, based on a dynamic high-low frequency decomposition: we will use classical energy estimates for low frequencies and tools from singular SPDEs for high frequencies.
3 First steps
To derive our energy estimate we start by iterating the Da Prato–Debussche trick to improve as much as possible the regularity of the right-hand side. The issue with using (2.3) to obtain an energy estimate is that formally such an estimate would require us to make sense of the pairing, which appears when differentiating in time the \( L^{2} \) norm \( t \mapsto \Vert v \Vert _{L^{2}}^{2}\):
Since \( \zeta \in \mathcal {C}^{-2 + 2 \kappa }, X \in \mathcal {C}^{- \kappa } \) and, at least locally, \( v \in \mathcal {C}^{2 \kappa }\), none of the pairings
are well defined for generic elements of these spaces. We can improve the situation by introducing the solution Y to the linear equation
and then setting \( w = v - Y \) so that, setting \( D = 2 (X + Y) \),
Since the worst term in (3.1) is \( \textbf{P} \Pi _{\times } \zeta \), we have \( Y \in \mathcal {C}^{2 \kappa } \), so that we expect \( w \in \mathcal {C}^{1 - \kappa } \), the worst term in (3.2) being given by \( \textbf{P} {\text {div}}( 2X \mathbin {\otimes _{\!s}}w) \in \mathcal {C}^{-1- \kappa }\). If we now consider the pairing
appearing in the time derivative of \(\Vert w\Vert ^2\), the only ill-defined term is
In fact, the main issue in deriving a-priori estimates on the solution is to give meaning to this pairing. At a very heuristic (and ultimately wrong) level, we would like to treat (3.4) as a random Dirichlet form. The problem with this approach is that the quadratic form is not semi-bounded from below, which reflects the necessity of renormalisation for the symmetrised version of the operator \( \varphi \mapsto \Delta \varphi + 2 {\text {div}}(X \mathbin {\otimes _{\!s}}\varphi ) \). This problem will be addressed by the already mentioned division of scales, so that at a fixed time we will require only a finite (but solution-dependent!) logarithmic renormalisation constant.
The second issue to address is how much regularity can be found in this quadratic form: by comparison, the quadratic form associated to the Laplacian guarantees one degree of regularity since \( \langle f, \Delta f \rangle = - \Vert \nabla f \Vert ^{2} \). In our case, for \( \mu \gg 1 \), the following resolvent (here \( \textrm{sym} \) stands for the symmetric part of the operator) is expected to be a bounded operator
In particular, because of the stochastic terms, it is expected to be less regularising than the Laplacian alone (which is bounded into \( H^{2} \)). Therefore, we could expect the quadratic form above to be bounded from above as follows, for some (random) \( c > 0 \)
This is a significant loss of regularity compared to the Laplacian and such a bound would not be sufficient to deduce our result. To solve this issue we observe that our argument only requires a fraction of regularity to treat the singular term \( {\text {div}}(X \mathbin {\otimes _{\!s}}w) \), so we split the quadratic form into
The first term yields an \( H^{1} \) bound and the second term is controlled by the division of scales. Note that this division is extremely artificial and highlights that our argument is somewhat rough and does not optimally capture the actual small scale structure of the solution.
3.1 Intermezzo: collecting the stochastic terms
In order to reduce the number of norms that we will later use in our bounds, it will be convenient to collect all stochastic quantities as elements of a large Banach space and use only one norm on that space. So far we have considered the following time-dependent processes, with associated “magnitude” \( \textbf{L}_{t} \):
for \( t \in [0, \infty ), \kappa > 0 \). In addition, in Section 6 we will consider the time-dependent Anderson-type operator \( \frac{1}{2} \Delta + 2 \nabla _{\!{\text {sym}}}X_{t} \). We therefore additionally consider the following “enhanced noise” process, for a given parameter \( \lambda \geqslant 1 \) and \( t \in [0, \infty ) \):
taking values in \( \mathcal {C}^{-1 - \kappa } \times \mathcal {C}^{- \kappa } \) (see Definition 4.1 for the definition of the projection \(\mathcal {L}_\lambda \), (6.5) for the definition of \(\mathfrak {r}_{\lambda }\), Lemma 6.2 for the definition of \(P^{\lambda }_{t}\), and Section A.1 for the definition of the “resonant product”
). Then we measure the magnitude of the enhanced noise together with the processes X and Y via
where \( \{ \lambda ^{i} \}_{i \in \textbf{N}} \) is defined in (4.8).
Lemma 3.1
Let \( (\Omega , \mathcal {F}, \mathbb {P}) \) be the probability space as in Assumption 2.1. There exist a null set \( \mathcal {N}^{\prime } \subseteq \Omega \) such that
Proof
For the terms involving \( \nabla _{\!{\text {sym}}}X \) see Lemma 6.2. The bounds on all other terms follow along similar lines. \(\square \)
For clarity, we collect all the stochastic terms required in our analysis in the following table.
Process | Definition | Regularity |
|---|---|---|
X | \( (\partial _{t} - \Delta ) X = \textbf{P} \Pi _{\times } \xi \) | \( \mathcal {C}^{- \kappa }\) |
Y | \( (\partial _{t} - \Delta ) Y = \textbf{P} {\text {div}}(2 X \mathbin {\otimes _{\!s}}Y + X^{\otimes 2}) + \textbf{P} \Pi _{\times } \zeta \) | \( \mathcal {C}^{2 \kappa } \) |
Q | \( (\partial _{t} - \Delta ) Q = 2 X \) | \( \mathcal {C}^{2 - \kappa }\) |
P | \( (- \frac{1}{2} \Delta +1 ) P = 2 \nabla _{\!{\text {sym}}}X \) | \( \mathcal {C}^{1 - \kappa } \) |
3.2 Recap: local well-posedness
Before we move on, let us recall the local well-posedness result for (3.2). The proof of a very similar result can be found in [8] and is by now classical. For \( \gamma , T > 0 \) and \( \beta \in \textbf{R}\), we consider the Banach space
We then say that \( w \in \mathcal {M}^{\gamma } \mathcal {C}^{\beta } \) is a mild solution to (3.2) if
where the definition of the products \( w^{\otimes 2} \) and \( D \mathbin {\otimes _{\!s}}w \) has to be justified, depending on the choice of the parameters \( \beta \) and \(\gamma \).
Proposition 3.2
Fix any \( 0< \kappa < 1/2\), set \(\gamma = 1 - \kappa /2 \), and assume that \( D \in C ([0, \infty ) ; \mathcal {C}^{- \kappa }) \) and \( Y^{\otimes 2} \in C ([0, \infty ); \mathcal {C}^{ 2 \kappa }) \). Then for all \( u_{0} \in \mathcal {C}^{-1 + 2\kappa } \), (3.2) admits a unique mild solution in the space \( \mathcal {M}^{\gamma /2}_{T^{{\text {fin}}}} \mathcal {C}^{3 \kappa /2}\), up to a maximal time \( 0 < T^{{\text {fin}}}(\textbf{L}_{t}^{\kappa }, u_{0}) \leqslant \infty \).
Note that one can improve the spatial regularity of the solution, at the cost of a higher blow-up at time \( t = 0 \) (roughly, one can obtain \( u \in \mathcal {M}^{1 - \kappa } \mathcal {C}^{1 - 2 \kappa }\) for all \( \kappa >0 \)). Yet if one does so, the non-linearity \( {\text {div}}(u^{\otimes 2}) \) would not be integrable (if measured in the better norm \( \mathcal {C}^{- 2 \kappa } \)) at \( t= 0 \). For this reason, we refrain from stating the optimal spatial regularity. Instead, we chose a space such that one can prove local well-posedness of the equation in that space through a classical Picard fixed point argument.
Remark 3.3
By Lemma 3.1, there exists a nullset \( \mathcal {N}\subseteq \mathcal {N}^{\prime } \) such that \( \textbf{L}^{\kappa }_{t}(\omega ) < \infty \) for all \( t \geqslant 0 \) and \( \omega \not \in \mathcal {N}\), so that the proposition above applies to our setting on \( \mathcal {N}\). Moreover, the maximal local existence time \( T^{{\text {fin}}} \) is the same as in Theorem 2.3, since mild solutions to (3.2) are equivalent to mild solutions to (2.3) through the mapping \( w \mapsto w + Y \).
4 A high-low energy estimate
We now analyse the most problematic term in deriving an energy estimate for w, namely the quadratic form (3.4). Since \( D \in \mathcal {C}^{- \kappa } \), we expect the solution w to be of regularity no better than \( \mathcal {C}^{1 - \kappa } \), also for smooth initial data. Hence to make sense of (3.4) there is no chance in treating the two terms \( \langle w, \Delta w \rangle \) and \( \langle w, \textbf{P} {\text {div}}( D \mathbin {\otimes _{\!s}}w) \rangle \) separately since both terms would be infinite. Instead, we have to exploit that there are cancellations between these two terms which make the quadratic form finite. Before we continue, let us assume that \( u_{0} \in L^{2} \): in any case Proposition 3.2 guarantees that \( w_{t} \in L^{2} \) for any \( t >0 \) up to the blow-up time \( T^{{\text {fin}}} \), also if \( u_{0} \) has worse regularity.
Assumption 4.1
Throughout this section we work under the assumption that \( u_{0} \in L^{2} \cap \mathcal {C}^{-1 + \kappa } \) for some \( \kappa >0 \).
4.1 High frequency paracontrolled decomposition
One way to observe the above mentioned cancellation is to look deeper into the structure of the solution w, using paracontrolled calculus to obtain a nonlinear expansion in terms of D. Let us define \(w^{\sharp } \) by
where the paraproduct 
is defined in Section A.1, and we note that \( Q \in \mathcal {C}^{2 - \kappa } \). Then \( w^{\sharp } \) solves
with the commutator 
defined by
Here we used that by the Leibnitz rule 
, which holds because for every Paley block \( \Delta _{j} \varphi \) we have \( \partial _{i} \Delta _{j} \varphi = \Delta _{j} \partial _{i} \varphi \). The term 
is expected to lie in \(\mathcal {C}^{1- 2\kappa }\) (see [13, Lemma 2.8], although here we are not using the parabolically scaled paraproduct, so the estimate will follow along a different line). Therefore, collecting all regularities we expect that \( w^{\sharp } \in \mathcal {C}^{1+ 2 \kappa } \), since the worst regularity term in the divergence is given by \( Y \mathbin {\otimes _{\!s}}w \in \mathcal {C}^{2 \kappa } \), assuming \( \kappa \) sufficiently small (recall that \(D = 2(X+Y)\)). This means that we have singled out the most irregular part of the solution w and we can now attempt to write an energy estimate for \( w^{\sharp } \). A naïve attempt will fail though, because now the pairing
appears to be cubic in the norm of w. By this we meant that the nonlinear term
does not vanish because of antisymmetry (as opposed to \( \langle w , {\text {div}}( w^{\otimes 2}) \rangle =0 \)), so that the naïve bound \( | \langle w^{\sharp }, {\text {div}}( (w - w^{\sharp } )^{\otimes 2}) \rangle | \lesssim \Vert w^{\sharp } \Vert _{H^{1}} \Vert w- w^{\sharp } \Vert _{L^{4}}^{2}\) is cubic in norms of \( w^{\sharp } \). On the other hand, if we knew that the irregular part \( w - w^{\sharp } \) is of order one in some appropriate norm, then we would be able to obtain an estimate that is quadratic in the norm of w, or in this case equivalently the norm of \( w^{\sharp } \). This is our aim, and the approach that we will follow to “make” the irregular part small is to take into account the paracontrolled structure only in high frequencies, where “high” will be defined in terms of the \( L^{2} \) norm of w.
4.1.1 High and low frequency projections
We start by introducing high and low frequency projections, together with some simple estimates.
Definition 4.1
For any \( \lambda > 0 \), define the projections
by respectively \(\mathcal {H}_{\lambda } w = \check{\mathfrak {h}}_{\lambda } * w\), and \(\mathcal {L}_{\lambda } w = w - \mathcal {H}_{\lambda } w = \check{\mathfrak {l}}_{\lambda } * w,\) where \( \check{\mathfrak {h}}_{\lambda }, \check{ \mathfrak {l}}_{\lambda } \in \mathcal {S}^{\prime } (\textbf{T}^{2}; \textbf{R}^{2}) \) are defined as the Fourier inverses
for smooth functions \( \mathfrak {h}, \mathfrak {l} :[0, \infty ) \rightarrow [0, \infty ) \) satisfying
The next result states that we can gain regularity in low frequencies by paying a price in powers of \( \lambda \). The spaces \( \mathcal {B}^{\alpha }_{p, \infty } \), for \( p \in [1, \infty ] \) and \( \alpha \in \textbf{R}\) are the Besov spaces with integrability parameter p introduced in Appendix A and agree with the spaces \( \mathcal {C}^{\alpha } \) for \( p = \infty \).
Lemma 4.2
For any \(p \in [1, \infty ]\) and \(\beta > \alpha \) one can estimate uniformly over \(\lambda \geqslant 1\):
Proof
We can write estimate, for some \( c > 0 \) by Young’s inequality for convolutions applied to \( \mathcal {L}_{\lambda } \Delta _{j} \varphi = \check{\mathfrak {l}}_{\lambda } * \Delta _{j} \varphi \)
from which the result immediately follows. \(\square \)
Similarly we can gain powers of \( \lambda \) in high frequencies by paying a price in regularity.
Lemma 4.3
For any \( p \in [1, \infty ] \) and \(\beta > \alpha \) one can estimate uniformly \(\lambda \geqslant 1\):
Proof
As above, we can bound for some \( c > 0 \)
Now we can simply estimate
where we used that by assumption \( \smallint _{\textbf{T}^{2}} \check{\mathfrak {l}}(x) \mathrm {\,d}x =1 \). Plugging this into the previous bound we obtain:
as required. \(\square \)
4.1.2 Construction of the high-frequency paracontrolled decomposition
For a time-dependent frequency level \( \lambda _{t} \geqslant 1 \) that will be introduced later on and with Q as in (4.1), let us define the high-frequency control \( Q^{\mathcal {H}} \) and the high-frequency component \( w^{\mathcal {H}} \) of w by
Clearly, \( w^{\mathcal {L}} \) should be interpreted as the low frequency component of w. In view of the two lemmas above, the gain in this decomposition is that if the frequency \( \lambda _{t} \) is large, then the control \( Q^{\mathcal {H}} \) is relatively small, provided that we are willing to measure it with a worse regularity. In particular, we can bound by Lemma 4.3:
To make sure that \( w^{\mathcal {H}} \) is of order one, independently of the size of w, it would be convenient to choose \( \lambda _{t} \simeq (1 + \Vert w_{t} \Vert ) \). Of course, such a decomposition eventually shifts the problem to the analysis of the low-frequency component \( w^{\mathcal {L}} \). For this purpose, such a choice of \( t \mapsto \lambda _{t} \) is not entirely convenient, because in deriving an equation for \( w^{\mathcal {L}} \) we will end up differentiating \( \lambda _{t} \) in time, which leads to a tedious term involving quantities such as the quadratic form (3.4), which is precisely what we set out to avoid. Instead we consider a discretised version of \( t \mapsto (1 + \Vert w_{t} \Vert )^{\mathfrak {a}} \), for a suitable \( \mathfrak {a} > 0 \).
Definition 4.4
Fix a parameter \( \mathfrak {a}> 0 \) and consider any initial condition \( u_{0} \) satisfying Assumption 4.1. Let us introduce the sequence of stopping times \( \{ T_{i} \}_{i \in \textbf{N}} \), with
defined for any \( \omega \in \Omega \) and \( u_{0} \in L^{2} \cap \mathcal {C}^{-1 + \kappa } \) as follows. For \( i \in \textbf{N}\setminus \{ 0 \} \) define
with w solving (3.2) and \( T^{{\text {fin}}} (\omega , u_{0}) \) as in Theorem 2.3. Then if we set
it holds that \(T_{i} = 0\) if and only if \(i \leqslant i_{0} (u_{0})\). Finally, for any \( i \in \textbf{N}\) set
Since \( u_{0}\in L^{2} \) by Assumption 4.1, we have \( i_{0}(u_{0}) < \infty \). Moreover \( \lambda _{t} \) is defined so that \( \lambda _{t} = \lambda ^{i} \) for all \( T_{i} \leqslant t < T_{i+1} \) and \( i \geqslant i_{0}(u_{0}) \).
Remark 4.5
We have defined the discretised frequency level \( t \mapsto \lambda _{t} \) in such a way that \( \lambda _{t} \in \{ \lambda ^{i} \}_{i \in \textbf{N}} \). In particular, it belongs to a fixed countable set independent of initial conditions, which will be of use in the approximation of the singular operator in Section 6 (else the null set in Lemma 6.2 could depend on the initial condition \( u_{0} \)). Moreover, we introduced the parameter \( \mathfrak {a} \), because it turns out that \( \mathfrak {a} = 1 \) (arguably the most natural choice) is not enough for our purposes. Instead choosing any \( \mathfrak {a} \in (2, 3] \) is sufficient. We left \( \mathfrak {a}\) as a free parameter, so that the reader can follow at what point the condition \( \mathfrak {a} > 2 \) is required.
Next we make use of the structure we have introduced so far to control the high-frequency term \( w^{\mathcal {H}} \).
Lemma 4.6
For any \( \delta > 0\) and \(\omega \not \in \mathcal {N}^{\prime } \) there exists a \( C(\delta ) > 0 \) such that
Observe that the formulation of the lemma above allows for t to depend on \( \omega \), and does not require it to be a stopping time.
Proof
The estimate follows from Lemma A.1, Lemma 4.3, the definition of \( w^{\mathcal {H}} \) in (4.4) and \( \lambda _{t} \) in Definition 4.4, since
Here, in the first estimate of the second line we made use of the continuous embedding \( \mathcal {B}^{\alpha }_{2, \infty } \subseteq H^{\alpha - \kappa }_{2} \) for any \( \kappa > 0 \). \(\square \)
4.2 Structure of the low-frequency energy estimate
In a nutshell, the question of global existence amounts then to proving that \( \lim _{i \rightarrow \infty } T_{i} = \infty \) (of course we still have to prove that \( T^{{\text {fin}}} \) coincides with the blow-up time of the \( L^{2} \) norm). To obtain such a result we now establish an \( L^{2} \) energy estimate on the low-frequency component \( w^{\mathcal {L}} \). Let us fix an \( i \in \textbf{N}, i > i_{0}\) and consider \( t \in [T_{i}, T_{i+1}) \), whenever \( T_{i}< T_{i +1} \), with the stopping times \( T_{i} \) defined as in (4.6). We find, in analogy to (4.2)
with initial condition 
, so that since \(D = 2(X+Y)\)
with 
as in (4.3). We will treat the four terms in (4.10) separately. The term (4.10a) gives rise to a paracontrolled quadratic form, which will need logarithmic (in \( \lambda _{t} \)) renormalisation. To bound the cubic term in (4.10d) we use our decomposition, in combination with Lemma 4.6.
Let us start with the quadratic form in (4.10a). Since both X and \( w^{\mathcal {L}} \) are divergence-free, we have
The factor 1/2 in front of the Laplacian is not a typo, that is, we did not consider the full term appearing in (4.10a) (there is a \( \Delta /2 \) missing), as we will split the Laplacian into two terms, see (4.13) below. This leads us to consider the following time-dependent family of operators:
where the “\( \infty \)” indicates the necessity of renormalisation. More precisely, \( \mathcal {A}_{t} \) will be constructed as the limit as \( \lambda \rightarrow \infty \) of the operators:
Here \( \mathfrak {r}_{\lambda }(t) \) is the renormalisation constant defined in (6.5) below. The fact that such a limit exists is the content of Proposition 6.1 and Lemma 6.2. Crucially, the convergence of the operators \( \mathcal {A}^{\lambda }_{t} \) is such that the quadratic form of the limiting operator is bounded from above (by a random, but finite, constant \( \textbf{m}_{t} \)), meaning that \( \langle \varphi , \mathcal {A}_{t} \varphi \rangle \leqslant \textbf{m}_{t} \Vert \varphi \Vert ^{2} \). For clarity let us formally write the action of these operators in components:
This allows us to rewrite (4.10a) as
The remaining terms in (4.10) will be treated as perturbations of this term. At this point we can thus already provide the heuristics of our approach, assuming (4.10b)–(4.10d) vanish. In this case we are left with the following bound, from the definition of \( \mathfrak {r}_{\lambda _{t}} (t) \) in (6.5) (where the constant \( c >0 \) appears) for \( t \in [T_{i}, T_{i+1}) \)
In addition, as we mentioned, by Proposition 6.1, there exists a continuous map \( \textbf{m} :\textbf{R}_{+} \rightarrow \textbf{R}_{+} \) such that the operator \( \mathcal {A}_{t} - \textbf{m}_{t} \) is negative. By Lemma 4.6 with \( \delta = 1/ \mathfrak {a} \) we additionally have \( \Vert w^{\mathcal {H}} \Vert \simeq 1 \) so that \( \Vert w \Vert \simeq \Vert w^{\mathcal {L}} \Vert + 1\), and we conclude
Roughly, this calculation shows that the norm grows at most like the solution to the ODE
for some \( c >0 \), which has double-exponential growth but does not blow up in finite time. More rigorously, we obtain that for \( t \in [T_{i}, T_{i+1}) \)
Now for \( t \geqslant 0 \) write \( \overline{\textbf{m}}_{t} = \max \{ \textbf{m}_{s} \; :\; s \in [0, t] \} \). If for the sake of our argument we assume that the blow-up time \( T^{{\text {fin}}} \) coincides with the blow-up time of the \( L^{2} \) norm of w (we will prove this in Corollary 5.4), then our aim is to prove that \( T_{i} \uparrow \infty \). In particular, if \( T^{{\text {fin}}} < \infty \), we would have \( T^{i}< T^{{\text {fin}}} < \infty \) for all \( i \in \textbf{N}\). On the other hand, we can bound for any \( i \geqslant 1 \), by using that \( \Vert w^{\mathcal {L}}_{T_{i}} \Vert ^{2} \simeq i^{2}\) and \( \Delta _{i} = T_{i+1} - T_{i}\)
whence
Since this quantity isn’t summable, \(\sum _i \Delta _i = \infty \) and we have found a contradiction to the assumption that \( T_{i}< T^{{\text {fin}}} < \infty \) for all i.
4.3 Energy estimate bounds
The next sections are devoted to making rigorous the argument sketched above. We start by obtaining the full energy estimate, taking into consideration the rest terms which we have ignored so far.
Proposition 4.7
Fix \( t \mapsto \lambda _{t} \) as in Definition 4.4 with \( \mathfrak {a}= 3 \). There exists a \( k \in \textbf{N}\), and a \( \kappa _{0} > 0 \) such that for some \( C > 0 \) and all \( \kappa \in (0, \kappa _{0} ) \) we can estimate uniformly over \( i \in \textbf{N}\) and \( t \in [T_{i} , T_{i +1}) \):
with \( \mathfrak {r}_{\lambda } (t) \) defined by (6.5).
Remark 4.8
The value \( \mathfrak {a} = 3 \) is arbitrary: for example the calculations below allow for any \( \mathfrak {a} \in (2, \infty ) \). Our choice \( \mathfrak {a} = 3 \) guarantees that \( \lambda ^{\frac{1}{3}}_{t} \lesssim 1 + \Vert w_{t} \Vert \), see also Remarks 4.5 and 4.11.
Proof
This estimate follows from the bound (4.13) for the term in (4.10a), together with Lemmas 4.9, 4.10, and 4.12 below for (4.10b)–(4.10d). The regularity \( 1 - \frac{3}{2} \kappa \) is the worst one appearing in all estimates, and comes from Lemma 4.12. \(\square \)
In the rest of this section we collect the bounds that lead to the energy estimate in Proposition 4.7. We start with a bound on the term (4.10b).
Lemma 4.9
Fix \( \lambda _{t} \) as in Definition 4.4 for any \( \mathfrak {a} \in [2, \infty ) \). There exists a \( \kappa _{0}> 0 \) and an \( \eta \in (0, 1 - \kappa _{0}) \) such that for all \( \kappa < \kappa _{0} \) we have the bound
Proof
We can bound for any \( \eta \in (0, 1) \)
so that overall
provided that \(\eta \geqslant \frac{1}{2} (1+ \kappa )\), which is the desired bound. \(\square \)
Next we pass to an estimate of (4.10c) and the first term of (4.10d).
Lemma 4.10
Fix \( \lambda _{t} \) as in Definition 4.4 for any \( \mathfrak {a} \in (2, \infty ) \). There exists a \( \kappa _{0}(\mathfrak {a}) > 0 \) and an \( \eta (\mathfrak {a}) \in (0, 1 - \kappa _{0}) \) such that for all \( \kappa < \kappa _{0} (\mathfrak {a}) \) we have the bounds
Remark 4.11
The factor \( \lambda ^{\frac{1}{3}}_{t} \) above could be replaced by \( \lambda ^{q}_{t} \) for an arbitrary \( q < 1/2\). Eventually we will need \( \lambda _{t}^{q} \lesssim 1 + \Vert w_{t}\Vert \), which is the case if \( \mathfrak {a} \leqslant q^{-1} \). Since any \( 2 < \mathfrak { a} \leqslant 3 \) will be sufficient for our needs we have fixed \( q =1/3 \).
Proof
First bound. By Lemma 4.6 with \( \delta = 1/2 \) and the assumption \( \mathfrak {a} \geqslant 2 \) one has
Applying in addition Lemma 4.2 we obtain
assuming that \( \kappa _{0} > 0 \) is sufficiently small so that \( 5/6 - 3 \kappa > 0 \). From the latter two estimates we can deduce as desired
for any \( \eta \in ( 2/3+ \kappa , 1) \), assuming that \( \kappa _{0} \) is small so that \( 1/2 - 3 \kappa \geqslant 1/3 - \kappa \).
Second bound. Here, since \( w^{\otimes 2} = ( w^{\mathcal {L}})^{\otimes 2} + ( w^{\mathcal {H}})^{\otimes 2} + 2 w^{\mathcal {L}} \mathbin {\otimes _{\!s}}w^{\mathcal {H}}\) and \( w^{\mathcal {L}} \) is divergence free, we find
For the term involving \( (w^{\mathcal {H}} )^{ \otimes 2} \) we estimate by Lemma A.1 and Sobolev embeddings in dimension \( d =2 \)
To close this first bound we apply Lemma 4.6 with \( \delta = 1/4 \) in order to deduce
since \( \mathfrak {a} \geqslant 2 \). Therefore we have obtained
where in the last step we used once again Lemma 4.6 with \( \delta = 1/2 \).
For the term involving \( w^{\mathcal {L}} \mathbin {\otimes _{\!s}}w^{\mathcal {H}} \) we proceed similarly, only this time we make use of the fact that \( \mathfrak {a} > 2 \) (with a strict inequality!). We use Lemma 4.6 with \( \delta = 1/ \mathfrak {a} \) and Besov embeddings (see (A.1)) to bound
Now, if \( 1/2 - 1/ \mathfrak {a} - \kappa > 0 \) – which is the case since \( \mathfrak {a} > 2 \), assuming \( \kappa _{0}(\mathfrak {a}) \) is sufficiently small – we conclude that
Therefore
provided \( \kappa >0 \) is sufficiently small with respect to \( \mathfrak {a} \) and \( \eta \geqslant (1/2 + 1/ \mathfrak {a} + 2 \kappa ) \vee (1 - 1/ \mathfrak {a} - \kappa ) \). The proof is complete. \(\square \)
We are left with the last terms in (4.10d).
Lemma 4.12
Fix \( \lambda _{t} \) as in Definition 4.4 for any \( \mathfrak {a} \in (2, \infty ) \). There exists a \( \kappa _{0}(\mathfrak {a}) > 0 \) and an \( \eta (\mathfrak {a}) \in (0, 1 - \kappa _{0}) \) such that for any \( \kappa \in (0, \kappa _{0} (\mathfrak {a})) \)
Proof
The \( 2 Y \mathbin {\otimes _{\!s}}w + Y^{\otimes 2} \) term. We can estimate via Lemma A.1 and Lemma 4.6 with \( \delta = 1/2 \), since \( \mathfrak {a} \geqslant 2 \):
Hence, since \( \frac{7}{4} \kappa - \frac{3}{2} \kappa > 0 \)
Similarly for the \( Y^{\otimes 2} \) term
where we used the estimate
The commutator term. Here by definition from (4.3) we have
As for the first term, from (3.2)
Let us start with the quadratic part, which has the worse homogeneity. By Sobolev embeddings we obtain \( \Vert w^{\otimes 2} \Vert _{L^{2}} \lesssim \Vert w \Vert _{L^{4}}^{2} \lesssim \Vert w \Vert ^{2}_{H^{1/2}}\) so that for any \( \gamma > 0 \), by Lemma A.1 and (4.5)
Therefore we find
Let us now use the decomposition \( w = w^{\mathcal {H}} + w^{\mathcal {L}} \), so that we can further bound
where in the last step we used Lemma 4.6 with \( \delta = 1/ \mathfrak {a} \) together with the assumption \( \mathfrak {a} > 2 \) so that, provided \( \kappa _{0}(\mathfrak {a}) > 0 \) is sufficiently small:
Next, we can use interpolation to bound, for any \( \eta \geqslant (1/2 + 2 \kappa ) \wedge (\gamma + 2 \kappa ) \):
Hence we obtain
To eventually find a useful estimate we must pick \( \eta , \gamma \) such that for all \(\kappa \) small
For example, if we fix \( \gamma = 1/2 \) and \( \eta = 3/4 + 2 \kappa \), then the first inequality is satisfied:
and the second inequality as well, since for \( \mathfrak {a} \geqslant 2 \):
With such a choice, we can finally bound
which is of the required order. Now we can proceed to the last two terms in (4.16). First of all, since \( D = 2(X + Y) \), we have
Therefore
Plugging this into the desired inner product we conclude
where in the last step we made use of Lemma 4.6.
Finally, we are left with the second term in (4.15). Here we bound
where in the last step we have used (4.17). We conclude that
which is again a bound of the correct order. This concludes the proof. \(\square \)
5 Global solutions
As in the previous section, we work under Assumption 4.1 and assume that the initial condition \( u_{0} \) to (3.2) satisfies
for some \( \kappa > 0 \). The objective of this section is to build on Proposition 4.7 to obtain global well-posedness for (2.3). The first step is to apply some interpolation inequalities to obtain a bound on the distance between the successive stopping times \( T_{i +1} - T_{i} \). We start with a corollary of Proposition 4.7.
Corollary 5.1
In the setting of Proposition 4.7, for some \( \kappa _{0} > 0 \) there exists a constant \( C_{1} >0 \) and increasing continuous maps \(C_{2}, C_{3} :\textbf{R}_{+} \rightarrow (0, \infty ) \) such that for all \( \kappa \leqslant \kappa _{0} \) we can estimate uniformly over \( i \in \textbf{N}, i \geqslant i_{0} \) and \( t \in [T_{i}, T_{i+1}) \)
In particular, we can estimate
Proof
From Proposition 4.7 we have that for some \( C >0 \)
Regarding the quadratic form associated to \( \mathcal {A}^{\lambda _{t}}_{t}\), it follows from Proposition 6.1 below that there exists an \( \textbf{m} (\textbf{N}^{\kappa }_{t}) \) such that
Regarding \( \mathfrak {r}_{\lambda }(t) \) we find for some \( c >0 \) that \( \mathfrak {r}_{\lambda } (t) \leqslant c \cdot \log {(\lambda _{t})} \), see (6.5). For the term involving \( \lambda _{t} \) we estimate \(\lambda _{t}^{\frac{1}{3}} \lesssim (1+ \Vert w_{t} \Vert ) \) for \( t \in [T_{i}, T_{i+1})\) since we have assumed that \( \mathfrak {a} = 3 \). Hence overall we find \( C_{1}, C_{2}, C_{3} \) as in the statement of the corollary, such that
Here we repeatedly use interpolation and Young’s inequality for products so that for any \( \eta , \varepsilon \in (0, 1) \) there exists a \( C(\varepsilon , \eta )> 0 \) such that
As for the second estimate, we find for any \( t \in [T_{i}, T_{i+1}) \) and \( \mu = C_{2}(\textbf{N}^{\kappa }_{T_{i+1}}) + C_{1} \log {(\lambda _{T_{i}})} \):
so that
which implies the desired result. \(\square \)
To complete the \( L^{2} \) estimate, we must control the jump of the norm at the stopping times \( T_{i} \).
Lemma 5.2
In the setting of Corollary 5.1, consider \( i \in \textbf{N}_{+} \) such that \( i \geqslant i_{0} (u_{0}) \), with \( i_{0} (u_{0}) \) as in (4.7), and fix \( t > 0 \). Then if \( T_{i+1} < T^{{\text {fin}}} \wedge t \) there exists a constant \( C (\textbf{N}_{t}^{\kappa }) > 0 \) such that
Proof
We can use Corollary 5.1 to bound
Now, since \( T_{i +1} < T^{{\text {fin}}} \), from the definition of the stopping time we have for some \( c > 1 \)
by Lemma 4.6 with \( \delta = 2/ \mathfrak {a} \in (0, 1 - 2\kappa ) \) (since \( \mathfrak {a} > 2 \), for \( \kappa > 0 \) sufficiently small). Recall here that since \(\lambda _t\) jumps at \(t = T_i\) by (4.8), we also have jumps in the definitions of \(w^\mathcal {L}\), see (4.4). Hence we obtain that
from which the result follows. \(\square \)
The previous lemma gives us a control on the explosion time of the \( L^{2} \) norm. Next we show that if \( T^{{\text {fin}}} < \infty \), then \( \lim _{t \uparrow T^{{\text {fin}}}} \Vert w^{\mathcal {L}}_{t} \Vert = \infty \), meaning that the explosion of the \( L^{2} \) norm is a necessary (and of course sufficient) condition for finite-time blow-up. For this purpose we require higher regularity estimates.
Lemma 5.3
In the setting of Corollary 5.1 there exists a \( \kappa _{0} > 0 \) such that the following holds for any \( \kappa \in (0, \kappa _{0})\) and \( \varepsilon \in (0, \kappa ) \) and. Fix any \( M>1, T > 0 \) such that
Then there exists a \( C (T, M, \textbf{N}_{T}^{\kappa } ) \in (0, \infty ) \) such that
Proof
To control the \( H^{\varepsilon } \) norm we have to control \( \langle w^{\mathcal {L}}, (- \Delta )^{\varepsilon } w^{\mathcal {L}} \rangle \). Here we find, as in (4.10a), (4.10b), (4.10c) and (4.10d):
We bound the right-hand side one term at the time. The value of the constants \( C >0\) may change from line to line. All calculations hold only for \( \kappa _{0}\) sufficiently small. For (5.1a) we have for any \( \delta \in (0, 1) \)
where we used the estimate
for \( \varepsilon \) sufficiently small. For (5.1b) we follow the proof of Lemma 4.9 to obtain for any \( \delta \in (0, 1) \)
where the last bound follows by interpolation on the Sobolev norms.
Next, following the proof of the first bound of Lemma 4.10, we obtain for (5.1c) and any choice of \( \delta \in (0, 1) \)
for any \( \eta > 2/3+ \kappa \), making use of the estimate \( \lambda _{t} \lesssim M^{\frac{\mathfrak {a}}{2} } \) and since \( \eta + 2 \varepsilon + \kappa < 1 + \varepsilon \) for \( \kappa _{0} \) sufficiently small.
Finally, for (5.1d) we start by estimating the cubic term. We can rewrite \( w^{\otimes 2} = ( w^{\mathcal {L}})^{\otimes 2} + ( w^{\mathcal {H}})^{\otimes 2} + 2 w^{\mathcal {L}} \mathbin {\otimes _{\!s}}w^{\mathcal {H}}\), and we will estimate one addend at a time. Starting with \( (w^{\mathcal {L}})^{\otimes 2} \), we obtain
Next, we can estimate via a Kato–Ponce type inequality (see for example [22, Thm A.13]) in dimension \( d =2 \) and by interpolation
Therefore we obtain that
where we used Young’s inequality with conjugate exponents 4/3 and 4.
For the other two terms we follow the proof of Lemma 4.10. In particular, we use the bound (4.14) to obtain
since \( \varepsilon \in (0, 1/6) \). As for the term involving \( w^{\mathcal {L}} \mathbin {\otimes _{\!s}}w^{\mathcal {H}} \), we follow once more the proof of Lemma 4.10 to obtain
so that for some \( \eta \in (0, 1)\) (assuming that \( \kappa _{0} \) is sufficiently small and since \( \mathfrak {a} =3 \)) and any \( \delta \in (0, 1) \):
for \( \varepsilon \) sufficiently small.
To conclude our estimate for (5.1d), we have to bound
Following the same steps as in Lemma 4.12, we obtain
since \( \varepsilon \leqslant \kappa \), which is again of the desired order.
Overall, choosing \( \delta \in (0, 1) \) sufficiently small we have obtained
Therefore, if we define \( g_{t} = 1 + \Vert w^{\mathcal {L}}_{t} \Vert ^{2}_{H^{\varepsilon }} \), we have
so that by Gronwall’s inequality
for all \( t \in [0, T] \), which is the desired bound. \(\square \)
Finally, we can deduce our \( L^{2} \) blow-up criterion.
Corollary 5.4
Under Assumption 4.1, if \( T^{{\text {fin}}} < \infty \), then \( \limsup _{t\uparrow T^{{\text {fin}}}} \Vert w_{t} \Vert = \infty \).
Proof
It suffices to prove that \( T_{i} < T^{{\text {fin}}} \) for all \( i \in \textbf{N}\). Note that under Assumption 4.1, by Proposition 3.2 for any \( \zeta < 1 - \kappa \) and \( 0< t < T^{{\text {fin}}} \) we have \( \Vert w^{\mathcal {L}}_{t} \Vert _{H^{\zeta }} < \infty \). If by contradiction there exists an \( i_{{\text {fin}}} \in \textbf{N}\) such that \( T_{i} = T^{{\text {fin}}} \) for all \( i \geqslant i_{{\text {fin}}} \), then by Corollary 5.1 and Lemma 5.3 we would find a \( C( T^{{\text {fin}}}, \textbf{N}^{\kappa }_{T^{{\text {fin}}}}) >0 \) and an \( \varepsilon > 0 \) such that
and as an application of Proposition 3.2 we would be able to extend the domain of definition of the mild solution. \(\square \)
Proof of Theorem 2.5
Suppose by contradiction that \( T^{{\text {fin}}} < \infty \) so that, by Corollary 5.4, \( T_{i} < T^{{\text {fin}}} \) for every \( i \in \textbf{N}\). Since on the other hand, Lemma 5.2 implies that for \( \kappa >0 \) sufficiently small
our initial assumption must be false. \(\square \)
6 The symmetrised operator
This section is devoted to the construction of the time-dependent operator \( t \mapsto \mathcal {A}_{t} \) as in (4.11) and its approximations \( (\mathcal {A}^{\lambda }_{t})_{\lambda \geqslant 1} \) as in (4.12). The construction is overall analogous to the construction of the 2D Anderson Hamiltonian by Allez and Chouk [1], although presently we are treating a vector-valued and time-dependent case. The fundamental step is the construction of a continuous map between the space \( \Xi \) of enhanced noises and the space \( \textbf{C}_{\textrm{op}} \) of closed self-adjoint operators with the graph distance [21, IV.2.4] (convergence in this distance is implied by convergence in the resolvent sense, which is the only one we will use here). We define the space of enhanced noises \(\Xi _{\kappa } \subseteq \mathcal {C}^{-1 - \kappa }(\textbf{T}^{2}; \textbf{M}^{2}) \times \mathcal {C}^{ - \kappa }(\textbf{T}^{2}; \textbf{M}^{2})\) by
where the closure is taken with respect to the \( \mathcal {C}^{-1 - \kappa }(\textbf{T}^{2}; \textbf{M}^{2}) \times \mathcal {C}^{ - \kappa }(\textbf{T}^{2}; \textbf{M}^{2})\) product norm. We refer to these as enhanced noises because our purpose is to define the operator
but if \( \textbf{X}_{1} \in \mathcal {C}^{-1 - \kappa } \) for some \( \kappa > 0 \), there is no canonical definition of such an operator and some additional information (in terms of functionals of \( \textbf{X}_{1} \)) is required. This is because, for generic \( \textbf{X}_{1} \in \mathcal {C}^{-1 - \kappa } \), the product 
is not well defined, cf. Lemma A.1. Eventually, we will associate to each element in the space \( \Xi _{\kappa } \) a closed operator, which will have as domain the space of so-called strongly paracontrolled functions, which embeds into the following space (with slightly simpler structure), for any \( \textbf{X} = (\textbf{X}_{1}, \textbf{X}_{2}) \in \Xi _{\kappa }\), for some \(\kappa >0\):
with the associated norm
Then let us recall the following result concerning singular Hamiltonians.
Proposition 6.1
(Allez–Chouk [1]) There exists a \( \kappa _{0} > 0 \) and a unique map \( \mathfrak {A} :\Xi \rightarrow \textbf{C}_{\textrm{op}} \), where
such that the following two properties are satisfied:
-
1.
For any smooth \( \textbf{X}= (\textbf{X}_{1}, \textbf{X}_{2}) \in \mathcal {S}(\textbf{T}^{2}; \textbf{M}^{2}) \times \mathcal {S}(\textbf{T}^{2}; \textbf{M}^{2}) \subseteq \Xi \) and \( \varphi \in H^{2} \) we have
with P as in (6.2) and the commutator
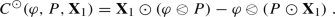
In particular, if
(for arbitrary \( c \in \textbf{R}\)) we recover \( \mathfrak {A} (\textbf{X}) \varphi = \frac{1}{2} \Delta \varphi + \textbf{X}_{1} \varphi {- c \varphi }\). -
2.
For any sequence \( \{\textbf{X}^{n}\}_{n \in \textbf{N}} \subseteq \mathcal {S}(\textbf{T}^{2}; \textbf{M}^{2}) \times \mathcal {S}(\textbf{T}^{2}; \textbf{M}^{2}) \) such that for some \( \kappa < \kappa _{0} \) and \( \textbf{X} \in \Xi _{\kappa } \), \( \textbf{X}^{n} \rightarrow \textbf{X} \) in \( \Xi _{\kappa } \) as \( n \rightarrow \infty \), we have that \(\mathfrak {A}(\textbf{X}^{n}) \) converges in resolvent sense to \( \mathfrak {A}(\textbf{X}) \).
(for arbitrary In addition, for any \( \kappa < \kappa _{0} \), there exist two continuous maps \( \textbf{m}, \textbf{c} :\Xi _{\kappa } \rightarrow \textbf{R}_{+} \) (depending on \( \kappa \)) such that \( [\textbf{m}(\textbf{X}), \infty ) \subseteq \varrho (\mathfrak {A}(\textbf{X}))\), for any \( \textbf{X} \in \Xi _{\kappa } \), where \( \varrho ( \cdot ) \) indicates the resolvent set of an operator, with the bound
Observe that the last statement implies that for \( m \geqslant \textbf{m}(\textbf{X}) \), the operator \( - \mathfrak {A}(\textbf{X}) +m \) is nonnegative, since from the spectral decomposition of self-adjoint operators with compact resolvents we immediately have \( \langle - \mathfrak {A}(\textbf{X}) \varphi , \varphi \rangle \geqslant - \sup \{ \textbf{R}\setminus \varrho ( \mathfrak {A}(\textbf{X})) \} \Vert \varphi \Vert ^{2} \). For a proof we refer for example to [1, Proposition 4.13]: the result is for the scalar setting, but its extension to the vector-valued case is immediate. Next we collect the Gaussian computations that are required for the construction of the symmetrised operator \( \mathcal {A}\). We start by rewriting the driving noise in Fourier coordinates. In particular, we are interested in the projection \(\textbf{P} \Pi _{\times } \xi \) on divergence-free functions, which can formally be represented in Fourier coordinates as follows:
where \(\{ \beta _{t}^{k, i} \}_{i=1,2, k \in \textbf{Z}^{2}_{*}}\) is a sequence of complex Brownian motions with covariance structure
For our purposes it will be more convenient to set \( \zeta _{s}^{k} = (\beta ^{k, 1}_{s} k_{2} - \beta ^{k, 2}_{s} k_{1}) / | k | \), which is again a sequence of two-sided complex Brownian motions, with covariance structure
With this notation, setting \( \{ e_{k} \}_{k \in \textbf{Z}^{d}_{*}} \) a basis for the space of divergence-free functions, we can represent
In this context we can write \( \mathcal {L}_{\lambda } X \) and \( (-\Delta / 2+1)^{-1} \mathcal {L}_{\lambda } X\) in Fourier coordinates as follows:
with F being the stochastic integral
We are now ready to state the main result of this subsection, namely the convergence of the stochastic terms required to make sense of the operator \( \mathcal {A}\).
Lemma 6.2
For any \( \kappa > 0 \), let \( \Xi _{\kappa } \subseteq \mathcal {C}^{-1 - \kappa }(\textbf{T}^{2}; \textbf{M}^{2}) \times \mathcal {C}^{ - \kappa }(\textbf{T}^{2}; \textbf{M}^{2})\) be as in (6.1). Furthermore, define for any \( \lambda > 1 \)
Then for any \( t \geqslant 0 \) there exists a distribution \( \nabla _{\!{\text {sym}}}X_{t} \diamond P_{t} \) in \( \mathcal {C}^{- \kappa } (\textbf{T}^{2}; \textbf{M}^{2 }) \), for which the following convergence holds, for any \( \kappa > 0 \), both in \( L^{p} ( \Omega ; C_{\textrm{loc}}(\textbf{R}_{+}; \Xi _{\kappa }) )\) for any \( p \in [1, \infty ) \) and almost surely:
as \( n \rightarrow \infty \)Footnote 1. In addition, the renormalisation constants \( \mathfrak {r}_{\lambda }(t) \) satisfy, for some \( c > 0 \) and uniformly over all \( \lambda \geqslant 1 \) and \( t \geqslant 0 \)
with \( \mathfrak {l} \) as in Definition 4.1.
Proof
We restrict ourselves to proving the convergence of the product 
, as the convergence of \( \mathcal {L}_{\lambda ^{n}} \nabla _{\!{\text {sym}}}X \) follows along similar calculations. We observe that both X and \( P^{\lambda } \) are Gaussian fields, so their product lives in the second and the zeroth chaos. We treat the two terms differently, since the renormalisation constant \( \mathfrak {r}_{\lambda } \) is chosen exactly to cancel out the zeroth chaos. In components, the problem amounts to studying the following product:
where \( X_{\lambda } = \mathcal {L}_{\lambda } X = (X^{i}_{\lambda })_{i = 1, 2} \). Hence we are lead to consider a product of the following form, for \( i, j, l, m \in \{ 1, 2 \} \)
Using (6.3) we can represent this product as follows:
Here the coefficient \( \mathfrak {c}^{i, l}_{j, m} \) is defined as
Zeroth chaos. In particular, the zeroth chaos (the average) is given by the contraction along the line \( k - k^{\prime } = - k^{\prime } \), so that we find
since \( \int _{0}^{t} e^{- 2 | k |^{2} (t -s)} \mathrm {\,d}s = \frac{1}{2 | k |^{2}} (1 - e^{- 2 | k |^{2}t})\). In particular, it follows that the average is nonzero only in two cases, namely if either \( i = j = l=m \) or exactly two of the indices are 1 and the other two are 2 (in all other cases the sum is anti-symmetric). As a consequence of this observation we immediately obtain that
We are thus left with computing the average 
. This amounts to considering four different terms. We start by observing that
Similarly also
In particular, we have reduced ourselves to computing
which is the required quantity.
Second chaos. Instead, for the second chaos we can bound for any \( p \geqslant 2 \) by Gaussian hypercontractivity
Then, for the second moment we can estimate with \( \psi _{0}(k, k^{\prime }) = \sum _{| c -d | \leqslant 1} \varrho _{c} (k) \varrho _{d}(k^{\prime })\)
since we are in dimension \( d =2 \). In this way we obtain for any \( \kappa > 0 \) and \( p \geqslant 2 \) that
From here to obtain convergence of the sequence in \( L^{p} \) for \( \lambda \rightarrow \infty \) follows along classical lines. Instead, let us address the almost sure convergence for the sequence \( \{ \lambda ^{i} \}_{i \in \textbf{N}} \). To this aim, we have to bound for any \( i \in \textbf{N}\) the difference
Following the previous calculation we are thus led to bound, for \( j \geqslant -1 \) and \( x \in \textbf{T}^{d} \)
where in the last step we follow the previous calculations. We deduce that
so that the almost sure convergence follows, since by (4.8) we have \( \sum _{i \in \textbf{N}} (\lambda ^{i})^{- \frac{\kappa p}{2}} < \infty \) for \( p \geqslant 2 \) sufficiently large. The convergence uniformly in time follows by similar estimates, and this concludes the proof. \(\square \)
7 Global high-low weak solutions
In this section we prove Theorem 2.6, regarding existence and uniqueness of global weak solutions to (2.3) with initial datum \( u_{0} \) in \( L^{2} \). We start by introducing a suitable concept of weak solution to (2.3).
Definition 7.1
(HL Solutions) For \( u_{0} \in L^{2} \) with \( {\text {div}}(u_{0}) = 0 \) we say that a divergence-free process v in \(C([0, \infty ); \mathcal {S}^{\prime } (\textbf{T}^{2}; \textbf{R}^{2})) \) is a global high-low weak solution to (2.3) (HL solution for short) with initial condition \( u_{0} \) if the following are satisfied by \( w = v - Y \), with Y given by (3.1):
-
1.
For any \( \lambda \geqslant 0 \) we can write w in the form \( w_{t} = w^{\mathcal {L}, \lambda }_{t} + w^{\mathcal {H}, \lambda }_{t} \), with
where \( Q_{t} \) is defined in (4.1). Then we assume that for any \( T > 0 \), \( w^{\mathcal {L}, \lambda } \) and \( w^{\mathcal {H}, \lambda } \) satisfy for all \( \delta \in (0, 1) \)
$$\begin{aligned}{} & {} w^{\mathcal {L}, \lambda } \in L^{2}([0, T]; H^{1}) \cap L^{\infty }([0, T]; L^{2}) \;, \\{} & {} \quad w^{\mathcal {H}, \lambda } \in L^{2}([0, T]; \mathcal {B}^{1 - \delta }_{4, \infty }) \cap L^{\infty } ([0, T]; L^{2})\;. \end{aligned}$$ -
2.
Equation (3.2) is satisfied by w in the weak sense. Namely, for any \( T > 0 \) and \( \varphi \in C^{\infty }([0, T] \times \textbf{T}^{2}; \textbf{R}^{2}) \) satisfying \( {\text {div}}(\varphi ) = 0 \):
$$\begin{aligned}{} & {} \langle w_{T}, \varphi _{T} \rangle - \langle w_{0}, \varphi _{0} \rangle \\{} & {} \quad = \int _{0}^{T} \langle w, (\partial _{t} \varphi + \Delta \varphi ) \rangle + \langle {\text {div}}(w^{\otimes 2} + D \mathbin {\otimes _{\!s}}w + Y^{\otimes 2} ), \varphi \rangle \mathrm {\,d}s \;. \end{aligned}$$
Remark 7.2
We observe that if the regularity assumption on \( w^{\mathcal {L}, \lambda } \) and \( w^{\mathcal {H}, \lambda } \) is satisfied for some \( \lambda > 0 \), then it is satisfied for all \( \lambda \).
Now we can establish existence of weak solutions.
Lemma 7.3
Let \( \mathcal {N}^{\prime } \) be the null set of Lemma 3.1. Then for any \( \omega \not \in \mathcal {N}^{\prime } \) and \( u_{0} \in L^{2} \) with \( {\text {div}}(u_{0}) = 0 \) there exists an HL solution to (2.3) with initial condition \( u_{0} \).
Proof
We construct a sequence of solutions to smooth approximations of (3.2) and prove a uniform energy estimate that guarantees compactness of the sequence. Let us define \( u_{0}^{n} = \mathcal {L}_{n} u_{0} \) and \( X^{n} = \mathcal {L}_{n} X \) and \( Y^{n} \) the solution to (3.1) with X replaced by \( X^{n} \). Then set \( D^{n} = 2 (X^{n} + Y^{n}) \) and let \( w^{n} \) be the smooth solution to
with \( w^{n}_{0} = u_{0}^{n} \). Furthermore, we introduce the following analogues of \( \textbf{N}^{\kappa }_{t} \) and \( \textbf{L}^{\kappa }_{t} \), cf. (3.6):
where we have defined for all \( \lambda \geqslant 1 \)
With this definition we have that \( \lim _{n \rightarrow \infty } \textbf{N}^{n , \kappa }_{t} (\omega ) = \textbf{N}^{\kappa }_{t} (\omega ) \) for all \( \omega \not \in \mathcal {N}^{\prime } \), the null set of Lemma 3.1, so in particular
Step 1: A priori bound. Our first objective is to show that for any \( T > 0 \) and \( \kappa > 0 \) sufficiently small there exists a \( C (T, \overline{\textbf{N}}_{T}^{\kappa }) \) such that
To this aim, in analogy to Definition 4.4 and (4.4), let us define \( T_{0}^{n} = 0 \) and
and set \(\lambda _{t}^{n} {\mathop {=}\limits ^{\textrm{def}}}(1 + \Vert w^{n}_{T_{i}} \Vert )^{3}\) for all \(T_{i} \leqslant t < T_{i+1}\). And finally, for \( Q^{n} \) solving \( (\partial _{t} - \Delta ) Q^{n} = 2 X^{n} \) with \( Q_{0}^{n} = 0\) and \( Q^{n, \mathcal {H}}_{t} = \mathcal {H}_{\lambda _{t}^{n}} Q^{n}_{t}\) we set
Now we follow verbatim the proofs of Corollary 5.1 and Proposition 4.7, so that we obtain for any \( T, \kappa > 0 \)
In particular, since for fixed \( n \in \textbf{N}\) the solution \( w^{n} \) is smooth for all times, we can follow Lemma 5.2 to obtain that for some increasing \( C :\textbf{R}_{+} \rightarrow \textbf{R}_{+} \) and uniformly over \( n, i \geqslant i_{0}(u_{0}) \) where \( i_{0} (u_{0})\) is as in (4.7):
Hence, from the divergence of the sequence \( \sum _{i \in \textbf{N}_{+}} (i \log {i})^{-1} = \infty \) we deduce that for every \( T>0, i \in \textbf{N}, i > i_{0} (u_{0}) \) there exists a time \( \mathfrak {t}(i, \overline{\textbf{N}}^{\kappa }_{T}) \in (0, T] \), satisfying \(\mathfrak {t}(i) = T \) for all i sufficiently large, such that
In addition we deduce that there exists a \( \overline{\lambda }_{T} > 0 \) such that
Then from (7.3) and (7.4) we can conclude that (7.2) holds true. In fact, we can go one step further and use (7.5) to introduce the processes
Then following all the previous calculations we obtain that for any \( \lambda \geqslant \overline{\lambda }_{T} \)
This leaves us roughly in the classical setting for solutions to the Navier–Stokes equations and we can follow, with a few modifications, [25, Chapter 3, Theorem 3.1].
Step 2: More a priori estimates. Of course control on \( w^{n, \mathcal {L}} \) alone is not sufficient, since we are interested in \( w^{n} = w^{n, \mathcal {H}} + w^{n, \mathcal {L}} \), so let us now include the high-frequency term. We find by Lemma A.1 that for any \( \alpha < 1 - \kappa - 1/ \mathfrak {a} \) and some \( C > 0 \)
where we have used Lemma 4.6. In particular, we obtain by (7.2) that for any \( \alpha < 1 - \kappa - 1 / \mathfrak {a} \)
Via Lemma A.1 we now bound \( \Vert w^{n}_{t} \Vert _{H^{1- \kappa }} \lesssim \Vert w^{n}_{t} \Vert \Vert Q^{n, \mathcal {H}}_{t} \Vert _{\mathcal {C}^{2 - \kappa }} + \Vert w^{n, \mathcal {L}}_{t} \Vert _{H^{1 - \kappa }} \), so that using (7.2) we further improve the estimate to
Next, to obtain the high-low frequency decomposition for w we have to establish a bound on \( w^{n, \mathcal {H}, \lambda } \). From (7.9) and the Besov embedding \( H^{1 - \kappa } \subseteq \mathcal {B}^{1/2 - 2\kappa }_{4, \infty } \), see (A.1), since
we then obtain, for every \( \lambda \geqslant 1 \)
We observe that we could in principle replace the \( L^{4} \) integrability with any \( L^{p} \) integrability for arbitrary \( p < \infty \), provided \( \kappa \) were chosen sufficiently small. Since this additional integrability will not be necessary, we fix \( p =4 \). Now we are ready to deduce the required convergence.
Step 3: Convergence and conclusion. In view of (7.8) and (7.9) there exists a subsequence \( \{ n_{k} \}_{k \in \textbf{N}} \) such that we have for \( k \rightarrow \infty \) and some w:
Here the arrows \( \rightharpoonup \) and \( \overset{*}{\rightharpoonup }\ \) indicate weak and weak-\( * \) convergence respectively. Now, weak convergence in \( L^{2}(\textbf{T}^{2}) \) is not sufficient to deduce that the limiting process satisfies (3.2). For this purpose we want to additionally establish the following strong convergence, for any \( \beta < 1- \kappa \):
To obtain this result, we would like to apply the Aubin–Lions lemma, so we bound via (7.1) and for \( \kappa > 0 \) sufficiently small
where we used the compact embedding \( (w^{n})^{\otimes 2} \in L^{1} \subseteq H^{- 1 - \kappa } \) in dimension \( d =2 \) for the nonlinear term. We therefore conclude that
so that (7.12) follows indeed from Aubin–Lions. Now we can deduce that the limit w of the subsequence \( w^{n_{k}} \) is a weak solution to (3.2). In fact by (7.12)
strongly in \( L^{2}([0, T]; L^{1}), L^{2}([0, T]; \mathcal {B}^{- \kappa }_{2, \infty }) \) and \( C([0, T]; \mathcal {C}^{2 \kappa }) \) respectively. Finally, we have to establish the high-low frequency decomposition for w. From the strong convergence in (7.12) we obtain that as \( n \rightarrow \infty \)
In addition (7.10) guarantees that \( w^{\mathcal {H}, \lambda } \) has the required regularity \( L^{2}([0, T]; \mathcal {B}^{1- 2 \kappa }_{4, \infty } ) \). That \( w^{\mathcal {H}, \lambda } \) lies in \( L^{\infty }([0, T]; L^{2}) \) follows from (7.7) with \( \alpha = 0 \). Similarly, from (7.6) we obtain that \( w^{\mathcal {L}, \lambda } = w - w^{\mathcal {H}, \lambda }\) lies in \( L^{\infty }([0, T]; L^{2}) \cap L^{2}([0, T]; H^{1}) \), as required. This completes the proof. \(\square \)
Next we show that HL solutions are unique.
Lemma 7.4
Let \( \mathcal {N}^{\prime } \) be the null set of Lemma 3.1. Then for any \( \omega \not \in \mathcal {N}^{\prime } \) and any initial condition \( u_{0} \in L^{2} \) with \( {\text {div}}(u_{0})=0 \) there exists at most one HL solution to (2.3) with initial condition \( u_{0} \) as in Definition 7.1.
Proof
Consider two HL solutions \( v = w + Y, \overline{v} = \overline{w} + Y \) to (2.3) and write \( z = w - \overline{w} \) and for any \( \lambda \geqslant \lambda _{T} \) define \( z^{\mathcal {L}, \lambda } = w^{\mathcal {L}, \lambda } - \overline{w}^{\mathcal {L}, \lambda } , z^{\mathcal {H}, \lambda }= z - z^{\mathcal {L}, \lambda }\). Since in the first few steps we do not care about the choice of \( \lambda \), we omit it from the notation (meaning that we write \( z^{\mathcal {L}}, z^{\mathcal {H}} \) in place of \( z^{\mathcal {L}, \lambda } \) and \( z^{\mathcal {H}, \lambda } \)), up to the last step. We can compute via (4.9):
Let us note that the equality we have written has to be justified, but its proof follows from the regularity assumptions in Definition 7.1 along the same estimate we will use below to obtain uniqueness. Also, recall that contrary to many previous calculations, \( \lambda \) is a fixed and arbitrary large parameter. As usual we proceed one term at a time.
Step 1: (7.14a). We estimate via Lemma 4.2
Step 2: (7.14b). Here we obtain for any \( \delta \in (0, 1) \)
where the last inequality follows by interpolation \( \Vert z^{\mathcal {L}} \Vert _{H^{2 \kappa }} \lesssim \Vert z^{\mathcal {L}} \Vert ^{1 - 2 \kappa } \Vert z^{\mathcal {L}} \Vert ^{2 \kappa }_{H^{1}} \) and by Young’s inequality for products with \( p = 2/(1+ 2\kappa ), q = 2/(1 - 2 \kappa ) \).
Step 3: (7.14c). Here we estimate
For the commutator 
we then proceed similarly to the proof of Lemma 4.12, namely from (4.3)
For the first term we have, since \( Q \in \mathcal {C}^{2 - \kappa } \):
For the second term we have
and from (3.2) we obtain that z solves
so that
Then, for the first quantity we have by Besov embedding, see (A.1), that
and for the second quantity \(\Vert D \mathbin {\otimes _{\!s}}Z \Vert _{H^{-1 + 2 \kappa }} \lesssim \Vert D \Vert _{\mathcal {C}^{- \kappa }} \Vert z \Vert _{H^{2 \kappa }}\). Hence in total for the commutator
So overall, via Lemmma 4.6 and by Young’s inequality for products we can conclude that for any \( \delta \in (0, 1) \)
Step 4: (7.14d). Here we estimate
Regarding the term involving \( z \mathbin {\otimes _{\!s}}(w + \overline{w}) \), we decompose it as
in order to use the different regularity and integrability bounds on the high and low frequency terms. For the low frequency term we use Gagliardo–Nirenberg to bound
For the cross term we bound via the Riesz–Thorin interpolation theorem
and in addition by Besov embeddings we find that (provided \( \kappa \) is sufficiently small), as we are in dimension \( d=2 \)
We can use similar bounds on all the remaining terms to eventually obtain
where for a function \( \varphi \), which for any \( \lambda \geqslant \lambda _{T} \) can be decomposed as \( \varphi = \varphi ^{\mathcal {L}, \lambda } + \varphi ^{\mathcal {H}, \lambda } \) we have defined
Then by Young’s inequality for products with conjugate exponents \( p = 4/3, q = 4 \) we can bound for any \( \delta \in (0, 1) \) and a suitable \( C(\delta ) > 0 \):
Step 5: Conclusion. Before we put together all our estimates, let us observe that in Steps 3 and 4 our bounds depend on the norms of z and \( z^{\mathcal {H}, \lambda } \) and not just \( z^{\mathcal {L}, \lambda } \). Here to obtain uniqueness we will make use of our freedom of choice for \( \lambda \). Let us start by considering the \( H^{\alpha } \) norm of z for \( 0 \leqslant \alpha < 1 - \kappa \). By Lemma 4.3 we obtain:
In particular, if we choose \( \overline{\lambda }(\alpha , \kappa , T)\geqslant 1 \) sufficiently large, so that
we obtain for all \( \lambda \geqslant \overline{\lambda }(\alpha , \kappa , T) \vee \lambda _{T} \):
Then choose \( \alpha = 1 - 2 \kappa \), so that from the Besov embedding \( H^{\alpha } \subseteq B^{\alpha -1}_{4, \infty } \), for all \( \lambda \geqslant \overline{\lambda } (1 -2 \kappa , \kappa , T) \vee \lambda _{T} \) we obtain
We deduce that for 
defined by (7.18) we have 
.
We are now ready to collect the bounds from the previous steps: (7.15), (7.16), (7.17) and (7.19) (for sufficiently small \( \delta \in (0, 1) \)), in combination with (7.20) and (7.21). We find that for any \( \lambda \geqslant \overline{\lambda } (1 - 2\kappa , \kappa , T ) \vee \lambda _{T} \), choosing \( \delta > 0 \) sufficiently small in the bounds above
As for the \( H^{3 \kappa } \) norm of \( z^{\mathcal {L}, \lambda } \), by interpolation \( \Vert z^{\mathcal {L}, \lambda } \Vert _{H^{3 \kappa }} \lesssim \Vert z^{\mathcal {L}, \lambda } \Vert ^{1 - 3 \kappa } \Vert z^{\mathcal {L}, \lambda } \Vert ^{3 \kappa }_{H^{1} }\). Hence by Young’s inequality for products with conjugate exponents \( p = \frac{2}{6 \kappa }, q = \frac{2}{2 - 6 \kappa }\) (as usual this is well-defined only for \( \kappa \) small) we obtain for any \( A > 0, \delta \in (0,1) \)
Of course, we want to apply this inequality with \( A^{\frac{1}{2} } = 1 + \Vert w \Vert _{H^{3 \kappa }} + \Vert \overline{w} \Vert _{H^{3 \kappa }} \), and for the last two terms we can apply the same line of inequalities to obtain, for \( \vartheta (\kappa ) = \frac{4 \kappa }{1 - 4\kappa } \)
Hence, since for \( \kappa \) small \( \frac{3 \kappa }{(1 - 3 \kappa )^{2}} \leqslant 2 \), we can further simplify our estimate to obtain
where we have additionally defined \( M_{T} = \Vert w \Vert _{L^{\infty }([0, T]; L^{2})} + \Vert \overline{w} \Vert _{L^{\infty }([0, T]; L^{2})}\), which is finite from the definition of HL solutions. We can now deduce that for any \( \mathfrak {t} \in (0, T] \)
From the regularity assumptions on HL solutions in Definition 7.1 we know that 
. In particular by dominated convergence
is a continuous map (and hence equicontinuous on the compact interval [0, T] ). From (7.22) we can conclude, by a contraction argument, that \( z = 0 \) on \( [0, \mathfrak {t}] \), for \( \mathfrak {t} \) sufficiently small depending only on the modulus of continuity of g. Hence we obtain also \( z_{\mathfrak {t}} = 0 \) for all \( \mathfrak {t} > 0\) by iterating the argument and the proof is complete. \(\square \)
Notes
Here we view all random variables as time-dependent, so that the map \( \textbf{R}_{+} \ni t \mapsto (2 \nabla _{\!{\text {sym}}}X_{t}, 2 \nabla _{\textrm{sym}}X_{t} \diamond P_{t}) \) is a continuous path with values in \( \Xi _{\kappa }\).
References
Allez, R., Chouk, K.: The continuous Anderson hamiltonian in dimension two. arXiv preprint (2015). https://arxiv.org/abs/1511.02718
Bahouri, H., Chemin, J.-Y., Danchin, R.: Fourier analysis and nonlinear partial differential equations, vol. 343 of Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences]. Springer, Heidelberg, 2011, xvi+523. https://doi.org/10.1007/978-3-642-16830-7
Bourgain, J.: Invariant measures for the \(2\)D-defocusing nonlinear Schrödinger equation. Comm. Math. Phys. 176(2), 421–445 (1996)
Chandra, A., Chevyrev, I., Hairer, M., Shen, H.: Langevin dynamic for the 2D Yang–Mills measure. Publications mathématiques de l’IHÉS (2022), 1–147.https://arxiv.org/abs/2006.04987
Chandra, A., Chevyrev, I., Hairer, M., Shen, H.: Stochastic quantisation of Yang-Mills-Higgs in 3D (2022). https://arxiv.org/abs/2201.03487
Chevyrev, I.: Stochastic quantisation of Yang-Mills (2022). https://arxiv.org/abs/2202.13359
Chandra, A., Moinat, A., Weber, H: A priori bounds for the \(\phi ^4\) equation in the full sub-critical regime, (2019). https://arxiv.org/abs/1910.13854
Prato, G. Da., Debussche, A.: Two-dimensional Navier-Stokes equations driven by a space-time white noise. J. Funct. Anal. 196, no. 1, 180–210, (2002). https://doi.org/10.1006/jfan.2002.3919
Gubinelli, M., Hofmanová, M.: Global solutions to elliptic and parabolic \(\Phi ^4\) models in Euclidean space. Comm. Math. Phys. 368(3), 1201–1266 (2019). https://doi.org/10.1007/s00220-019-03398-4
Gubinelli, M., Hofmanová, M.: A PDE construction of the Euclidean \(\phi _3^4\) quantum field theory. Comm. Math. Phys. 384(1), 1–75 (2021). https://doi.org/10.1007/s00220-021-04022-0
Gubinelli, M., Imkeller, P., Perkowski, N.: Paracontrolled distributions and singular PDEs. Forum Math. Pi 3, e6, 75. (2015) https://doi.org/10.1017/fmp.2015.2
Gallagher, I., Planchon, F.: On global infinite energy solutions to the Navier-Stokes equations in two dimensions. Archive for Rational Mechanics and Analysis 161(4), 307–337 (2002)
Gubinelli, M., Perkowski, N.: KPZ reloaded. Comm. Math. Phys. 349(1), 165–269 (2017) https://arxiv.org/abs/1508.03877
Hairer, M.: A theory of regularity structures. Invent. Math. 198(2), 269–504 (2014). https://doi.org/10.1007/s00222-014-0505-4
Hairer, M.: Introduction to Malliavin calculus, (2021)
Hairer, M., Stuart, A.M., Voss, J.: Analysis of SPDEs arising in path sampling. II. The nonlinear case. Ann. Appl. Probab. 17(5–6), 1657–1706 (2007). https://doi.org/10.1214/07-AAP441
Hofmanová, M., Zhu, R., Zhu, X.: Global existence and non-uniqueness for 3D Navier–Stokes equations with space-time white noise. arXiv preprint (2021). https://arxiv.org/abs/2112.14093
Hofmanová, M., Zhu, R., Zhu, X.: Global-in-time probabilistically strong and Markov solutions to stochastic 3D Navier–Stokes equations: existence and non-uniqueness. arXiv preprint (2021). https://arxiv.org/abs/2104.09889
Hofmanová, M., Zhu, R., Zhu, X.: A class of supercritical/critical singular stochastic PDEs: existence, non-uniqueness, non-Gaussianity, non-unique ergodicity. arXiv preprint (2022). https://arxiv.org/abs/2205.13378
Hofmanová, M., Zhu, R., Zhu, X.: Non-unique ergodicity for deterministic and stochastic 3D Navier–Stokes and Euler equations. arXiv preprint (2022). https://arxiv.org/abs/2208.08290
Kato, T.: Perturbation theory for linear operators. Classics in Mathematics. Springer-Verlag, Berlin, 1995, xxii+619. Reprint of the 1980 edition
Kenig, C.E., Ponce, G., Vega, L.: Well-posedness and scattering results for the generalized Korteweg-de Vries equation via the contraction principle. Comm. Pure Appl. Math. 46(4), 527–620 (1993). https://doi.org/10.1002/cpa.3160460405
Mourrat, J.-C., Weber, H.: The dynamic \(\Phi ^4_3\) model comes down from infinity. Comm. Math. Phys. 356(3), 673–753 (2017). https://doi.org/10.1007/s00220-017-2997-4
Nelson, E.: A quartic interaction in two dimensions. In Mathematical Theory of Elementary Particles (Proc. Conf., Dedham, Mass., 1965), 69–73. M.I.T. Press, Cambridge, Mass., (1966)
Temam, R.: Navier-Stokes equations: theory and numerical analysis, vol. 343. American Mathematical Soc., (2001)
Zhu, R., Zhu, X.: Strong-Feller property for Navier-Stokes equations driven by space-time white noise. arXiv preprint (2017). https://arxiv.org/abs/1709.09306
Acknowledgements
This article was written in vast majority while TR was employed at Imperial College London. Financial support through the Royal Society research professorship of MH, grant number RP\R1\191065, is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A Function spaces and paraproducts
Appendix A Function spaces and paraproducts
We define the space of Schwartz functions \(\mathcal {S}(\textbf{T}^{2}; \textbf{R}^{d})= \bigcap _{k \in \textbf{N}}C^{k}(\textbf{T}^{2}; \textbf{R}^{d})\) and their topological dual, the set of Schwartz distributions \(\mathcal {S}^{\prime }(\textbf{T}^{2}; \textbf{R}^{d})\). Then the Fourier transform \(\hat{\varphi }\) is defined for any distribution \(\varphi \in \mathcal {S}^{\prime }(\textbf{T}^2 ; \textbf{R}^d)\):
We additionally define the space of mean-free Schwartz distributions \( \mathcal {S}^{\prime }_{\times } (\textbf{T}^{2}; \textbf{R}^{d}) = \{ \varphi \in \mathcal {S}^{\prime } (\textbf{T}^{2}; \textbf{R}^{d} ) \; :\; \hat{\varphi } (0) = 0 \}\). Then, for any \(p\in [1,\infty ], d\in \textbf{N}\) and \(O \subseteq \textbf{R}^{d}\) we denote with \(L^p(\textbf{T}^2;O)\) the Banach space of measurable functions (modulo modifications on a null set) \(\varphi :\textbf{T}^2 \rightarrow \textbf{R}^d\) such that the norm
is finite, with the usual convention for \( p = \infty \). For brevity we write
Next we introduce the scale of mean-free Besov spaces \(\mathcal {B}^{\alpha }_{p,q}(\textbf{T}^{2} ; \textbf{R}^{d}) \subseteq \mathcal {S}^{\prime }_{\times } (\textbf{T}^{2}; \textbf{R}^{d})\), for \(\alpha \in \textbf{R}\), \(p,q \in [1, \infty ]\). Having fixed a \(2-\)dimensional dyadic partition of the unity \(\{\varrho _{j}\}_{j \geqslant -1}\) (see [2]), the spaces \(\mathcal {B}^{\alpha }_{p,q}(\textbf{T}^{2}; \textbf{R}^{d})\) are defined via the norms:
with the Paley block \( \Delta _{i} \varphi \) defined in Section A.1 below. In particular we will distinguish the Bessel potential spaces, corresponding to \( p = q = 2 \):
over which we will use the equivalent norm (recall that we are only considering mean-free functions)
Next we also distinguish the Hölder-Besov spaces
For time-dependent functions we consider the space of Schwartz functions
and its topological dual \(\mathcal {S}^{\prime }(\textbf{R}\times \textbf{T}^{2})\), the space of Schwartz distributions. For time-dependent measurable functions \(\varphi :[0,t] \rightarrow X\) for some \(t>0\) and a Banach space \(X\) we introduce the spaces \(L^{p}_{t} X\), for \(p \in [1, \infty ]\) via the norm
1.1 A.1 Paraproducts
Next consider, for \( \varphi \in \mathcal {S}^{\prime } (\textbf{T}^{2}; \textbf{R}^{d}),\) the Paley block
as well as the paraproducts (the sum is only formal and its convergence has to be justified), for \( \varphi , \psi \in \mathcal {S}^{\prime } (\textbf{T}^{2}; \textbf{R}^{d}) \):
So one can formally decompose the tensor product between two distributions \( \varphi , \psi \) as:
In the hope that no confusion can occur, we will slightly abuse of the notation of paraproducts, allowing it to denote both tensor products as the one we just described, and matrix multiplication (which is just a contraction along some index of the former). In particular, we will consider the situation in which we are give a matrix \( M \in \mathcal {S}^{\prime } (\textbf{T}^{2}; \textbf{M}^{2}) \) and a vector \( \varphi \in \mathcal {S}^{\prime } (\textbf{T}^{2}; \textbf{R}^{2}) \). In this case we write
and similarly all other paraproducts. Note that in this definition 
is not the same as 
. Similarly, for two matrices \( M, N \in \mathcal {S}^{\prime } (\textbf{T}^{2}; \textbf{M}^{2}) \) we define
The following lemma collects the fundamental estimates on paraproducts that we will make use of: these hold both for vector-valued and matrix-valued distributions.
Lemma A.1
(Theorems 2.82 and 2.85 [2]) Fix \(\alpha , \beta \in \textbf{R}\) and \(p, q \in [1, \infty ]\) such that \(\frac{1}{r} = \frac{1}{p} {+} \frac{1}{q} \le 1\). Then uniformly over \(\varphi , \psi \in \mathcal {S}^{\prime }\)
Note that in the lemma above we have set the fine-tuning parameter \( \ell \) in \( \mathcal {B}^{\alpha }_{p, \ell } \) to \( \ell = \infty \). This causes no issues, since by giving up an arbitrarily small regularity we can change the fine-tuning parameter at will. Namely, we will use that for any \( \alpha < \beta \):
For the convenience of the reader we conclude this appendix by recalling the following embedding between Besov spaces in dimension \( d =2 \) (since no other dimension is used), and for arbitrary \( p, q, p^{\prime } \in [1, \infty ] \) and \( \alpha \in \textbf{R}\) such that \( p \leqslant p^{\prime } \):
These are often used in combination with the fact that for \( p = q =2 \) the Besov space \( \mathcal {B}^{\alpha }_{2,2} \) coincides with the Bessel potential space \( H^{\alpha } \).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hairer, M., Rosati, T. Global existence for perturbations of the 2D stochastic Navier–Stokes equations with space-time white noise. Ann. PDE 10, 3 (2024). https://doi.org/10.1007/s40818-023-00165-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40818-023-00165-6