Group Multi-criteria Decision Making Method with Triangular Type-2 Fuzzy Numbers

Abstract

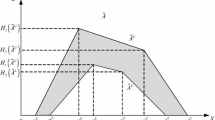
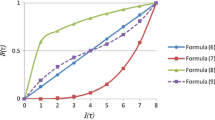
Type-2 fuzzy sets/numbers (T2FSs/T2FNs) attract more and more attention in fuzzy decision field. The existing studies mostly focus on the general properties of T2FS, or interval type-2 fuzzy number whose membership degrees are denoted by intervals. A new form of T2FN named triangular type-2 fuzzy number is proposed, whose primary and secondary memberships both have the continuous triangular feature. For aggregating the triangular type-2 fuzzy information, two operators are also defined. Based on them, a method is developed to handle the duplex linguistic group multi-criteria decision making problems and rank the alternatives. Finally, an example is provided to show the feasibility of the method.

Appendix

The Proof of Property 1

Since the properties (1), (3), (4) are easy to proof, here the property (2) is proofed. As $a_{i} \ge 0$ $\left( {i = 1,2,3} \right)$, from definition 3:

$$\tilde{a}_{1} + \tilde{a}_{2} = \left\langle {\left[ {a_{1} + a_{2} ,b_{1} + b_{2} ,c_{1} + c_{2} } \right];\left[ {\frac{{\left\| {\tilde{a}_{1} } \right\|\mu_{1}^{L} + \left\| {\tilde{a}_{2} } \right\|\mu_{2}^{L} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\|}},\frac{{\left\| {\tilde{a}_{1} } \right\|\mu_{1}^{M} + \left\| {\tilde{a}_{2} } \right\|\mu_{2}^{M} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\|}},\frac{{\left\| {\tilde{a}_{1} } \right\|\mu_{1}^{R} + \left\| {\tilde{a}_{2} } \right\|\mu_{2}^{R} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\|}}} \right]} \right\rangle$$

Thus,

$$(\tilde{a}_{1} + \tilde{a}_{2} ) + \tilde{a}_{3} = \left\langle {[a_{1} + a_{2} ,b_{1} + b_{2} ,c_{1} + c_{2} ];\left[ {\frac{{\left\| {\tilde{a}_{1} } \right\|\mu _{1}^{L} + \left\| {\tilde{a}_{2} } \right\|\mu _{2}^{L} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\|}},\frac{{\left\| {\tilde{a}_{1} } \right\|\mu _{1}^{M} + \left\| {\tilde{a}_{2} } \right\|\mu _{2}^{M} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\|}},\frac{{\left\| {\tilde{a}_{1} } \right\|\mu _{1}^{R} + \left\| {\tilde{a}_{2} } \right\|\mu _{2}^{R} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\|}}} \right]} \right\rangle + \left\langle {\left[ {a_{3} ,b_{3} ,c_{3} } \right];\left[ {\mu _{3}^{L} ,\mu _{3}^{M} ,\mu _{3}^{R} } \right]} \right\rangle = \left\langle [(a_{1} + a_{2} ) + a_{3} ,(b_{1} + b_{2} ) + b_{3} ,(c_{1} + c_{2} ) + c_{3} ];\left[\frac{{\frac{1}{4}(a_{1} + a_{2} + c_{1} + c_{2} + 2b_{1} + 2b_{2} ) \cdot \frac{{\left\| {\tilde{a}_{1} } \right\|\mu _{{\tilde{a}_{1} }}^{L} + \left\| {\tilde{a}_{2} } \right\|\mu _{{\tilde{a}_{2} }}^{L} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\|}} + \left\| {\tilde{a}_{3} } \right\|\mu _{{\tilde{a}_{3} }}^{L} }}{{\frac{1}{4}(a_{1} + a_{2} + c_{1} + c_{2} + 2b_{1} + 2b_{2} ) + \frac{1}{4}(a_{3} + c_{3} + 2b_{3} )}}, \frac{{\frac{1}{4}(a_{1} + a_{2} + c_{1} + c_{2} + 2b_{1} + 2b_{2} ) \cdot \frac{{\left\| {\tilde{a}_{1} } \right\|\mu _{{\tilde{a}_{1} }}^{M} + \left\| {\tilde{a}_{2} } \right\|\mu _{{\tilde{a}_{2} }}^{M} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\|}} + \left\| {\tilde{a}_{3} } \right\|\mu _{{\tilde{a}_{3} }}^{M} }}{{\frac{1}{4}(a_{1} + a_{2} + c_{1} + c_{2} + 2b_{1} + 2b_{2} ) + \frac{1}{4}(a_{3} + c_{3} + 2b_{3} )}},\frac{{\frac{1}{4}(a_{1} + a_{2} + c_{1} + c_{2} + 2b_{1} + 2b_{2} ) \cdot \frac{{\left\| {\tilde{a}_{1} } \right\|\mu _{{\tilde{a}_{1} }}^{R} + \left\| {\tilde{a}_{2} } \right\|\mu _{{\tilde{a}_{2} }}^{R} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\|}} + \left\| {\tilde{a}_{3} } \right\|\mu _{{\tilde{a}_{3} }}^{R} }}{{\frac{1}{4}(a_{1} + a_{2} + c_{1} + c_{2} + 2b_{1} + 2b_{2} ) + \frac{1}{4}(a_{3} + c_{3} + 2b_{3} )}}\right] \right\rangle = \left\langle [a_{1} + a_{2} + a_{3} ,b_{1} + b_{2} + b_{3} ,c_{1} + c_{2} + c_{3} ];\left[\frac{{\left\| {\tilde{a}_{1} } \right\|\mu _{{\tilde{a}_{1} }}^{L} + \left\| {\tilde{a}_{2} } \right\|\mu _{{\tilde{a}_{2} }}^{L} + \left\| {\tilde{a}_{3} } \right\|\mu _{{\tilde{a}_{3} }}^{L} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\| + \left\| {\tilde{a}_{3} } \right\|}},\frac{{\left\| {\tilde{a}_{1} } \right\|\mu _{{\tilde{a}_{1} }}^{M} + \left\| {\tilde{a}_{2} } \right\|\mu _{{\tilde{a}_{2} }}^{M} + \left\| {\tilde{a}_{3} } \right\|\mu _{{\tilde{a}_{3} }}^{M} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\| + \left\| {\tilde{a}_{3} } \right\|}}, \frac{{\left\| {\tilde{a}_{1} } \right\|\mu _{{\tilde{a}_{1} }}^{R} + \left\| {\tilde{a}_{2} } \right\|\mu _{{\tilde{a}_{2} }}^{R} + \left\| {\tilde{a}_{3} } \right\|\mu _{{\tilde{a}_{3} }}^{R} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\| + \left\| {\tilde{a}_{3} } \right\|}}\right]\right\rangle$$

Similarly,

$$\begin{aligned} \tilde{a}_{1} + (\tilde{a}_{2} + \tilde{a}_{3} ) &= \left\langle {\left[ {a_{1} ,b_{1} ,c_{1} } \right];\left[ {\mu _{1}^{L} ,\mu _{1}^{M} ,\mu _{1}^{R} } \right]} \right\rangle\,+\,\left\langle {[a_{2} + a_{3} ,b_{2} + b_{3} ,c_{2} + c_{3} ]; \left[ {\frac{{\left\| {\tilde{a}_{2} } \right\|\mu _{2}^{L} + \left\| {\tilde{a}_{3} } \right\|\mu _{3}^{L} }}{{\left\| {\tilde{a}_{2} } \right\| + \left\| {\tilde{a}_{3} } \right\|}},\frac{{\left\| {\tilde{a}_{2} } \right\|\mu _{2}^{M} + \left\| {\tilde{a}_{3} } \right\|\mu _{3}^{M} }}{{\left\| {\tilde{a}_{2} } \right\| + \left\| {\tilde{a}_{3} } \right\|}},\frac{{\left\| {\tilde{a}_{2} } \right\|\mu _{2}^{R} + \left\| {\tilde{a}_{3} } \right\|\mu _{3}^{R} }}{{\left\| {\tilde{a}_{2} } \right\| + \left\| {\tilde{a}_{3} } \right\|}}} \right]} \right\rangle \\ & = \left\langle {\left[ {a_{1} + a_{2} + a_{3} ,b_{1} + b_{2} + b_{3} ,c_{1} + c_{2} + c_{3} } \right];\left[ \begin{aligned} \frac{{\left\| {\tilde{a}_{1} } \right\|\mu_{{\tilde{a}_{1} }}^{L} + \left\| {\tilde{a}_{2} } \right\|\mu_{{\tilde{a}_{2} }}^{L} + \left\| {\tilde{a}_{3} } \right\|\mu_{{\tilde{a}_{3} }}^{L} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\| + \left\| {\tilde{a}_{3} } \right\|}},\frac{{\left\| {\tilde{a}_{1} } \right\|\mu_{{\tilde{a}_{1} }}^{M} + \left\| {\tilde{a}_{2} } \right\|\mu_{{\tilde{a}_{2} }}^{M} + \left\| {\tilde{a}_{3} } \right\|\mu_{{\tilde{a}_{3} }}^{M} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\| + \left\| {\tilde{a}_{3} } \right\|}}, \hfill \\ \quad \frac{{\left\| {\tilde{a}_{1} } \right\|\mu_{{\tilde{a}_{1} }}^{R} + \left\| {\tilde{a}_{2} } \right\|\mu_{{\tilde{a}_{2} }}^{R} + \left\| {\tilde{a}_{3} } \right\|\mu_{{\tilde{a}_{3} }}^{R} }}{{\left\| {\tilde{a}_{1} } \right\| + \left\| {\tilde{a}_{2} } \right\| + \left\| {\tilde{a}_{3} } \right\|}} \hfill \\ \end{aligned} \right]} \right\rangle \\ \end{aligned}$$

So $(\tilde{a}_{1} + \tilde{a}_{2} ) + \tilde{a}_{3} = \tilde{a}_{1} + (\tilde{a}_{2} + \tilde{a}_{3} )$.□

The Proof of Property 3

$0 \le P(\tilde{a}_{1} \ge \tilde{a}_{2} ) \le 1$ is easy to proof.

$$\begin{aligned} P(\tilde{a}_{1} \ge \tilde{a}_{1} ) & = \frac{{\hbox{min} \left\{ {l_{1} \mu_{1} + l_{1} \mu_{1} ,\hbox{max} ((b_{1} + c_{1} )\mu_{1} - (a_{1} + b_{1} )\mu_{1} ,0)} \right\}}}{{l_{1} \mu_{1} + l_{1} \mu_{1} }} \\ & = \frac{{\hbox{min} \left\{ {l_{1} \mu_{1} + l_{1} \mu_{1} ,\hbox{max} (\mu_{1} l_{1} ,0)} \right\}}}{{l_{1} \mu_{1} + l_{1} \mu_{1} }} = \frac{{l_{1} \mu_{1} }}{{l_{1} \mu_{1} + l_{1} \mu_{1} }} = 0.5. \\ \end{aligned}$$

□

The Proof of Property 4

$$P(\tilde{a}_{1} \ge \tilde{a}_{2} ) = \frac{{\hbox{min} \left\{ {l_{1} \mu_{1} + l_{2} \mu_{2} ,\hbox{max} ((b_{1} + c_{1} )\mu_{1} - (a_{2} + b_{2} )\mu_{2} ,0)} \right\}}}{{l_{1} \mu_{1} + l_{2} \mu_{2} }}$$

$$P(\tilde{a}_{2} \ge \tilde{a}_{1} ) = \frac{{\hbox{min} \left\{ {l_{1} \mu_{1} + l_{2} \mu_{2} ,\hbox{max} ((b_{2} + c_{2} )\mu_{2} - (a_{1} + b_{1} )\mu_{1} ,0)} \right\}}}{{l_{1} \mu_{1} + l_{2} \mu_{2} }}$$

• (1) If $(b_{1} + c_{1} )\mu_{1} \le (a_{2} + b_{2} )\mu_{2}$, So, $(a_{1} + b_{1} )\mu_{1} \le (b_{1} + c_{1} )\mu_{1} \le (a_{2} + b_{2} )\mu_{2} \le (b_{2} + c_{2} )\mu_{2}$,

  $$P(\tilde{a}_{1} \ge \tilde{a}_{2} ) = 0,$$
  $$\begin{aligned} P(\tilde{a}_{2} \ge \tilde{a}_{1} ) = \frac{{\hbox{min} \left\{ {l_{1} \mu_{1} + l_{2} \mu_{2} ,(b_{2} + c_{2} )\mu_{2} - (a_{1} + b_{1} )\mu_{1} } \right\}}}{{l_{1} \mu_{1} + l_{2} \mu_{2} }} \hfill \\ \quad \quad \quad \quad \,\, = \frac{{\hbox{min} \left\{ {(c_{1} - a_{1} )\mu_{1} + (c_{2} - a_{2} )\mu_{2} ,(b_{2} + c_{2} )\mu_{2} - (a_{1} + b_{1} )\mu_{1} } \right\}}}{{(c_{1} - a_{1} )\mu_{1} + (c_{2} - a_{2} )\mu_{2} }}. \hfill \\ \end{aligned}$$

  Because $[(c_{1} - a_{1} )\mu_{1} + (c_{2} - a_{2} )\mu_{2} ] - [(b_{2} + c_{2} )\mu_{2} - (a_{1} + b_{1} )\mu_{1} ] = (\mu_{1} c_{1} - \mu_{2} a_{2} ) - (\mu_{2} b_{2} - \mu_{1} b_{1} )$, and $(\mu_{1} c_{1} - \mu_{2} a_{2} ) - (\mu_{2} b_{2} - \mu_{1} b_{1} ) = (b_{1} + c_{1} )\mu_{1} - (a_{2} + b_{2} )\mu_{2} \le 0$, so $\mu_{1} c_{1} - \mu_{2} a_{2} \le \mu_{2} b_{2} - \mu_{1} b_{1}$,$(c_{1} - a_{1} )\mu_{1} + (c_{2} - a_{2} )\mu_{2} \le (b_{2} + c_{2} )\mu_{2} - (a_{1} + b_{1} )\mu_{1}$. That is $P(\tilde{a}_{2} \ge \tilde{a}_{1} ) = 1$. So $P(\tilde{a}_{1} \ge \tilde{a}_{2} ) + P(\tilde{a}_{2} \ge \tilde{a}_{1} ) = 1.$

• (2) If $(b_{1} + c_{1} )\mu_{1} > (a_{2} + b_{2} )\mu_{2}$, $(b_{2} + c_{2} )\mu_{2} \le (a_{1} + b_{1} )\mu_{1}$, it is the same as 1)

• (3) If $(b_{1} + c_{1} )\mu_{1} > (a_{2} + b_{2} )\mu_{2}$, $(b_{2} + c_{2} )\mu_{2} > (a_{1} + b_{1} )\mu_{1}$, then

  $$\begin{aligned} P(\tilde{a}_{1} \ge \tilde{a}_{2} ) & = \frac{{\hbox{min} \left\{ {(c_{1} - a_{1} )\mu_{1} + (c_{2} - a_{2} )\mu_{2} ,(b_{1} + c_{1} )\mu_{1} - (a_{2} + b_{2} )\mu_{2} } \right\}}}{{(c_{1} - a_{1} )\mu_{1} + (c_{2} - a_{2} )\mu_{2} }} \\ & = \frac{{\hbox{min} \left\{ {c_{1} \mu_{1} - a_{1} \mu_{1} + c_{2} \mu_{2} - a_{2} \mu_{2} ,b_{1} \mu_{1} + c_{1} \mu_{1} - a_{2} \mu_{2} - b_{2} \mu_{2} } \right\}}}{{(c_{1} - a_{1} )\mu_{1} + (c_{2} - a_{2} )\mu_{2} }}. \\ \end{aligned}$$

  Because $(c_{1} \mu_{1} - a_{1} \mu_{1} + c_{2} \mu_{2} - a_{2} \mu_{2} ) - (b_{1} \mu_{1} + c_{1} \mu_{1} - a_{2} \mu_{2} - b_{2} \mu_{2} ) = c_{2} \mu_{2} - a_{1} \mu_{1} - b_{1} \mu_{1} + b_{2} \mu_{2}$, and $c_{2} \mu_{2} - a_{1} \mu_{1} - b_{1} \mu_{1} + b_{2} \mu_{2} = (b_{2} + c_{2} )\mu_{2} - (a_{1} + b_{1} )\mu_{1} > 0$, so $c_{1} \mu_{1} - a_{1} \mu_{1} + c_{2} \mu_{2} - a_{2} \mu_{2} > b_{1} \mu_{1} + c_{1} \mu_{1} - a_{2} \mu_{2} - b_{2} \mu_{2}$, that is $P(\tilde{a}_{1} \ge \tilde{a}_{2} ) = \frac{{b_{1} \mu_{1} + c_{1} \mu_{1} - a_{2} \mu_{2} - b_{2} \mu_{2} }}{{(c_{1} - a_{1} )\mu_{1} + (c_{2} - a_{2} )\mu_{2} }}$. There also have $P(\tilde{a}_{2} \ge \tilde{a}_{1} ) = \frac{{(b_{2} + c_{2} )\mu_{2} - (a_{1} + b_{1} )\mu_{1} }}{{l_{1} \mu_{1} + l_{2} \mu_{2} }} = \frac{{b_{2} \mu_{2} + c_{2} \mu_{2} - a_{1} \mu_{1} - b_{1} \mu_{1} }}{{(c_{1} - a_{1} )\mu_{1} + (c_{2} - a_{2} )\mu_{2} }}$, and $P(\tilde{a}_{1} \ge \tilde{a}_{2} ) + P(\tilde{a}_{2} \ge \tilde{a}_{1} )$ $= \frac{{b_{1} \mu_{1} + c_{1} \mu_{1} - a_{2} \mu_{2} - b_{2} \mu_{2} }}{{(c_{1} - a_{1} )\mu_{1} + (c_{2} - a_{2} )\mu_{2} }} + \frac{{b_{2} \mu_{2} + c_{2} \mu_{2} - a_{1} \mu_{1} - b_{1} \mu_{1} }}{{(c_{1} - a_{1} )\mu_{1} + (c_{2} - a_{2} )\mu_{2} }} = \frac{{c_{1} \mu_{1} - a_{2} \mu_{2} + c_{2} \mu_{2} - a_{1} \mu_{1} }}{{(c_{1} - a_{1} )\mu_{1} + (c_{2} - a_{2} )\mu_{2} }}$ $= 1$. So $P(\tilde{a}_{1} \ge \tilde{a}_{2} ) + P(\tilde{a}_{2} \ge \tilde{a}_{1} ) = 1$. □

The Proof of Theorem 2

Obviously, from definition 3, the sum of PTT2FNs is also a PTT2FN. In the following, equation (2) is proved by using mathematical induction on $n$.

• (1) For $n = 2$, since

  $$\begin{aligned} &\sum\limits_{i = 1}^{2} {\omega_{i} \tilde{a}_{i} } = \langle \left[ {\omega_{1} a_{1} + \omega_{2} a_{2} ,\omega_{1} b_{1} + \omega_{2} b_{2} ,\omega_{1} c_{1} + \omega_{2} c_{2} } \right]; \\ &\left[ {\frac{{\left\| {\tilde{a}_{1} } \right\|\omega_{1} \mu_{1}^{L} + \left\| {\tilde{a}_{2} } \right\|\omega_{2} \mu_{2}^{L} }}{{\omega_{1} \left\| {\tilde{a}_{1} } \right\| + \omega_{2} \left\| {\tilde{a}_{2} } \right\|}},\frac{{\left\| {\tilde{a}_{1} } \right\|\omega_{1} \mu_{1}^{M} + \left\| {\tilde{a}_{2} } \right\|\omega_{2} \mu_{2}^{M} }}{{\omega_{1} \left\| {\tilde{a}_{1} } \right\| + \omega_{2} \left\| {\tilde{a}_{2} } \right\|}},\frac{{\left\| {\tilde{a}_{1} } \right\|\omega_{1} \mu_{1}^{R} + \left\| {\tilde{a}_{2} } \right\|\omega_{2} \mu_{2}^{R} }}{{\omega_{1} \left\| {\tilde{a}_{1} } \right\| + \omega_{2} \left\| {\tilde{a}_{2} } \right\|}}} \right]\rangle \\ \end{aligned}$$

  then the Eq. (2) is clearly true.

• (2) If Eq. (2) holds for $n = k$, that is

  $$\sum\limits_{i = 1}^{k} {\omega_{i} \tilde{a}_{i} = \left\langle {\left[ {\sum\limits_{i = 1}^{k} {\omega_{i} a_{i}^{{}} } ,\sum\limits_{i = 1}^{k} {\omega_{i} b_{i} } ,\sum\limits_{i = 1}^{k} {\omega_{i} c_{i} } } \right];\left[ {\frac{{\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} \mu_{i}^{L} } }}{{\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} } }},\frac{{\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} \mu_{i}^{M} } }}{{\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} } }},\frac{{\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} \mu_{i}^{R} } }}{{\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} } }}} \right]} \right\rangle }$$

Then, when $n = k + 1$, by the operational laws in Definition 3, there is:

$$\sum\limits_{i = 1}^{k + 1} {\omega_{i} \tilde{a}_{i} } = \sum\limits_{i = 1}^{k} {\omega_{i} \tilde{a}_{i} } + \omega_{k + 1} \tilde{a}_{k + 1} = \left\langle \left[ {\sum\limits_{i = 1}^{k} {\omega_{i} a_{i} } ,\sum\limits_{i = 1}^{k} {\omega_{i} b_{i} } ,\sum\limits_{i = 1}^{k} {\omega_{i} c_{i} } } \right]; \left[ {\frac{{\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} \mu_{i}^{L} } }}{{\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} } }},\frac{{\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} \mu_{i}^{M} } }}{{\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} } }},\frac{{\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} \mu_{i}^{R} } }}{{\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} } }}} \right] \right\rangle + \left\langle {\left[ {\omega_{k + 1} a_{k + 1} ,\omega_{k + 1} b_{k + 1} ,\omega_{k + 1} c_{k + 1} } \right];\mu_{k + 1}^{L} ,\mu_{k + 1}^{M} ,\mu_{k + 1}^{R} } \right\rangle = \left\langle \left[ {\sum\limits_{i = 1}^{k} {\omega_{i} a_{i} } + \omega_{k + 1} a_{k + 1} ,\sum\limits_{i = 1}^{k} {\omega_{i} b_{i} } + \omega_{k + 1} b_{k + 1} ,\sum\limits_{i = 1}^{k} {\omega_{i} c_{i} } + \omega_{k + 1} c_{k + 1} } \right]; \left[\frac{{\frac{{\left( {\sum\nolimits_{i = 1}^{k} {a_{i} } + 2\sum\nolimits_{i = 1}^{k} {b_{i} } + \sum\nolimits_{i = 1}^{k} {c_{i} } } \right)\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\mu_{i}^{L} } }}{{4\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|} }}\omega_{i} + \frac{1}{4}(a_{k + 1} + 2b_{k + 1} + c_{k + 1} )\omega_{k + 1} \mu_{k + 1}^{L} }}{{\frac{1}{4}\left( {\sum\nolimits_{i = 1}^{k} {a_{i} } + 2\sum\nolimits_{i = 1}^{k} {b_{i} } + \sum\nolimits_{i = 1}^{k} {c_{i} } } \right)\omega_{i} + \frac{1}{4}(a_{k + 1} + 2b_{k + 1} + c_{k + 1} )\omega_{k + 1} }}, \frac{{\frac{{\left( {\sum\nolimits_{i = 1}^{k} {a_{i} } + 2\sum\nolimits_{i = 1}^{k} {b_{i} } + \sum\nolimits_{i = 1}^{k} {c_{i} } } \right)\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\mu_{i}^{M} } }}{{4\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|} }}\omega_{i} + \frac{1}{4}(a_{k + 1} + 2b_{k + 1} + c_{k + 1} )\omega_{k + 1} \mu_{k + 1}^{M} }}{{\frac{1}{4}\left( {\sum\nolimits_{i = 1}^{k} {a_{i} } + 2\sum\nolimits_{i = 1}^{k} {b_{i} } + \sum\nolimits_{i = 1}^{k} {c_{i} } } \right)\omega_{i} + \frac{1}{4}(a_{k + 1} + 2b_{k + 1} + c_{k + 1} )\omega_{k + 1} }}, \frac{{\frac{{\left( {\sum\nolimits_{i = 1}^{k} {a_{i} } + 2\sum\nolimits_{i = 1}^{k} {b_{i} } + \sum\nolimits_{i = 1}^{k} {c_{i} } } \right)\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\mu_{i}^{R} } }}{{4\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|} }}\omega_{i} + \frac{1}{4}(a_{k + 1} + 2b_{k + 1} + c_{k + 1} )\omega_{k + 1} \mu_{k + 1}^{R} }}{{\frac{1}{4}\left( {\sum\nolimits_{i = 1}^{k} {a_{i} } + 2\sum\nolimits_{i = 1}^{k} {b_{i} } + \sum\nolimits_{i = 1}^{k} {c_{i} } } \right)\omega_{i} + \frac{1}{4}(a_{k + 1} + 2b_{k + 1} + c_{k + 1} )\omega_{k + 1} }}\right] \right\rangle = \left\langle \left[\sum\limits_{i = 1}^{k + 1} {\omega_{i} a_{i} } ,\sum\limits_{i = 1}^{k + 1} {\omega_{i} b_{i} } ,\sum\limits_{i = 1}^{k + 1} {\omega_{i} c_{i} } \right];\left[\frac{{\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} \mu_{i}^{L} } + \frac{1}{4}(a_{k + 1} + 2b_{k + 1} + c_{k + 1} )\omega_{k + 1} \mu_{k + 1}^{L} }}{{\frac{1}{4}\left( {\sum\nolimits_{i = 1}^{k} {\omega_{i} a_{i} } + \omega_{k + 1} a_{k + 1} + 2\sum\nolimits_{i = 1}^{k} {\omega_{i} b_{i} } + 2\omega_{k + 1} b_{k + 1} + \sum\nolimits_{i = 1}^{k} {\omega_{i} c_{i} } + \omega_{k + 1} c_{k + 1} } \right)}}, \frac{{\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} \mu_{i}^{M} } + \frac{1}{4}(a_{k + 1} + 2b_{k + 1} + c_{k + 1} )\omega_{k + 1} \mu_{k + 1}^{M} }}{{\frac{1}{4}\left( {\sum\nolimits_{i = 1}^{k} {\omega_{i} a_{i} } + \omega_{k + 1} a_{k + 1} + 2\sum\nolimits_{i = 1}^{k} {\omega_{i} b_{i} } + 2\omega_{k + 1} b_{k + 1} + \sum\nolimits_{i = 1}^{k} {\omega_{i} c_{i} } + \omega_{k + 1} c_{k + 1} } \right)}}, \frac{{\sum\nolimits_{i = 1}^{k} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} \mu_{i}^{R} } + \frac{1}{4}(a_{k + 1} + 2b_{k + 1} + c_{k + 1} )\omega_{k + 1} \mu_{k + 1}^{R} }}{{\frac{1}{4}\left( {\sum\nolimits_{i = 1}^{k} {\omega_{i} a_{i} } + \omega_{k + 1} a_{k + 1} + 2\sum\nolimits_{i = 1}^{k} {\omega_{i} b_{i} } + 2\omega_{k + 1} b_{k + 1} + \sum\nolimits_{i = 1}^{k} {\omega_{i} c_{i} } + \omega_{k + 1} c_{k + 1} } \right)}}\right] \right\rangle = \left\langle \left[\sum\limits_{i = 1}^{k + 1} {\omega_{i} a_{i} } ,\sum\limits_{i = 1}^{k + 1} {\omega_{i} b_{i} } ,\sum\limits_{i = 1}^{k + 1} {\omega_{i} c_{i} } \right];\left[\frac{{\sum\nolimits_{i = 1}^{k} {\frac{{a_{i} + 2b_{i} + c_{i} }}{4}\omega_{i} \mu_{i}^{L} } + \frac{{a_{k + 1} + 2b_{k + 1} + c_{k + 1} }}{4}\omega_{k + 1} \mu_{k + 1}^{L} }}{{\frac{1}{4}\left( {\sum\nolimits_{i = 1}^{k + 1} {\omega_{i} a_{i} } + 2\sum\nolimits_{i = 1}^{k + 1} {\omega_{i} b_{i} } + \sum\nolimits_{i = 1}^{k + 1} {\omega_{i} c_{i} } } \right)}}, \frac{{\sum\nolimits_{i = 1}^{k} {\frac{{a_{i} + 2b_{i} + c_{i} }}{4}\omega_{i} \mu_{i}^{M} } + \frac{{a_{k + 1} + 2b_{k + 1} + c_{k + 1} }}{4}\omega_{k + 1} \mu_{k + 1}^{M} }}{{\frac{1}{4}\left( {\sum\nolimits_{i = 1}^{k + 1} {\omega_{i} a_{i} } + 2\sum\nolimits_{i = 1}^{k + 1} {\omega_{i} b_{i} } + \sum\nolimits_{i = 1}^{k + 1} {\omega_{i} c_{i} } } \right)}},\;\frac{{\sum\nolimits_{i = 1}^{k} {\frac{{a_{i} + 2b_{i} + c_{i} }}{4}\omega_{i} \mu_{i}^{R} } + \frac{{a_{k + 1} + 2b_{k + 1} + c_{k + 1} }}{4}\omega_{k + 1} \mu_{k + 1}^{R} }}{{\frac{1}{4}\left( {\sum\nolimits_{i = 1}^{k + 1} {\omega_{i} a_{i} } + 2\sum\nolimits_{i = 1}^{k + 1} {\omega_{i} b_{i} } + \sum\nolimits_{i = 1}^{k + 1} {\omega_{i} c_{i} } } \right)}}\right] \right\rangle = \left\langle {\left[ {\sum\limits_{i = 1}^{k + 1} {\omega_{i} a_{i} } ,\sum\limits_{i = 1}^{k + 1} {\omega_{i} b_{i} } ,\sum\limits_{i = 1}^{k + 1} {\omega_{i} c_{i} } } \right];\frac{{\sum\nolimits_{i = 1}^{k + 1} {\frac{{a_{i} + 2b_{i} + c_{i} }}{4}\omega_{i} \mu_{i}^{L} } }}{{\sum\nolimits_{i = 1}^{k + 1} {\omega_{i} \left\| {\tilde{a}_{i} } \right\|} }},\frac{{\sum\nolimits_{i = 1}^{k + 1} {\frac{{a_{i} + 2b_{i} + c_{i} }}{4}\omega_{i} \mu_{i}^{M} } }}{{\sum\nolimits_{i = 1}^{k + 1} {\omega_{i} \left\| {\tilde{a}_{i} } \right\|} }},\frac{{\sum\nolimits_{i = 1}^{k + 1} {\frac{{a_{i} + 2b_{i} + c_{i} }}{4}\omega_{i} \mu_{i}^{R} } }}{{\sum\nolimits_{i = 1}^{k + 1} {\omega_{i} \left\| {\tilde{a}_{i} } \right\|} }}} \right\rangle = \left\langle {\left[ {\sum\limits_{i = 1}^{k + 1} {\omega_{i} a_{i} } ,\sum\limits_{i = 1}^{k + 1} {\omega_{i} b_{i} } ,\sum\limits_{i = 1}^{k + 1} {\omega_{i} c_{i} } } \right];\left[ {\frac{{\sum\nolimits_{i = 1}^{k + 1} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} \mu_{i}^{L} } }}{{\sum\nolimits_{i = 1}^{k + 1} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} } }},\frac{{\sum\nolimits_{i = 1}^{k + 1} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} \mu_{i}^{M} } }}{{\sum\nolimits_{i = 1}^{k + 1} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} } }},\frac{{\sum\nolimits_{i = 1}^{k + 1} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} \mu_{i}^{R} } }}{{\sum\nolimits_{i = 1}^{k + 1} {\left\| {\tilde{a}_{i} } \right\|\omega_{i} } }}} \right]} \right\rangle.$$

i.e. equation (2) holds for $n = k + 1$.

Therefore, based on (1) and (2), Eq. (2) holds for all $n \in N$, which completes the proof.□