An epidemic model of childhood disease dynamics with maturation delay and latent period of infection

Abstract

In the present study, an epidemic model is proposed with maturation delay and latent period of infection, keeping in view the childhood disease dynamics and studied the asymptotic behavior of the model for all the feasible equilibrium states. The criterion for local stability of the system around steady states are established in terms of delay, latent period and system parameters. Further explored the possibility of Hopf bifurcation at the endemic equilibrium state and threshold is determined. We also performed the sensitivity analysis of the state variables at the endemic equilibrium state with respect to the model parameters and identified the respective sensitive indices. Further numerical simulations have been carried out to justify our analytic findings.

Introduction

Epidemics is defined as a rapid spread of a infectious disease that infects a large portion of the population in a particular region and this study of disease dynamics is a dominating theme for many biologists and mathematicians (Singh et al. 2016; Samanta 2010; Zhang et al. 2013; Xu and Ma 2010; Zhou and Cui 2011; Kang and Fu 2015; Upadhyay and Roy 2014; Bansal and Meyers 2012; Liu et al. 2013; Gao et al. 2013; Tharakaraman et al. 2013; Chao et al. 2012; Safi and Gumel 2013; Hu et al. 2012, 2014; Alexander and Moghadas 2005; Kaddar et al. 2010; Zhang et al. 2009; Samsuzzoha et al. 2013; Sahu and Dhar 2012; He et al. 2013; Sun et al. 2011; Liu et al. 2007; Tchuenche et al. 2011; Liu and Cui 2008; Cui et al. 2008a, b; Funk et al. 2009). Further, there are a number of diseases, which affects mostly the children, for example, Rubella, Measles, Chickenpox, Polio, Mumps, etc., because pre-mature (child) population is more prone to the diseases than the mature (adult) population Reef et al. (2002). Therefore, in disease dynamics the population can be divided into two major categories: pre-mature population and mature population. The pre-mature population takes a constant time to become mature and this constant time is called maturation delay. Also, in disease dynamics, disease cannot spread instantaneously, it will take some time in the host body before the outbreak and that time period is known as the latent period of the particular disease. The simplest disease models cannot capture the rich variety of dynamics and the inclusion of temporal delays in these models makes them more realistic (Beretta and Takeuchi 1995; Brauer 1990; Jin and Ma 2006; Ma et al. 2004).

Keeping in view of the childhood disease dynamics, in this paper, we proposed and analyzed an epidemic model incorporating maturation delay and latent period of infection. This paper is organized as follows: in Sect. 2, formulation of epidemic model is presented. In Sect. 3, positivity and boundedness of the system has been obtained. In Sect. 4, the system is analyzed for the asymptotic stability at all the feasible equilibrium states and obtained the conditions for the existence of Hopf bifurcation at the endemic equilibrium state. In Sect. 5, the sensitivity analysis of the state variables at endemic equilibrium state with respect to model parameters is performed. In Sect. 6, we presented some numerical simulations to support our analytical findings and in the last section, a brief conclusion is given.

Formulation of mathematical model

The assumptions of the proposed model are:

• (i) The population exhibit age structure and the total population at time t is divided into three mutually exclusive compartments, namely, pre-mature (P), mature (M) and infected (I).

• (ii) $\tau _1$ is maturation delay (i.e. the pre-mature period) and $d_1$ is the death rate of pre-mature population. The transformation from pre-mature to mature population is $\gamma e^{-d_1 \tau _1} M(t-\tau _1)$, where $\gamma$ is the birth rate of pre-mature, who was born at time $t-\tau _1$ and survive at time t.

• (iii) $\tau _2$ is a latent period of infection.

• (iv) No vertical transmission of the disease from mature to pre-mature compartment.

• (v) Treatment limitation is shown as the overcrowding in disease compartment.

• (vi) Resource limitation is shown as the overcrowding in mature compartment.

The proposed system is of the form:

$$\begin{aligned} \frac{dP}{dt}= & \,\gamma M-d_1 P-\gamma e^{-d_1 \tau _1}M(t-\tau _1)-\alpha P(t-\tau _2)I, \end{aligned}$$

(1)

$$\begin{aligned} \frac{dM}{dt}= & \,\gamma e^{-d_1 \tau _1}M(t-\tau _1)-d_2 M-\beta _1 M^2,\end{aligned}$$

(2)

$$\begin{aligned} \frac{dI}{dt}= & \,\alpha P(t-\tau _2)I-d_3 I-\beta _2 I^2, \end{aligned}$$

(3)

with initial conditions:

$$\begin{aligned} {P}(\theta )=\phi _1(\theta ),\ {M}(\theta )=\phi _2(\theta ),\ {I}(\theta )=\phi _3(\theta ),\quad \phi _1(0)>0,\ \phi _2(0)>0,\ \phi _3(0)>0, \end{aligned}$$

where $\theta \in [-\tau ,0]$ and $\phi _1(\theta )$, $\phi _2(\theta )$, $\phi _3(\theta )$ $\in \mathcal {C}([-\tau ,0], R_+^3)$, the Banach space of continuous functions mapping the interval $[-\tau ,0]$ into $R_+^3$, where $R_+^3=\{(x_1, x_2, x_3): x_i\ge 0, i=1,2,3\}.$

Here $d_2$ and $d_3$ are the death rates of mature and infected populations respectively; $\alpha$ is the rate of infection to the pre-mature individuals; $\beta _1$ and $\beta _2$ are respectively the overcrowding rates of mature and infected individuals.

Positivity and boundedness of the system

We state and prove the following lemmas for the positivity and boundedness of the solution of the system (1) (2) (3):

Lemma 1

The solution of the system (1)-(3) with initial conditions are positive, for all $t\ge 0$.

Proof

Let (P(t), M(t), I(t)) be a solution of the system (1)-(3) with initial conditions. Let us consider I(t) for $t\in [0,\tau ^*]$, where $\tau ^*=min\{\tau _1,\tau _2\}$. We obtain from the equation (3) that

$$\begin{aligned} \frac{dI}{dt}\ge -d_3I-\beta _2 I^2, \end{aligned}$$

it follows that

$$\begin{aligned} I(t)\ge \frac{d_3 I(0)}{\beta _2 I(0)(e^{d_3 t}-1)+d_3 e^{d_3 t} }>0. \end{aligned}$$

For $t\in [0,\tau ^*]$, the equation (2) can be rewritten as

$$\begin{aligned} \frac{dM}{dt}\ge -d_2 M-\beta _1 M^2, \end{aligned}$$

which implies that

$$\begin{aligned} M(t)\ge \frac{d_2 M(0)}{\beta _1 M(0)(e^{d_2 t}-1)+d_2 e^{d_2 t} }>0. \end{aligned}$$

The equation (1) for $t\in [0,\tau ^*]$ can be rewritten as

$$\begin{aligned} \frac{dP}{dt}\ge -d_1 P-\gamma e^{-d_1 \tau _1}M(t-\tau _1)-\alpha P(t-\tau _2)I, \end{aligned}$$

which evidences that

$$\begin{aligned} P(t)= e^{-\tilde{I}}\left[ P(0)-\int _0^t \gamma e^{-d_1 \tau _1}M(r-\tau _1) e^{\tilde{I}}dr\right] >0, \end{aligned}$$

where $\tilde{I}=\int _0^t (d_1+\alpha I(s))ds.$

In the similar way, we can treat the intervals $[\tau ^*,2\tau ^*],....,[n\tau ^*,(n+1)\tau ^*], n\in N$. Thus by induction, we establish that $P(t)>0, M(t)>0$ and $I(t)>0$ for all $t\ge 0$. $\square$

Lemma 2

The solution of the system of equations (1)-(3) with initial conditions is uniformly bounded in $\Omega$, where

$$\begin{aligned} \Omega = \left\{(P,M,I):0 \le P(t)+M(t)+I(t) \le \frac{k_2}{k_1}\right\}, \end{aligned}$$

$k_1=min\{d_1,d_2,d_3\}$ and $k_2=\frac{\gamma ^2}{4 \beta _1}$.

Proof

Let $V(t)=P(t)+M(t)+I(t)$. Calculating the derivative of V(t) with respect to t, we have

$$\begin{aligned} \frac{dV(t)}{dt}= &\, \gamma M-d_1 P-d_2 M-\beta _1 M^2-d_3I-\beta _2I^2 \\\le & {} \gamma M-d_1 P-d_2 M-\beta _1 M^2-d_3I. \end{aligned}$$

Taking $k_1=min\{d_1,d_2,d_3\}$, we obtain that

$$\begin{aligned} \frac{dV(t)}{dt}+k_1V\le \gamma M-\beta _1 M^2. \end{aligned}$$

There exists a positive constant $k_2=\frac{\gamma ^2}{4 \beta _1}$, such that

$$\begin{aligned} \frac{dV(t)}{dt}+k_1V\le k_2. \end{aligned}$$

Thus we get

$$\begin{aligned} 0<V(t)\le V(0)e^{-k_1t}+\frac{k_2}{k_1}. \end{aligned}$$

As $t\rightarrow \infty$, we have

$$\begin{aligned} 0\le V(t)\le \frac{k_2}{k_1}. \end{aligned}$$

Therefore, V(t) is bounded. So, each solution of the system (1)-(3) is bounded. $\square$

Dynamical behavior of the system

The system (1)-(3) has three non-negative equilibrium points:

• (i) Trivial equilibrium $E_0(0,0,0)$ always exists.

• (ii) Boundary equilibrium $E_1(P_1,M_1,0)$ exists, if (${H_1}$) holds, where $P_1=\frac{\gamma \left( 1-e^{-d_1\tau _1}\right) \left( \gamma e^{-d_1 \tau _1}-d_2\right) }{\beta _1 d_1}$, $M_1=\frac{\left( \gamma e^{-d_1 \tau _1}-d_2\right) }{\beta _1}$ and

  $$\begin{aligned} (\mathbf {H_1}): \tau _1<\frac{1}{d_1}\ln \left( \frac{\gamma }{d_2}\right) :=\tau _{10}. \end{aligned}$$

• (iii) Endemic equilibrium $E^*(P^*,M^*,I^*)$ exists, if (${H_1}$), (${H_2}$) and (${H_3}$) holds, where $M^{*}=\frac{\gamma e^{-d_1 \tau _1}-d_2}{\beta _1}, I^{*}=\frac{\alpha P^*-d_3}{\beta _2}$ and $P^*$ satisfy

  $$\begin{aligned} AP^{*2}-BP^*-C=0 \end{aligned}$$

  and

  $$\begin{aligned} \begin{array}{l} A=\alpha ^2 \beta _1,\\ B=\alpha \beta _1 d_3-d_1 \beta _1 \beta _2,\\ C=\beta _2 \gamma \left( 1-e^{-d_1 \tau _1}\right) \left( \gamma e^{-d_1 \tau _1}-d_2\right) . \end{array} \end{aligned}$$

  Here

  $$\begin{aligned} \begin{array}{l} (\mathbf {H_2}): B^2+4AC\ge 0,\ \ (\mathbf {H_3}): P^*>\frac{d_3}{\alpha }. \end{array} \end{aligned}$$

  Now, if $({H_1})$ holds, then $M^*$, $P^*$ are positive and $P^*$ is uniquely defined by $P^* = \frac{B + \sqrt{B^2 + 4 A C}}{2 A}$. Also $P^*$ is real if ($H_2$) holds. Further $I^*$ is positive if ($H_3$) holds.

Now, the transcendental polynomial equation of the second degree

$$\begin{aligned} \lambda ^2+p\lambda +r +(s\lambda +q)e^{-\lambda \tau }=0, \end{aligned}$$

(4)

has been studied by Ruan (2001) and the following results have been discussed:

• (A1) $p+s>0$;

• (A2) $q+r>0$;

• (A3) either $s^2-p^2+2r<0$ and $r^2-q^2>0$ or $(s^2-p^2+2r)^2<4(r^2-q^2)$;

• (A4) either $r^2-q^2<0$ or $s^2-p^2+2r>0$ and $(s^2-p^2+2r)^2=4(r^2-q^2)$;

• (A5) either $r^2-q^2>0$, $s^2-p^2+2r>0$ and $(s^2-p^2+2r)^2>4(r^2-q^2)$.

Lemma 3

(see Ruan (2001)) For equation (4);

• (i) If (A1)-(A3) holds, then all the roots of (4) have negative real parts for all $\tau \ge 0$.

• (ii) If (A1), (A2) and (A4) hold and $\tau =\tau ^+_j$, then equation (4) has a pair of purely imaginary roots $\pm iw_+.$ When $\tau =\tau _j^+$ then all roots of (4) except $\pm iw_+$ have negative real parts.

• (iii) If (A1), (A2) and (A5) hold and $\tau =\tau ^+_j$($\tau =\tau ^-_j$ respectively) then equation (4) has a pair of purely imaginary roots $\pm iw_+$ ($\pm iw_-,$ respectively). Furthermore $\tau =\tau _j^+$ ($\tau _j^-,$ respectively), then all roots of (4) except $\pm iw_+$ ($\pm iw_-$, respectively)have negative real parts.

Now, we will discuss the local behavior of all the equilibrium points of the system (1)-(3).

Theorem 1

The local behavior of different equilibria of the system (1)-(3) is as follows;

• (i) If $\tau _1\ge \tau _{10},$ then trivial equilibrium $E_0$ is locally asymptotically stable for all $\tau _2$ and if $\tau _1<\tau _{10},$ then it is unstable.

• (ii) If $(H_1)$ and $(H_4)$ holds, then boundary equilibrium $E_1$ is locally asymptotically stable for all $\tau _2,$ otherwise it is unstable.

• (iii) If $(H_1)$-$(H_3)$ and $(H_5)$ holds, then the endemic equilibrium $E^*$ is locally asymptotically stable for all $\tau _2,$ otherwise it is unstable.

Proof

• (i) The characteristic equation for $E_0 (0,0,0)$ is

  $$\begin{aligned} (\lambda +d_1)(\lambda -\gamma e^{-d_1\tau _1}e^{-\lambda \tau _1}+d_2)(\lambda +d_3)=0. \end{aligned}$$

  (5)

  Clearly $\lambda =-d_1, \lambda =-d_3$ are negative eigenvalues. If $\gamma e^{-d_1\tau _1}\le d_2$, then all the eigenvalues of (5) have negative real part. Therefore, the equilibrium $E_0(0,0,0)$ is locally asymptotically stable, if $\gamma e^{-d_1\tau _1}\le d_2$, that is, if

  $$\begin{aligned} \tau _1\ge \frac{1}{d_1}\ln \left( \frac{\gamma }{d_2}\right) =\tau _{10}. \end{aligned}$$

  Thus, if $\tau _1\ge \tau _{10}$, then the equilibrium $E_0(0,0,0)$ is locally asymptotically stable for all $\tau _2$. Moreover, $E_0(0,0,0)$ is unstable for all $\tau _1<\tau _{10}$, because one of the eigenvalues of (5) has positive real part.

• (ii) The characteristic equation for $E_1(P_1, M_1, 0)$ is

  $$\begin{aligned} (\lambda +d_1)F_1(\lambda )F_2(\lambda )=0, \end{aligned}$$

  (6)

  where $F_1(\lambda )=\lambda -\alpha P_1+d_3,$ $F_2(\lambda )=\lambda -\gamma e^{-d_1 \tau _1} e^{-\lambda \tau _1}+d_2+2\beta _1 M_1$. Now $d_2+2\beta _1 M_1-\gamma e^{-d_1 \tau _1} e^{-\lambda \tau _1}>0$, if $(H_1)$ holds. Further $d_3-\alpha P_1>0$, if $(H_4)$ holds, where

  $$\begin{aligned} (\mathbf {H_4}): \alpha P_1<{d_3}. \end{aligned}$$

  Thus, if $(H_1)$ and (${H_4}$) holds, than all the eigen values of (6) have negative real parts and hence non-negative equilibrium $E_1(P_1, M_1, 0)$ is locally asymptotically stable for all $\tau _2$, otherwise it is unstable.

• (iii) The characteristic equation of the Jacobian matrix at the equilibrium point $E^ {*} (P^ {*}, M^ {*}, I^*)$ can be written as:

  $$\begin{aligned} (\lambda +A)F(\lambda )=0, \end{aligned}$$

  (7)

  where

  $$\begin{aligned} F(\lambda )=(\lambda +\beta _2 I^*)(\lambda +d_1+\alpha e^{-\lambda \tau _2 }I^*)+\alpha ^2 I^* P^* e^{-\lambda \tau _2} \end{aligned}$$

  and

  $$\begin{aligned} A=\gamma e^{-d_1 \tau _1}(2-e^{-\lambda \tau _1})-d_2. \end{aligned}$$

  Here $A>0$ if $(H_1)$ holds. From (7), we obtain that $\lambda =-A$ or $F(\lambda )=0$. If $F(\lambda )=0$, then we have

  $$\begin{aligned} (\lambda +\beta _2 I^*)(\lambda +d_1+\alpha e^{-\lambda \tau _2 }I^*)+\alpha ^2 I^* P^* e^{-\lambda \tau _2}=0. \end{aligned}$$

  (8)

  Separating real and imaginary parts of (8) after substituting $\lambda =\xi + i \omega$, we obtain

  $$\begin{aligned} G_1 G_2-\omega H= & {} -\alpha ^2 I^* P^* e^{-\xi \tau _2}cos \omega \tau _2,\\ G_1 H+\omega G_2= & {} \alpha ^2 I^* P^* e^{-\xi \tau _2}sin \omega \tau _2, \end{aligned}$$

  where

  $$\begin{aligned} G_1 &= \xi +\beta _2 I^*,\\ G_2 & = \xi +d_1+\alpha I^* e^{-\xi \tau _2}cos \omega \tau _2,\\ H &= \omega -\alpha I^* e^{-\xi \tau _2}sin \omega \tau _2. \end{aligned}$$

  Thus we have

  $$\begin{aligned} (G_1G_2)^2+(\omega H)^2+(G_1H)^2+(\omega G_2)^2=(\alpha ^2 I^* P^*)^2 e^{-2 \xi \tau _2}. \end{aligned}$$

  (9)

  Now we assume that ($\mathbf {H_5}$): $\beta _2d_1>\alpha ^2 P^*$. We have to show that $\xi$ is negative. If possible, suppose that $\xi \ge 0.$ We have

  $$\begin{aligned} G_1=\xi +\beta _2 I^*, G_2=\xi +d_1+\alpha I^* e^{-\xi \tau _2}cos \omega \tau _2>\xi +d_1. \end{aligned}$$

  Therefore

  $$\begin{aligned} (G_1G_2)^2>(\alpha ^2 I^* P^*)^2 e^{-2 \xi \tau _2}, \end{aligned}$$

  which is a contradiction of (9). Therefore, $\xi <0$ if $(H_5)$ holds. Thus, each solution of (8) has negative real part, if $(H_5)$ holds. Therefore, the endemic equilibrium $E^*(P^*, M^*, I^*)$ is locally asymptotically stable if $(H_1)$-$(H_3)$ and (${H_5}$) holds for all $\tau _2.$

$\square$

Next, we will discuss the behavior of (1)-(3) taken all possible cases of $\tau _1$ and $\tau _2$. From (8), we have

$$\begin{aligned} {\lambda }^2+A_1\lambda +A_2+(B_1\lambda +B_2)e^{-\lambda \tau _2}+Ce^{-\lambda \tau _1}=0, \end{aligned}$$

(10)

where

$$\begin{aligned} \begin{array}{l} A_1=d_1+\beta _2 I^*,\\ A_2=\beta _2 d_1 I^*,\\ B_1=\alpha I^*,\\ B_2=\alpha \beta _2 I^{*2}+{\alpha }^2 I^* P^*,\\ C=0. \end{array} \end{aligned}$$

Case I: If $\tau _2=0$, then we get

$$\begin{aligned} {\lambda }^2+(A_1+B_1)\lambda +(A_2+B_2)=0. \end{aligned}$$

(11)

In this case, all the roots of (11) have negative real parts and therefore, the endemic equilibrium $E^*(P^*,M^*,I^*)$ is locally asymptotically stable.

Case II: If $\tau _2>0$, then we get

$$\begin{aligned} {\lambda }^2+p\lambda +r+(s\lambda +q)e^{-\lambda \tau _2}=0, \end{aligned}$$

(12)

where

$$\begin{aligned} \begin{array}{l} p=d_1+\beta _2 I^*,\\ r=\beta _2 d_1 I^*,\\ s=\alpha I^*,\\ q=\alpha \beta _2 I^{*2}+{\alpha }^2 I^* P^*.\\ \end{array} \end{aligned}$$

We have

$$\begin{aligned} q+r=\alpha \beta _2 I^{*2}+\alpha ^2 I^* P^*+\beta _2 d_1 I^*>0,\\ p+s=d_1+\beta _2 I^*+\alpha I^*>0,\\ s^2-p^2+2r=-d_1^2-(\beta _2^2-\alpha ^2) I^{*2},\\ r^2-q^2=(\beta _2 d_1 I^*)^2-(\alpha \beta _2 I^{*2}+{\alpha }^2 I^* P^*)^2. \end{aligned}$$

We have $s^2-p^2+2r<0,$ if (${H_6}$) holds and $r^2-q^2>0,$ if (${H_7}$) holds, where

$$\begin{aligned} (\mathbf {H_6})&: (\alpha ^2-\beta _2^2)I^{*2}<d_1^2,\\ (\mathbf {H_7})&: \frac{d_3}{\alpha }<P^*<\frac{1}{2\alpha }(d_3+\frac{\beta _2 d_1}{\alpha }). \end{aligned}$$

Using Lemma 3, if $(H_6)$ and $(H_7)$ holds, then all the roots of (1)-(3) have negative real parts for all $\tau _2$ and hence $E^*(P^*, M^*, I^*)$ is locally asymptotically stable.

Further $r^2-q^2<0,$ if ($\mathbf {H_8}$): $P^*>\frac{1}{2\alpha }(d_3+\frac{\beta _2 d_1}{\alpha })$ holds.

Using Lemma 3, if $(H_8)$ holds, then the system (1)-(3) has a pair of purely imaginary roots.

Put $\lambda =iw$ in (12), we get

$$\begin{aligned} {(iw) }^2+p(iw)+r+(iws +q)e^{-iw \tau _2}=0. \end{aligned}$$

Equating real and imaginary parts, we get

$$\begin{aligned} -w^2+r+sw\sin {w\tau _2}+q\cos w\tau _2=0,\end{aligned}$$

(13)

$$\begin{aligned} pw+sw\cos w\tau _2-q\sin w\tau _2=0. \end{aligned}$$

(14)

Solving (13) and (14), we get

$$\begin{aligned} \sin w\tau _2 = \frac{sw^3+(pq-rs)w}{s^2w^2+q^2},\end{aligned}$$

(15)

$$\begin{aligned} \cos w\tau _2 = \frac{(q-ps)w^2-qr}{s^2w^2+q^2}, \end{aligned}$$

(16)

and

$$\begin{aligned} w^4+(p^2-2r-s^2)w^2+(r^2-q^2)=0. \end{aligned}$$

(17)

We define

$$\begin{aligned} F(w)=w^4+(p^2-2r-s^2)w^2+(r^2-q^2)=0. \end{aligned}$$

Now, $F(0)=(r^2-q^2)<0$, if ($H_8$) holds. By Descartes’ rule of sign, there is at least one positive root of $F (w) =0$. Let $w_0$ is the positive root of $F(w)=0.$

From (16), we get

$$\begin{aligned} \tau _{2k}^+=\frac{1}{w_0}\left[ \cos ^{-1}\left( \frac{(q-ps){w_0}^2-qr}{s^2{w_0}^2+q^2}\right) + 2k\pi \right] , \end{aligned}$$

where $k=0,1,2,....$

Now, differentiating (12) with respect to $\tau _2$, we get

$$\begin{aligned} \frac{d\lambda }{d\tau _2}=\frac{\lambda (s\lambda +q)e^{-\lambda \tau _2}}{2\lambda +p-(s\lambda +q)\tau _2 e^{-\lambda \tau _2}+se^{-\lambda \tau _2}}. \end{aligned}$$

At $\lambda =iw_0$ and $\tau _2=\tau _{20}^+$, we have

$$\begin{aligned} Re\left( \frac{d\lambda }{d\tau _2}\right) ^{-1}=\frac{(sw_0p+2w_0q)cosw_0\tau _2+(pq-2sw_0^2)sinw_0\tau _2+s^2w_0}{w_0(q^2+s^2w_0^2)}. \end{aligned}$$

(18)

Fig. 1

$E_0$ is stable for parameter values $\gamma = 0.8, \alpha =0. 04, \beta _1 = 0.8, \beta _2 = 0.3, d_1= 0.3, d_2 = 0.01, d_3 = 0.09, \tau _1=15>\bar{\tau }_{10}=14.6$ and $\tau _2=7.2$

Simplifying (18), we have

$$\begin{aligned} Re\left[ \left( \frac{d\lambda }{d\tau _2}\right) ^{-1}\right] _{\tau _2=\tau _{20}^+}\ne 0, \end{aligned}$$

for $pq>2sw_0^2$, which is one of the sufficient condition.

Theorem 2

Let $(H_1)$-$(H_3)$ holds. For the system (1)-(3), we have

• (i) If $(H_6)$ and $(H_7)$ holds, then the endemic equilibrium $E^*(P^*,M^*,I^*)$ is locally asymptotically stable for all $\tau _2.$

• (ii) If $(H_8)$ holds, then the endemic equilibrium $E^*(P^*,M^*,I^*)$ is locally asymptotically stable for all $\tau _2\in [0,\tau _{20}^+),$ and unstable when $\tau _2\ge \tau _{20}^+.$

Sensitivity analysis

Table 1 The sensitivity indices $\gamma _{y_j}^{x_i}=\frac{\partial x_i}{\partial y_j}\times \frac{y_j}{x_i}$ of the state variables of the system (1)-(3) to the parameters $y_j$ for the parameter values $\gamma = 0.8, \,\alpha =0.09,\,\beta _1 = 0.2,\,\beta _2 = 0.3,\,d_1= 0.05,\,d_2 = 0.01,\,d_3 = 0.01,\,\tau _1=12.2, \,\tau _2=7.2$

In this section, we perform the sensitivity analysis of the endemic equilibrium with respect to model parameters, for a particular set of parameters $\gamma = 0.8,$ $\alpha =0.09,$ $\beta _1 = 0.2,$ $\beta _2 = 0.3,$ $d_1= 0.05,$ $d_2 = 0.01,$ $d_3 = 0.01,$ $\tau _1=12.2$ and $\tau _2=7.23$. The normalized sensitive indices of the endemic equilibrium with respect to parameters are shown in Table 1. From the Table 1, it is observed that $\gamma ,$ $\beta _2,$ $d_3$ have a positive impact on the $P^*$ and the rest of the parameters have a negative impact. Moreover $\gamma$ and $\alpha$ are most sensitive parameter to $P^*$, hence, the significant change in $P^*$ is observed by small changes in these parameters. Again $\gamma$ and $\beta _1$ are most sensitive parameters to both $M^*$ and $I^*$.

Fig. 2

$E_1$ is stable for parameter values $\gamma = 0.8, \alpha =0. 04, \beta _1 = 0.8, \beta _2 = 0.3, d_1= 0.3, d_2 = 0.01, d_3 = 0.09, \tau _1=12.2<\bar{\tau }_{10}=14.6$ and $\tau _2=7.2$

Fig. 3

$E^{*}$ is stable for parameter values $\gamma = 0.8, \alpha =0. 04, \beta _1 = 0.2, \beta _2 = 0.3, d_1= 0.2, d_2 = 0.05, d_3 = 0.01, \tau _1=11.2<\bar{\tau }_{10}=13.86$ and $\tau _2=7.2$

Fig. 4

$E^{*}$ is stable for parameter values $\gamma = 0.8,\,\alpha =0. 09,\,\beta _1 = 0.2,\,\beta _2 = 0.3, \,d_1= 0.05, \,d_2 = 0.01,\,d_3 = 0.01,\,\tau _1=12.2,\,\tau _2=7.2<\tau _{20}^+=7.25$

Fig. 5

$E^{*}$ is unstable for parameter values $\gamma = 0.8,\,\alpha =0. 09,\,\beta _1 = 0.2,\,\beta _2 = 0.3,\,d_1= 0.05,\,d_2 = 0.01,\,d_3 = 0.01,\,\tau _1=12.2,\,\tau _2=7.35>\tau _{20}^+=7.25$

Numerical simulations

We perform the numerical simulations of the system (1)-(3) keeping the parameters $\gamma = 0.8$, $\alpha =0.04$, $\beta _1 = 0.8$, $\beta _2 = 0.3$ as fixed and varying the parameters $d_1$, $d_2$ and $d_3$. We use initial population sizes as $P_0=0.3,$ $M_0=0.9$ and $I_0=0.4$.

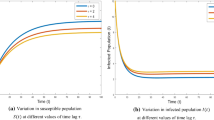
The trivial equilibrium $E_0(0,0,0)$ is locally asymptotically stable for the parameter values $d_1= 0.3$, $d_2=0.01$ and $d_3 = 0.09$, when $\tau _1=15 \ge \bar{\tau }_{10}=14.6$ and $\tau _2=7.2$ (see Fig. 1). For the same set of parametric values the boundary equilibrium $E_1(P_1,M_1,0)$ is locally asymptotically stable when $\tau _1=12.2<\bar{\tau }_{10}=14.6$ and $\tau _2=7.2$ as shown in Fig. 2. Further, the endemic equilibrium $E^ {*} (P^*, M^*, I^*)$ is locally asymptotically stable when $\tau _1=11.2<\bar{\tau }_{10}=13.86$ and $\tau _2=7.2$ for parameter values $d_1= 0.2$, $d_2=0.05$ and $d_3 = 0.01$ (see Fig. 3). These results show that the Theorem 1 is true.

Again, we take parameter values as $d_1= 0.05$, $d_2=0.01$, $d_3 = 0.01$ and $\tau _1=12.2$. The endemic equilibrium $E^{*}(P^*,M^*,I^*)$ is stable when $\tau _2=7.2<\tau _{20}^+=7.25$ as shown in Fig. 4. Further, $E^{*}(P^*,M^*,I^*)$ is unstable and Hopf bifurcation appears when $\tau _2=7.35 \ge \tau _{20}^+=7.25$ as shown in Fig. 5, which is in accordance with the results stated in Theorem 2.

Conclusions

In this paper, an epidemic model for childhood disease with maturation delay and latent period of infection is proposed. The asymptotic stability of the model is investigated at all the feasible equilibrium states. The existence of Hopf bifurcation at the endemic equilibrium state is explored. The endemic equilibrium is locally asymptotically stable for all $\tau _2\in [0,\tau _{20}^+)$, and exhibits Hopf bifurcation, when the latent period ($\tau _2$) is greater than or equal to some critical value ($\tau _{20}^+$) under specific conditions. Finally, the normalized forward sensitivity indices are calculated for state variables at endemic equilibrium with respect to various parameters. Numerical simulations of the system are performed with a particular set of parameters to justify our analytic findings.