Introduction

Random vibration loadings exposed on electronic systems may cause fatigue failure in electronic components mounted on printed circuit boards (PCB). Many good examples of using finite element (FE) method to calculate the vibration response of the PCB and to predict when fatigue failure may occur exist in current literature. The complexity of these models depends on if the internal stresses of components are required. Yu et al. related the fatigue parameters obtained with harmonic excitation to the fatigue life of ball grid array (BGA) solder joints under the random excitation [1]. Li considered a detailed modeling approach for random vibration analysis and fatigue prediction of electronic components [2]. Mei-Ling Wu developed a rapid assessment methodology that can determine the solder joint fatigue life of BGA and chip scale packages (CSP) under vibration loading [3]. Wong et al. developed an experimentally validated vibration fatigue damage model for a PBGA solder joint assembly [4]. Effective strains were calculated and combined with the three-band techniques to predict solder joint survivability. Lead spring constants can be used in place of detailed lead models when only the PCB response is required [5, 6]. Further simplification can be made by including the effect of the component with artificially increased stiffness and density of the underlying PCB properties in the FE model or with simple block 3D elements [7–10]. Using experimental data, Lim et al. and Barker et al. give examples of how the edge rotational stiffness can be calculated for use in a PCB FE model [11, 12].

The accuracy of the FE model is essential for predicting fatigue life under random vibration. Although there are literatures showing that the uncertainties of the material properties and the boundary condition of PCB have strong effects on the simulation results [13, 14], very few author presented the model updating procedure for PCBs. Finite element model updating is a procedure that uses test results to update the uncertain parameters in the original FE model so that a more realistic model can be obtained. Early FE model updating methods include direct methods [15–18] and iterative methods [19–22]. Direct methods update the elements of mass and stiffness matrices directly and reproduce the test results well. However, the updated matrices do not generally maintain structural connectivity and the corrections suggested are not always physically meaningful. The iterative method calculates the sensitivity of the parameters in each iteration and use Taylor expansions to find the changes of input parameters. Time consuming and convergence problem arise when the model is complicated. The response surface method is becoming popular for its fast-running and good convergence properties [23–27]. This method uses design of experiment (DOE) method to create samples for updating parameters and calculate the response at each sample. The updating parameters and response are then used to create a model to replace the original FE model. Objective functions are formed with simulation and test results and minimized with optimization algorithm by correcting the updating parameters.

This paper presents a procedure to predict the fatigue life of PBGA components under random vibration loading based on FE analysis and vibration tests. The FE models of the specially designed daisy chain PCBs with attached PBGA components are updated through three consecutive stages. The random vibration test response of the PCB is compared with simulation results. The resistance of the daisy chained circuits is monitored and the failure time of the PBGA is fitted by a two-parameter Weibull distribution. The Von Mises stress power spectral density (PSD) of the critical solder joint is calculated and transferred into time-history data. The rainflow cycle counting (RFCC), the S–N curve and the Miner’s rule are combined to estimate the cumulative damage of the critical solder joints.

Model Updating Using Response Surface Method

Response surface-based model updating approach uses an approximation model to replace the original FE model. The main steps include:

  1. 1.

    The selection of updating parameters (using sensitivity analysis, if necessary);

  2. 2.

    The sampling of updating parameters using the design of experiment (DOE) method and the calculation of response using FE model;

  3. 3.

    The creation of response surface using regression analysis between the updating parameters and the response followed by a regression error analysis;

  4. 4.

    The construction of objective functions using simulated and measured response features of the structure;

  5. 5.

    The iteration and optimization of objective functions within the established response surface model.

The selected updating parameters should be able to clarify the ambiguity of the model, and the response should be sensitive to these parameters. If the number of updating parameters exceeds the number of structural response available, ill-conditioned optimization problem may appear. To reduce the number of updating parameters, the sensitivity analysis can be used to determine the key parameters.

The sampling of updating parameters affects the accuracy and computation efficiency of the response surface model. A commonly used DOE method, the central composite design (CCD) method, is used in this paper for parameter sampling and response surface construction. The CCD method uses the orthogonal table to perform the experimentation to determine the sample points of selected parameters [25].

Polynomials are popular forms representing a response surface because the calculation is simple and the resulting function is a closed-form expression. A quadratic polynomial response surface is used in this paper:

$$ y={\beta}_0+{\displaystyle \sum_{i=1}^k{\beta}_i{x}_i}+{\displaystyle \sum_{i=1}^k{\displaystyle \sum_{j=1}^k{\beta}_{ij}{x}_i{x}_j}} $$
(1)

where β 0, β i , β ij are the regression coefficients, y is the response surface, x is the updating parameters, k is the number of updating parameters.

The least-square fitting is used to fit the response surface to the sample data, and the accuracy of the response surface should be checked before put to use. The R 2 criterion is used here for verification:

$$ {R}^2=1-\frac{{\displaystyle \sum_{i=1}^N{\left({\widehat{y}}_i-{y}_i\right)}^2}}{{\displaystyle \sum_{i=1}^N{\left({y}_i-\overline{y}\right)}^2}} $$
(2)

where N is the number of sampling points, y i is the true response at the ith sampling point, ŷ i is the regression response at the ith sampling point, \( \overline{y} \) is the mean value of y i .

With values ranging from 0 to 1, high values of R 2 indicate good regression accuracy of the response surface model. The FE model of a specially designed daisy chain PCB mounted with two PBGA components is updated through three consecutive stages. The updating parameters in these stages are the material properties of the PCB, the material properties of the PBGA components, and the boundary condition of the PCB, respectively. The boundary condition of typical plug-in PCBs used in airborne electronic cases (AEC) is considered in this paper [28]. The PCB is plugged into the AEC through a plug-in connector and two wedge lock retainers, as shown in Fig. 1.

Fig. 1
figure 1

Typical plug-in PCB and AEC

Full size image

In each stage, the first three resonant frequencies of the PCB are calculated using ANSYS and correlated with modal test results. Two objective functions are created, one using the first simulated and measured resonant frequency, the other using the square of residuals between the first three simulated and measured resonant frequencies, each resonant frequency with the same weight.

$$ {O}_{bj1}^m(x)=\left|{f}_{{}_{a1}}^m-{f}_{{}_{e1}}^m\right|,m=1,2,3,{x}_l\le x\le {x}_u $$
(3)
$$ {O}_{bj2}^m(x)={\displaystyle \sum_{i=1}^3{\left({f}_{{}_{ai}}^m-{f}_{{}_{ei}}^m\right)}^2},m=1,2,3,{x}_l\le x\le {x}_u $$
(4)

where m is the stage number, f ai is the simulated resonant frequency, f ei is the measured resonant frequency, i is the mode number, x is the updating parameters, x l and x u are the lower and upper bounds of updating parameters.

A multi-objective genetic algorithm (MOGA) was used to minimize the objective function. In this algorithm, the mutation probability and the crossover probability are set to be 0.01 and 0.98 respectively. The maximum allowable Pareto ratio is used as the convergence criterion [29].

Stage 1 – PCB Model Updating

The daisy chain PCB under investigation is made of FR4 with 203 mm in length, 140 mm in width, and 1.6 mm in thickness. The modal test arrangement used in this paper is based upon the concept of “roving hammer”. In this test, the accelerometer is fixed at one DOF, and the structure is impacted at as many DOFs as desired to define the mode shapes of the structure. The accelerometer and the instrumented hammer are connected to a multi-channel Fast Fourier Transform (FFT) analyzer which collects both input and output responses and calculated the FRF. By cycling through all the test points, sufficient frequency response functions are collected to build the transfer matrix. Time domain least square complex exponential technique and frequency domain curve fitting technique are used to extract the modal parameters. The modal test setup and measurement points are shown in Fig. 2.

Fig. 2
figure 2

Modal test setup and measurement points in stage 1

Full size image

The modal assurance criterion (MAC) matrix is used for assessing the degree of correlation between any two (i.e., analytical and experimental) vectors and is formulated as:

$$ {\mathrm{MAC}}_{ij}=\frac{{\left({{\boldsymbol{u}}_i}^{\mathrm{T}}{\boldsymbol{e}}_j\right)}^2}{\left({{\boldsymbol{u}}_i}^{\mathrm{T}}{\boldsymbol{u}}_i\right)\left({{\boldsymbol{e}}_j}^{\mathrm{T}}{\boldsymbol{e}}_j\right)} $$
(5)

Where u i denotes the ith vector from analytical modal matrix, and e j the jth vector from experimental modal matrix.

With values ranging from 0 to 1, low values of MAC indicate very little correlation between the two vectors and high values indicate very high correlation. The MAC value of the first three test modes are shown in Table 1. From Table 1 we can see that all modes are independent.

Table 1 MAC value of test modes
Full size table

The initial material properties of the PCB are shown in Table 2. The FE model is created in ANSYS, as shown in Fig. 3. The model consists of 200 shell elements, 4 nodes for each element and 6° of freedom (DOFs) for each node. Using this FE model, a free-free analytical solution is obtained for the first three flexural modes.

Table 2 Initial material properties of PCB
Full size table
Fig. 3
figure 3

Finite element model of the PCB

Full size image

The MAC value of simulated and test modes is shown in Table 3. From Table 3 we can see that a good correlation is obtained. A comparison of the first three simulated and measured resonant frequencies is shown in Table 5.

Table 3 MAC value of FEA and test modes
Full size table

In this stage, the orthogonal material properties of the PCB (3 Young’s modulus, 3 Poisson ratio and 3 Shear modulus) are used as initial updating parameters. The sensitivity analysis of updating parameters are shown in Fig. 4. From Fig. 4 we can see that the objective functions are only sensitive to E y and G xy . Positive sensitivity indicates that the response increases as the updating parameters increase, and negative sensitivity indicates that the response decreases as the updating parameters increase.

Fig. 4
figure 4

Sensitivity analysis in stage 1

Full size image

The E y and G xy are used as final updating parameters. Within the parameter constraints, 10 sampling points are created using the DOE method. The response surface of two objective functions are shown in Fig. 5. The R 2 value of the first three resonant frequencies are all close to 1, indicating a good fit.

Fig. 5
figure 5

Response surface of two objective functions in stage 1

Full size image

The iteration process of the two objective functions is shown in Fig. 6. The updated material properties of the PCB and the updated resonant frequencies are shown in Tables 4 and 5. From Table 5 we can see that the errors are reduced for all modes.

Fig. 6
figure 6

Iteration process of two objective functions in stage 1

Full size image
Table 4 Updated material properties
Full size table
Table 5 Comparison of the first three resonant frequencies
Full size table

Stage 2 – PBGA Model Updating

In this stage, two PBGA components are mounted on the PCB. The geometry of solder joints is shown in Fig. 7. The PBGA is 35 mm in length, 35 mm in width and 1.9 mm in thickness.

Fig. 7
figure 7

PBGA and solder joints (A = 0.76 mm, B = 0.60 mm, C = 0.52 mm)

Full size image

The modal test setup is shown in Fig. 8. The test method and measurement points are the same as in stage 1. The MAC value of test modes are shown in Table 6. From Table 6 we can see that all modes are independent. A comparison of the first three simulated and measured resonant frequencies is shown in Table 10.

Fig. 8
figure 8

Modal test setup in stage 2

Full size image
Table 6 MAC value of test modes
Full size table

The material property of the PBGA is assumed to be isotropic, as shown in Table 7. The FE model is created in ANSYS, as shown in Fig. 9. The PCB model is the same as in Fig. 3. The components and solder joints are modeled by solid elements, 20 nodes for each element and 3 DOFs for each node. The four corner solder joints of each PBGA are modeled in detail, the others are approximated by cubes. Using this FE model, a free-free analytical solution is obtained for the first three flexural modes.

Table 7 Initial material properties of PBGA
Full size table
Fig. 9
figure 9

Finite element model of PCB and PBGA

Full size image

The MAC of simulated and test modes is shown in Table 8. From Table 8 we can see that a good correlation is obtained. A comparison of analytical and test resonant frequencies is shown in Table 10.

Table 8 MAC value of FEA and test modes
Full size table

The density and geometry size of the PBGA components are treated as constants. The Young’s modulus and Poisson ratio of the PBGA components are used as updating parameters. Sensitivity analysis of updating parameters is not necessary in this stage since there are only two parameters. The response surface is shown in Fig. 10. The R 2 value of the first three resonant frequencies are all close to 1, indicating a good fit.

Fig. 10
figure 10

Response surface of two objective functions in stage 2

Full size image

The iteration process of the two objective functions is shown in Fig. 11. The updated material properties of the PBGA and the updated resonant frequencies are shown in Tables 9 and 10. From Table 10 we can see that the errors are reduced for all modes.

Fig. 11
figure 11

Iteration process of two objective functions in stage 2

Full size image
Table 9 Material property parameters before and after updating
Full size table
Table 10 A comparison of the first three resonant frequencies
Full size table

Stage 3 – Boundary Condition Model Updating

In this stage, the boundary condition of the plug-in PCB is simulated and updated. Since ‘clamped’ boundary condition does not exist in practice, simulating the boundary condition by constraining all DOFs that corresponding to the plug-in connector and wedge lock retainers will lead to large error. To better simulate the boundary condition of the plug-in PCB, the PCB and a specially designed fixture were model together in ANSYS (as shown in Fig. 12). Rotational springs are used to constrain the rotational DOFs of nodes that correspond to the plug-in connector and wedge lock retainers. The corresponding translational DOFs are coupled with the fixture. A spring stiffness of K 1 (1*104Nmm/rad) is assumed for the springs that correspond to the wedge lock retainers, and K 2 (1*106Nmm/rad) for the springs that correspond to the plug-in connector.

Fig. 12
figure 12

Finite element model of PCB and fixture

Full size image

The modal test setup is shown in Fig. 13. The test method and measurement points are the same as in stage 1. The MAC value of test modes is shown in Table 11. From Table 11 we can see that all modes are independent. A comparison of the first three simulated and measured resonant frequencies is shown in Table 14. The MAC value of simulated and test modes is shown in Table 12. From Table 12 we can see that a good correlation is obtained.

Fig. 13
figure 13

Modal test setup in stage 3

Full size image
Table 11 MAC of test modes
Full size table
Table 12 MAC value of FEA and test modes
Full size table

The response surface of two objective functions is shown in Fig. 14. The R 2 value of the first three resonant frequencies are all close to 1, indicating a good fit.

Fig. 14
figure 14

Response surface of two objective functions in stage 3

Full size image

The iteration process of the two objective functions is shown in Fig. 15. The updated spring stiffness coefficients and the updated resonant frequencies are shown in Tables 13 and 14. From Table 14 we can see that, although the error of the second resonant frequency is still relatively large, the first and third resonant frequencies agree well with the test results. The relatively large discrepancy between the second resonant frequencies may originate from the defect in the design of the fixture, e.g., the fixture is not stiff enough so that it tends to bend when being tightened, which makes the boundary condition even more complicated. Except for the second mode, from Table 5, Tables 10 and 14 we can see that good agreement of natural frequencies has been achieved after carrying out the response surface-based FE model updating. The updated FE model is used to perform random vibration analysis and fatigue life prediction in “Vibration Test and Analysis” section.

Fig. 15
figure 15

Iteration process of two objective functions in stage 3

Full size image
Table 13 Comparison of the spring stiffness before and after updating
Full size table
Table 14 Comparison of the first three resonant frequencies
Full size table

Vibration Test and Analysis

The flow chart of fatigue life prediction under random vibration is shown in Fig. 16. With the updated FE model, the vibration analysis is performed in ANSYS and compared with test result. The resistance of the specially designed daisy chain PCB is monitored. A two-parameter Weibull distribution is used to fit the PBGA failure time. The Von Mises stress PSD of the critical solder joints are calculated in ANSYS and transferred into time-history data. The RFCC, the S–N curve and the Miner’s rule are used to estimate the cumulative damage.

Fig. 16
figure 16

Flowchart of fatigue life prediction under random vibration

Full size image

Random Vibration Test and Analysis

The daisy chain PCB with two PBGA components attached is mounted to the electro-dynamic shaker and subjected to random vibration excitations at the supports, as shown in Fig. 17. The input PSD has a level of 0.1 G^2/Hz over 50 to 1000Hz, as shown in Fig. 18.

Fig. 17
figure 17

Random vibration test set-up

Full size image
Fig. 18
figure 18

Input acceleration PSD

Full size image

The acceleration response at a specified point on the PCB is measured (as shown in Fig. 17) and shown in Fig. 19. The modal damping ratio is calculated using equation 6:

$$ {\xi}_i=\frac{\varDelta {f}_i}{2{f}_{n,i}} $$
(6)

where Δf i is the frequency interval between two half-power points of the ith mode, f n,i is the ith resonant frequency.

Fig. 19
figure 19

Comparison of response acceleration PSD on the test item

Full size image

Using the calculated modal damping ratio, the simulated response was compared with measured result to further validate the accuracy of the FE model, as shown in Fig. 19. As we can see from Fig. 19, a good correlation was obtained between the test and simulation results (except for the second resonant frequency, as indicated in “Stage 3 – Boundary Condition Model Updating” section).

Fatigue Life Test and Analysis

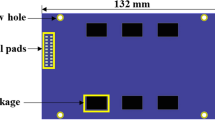
Five daisy chain PCBs are used to perform the fatigue life test. The detail of the daisy chain PCB is shown in Fig. 20. The upper and lower PBGA components are attached to the PCB using Sn37Pb and SAC305 solder material respectively. A milliohm meter is used to monitor the resistance of the daisy chained circuits and record the failure time (indicated by AA1 and BB2) of these two PBGA components.

Fig. 20
figure 20

Detail of the daisy chain PCB

Full size image

A two-parameter Weibull distribution is used to fit the time to failure data and to calculate the mean life:

$$ F(t)=1- \exp \left[-{\left(\frac{t}{\eta}\right)}^{\beta}\right] $$
(7)

where, F(t) is the cumulated distribution function, η is the scale parameter, β is the shape parameter.

The result is shown in Fig. 21. Random vibration analysis is performed in ANSYS to obtain the response Von Mises (equivalent) stress of the critical solder joint. The RMS of the equivalent stress of the Sn37Pb and SAC305 solder joints are shown in Fig. 22 and Fig. 23. As we can see, the outmost corner solder ball is observed to have stress concentration along the solder/PCB interface.

Fig. 21
figure 21

Weibull distribution of time to failure for different solder joints

Full size image
Fig. 22
figure 22

Equivalent stress RMS of Sn37Pb solder joints

Full size image
Fig. 23
figure 23

Equivalent stress RMS of SAC305 solder joints

Full size image

To compensate for the effects of mesh density, the volume-averaged stress over the critical solder joint is calculated:

$$ {\sigma}_{av}=\frac{{\displaystyle \sum_{i=1}^{N_e}{\sigma}_{eq}^i\ast {V}_i}}{{\displaystyle \sum_{i=1}^{N_e}{V}_i}} $$
(8)

where, σ av is the volum average Von Mises stress, σ i eq is the Von Mises stress of the ith element, V i is the volum of the ith element, N e is the number of elements.

The volume-averaged equivalent stress PSD is shown in Fig. 24 (a) and Fig. 25 (a). The PSD is then transformed into time-history data (see Fig. 24 (b) and Fig. 25 (b)) using the IFFT method [30]. A unit sample of 10 s time-history data is generated. The total record is then assumed to be the repetition of the unit sample over the test time.

Fig. 24
figure 24

Equivalent stress PSD and time history of critical Sn37Pb solder joints

Full size image
Fig. 25
figure 25

Equivalent stress PSD and time history of critical SAC305 solder joints

Full size image

The RFCC method is applied in the analysis of fatigue data in order to reduce the spectrum of varying stress into sets of simple stress reversals for different amplitudes [31]. The results are shown in Fig. 26.

Fig. 26
figure 26

RFCC results of equivalent stress

Full size image

The S-N curve of the Sn37Pb [32] and SAC305 [1] solder joints can be formulated as:

$$ N{\sigma}^{8.3}={(71.5MPa)}^{8.3}\ \mathrm{f}\mathrm{o}\mathrm{r}\ \mathrm{S}\mathrm{n}37\mathrm{P}\mathrm{b} $$
(9)
$$ N{\sigma}^{6.93}={(64.8MPa)}^{6.93}\kern0.5em \mathrm{f}\mathrm{o}\mathrm{r}\ \mathrm{S}\mathrm{A}\mathrm{C}305 $$
(10)

Palmgren-Miner’s rule is used to assess the fatigue life [33]. This rule states that the incremental damage due to each cycle can be simply added to estimate the fatigue life:

$$ D={\displaystyle \sum_{i=1}^p\frac{n_i}{N_i}} $$
(11)

where n i is the number of cycle at stress level σ i (i = 1, 2, …, p), p is the number of considered stress level, N i is the fatigue life at stress level σ i .

Within 10s, the fatigue damage of Sn37Pb and SAC305 solder joints are 0.0029 and 0.0073 respectively. The fatigue life is 57.5 min for Sn37Pb and 22.8 min for SAC305. The comparison between predicted and measured fatigue life results is shown in Table 15. From Table 15 we can see that relatively good agreement is obtained, indicating the validity of the method.

Table 15 Comparison between predicted and measured fatigue life results
Full size table

Conclusions

A procedure based on FE modeling, response surface-based model updating and random vibration analysis for predicting the fatigue life of PBGA components mounted on daisy chain PCBs is presented. Modal test, random vibration test and fatigue life test are used to validate the procedure. Conclusions are as below:

  1. (1)

    A multi-stage model updating procedure can be used to calibrate FE models of plug-in PCBs which consist of many uncertain parameters. Further reduction of updating parameters can be performed in each stage by using sensitivity analysis;

  2. (2)

    The response surface based model updating technique can be implemented directly in commercial FE software to improve the accuracy of FE model, which provides a practical way for engineering application;

  3. (3)

    The fatigue life prediction procedure is validated by vibration test and fatigue life test, good agreement between predicted and test results is obtained;

  4. (4)

    The accuracy of the S-N curve has a huge impact on the predicted result, more test items can be used in future to obtain more accurate S-N curve and to further validate the accuracy of the procedure.