Picture fuzzy tolerance graphs with application

Abstract

In this study, the notions of picture fuzzy tolerance graphs, picture fuzzy interval containment graphs and picture fuzzy $\phi$-tolerance graphs are established. Three special types of picture fuzzy tolerance graphs having bounded representations are introduced and studied corresponding properties of them taking $\phi$ as max, min and sum functions. Also, picture fuzzy proper and unit tolerance graphs are established and some related results are investigated. The class of picture fuzzy $\phi$-tolerance chaingraphs which is the picture fuzzy $\phi$-tolerance graphs of a nested family of picture fuzzy intervals are presented. A real-life application in sports competition is modeled using picture fuzzy min-tolerance graph. Also a comparison is given between picture fuzzy tolerance graphs and intuitionistic fuzzy tolerance graphs.

Introduction

Research background

In 1965, the notion of fuzzy set (FS) was initially posed by Zadeh [51] to model the problems having uncertainties. It was seen that FS with one component may fail to modeled some problems properly. To illustrate those problems Atanassov [2] invited another component namely non-membership value and defined intuitionistic fuzzy (IF) set. But, in some cases, an extra component namely ‘neutrality’ is needed to explain an existing information completely. To recover this situation, Cuong [6] initiated the idea of picture fuzzy (PF) set as an extended version of IF set. After that, Son [43] introduced generalized picture distance measure with its applications in PF clustering (PFC) and he described some measuring analogousness in PF sets [44]. Based on PFC method, Thong and Son presented weather now casting from satellite image sequences in [45] and particle swarm optimization with picture composite cardinality in [46]. They also explained PFC: a new computational intelligence method [47] and PFC for complex data [48]. Graph theory was well studied by many researcher in discrete mathematics, computer science, railway network, traffic network, ecological modeling, archaeology, etc. for its wide applications. The concept of fuzziness was initiated in graph theory by Rosenfeld [33] and defined fuzzy graph (FG), whereas in 1973 Kauffman [22] initially posed its basic idea. After that, in the domain of FG many works have been done by the researchers in several directions such as Samanta and Pal defined the notion of fuzzy competition graphs (CGs) [36] and fuzzy planar graphs (FPGs) [37]. Samanta et al. explained m-step fuzzy CGs [38] and they investigated completeness and regularity of generalized FGs in [39]. Several new concepts of bipolar FGs with applications were proposed by Poulik and Ghorai in [29,30,31]. Later on, Naz et al. [26] introduced the novel concepts of energy of a graph in the context of a bipolar fuzzy environment with its application in decision making problem. Ghorai and Pal introduced some operations on m-polar FGs [15], some isomorphic properties of m-polar FGs with applications [16] and m-polar FPGs [17]. They also studied certain types of product bipolar FGs in [18]. The concept of IF graph was first given by Shannon and Atanassov [34]. Sahoo and Pal introduced IF competition graph [40] and explained certain types of edge irregular IF graphs in [42]. Next, Karaaslan [24] exhibited structure of hesitant FGs with their applications in decision making. Recently, Akram et al. [3] proposed the concept of CGs under complex fuzzy environment and designed an application of it in ecology.

Al-Hawary et al. [1] proposed the notion of PF graph (PFG) with some operations as an extended version of IF graph. Later on, Zuo et al. presented the new concepts of PFGs with application in [50]. Mohamedlsmayil and AshaBosely [25] described domination in PFGs. Recently, Das and Ghorai [8] have defined picture FPGs and applied it to construct road map designs. They have also applied the idea of PF sets to CGs, PF genus graphs [9,10,11]. Xiao et al. studied on regular PFG and its application in communication networks in [49].

Golumbic and Monma [12] first initiated tolerance graphs (TGs) as a natural generalization of interval graphs (IGs) using tolerances and examined TG in [13]. Jacobson et al. [19, 20] introduced tolerance intersection graph and established some general results of it. The equivalence relation between proper and unit intervals for sum-TGs are explained by Jacobson and McMorris in [21]. Bogart and Fishburn [5] described proper and unit TGs. The idea of tolerance CGs was initiated by Brigham et al. [4]. Samanta and Pal [35] defied fuzzy TGs. Pramanik et al. introduced fuzzy $\phi$-tolerance CGs [27] and interval-valued fuzzy $\phi$-tolerance CGs [28]. Then TGs with application in IF environment were explained by Sahoo and Pal [41]. Kiersteada and Saoubb [23] discussed about the first-fit coloring of bounded TGs. Max-point-TGs were studied by Catanzaro et al. [7] in 2017 and recently, Paul [32] discussed on central max-point-TGs.

Research challenges and gaps

• The TG is a well-known topic. But till now, no work has been done on it in PF environment.

• The PF tolerance graph (PFTG) can model the conflicts of events occurring in a block of time and can also fix up the relation between them.

• PFTG models are very effective to solve certain scheduling and resource allocation problems in operations research than the models in other fields.

• All the introduced TGs are crisp graphs which cannot describe all the real-world problems that contains uncertainty or haziness and fuzzy in nature.

• The PFTG models give more legibility, flexibility and suitability to the system as compared with the models in other fields due to uncertainty.

Motivation and contribution of this study

In graph theory, an intersection graph represents the pattern of overlap of collection of sets. An IG is the intersection of the intervals on a real line $R_{L}$. In certain scheduling and resource allocation problems of operations research the IG model is very fruitful. Moreover, IGs have numerous applications in several fields such as ecological model, developmental psychology, archaeology, mathematical modeling, etc. TGs were invited to generalize few well-known applications of IGs. The original purpose was to model certain scheduling and resource allocation problems for sharing of vehicles and rooms, etc. We have presented a new classification of TGs in PF environment. Due to uncertainty in the description of TGs, it is a necessity to design PFTG models. We have generalized IGs by using tolerance and constructed PFTG models by assuming PFIs as the vertices. And two vertices are combined by an edge iff the intersection of the corresponding picture fuzzy intervals (PFIs) are at least as large as the picture fuzzy tolerance (PFT) associated with one of the PF vertices. The PFTG, a worthwhile generalization of IF tolerance graph (IFTG), is a proficient model to deal with uncertainties of human judgement in more comprehensive and logical way due to the presence of an additional term known as ‘neutral membership’. This graph has an acuity over the other existing models of the literature due to its additional features of handling the uncertainties. On the other hand, if we remove the ‘neutral membership’ of PFTG, the PFTG reduces to conventional IFTG. Thus, PFTG is an effective generalization of IFTG. The TGs developed under PF environment are useful enough to tackle all the tolerances of real world which possess the information with more possible types of vagueness and uncertainties.

In this research article, we present the innovative concept of PFTGs. Moreover, we consider PF $\phi$-tolerance graphs (PF$\phi$-TGs), PF max, min and sum TGs, PF unit TGs, PF proper TGs and PF $\phi$-tolerance chain graphs (PF$\phi$-TCGs) with interesting properties. In addition, we discuss an application of PFmin TG in sports competition to emphasize the superiority of this graphs in real life. The main contribution to this article is TGs with its remarkable specializations are developed in PF environment to overcome the deficiencies of other existing TGs of the literature. An algorithm is initiated to find the tolerances among the real-world entities with an application in sports competition. A comparison between PFTG and IFTG is provided to show the superiority and authenticity of our proposed TGs.

Framework of this study

This work is constructed as follows: some basic observations connected to PFTGs are provided in “Preliminaries”. “Picture fuzzy tolerance graphs” presents new notions of PF max, min and sum TGs and studies several properties of them. “Picture fuzzy $\phi$-tolerance chain graph” gives the idea of PF$\phi$-TCGs with some properties. An application of PFmin TG in sports competition is given in “Application of tolerance graph in sports competition”. Before the concluding section, comparison of the proposed TGs with existing IFTGs is given. Finally, the conclusion is presented in “Conclusion”.

Preliminaries

This section, we reminisce some preliminary observations related to our study such as TG, bounded TG, unit TG, proper TG, interval containment graph, max TG, PF set and PFG.

Definition 2.1

[13] A graph $G=(V,B)$ is a TG if $\exists$ a collection of the closed intervals $I=\{I_{r}: r\in V\}$ on $R_{L}$ with the corresponding positive tolerances $t=\{t_{r}: r\in V\}$ satisfying $rs\in B\Leftrightarrow |I_{r}\cap I_{s}|\ge \min \{t_{r},t_{s}\}$, where |I| is the length of I and the pair (I, t) is known as tolerance representation (TR) of G.

A TR (I, t) is bounded if $t_{r}\le |I_{r}|$ for all $r\in V$. A TG is bounded [13] if it confess a bounded TR. An interval representation (IR) is an unit-IR when all intervals are of equal length and it will be proper-IR when no interval contained completely in another.

Definition 2.2

[13] A vertex $r\in G$ is an assertive if for every TR (I, t) of G replacing $t_{r}$ by $\min \{t_{r},|I_{r}|\}$ leaves the TG unchanged. An assertive vertex is one which never requires unbounded tolerance. If each vertex of a TG G is assertive, then G is bounded TG.

If r be a vertex of G and $\mathrm{{adj}}(r)-\mathrm{{adj}}(s)\ne \emptyset$, $\forall s\ne r$ in G, then r is assertive, where $\mathrm{{adj}}(r)$ is the set of all vertices adjacent to r by an edge in G.

Definition 2.3

[5] A unit TG is one that has a TR in which all intervals are of equal length and proper TG is one that has a TR in which no interval contained properly in another.

Now we define interval containment (IC) graph and max TG below.

Definition 2.4

[13] An IC graph $G=(V,B)$ is represented by the set of intervals $I=\{I_{r}: r\in V\}$ such that an edge $(r,s)\in B(G)$ if one of $I_{r},I_{s}$ contains the other. This representation is known as IC representation.

Definition 2.5

[14] A graph $G=(V,B)$ is a max TG if $\exists$ a collection of the closed intervals $I=\{I_{r}: r\in V\}$ on $R_{L}$ with the corresponding positive tolerances $t=\{t_{r}: r\in V\}$ satisfying $rs\in B\Leftrightarrow |I_{r}\cap I_{s}|\ge \max \{t_{r},t_{s}\}$. For max TGs, we may assume $t_{r}\le |I_{r}|$ $\forall$ $r\in V$; otherwise, r becomes isolated. A max TG is a unit-max TG if $I_{r}=I_{s}$ $\forall$ $r,s\in V$.

Definition 2.6

[6] A PF set A is defined on an universe X as $A=\{p,(\mu _{A}(p),\eta _{A}(p),\nu _{A}(p)):p\in X\}$, where $\mu _{A}(p),\eta _{A}(p),\nu _{A}(p)\in [0,1]$ are the degree of truth membership (TMS), degree of abstinence membership (AMS), degree of false membership (FMS) of $p\in A$, respectively, with $0\le \mu _{A}(p)+\eta _{A}(p)+\nu _{A}(p)\le 1$ $\forall p\in X$. Also $\forall p\in X$, $D_{A}(p)=1-(\mu _{A}(p)+\eta _{A}(p)+\nu _{A}(p))$ represent denial degree of $p\in A$.

Now, we define support, core and height of a PF set. Also, define PFG with an example as follows:

Definition 2.7

[9] Let $A=\{p,(\mu _{A}(p),\eta _{A}(p),\nu _{A}(p)):p\in X\}$ be a PF set. The support of A is defined as $\mathrm{{Supp}}(A)$=$\{p\in V$: $\mu _{A}(p)\ge 0,\eta _{A}(p)\ge 0$ and $\nu _{A}(p)\ge 0\}$ and its support length (SL) is $s(A)=|\mathrm{{Supp}}(A)|$. The core of A is defined as $\mathrm{{Core}}(A)$=$\{p\in V$: $\mu _{A}(p)= 1,\eta _{A}(p)= 0$ and $\nu _{A}(p)= 0\}$ and its core length (CL) is $c(A)=|\mathrm{{Core}}(A)|$. The height of A is defined as $h(A)=(\sup \nolimits _{p\in V}\mu _{A}(p),$ $\sup \nolimits _{p\in V}\eta _{A}(p),$ $\inf \nolimits _{p\in V} \nu _{A}(p))=(h_{\mu }(A),h_{\eta }(A),h_{\nu }(A))$.

Definition 2.8

[1] A PFG is $G=(V,A,B)$ where $A=(\mu _{A},\eta _{A},\nu _{A})$, $B=(\mu _{B},\eta _{B},\nu _{B})$ and

• (i) $V=\{r_{1},r_{2}, \ldots ,r_{n}\}$ such that $\mu _{A},\eta _{A},\nu _{A}:V\rightarrow [0,1]$ are the TMS, AMS and FMS of $r_{i}\in V$, respectively, with $0\le \mu _{A}(r_{i})+\eta _{A}(r_{i})+\nu _{A}(r_{i})\le 1$ $\forall r_{i}\in V$, $({i=1,2,\ldots ,n})$.

• (ii) $\mu _{B},\eta _{B},\nu _{B}:V\times V\rightarrow [0,1]$ are the TMS, AMS and FMS of edge $(r_{i},r_{j})$, respectively, such that $\mu _{B}(r_{i},r_{j})\le \min \{\mu _{A}(r_{i}),\mu _{A}(r_{j})\},$ $\eta _{B}(r_{i},r_{j})\le \min \{\eta _{A}(r_{i}),\eta _{A}(r_{j})\}$ and $\nu _{B}(r_{i},r_{j})\le \max \{\nu _{A}(r_{i}),\nu _{A}(r_{j})\}$ with $0\le \mu _{B}(r_{i},r_{j})+\eta _{B}(r_{i},r_{j})+\nu _{B}(r_{i},r_{j})\le 1$ for every $(r_{i},r_{j})$, $({i,j=1,2, \ldots ,n})$.

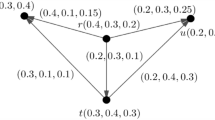
Example 2.9

We consider a PFG $G=(V,A,B)$ as shown in Fig. 1, where $V=\{r_1,r_2,r_3,r_4\}$, $A=\{(r_1,(0.35,0.2,0.1)), (r_2,(0.4,0.3,0.2)),(r_3,(0.3,0.1,0.5)),(r_4,(0.15,0.4,0.3))\}$ is a PF set on V and $B=\{(r_1r_2,(0.3,0.2,0.2)), (r_1r_4,(0.15,0.2,0.3)),(r_2r_3,(0.2,0.1,0.5)),(r_2r_4,(0.1,0.3,0.3)), (r_3r_4,(0.15,0.1,0.5))\}$ is the PF relation on a PF subset of $V \times V$. The TMS, AMS and FMS of the vertex $r_1$ are 0.35, 0.2 and 0.1, respectively, and similarly for other vertices and edges.

Fig. 1

Example of a PFG

Picture fuzzy tolerance graphs

In this section, first we define PF intersection graph and then PF$\phi$-TG. Here $\phi$ is restricted as one of the functions of maximum, minimum and sum. We describe PF max, min and sum TGs, respectively, and study some important properties of them.

Definition 3.1

Let $F=\{A_{i}:{i=1,2,\ldots ,n}\}$ be the finite collection of PF sets defined on X and consider each PF set as vertex of the PFG. Let $V=\{r_{i}:{i=1,2,\ldots ,n}\}$ be the vertex set. Then the PF intersection graph of F is a PFG $\mathrm{{Int}}(F)=(V,A,B)$. The TMS, AMS and FMS of the vertices are given by $\mu _{A}(r_{i})=h_{\mu }(A_{i})$, $\eta _{A}(r_{i})=h_{\eta }(A_{i})$ and $\nu _{A}(r_{i})=h_{\nu }(A_{i})$. Also, the TMS, AMS and FMS of an edge $(r_{j},r_{k})\in \mathrm{{Int}}(F)$ are given by $\mu _{B}(r_{j},r_{k})=\left\{ \begin{array}{ll} h_{\mu }(A_{j}\cap A_{k}), &{} \mathrm{if }\;\; j\ne k \;\;\\ 0, &{} \mathrm{if}\;\; j=k, \;\; \end{array}\right.$

$\eta _{B}(r_{j},r_{k})=\left\{ \begin{array}{ll} h_{\eta }(A_{j}\cap A_{k}), &{} \mathrm{if }\;\; j\ne k \;\;\\ 0, &{} \mathrm{if}\;\; j=k, \;\; \end{array}\right.$ and

$\nu _{B}(r_{j},r_{k})=\left\{ \begin{array}{ll} h_{\nu }(A_{j}\cap A_{k}), &{} \mathrm{if }\;\; j\ne k \;\;\\ 0, &{} \mathrm{if}\;\; j=k. \;\; \end{array}\right.$

Now, we will discuss about the notion of PFI, PFTG and PF$\phi$-TG.

Definition 3.2

A PFI I on a real interval $I$ is a PF set $I: I \rightarrow [0,1]$, it is denoted by $I=\big (I ,(\mu _{A}(I ),\eta _{A}(I ),\nu _{A}(I ))\big )$. A PFI I is normal and convex PF-subset of $I$. A PFI I is normal if $\exists$ a $r\in I$ such that $h(r)=(1,0,0)$ and convex if the ordering $r\le s\le t$ implies that

$$\begin{aligned}&\mu _{A}(s)\ge \min \{\mu _{A}(r),\mu _{A}(t)\},\\&\eta _{A}(s)\le \min \{\eta _{A}(r),\eta _{A}(t)\}, \\&\nu _{A}(s)\le \max \{\nu _{A}(r),\nu _{A}(t)\}. \end{aligned}$$

Definition 3.3

The PFT T of a PFI is an arbitrary PFI whose CL is a positive real number. If the real number is taken as L and $|i_{n}-i_{n-1}|=L$, where $i_{n},i_{n-1}\in R$, then the PFT is the PF set of the interval $[i_{n}-i_{n-1}]$. s(T) and c(T) are, respectively, the SL and CL of T. PFT may be a PF number. The PFT is shown in Fig. 2.

Fig. 2

Example of a PFT

PF$\phi$-TG is the generalization of PF interval graph (PFIG) which is defined below and explained a general characterization of it as follows:

Definition 3.4

Let $\phi :R^{+}\times R^{+}\rightarrow R^{+}$ be a function, where $R^{+}$ is the set of all positive real numbers. Let $I=\{I_{i}:{i=1,2,\ldots ,n}\}$ be a finite family of PFIs on $R_{L}$ along with corresponding PFTs $T=\{T_{i}:{i=1,2,\ldots ,n}\}$. Consider each PFI as vertex of the PF$\phi$-TG. Let $V=\{r_{i}:{i=1,2,\ldots ,n}\}$ be the vertex set and corresponding PF$\phi$-TG is the PF graph $G=(V,A,B)$. The TMS, AMS and FMS of the vertices are given by $\mu _{A}(r_{i})=h_{\mu }(I_{i})$, $\eta _{A}(r_{i})=h_{\eta }(I_{i})$ and $\nu _{A}(r_{i})=h_{\nu }(I_{i})$. Also the TMS, AMS and FMS of the edge $(r_{i},r_{j})$ in G are, respectively,the following:

$$\begin{aligned} \mu _{B}(r_{i},r_{j})=\left\{ \begin{array}{ll} 1, &{} \mathrm{if}\;\; c(I_{i}\cap I_{j})\ge \phi \{c(T_{i}),c(T_{j})\} \;\;\\ \frac{s(I_{i}\cap I_{j})- \phi \{s(T_{i}),s(T_{j})\}}{s(I_{i}\cap I_{j})}h_{\mu }(I_{i}\cap I_{j}), &{} \mathrm{if }\;\; s(I_{i}\cap I_{j})\ge \phi \{s(T_{i}),s(T_{j})\} \;\;\\ 0, &{} \mathrm{}\;\; \mathrm{{otherwise}}. \;\;\\ \end{array}\right. \\ \eta _{B}(r_{i},r_{j})=\left\{ \begin{array}{ll} 0, &{} \mathrm{if}\;\; c(I_{i}\cap I_{j})\ge \phi \{c(T_{i}),c(T_{j})\} \;\;\\ \frac{s(I_{i}\cap I_{j})- \phi \{s(T_{i}),s(T_{j})\}}{s(I_{i}\cap I_{j})}h_{\eta }(I_{i}\cap I_{j}), &{} \mathrm{if }\;\; s(I_{i}\cap I_{j})\ge \phi \{s(T_{i}),s(T_{j})\} \;\;\\ 0, &{} \mathrm{}\;\; \mathrm{{otherwise}}. \;\;\\ \end{array}\right. \\ \nu _{B}(r_{i},r_{j})=\left\{ \begin{array}{ll} 0, &{} \mathrm{if}\;\; c(I_{i}\cap I_{j})\ge \phi \{c(T_{i}),c(T_{j})\} \;\;\\ \frac{s(I_{i}\cap I_{j})- \phi \{s(T_{i}),s(T_{j})\}}{s(I_{i}\cap I_{j})}h_{\nu }(I_{i}\cap I_{j}), &{} \mathrm{if }\;\; s(I_{i}\cap I_{j})\ge \phi \{s(T_{i}),s(T_{j})\} \;\;\\ 1, &{} \mathrm{}\;\; \mathrm{{otherwise}}. \;\;\\ \end{array}\right. \end{aligned}$$

where $c(I_{i}\cap I_{j})$ and $s(I_{i}\cap I_{j})$ are the CL and SL of $I_{i}\cap I_{j}$, respectively. Also, $h_{\mu }(I_{i}\cap I_{j})$, $h_{\eta }(I_{i}\cap I_{j})$ and $h_{\nu }(I_{i}\cap I_{j})$ are the TMS, AMS and FMS of the height of $I_{i}\cap I_{j}$, respectively.

Theorem 3.5

Let $G=(V,A,B)$ be the PF$\phi$-TG. If $h(I_{i}\cap I_{j})=(1,0,0)$ and $s(I_{i}\cap I_{j})\ge 2\phi \{s(T_{i}),s(T_{j})\}$. Then $\mu _{B}(r_{i},r_{j})\le \frac{1}{2}$, $\eta _{B}(r_{i},r_{j})\le \frac{1}{2}$ and $\nu _{B}(r_{i},r_{j})\le \frac{1}{2}$ $\forall (r_{i},r_{j})\in G$.

Proof

Let $G=(V,A,B)$ be a PF$\phi$-TG of the PFIs $I=\{I_{i}:{i=1,2,\ldots ,n}\}$ with the corresponding PFTs $T=\{T_{i}:{i=1,2,\ldots ,n}\}$. Since $h(I_{i}\cap I_{j})=(1,0,0)$, then $h_{\mu }(I_{i}\cap I_{j})=1$, $h_{\eta }(I_{i}\cap I_{j})=0$ and $h_{\nu }(I_{i}\cap I_{j})=0$. Also, since $s(I_{i}\cap I_{j})\ge 2\phi \{s(T_{i}),s(T_{j})\}$, then $s(I_{i}\cap I_{j})\ge \phi \{s(T_{i}),s(T_{j})\}$. Therefore, $\mu _{B}(r_{i},r_{j})=\frac{s(I_{i}\cap I_{j})- \phi \{s(T_{i}),s(T_{j})\}}{s(I_{i}\cap I_{j})}h_{\mu }(I_{i}\cap I_{j})=[1-\frac{\phi \{s(T_{i}),s(T_{j})\}}{s(I_{i}\cap I_{j})}]\times 1\le 1-\frac{1}{2}=\frac{1}{2}$, $\eta _{B}(r_{i},r_{j})=\frac{s(I_{i}\cap I_{j})- \phi \{s(T_{i}),s(T_{j})\}}{s(I_{i}\cap I_{j})}h_{\mu }(I_{i}\cap I_{j})=[1-\frac{\phi \{s(T_{i}),s(T_{j})\}}{s(I_{i}\cap I_{j})}]\times 0=0<\frac{1}{2}$ and $\nu _{B}(r_{i},r_{j})=\frac{s(I_{i}\cap I_{j})- \phi \{s(T_{i}),s(T_{j})\}}{s(I_{i}\cap I_{j})}h_{\mu }(I_{i}\cap I_{j})=[1-\frac{\phi \{s(T_{i}),s(T_{j})\}}{s(I_{i}\cap I_{j})}]\times 0=0<\frac{1}{2}$.

Picture fuzzy min-tolerance graphs

The PF min-tolerance graph (PFmin TG) is a PF$\phi$-TG in which $\phi$ is restricted to the minimum (min) function defined by $\phi (r,s)=\min \{r,s\}$. The PFmin-TG is defined below.

Definition 3.6

Let $I=\{I_{i}:{i=1,2,\ldots ,n}\}$ be a finite collection of PFIs on $R_{L}$ along with corresponding PFTs $T=\{T_{i}:{i=1,2,\ldots ,n}\}$. Consider each PFI as vertex of the PFmin-TG. Let $V=\{r_{i}:{i=1,2,\ldots ,n}\}$ be the vertex set and corresponding PFmin-TG is the PF graph $G=(V,A,B)$. The TMS, AMS and FMS of the vertices are given by $\mu _{A}(r_{i})=h_{\mu }(I_{i})$, $\eta _{A}(r_{i})=h_{\eta }(I_{i})$ and $\nu _{A}(r_{i})=h_{\nu }(I_{i})$. Also the TMS, AMS and FMS of the edge $(r_{i},r_{j})$ in G are, respectively, the following:

$$\begin{aligned} \mu _{B}(r_{i},r_{j})= \left\{ \begin{array}{ll} 1, &{} \mathrm{if}\;\; c(I_{i}\cap I_{j})\ge \min \{c(T_{i}),c(T_{j})\} \;\;\\ \frac{s(I_{i}\cap I_{j})- \min \{s(T_{i}),s(T_{j})\}}{s(I_{i}\cap I_{j})}h_{\mu }(I_{i}\cap I_{j}), &{} \mathrm{if }\;\; s(I_{i}\cap I_{j})\ge \min \{s(T_{i}),s(T_{j})\} \;\;\\ 0, &{} \mathrm{}\;\; \mathrm{{otherwise}}. \;\;\\ \end{array}\right. \\ \eta _{B}(r_{i},r_{j})= \left\{ \begin{array}{ll} 0, &{} \mathrm{if}\;\; c(I_{i}\cap I_{j})\ge \min \{c(T_{i}),c(T_{j})\} \;\;\\ \frac{s(I_{i}\cap I_{j})- \min \{s(T_{i}),s(T_{j})\}}{s(I_{i}\cap I_{j})}h_{\eta }(I_{i}\cap I_{j}), &{} \mathrm{if }\;\; s(I_{i}\cap I_{j})\ge \min \{s(T_{i}),s(T_{j})\} \;\;\\ 0, &{} \mathrm{}\;\; \mathrm{{otherwise}}. \;\;\\ \end{array}\right. \\ \nu _{B}(r_{i},r_{j})= \left\{ \begin{array}{ll} 0, &{} \mathrm{if}\;\; c(I_{i}\cap I_{j})\ge \min \{c(T_{i}),c(T_{j})\} \;\;\\ \frac{s(I_{i}\cap I_{j})- \min \{s(T_{i}),s(T_{j})\}}{s(I_{i}\cap I_{j})}h_{\nu }(I_{i}\cap I_{j}), &{} \mathrm{if }\;\; s(I_{i}\cap I_{j})\ge \min \{s(T_{i}),s(T_{j})\} \;\;\\ 1, &{} \mathrm{}\;\; \mathrm{{otherwise}}. \;\;\\ \end{array}\right. \end{aligned}$$

We explain it by the following example:

Example 3.7

We consider four PFIs $\{I_{i}:i=1,2,3,4\}$ on $R_{L}$ along with corresponding PFTs $\{T_{i}:i=1,2,3,4\}$. Suppose PFIs are the vertices and $V=\{r_{i}:i=1,2,3,4\}$ is the vertex set of PFmin TG $G=(V,A,B)$. Let the support of these PFIs are respectively [1, 7.5], [3.5, 10], [5, 11], [10.5, 17]. Also the cores are respectively [2, 6], [4, 8], [6.5, 9], [12, 15.5] and $s(T_{1})=5$, $s(T_{2})=4.25$, $s(T_{3})=2$, $s(T_{4})=2.75$ and $c(T_{1})=1.5$, $c(T_{2})=3$, $c(T_{3})=4.5$, $c(T_{4})=1.25$. The corresponding PFIs are shown in Fig. 3.

We have $I_{1}\cap I_{2}=[3.5,7.5]$, $I_{1}\cap I_{3}=[5,7.5]$, $I_{2}\cap I_{3}=[5,10]$, $I_{3}\cap I_{4}=[10.5,11]$. Also, $s(I_{1}\cap I_{2})=4$, $s(I_{1}\cap I_{3})=2.5$, $s(I_{2}\cap I_{3})=5$, $s(I_{3}\cap I_{4})=0.5$ and $c(I_{1}\cap I_{2})=2$, $c(I_{1}\cap I_{3})=0$, $c(I_{2}\cap I_{3})=1.5$, $c(I_{3}\cap I_{4})=0$. Here, $h(I_{1}\cap I_{2})=(1,0,0)$, $h(I_{1}\cap I_{3})=(0.83,0.05,0.12)$, $h(I_{2}\cap I_{3})=(1,0,0)$, $h(I_{3}\cap I_{4})=(0.14,0.22,0.64)$. Since, $I_{1}\cap I_{2}\ne \emptyset$ and $c(I_{1}\cap I_{2})\ge \min \{c(T_{1}),c(T_{2})\}$, $(r_{1},r_{2})$ is an edge of G with TMS, AMS and FMS (1, 0, 0). Also, $I_{1}\cap I_{3}\ne \emptyset$ and $s(I_{1}\cap I_{3})\ge \min \{s(T_{1}),s(T_{3})\}$. Hence $(r_{1},r_{3})$ is an edge of G with TMS, AMS and FMS (0.16, 0.01, 0.02). Again, $I_{2}\cap I_{3}\ne \emptyset$ and $s(I_{2}\cap I_{3})\ge \min \{s(T_{2}),s(T_{3})\}$. So $(r_{2},r_{3})$ is an edge of G with TMS, AMS and FMS (0.6, 0, 0). As, $I_{3}\cap I_{4}\ne \emptyset$ and $c(I_{3}\cap I_{4})\ngeq \min \{c(T_{3}),c(T_{4})\}$, $s(I_{3}\cap I_{4})\ngeq \min \{s(T_{3}),s(T_{4})\}$, then $(r_{3},r_{4})$ is an edge of G with TMS, AMS and FMS (0, 0, 1). The corresponding PFmin TG is shown in Fig. 4.

Fig. 3

Representation of PFIs

Fig. 4

Corresponding PFmin-TG

Definition 3.8

Let $I=\{I_{i}:{i=1,2,\ldots ,n}\}$ be a finite collection of PFIs on $R_{L}$ along with corresponding PFTs $T=\{T_{i}:{i=1,2,\ldots ,n}\}$. Let $c(I_{i})$, $s(I_{i})$ be the CL and SL of the PFI $I_{i}$ and $c(T_{i})$, $s(T_{i})$ be the CL and SL of the PFT $T_{i}$, respectively, such that $c(I_{i})\ge c(T_{i})$ and $s(I_{i})\ge s(T_{i})$ of the PFTG. Then the PFTG is called bounded PFTG.

Theorem 3.9

If G is a PFIG, then G is PFmin TG with constant CL and constant SL.

Proof

Let G be a PFIG with PFI $I_{i}$ that is assigned to be the vertex of V. Let CL of the PFIs $I_{i}$, $I_{j}$ be denoted by $c(I_{i})$, $c(I_{j})$ and SL of that be denoted by $s(I_{i})$, $s(I_{j})$, respectively. Let $c(I_{i}\cap I_{j})= \min \{c(I_{i}),c(I_{j})\}$ and $s(I_{i}\cap I_{j})= \min \{s(I_{i}),s(I_{j})\}$.

Let $n_{1}$, $n_{2}$ be two positive real numbers such that $c(I_{i}\cap I_{j})>n_{1}$ and $s(I_{i}\cap I_{j})>n_{2}$. Then $\min \{c(I_{i}),c(I_{j})\}>n_{1}$ and $\min \{s(I_{i}),s(I_{j})\}>n_{2}$. Therefore, the PFI $I_{i}$ together with PFT with CL $n_{1}$ and SL $n_{2}$ give PFT representation.

Theorem 3.10

If G is a PFTG with constant CL and constant SL, then G is bounded PFTG.

Proof

Let $I=\{I_{i}:{i=1,2,\ldots ,n}\}$ be a finite collection of PFIs on $R_{L}$ along with corresponding PFTs $T=\{T_{i}:{i=1,2,\ldots ,n}\}$. Let $G=(V,A,B)$ be PFTG with PFI I and PFT T. Let $n_{1}$, $n_{2}$ be two positive real numbers such that $c(T_{i})=n_{1}$ and $s(T_{i})=n_{2}$ for ${i=1,2,\ldots ,n}$.

If $c(I_{i})\ge n_{1}$ and $s(I_{i})\ge n_{2}$, then $c(I_{i})\ge c(T_{i})$ and $s(I_{i})\ge s(T_{i})$ $\forall$ ${i=1,2,\ldots ,n}$. Then G is bounded PFTG.

If $c(I_{i})< n_{1}$ and $s(I_{i})<n_{2}$ for some i and j, we take $c(I_{i})=n_{1}$ and $s(I_{i})=n_{2}$ to make G is bounded. Therefore, G is bounded PFTG.

Definition 3.11

Let G be a PFTG. A vertex r of G is an assertive if for every PFTR of G replacing $c(T_{r})$ by $\min \{c(T_{r}),|c(I_{r})|\}$ and $s(T_{r})$ by $\min \{s(T_{r}),|s(I_{r})|\}$ leaves the PFTG unchanged. An assertive vertex is one which never requires unbounded PFT. If each vertex of a PFTG G is assertive, then G is bounded PFTG.

If r be a vertex of G and $\mathrm{{adj}}(r)-\mathrm{{adj}}(s)\ne \emptyset$, $\forall s\ne r$ in G, then r is assertive, where $\mathrm{{adj}}(r)$ is the set of all vertices adjacent to r by an edge in G.

Theorem 3.12

Let G be a PFTG that is not bounded and let U be the set of all non assertive vertices. Then, the graph $G^{*}$ formed in addition to a new pendant vertex to each member of U, is not a PFTG.

Proof

If possible let, $G^{*}$ be a PFTG along with arbitrary PFTs associated to each vertex of $G^{*}$. Since each $r\in U$ has an exclusive new neighbor in $G^{*}$, then each r of U is assertive in $G^{*}$. Therefore, we may assume that $c(I_{r})\ge c(T_{r})$ and $s(I_{r})\ge s(T_{r})$ $\forall r\in U$. Thus, we obtain a TR for G in which all non assertive vertices have bounded PFT. This shows that G is a bounded PFTG, which contradicts the assumption that G is not a bounded PFTG. Hence $G^{*}$ is not a PFTG.

We will explain it by the following example:

Example 3.13

We consider an unbounded PFTG T. The non assertive vertices of T are its three leaves $r_1$, $r_5$ and $r_7$. If we add a new pendant vertex to each non assertive vertices of T, then it will form a new graph $T^{*}$ as shown in Fig. 5. By Theorem 3.12, it is not a PFTG.

Fig. 5

Unbounded PFTG (T) and non PFTG $(T^{*})$

Picture fuzzy interval containment graphs

Now, we define PF interval containment graphs (PFICGs).

Definition 3.14

Let $I=\{I_{i}:{i=1,2,\ldots ,n}\}$ be a finite collection of PFIs on $R_{L}$. Consider each PFI as vertex as the PFICG. Let $V=\{r_{i}:{i=1,2,\ldots ,n}\}$ be the vertex set and corresponding PFICG $G=(V,A,B)$. The TMS, AMS and FMS of the vertices are given by $\mu _{A}(r_{i})=h_{\mu }(I_{i})$, $\eta _{A}(r_{i})=h_{\eta }(I_{i})$ and $\nu _{A}(r_{i})=h_{\nu }(I_{i})$. Also the TMS, AMS and FMS of the edge $(r_{i},r_{j})$ in G are, respectively, as follows:

$$\begin{aligned}&\mu _{B}(r_{i},r_{j})=\left\{ \begin{array}{ll} 1, \mathrm{\ if \ support \ and \ core \ of \ one \ of \ I_{i}, \ I_{j} \ include \ the \ other} \;\;\\ \frac{1}{2}\bigg [\frac{c(I_{i}\cap I_{j})}{\min \{c(I_{i}),c(I_{j})\}}+\frac{s(I_{i}\cap I_{j})}{\min \{s(I_{i}),s(I_{j})\}}\bigg ]h_{\mu }(I_{i}\cap I_{j}), \mathrm{\ otherwise} \;\;\\ \end{array}\right. \\&\eta _{B}(r_{i},r_{j})=\left\{ \begin{array}{ll} 0, \mathrm{\ if \ support \ and \ core \ of \ one \ of \ I_{i}, \ I_{j} \ include \ the \ other} \;\;\\ \frac{1}{2}\bigg [\frac{c(I_{i}\cap I_{j})}{\min \{c(I_{i}),c(I_{j})\}}+\frac{s(I_{i}\cap I_{j})}{\min \{s(I_{i}),s(I_{j})\}}\bigg ]h_{\eta }(I_{i}\cap I_{j}), \mathrm{\ otherwise} \;\;\\ \end{array}\right. \\&\nu _{B}(r_{i},r_{j})=\left\{ \begin{array}{ll} 0, \mathrm{\ if \ support \ and \ core \ of \ one \ of \ I_{i}, \ I_{j} \ include \ the \ other} \;\;\\ \frac{1}{2}\bigg [\frac{c(I_{i}\cap I_{j})}{\min \{c(I_{i}),c(I_{j})\}}+\frac{s(I_{i}\cap I_{j})}{\min \{s(I_{i}),s(I_{j})\}}\bigg ]h_{\nu }(I_{i}\cap I_{j}), \mathrm{\ otherwise} \;\;\\ \end{array}\right. \end{aligned}$$

We will explain it by the following example:

Example 3.15

We consider four PFIs $\{I_{i}:i=1,2,3,4\}$ on $R_{L}$ along with corresponding PFTs $\{T_{i}:i=1,2,3,4\}$. Let the support of these PFIs be, respectively, [1, 7.5], [3.5, 10], [5, 11], [10.5, 17]. Also the cores are, respectively, [2, 6], [4, 8], [6.5, 9], [12, 15.5] and $s(T_{1})=5$, $s(T_{2})=4.25$, $s(T_{3})=2$, $s(T_{4})=2.75$ and $c(T_{1})=1.5$, $c(T_{2})=3$, $c(T_{3})=4.5$, $c(T_{4})=1.25$. The corresponding PFIs are shown in Fig. 6.

Then $h(I_{1}\cap I_{2})=(1,0,0)$, $h(I_{1}\cap I_{3})=(0.83,0.05,0.12)$, $h(I_{2}\cap I_{3})=(1,0,0)$, $h(I_{3}\cap I_{4})=(0.14,0.22,0.64)$. Therefore, the TMS, AMS and FMS of the edges $(r_{1},r_{2})$, $(r_{2},r_{3})$, $(r_{1},r_{3})$ and $(r_{3},r_{4})$ are, respectively, (0.55, 0, 0), (0.71, 0, 0), (0.17, 0.01, 0.02) and (0.005, 0.009, 0.026). The corresponding PFICG is shown in Fig. 7.

Fig. 6

Representation of PFIs

Fig. 7

Corresponding PFICG

Theorem 3.16

If $G=(V,A,B)$ is a PFICG with either $(\mu _{B}(r,s),\eta _{B}(r,s),\nu _{B}(r,s))=(1,0,0)$ or (0, 0, 1) for any edge $(r,s)\in B$, then G has PFT representation with CL and SL of a PFI are equal to the CL and SL of the corresponding PFT, respectively.

Proof

Let $I=\{I_{i}:{i=1,2,\ldots ,n}\}$ be a finite collection of PFIs on $R_{L}$. Consider each PFI as vertex of the PFICG. Let $V=\{r_{i}:{i=1,2,\ldots ,n}\}$ be the vertex set. If $(\mu _{B}(r,s),\eta _{B}(r,s),\nu _{B}(r,s))=(1,0,0)$ for the edge $(r,s)\in B$. Then the support and core of one PFI include the other PFI. Let $G^{*}=(V,A,B^{\prime })$ be a PFTG with PFI I with the corresponding PFT $T=\{T_{i}:{i=1,2,\ldots ,n}\}$ such that $c(I_{r})=c(T_{r})$ and $s(I_{r})=s(T_{r})$. Then, $c(I_{r}\cap I_{s})=\min \{c(I_{r}),c(I_{s})\}=\min \{c(T_{r}),c(T_{s})\}$. So, $(\mu _{B^{\prime }}(r,s),\eta _{B^{\prime }}(r,s),\nu _{B^{\prime }}(r,s))=(1,0,0)$.

Again, if $(\mu _{B}(r,s),\eta _{B}(r,s),\nu _{B}(r,s))=(0,0,1)$. Then there is no common part of the support and core between two PFIs. Therefore, $(\mu _{B^{\prime }}(r,s),\eta _{B^{\prime }}(r,s),\nu _{B^{\prime }}(r,s))=(0,0,1)$.

This proves that G has PFT representation with CL and SL of a PFI are equal to the CL and SL of the corresponding PFT, respectively.

Picture fuzzy max-tolerance graphs

A PF max-tolerance graph (PFmax TG) is a PF$\phi$-TG in which $\phi$ is restricted to the maximum (max) function defined by $\phi (r,s)= \max \{r,s\}$. The PFmax TG is defined below as follows:

Definition 3.17

Let $I=\{I_{i}:{i=1,2,\ldots ,n}\}$ be a finite collection of PFIs on $R_{L}$ along with corresponding PFTs $T=\{T_{i}:{i=1,2,\ldots ,n}\}$. Consider each PFI as vertex of the PFmax-TG. Let $V=\{r_{i}:{i=1,2,\ldots ,n}\}$ be the vertex set and corresponding PFmax-TG is the PF graph $G=(V,A,B)$. The TMS, AMS and FMS of the vertices are given by $\mu _{A}(r_{i})=h_{\mu }(I_{i})$, $\eta _{A}(r_{i})=h_{\eta }(I_{i})$ and $\nu _{A}(r_{i})=h_{\nu }(I_{i})$. Also the TMS, AMS and FMS of the edge $(r_{i},r_{j})$ in G are, respectively, as fpllows:

$$\begin{aligned}&\mu _{B}(r_{i},r_{j})=\left\{ \begin{array}{ll} 1, &{} \mathrm{if}\;\; c(I_{i}\cap I_{j})\ge \max \{c(T_{i}),c(T_{j})\} \;\;\\ \frac{s(I_{i}\cap I_{j})- \max \{s(T_{i}),s(T_{j})\}}{s(I_{i}\cap I_{j})}h_{\mu }(I_{i}\cap I_{j}), &{} \mathrm{if }\;\; s(I_{i}\cap I_{j})\ge \max \{s(T_{i}),s(T_{j})\} \;\;\\ 0, &{} \mathrm{}\;\; \mathrm{{otherwise}}. \;\;\\ \end{array}\right. \\&\eta _{B}(r_{i},r_{j})=\left\{ \begin{array}{ll} 0, &{} \mathrm{if}\;\; c(I_{i}\cap I_{j})\ge \max \{c(T_{i}),c(T_{j})\} \;\;\\ \frac{s(I_{i}\cap I_{j})- \max \{s(T_{i}),s(T_{j})\}}{s(I_{i}\cap I_{j})}h_{\eta }(I_{i}\cap I_{j}), &{} \mathrm{if }\;\; s(I_{i}\cap I_{j})\ge \max \{s(T_{i}),s(T_{j})\} \;\;\\ 0, &{} \mathrm{}\;\; \mathrm{{otherwise}}. \;\;\\ \end{array}\right. \\&\nu _{B}(r_{i},r_{j})=\left\{ \begin{array}{ll} 0, &{} \mathrm{if}\;\; c(I_{i}\cap I_{j})\ge \max \{c(T_{i}),c(T_{j})\} \;\;\\ \frac{s(I_{i}\cap I_{j})- \max \{s(T_{i}),s(T_{j})\}}{s(I_{i}\cap I_{j})}h_{\nu }(I_{i}\cap I_{j}), &{} \mathrm{if }\;\; s(I_{i}\cap I_{j})\ge \max \{s(T_{i}),s(T_{j})\} \;\;\\ 1, &{} \mathrm{}\;\; \mathrm{{otherwise}}. \;\;\\ \end{array}\right. \end{aligned}$$

An example is given to explain the above.

Example 3.18

We consider three PFIs $\{I_{i}:i=1,2,3\}$ on $R_{L}$ along with corresponding PFTs $\{T_{i}:i=1,2,3\}$. Let the support of these PFIs are respectively [1, 6], [4.5, 13], [9.5, 16.5] and also the cores are respectively [2, 5], [7, 10], [12, 15] and $s(T_{1})=1.5$, $s(T_{2})=2.5$, $s(T_{3})=3$ and $c(T_{1})=0.75$, $c(T_{2})=1.25$, $c(T_{3})=2$. The corresponding PFIs are shown in Fig. 8.

Then $h(I_{1}\cap I_{2})=(0.42,0.17,0.41)$, $h(I_{2}\cap I_{3})=(0.63,0.03,0.34)$. Therefore the TMS, AMS and FMS of the edges $(r_{1},r_{2})$ and $(r_{2},r_{3})$ are,respectively, (0, 0, 1) and (0.09, 0.004, 0.04). The corresponding PFmax TG is shown in Fig. 9.

Fig. 8

Representation of PFIs

Fig. 9

Corresponding PFmax TG

Now, we define PF unit TG and PF proper TG. The class of PF unit TG is a subset of the class of PF proper TG.

Definition 3.19

The PF unit max TG is a PFTG that has TR in which all PFIs have same SL and same CL. A PF proper TG is one that has a TR in which no PFI support and core contain completely in another PFI support and core.

Theorem 3.20

The chordless PF cycle $C_{n}$ is a PF unit max TG.

Proof

For $1\le i\le n$, we define core of PFI $I_{i}=[i,i+n]$. Then the CL of PFI $I_{i}$ is $c(I_{i})=n$. Also, let the CL of the corresponding PFT $c(T_{1})=c(T_{n})=1$ and $c(T_{j})=n-1$ for $2\le j\le n-1$. Then it is simple to verify that this is a PF unit max TG.

Picture fuzzy sum-tolerance graphs

A PF sum-tolerance graph (PFsum TG) is a PF$\phi$-TG in which $\phi$ is restricted to the sum function defined by $\phi (r,s)=\mathrm{{sum}}\{r,s\}$. The PFsum TG is defined below as follows:

Fig. 10

Representation of PFIs

Definition 3.21

Let $I=\{I_{i}:{i=1,2,\ldots ,n}\}$ be a finite collection of PFIs on $R_{L}$ along with corresponding PFTs $T=\{T_{i}:{i=1,2,\ldots ,n}\}$. Consider each PFI as vertex of the PFsum TG. Let $V=\{r_{i}:{i=1,2,\ldots ,n}\}$ be the vertex set and corresponding PFsum-TG is the PF graph $G=(V,A,B)$. The TMS, AMS and FMS of the vertices are given by $\mu _{A}(r_{i})=h_{\mu }(I_{i})$, $\eta _{A}(r_{i})=h_{\eta }(I_{i})$ and $\nu _{A}(r_{i})=h_{\nu }(I_{i})$. Also the TMS, AMS and FMS of the edge $(r_{i},r_{j})$ in G are,respectively, as follows:

$$\begin{aligned}&\mu _{B}(r_{i},r_{j})=\left\{ \begin{array}{ll} 1, &{} \mathrm{if}\;\; c(I_{i}\cap I_{j})\ge \mathrm{{sum}} \{c(T_{i}),c(T_{j})\} \;\;\\ \frac{s(I_{i}\cap I_{j})- \mathrm{{sum}} \{s(T_{i}),s(T_{j})\}}{s(I_{i}\cap I_{j})}h_{\mu }(I_{i}\cap I_{j}), &{} \mathrm{if }\;\; s(I_{i}\cap I_{j})\ge \mathrm{{sum}} \{s(T_{i}),s(T_{j})\} \;\;\\ 0, &{} \mathrm{}\;\; \mathrm{{otherwise}}. \;\;\\ \end{array}\right. \\&\eta _{B}(r_{i},r_{j})=\left\{ \begin{array}{ll} 0, &{} \mathrm{if}\;\; c(I_{i}\cap I_{j})\ge \mathrm{{sum}} \{c(T_{i}),c(T_{j})\} \;\;\\ \frac{s(I_{i}\cap I_{j})- \mathrm{{sum}} \{s(T_{i}),s(T_{j})\}}{s(I_{i}\cap I_{j})}h_{\eta }(I_{i}\cap I_{j}), &{} \mathrm{if }\;\; s(I_{i}\cap I_{j})\ge \mathrm{{sum}} \{s(T_{i}),s(T_{j})\} \;\;\\ 0, &{} \mathrm{}\;\; \mathrm{{otherwise}}. \;\;\\ \end{array}\right. \\&\nu _{B}(r_{i},r_{j})=\left\{ \begin{array}{ll} 0, &{} \mathrm{if}\;\; c(I_{i}\cap I_{j})\ge \mathrm{{sum}} \{c(T_{i}),c(T_{j})\} \;\;\\ \frac{s(I_{i}\cap I_{j})- \mathrm{{sum}} \{s(T_{i}),s(T_{j})\}}{s(I_{i}\cap I_{j})}h_{\nu }(I_{i}\cap I_{j}), &{} \mathrm{if }\;\; s(I_{i}\cap I_{j})\ge \mathrm{{sum}} \{s(T_{i}),s(T_{j})\} \;\;\\ 1, &{} \mathrm{}\;\; \mathrm{{otherwise}}. \;\;\\ \end{array}\right. \end{aligned}$$

We explain it by the following example:

Example 3.22

We consider three PFIs $\{I_{i}:i=1,2,3\}$ on $R_{L}$ along with corresponding PFTs $\{T_{i}:i=1,2,3\}$. Let the support of these PFIs are,respectively,[1.5, 7.5], [3.5, 9.5], [6, 14.5] and also the cores are,respectively, [3, 6], [5, 8], [9, 12] and $s(T_{1})=1.5$, $s(T_{2})=1$, $s(T_{3})=2$ and $c(T_{1})=1$, $c(T_{2})=0.5$, $c(T_{3})=1.5$. The corresponding PFIs are shown in Fig. 10.

Then $h(I_{1}\cap I_{2})=(1,0,0)$, $h(I_{1}\cap I_{3})=(0.33,0.07,0.6)$, $h(I_{2}\cap I_{3})=(0.77,0.01,0.22)$. Therefore,the TMS, AMS and FMS of the edges $(r_{1},r_{2})$, $(r_{1},r_{3})$ and $(r_{2},r_{3})$ are, respectively,(0.37, 0, 0), (0, 0, 1) and (0.11, 0.001, 0.03). The corresponding PFsum TG is shown in Fig. 11.

Fig. 11

Corresponding PFsum TG

Theorem 3.23

Every PFmin TG $G=(V,A,B)$ with $c(T_{i})=c(I_{i})$ and $s(T_{i})=s(I_{i})$ $\forall$ $i\in V(G)$ is a PFICG.

Proof

Let $G=(V,A,B)$ be a PFmin TG with PFIs $I=\{I_{i}:{i=1,2,\ldots ,n}\}$ and PFTs $T=\{T_{i}:{i=1,2,\ldots ,n}\}$ such that $c(T_{i})=c(I_{i})$ and $s(T_{i})=s(I_{i})$ $\forall$ $i\in V(G)$. We have by the definition of PFmin TG

$$\begin{aligned} \mu _{B}(r_{i},r_{j})=\left\{ \begin{array}{ll} 1, &{} \mathrm{if}\;\; c(I_{i}\cap I_{j})\ge \min \{c(T_{i}),c(T_{j})\} \;\;\\ \frac{s(I_{i}\cap I_{j})- \min \{s(T_{i}),s(T_{j})\}}{s(I_{i}\cap I_{j})}h_{\mu }(I_{i}\cap I_{j}), &{} \mathrm{if }\;\; s(I_{i}\cap I_{j})\ge \min \{s(T_{i}),s(T_{j})\} \;\;\\ 0, &{} \mathrm{}\;\; \mathrm{{otherwise}}. \;\;\\ \end{array}\right. \\ \eta _{B}(r_{i},r_{j})=\left\{ \begin{array}{ll} 0, &{} \mathrm{if}\;\; c(I_{i}\cap I_{j})\ge \min \{c(T_{i}),c(T_{j})\} \;\;\\ \frac{s(I_{i}\cap I_{j})- \min \{s(T_{i}),s(T_{j})\}}{s(I_{i}\cap I_{j})}h_{\eta }(I_{i}\cap I_{j}), &{} \mathrm{if }\;\; s(I_{i}\cap I_{j})\ge \min \{s(T_{i}),s(T_{j})\} \;\;\\ 0, &{} \mathrm{}\;\; \mathrm{{otherwise}}. \;\;\\ \end{array}\right. \\ \nu _{B}(r_{i},r_{j})=\left\{ \begin{array}{ll} 0, &{} \mathrm{if}\;\; c(I_{i}\cap I_{j})\ge \min \{c(T_{i}),c(T_{j})\} \;\;\\ \frac{s(I_{i}\cap I_{j})- \min \{s(T_{i}),s(T_{j})\}}{s(I_{i}\cap I_{j})}h_{\nu }(I_{i}\cap I_{j}), &{} \mathrm{if }\;\; s(I_{i}\cap I_{j})\ge \min \{s(T_{i}),s(T_{j})\} \;\;\\ 1, &{} \mathrm{}\;\; \mathrm{{otherwise}}. \;\;\\ \end{array}\right. \end{aligned}$$

Now, $c(I_{i}\cap I_{j})\ge \min \{c(T_{i}),c(T_{j})\}= \min \{c(I_{i}),c(I_{j})\}$ is true iff when the core of $I_{i}$, $I_{j}$contains another. Also, $s(I_{i}\cap I_{j})\ge \min \{s(T_{i}),s(T_{j})\}= \min \{s(I_{i}),s(I_{j})\}$ is true iff when the support of $I_{i}$, $I_{j}$ contains another. This gives $\mu _{B}(r_{i},r_{j})\ge 0$, $\eta _{B}(r_{i},r_{j})\ge 0$ and $\nu _{B}(r_{i},r_{j})\ge 0$. Therefore,one of $I_{i}$, $I_{j}$ contains another. Hence G is a PFICG.

Theorem 3.24

Any PF proper or unit TR be assumed to have bounded PFT.

Proof

Let $G=(V,A,B)$ be a PF proper or unit TG with PFIs $I=\{I_{r}:r\in V\}$ and PFTs $T=\{T_{r}:r\in V\}$. We assume that all endpoints of support and core in this representation are distinct. We replace $c(T_{r})$ by $|c(I_{r})|$ for each $r\in V$ when $c(T_{r})\ge |c(I_{r})|$ and $s(T_{r})$ by $|s(I_{r})|$ for each $r\in V$ when $s(T_{r})\ge |s(I_{r})|$. Since there are no containment of support and core of the PFIs, this will not change any adjacency. Therefore, any PF proper or unit TR be assumed to have bounded PFT.

: We explain it by the following example:

Example 3.25

We consider four PFIs $\{I_{i}:i=1,2,3\}$ on $R_{L}$ along with corresponding PFTs $\{T_{i}:i=1,2,3\}$. Assume that PFIs are the vertices and $V=\{r_{i}:i=1,2,3\}$ be the vertex set of the TG. Let the support of these PFIs are,respectively,[1, 7.5], [3.5, 10], [8.5, 15] and cores are,respectively,[2, 6], [4, 8], [9, 13] and $s(T_{1})=6.5$, $s(T_{2})=4$, $s(T_{3})=1$ and $c(T_{1})=4$, $c(T_{2})=2$, $c(T_{3})=0.5$. The corresponding PFIs are shown in Fig. 12.

We have $I_{1}\cap I_{2}=[3.5,7.5]$, $I_{2}\cap I_{3}=[8.5,10]$. Also, $s(I_{1}\cap I_{2})=4$, $s(I_{2}\cap I_{3})=1.5$ and $c(I_{1}\cap I_{2})=2$, $c(I_{2}\cap I_{3})=0$. Here, $h(I_{1}\cap I_{2})=(1,0,0)$, $h(I_{2}\cap I_{3})=(0.6,0.1,0.3)$. Therefore,the TMS, AMS and FMS of the edges $(r_{1},r_{2})$ and $(r_{2},r_{3})$ are,respectively,(1, 0, 0) and (0.2, 0.03, 0.1). Here, no PFI core and support properly contain another PFI core and support. Also, all PFIs have same CL(=4) and same SL (=6.5). So the PFIs together with PFTs represent PF proper (unit)-TG. The corresponding PF proper (unit) TG is shown in Fig. 13. It has bounded PFTs as $c(I_{r})\ge c(T_{r})$ and $s(I_{r})\ge s(T_{r})$ for each $r\in V$. Otherwise, to make bounded PFTs we may replace $c(T_{r})$ by 4 and $s(T_{r})$ by 6.5. This replacement will not change any adjacency, as there are no containment of support and core of the PFIs.

Fig. 12

Representation of PFIs

Fig. 13

Corresponding proper (unit)- TG

Theorem 3.26

All PFmax TGs and PFsum TGs have bounded representations.

Proof

Let $r\in V$ be a vertex in a PFmax TG or PFsum TG such that $c(T_{r})>c(I_{r})$ and $s(T_{r})>s(I_{r})$;then r is an isolated vertex. In that case we reassign this vertex with a different PFI which is disjoint from other PFIs and an arbitrary bounded PFT. This theorem is true for any PF$\phi$-TG and also applies to PF proper and unit TRs.

Picture fuzzy $\phi$-tolerance chain graphs

We introduce the normalized representation of PFIs and define a special case of PF$\phi$-TG, known as the class of PF$\phi$-TCG which consists of a nested family of PFIs. Here we investigated some specific results when $\phi$ is the max, min and sum functions.

Definition 4.1

Any nested family of PFIs $I_{i}$ can be normalized by replacing each PFI $I_{i}$ by the intervals $[0,r_{i}]$, where $r_{i}=|I_{i}|$. Thus the normalized representation of the nested family of PFIs $I_{i}$ is of the form $N=\{I^{*}_{i}:{i=1,2,\ldots ,n}\}$, where $I^{*}_{i}=[0, r_{i}]$ and $0<r_{1}\le r_{2}\le ..\le r_{n}$.

Definition 4.2

In a PFG G, a vertex is an universal if it is adjacent to all other vertices and an isolated if is adjacent to no other vertex of G.

Definition 4.3

A PFG G is a threshold graph iff for each subset $S\subseteq V$, $\exists$ a vertex $r\in S$ which is either isolated or universal in the induced subgraph $G_{S}$ of G.

Theorem 4.4

A PF min-tolerance chain graph (PFmin-TCG) is a PF threshold graph.

Proof

Let $N=\{I^{*}_{i}:{i=1,2,\ldots ,n}\}$ be a nested family of PFIs along with corresponding PFTs $T^{*}=\{T^{*}_{i}:{i=1,2,\ldots ,n}\}$, where $I^{*}_{i}=[0, r_{i}]$ and $0<r_{1}\le r_{2}\le \cdots \le r_{n}$. Consider each nested family of PFI as vertex of the PFmin TCG. Let $V=\{u_{i}:{i=1,2,\ldots ,n}\}$ be the vertex set and corresponding PFmin TCG be the PFG $G^{*}$. We have to prove $G^{*}$ has an universal or an isolated vertex.

If $c(T_{1})\le c(I_{1})$ and $s(T_{1})\le s(I_{1})$, then $u_{1}$ is an universal vertex as $c(I_{1}\cap I_{j})= c(I_{1})\ge c(T_{1})\ge \min \{c(T_{1}), c(T_{j})\}$ and $s(I_{1}\cap I_{j})= s(I_{1})\ge s(T_{1})\ge \min \{s(T_{1}), s(T_{j})\}$, $\forall j$.

Again if $c(T_{1})> c(I_{1})$ and $s(T_{1})> s(I_{1})$, then $u_{1}$ is not an isolated vertex, then $u_{1}$ has a neighbor $u_{k}$. This implies that $c(T_{k})\le c(I_{1})$ and $c(T_{k})\le c(I_{1})$, that means $u_{k}$ is an universal vertex as $c(I_{k}\cap I_{j})= \min \{c(I_{k}), c(I_{j})\}\ge c(I_{1})\ge c(T_{k})\ge \min \{c(T_{k}), c(T_{j})\}$ and $s(I_{k}\cap I_{j})=\min \{s(I_{k}), s(I_{j})\}\ge s(I_{1})\ge s(T_{k})\ge \min \{s(T_{k}), s(T_{j})\}$, $\forall j$.

This proves that $G^{*}$ is a PF threshold graph.

Theorem 4.5

A PF max-tolerance chain graph (PFmax TCG) is an PFIG.

Proof

Let $N=\{I^{*}_{i}:{i=1,2,\ldots ,n}\}$ be a nested family of PFIs along with corresponding PFTs $T^{*}=\{T^{*}_{i}:{i=1,2,\ldots ,n}\}$, where $I^{*}_{i}=[0, r_{i}]$ and $0<r_{1}\le r_{2}\le \ldots \le r_{n}$. Consider each nested family of PFI as vertex of the PFmax TCG. Let $V=\{u_{i}:{i=1,2,\ldots ,n}\}$ be the vertex set and corresponding PFmax TCG is the PFG $G^{*}$.

Assume that $c(T_{i})\le c(I_{i})$ and $s(T_{i})\le s(I_{i})$, for ${i=1,2,\ldots ,n}$, for if $c(T_{i})> c(I_{i})$ and $s(T_{i})> s(I_{i})$, then $u_{i}$ is an isolated and we disregard $u_{i}$. Consequently, $u_{i}$ and $u_{j}$ are adjacent iff $\min \{c(I_{i}), c(I_{j})\}\ge \max \{c(T_{i}), c(T_{j})\}$ and $\min \{s(I_{i}), s(I_{j})\}\ge \max \{s(T_{i}), s(T_{j})\}$.

This will be true iff $[T_{i},r_{i}]$ and $[T_{j},r_{j}]$ have a non-empty intersection.

Thus, the PFmax TCG of N is the PFIG of the intervals $\{[T_{i},r_{i}]:{i=1,2,\ldots ,n}\}$.

Theorem 4.6

A PF sum-tolerance chain graphs (PFsum TCGs) are chordal.

Proof

Let $N=\{I^{*}_{i}:{i=1,2,\ldots ,n}\}$ be a nested family of PFIs along with corresponding PFTs $T^{*}=\{T^{*}_{i}:{i=1,2,\ldots ,n}\}$, where $I^{*}_{i}=[0, r_{i}]$ and $0<r_{1}\le r_{2}\le \ldots \le r_{n}$. Consider each nested family of PFI as vertex of the PFsum TCG. Let $V=\{u_{i}:{i=1,2,\ldots ,n}\}$ be the vertex set and corresponding PFsum TCG is the PFG $G^{*}$.

Let $u_{j}$ be a vertex with maximum tolerance and let $u_{i}$ and $u_{k}$ be two distinct neighbors of $u_{j}$. Then we have $c(T_{i})+c(T_{k})\le c(T_{i})+c(T_{j})\le \min \{c(I_{i}), c(I_{j})\}\le c(I_{i})$. $s(T_{i})+s(T_{k})\le s(T_{i})+s(T_{j})\le \min \{s(I_{i}), s(I_{j})\}\le s(I_{i})$ and $c(T_{i})+c(T_{k})\le c(T_{j})+c(T_{k})\le \min \{c(I_{j}), c(I_{k})\}\le c(I_{k})$. $s(T_{i})+s(T_{k})\le s(T_{j})+s(T_{k})\le \min \{s(I_{j}), s(I_{k})\}\le s(I_{k})$.

So that, $c(T_{i})+c(T_{k})\le \min \{c(I_{i}), c(I_{k})\}$ and $s(T_{i})+s(T_{k})\le \min \{s(I_{i}), s(I_{k})\}$.

This shows that PFsum TCGs are chordal.

Application of tolerance graph in sports competition

The PFTG is an important tool that can be applied in different types of real life problems. We consider a PFG model of PFIs in Fig. 14 representing the $4\times 100$ meter relay race competition of a group of team, each having 4 runners and assigned them to run for a fixed interval of distance in a lane. The lead off runner starts the race with baton in-hand from the starting point when he hears the starter’s gun. Each runner tries to handover the baton without dropping to his next teammate after completing own assigned distance. Also, that teammate must have to receive this baton within 20 m area from his starting point, otherwise his team will be disqualified. A team will win this competition if its last runner successfully cross the finish line first. Each team has some tolerances, because runners have to wait some distances for other. The problem is to schedule the teams to finish the race under certain rules. This problem can be modeled by the PFmin TG, where the runners are considered as vertices and there is an edge between the vertices if interval of distances of two runners intersect. In practical situation, the tolerance of a graph may be a PF-number. For example, each runner tries to receive baton from his earlier teammate in between 0 and 20 m distance, i.e., the baton will be handed over within any distance in between 0 and 20 m. This is an uncertainty. So, we may consider the tolerances as a PF-number. The following algorithm finds the minimum tolerance between two runners when they run on the same lane.

Fig. 14

PFI representation of the problem

Algorithm

Aim: To get a PFTG of the competition such that there is a minimum tolerance between two runners when they run on the same lane under certain rules.

Input: Four PFIs of distances with their cores and supports and the corresponding PFTs with their CLs and SLs.

Output: A PFmin TG having minimum tolerances among the runners.

Step 1: Assign PFIs of distances $\{I_{i}: i=1,2,3,4\}$ with their respective cores and supports for the set of runners $\{r_{i}: i=1,2,3,4\}$ in the competition.

Step 2: Assign PFTs $\{T_{i}: i=1,2,3,4\}$ corresponding to the PFIs with their respective CLs and SLs.

Step 3: Compute $I_{i}\cap I_{j}$, $c(I_{i}\cap I_{j})$, $s(I_{i}\cap I_{j})$ and $h(I_{i}\cap I_{j})$, where $i,j=1,2,3,4$ $(i\ne j)$.

Step 4: If $I_{i}\cap I_{j}\ne \emptyset$, then draw an edge $(r_{i},r_{j})$, where $i\ne j$.

Step 5: Calculate the TMS, AMS and FMS for each of vertices by using the formula $\mu _{A}(r_{i})=h_{\mu }(I_{i})$, $\eta _{A}(r_{i})=h_{\eta }(I_{i})$ and $\nu _{A}(r_{i})=h_{\nu }(I_{i})$.

Step 6: Calculate the TMS, AMS and FMS of edges by using the respective formulas as follows:

$$\begin{aligned} \mu _{B}(r_{i},r_{j})=\left\{ \begin{array}{ll} 1, &{} \mathrm{if}\;\; c(I_{i}\cap I_{j})\ge \min \{c(T_{i}),c(T_{j})\} \;\;\\ \frac{s(I_{i}\cap I_{j})- \min \{s(T_{i}),s(T_{j})\}}{s(I_{i}\cap I_{j})}h_{\mu }(I_{i}\cap I_{j}), &{} \mathrm{if }\;\; s(I_{i}\cap I_{j})\ge \min \{s(T_{i}),s(T_{j})\} \;\;\\ 0, &{} \mathrm{}\;\; \mathrm{{otherwise}}. \;\;\\ \end{array}\right. \\ \eta _{B}(r_{i},r_{j})=\left\{ \begin{array}{ll} 0, &{} \mathrm{if}\;\; c(I_{i}\cap I_{j})\ge \min \{c(T_{i}),c(T_{j})\} \;\;\\ \frac{s(I_{i}\cap I_{j})- \min \{s(T_{i}),s(T_{j})\}}{s(I_{i}\cap I_{j})}h_{\eta }(I_{i}\cap I_{j}), &{} \mathrm{if }\;\; s(I_{i}\cap I_{j})\ge \min \{s(T_{i}),s(T_{j})\} \;\;\\ 0, &{} \mathrm{}\;\; \mathrm{{otherwise}}. \;\;\\ \end{array}\right. \\ \nu _{B}(r_{i},r_{j})=\left\{ \begin{array}{ll} 0, &{} \mathrm{if}\;\; c(I_{i}\cap I_{j})\ge \min \{c(T_{i}),c(T_{j})\} \;\;\\ \frac{s(I_{i}\cap I_{j})- \min \{s(T_{i}),s(T_{j})\}}{s(I_{i}\cap I_{j})}h_{\nu }(I_{i}\cap I_{j}), &{} \mathrm{if }\;\; s(I_{i}\cap I_{j})\ge \min \{s(T_{i}),s(T_{j})\} \;\;\\ 1, &{} \mathrm{}\;\; \mathrm{{otherwise}}. \;\;\\ \end{array}\right. \end{aligned}$$

Illustration of algorithm

Step 1: Assume that the runners $r_{1}$, $r_{2}$, $r_{3}$ and $r_{4}$ can run for the interval of distances $I_{1}$, $I_{2}$, $I_{3}$ and $I_{4}$, respectively. They run actively in the intervals [0, 100], [100, 200], [200, 300] and [300, 400];these are considered as core of the intervals. Also, they run both actively and inactively in the interval of distances [0, 112], [100, 215], [200, 318] and [300, 430]; these are considered as support of the intervals as shown in the diagram of Fig. 14.

Step 2: Let $\{T_{i}: i=1,2,3,4\}$ are the tolerances corresponding to the intervals $\{I_{i}: i=1,2,3,4\}$ with $c(T_{1})=8$, $c(T_{2})=9$, $c(T_{3})=13$, $c(T_{4})=16$ and $s(T_{1})=10$, $s(T_{2})=12$, $s(T_{3})=15$, $s(T_{4})=22$.

Step 3: Here, $I_{1}\cap I_{2}=[100,112]$, $I_{2}\cap I_{3}=[200,215]$, $I_{3}\cap I_{4}=[300,318]$; $s(I_{1}\cap I_{2})=12$, $s(I_{2}\cap I_{3})=15$, $s(I_{3}\cap I_{4})=18$; $c(I_{1}\cap I_{2})=0$, $c(I_{2}\cap I_{3})=0$, $c(I_{3}\cap I_{4})=0$; $h(I_{1}\cap I_{2})=(1,0,0)$, $h(I_{2}\cap I_{3})=(1,0,0)$, $h(I_{3}\cap I_{4})=(1,0,0)$.

Step 4: Since some interval of distances overlapped, then tolerance arises between some runners. There exist tolerances between the runners $r_{1}$ and $r_{2}$; $r_{2}$ and $r_{3}$; $r_{3}$ and $r_{4}$.

Step 5: The TMS, AMS and FMS of each vertex are obtained as follows: $(\mu _{A}(r_{i}),\eta _{A}(r_{i}),\nu _{A}(r_{i}))=(h_{\mu }(I_{i}), h_{\eta }(I_{i}),h_{\nu }(I_{i}))=(1,0,0)$, $i=1,2,3,4$

Fig. 15

Corresponding PFmin-TG

Table 1 The characteristic comparison of PFTGs with IFTGs

Step 6: Using the formula of Definition 3.6, we have the TMS, AMS and FMS of the edges $(r_{1},r_{2})$, $(r_{2},r_{3})$ and $(r_{3},r_{4})$ as (0.166, 0, 0), (0.2, 0, 0) and (0.166, 0, 0) respectively,in the corresponding PFmin TG (see Fig. 15).

The following observations are made from the PFmin TG:There are tolerances between the runners $r_{1}$ and $r_{2}$; $r_{2}$ and $r_{3}$; $r_{3}$ and $r_{4}$. But there is no tolerance between $r_{1}$ and $r_{3}$; $r_{1}$ and $r_{4}$; $r_{2}$ and $r_{4}$. Thus, the runners are assigned to run for a fixed interval of distance in own lane such that there is a minimum tolerance.

Comparative study with existing IFTG models

In existing papers on IFTGs, all information was taken in IF sense. When more possible types of vagueness and uncertainty occur in information,then the IFTG models are not appropriate to handle such situation. For these cases, the information should be collected or represented as PF sense. The currently developed model plays a vital role in such cases to give a fruitful conclusion.

Sahoo and Pal [41] proposed an IFTG model by considering each vertex and edge with IF information and determined the minimum tolerance among the employees in a company when they scheduled to work on the same work station. In IFTG models, only membership and non-membership values of vertices and edges are considered. So these models are not applicable when the models are considered in other environment like in PF environment. In our currently developed PFTG model, we include another parameter called neutral membership value and it is practically useful in case of real life problem. The PFTG models are more generalized and superior than the IFTG models. Moreover, it will be capable to accommodate more vagueness and uncertainties and provides better results than the existing models. On removing the neutral membership value of PFTG, the PFTG reduces to conventional IFTG. Thus, PFTG can be viewed as an effective generalization of IFTG. The characteristics comparison of our proposed PFTGs with IFTGs is given in Table 1.

Conclusion

In this study, we have applied the powerful tool of fuzziness to generalize PFIGs using tolerances under the PF environment. Our proposed PF model provides more legibility, flexibility and suitability to the system as compared with the models in other fields due to the existence of additional term named as ‘neutrality’ and which discriminate this model from all other existing models of literature. We have mainly studied the construction methods of several types of PFTGs. Adding more uncertainty to fuzzy $\phi$-TGs and IF $\phi$-TGs, we have introduced PF$\phi$-TGs. Some specific results are established when $\phi$ is the max, min and sum functions. Also, PF proper TGs and unit TGs are defined and investigated few strong properties related to the stated TGs. Later on, PF$\phi$-TCGs have been studied with some results. In addition, to reveal the importance of these TGs in realistic situations, we have applied our proposed model in sports competition. Finally, we have compared our proposed PFTGs with IFTGs to check the superiority and authenticity of proposed graphs which leads us to handle the problems having more possible types of vagueness and uncertainties. In future, we will extend this work to PFT CGs and m-Step PFT CGs.