ML-based group method of data handling: an improvement on the conventional GMDH

Abstract

Machine learning (ML) has been recognized as a feasible and reliable technique for the modeling of multi-parametric datasets. In real applications, there are different relationships with various complexities between sets of inputs and their corresponding outputs. As a result, various models have been developed with different levels of complexity in the input–output relationships. The group method of data handling (GMDH) employs a family of inductive algorithms for computer-based mathematical modeling grounded on a combination of quadratic and higher neurons in a certain number of variable layers. In this method, a vector of input features is mapped to the expected response by creating a multistage nonlinear pattern. Usually, each neuron of the GMDH is considered a quadratic partial function. In this paper, the basic structure of the GMDH technique is adapted by changing the partial functions to enhance the complexity modeling ability. To accomplish this, popular ML models that have shown reasonable function approximation performance, such as support vector regression and random forest, are used, and the basic polynomial functions in the GMDH are replaced by these ML models. The regression feasibility and validity of the ML-based GMDH models are confirmed by computer simulation.

Introduction

The group method of data handling (GMDH) was first introduced by Ivakhnenko as a proper approach for detecting nonlinear systems [1]. The GMDH approach employs a family of inductive algorithms for the computer-based mathematical modeling of multiparameter datasets. This method uses fully automatic parametric and structural optimization. The GMDH is a combination of quadratic and higher neurons in a certain number of variable layers that map a vector of input features to the expected response by creating a multistage nonlinear pattern; it is mainly based on decomposition and dominance. In every layer of this network, a different subset of possible combinations in each neuron among the existing features is mapped to the expected response using polynomial functions [2, 3]. Based on the accuracy achieved for each combination, some weaker combinations are removed in favor of stronger ones. In other words, different layers of the network are configured by reducing the mapping error from the input feature space to the expected response. Like real structures in nature, the GMDH creates a complex combination of relatively simple structures, and each section is adjusted by an evolutionary approach.

GMDH algorithms are characterized by a reasoning method in which sorting is performed on polynomial models that gradually increase in complexity to select the best solution via a specified external criterion. In the basic structure proposed by Ivakhnenko, polynomial mapping functions (mostly quadratic functions) are used in each GMDH neuron and fitted by the least-squares method. A more complex model is configured for mapping from the input space to the output space by multilayer combinations of mapping created by relatively simple polynomial functions. Since it was first developed, several improvements have been proposed for the GMDH. For example, Ohtani et al. [4] used the M-apoptosis concept to propose a neuro-fuzzy GMDH. Kondo [5] changed the basic GMDH structure and replaced the mechanism for using the output of the neuron in the next layer with backpropagation (BP) and feedback structures to the input layer. Elattar et al. [6] combined GMDH and local regression to develop a generalized locally weighted GMDH. Moreover, Zhang et al. [7] developed the diversity-GMDH (D-GMDH) model by using the diversity concept in the GMDH to improve the noise-immunity ability. Shahsavar et al. [8] changed the GMDH structure and added initial inputs to the input binary combinations in the next layers to propose a generalized GMDH structure for modeling thermal conductivity. Band et al. [9] added a sigmoid transfer function to the basic polynomial function of the GMDH method, introduced a neural network-based GMDH (GMDH-NN), and tested it for voltage regulation. Zounemat-Kermani and Mahdavi-Meymand [10] developed the GMDH-FA by the automatic tuning of the GMDH with the silkworm moth algorithm and employed it for the aeration modeling of spillways.

Some studies have combined GMDH with other methods for improving its accuracy. For example, reference [11] predicted bridge pier scour depth under debris flow effects by combining the Adaptive Nero-Fuzzy Inference System (ANFIS) and GMDH and constructing FN-GMDH. Reference [12], proposed a GMDH-based hybrid model to forecast the container throughput. Considering the complexity of forecasting nonlinear subseries, the proposed model adopts three nonlinear single models—namely, support vector regression (SVR), BP neural network, and genetic programming (GP), to predict the nonlinear subseries. Then, the model establishes selective combination forecasting by the GMDH neural network on the nonlinear subseries and obtains its combination forecasting results. Finally, the predictions of the two parts are integrated to obtain the forecasting results of the original container throughput time series. In reference [13], the GMDH network was developed using a gene-expression programming (GEP) algorithm. In this study, GEP was performed in each GMDH neuron instead of the polynomial quadratic neuron. Effective parameters on the three-dimensional scour rates include sediment size, pipeline geometry, and wave characteristics upstream of the pipeline. Four dimensionless parameters were considered input variables by means of the dimensional analysis technique. Furthermore, scour rates along the pipeline, the vertical scour rate, and scour rates to the left and right of the pipeline are determined as output parameters. Reference [14] combined GMDH with ANFIS to combine their abilities in forecasting ultimate pile bearing capacity. In this study, uncertainty in the data is handled using ANFIS, and the complexity of the input–output relationship is considered using GMDH. In addition, Particle Swarm Optimization (PSO) was used to determine the parameters of these methods. Reference [15] developed a novel hybrid intelligent model for solving engineering problems using a new combination of the GMDH algorithm. In this study, the conventional structure of GMDH is combined with new polynomial functions to form a new version of the GMDH algorithm by combining fuzzy logic theory, GMDH, and a gravitational search algorithm (GSA). The developed model was leveraged to predict rock tensile strength based on experimental datasets. In this method, simple polynomial functions are replaced with fuzzy if–then rules, which are constructed using Gaussian membership functions, and GSA is used for determining parameters of Gaussian membership functions.

In reference [17], the authors designed a special classifier ensemble selection approach called GMDH-PSVM. The presented work proposed taking advantage of GMDH-NN to further increase the classification performance of SVM. One weakness of the symmetric regularity criterion of GMDH-NN is that if one of the input attributes has a relatively large range, it may overcome the other attributes. Thus, authors first define a standardized symmetric regularity criterion (SSRC) to evaluate and select the candidate models and optimize a classifier ensemble selection approach. Second, they define a novel structure of the initial model of GMDH-NN, which is from the posterior probability outputs of SVMs. These probabilistic outputs were generated from the improved version of Platt’s probabilistic outputs. Third, in real classification tasks, different classifiers usually have different classification advantages. Reference [18] proposed a novel hybrid wavelet time series decomposer and GMDH-extreme learning machine (ELM) ensemble method called Wavelet-GMDH-ELM (WGE) for workload forecasting, which predicts and ensembles workload in different time–frequency scales. In [19], GMDH and Genetic Algorithm (GA) were integrated to optimize the ability of GMDH. The efficiency and effectiveness of the GMDH network structure were optimized by the GA, enabling each neuron to search for its optimum connections set from the previous layer. With this proposed model, monitoring data, including the shield performance database, disc cutter consumption, geological conditions, and operational parameters, could be analyzed.

Following the aforementioned works, this study aims to enhance the ability of GMDH to handle more complex relationships between inputs and outputs, which has not been considered before. Considering the reasonable results of ML models in different regression and pattern recognition applications [20,21,22,23,24,25,26,27,28,29,30], it is valuable for us to study whether the combination of ML models and GMDH leads to better performance. A modified version of the GMDH is proposed, in which the basic polynomial functions are replaced by ML models. Given the ability of ML models to establish linear and nonlinear mapping, these methods replace the polynomial functions for the mapping from the inputs to the output in each GMDH neuron. Accordingly, the ML-based GMDH aims to find an optimal approximation in the spanned space by layers that consist of neurons in the ML models. Tests confirm the feasibility and validity of the proposed model in approximation tasks. The main contributions of this paper are as follows:

• 1. Improving the accuracy of the GMDH model in forecasting more complex relationships.

• 2. Replacing conventional polynomial functions with ML models to handle complexities in the datasets.

The rest of this paper is organized as follows: the GMDH mechanism is presented in Sect. 2. The ML-based GMDH is introduced in Sect. 3. The simulation experiments are discussed in Sect. 4, and finally, concluding remarks are presented in Sect. 5.

Group method of data handling (GMDH)

The GMDH is a nature-inspired learning method that approximates the relationship of inputs and the output by a nonlinear mapping composed of successive layers of neurons using polynomial transfer functions. A basic explanation for the mapping problem is to identify a function ($\hat{f}$) as an alternative for a latent utility function ($f$) to predict $\hat{y}$ from the input $X = \left( {x_{1} ,x_{2} ,x_{3} , \ldots ,x_{n} } \right)$ to be as close to the expected output ($y$) as possible. To this end, M observations, including the multivariable unit–single variable output, are considered as follows [1,2,3, 10, 31]:

$$ y_{i} = f\left( {x_{i1} ,x_{i2} ,x_{i3} , \ldots ,x_{in} } \right),\quad \left( {i = 1,2,3, \ldots M} \right). $$

(1)

The GMDH network is trained by the input vector X for predicting the $\hat{y}$ values:

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y}_{i} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} \left( {x_{i1} ,x_{i2} ,x_{i3} , \ldots ,x_{in} } \right){,}\quad \left( {i = 1,2,3, \ldots M} \right). $$

(2)

The main issue is to determine a GMDH model to ensure the minimization of the squares of the difference between the predicted and expected values, as in the following [10]:

$$ \sum\limits_{i = 1}^{M} {\left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} \left( {x_{i1} ,x_{i2} ,x_{i3} , \ldots ,x_{in} } \right) - y_{i} } \right]}^{2} \Rightarrow \min . $$

(3)

The detailed representation of the Volterra functional series may represent the relationship between the inputs and the output by referring to the Kolmogorov–Gabor polynomial. The output is as follows [1, 2, 31]:

$$ \begin{aligned} y = f(x_{1} , \ldots ,x_{n} ) & = a_{0} + \sum\limits_{i = 1}^{n} {a_{i} } x_{i} + \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {a_{ij} x_{i} x_{j} } } \\ & \quad + \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{n} {a_{ij} x_{i} x_{j} x_{k} } } } + \cdots , \\ \end{aligned} $$

(4)

where, $a_{0}$, $a_{i}$, and $a_{ij}$ are coefficients of polynomial functions. The complete form of mapping the modeling in each neuron is simplified by the output obtained from the partial polynomial functions with two variables as inputs (neurons) [1], as shown in the following equation:

$$ \begin{aligned} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} & = G_{pq} (x_{p} ,x_{q} ) \\ & = a_{0} + a_{1} x_{p} + a_{2} x_{q} + a_{3} x_{p} x_{q} + a_{4} x_{p}^{2} + a_{5} x_{q}^{2} . \\ \end{aligned} $$

(5)

In this approach, a recursive polynomial function is applied to the neurons connected to the network to develop the standard relationship between the input and the output in Eq. 4. The $a_{i}$ coefficients in Eq. 5 are calculated by regression to reduce the difference between the observed output ($\hat{y}$) and the expected output (y) for each pair of inputs ($x_{p} ,x_{q}$). In other words, a tree set of polynomial functions in Eq. 5 is developed in which its coefficients are calculated by the least-squares method. The coefficients of each polynomial function (G_pq) are determined to apply the optimal fitting for the output that corresponds to the input–output pair in the dataset [2, 31] as follows:

$$ {\text{MSE}} = \frac{{\sum\nolimits_{i = 1}^{M} {\left( {y_{i} - G_{pq} (x_{ip} ,x_{iq} )} \right)}^{2} \, }}{M} \Rightarrow \min . $$

(6)

To avoid overfitting, 70%–80% (P_train) of the total of M observations is used practically for fitting by the least-squares method, and the rest are used as a validation set for evaluating the approximation error. In other words, Eq. 7 is minimized by the least-squares method, and the value calculated by Eq. 8 is considered the error criterion for each neuron [3]:

$$ \begin{aligned} {\text{MSE}}_{{{\text{train}}}} & = \frac{{\sum\limits_{{i \in {\text{Train}}}}^{{}} {\left( {y_{i} - G_{pq} (x_{ip} ,x_{iq} )} \right)}^{2} \, }}{M},\; \Rightarrow \min \\ {\text{Train}} & = (P_{{{\text{train}}}} *M)\;{\text{number}}\;{\text{of}}\;{\text{observations}}\;{\text{selected}}\;{\text{randomly}}. \\ \end{aligned} $$

(7)

$$ \begin{aligned} {\text{MSE}}_{{{\text{validation}}}} & = \frac{{\sum\limits_{{i \in {\text{Validation}}}}^{{}} {\left( {y_{i} - G_{pq} (x_{ip} ,x_{iq} )} \right)}^{2} \, }}{M}, \\ {\text{Validation}} & = ((1 - P_{{{\text{train}}}} )*M)\,{\text{number}}\;{\text{of}}\;{\text{observations}}\;{\text{selected}}\;{\text{randomly}}. \\ \end{aligned} $$

(8)

In the standard GMDH, all the possible binary combinations of the n input variables are considered for creating the regression polynomial in Eq. 5 to find the best fitting variables using independent observations $\left( {\begin{array}{*{20}c} {y_{i} ,} & {i \in {\text{Train}}} \\ \end{array} } \right)$ and the least-squares method. Hence, $\left( {\begin{array}{*{20}c} n \\ 2 \\ \end{array} } \right) = \frac{n(n - 2)}{2}$ neurons exist in the first GMDH layer using $\left\{ {(y_{i} ,x_{ip} ,x_{iq} );\quad i \in {\text{Train}}} \right\}$ observations [2, 3, 19], as shown in the following:

$$ \left[ {\begin{array}{*{20}c} {x_{1p} } & {x_{1q} } & \vdots & {y_{1} } \\ {x_{2p} } & {x_{2q} } & \vdots & {y_{2} } \\ \cdots & \cdots & \cdots & \cdots \\ {x_{Mp} } & {x_{Mq} } & \vdots & {y_{M} } \\ \end{array} } \right], $$

(9)

where,$p,q \in \left\{ {i = 1,2, \ldots n} \right\}$. The matrix factorization relations are respectively obtained by Eqs. 10–14 by adding the quadratic sub-equations using Eq. 5 for each row of the M three-member sets $(y_{i} ,x_{ip} ,x_{iq} ),$:

$$ Aa = Y, $$

(10)

$$ a = \{ a_{0} ,a_{1} ,a_{2} ,a_{3} ,a_{4} ,a_{5} \} , $$

(11)

$$ Y = \{ y_{1} ,y_{2} ,y_{3} ,...,y_{5} \}^{T} , $$

(12)

$$ A = \left[ {\begin{array}{*{20}c} 1 & {x_{1p} } & {x_{1q} } & {x_{1p} x_{1q} } & {x_{1p}^{2} } & {x_{2p}^{2} } \\ 1 & {x_{2p} } & {x_{2q} } & {x_{2p} x_{2q} } & {x_{2p}^{2} } & {x_{2p}^{2} } \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 1 & {x_{Mp} } & {x_{Mq} } & {x_{Mp} x_{Mq} } & {x_{Mp}^{2} } & {x_{Mp}^{2} } \\ \end{array} } \right]. $$

(13)

The parameters are obtained as follows, using the least-squares method and the above equations:

$$ a = (A^{T} A)^{ - 1} A^{T} Y. $$

(14)

The result gives a in Eq. 5 for all three values of $(y_{i} ,x_{ip} ,x_{iq} )$ of the dataset. This process is repeated for all the neurons in the following layers, which are specified by the internal linkage of the GMDH network [1, 3].

To prevent computational overburden, some neurons in each layer of the GMDH are excluded by a natural selection mechanism. By comparing the sum of squares of the fitting errors for each neuron with a threshold, some neurons and their outputs are excluded from the network. The threshold is calculated from the following equation [10]:

$$ T_{l} = \alpha \mathop {{\text{MSE}}_{{{\text{validation}}}} }\nolimits_{l}^{\min } + (1 - \alpha )\mathop {{\text{MSE}}_{{{\text{validation}}}} }\nolimits_{l}^{\max } , $$

(15)

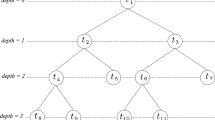
where I represents the lth layer; $T_{l}$ is the threshold value; and $\mathop {{\text{MSE}}_{{{\text{validation}}}} }\nolimits_{l}^{\min }$ and $\mathop {{\text{MSE}}_{{{\text{validation}}}} }\nolimits_{l}^{\max }$ show the minimum and maximum mean square errors (MSEs) of the fitting among neurons of each layer, respectively; and α is the selection leverage and a regulatory parameter of the GMDH network. The other regulatory parameters include the number of layers and the maximum allowable number of neurons in each layer (another variable for controlling the model complexity) that controls the GMDH complexity. Figure 1 shows the structure of a hypothetical GMDH network with three middle layers and four inputs [32].

Fig. 1

GMDH with three layers and four inputs [19]

In the next section, the developed ML-based GMDH is presented.

Machine learning-based group method of data handling (ML-based GMDH)

As mentioned in Sect. 2, in each neuron of the GMDH, a polynomial function is fitted between two (or more) inputs and outputs. In the ML-based GMDH models, the partial polynomial functions in the GMDH model are replaced by the ML models. In other words, while preserving the original GMDH structure, the function used for mapping the input pair $\begin{array}{*{20}c} {(x_{ip} ,x_{jq} ),} & {i = 1,2,...,M} \\ \end{array}$, to $(\begin{array}{*{20}c} {y_{i} ,} & {i = 1,2,...,M} \\ \end{array} )$ is made more complex than the basic function to model more complex mappings. In cases where there are complex patterns between the input and output pairs, the use of ML models provides GMDH building blocks with more precise approximations.

Unlike the basic GMDH structure in which the a values in Eq. 5 are obtained by solving Eq. 15, in each neuron of the ML-based GMDH, the ML model is trained once by observations to determine a list of weights and ML parameters. The approximation error for validation observations was calculated by evaluating the outputs of the ML model. Each partial function (neuron) in the ML-based GMDH is considered a black box, and like the basic GMDH structure, the outputs of neurons in each layer are considered inputs to the next layer. The mean square error of validation observations in each neuron of the ML-based GMDH is calculated from the following equation:

$$ \begin{aligned} {\text{MSE}}_{{{\text{validation}}}} & = \frac{{\sum\limits_{{i \in {\text{Validation}}}}^{{}} {\left( {y_{i} - ML_{pq} (x_{ip} ,x_{iq} )} \right)}^{2} \, }}{M}, \\ {\text{Validation}} & = ((1 - P_{{\text{train}}} )*M)\,{\text{number}}\,{\text{of}}\;{\text{observations}}\;{\text{selected}}\;{\text{randomly,}} \\ \end{aligned} $$

(16)

where, $ML_{pq}$ is the trained ML model on $\left\{ {(y_{i} ,x_{ip} ,x_{iq} );\;i \in {\text{Train}}} \right\}$ observations. Like the basic GMDH model and the selection mechanism of neurons in each layer, in ML-based GMDH, the neurons in each layer were selected and excluded based on the MSE values obtained from analyzing the trained ML models using Eq. 15. Figure 2 displays the ML-based GMDH model with four input variables; two middle layers; and multilayer perceptron (MLP) [33] partial functions of the ML model, with a middle layer containing three neurons.

Fig. 2

ML-based GMDH model with four input variables, two middle layers, and MLP partial functions

Various ML models can be used as partial functions in ML-based GMDH. The four conventional models of MLP, SVR [34], random forest (RF) [35], and ELM [36] are considered alternatives to be used as partial functions in this case.

The following hyperparameters in the ML-based GMDH models should be tuned:

• 1. The selection leverage (α) that determines the selection threshold of neurons in each layer.

• 2. The number of network layers (N-layer).

• 3. The maximum allowable number of neurons in each layer (Max-Neurons).

• 4. The type of ML model as the partial function (among MLP, SVR, RF, and ELM).

• 5. The percentage of observations used for training (P_train).

In the next section, the simulation results and comparisons with other ML models are presented.

Simulation experiment

The performance of the ML-based GMDH model was validated by the five following simulation experiments: a six-dimensional non-polynomial function and four real-world datasets in the UCI repository¹—namely, household electric power consumption approximation, air-quality approximation, Hungarian chickenpox, and Seoul bike sharing demand. For comparison, the results of the GMDH and ML-based GMDH models are presented separately. The parameters α, N-layer, Max-Neurons, and P_train are the same in both the GMDH and ML-based GMDH models and are determined by the commonly used cross-validation method [37]. The results are listed in Table 1.

Table 1 Similar parameters in the GMDH and ML-based GMDH models

The evaluation metrics used for comparing the results were the correlation coefficient (R), root mean square error (RMSE), mean of absolute errors (MAE), and standard deviation of the absolute errors (STD errors), as follows:

$$ {\text{MSE}}_{{{\text{train}}}} = \frac{{ 1}}{M}\sqrt {\sum\limits_{i = 1}^{M} {\left( {y_{i} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y}_{i} } \right)}^{2} } , $$

(17)

$$ {\text{MAE}} = \frac{{ 1}}{M}\sum\limits_{i = 1}^{M} {\left| {y_{i} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y}_{i} } \right|} , $$

(18)

$$ {\text{STD}}\;{\text{errors}} = \sum\limits_{i = 1}^{M} {\sqrt {\frac{{(y_{i} - {\text{MAE}})}}{M - 1}} } , $$

(19)

$$ R = \frac{{\sum\nolimits_{i = 1}^{M} {\left( {y_{i} - \overline{y}_{i} } \right)\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y}_{i} - \overline{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} }_{i} } \right)} }}{{\sum\nolimits_{i = 1}^{M} {\left( {y_{i} - \overline{y}_{i} } \right)^{2} } *\sum\nolimits_{i = 1}^{M} {\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y}_{i} - \overline{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} }_{i} } \right)^{2} } }}. $$

(20)

Approximation of a six-dimensional non-polynomial function

In this experiment, a six-dimensional non-polynomial function was approximated as follows [38]:

$$ f(x_{1} ,x_{2} ,x_{3} ,x_{4} ,x_{5} ,x_{6} ) = x_{1}^{{}} + x_{2}^{0.5} + x_{3} x_{4} + 2e^{{2(x_{5} - x_{6} )}} , $$

(21)

where,$x_{1,} x_{2} \in \left[ {1,5} \right]$, $x_{3} \in \left[ {0,4} \right]$, $x_{4} \in \left[ {0,0.6} \right]$, $x_{5} \in \left[ {0,1} \right]$, and $x_{6} \in \left[ {0,1.2} \right]$. Of the total data points, 80% (72,000) were considered for training and the rest (18,000) for testing the network. Figure 3 compares the expected values of function f with the GMDH and ML-based GMDH outputs (using different types of partial ML). As can be seen in Fig. 3, the different types of ML-based GMDH models presented closer approximations to real values compared with the basic GMDH. For more comparative information, Table 2 provides a detailed comparison between the basic GMDH model and different types of ML-based GMDH models in terms of the evaluation metrics. Table 2 shows that the ML-based GMDH models dominate the basic GMDH in terms of all the evaluation metrics. Overall, the RMSE metric is improved 25%, 18%, 28%, and 27% by MLP-based GMDH, SVR-based GMDH, RF-based GMDH, and ELM-based GMDH, respectively. In terms of the MAE metric, 16%, 10%, 19%, and 18% improvements resulted from the MLP-based GMDH, SVR-based GMDH, RF-based GMDH, and ELM-based GMDH, respectively.

Fig. 3

Results of the GMDH and ML-based GMDH models on a six-dimensional non-polynomial function

Table 2 Results of the GMDH and ML-based GMDH models on a six-dimensional non-polynomial function

In addition, 42%, 35%, 44%, and 63% improvements are returned by MLP-based GMDH, SVR-based GMDH, RF-based GMDH, and ELM-based GMDH, respectively, in terms of the R metric. Regarding the STD error metric, 38%, 29%, 41%, and 39% improvements are shown by MLP-based GMDH, SVR-based GMDH, RF-based GMDH, and ELM-based GMDH, respectively. It can be concluded that different types of ML-based GMDH models provide better results in approximating the considered six-dimensional non-polynomial function compared with the conventional GMDH.

Approximation of household electric power consumption

In this task, individual household electric power consumption was approximated. This archive² contained 2,075,259 measurements gathered in a house located in Sceaux, France (7 km from Paris), from December 2006 to November 2010 (47 months). Of all the observations, 80% (179,209) were considered for training and the rest (716,835) for testing the network. Table 3 lists the evaluation metrics calculated for the predictions made by the basic GMDH model and the various ML-based GMDH models.

Table 3 Results of the GMDH and ML-based GMDH models on household electric power consumption

According to the results presented in Table 3, the ML-based GMDH models outperformed the basic GMDH model in approximating the household electric power consumption pattern in terms of all evaluation metrics. In addition, as illustrated in Fig. 4. ELM-based GMDH as an ML-based GMDH performed much better than the basic GMDH method in terms of the RMSE, MAE, and STD error metrics. Even the MLP-based GMDH method with the weakest performance among ML-based GMDH models exhibited good improvement over the base model in terms of all metrics.

Fig. 4

Visual comparison of the GMDH and ML-based GMDH models on household electric power consumption

Approximation of air quality

In this task, the PM2.5 concentration at Shunyi Railway Station in China was approximated. The dataset³ used for this purpose included the concentrations of pollutants recorded at 12 different railway stations in China from March 1, 2013, to February 28, 2017. Shunyi Station was randomly selected for this evaluation, and its PM2.5 concentration data were used. Of 34,151 observations (after preprocessing), 80% (27,314) were considered for training and 20% (6828) for testing the network. Table 4 shows the calculated evaluation metrics for the predictions made by the basic GMDH model and the various ML-based GMDH models.

Table 4 Results of the GMDH and ML-based GMDH models for air quality

According to the results, the ML-based GMDH models outperformed the basic GMDH model in approximating the PM2.5 concentration. As shown in Fig. 5 (for greater clarity, the R values are multiplied by 10), all ML-based GMDH performed much better than the basic GMDH method did in terms of R, RMSE, MAE, and STD error metrics. The extent of the improvement I the ML-based GMDH is clear in approximating the PM2.5 concentration.

Fig. 5

Visual comparison of the GMDH and ML-based GMDH models on approximating the PM2.5 concentration

Approximation of Hungarian chickenpox

In this task, a spatiotemporal dataset of weekly chickenpox cases from Hungary is approximated. This dataset⁴ consists of a county-level adjacency matrix and a time series of the county-level reported cases between 2005 and 2015. Of the 520 observations (after preprocessing), 80% (416) were considered for training and 20% (104) for testing the network. Table 5 shows the calculated evaluation metrics for the predictions made by the basic GMDH model and the various ML-based GMDH models.

Table 5 Results of the GMDH and ML-based GMDH models for approximating chickenpox

According to the results, the ML-based GMDH models outperformed the basic GMDH model in approximating chickenpox.

In addition, as observed in Fig. 6 (for greater clarity, the R values are multiplied by 10), MLP-based GMDH, RF-based GMDH, and ELM-based GMDH exhibited weaker performance compared with the basic GMDH method in terms of RMSE and MAE metrics. Regarding the STD error metric, the basic GMDH method performed better than the other methods did. Only the MLP-based GMDH method presented better results in the RMSE and MAE metrics compared with the basic GMDH method. Overall, in approximating chickenpox, ML-based GMDH did not show considerable improvement in relation to the basic GMDH method. This matter may have arisen either because the complexity in this dataset was negligible/minimal or more observations may have produced a different result.

Fig. 6

Visual comparison of the GMDH and ML-based GMDH models on approximating chickenpox

Approximation of bike-sharing demand

In the next task, the Seoul bike sharing demand was approximated. The dataset⁵ contained a count of public bikes rented at each hour in the Seoul bike-sharing system with the corresponding weather data and holiday information. Currently, rental bikes are available in many urban centers for the enhancement of mobility comfort. It is important to make rental bikes available and accessible to the public at the right time because this will lessen users’ waiting time. Eventually, providing the city with a stable supply of rental bikes becomes a major concern. The crucial part is the prediction of the bike count required at each hour for the stable supply of rental bikes. The dataset contains weather information (temperature, humidity, wind speed, visibility, dew point, solar radiation, snowfall, rainfall), the number of bikes rented per hour, and date information. Of the 8760 observations (after preprocessing), 80% (7008) were considered for training and 20% (1752) for testing the network. Table 6 shows the calculated evaluation metrics for the predictions made by the basic GMDH model and the various ML-based GMDH models.

Table 6 Results of the GMDH and ML-based GMDH models bike-sharing demand

According to the results, the ML-based GMDH models outperformed the basic GMDH model in approximating the bike-sharing demand. For comparing results in a graphical shape, evaluation metrics calculated for each method are depicted in Fig. 7 as a bar chart.

Fig. 7

Visual comparison of the GMDH and ML-based GMDH models on approximating bike sharing demand

As shown in Fig. 7 (for greater clarity, the R values are multiplied by 10), all ML-based GMDH performed much better than the basic GMDH method did in terms of the R, RMSE, MAE, and STD error metrics. The extent of the improvement made by ML-based GMDH is clear in approximating the bike-sharing demand.

To validate the significant difference between the results obtained by all the methods, we applied a Wilcoxon signed-rank test to four evaluation metrics—RMSE, MAE, R, and STD error. The obtained results are presented in Table 7 in terms of p values.

Table 7 Wilcoxon signed-rank test for evaluating significance on approximating results

From the results in Table 7 and the obtained p values, the null hypotheses are rejected and all differences are significant. In other words, all ML-based GMDH models showed significantly better results in approximating the power consumption, PM2.5 concentration, and bike-sharing demand compared with the conventional GMDH model. Only in approximating Hungarian chickenpox did the ML-based GMDH models fail to show better results in all evaluation metrics. Regarding the number of observations in this dataset, the performance of ML-based GMDH models—with their complexities related to the basic GMDH model—may have been affected by under-fitting. This is suggested because the ML-based GMDH models showed significantly better results in three cases with a greater number of observations.

Conclusion

The approximation capability of the GMDH model was improved by combining it with conventional ML models—namely, SVR, RF, MLP, and ELM. To this end, the basic partial functions (polynomial) in the GMDH model, which are used as transfer functions in neurons, were replaced by ML models. Given the GMDH mechanism and the role of the polynomial partial functions in this method, the ML models were considered black boxes in the sequential structure of the GMDH to approximate the relationship between the input and output pairs. The simulation results on a non-polynomial function and four real-world datasets confirmed the better performance of the ML-based GDMH models compared with the GMDH model in terms of the RMSE, MAE, R, and STD error. In the proposed ML-based GMDH model, in each neuron, an ML model is trained between two (or more) inputs and targets. This mechanism may be time-consuming in cases with many inputs and observations. This matter can be addressed by incorporating information theory-based methods and feature selection approaches into the models in future work.