Introduction

The last 20 years have witnessed an explosion of e-commerce, which has prompted customers to purchase online instead of visiting physical stores. Platforms like MeiTuan and UberEATS are selling many foods every day and have become more and more popular because of their convenient online catering service. These platforms provide end-to-end services for customers and restaurants, This means that after customers make requests on platforms, restaurants prepare food in the central kitchen once they receive orders from platforms, find drivers to deliever the food, and finally deliver the food from restaurants to customers according to the arrangement of platforms [1]. There is no doubt that platforms play an essential role in this food delivery service; however, one key challenge they have to face is how quickly and efficiently they deliver food from restaurants to customers with limited drivers. This problem is consistent with the well-known Last-Mile Problem (LMP) [2], which transports goods from a public node to customers and can be formulated by a modified VRP (Vehicle Routing Problem) model. In our case, the public node could be the nearest local logistics service center or central kitchen, and the transport means of food LMP include walking, taking a taxi, or driving a private vehicle.

LMP is potentially very expensive and accounts for a large part expenditure of the whole business activity of food platforms [3]. With the increasing business competition and fast delivery requirement, online platforms have to improve the performance of Last-Mile Transportation Systems (LMTS), to gain a large market share, control cost and ensure delivery timeliness. So, it is a vital task for online food platforms to solve LMP effectively. What’s more, the last-mile delivery problem is a computational challenge because VRP is an NP-hard problem in theory, and there are many uncertainty factors in practice that affect the parameter values [4]. Using optimization theories and methods, related managers can make order assignment and routing decisions for LMP by solving an improved VRP, which has been solved effectively by exact or heuristic algorithms. However, realistic uncertain factors in last-mile delivery, such as drivers’ behavior characteristics and traffic conditions, are difficult to be predicted exactly using general statistical methods for their inherent complexities, This leads to the inaccurate estimation of optimization parameters, such as service time or service cost. Consequently, the uncertain factors will result in an unreasonable optimization formulation and ineffective management decision.

Early related studies usually assume that optimization models’ parameters are constant and estimate those parameters by sample statistics or specialist experience. In those works, researchers focus on how to design efficient algorithms to derive exact or satisfactory solutions. Considering the existence of uncertainties in practice, optimization problems involving uncertain factors began to receive more attention. In the beginning, stochastic programming theory is proposed to handle the randomness of parameters [5]. For example, as one of the widely used stochastic programming measures, chance constraint requires the probability of reference target to satisfy a given threshold. In the past decade, robust optimization (RO) and distributionally robust optimization (DRO) have been drawing more and more attention for their advantages in using real data by combining statistical techniques [6,7,8]. In the robust optimization framework, it is crucial to construct the uncertain set of parameters based on the sample data, which also has a significant impact on the optimization results and decision.

Nowadays, with the development of information technology, massive data have been accumulated in many fields. In the meanwhile, AI technologies include machine learning, deep learning, and reinforcement learning have exhibited high effectiveness in prediction, classification, and other problems for many practical applications. Sequentially, data-driven optimization, which combines traditional optimization methods with AI prediction tools, has become a new research frontier in the operations research field. Typically, the optimization decision can be improved dramatically due to the accessibility and excellence in parameter estimation of the machine learning method. The data-driven combination form has been applied in many real analytics fields [9,10,11]. However, most of the present studies execute the procedures of machine learning and optimization separately. More specifically, the machine learning method is only used to generate parameters’ prediction, and the optimization model is only used to generate an optimal decision based on the estimated parameters given by machine learning. This procedure takes the same paradigm as stochastic programming, robust optimization, and distributionally robust optimization. The paradigm is defined as predict-then-optimize [12]. In essence, the predict-then-optimize paradigm does not account for how the predictions would be used in the downstream optimization model, no matter how the prediction methods are used. This asynchronous procedure leads to an inconsistency phenomenon in the predict-then-optimize paradigm, that is, the quality of a prediction is not equivalent to the quality of a decision.

To overcome the shortcomings of the predict-then-optimize paradigm, Elmachtoub and Grigas [12] propose a smart predict-then-optimize (SPO) framework. Although the SPO approach also maintains the sequence that first prediction then optimization, but the quality of parameter prediction is measured by decision error rather than prediction error. The authors also present some simple examples to demonstrate the SPO strongly outperforms the ordinary optimization models with regular machine learning prediction.

In this paper, we aim to improve online platforms’ last-mile delivery performance using the SPO framework. We consider a simplified scenario: an online delivery service provider first prepares packages at his central depot and then deliver all packages to the customers by drivers within a certain radius from the depot. Each driver has a limited capacity, and the service provider needs to ensure that each driver’s total travel time is less than a given threshold. This setting is a typical and straightforward LMP case for online food platforms or logistics companies, and the problem can be formulated by a Capacitated Vehicle Routing Problem (CVRP) model. However, different from the previous conventional models, we assume the travel time between any two customers is uncertain and can be predicted by the large volume and multi-source data. The data may incorporate the distance, weather, season, driver’s profile, and real-time traffic data from mobile applications. The booming online platforms provide a convenient shopping experience for customers and accumulate enough relevant data for smart decisions. Therefore, adequate data guarantee the basic requirements of our methods.

What’s more, this paper assumes that the driver's behavior impacts his travel time, which leads to a mutual effect between parameters and decision variables. The problem setting is similar to [1], which integrates order assignment optimization with a travel time prediction model. However, they do not take the decision error caused by inaccurate prediction into consideration, while our work involving this point by using a different mathematic formulation and SPO data-driven optimization implementation framework. Furthermore,this work provides a specific solution algorithm to handle the coupled problem of parameters and decision variables.

The remainder of this paper is organized as follows: we review the relevant studies about data-driven optimization and LMP in Sect. 2. Then Sect. 3 provides the corresponding model and the solving algorithms. In Sect. 4, we compare the proposed model with other methods to indicate our model’s advantage by numerical studies. Finally, the conclusion and future research directions are presented in Sect. 5.

Related literature

There are several literature streams relevant to our work. This section presents a brief overview of those researches from two domains: LMP and data-driven optimization.

Last-mile problem

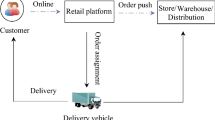
The classical LMP can be described schematically as Fig. 1, which contains a central depot that prepares packages and several customers distributed around the central depot in a fixed area. A fleet of vehicles visit customers and return to the central depot after all the packages are delivered. There are also some variants of the classical LMP. For example, Wang and Odoni [2] study the last-mile problem for passenger transportation in a stochastic setting. This paper studies the last-mile problem following a classical VRP framework, which is a packages’ assignment and delivery problem and has been widely studied in the operations research literature [13]. Jiang et al. [14] consider a similar last-mile delivery problem and aim to reduce the total costs and carbon emissions, their model is a variant of the traveling salesman problem. Zhou et al. [15] study a green VRP considering dual last-mile delivery services with stochastic travel times. However, both of them do not consider the prediction problem with multivariate data. VRP is first introduced by Dantzig and Ramser [16], they concern the gasoline delivery problem for a gas station by truck. After their seminal paper, a vast number of various extensional works of VRP have been published, range from stochastic context [17], dynamic environment [18], delivery time constraint [19] to time window constraint [20]. For a broad overview of VRP variants, the readers are recommended to refer to Toth and Vigo [13].

Fig. 1
figure 1

Schematic of the last-mile transportation

Full size image

Due to the complexity and NP-hard of VRP, designing an effective algorithm is always a critical job in this field. Various heuristic or exact algorithms have been proposed and verified. The history of VRP heuristic algorithms is as old as the problem itself. Dantzig and Ramser [16] sketch a simple heuristic based on successive matchings of vertices through the solution of relaxed linear programs. Clarke and Wright [21] propose a useful greedy heuristic to derive the approximate solution of VRP. Since then, a wide variety of constructive and improvement heuristics have been proposed. Such as constructive heuristics provide a starting solution to improve algorithms [22, 23], classical improvement heuristics perform intra-route and inter-route moves [24, 25], metaheuristics include local search methods [26] and population-based heuristics [27]. In essence, VRP is a combinatorial optimization which can also be solved by classical exact algorithms, such as brand-and-bound algorithms with assignment problem relaxation [28, 29], brand-and-bound algorithms with shortest spanning tree [30], branch-and-cut algorithms [31] and column generation algorithms [32]. This paper’s proposed LMP model is a kind of capacitated VRP, but it has a prominent characteristic that there are mutual effects between parameters and decision variable. In this paper, a data-driven SPO framework and design-related algorithm is used for the proposed complex model.

Data-driven optimization

The main purpose of this study is to improve the optimal vehicle routing decision for last-mile delivery using real data. Therefore, this paper is also closely related to the stream of data-driven optimization. Generally speaking, data-driven optimization approaches find suboptimal solutions from data and highlight the importance of real data on the decision. Previous data-driven optimization approaches can be roughly classified as operational statistics, sample average approximation, and robust optimization. Operational statistics are recognized as the beginning work of data-driven optimization in operational research, this approach integrates parameter estimation and optimization to obtain better solutions compared with the traditional approach. Liyanage and Shanthikumar [33] apply it to a single period newsvendor problem, and Chu et al. [34] investigate how to find the optimal operational statistic with a similar problem setting. The sample average approximation’s (SAA) basic idea is using sample average function to approximate expected value function, and then solving sample average optimization problem to derive an optimal solution. Kleywegt et al. [35] introduce this approach and present the convergence rates, stopping rules, and computational complexity of this procedure. After then, the SAA approach is widely used in different problems. For example, Schütz et al. [36] use SAA to solve a two-stage supply chain design problem for a Norwegian meat industry, Chang et al. [37] apply SAA scheme to solve a flood emergency logistics problem. Mathematical programming’s solution is usually incorrect when there are random parameters. The reason is that we cannot use a specific distribution to describe the ambiguity of uncertainty parameters. Robust optimization, and its extension distributionally robust optimization are proposed to overcome this shortcoming. Those approaches represent random parameters by some uncertainty sets which do not have a specific distribution expression but can be constructed by historical data. Delage and Ye [8] propose a distributionally robust model that describes the uncertainty by mean and covariance matrix constraints, then provide probabilistic arguments to design optimization model. Bertsimas et al. [38] develop a tractable framework for solving an adaptive distributionally robust linear optimization problem, they minimize the worst-case objective over a class of second-order conic representable ambiguity set.

Although the above data-driven approaches perform well with real data, they do not have a clear way to use feature data. The machine learning model has a prominent advantage in exploiting multi-source data, so recent advanced researches attempt to integrate the machine learning model with the optimization model. Most of this integration follows a predict-then-optimize framework mentioned in the introduction, such as Ferreira et al. [9] first adopt regression tree to estimate lost sales and predict future demand using historical sale data, then develop an algorithm to solve multiproduct price optimization for the online retailer. Liu et al. [1] use a class of machine learning models, such as LASSO regression, ridge regression, and support vector machine (SVM), to predict travel time, then integrate the predictors within the optimization model to solve the last-mile delivery problem. However, in those papers, the machine learning method only accounts for exact prediction, and does not guarantee optimal decisions in uncertain environments. Therefore, researchers begin to consider improving the prediction model by the decision error instead of prediction error. Kao et al. [39] seek to train a machine learning model that minimizes loss for a nominal unconstraint optimization problem. Considering a similar problem with [39], Donti et al. [40] develop a heuristic algorithm to address a more general setting. Unfortunately, both Kao et al.[39] and Donti et al.[40] focus on the unconstrained optimization models. More recently, Elmachtoub and Grigas [12] design a new predictive framework to incorporate the general optimization problem structure, which enables robust performance against model Misspecification. This paper investigates the LMDP using the SPO framework presented in [12], and proposes an algorithm to deal with the mutual effect between decision variables and uncertainty parameters.

Problem description and assumptions

We first provide an overview of the concerned online platforms in the last-mile delivery problem, then introduce the SPO framework to integrate prediction model and optimization formulation. Finally, we present relevant algorithms to solve the proposed SPO-LMP model.

A. LMP modeling

In the beginning, we describe the LMP of the online platforms shown in Fig. 1 in detail. One single provider (platform or logistics company) takes charge of LMP service for a given area. The delivered item can be food or package which has been prepared in the central depot. The provider has known the location and demand quantity of each custom before the delivery service. Furthermore, the provider’s LMP consists of two procedures: first, the provider should assign the delivery task to a fleet of vehicles and then decides the delivery sequence for each vehicle. The vehicles are assumed to be heterogeneous with different capacities. The drivers have different driving habits and preferences, which will lead to different travel durations in the same service arc. Once the provider schedules an arrangement plan, the driver will execute a given delivery route, i.e., visiting each customer’s destination, and then return to central deport to pick up the items for the next delivery tour. Delays are inevitable, primarily when the orders are poorly assigned to drivers. For this reason, the provider’s primary focus on the timeliness of delivery due to the intense market competition and customer faster delivery expectation. According to the above explanation, the concerned last-mile problem could be formulated as a capacitated vehicle routing problem with the on-time delivery objective function, whose notations and formulation are presented in the following.

We denote the central depot as node 0, and all customers are given by a set \(N = \left\{ {1,2, \ldots ,n} \right\}\). The demand of customer \(i { }\left( {i \in N} \right)\) is given by a scalar \(d_{i} \ge 0\), e.g., the weight or number of the goods needed to deliver. Suppose there are \(k\) drivers who have diverse vehicles with different capacity \(Q_{k}\) and fixed identical operating cost \(C\), and the set of drivers is defined as \(k \in \left\{ {1,2, \ldots ,K} \right\}\). The drivers make deliveries for customers’ pooling \(N\) starting from central depot node 0, the traveling time from customer node \(i\) to node \(j\) is denoted by \(t_{ij}\). We need to find the optimal routing for each vehicle to minimize the total delivery time and total operating cost under vehicle capacity constraints.

With the above-given notations, we can construct a delivery model by network optimization framework. Let \(V = \left\{ 0 \right\} \cup N = \left\{ {0,1, \ldots ,n} \right\}\) be the set of nodes and \(E = \left\{ {\left( {i j} \right):i,j \in V,i \ne j and \left( {i j} \right) \ne \left( {j i} \right)} \right\}\) be the set of edges, then we get a directed graph \(G = \left( {V,E} \right)\). Notice that \(\left| E \right| = n\left( {n + 1} \right)\) since \(t_{ij} \ne t_{ji}\). It is reasonable because of the complex road conditions in reality, which make the trip between two customers has different travel time in a different direction. In sum, the last-mile delivery problem is defined by a directed and weighted graph \(G = \left( {V,E,{ }t_{ij} ,d_{i} } \right)\) together with a driver set \(K\), each vehicle has a delivery capacity \(Q\).

To present the corresponding formulation concisely, some condensed notations will be further defined. Suppose \(S\) is an arbitrary non-empty subset of \(V\),\( S \subseteq V\), let the in-arcs and out-arcs of \(S\) be \(\delta^{ - } \left( S \right) = \left\{ {\left( {i,j} \right) \in E:i \notin S,j \in S} \right\}\) and \(\delta^{ + } \left( S \right) = \left\{ {\left( {i,j} \right) \in E:i \in S,j \notin S} \right\}\). the in-arcs and out-arcs of a node \(i\) are calculated by setting \(S = \left\{ i \right\}\). For a customer subset \(S\), it is assumed that the minimum number of drivers used to serve \(S\) is \(r\left( S \right)\). It is clear that \(r\left( S \right)\) is dependent on customer demand \(d_{i}\),\( i \in S\) and vehicle capacity \(Q\), and \(r\left( S \right)\) can be computed by solving a bin packing problem. A simple formulation without considering the heterogeneity of drivers can be presented by two-index decision variable \(x_{ij}\) with \(\left( {i,j} \right) \in E\), \(x_{ij}\) is binary variable indicating a driver first deliver \(i\) then \(j\) if \(x_{ij} = 1\), no driver moves from \(i\) to \(j\) if \(x_{ij} = 0\). Another decision variable is the exact number of used drivers, \(m\). With the above notations, the last-mile delivery model can be given as follows:

$$ \mathop {\min }\limits_{m \le K,x} \mathop \sum \limits_{{\left( {i,j} \right) \in E}} t_{ij} x_{ij} + \beta Cm, $$
(1)
$$ {\text{s}}.{\text{t}}.{ }\mathop \sum \limits_{{j \in \delta^{ + } \left( i \right)}} x_{ij} = 1, \,\forall i \in N, $$
(2)
$$ \mathop \sum \limits_{{i \in \delta^{ - } \left( j \right)}} x_{ij} = 1, \,\forall j \in N, $$
(3)
$$ \mathop \sum \limits_{{j \in \delta^{ + } \left( 0 \right)}} x_{0j} = m, $$
(4)
$$ \mathop \sum \limits_{{i,j \in \delta^{ + } \left( S \right)}} x_{ij} \ge r\left( S \right), \,\forall S \subseteq V, $$
(5)
$$ x_{ij} \in \left\{ {0,1} \right\}, \forall \left( {i,j} \right) \in E. $$
(6)

In this model, \(\beta\) is a constant parameter that adjusts service quality and operating cost. The objective function (1) contains the total travel time cost and total operating cost. Constraints (2) and (3) ensure that each customer can be visited precisely once in a route. Constraint (4) ensures that the number of drivers at work is no more than \(k\). Constraint (5) works for eliminating illegal routes and serves as capacity constraints.

Following the assumptions commonly used in previous researches, travel time \(t\) is assumed to be uncertain. However, unlike previous studies that define travel time as continuous or discrete random variables, this study tends to emphasize the predictability of random travel time. In reality, travel time is highly dependent on several relevant factors, such as road conditions, weather, transportation distance, and driver characteristics. One of the difficulties in our LMP is that the travel time is dependent on the driver’s behavior. Therefore, we introduce a three-index decision 0–1 variable \(x = \left( {x_{ijk} } \right)\) to describe the driver’s behavior. \(x_{ijk} = 1\) if driver \(k \) services customer \(i\) and customer \(j\) successively; otherwise, \(x_{ijk} = 0\). Let \(y_{ik} = 1\) if driver \(k \) services customer \(i\), else \(y_{ik} = 0\) for \(i \in \{ 1, \ldots ,n\)}, and \(y_{0k} = m\) represents that every driver must start from a central depot. For simplification, let \(t = \left( {t_{ij} } \right)\) and the proposed LMP can be formulated as:

$$ \mathop {\min }\limits_{m \le K,x} \mathop \sum \limits_{i} \mathop \sum \limits_{j} \mathop \sum \limits_{k} t_{ij} x_{ijk} + \beta Cm, $$
(7)
$$ {\text{s}}.{\text{t}}.{ }\mathop \sum \limits_{j} x_{ijk} = 1, \,\forall i \in N, k = 1, \ldots ,m, $$
(8)
$$ \mathop \sum \limits_{i} x_{ijk} = 1, \,\forall j \in N,k = 1, \ldots ,m, $$
(9)
$$ \mathop \sum \limits_{i} d_{i} y_{ik} \le Q_{k} , k = 1, \ldots ,m, $$
(10)
$$ \mathop \sum \limits_{k} y_{ik} = \left\{ {\begin{array}{*{20}l} {1, i = 1, \ldots ,n} \\ {m, i = 0 } \\ \end{array} } \right. $$
(11)
$$ x_{ijk} \in \left\{ {0,1} \right\}, \,\forall \left( {i,j} \right) \in E,k = 1, \ldots ,m . $$
(12)

As mentioned above, online platforms have abundant available data for prediction to make more accurate decisions. Therefore, how to generate a smart decision by exploiting real data is a crucial problem. In this paper, an SPO framework is adopted to solve the LMDP of online platforms.

B. SPO paradigm

The SPO framework trains prediction models based on a new loss function represented by decision error instead of decision error. In our setting, actual travel time \(t\) is not known when the service provider makes a delivery decision, but some associated features can be observed. We assume \(p\) available features are denoted by vector \(f \in R^{p}\), such as the above-mentioned driver’s profile, routing length, weather, season or traffic information. Let \(F\left( {t,x,m} \right)\) be the objective function represented by Eq. (7), i.e., \(F\left( {t,x,m} \right) = \mathop \sum \nolimits_{{\left( {i,j} \right) \in E,k}} t_{ij} x_{ijk} + \beta mC\). For simplicity, we condense the decision variable \(x: = (x,m)\), then the objective function is simplified to \(F\left( {t,x} \right)\). Traditional optimization frameworks usually figure out the conditional distribution of \(t\) with given feature data \(f\), and then solve the corresponding model with the expected objective function. For example, stochastic programming uses chance constraints or a two-stage model to handle the random variables. However, the SPO framework we adopted integrates the machine learning method with optimization programming. Next, some notations are replinshed and the key ingredients of the SPO paradigm are introduced.

Assume that \(\left( {f_{1} ,t_{1} } \right),\left( {f_{2} ,t_{2} } \right), \ldots ,{ }\left( {f_{s} ,t_{s} } \right)\) denotes the training data for machine learning, where \(f_{i} \in \chi \subset R^{p}\) is a feature vector representing contextual information associated with travel time \(t_{i}\). A hypothesis class of travel time vector prediction models is \({ }H: \chi \to R^{q}\), which predicts travel time \(\hat{t}\) associated with feature \(f\) by \(\hat{t}: = H\left( f \right)\). A loss function \(l\left( {\hat{t},t} \right){ }\) quantifies the error in predicting \(\hat{t}\) when the realized true travel time is \(t\). In general, given the training data \({ }\left( {f_{1} ,t_{1} } \right),\left( {f_{2} ,t_{2} } \right), \ldots ,{ }\left( {f_{s} ,t_{s} } \right)\), an optimal prediction model \(H^{*}\) is derived to minimize the empirical loss function:

$$ \mathop {\min }\limits_{H} \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} l\left( {H\left( {f_{i} } \right),t_{i} } \right). $$
(13)

After deriving the prediction model \(H^{*}\), we can solve the LMP model (7–12) and induce an optimal decision \(X^{*} \left( f \right)\) according to an observed feature vector \(f\).

In the traditional predict-then-optimize framework, the loss function is usually wholly independent of the LMP optimization problem. For example, the mean squared error loss function \(l\left( {\hat{t},t} \right) = \frac{{\hat{t} - t_{2}^{2} }}{2}\) is widely used in the linear regression models of machine learning. The corresponding prediction problem is to find the best linear model \(H^{*}\) to minimize \( \frac{1}{n}\sum\nolimits_{{i = 1}}^{n} {H^{*} f_{i} - t_{{i_{2}^{2} }} } \) without considering the underlying structure of the optimization problem.

The SPO framework takes advantage of problem structure to train the prediction model, predict travel time, and then construct the loss function intelligently. According to the defined notations, \(p\) is the dimension of the feature vector,\( s\) is the number of training samples, and \(q\) is the dimension of the decision matrix, i.e., \(q = i*j\), \(i,j \in V\). The nominal LMP model (1–5) can be simplified as

$$ \mathop {\min }\limits_{x} F\left( {t,x} \right), $$
(14)
$$ s.t.{ }x \in \Gamma . $$
(15)

In this model, \(\Gamma\) is a non-empty feasible region generated by constraints (8–12). \(F\left( {t,x} \right)\) is a linear function concerning \(x\) with redefining \(t: = (t,\beta C)\), then the optimal solution set can be expressed as \( X^{*} \left( t \right): = \arg \min _{{x \in \Gamma }} t^{{\text{T}}} x \).

The SPO loss function is \(l_{spo}^{{X^{*} }} (\hat{t},t): = t^{T} X^{*} (\hat{t}) - F^{*} (t)\), in which \(\hat{t}\) is a travel time prediction and \(X^{*} \left( {\hat{t}} \right)\) is a decision obtained by solving (11–12). After implementing the routing decision \(X^{*} \left( {\hat{t}} \right)\), the actual travel time \(t\) and objective cost \(F^{*} \left( t \right)\) is realized, then excess cost \(t^{T} X^{*} \left( {\hat{t}} \right) - F^{*} \left( t \right)\) can be derived. Since \(X^{*} \left( {\hat{t}} \right)\) may contain more than one solution, another definition that does not depend on the particular choice of the optimization oracle \(X^{*} \left( {\hat{t}} \right)\) is provided by

$$ l_{SPO} \left( {\hat{t},t} \right) = \mathop {{\text{max}}}\limits_{{x \in X^{*} \left( {\hat{t}} \right)}} t^{T} x - F^{*} \left( t \right). $$
(16)

Given the training data and definition of SPO loss function, we need to determine a travel time prediction model with minimal SPO loss function \(l_{SPO} \left( {\hat{t},t} \right)\). The prediction model would be determined by empirical risk minimization principle similar to Eq. (13), which leads to the following optimization problem:

$$ \mathop {\min }\limits_{H} \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} l_{SPO} \left( {H\left( {f_{i} } \right),t_{i} } \right). $$
(17)

To overcome the difficulty in solving the above optimization problem, Elmachtoub and Grigas [12] provide a useful approximate loss function. Indeed, the SPO loss function \(l_{SPO} \left( {\hat{t},t} \right)\) may not be continuous with \(\hat{t}\) because \(X^{*} \left( {\hat{t}} \right)\) cannot be guaranteed to be continuous with respect to \(\hat{t}\). However, the approximate surrogate loss function is convex and can be defined as

$$ l_{SPO + } \left( {\hat{t},t} \right) = \xi_{\Gamma } \left( {t - 2\hat{t}} \right) + 2\hat{t}^{T} X^{*} \left( t \right) - F^{*} \left( t \right). $$
(18)

In Eq. (18), the support function of feasible region \(\Gamma\), \(\xi_{\Gamma } \left( t \right) = \max_{x \in S} \left\{ {t^{T} x} \right\}\) is convex in \(t\). \(\xi_{\Gamma } \left( \cdot \right)\) is finite and for all \(t \in R^{q}\), there is \(\xi_{\Gamma } \left( t \right) = - F^{*} \left( { - t} \right) = t^{T} x^{*} \left( { - t} \right)\). Consequently, the optimization problem (17) has the following empirical risk counterpart:

$$ \mathop {\min }\limits_{H} \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} l_{SPO + } \left( {H\left( {f_{i} } \right),t} \right). $$
(19)

This paper uses the linear prediction function \(H\left( f \right) = B{*}f,{ }B \in R^{q \times p}\) to predict travel time. To improve accuracy and preserve convexity of the prediction model, we incorporate ridge penalty \({\Omega }\left( B \right) = B_{F}^{2} /2\) into Eq. (19), where \(B_{F}\) denotes the Frobenius norm of matrix \(B\). These presumptions lead to the following version of the risk model:

$$ \mathop {\min }\limits_{{B \in R^{d \times p} }} \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} l_{SPO + } \left( {Bf_{i} ,t_{i} } \right) + \lambda {\Omega }\left( B \right), $$
(20)

where \(\lambda \ge 0\) is a regularization parameter and selected by adjusting. The above optimization problem (20) is a convex optimization since both \({\Omega }\left( B \right){ }\) and SPO + loss function \(l_{SPO + }\) are convex.

The classical gradient approach can be used to solve the SPO+ problem due to the convexity of (20). For convenience, let \(\phi_{i} \left( B \right) = l_{SPO + } \left( {Bf_{i} ,t_{i} } \right) + \lambda {\Omega }\left( B \right)\), then the optimization objective function is reformulated as \(\mathop \sum \limits_{i = 1}^{n} \phi_{i} \left( B \right)\). As mentioned above, \(l_{SPO + } \left( { \cdot ,t} \right)\) is convex for a given \(t\), and \({\Omega }\left( B \right)\) is a convex ridge penalty function, then the sum of \(\phi_{i} \left( B \right)\) is also convex. Furthermore, the sub-gradients of \(\phi_{i} \left( B \right)\) is \(2\left( {X^{*} \left( t \right) - X^{*} \left( {2\hat{t} - t} \right)} \right)x_{i}^{T} + \lambda \nabla {\Omega }\left( B \right)\), and according to Nemirovski et al. [41], we set the \(i\)-th update step-size from the reverse gradient direction to be \(\Upsilon_{i} = 2/\lambda \left( {i + 2} \right)\). Given the travel information data \(\left( {f_{1} ,t_{1} } \right),\left( {f_{2} ,t_{2} } \right), \ldots ,{ }\left( {f_{s} ,t_{s} } \right)\), problem (20) can be solved by the mini-batching gradient descent approach. The algorithm is as follows:

figure a

In Algorithm 1, we use the sample data successively, resulting in early stopping if there is large-scale sample data. Therefore, the batch data can also be constructed uniformly at random from a given sample set a standard application of the stochastic gradient descent approach. It is important to emphasize that the optimal solution of the LMP problem is required several times in each iteration of Algorithm 1. To guarantee efficiency, we need to choose a suitable algorithm for LMP to accelerate the convergent speed. This paper adopts a simulated annealing (SA) algorithm to compute \(X^{*} \left( \cdot \right)\) in each iteration step of Algorithm 1. Because the travel time and optimal routing have a mutual effect on each other, after implementing the prediction Algorithm 1, we leverage the idea of classical improvement heuristics of VRP to retrieve the final optimal routing.

Classical local search descent methods do not accept non-improvement moves at each iteration, whereas the SA algorithm does with specific probabilities. Therefore, the SA method can reach a satisfactory suboptimal solution much faster than local search descent methods. However, the SA algorithm is still based on a local search mechanism for iterating. We first present two commonly used exchange operators and the classical local search descent method of VRP.

Suppose a feasible routing solution for LMP have been already obtained, \(X = \left\{ {R_{1} , \ldots ,R_{i} , \ldots ,R_{j} , \ldots R_{k} } \right\}\), where \(R_{i}\) is the ordered set of customers serviced by driver \(i\). The following procedure easily derives the initial feasible solution: let each customer being served by a driver, and then compute travel time-saving \(t_{0i} + t_{0j} - t_{ij}\) about customers \(i\) and \(j\) which are served by one vehicle from the central deport. These savings are sorted in decreasing order. Finally, this procedure merges customers corresponding to the highest saving without violating the capacity restriction until no further merges are possible.

Define a non-empty subset of \(R_{i}\) and \(R_{j}\) as \(S_{1}\) and \(S_{2}\), respectively. An interchange between \(R_{i}\) and \(R_{j}\) is a replacement by \(R_{i}^{^{\prime}} = \left( {R_{i} - S_{1} } \right) \cup S_{2}\) and \( R_{j}^{^{\prime}} = \left( {R_{j} - S_{2} } \right) \cup S_{1}\). Then we get a new neighboring solution \(X^{\prime} = \left\{ {R_{1} , \ldots ,R_{i}^{^{\prime}} , \ldots ,R_{j}^{^{\prime}} , \ldots R_{k} } \right\}\). In general, the interchange is defined according to the threshold size of the subset. For example, if the size of \(S_{1}\) and \(S_{2}\) is less than \(\lambda\), i.e., \(\left| {S_{1} } \right| \le \lambda\) and \(\left| {S_{2} } \right| \le \lambda\), the interchange is called \(\lambda\)-exchange. In this paper, we set \(\lambda = 1\). Correspondingly, the search order of a given pair \(\left( {R_{i} ,R_{j} } \right)\) has two standard operators described in Fig. 2. The 1–0 exchange wipes off a customer in a route and relocates the customer to another route. The 1–1 exchange swaps two customers in a routing pair.

Fig. 2
figure 2

exchange local search operators for the VRP

Full size image

For a given routing pair, the above exchange operators will generate a series of neighbors. In practical calculation, we can specify the searching order of neighbors following the permutation of routing pairs, which has a total number of \(k\left( {k - 1} \right)/2\) different pairs:

$$ \left( {R_{1} ,R_{2} } \right), \ldots ,\left( {R_{1} ,R_{k} } \right),\left( {R_{2} ,R_{3} } \right), \ldots ,\left( {R_{k - 1} ,R_{k} } \right).{ } $$
(21)

Following the above searching order of neighborhood, local search algorithms improve solution performance from the current \(X_{t}\) to another \(X_{t + 1}\) in its neighborhood \(N\left( {X_{t} } \right)\) if the objective value \(F\left( {X_{t + 1} } \right)\) is less than \(F\left( {X_{t} } \right)\). However, the SA algorithm accepts the improvement according to probabilities that are determined by a temperature parameter. The temperature parameter tends to zero following a deterministic cooling schedule. We adopt SA with a 1-interchange mechanism to solve \(X^{*} \left( \cdot \right)\) in Algorithm 1, and the SA is introduced as Algorithm 2:

figure b
figure c

Experimental design

This section presents numerical experiments to show the performance of the data-driven SPO + framework for solving LMP. Specifically, we use Matlab R2017b to implement the programming of Algorithms 1–3. To provide suitable training samples, we generate experimental data according to Elmachtoub and Grigas [12]. Notice that there are \(n\) customers and one central depot, the dimension of the travel time vector is \(q = n \times \left( {n - 1} \right)\). We firstly determine a matrix \(B^{*} \in R^{q \times p}\) whose entries is generated by Bernoulli distribution with probability 0.5, and then generate the training data as follows:

1. Generate the feature vector \(\hat{f}_{i} \in R^{p - 1}\) by a multivariate Gaussian distribution with i.i.d. standard regular entries, i.e., \(\hat{f}_{i} \sim N\left( {0,I_{p - 1} } \right)\), where \(I_{p - 1}\) is an identity matrix. Notice that \(\hat{f}_{i}\) is a part of the total feature vector \(f_{i} = \left( {\hat{f}_{i} ,f_{i}^{k} } \right)\), \(f_{i}^{k}\) represents the driver’s feature.

2. The travel time vector \(t_{ij}\) is generated by employing a polynomial kernel function and is according to \(t_{ij} = \left( {\left[ {\left( {\frac{1}{\sqrt p }\left( {B^{*} f} \right) + 3} \right)^{deg} + 1} \right]{*}\varepsilon } \right)_{{\left( {i - 1} \right)j + j}}\), where \(\varepsilon\) is a multiplicative noise matrix whose entries are generated independently from the uniform distribution on \(\left[ {1 - \overline{\varepsilon }, 1 + \overline{\varepsilon }} \right]\) for some given parameter \(\overline{\varepsilon } \ge 0\).

The parameter \(deg\) controls the amount of model misspecification. When \(deg = 1\), the expected value of travel time \(t\) is indeed a linear function. When \(deg\) takes a large value, the traditional regression methods will be sensitive to outliers and have poor performance. In this experiment, we set \(deg = 2\) which will generate enough outliers to compare SPO + framework against the normal loss approach. Furthermore, we set \(f_{i}^{k} = \sqrt {\left| {i + j - k} \right|}\) which construct a larger expectation value \(t_{ij}\) if \(i + j\) is far away from \(k\), and \(t_{ij}\) is small if \(i + j\) closes to \(k\).

Following the generating process above, experiments are implemented whose specific procedure and parameters setting are described as follows. Assuming there are \(p = 5\) features, and the nodes-vehicles pair is \({ }\left( {15,3} \right)\) in which further entry is a total number of customers and the latter is the number of total drivers. The customer demand is random generated as \(d_{i} = \left[ {24, 20, 20, 25, 24, 13, 16, 20, 25, 25, 16, 17, 22, 19, 15} \right]\) and vehicle capacity vector is \(Q = \left[ {94, 108, 100} \right]\). We generate customers’ positions in a 100*100 region and suppose the initial deport is situated in the central position. In case \(\left( {15,5} \right)\), the travel time dimension is \(q = 15{*}14\), and \(B\) has \(q \times p\) parameters to estimate. For the sample size that has a heavy impact on the practical performance, we choose the training set size \(S = 10000\), i.e., for a driver, we generate \({\text{s}}/k\) training data and let mini-batching be 100. The other parameters are set as follows: discounted operating cost \(\beta C = 10\), \(\overline{\varepsilon } = 0.5\), and the regularization parameter \({\uplambda }\) is selected by validating the ten different values evenly spaced between 0 and 1.

After training the prediction model by algorithms 1 and 2, we generate random testing data \(\left( {f,t} \right)\) and compute the optimal routing solution \(X^{*}\). We compare our model with the general least square predict and optimization model, the expected optimization model. The results are summarized in Figs. 3, 4, 5, 6.

Fig. 3
figure 3

The LMP routing of SPO

Full size image
Fig. 4
figure 4

The LMP routing of least square

Full size image
Fig. 5
figure 5

The LMP routing of expectation

Full size image
Fig. 6
figure 6

The LMP routing results of SPO, least-square and expectation methods

Full size image

Figures 3, 4, 5 present the online platforms’ detailed routing decisions by SPO, Least Square and expectation methods, respectively. In these figures, the customer deports represented by the circles, the square is the central service deport, and each polyline with the same color is the routing path of a given driver. We can see that the routing results of the three models have significant differences; even the driver visits the same customer set. For example, the top right corner customer point is connected with a different customer set. The SPO model assigns a driver to take charge of the bottom right five customers, which is in line with the results in the expectation model; however, comparing Fig. 3 and Fig. 5, it is clear that the service sequence of the SPO solution is quite different from that of the expected solution.

Furthermore, we make a thousand simulation that contains 1000 feature vectors for prediction. After predicting and optimizing, we compute the travel costs of three routing solutions according to actual travel time. Box plots in Fig. 6 draw the results. It is clear that the SPO model has a lower travel cost compare with the other two methods; the gap is about 5%. From the box plots, we can also find that the least square model has a similar performance as the expectation model, which indicates the traditional predict-then-optimize paradigm has a bottleneck, although the prediction model is effective in our numerical setting.

Conclusion

In this paper, a novel SPO framework is adopted to solve the emerging LMP of online food platforms. Our study mainly contains two innovations, the first one is that we provide a completed data-driven framework to solve the LMP more effectively, the second one is that we consider the drivers’ behavior in the model and propose the corresponding solving algorithms. The experimental results indicate that the proposed SPO framework provides a more effective delivery routing than the other methods.

Prediction and optimization are two significant challenges in analyzing real world problems. In the era of big data, a new regulatory principle to decide is combing data from Multi-Dimension. Data-driven optimization methods, especially the combination of optimization models and machine learning methods, are causing more and more attention. This work provides an effective model for LMP, and the implementation framework can be embedded to the management system for the daily operation of food delivery platforms.

Naturally, this work has many further improvement directions for future studies. First, this paper does not consider the pickup problem, which will make the LMP more difficult to solve. Second, a faster and more effective algorithm should be proposed for other more complex conditions, such as unknown parameters in the constraints, nonlinear objective function, and so on.