Multitasking scheduling with batch distribution and due date assignment

Abstract

This study addresses the multitasking scheduling problems with batch distribution and due date assignment (DDA). Compared with classical scheduling problems with due date-related optimization functions, the job due dates are decision variables rather than given parameters. The jobs completed are distributed in batches, and the sizes of all batches are identical, which may be bounded or unbounded. The jobs in every batch are scheduled one by one. Each batch incurs a fixed cost. Under multitasking environment, it allows the machine to put an uncompleted job on hold and turn to another uncompleted job. The goal is to identify the optimal primary job sequence, the optimal job due dates, and the optimal batch production and distribution strategy so that one of the following two optimization functions is minimised: the total cost composed of the earliness penalty, DDA cost, tardiness penalty and batch distribution cost, and the total cost composed of the earliness penalty, weighted number of late jobs, DDA cost and batch distribution cost. We devise efficient exact algorithms for the problems we consider, and perform numerical experiments to check how multitasking affects the scheduling cost or value, the results of which can assist decision-makers to justify the extent to put to use or refrain from multitasking.

Introduction

The problem we investigate in this study covers three momentous sub-areas of scheduling research, i.e., multitasking scheduling, scheduling with DDA, and batch distribution scheduling. All of these three sub-areas have been widely investigated in the literature. In the remaining part of this section, we briefly review some related research from these sub-areas.

The research about multitasking scheduling is initialized by Hall et al. [12], where the processing of a chosen job can be suspended by other uncompleted jobs. The authors demonstrate that the solution algorithms for some classical scheduling criteria are more complex in terms of time complexity than the corresponding problems without multitasking, and verify the effects of multitasking on the schedule criteria through computational experiments. Subsequently, the research on this line has attracted increasing attention. Hall et al. [13] introduce two different multitasking scheduling problems, in which the first one addresses alternate period processing and the second one investigates shared processing. Ji et al. [15] consider the identical parallel-machine scheduling problem with slack due-window assignment (DWA) under multitasking, in which the slack due windows are machine dependent. Hall et al. [19] consider the multitasking scheduling problem with common DDA such that all the jobs have a common due date. Xiong et al. [24] investigate the unrelated parallel-machine scheduling problem under multitasking, and present an exact mathematical-based programming for the problem with the goal of minimising the total completion time. Li et al. [18] and Wang et al. [23] address multitasking scheduling with two competing agents, and study the computational complexity and present exact algorithms for the problems, in which every agent requires to process its respective jobs and wishes to minimise its respective optimization function that is related to its respective jobs. As for due window assignment scheduling, Zhu et al. [34] address the multitasking scheduling problem with DDA and a rate-modifying activity (RMC), and Zhu et al. [33] further generalize the model to the case with multiple RMCs, in which the RMC may alter the process speed of the machine.

In the aforementioned studies, Ji et al. [15], Liu et al. [19] and Zhu et al. [34] address the due date-related optimization functions, in which the jobs’ due dates or time windows require to be decided by the decision-makers in the decision-making process along with the primary job sequence. This kind of scheduling problems is referred to scheduling with DDA or due window assignment in the literature, which has been extensively studied in the area of just-in-time scheduling and has been receiving widespread attention during the past four decades. The literature on this topic is abound, the interested readers are referred to the review papers by Gordon et al. [9, 10], and Kaminsky and Hochbaum [11]. Nevertheless, in contrast to our study, all the aforementioned studies as well as the review papers concentrate only on the problem of how to process the jobs while neglecting the problem of scheduling job delivery.

Recently, some researchers pay attention to the study of DDA (due window assignment) and batch distribution scheduling. Chen [4] address the common DDA and batch distribution scheduling, and devise an algorithm with polynomial running time to minimise the weighted sum of tardiness penalty, earliness penalty, batch distribution cost and DDA cost. Shabtay [22] considers the unrestricted DDA and batch distribution scheduling with acceptable lead-times, in which the jobs can be assigned different due dates, and prove that the considered problem is NP-hard and demonstrate that several special cases may be solved in polynomial time. Yin et al. [29] consider the common DDA and batch distribution scheduling with a RMC to minimise the weighted sum of earliness penalty, holding cost, tardiness penalty, batch distribution cost and DDA cost, and demonstrate that several special cases are polynomial time solvable. Yin et al. [26, 28] focus on the common DDA and batch distribution scheduling, where we can reduce the job processing times by assigning a certain amount of resources to process the jobs. Mor and Mosheiov [20] and Yin et al. [30, 32] study the DDA and batch distribution scheduling with two competing agents. Yin et al. [27] consider the common DWA and batch distribution scheduling problem such that the due windows of all jobs are identical, which specify the earliest and latest delivery date, and show that the problem with the goal to minimise the weighted sum of earliness cost, window location cost, window size cost, holding cost, tardiness cost, and batch distribution cost is polynomial time solvable. For more results on DDA and batch distribution scheduling, the interested readers are recommended to read the recent papers by Ahmadizar and Farhadi [1], Agnetis et al. [2, 3], Gong et al. [8], Kovalyov et al. [16], Li et al. [17], Xu et al. [25] and Yin et al. [31], and the review papers by Chen [5] and Hall and Potts [14].

What is noteworthy is that, as far as our information goes, there is no study addressing the batch delivery schedule in the field of multitasking setting. This study tries to fill up this gap, the contributions of which to the literature can be summarized as follows.

• We introduce a new scheduling model which simultaneously considers batch delivery, multitasking and DDA with the goal to identify the optimal primary job sequence, the optimal job due dates, and the optimal batch production and delivery strategy such that two objective functions considered are minimised.

• We demonstrate that the problem with the first optimization function may be solved in polynomial time and that the problem with the second optimization function is pseudo-polynomial time solvable.

• We perform computational experiments to assess how multitasking affects the scheduling cost or value, the results of which can assist decision-makers to justify the extent to put to use or refrain from multitasking.

We organize the study as follows. The next section formally describes the studied problem, followed by which the preliminary analysis and several properties about the optimal schedule for the studied problems are presented. The subsequent section focuses on developing the solution procedures for solving the problems. The computational experiments to verify the effects of multitasking on the objective function values are shown before the concluding section. The last section provides the conclusions and future studies.

Problem description

This section formally describes the studied problems. Table 1 summarizes the main notation used throughout this study.

Table 1 Notation used in this study

To be precise, a set of n jobs $N=\{J_1,\ldots ,J_n\}$ needs to be scheduled on a machine, which may schedule at most one job at a time. Every job $J_j,j=1,\ldots ,n$, has a non-negative processing time $p_j$ and a non-negative due date $d_j$. Different from the classical assumption that the due date $d_j$ is pre-defined, it is a decision variable in this study.

As in Hall et al. [12] and Wang et al. [23], we allow uncompleted jobs to suspend the jobs being processing, i.e., it permits the machine to suspend an uncompleted job and turn to another uncompleted job. We regard the job scheduled in anytime as the primary job, and the other uncompleted jobs as the waiting jobs, which may interrupt the processing of the primary job. We assume that each job may be handled as a primary job only once and immediately after another primary job completing its processing.

In the execution of a primary job, two types of times, say interruption time and switching time, are incurred, in which the former represents the time during which the primary job’s waiting jobs interrupt its processing, and the latter measures the time spent in the inspecting its waiting jobs. Specially, given any primary job $J_j$ and each waiting job $J_k\in W_j$, the time that job $J_k$ suspends the processing of job $J_j$ is defined as $\alpha r_k^j$, which is proportional to the remaining processing time of job $J_k$. The switching time for reviewing the waiting jobs of job $J_j$ is defined as $\varphi (|W_j|)$, which only depends on the number of waiting jobs. As a consequence, it is evident that the remaining processing time of job $J_k$ after interrupting r, $r=1,\ldots ,n-1$, primary jobs equals

$$\begin{aligned} f_k(r-1)-\alpha f_k(r-1)=(1-\alpha )^rp_k. \end{aligned}$$

(1)

Thus, the time that job $J_k$ suspends the $(r+1)$th primary job equals

$$\begin{aligned} \alpha f_k(r)=\alpha (1-\alpha )^rp_k. \end{aligned}$$

(2)

We distribute the completed jobs to the customers in batches, and process the jobs in a batch sequentially. We refer to the sum of the processing times of all the jobs in a batch to the processing time of the batch. The sizes of all batches are identical, which may be bounded or unbounded. By bounded batch size, we mean that there may be at most b jobs in each batch. In this study, we mainly concentrate on the case with bound batch size, and show how to extend the results to the unbounded case. We distribute each batch to the customers immediately after the last job in it completing its processing, and each distribution incurs a fixed cost $\vartheta$. We call the corresponding time as the delivery time of the jobs in the batch.

If we distribute a job to its customer before its due date, an earliness penalty is incurred which depends on how early it is ($E_j$). In addition, if we distribute a job to its customer after its due date, a lateness penalty is incurred, which depends on how late it is ($T_j$) or whether it is late ($U_j$=0 or 1). A job is referred to be early if $U_j\,=\,0$, and late otherwise.

The goal is to find (1) the optimal primary job sequence, (2) the optimal due dates, (3) the optimal number of batches m, and (4) the optimal batch distribution partition $(B_1, B_2, \ldots , B_{m})$ such that the optimization function

$$\begin{aligned} \digamma _1=\sum \limits _{J_j\in N}\left( \mu E_j+ \eta T_j+ \gamma d_j \right) + m \vartheta \end{aligned}$$

or

$$\begin{aligned} \digamma _2=\sum \limits _{J_j\in N}\left( \mu E_j+ \omega _j U_j+ \gamma d_j \right) + m \vartheta \end{aligned}$$

is minimised. In the remaining part of this study, we refer to the problems of minimizing the objective functions $\digamma _1$ and $\digamma _2$ as problems P1 and P2, respectively. In addition, as for problem P2, we assume that the jobs which would be late are not processed.

The following practical example concerning a two-level supply chain, which involves a steel manufacturer and a set of orders from several customers, motivates the studied problems, where each order consists of producing numbers of various medium to small steel coils. In this example, the manufacturer is referred to as a single “machine” and the orders are referred to as “jobs”. A sufficient number of transport vehicles are available to distribute the completed orders to the customers, where the transport vehicles have fixed capacity, and the cost per distribution is fixed. The processing requirement dictates that the orders containing in the same batch are processed contiguously and the distribution date of a batch equals the completion time of the last order in the batch. To reduce the setup times that are needed to perform some cleaning operations, or remove a previous container and install a new one when the manufacturer switches processing from one type of steel coil to another type of steel coil, multitasking is permitted, which allows unfinished orders to seize the production resources and suspend the orders under processing. The steel manufacturer will negotiate with customers to set the due dates for completing their orders. To reduce the operating cost and improve the overall satisfaction of the customers, the steel manufacturer requires to determine an effective way to allocate its services over time to perform the orders of the customers in a timely and cost-effective manner. This situation can be modeled as the studied models.

Structure property analysis

This section provides some structure properties on the optimal solution for problems P1 and P2.

Given a job sequence, we let $J_{[j]}$ be the jth primary job in the sequence, and let $B_k$ and $|B_k|$ represent the set of primary jobs scheduled in the kth batch and the number of primary jobs in $B_k$ ($k = 1, 2, \cdots$), respectively. The following lemma illustrates the property about assignment due dates.

Proposition 3.1

There is an optimal solution to the problem so that

• (i) $d_j= D_j$ if $\gamma <\eta$ and $d_j= 0$ otherwise for all $j=1,2,\ldots ,n$ when objective function is $\digamma _1$;

• (ii) $d_j= D_j$ if $\gamma D_j<\omega _j$ and $d_j= 0$ otherwise for all $j=1,2,\ldots ,n$ when the objective function is $\digamma _2$.

Proof

It is similar to the proof of Yin et al. [30]. For completeness, we provide a brief proof for (i). The proof for (ii) is similarly. To be precise, we require to address two cases.

• (1) $\gamma <\eta$. Assume there exists a solution S such that there is a job $J_j$ with $d_j= D_j$, i.e., $d_j< D_j$ or $d_j>D_j$. In what follows, we prove that a shift of $d_j$ to the right (resp., left) if $d_j< D_j$ (resp., $d_j>D_j$) such that $d_j=D_j$ can only reduce the optimization function value of $\digamma _1$. When $d_j< D_j$, the change in the optimization function value of $\digamma _1$ is $(\gamma -\eta )(D_j-d_j)<0$. On the other hand, when $d_j>D_j$, the change in the optimization function value of $\digamma _1$ is $-(\gamma +\mu )(d_j-D_j)<0$.

• (2) $\gamma \le \eta$. Assume there exists a solution S such that there is a job $J_j$ with $d_j>0$. In what follows, we prove that a shift of $d_j$ to the left such that $d_j=0$ can only reduce the optimization function value of $\digamma _1$. When $d_j\ge D_j$, the change in the optimization function value of $\digamma _1$ is $\eta D_j-(\gamma d_j+\mu (d_j-D_j))\le 0$. When $d_j< D_j$, the change in the optimization function value of $\digamma _1$ is $\eta D_j-(\gamma d_j+\eta (D_j-d_j))=(\eta -\gamma )d_j\le 0$. $\square$

The proposition above demonstrates that an optimal solution to each of the problems exists where the earliness of each job equals zero. It follows that the optimization functions $\digamma _1$ and $\digamma _2$ reduce to

$$\begin{aligned} \sum \limits _{J_j\in N} \xi D_j+ m \vartheta \end{aligned}$$

(3)

and

$$\begin{aligned} \sum \limits _{J_j\in N}\left( \omega _j U_j+ \gamma D_j \right) + m \vartheta , \end{aligned}$$

(4)

respectively, in which $\xi =\min \{\gamma ,\eta \}$. As a consequence, it is beneficial to process the primary jobs consecutively from time 0 (exclude the interruption and switching times).

In what follows, we limit our attention to solutions fulfilling the properties above. Now we analyze the formulation of the optimization function $\digamma _1$ of a given schedule. Given any such primary job sequence S, which is partitioned into m batches $B_1 = \{J_{ [1]}, J_{[2]}, \ldots , J_{[h_1]}\}, \ldots$, $B_{m} = \{J_{[h_{m-1}+ 1]}, J_{[h_{m-1}+ 2]}, \ldots , J_{[n]}\}$, in which $h_k$ is the number of primary jobs contained in the first k batches for $k= 0, 1, 2, \ldots , m$, with $h_0 = 0$ and $h_{m}= n$. Thus, for each $j=1,\ldots ,n$, job $J_{[j]}$’s completion time is equal to

$$\begin{aligned} C_{[j]}=\sum _{l=1}^{j}p_{[l]}+\left( 1-\left( 1-\alpha \right) ^j \right) \sum _{l=j+1}^{n}p_{[l]}+\sum _{l=1}^j \varphi (n-l), \end{aligned}$$

(5)

in which the first term is the sum of the total processing times of the first j primary jobs, the second term denotes the sum of the interruption times that the last $n-j$ jobs interrupt the first j primary jobs, and the third term gives the sum of the switching times during processing the first j primary jobs.

By Eq. (5), the distribution time $D_{[j]}$ of job $J_{[j]}$ such that $h_{k-1}+ 1 \le j\le h_k$ for some $k= 0, 1, \ldots , m$ is

$$\begin{aligned} D_{[j]}=\sum _{l=1}^{h_k}p_{[l]}+\left( 1-(1-\alpha )^{h_k}\right) \sum _{l=h_k+1}^{n}p_{[l]}+\sum _{l=1}^{h_k} \varphi (n-l), \end{aligned}$$

(6)

and thus the optimization function $\digamma _1$ of schedule S can be formulated as

$$\begin{aligned} \digamma _1&= \sum \nolimits _{J_j\in N} \xi D_j+ m \vartheta \nonumber \\&= \xi \sum _{k=1}^{m}\sum _{j=h_{k-1}+1}^{h_k}D_{[j]}+m \vartheta \nonumber \\&= \xi \Bigg (\sum _{k=1}^{m}\sum _{j=h_{k-1}+1}^{h_k}\Bigg (\sum _{l=1}^{h_k}p_{[l]}+(1-(1-\alpha )^{h_k})\nonumber \\&\quad \sum _{l=h_k+1}^{n}p_{[l]}+\sum _{l=1}^{h_k} \varphi (n-l)\Bigg )\Bigg )+m \vartheta \nonumber \\&= \xi \Bigg (\sum _{k=1}^{m}\Bigg ((n-h_{k-1})P_k+P_k\sum _{l=1}^{k-1}(1-(1-\alpha )^{h_l})|B_l|\nonumber \\&\quad +(n-h_{k-1})\sum _{j=h_{k-1}+1}^{h_k}\varphi (n-j) \Bigg )\Bigg )+m \vartheta , \end{aligned}$$

(7)

in which $P_k=\sum _{j=h_{k-1}+1}^{h_k} p_{[j]}$ represents the processing time of batch $B_k$.

As for the optimization function $\digamma _2$, given any primary job sequence S with $n_e$ early jobs, in which the early jobs are partitioned into $m_e$ batches $B_1 = \{J_{[1]}, J_{ [2]}, \ldots , J_{[h_1]}\}, \ldots$, $B_{m_e} = \{J_{[h_{m_e-1}+ 1]}, J_{[h_{m_e-1}+ 2]}, \ldots , J_{[n_e]}\}$, then the optimization function $\digamma _2$ of schedule S can be formulated as

$$\begin{aligned} \digamma _2&= \sum \nolimits _{J_j\in N} (\gamma D_j+\omega _jU_j)+ m \vartheta \nonumber \\&= \gamma \Bigg (\sum _{k=1}^{m_e}\Bigg ((n-h_{k-1})P_k+P_k\sum _{l=1}^{k-1}\left( 1-(1-\alpha )^{h_l}\right) |B_l|\nonumber \\&\quad +(n-h_{k-1})\sum _{j=h_{k-1}+1}^{h_k}\varphi (n-j) \Bigg )\Bigg )+\sum \nolimits _{J_j\in L}w_j+m \vartheta \end{aligned}$$

(8)

in which L stands for the set of late jobs in solution S.

Based on Eqs. (7) and (8), one can draw the following conclusion.

Proposition 3.2

There is an optimal solution to each of the problems P1 and P2 so that the maximum processing time among the primary jobs scheduled in any batch $B_k$, $k=1,2,\ldots$, is equal to or less than the minimum processing time among the primary jobs scheduled in batch $B_{k+1}$.

Proof

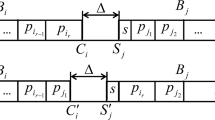
We provide the proof for problem P1. The proof for problem P2 is analogous. Assume there exists a solution S with two continuous batches $B_k$ and $B_{k+1}$ such that $p_i>p_j$ for some primary jobs $J_i\in B_k$ and $J_j\in B_{k+1}$. We create a new solution $S'$ from S by exchanging primary jobs $J_i$ and $J_j$ while keeping the other primary jobs being the same. According to Eq. (7), the difference between the optimization function values of solutions S and $S'$ is

$$\begin{aligned}&p_i \left( (n-h_{k-1})+\sum _{l=1}^{k-1}\left( 1-(1-\alpha )^{h_l}\right) |B_l|\right) \\&\qquad +p_j \left( (n-h_{k})+\sum _{l=1}^{k}\left( 1-(1-\alpha )^{h_l}\right) |B_l|\right) \\&\qquad -\Bigg (p_j \left( (n-h_{k-1})+\sum _{l=1}^{k-1}\left( 1-(1-\alpha )^{h_l}\right) |B_l|\right) \\&\qquad +p_i \left( (n-h_{k})+\sum _{l=1}^{k}\left( 1-(1-\alpha )^{h_l}\right) |B_l|\right) \Bigg )\\&\quad =(p_i-p_j)\left( h_{k}-h_{k-1}-\left( 1-(1-\alpha )^{h_k}\right) |B_k|\right) \\&\quad =(p_i-p_j)(1-\alpha )^{h_k}|B_k|>0. \end{aligned}$$

As a consequence, solution $S'$ is no worse than S, as required. $\square$

The proposition above demonstrates that both problems P1 and P2 allow an optimal solution so that the primary jobs are proceeded in terms of the SPT (Shortest Processing Time first) rule. In what follows, we re-arrange the jobs in terms of the SPT rule so that $d_1\le d_2\le \cdots \le d_n$.

Dynamic programming algorithms

This section devises dynamic programming (DP) algorithms for problems P1 and P2 which relies on the properties given in Lemmas 3.1 and 3.2. Specially, we prove that problem P1 is polynomial time solvable, whereas problem P2 may be solved in pseudo-polynomial time.

Let us begin with devising a polynomial-time forward DP algorithm, denoted as Algorithm $MDB_T$, for problem P1. The procedure of the algorithm is as follows. For each $j=0,1,\ldots ,n$, we let $H_j$ stand for the set of states encoding the partial solutions for the first j jobs $J_1,\ldots ,J_j$. Each state in $H_j$ is in the form of (a, g) such that

• There is exactly a primary jobs contained in the last batch of the partial solution.

• The optimization function value of the partial solution is g.

Algorithm $MDB_T$ begins with an initial tag set $F_0=\{(0,0)\}$. For each $j=1,\ldots ,n$, the tag set $F_j$ is constructed from tag set $F_{j-1}$. To be precise, for each tag $(a,g)\in F_{j-1}$ that corresponds to a partial solution for the jobs $J_1,\ldots ,J_{j-1}$, to create a new solution by appending the next unassigned job $J_j$ to the end of the above partial solution, one requires to take the following two cases into account.

Case T1: Start a new batch and append job $J_j$ to it. What is noteworthy is that we take into account the contributions of the jobs to the optimization function value in batches, i.e., the contributions of all jobs contained in a batch are added to the optimization function value of $\digamma _1$ immediately when we complete the processing of all the jobs contained in the batch. Thus, the contributions of all the jobs contained in the previous batch to the optimization function value of $\digamma _1$ in this case equals

$$\begin{aligned}&\xi \Big ((n-(j-1-a))\sum \limits _{l=j-a}^{j-1}p_l+a\\&\quad \left( 1-(1-\alpha )^{j-1}\right) \sum \limits _{l=j}^np_l\\&\quad +(n-(j-1-a))\sum \limits _{l=0}^{a-1}\varphi (n-j+1+l)\Big ) \end{aligned}$$

according to Eq. (7), in which $j-1-a$ gives the number of primary jobs processed before the previous batch, $\sum \nolimits _{l=j-a}^{j-1}p_l$ gives the total processing times of all the jobs contained in the previous batch, and $\sum \nolimits _{l=j}^np_l$ measures the total processing times of all the primary jobs processed after the previous batch. Therefore, the value that increases in the optimization function $\digamma _1$ due to this operation in thi

s case is

$$\begin{aligned}&\xi \Big ((n-(j-1-a))\sum \limits _{l=j-a}^{j-1}p_l+a\\&\quad \left( 1-(1-\alpha )^{j-1}\right) \sum \limits _{l=j}^np_l\\&\quad +(n-(j-1-a))\sum \limits _{l=0}^{a-1}\varphi (n-j+1+l)\Big )+\vartheta . \end{aligned}$$

As a consequence, one can construct a new tag

$$\begin{aligned}&\Bigg (1,g+\xi \Big ((n-(j-1-a))\sum \limits _{l=j-a}^{j-1}p_l\\&\quad +a \left( 1-(1-\alpha )^{j-1}\right) \sum \limits _{l=j}^np_l\\&\quad +(n-(j-1-a))\sum \nolimits _{l=0}^{a-1}\varphi (n-j+1+l)\Big )+\vartheta \Bigg ) \end{aligned}$$

and add it into $F_j$.

Case T2: Append job $J_j$ to the last batch. To ensure the feasibility, there must be $1\le a<b$ by the restriction on the batch size. By the analysis in Case 1, the value that increases in the optimization function $\digamma _1$ due to this operation in this case is zero if $j<n$, and $\xi (a+1)\left( \sum \nolimits _{l=j-a}^jp_l+\sum \nolimits _{l=0}^{a}\varphi (l)\right)$ otherwise. Thus, if $a<b$, one can construct a new tag $(a+1,{\widetilde{g}})$ and add it into $F_j$, in which ${\widetilde{g}}=g$ if $j<n$ and ${\widetilde{g}}=g+\xi (a+1)\left( \sum \nolimits _{l=j-a}^jp_l+\sum \nolimits _{l=0}^{a}\varphi (l)\right)$ otherwise.

What is noteworthy is that not all the generated tags during the procedure above will form a complete better schedule. Thus, it is necessary to find the tags that can be discarded for further consideration by the following dominant rule.

Lemma 4.1

Given any tags (a, g) and $(a',g')$ in $F_j$ such that $a\le a'$, and $g\le g'$, one can discard the latter tag.

Proof

Given the conditions stated in the lemma, it is evident that every feasible extension of the partial solution corresponding to the latter one is also feasible for the partial solution corresponding to the former one, and leads to a complete solution whose objective function value is equal to or less tan that of the solution constructed by using the same extension to the former one. $\square$

According to the above analyses, we provide the following procedure for Algorithm ${\text {MDB}}_T$:

Theorem 4.2

Problem P1 may be solved by Algorithm ${\text {MDB}}_T$ with running time O(nb).

Proof

Due to the fact that all possible scheduling choices for each job $J_j$ are addressed in Step 3, Algorithm 1 can find an optimal schedule. In Step 1, we execute a sorting procedure requiring $n\log n$ time. In Step 3, since there are b different values of a, there are at most b different combinations of $\{a,g\}$ according to the dominant rule. For any state, at most two new states can be constructed. As a consequence, going through n iterations, Step 3 may be implemented in O(nb) time, which completes the proof. $\square$

In what follows, we use the following example to demonstrate Algorithm ${\text {MDB}}_T$.

Example 4.3

Let $n=3$, $\alpha =0.1, \mu =\eta =3,\gamma =1, \vartheta =10, p_1=30,p_2=20,p_3=15, b=2$, and $\varphi (x)=x$ for all $x\in [0,+\infty )$. We implement Algorithm ${\text {MDB}}_T$ to solve this example in the following way.

• Step 1: The jobs are already re-arranged in the LPT order.

• Step 2: Set $F_0=\{(0,0)\}$ and $\xi =\min \{\gamma ,\eta \}=1$.

• Step 3: For $j=1$, we generate a tag $(1,\vartheta )=(1,10)$ from the tag $(0,0)\in F_{0}$. Thus, $F_{1}=\{(1,10)\}$.

For $j=2$, we generate two tags $(1,10+3p_1+0.1(p_2+p_3)+3 \varphi (2)+\vartheta )=(1,119.50)$ and (2, 10) from the tag $(1,10)\in F_{1}$. Thus, $F_{2}=\{(1,119.50),(2,10)\}$.

For $j=3$, we generate two tags $(1,119.5+2p_2+(1-(1-\alpha )^2)p_3+2 \varphi (1)+\vartheta )=(1,174.35)$ and $(2,119.50+2(p_2+p_3+\varphi (1)))=(2,191.50)$ from the tag $(1,119.50)\in F_{2}$; and a tag $(1,10+3(p_1+p_2)+2(1-(1-\alpha )^2)p_3+3 (\varphi (1)+\varphi (2))+\vartheta )=(1,184.70)$ from the tag (2, 10). During the elimination process, (1,184.70) is deleted. Thus, $F_{2}=\{(1,174.35),(2,191.50)\}$, and the optimal solution value is 174.35 and the optimal primary job sequence is $(J_1,J_2,J_3)$, where each single job forms a batch.

What is noteworthy is that Algorithm ${\text {MDB}}_T$ with a slight amendment by deleting the constraint on a can be applied for solving problem P1 with unbound batch size. In terms of this modification, there are at most n possible values for a. Thus, problem P1 with unbounded batch size may be solved in $O(n^2)$ time.

Now we turn to the solution algorithm for problem P2. It’s worth noting that Algorithm ${\text {MDB}}_T$ with directly amendments cannot be used to solve problem P2 since we cannot determine which jobs would be scheduled after the current batch. Instead, we devise a backward dynamic programming algorithm, denoted as ${\text {MDB}}_L$, that appends a job immediately before the partial schedule. To keep things simple, in the sequel we re-arrange the jobs so that $p_1\ge p_2\ge \cdots \ge p_n$.

Specially, we need to enumerate all possible values of the number of early jobs in the complete optimal solution. Given each such value e and each j, $e,j=0,1,\ldots ,n$, we let $H_{(e,j)}$ represent the set of tags encoding the partial solutions for jobs $J_1,\ldots ,J_j$ so that the number of early jobs in the complete optimal solution is exactly e. Each tag in $H_{(e,j)}$ is in the form of $(x,a,t_1,t_2,g)$ such that

• there is exactly x primary jobs processed after the first batch of the partial solution,

• there is exactly a primary jobs in the first batch of the partial solution,

• the total processing time of the primary jobs processed after the first batch of the partial solution is $t_1$,

• the total processing time of the primary jobs processed in the first batch of the partial solution is $t_2$,

in which g is defined similarly as that in Algorithm $MDB_T$.

The algorithm begins with an initial tag set $H_{(e,0)}=\{(0,0,0,0,0)\}$. For each $j=1,\cdots ,n$, the tag set $H_{(e,j)}$ is generated from tag set $H_{(e,j-1)}$. To be exact, given any tag $(x,a,t_1,t_2,g)\in F_{(e,j-1)}$ that corresponds to a partial solution for the jobs $J_1,\ldots ,J_{j-1}$, to generate a new schedule by appending the next unassigned job $J_j$ to the start of the above partial solution, one require to take the following two cases into account.

• Case L1: assign job $J_j$ as a late job. The value that increases in the optimization function $\digamma _2$ due to this operation is $\omega _j$. Thus, one can construct a new tag $(x,a,t_1,t_2,g+w_j)$ and add it into $H_{(e,j)}$.

• Case L2: assign job $J_j$ as an early job. There must be $a+x<e$ in this case, and we require to further address two subcases.

  • Subcase L21: Start a new batch and append job $J_j$ to the new batch. The contributions of all jobs in the previous batch to the objective function value of $\digamma _2$ in this case is

    $$\begin{aligned}&\gamma \Bigg ((x+a)t_2+a \left( 1-(1-\alpha )^{e-x}\right) t_1\\&\quad +(x+a)\sum \limits _{l=0}^{a-1}\varphi (x+l)\Bigg ) \end{aligned}$$

    by Eq. (8). Thus, the value that increases in the optimization function of $\digamma _2$ due to this operation in this case equals

    $$\begin{aligned}&\gamma \Bigg ((x+a)t_2+a\left( 1-(1-\alpha )^{e-x}\right) t_1\\&\quad +(x+a)\sum \limits _{l=0}^{a-1}\varphi (x+l)\Bigg )+\vartheta . \end{aligned}$$

    As a consequence, one can construct a new tag

    $$\begin{aligned}&\Bigg (x+a,1,t_1+t_2,p_j,g+\gamma ((x+a)t_2.\\&\quad +a\left( 1-(1-\alpha )^{e-x}\right) t_1 +(x+a)\\&\qquad \sum \nolimits _{l=0}^{a-1}\varphi (x+l)\Bigg )+\vartheta ) \end{aligned}$$

    and add it into $H_{(e,j)}$.

  • Subcase L22: Append job $J_j$ to the first batch. In this case, there must be $a<b$ by the restriction on the batch size. The value that increases in the optimization function $\digamma _2$ due to this operation is zero if $j<n$, and $\gamma (x+a)\left( t_2+\sum \nolimits _{l=0}^{a-1}\varphi (x+l)\right)$, otherwise. Thus, if $a<b$, one can construct a new tag $(x,a+1,t_1,t_2+p_j,{\widetilde{g}})$ and add it into $H_{(e,j)}$, in which ${\widetilde{g}}=g$ if $j<n$ and ${\widetilde{g}}=g+\gamma (x+a)\left( t_2+\sum \nolimits _{l=0}^{a-1}\varphi (x+l)\right)$ otherwise.

To cut down the number of states, one can use the following dominant rule.

Lemma 4.4

Given any tags $(x,a,t_1,t_2,g)$ and $(x',a',t'_1,t'_2, g')$ in $F_j$ such that $x\le x'$, $a\le a'$, $t_1\le t'_1$, $t_2\le t'_2$, and $g\le g'$, one can discard the latter one.

Proof

It is similar to the proof Lemma 3.1. $\square$

According to the analyses above, we provide the following procedure for Algorithm ${\text {MDB}}_L$.

Theorem 4.5

Problem P2 may be solved by Algorithm ${\text {MDB}}_L$ with running time $O(n^3bP^2)$.

Proof

It is analogous to the proof of Theorem 3.2, in which the only differences lie in that: x, $t_1$ and $t_2$ take at most n, P and P different values, respectively. $\square$

Similarly, Algorithm ${\text {MDB}}_L$ with a slight amendment by deleting the constraint on a can be applied for solving problem P2 with unbound batch size, which runs in $O(n^4P^2)$ time.

Computational experiments

This section assesses how multitasking affects the scheduling cost or value through computational experiments. In terms of the parameter settings in Hall et al. [12] and Wang et al. [23], we generate different sets of parameter values as follows.

• We selected n from the set $\{50,60, \ldots , 120\}$ for problem P1 and from the set $\{5,10,15,20\}$ for problem P2.

• We randomly selected $p_j$ from the uniform distribution [10, 50].

• We randomly selected $\eta$ and $\gamma$ from the uniform distribution [1, 10].

• We randomly selected $\vartheta$ from the uniform distribution [20, 100], and b from the discrete uniform [2, n].

• We randomly selected $\omega _j$ from the uniform distribution [bP/n, P/2].

• We selected $\alpha$ from the set $\{0.01,0.05,0.10,0.15\}$.

The reason for the setting of n is as follows: the preliminary computational test indicates that Algorithm ${\text {MDB}}_T$ takes 2 h on average for solving the instances with $n=120$ of problem P1, and Algorithm ${\text {MDB}}_l$ takes more 2 h on average for solving the instances with $n=20$ of problem P2. The average running times of the algorithms on testing instances with different numbers of jobs are depicted in Tables 2 and 3, respectively.

Given any combination of the parameters above, we perform two computational experiments, i.e., $\varphi (x) = 0.05x$ and $\varphi (x) = -\,0.05x$. And for any combination of n and $\alpha$, 30 instances were randomly chosen and the average results were reported.

We apply the algorithm for each problem by setting $\alpha =0$ for solving the corresponding problem without multitasking. The developed DP algorithms are coded in MATLAB and the numerical experiments are performed on a notebook computer with a 3.80-GHz CPU and 16 GB memory.

Let $\digamma _1$ and $\digamma '_1$ be the optimal optimization function values to the multitasking problem P1 and the corresponding problem without multitasking, respectively, and $LT_{\text {avg}}$ be the mean value of $\frac{\digamma _1-\digamma '_1}{\digamma '_1}$ over the 50 chosen instances for any combination of n and $\alpha$, which demonstrates the average multitasking cost or value. In a similar way, we let $\digamma _2$ and $\digamma '_2$ be the optimal optimization function values to the multitasking problem P2 and the corresponding problem without multitasking, respectively, and $LL_{\text {avg}}$ be the mean value of $\frac{\digamma _2-\digamma '_2}{\digamma '_2}$ over the 50 chosen instances.

The results for problems P1 and P2 are summarized in Tables 2 and 3, from which we have the following observations.

• As expected, the affect of multitasking on the scheduling cost or value increases as the $\alpha$ value increases, especially for problem P1. For instances, when $\varphi (x) = 0.05x$, the $LT_{\text {avg}}$ value for $\alpha =0.15, 0.10$ and 0.05 respectively increases 54.02%, 39.12% and 28.17% on average compared to that for $\alpha =0.01$ for problem P1, and the $LL_{\text {avg}}$ value for $\alpha =0.15, 0.10$ and 0.05 respectively increases 512.17%, 158.37% and 158.71% on average compared to that for $\alpha =0.01$ for problem P2. In addition, when $\varphi (x) =-\,0.05x$, the $LT_{avg}$ value for $\alpha =0.15, 0.10$ and 0.05, respectively increases 96.81%, 84.05% and 43.47% on average compared to that for $\alpha =0.01$ for problem P1, and the $LL_{\text {avg}}$ value for $\alpha =0.15, 0.10$ and 0.05, respectively, increases 301.63%, 196.56% and 112.32% on average compared to that for $\alpha =0.01$ for problem P2. The reason behind this is that the interruption time that the waiting jobs suspend the primary jobs becomes large when $\alpha$ increases.

• The affect of the number of jobs on the $LT_{\text {avg}}$ and $LL_{\text {avg}}$ values is obviously. From Tables 1 and 2, we can see that the instances with more larger n induce more lager cost of multitasking for most problem instances. For instance, the average cost of multitasking ranges from 98.15 to 143.61% when $(\alpha ,\varphi (x))=(0.10,-\,0.05x)$ and ranges from 98.50 to 116.67% when $(\alpha ,\varphi (x))=(0.10,-\,0.05x)$, which increases approximately in proportion to the number of jobs.

• Negative $LT_{\text {avg}}$ or $LL_{\text {avg}}$ value is possible, implying that we can get some revenue from multitasking. For instance, when $n=5$, we can get 0.01% revenue from multitasking when $(\alpha ,\varphi (x))=(0.05,-\,0.05x)$, and get 0.05% revenue from multitasking when $(\alpha ,\varphi (x))=(0.01,-\,0.05x)$ for problem P2. However, this result does not continue as the number of jobs increases.

• The affect of multitasking for problem P1 is more larger than that for problem P2. This is due to the fact that multitasking will affect the completion times of jobs, and the optimization function of problem P1 is more related to the completion times of jobs compared to that of problem P2.

Table 2 The results for problem P1

Table 3 The results for problem P2

Conclusions

In this study, we investigate a novel scheduling model that coinstantaneously involves batch distribution, multitasking and DDA. In the developed model, the job due dates are to be decided by the decision-makers in the decision-making process. The completed jobs are distributed to their customers in batches, and the sizes of all batches are identical, which may be bounded or unbounded. The jobs contained in each batch are scheduled sequentially. In addition, it permits the machine to suspend an uncompleted job and turn to another uncompleted job. The goal is to identify the optimal primary job sequence, the optimal job due dates, and the optimal batch production and delivery strategy so that one of the following optimization functions are minimised: the total cost composed of the earliness penalty, DDA cost, tardiness penalty and batch distribution cost, and the total cost composed of the earliness penalty, weighted number of late jobs, DDA cost and batch distribution cost. We prove that the problem with the first optimization function may be solved in polynomial time and that the problem with the second optimization function is pseudo-polynomial time solvable. We also conduct numerical experiments on randomly chosen instances to assess how multitasking affects the scheduling cost or value, the results of which can assist decision-makers to justify the extent to put to use or refrain multitasking.

As for future research, the following topics are interesting and necessary.

• Providing the computational complexity status of the problem P2, i.e. whether it is NP-hard.

• Investigating the model with other due date assignment methods.

• Extending the model to other machine setting, for example, flowshop or parallel-machine setting.

• Investigating the model in a uncertain or dynamic environment, for example in the present of random processing times, unexpected machine breakdown, etc.

• Extending the model to the case with energy efficiency, consumption, or cost as constraints or objectives (Gao et al. [7]).

• Developing effective intelligent optimization algorithms for solving large-scale problem, such as Tabu search, genetic algorithm, or genetic programming (Nguyen et al. [21]).