1 Introduction

Support vector machines (SVMs) [1–7] using the well established concepts in statistical learning theory (SLT) and optimization theory, maybe the most widely used techniques for data mining, and have been successfully applied in many fields ranging from text categorization, face verification, speech recognition, information and image retrieval, to remote sensing image analysis, time series forecasting, information security, bankruptcy prediction and etc. [8–20]. For the standard SVM, the principal of maximizing the margin between two parallel support hyperplanes leads to solving a convex quadratic programming problem (QPP), dual theory makes introducing the kernel function possible, then the kernel trick is applied to solve nonlinear cases.

Recently, different with the standard SVM searching for two parallel hyperplanes, some nonparallel hyperplane classifiers have been proposed, such as the generalized eigenvalue proximal support vector machine (GEPSVM) [21] and the twin support vector machine (TWSVM) [22], which have become one of the researching hot spots in the field of matching learning. For the TWSVM, it seeks two nonparallel proximal hyperplanes such that each hyperplane is closer to one of the two classes and is at least one distance from the other. This strategy results the fundamental difference between TWSVM and the standard SVM, i.e, the former solves two smaller sized QPPs, whereas the latter solves a larger one, which increases the TWSVM training speed by approximately fourfold compared to that of SVM. Furthermore, experimental results in [22] have shown the effectiveness of TWSVM over standard SVM and even GEPSVM on UCI datasets. Therefore, in the last few years, TWSVM has been studied extensively and developed rapidly. Considering the many variants of TWSVM, a systematic survey is needed and helpful to understand and use this family of data mining techniques more easily although there are several limited reviews about TWSVMs [23, 24]. The goal of this paper is to closely review TWSVMs and provide an insightful understanding of current developments, at the same time point out their limitations and highlight the major opportunities and challenges, as well as potential important research directions.

Section 2 of the paper reviews four representative TWSVMs: original TWSVM, twin bounded support vector machine (TBSVM) [25], improved TWSVM (ITSVM) [26] and nonparallel SVM (NPSVM) [27]. Section 3 describes the variants and extensions of TWSVMs for different learning problems. Section 4 introduces several applications of TWSVMs. Finally, concluding remarks and future research directions are provided in Sect. 5.

2 TWSVM, TBSVM, ITSVM and NPSVM

In this section, we review four representative nonparallel hyperplane classifiers, on which almost all the improved models are based. Here we consider their originally proposed models for the binary classification problem with the training set

$$\begin{aligned} T=\{(x_1,+1),\ldots ,(x_p,+1),(x_{p+1},-1),\ldots ,(x_{p+q},-1)\}, \end{aligned}$$
(1)

where \(x_i\in R^n, i=1,\ldots ,p+q\). Let \(l=p+q\) and

$$\begin{aligned} A=(x_1,\ldots ,x_p)^{\top }\in R^{p\times n}, \ B=(x_{p+1},\ldots , x_{p+q})^{\top }\in R^{q\times n}. \end{aligned}$$
(2)

2.1 TWSVM

Unlike the standard SVM solving one QPP and similar to the GEPSVM [21, 28], TWSVM [22] constructs two smaller QPPs

(3)

and

(4)

to seek a pair of nonparallel hyperplanes

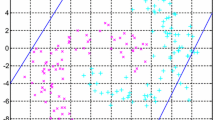
$$\begin{aligned} (w_+\cdot x)+b_+=0 \, \hbox {and} \, (w_-\cdot x)+b_-=0, \end{aligned}$$
(5)

such that the positive hyperplane \((w_+\cdot x)+b_+=0\) is proximal to the positive class (measured by the quadratic loss \(\displaystyle \frac{1}{2}(Aw_++e_+b_+)^{\top }(Aw_++e_+b_+)\)) and far from the negative class (measured by the hinge loss \(\xi _-=\max \{0, e_-+(Bw_++e_-b_+)\}\)), and vice visa for the negative hyperplane \((w_-\cdot x)+b_-=0\), see Fig. 1. \(c_i,i=1,2\) are the penalty parameters and \(e_+\) and \(e_-\) are vectors of ones of appropriate dimensions.

Fig. 1
figure 1

Geometrical illustration of TWSVM in \(R^2\): The “\(+\)” (class 1) and “\(*\)” (class 2) points are generated following two normal distributions respectively, two nonparallel lines (red and blue lines) are obtained from linear TWSVM [26]. (Color figure online)

Full size image

In order to get the solutions of the above QPPs, their dual problems

$$\begin{aligned} \begin{aligned}&\max _{\alpha }\quad e_-^{\top }\alpha -\frac{1}{2}\alpha ^{\top }G(H^{\top }H)^{-1}G^{\top }\alpha ,\\&\quad \mathrm{s.t.} \quad 0\leqslant \alpha \leqslant c_1e_-,\\ \end{aligned} \end{aligned}$$
(6)

and

$$\begin{aligned} \begin{aligned}&\max _{\gamma } \quad e_+^{\top }\gamma -\frac{1}{2}\gamma ^{\top }H(G^{\top }G)^{-1}H^{\top }\gamma ,\\&\quad \mathrm{s.t.} \quad 0\leqslant \gamma \leqslant c_2e_+,\\ \end{aligned} \end{aligned}$$
(7)

are solved respectively, where

$$\begin{aligned} H=[A \ e_+]\in R^{p\times (n+1)},\ G=[B\ e_-]\in R^{q\times (n+1)}, \end{aligned}$$
(8)

therefore the solutions of problems (3) and (4) can be obtained by

$$\begin{aligned} (w_+^{\top },b_+)^{\top }=-(H^{\top }H)^{-1}G^{\top }\alpha ,\end{aligned}$$
(9)
$$\begin{aligned} (w_-^{\top },b_-)^{\top }=-(G^{\top }G)^{-1}H^{\top }\gamma . \end{aligned}$$
(10)

Thus an unknown point \(x\in R^n\) is predicted to the Class by

$$\begin{aligned} Class =\arg \min _{k=-,+} |(w_k\cdot x)+b_k|, \end{aligned}$$
(11)

where \(|\cdot |\) is the perpendicular distance of point \(x\) from the planes \((w_k\cdot x)+b_k=0, k=-,+\).

TWSVM has several advantages such as

  1. (1)

    The dual problems (6) and (7) has \(q\) and \(p\) variables respectively as opposed to \(l=p+q\) in the standard SVM. This strategy of solving a pair of smaller sized QPPs instead of a large one makes the learning speed of TWSVM be approximately four times faster;

  2. (2)

    By using the quadratic loss function, TWSVM fully considers the prior information within classes in data and is less sensitive to the noise;

  3. (3)

    TWSVM is useful for automatically discovering two-dimensional projections of the data;

However, it still has the following drawbacks:

  1. (I)

    In the primal problems (3) and (4) of TWSVM, only the empirical risk is minimized, whereas the structural risk is minimized in the standard SVM;

  2. (II)

    The inverse matrices of \(H^{\top }H\) and \(G^{\top }G\) are approximately replaced by \(H^{\top }H+\epsilon I\) and \(G^{\top }G+\epsilon I\) respectively in order to deal with the singular case and avoid the possible ill conditioning, where \(I\) is an identity matrix of appropriate dimensions, \(\epsilon \) is a small positive scalar to keep the structure of data. This replacements means TWSVM only get the approximate solutions;

  1. (III)

    Though TWSVM solves two smaller sized QPPs, it needs to compute the inverse matrices before training the models. So the computational complexity of TWSVM should include two parts: the complexity of computing the inverse matrices and the complexity of solving the dual problems. For a large data set, TWSVM will fail since it is in practice intractable or even impossible to compute the inverse matrices by the classical methods, though Sherman-Morrison-Woodbury [29] formula or the rectangular kernel technique [30] were used in [22];

  2. (IV)

    The above TWSVM is only for the linear classification problem since it can not be extended to the nonlinear case directly as standard SVMs usually do. For the nonlinear case [22], two kernel-generated surfaces

    $$\begin{aligned} K(x^{\top }, C^{\top })u_++b_+=0 \ \mathrm{and} \ K(x^{\top }, C^{\top })u_-+b_-=0, \end{aligned}$$
    (12)

    instead of hyperplanes (5) were considered, where

    $$\begin{aligned} C^{\top }=[A\ B]^{\top }\in R^{n\times l}, \end{aligned}$$
    (13)

    and \(K\) is an appropriately chosen kernel. Two primal problems different with (3) and (4) were constructed and their corresponding dual problems were solved. Similar with the linear case, the nonlinear TWSVM still has the drawbacks (i) (ii) and (iii) and the folloing (V) and (VI) . Furthermore, the nonlinear TWSVM with the linear kernel is not equivalent to the linear TWSVM [26], which is also different with the standard SVM;

  1. (V)

    TWSVM needs fast solvers such as the sequential minimization optimization (SMO) [31] algorithm for the standard SVMs;

  2. (VI)

    TWSVM loses the sparseness by using the quadratic loss function for each class to make the proximal hyperplane close enough to the class itself, which results that almost all the points in this class contribute to each final decision function.

2.2 TBSVM

The twin bounded support vector machines (TBSVM) [25] was proposed to overcome the drawbacks (I) and (II). For the linear case, two primal problems constructed in TBSVM are

$$\begin{aligned} \begin{aligned}&\min _{w_{+},b_{+},\xi _{-}}\quad \frac{1}{2}c_3(\Vert w_+^2\Vert +b_+^2)+ \frac{1}{2}(Aw_++e_+b_+)^{\top }(Aw_++e_+b_+)+c_{1}e_-^{\top }\xi _-,\\&\quad \hbox {s.t.}\quad \quad \quad -(Bw_++e_-b_+)+\xi _-\geqslant e_-,\ \xi _- \geqslant 0,\\ \end{aligned} \end{aligned}$$
(14)

and

$$\begin{aligned} \begin{aligned}&\underset{w_{-},b_{-},\xi _{+}}{\min }\quad \frac{1}{2}c_4(\Vert w_-\Vert ^2+b_-^2)+\frac{1}{2}(Bw_-+e_-b_-)^{\top }(Bw_-+e_-b_-)+c_{2}e_+^{\top }\xi _+,\\&\quad \hbox {s.t.} \quad \quad \qquad (Aw_-+e_+b_-)+\xi _+\geqslant e_+,\ \xi _+ \geqslant 0,\\ \end{aligned} \end{aligned}$$
(15)

where \(c_i,i=1,2,3,4\) are the penalty parameters and \(e_+\) and \(e_-\) are vectors of ones of appropriate dimensions. Compared with the primal problems (3) and (4) of TWSVM, the regularization terms \(\displaystyle \frac{1}{2}c_3(\Vert w_+^2\Vert +b_+^2)\) and \(\displaystyle \frac{1}{2}c_4(\Vert w_-\Vert ^2+b_-^2)\) are added to minimize that the structural risk, and this modification leads to two dual problems

(16)

and

(17)

with nonsingular matrices \((H^{\top }H+c_3I)\) and \((G^{\top }G+c_4I)\). Different with the fixed small scalar \(\epsilon \) in TWSVM, the parameter \(c_3\) or \(c_4\), is the weighting factor which determines the tradeoff between the regularization term and the empirical risk. For the nonlinear case, two other regularization terms \((\Vert u_+\Vert ^2+b_+^2)\) and \((\Vert u_-\Vert ^2+b_-^2)\) are introduced to implement the structural risk minimization principle. However, TBSVM still has the drawbacks (III)\(\sim \)(VI). Though it claimed that the successive overrelaxation (SOR) [32] technique was used to solve the dual problems to speed up the training procedure, and seems to be able to deal with the large scale problems, it in fact took no account of the computation of the inverse matrices. Its similar model [33], a coordinate descent margin based TWSVM (CDMTSVM), was presented and a coordinate descent method was proposed for fast training which handles one data point at a time, but the inverse matrices still need to be computed at first.

2.3 ITSVM

The improved twin support vector machine (ITSVM) [26] was proposed to overcome the drawbacks (I)\(\sim \)(V). By introducing the different Lagrangian functions for the primal problems (14) and (15) in the TBSVM, we get the improved dual formulations

$$\begin{aligned} \begin{aligned}&\max _{\lambda ,\alpha }\quad -\frac{1}{2}(\lambda ^{\top }\ \alpha ^{\top }){\hat{Q}}(\lambda ^{\top }\ \alpha ^{\top })^{\top }+c_3e_-^{\top }\alpha ,\\&\mathrm{s.t.} \quad \quad \quad 0\leqslant \alpha \leqslant c_1e_-, \end{aligned} \end{aligned}$$
(18)

and

$$\begin{aligned} \begin{aligned}&\max _{\theta ,\gamma }\quad -\frac{1}{2}(\theta ^{\top }\ \gamma ^{\top }){\tilde{Q}}(\theta ^{\top }\ \gamma ^{\top })^{\top }+c_4e_+^{\top }\gamma ,\\&\mathrm{s.t.} \quad \quad \quad 0\leqslant \gamma \leqslant c_2e_+, \end{aligned} \end{aligned}$$
(19)

respectively, where

$$\begin{aligned} {\hat{Q}}=\left( \begin{array}{ll} AA^{\top } +c_3\hat{I} &{} AB^{\top }\\ AB^{\top } &{} BB^{\top } \end{array} \right) +E, {\tilde{Q}}=\left( \begin{array}{ll} BB^{\top } +c_4\tilde{I} &{} BA^{\top }\\ BA^{\top } &{} AA^{\top } \end{array} \right) +E, \end{aligned}$$
(20)

and \(\hat{I}\) is the \(p\times p\) identity matrix, \(\tilde{I}\) is the \(q\times q\) identity matrix, \(E\) is the \(l\times l\) matrix with all entries equal to one. The pair of nonparallel hyperplanes (5) are then obtained from the solutions \((\lambda ^*,\alpha ^*)\) and \((\theta ^*,\gamma ^*)\) of (18) and (19)

$$\begin{aligned} w_+^*=-(A^{\top }\lambda ^* +B^{\top }\alpha ^*),\ b_+^*=-(e_+^{\top }\lambda ^*+e_-^{\top }\alpha ^*), \end{aligned}$$
(21)

and

$$\begin{aligned} w_-^*=-(B^{\top }\theta ^* +A^{\top }\gamma ^*),\ b_-^*=-(e_-^{\top }\theta ^*+e_+^{\top }\gamma ^*). \end{aligned}$$
(22)

ITSVM overcomes several drawbacks listed above of the TWSVM. (1) ITSVM implements the structural risk minimization principle since its primal problems are the same with those of TBSVM; (2) ITSVM has no inverse matrices to be computed before training since it only needs to solve the QPPs (18) and (19); (3) Linear ITSVM can be easily extended to the nonlinear case since the dual problems (18) and (19) can be applied with the kernel functions just as the standard SVMs do, i.e., take the \(K(A,B^{\top })\), \(K(A,A^{\top })\), \(K(B,B^{\top })\), \(K(B,A^{\top })\) instead of \(AB^{\top }\), \(AA^{\top }\), \(BB^{\top }\), \(AB^{\top }\), \(BA^{\top }\) in \(\tilde{Q}\) and \(\hat{Q}\); (4) SOR technique is also used to solve the dual problems (18) and (19). Here we should point out that the computational complexity of SOR for ITSVM is different with that for TBSVM. Since the dual problems (18) and (19) have \(l=p+q\) variables respectively, ITSVM has the same scale with the standard SVM and is almost 2 times larger than TWSVM or TBSVM, which means that ITSVM sacrifices more model training time to skillfully avoids the computation of the inverse matrix. At a first glance, it seems that ITSVM has more computational complexity than TWSVM or TBSVM, in fact when the complexity of computing the inverse matrices are considered in TWSVM or TBSVM, ITSVM is faster since

$$\begin{aligned} O(p^3)+ \sharp iteration\times O(p) > \sharp iteration\times O(l), \end{aligned}$$
(23)

where \(O(p^3)\) is the complexity of computing \(p\times p\) inverse matrix, and \(\sharp iteration\times O(p)\) is of SOR for \(p\) sized problem, \(\sharp iteration\times O(l)\) is of SOR for \(l\) sized problem (\(\sharp iteration\) is the number of the iterations, experiments in [32] has shown that \(\sharp iteration\) is almost linear scaling with the problem size) [26].

2.4 NPSVM

The nonparallel support vector machine (NPSVM) [27] was proposed to further overcome the sparseness drawback (VI). By taking the \(\varepsilon \)-insensitive loss function instead of the quadratic loss function in TWSVM, TBSVM or ITSVM, NPSVM constructs two primal problems

$$\begin{aligned} \begin{aligned}&\min _{w_+,b_+,\eta _+^{(*)},\xi _-}\quad \frac{1}{2}\Vert w_+\Vert ^2+c_1\sum _{i=1}^p(\eta _i+\eta _i^*)+c_2\sum _{j=p+1}^{p+q}\xi _j,\\&\qquad \hbox {s.t.}\quad \qquad \quad (w_+\cdot x_i)+b_+\leqslant \varepsilon +\eta _i,\ i=1,\cdots ,p,\\&\quad \qquad \quad \qquad \qquad -(w_+\cdot x_i)-b_+\leqslant \varepsilon +\eta _i^*,\ i=1,\cdots ,p,\\&\quad \qquad \quad \qquad \qquad (w_+\cdot x_j)+b_+\leqslant -1+\xi _j, \ j=p+1,\cdots ,p+q,\\&\quad \qquad \quad \qquad \qquad \eta _i,\eta _i^*\geqslant 0, \ i=1,\cdots ,p,\\&\quad \qquad \quad \qquad \qquad \xi _j\geqslant 0, \ j=p+1,\cdots ,p+q,\\ \end{aligned} \end{aligned}$$
(24)

and

$$\begin{aligned}&\min _{w_-,b_-,\eta _-^{(*)},\xi _+}\quad \frac{1}{2}\Vert w_-\Vert ^2+c_3\sum _{i=p+1}^{p+q}(\eta _i+\eta _i^*)+c_4\sum _{j=1}^{p}\xi _j,\nonumber \\&\quad \mathrm{s.t.}\quad \quad \quad \quad \quad (w_-\cdot x_i)+b_-\leqslant \varepsilon +\eta _i,\ i=p+1,\cdots ,p+q,\nonumber \\&\quad \quad \qquad \quad \qquad -(w_-\cdot x_i)-b_-\leqslant \varepsilon +\eta _i^*,\ i=p+1,\cdots ,p+q,\nonumber \\&\quad \quad \qquad \quad \qquad \quad (w_-\cdot x_j)+b_-\geqslant 1-\xi _j, \ j=1,\cdots ,p,\nonumber \\&\quad \quad \qquad \quad \qquad \quad \eta _i,\eta _i^*\geqslant 0, \ i=p+1,\cdots ,p+q,\nonumber \\&\quad \quad \qquad \quad \qquad \quad \xi _j\geqslant 0, \ j=1,\cdots ,p, \end{aligned}$$
(25)

where \(\varepsilon \geqslant 0\) is the sparseness parameter, \(c_i\geqslant 0, i=1,\cdots ,4\) are penalty parameters, \(\xi _{+}\!=\!(\xi _{1},\cdots ,\xi _{p})^{\top }\), \(\xi _{-}\!=\!(\xi _{p+1},\cdots ,\xi _{p+q})^{\top }\), \(\eta _+^{(*)}\!=\!(\eta _+^{\top },\eta _+^{*\top })^{\top }\!=\!(\eta _1,\cdots ,\eta _p,\eta _1^*,\cdots ,\eta _p^*)^{\top }\), \(\eta _-^{(*)}\!=\!(\eta _-^{\top },\eta _-^{*\top })^{\top }\!=\!(\eta _{p+1},\cdots ,\eta _{p+q},\eta _{p+1}^*,\cdots ,\eta _{p+q}^*)^{\top }\), are slack variables. Figure 2 illustrates its geometrical explanation in \(R^2\), where class 1 locates as much as possible in the \(\varepsilon \)-band of the positive hyperplane \((w_+\cdot x)\,+\,b_+=0\) (measured by the \(\varepsilon \)-insensitive loss function) and far from class 2 (measured by the hinge loss \(\xi _-=\max \{0, e_-+(Bw_++e_-b_+)\}\)), and vice visa for the negative hyperplane \((w_-\cdot x)+b_-=0\).

Fig. 2
figure 2

Geometrical illustration of NPSVM in \({R}^2\): The “\(+\)” (class 1) and “\(*\)” (class 2) points are generated following two normal distributions respectively, two nonparallel lines (red and blue bold lines) are obtained from linear NPSVM [27]. (Color figure online)

Full size image

The corresponding dual problems has the similar formulation with that of standard SVM but almost 1.5 times larger

$$\begin{aligned} \begin{aligned}&\min _{\pi } \quad \frac{1}{2} \pi ^{\top }\varLambda \pi +\kappa ^{\top } \pi , \\&\quad \mathrm{s.t.} \quad e^{\top }{ \pi }=0,\\&\qquad \quad \,\,\, 0\leqslant \pi \leqslant C, \end{aligned} \end{aligned}$$
(26)

where \(\varLambda \in R^{1.5l\times 1.5l}\) is semi-definite positive, therefore (26) can be solved efficiently by the SMO-type technique. NPSVM also implements the structural risk minimization principle, has no inverse matrices to be computed, introduces the kernels directly to deal with the nonlinear case, and most importantly has the sparseness because of the \(\varepsilon \)-insensitive loss function and hinge loss function adopted simultaneously in each primal problem. NPSVM overcomes all the listed drawbacks of TWSVM and in some sense is a true nonparallel classifier with solid theoretical foundation.

3 Variants and Extensions of TWSVMs

TWSVMs have attracted many interests in recent years and many improved algorithms were proposed. In this section, we will review them based on the problems they solved.

3.1 Variants of Binary TWSVMs

3.1.1 \(\nu \)-TWSVMs

\(\nu \)-NPSVM [34] is an equivalent formulation of NPSVM inheriting all the advantages of NPSVM model, but has more excellent properties. It is parameterized by the quantity \(\nu \) to let ones effectively control the number of support vectors, since the value of \(\nu \) is the lower bound of the percentage of support vectors. Furthermore, for each class, different sparseness can be obtained by using different parameter \(\nu \), which enable us to solve unbalanced classification problems. A \(\nu \)-TWSVM based on the original TWSVM was proposed in [35], which was interpreted as a pair of minimum generalized Mahalanobis-norm problems on two reduced convex hulls, and an improved geometric algorithm (GA) was developed to improve its efficiency. A rough margin-based \(\nu \)-TWSVM incorporating the rough set theory [36] was proposed in [37] to give the different penalties to the misclassified points. The twin parametric-margin SVM (TPMSVM) [38], motivated by the TWSVM and the par-\(\nu \)-SVM [39], determines a pair of parametric-margin hyperplanes, which can automatically adjust a flexible margin and are suitable for the heteroscedastic error structure. Its least squares version can be found in [40]. [41] smoothed the TPMSVM by introducing a quadratic function and suggested a genetic algorithm GA-based model selection for TPMSVM.

3.1.2 Least Squares TWSVMs

A least squares version of TWSVM (LSTWSVM) [42] was proposed in line with the lease squares SVM (LSSVM) [43]. The solution of the two modified primal problems reduces to solving just two systems of linear equations and leads to an extremely fast and efficient performance. Weighted LSTWSVM [44] put different weights on the error variables in order to eliminate the impact of noise data and obtain the robust estimation, and also for the imbalanced problem [45]. 1-norm LSTWSVM [46] was designed for automatically selecting the relevant features, by replacing all the 2-norm terms in the regularized LSTWSVM [47] with 1-norm ones and then converting its formulation to a linear programming (LP) problem. A least squares version of twin support hypersphere (TSVH) [48, 49] can be referred to [50], where TSVH aims to find a pair of hyperspheres not hyperplanes by solving two smaller sized QPPs, each QPP is based on the support vector data description (SVDD) [51]. A multiple-surface classification (MSC) algorithm, named projection twin support vector machine (PTSVM) [52–54], seeks projection directions such that the projected samples of one class are well separated from those of the other class in its own subspace, and a recursive algorithm for PTSVM was proposed to further boost the performance. Its least squares version, LSPTSVM, was formulated in [55], where a regularization term was added to ensure the optimization problems are positive definite and for better generalization ability. A nonlinear LSPTSVM for binary nonlinear classification by introducing nonlinear kernel into LSPTSVM was proposed in [56]. FLSPTSVM (feature selection for LSPTSVM) [57] can perform the feature selection and reduce the number of kernel functions required for the classifier. Nonparallel plane proximal classifier (NPPC) [58] was very similar to the LSTWSVM by introducing a technique as used in the proximal support vector machine(PSVM) [30] classifier, which leads to solving two small systems of linear equations in input space.

3.1.3 Localized TWSVMs

Weighted TWSVM with local information (WLTSVM) [59] explored the similarity information between pairs of samples by finding the \(k\)-nearest neighbors for all the samples. Ye et al. [60] proposed a reduced algorithm termed localized TWSVM via convex minimization (LCTSVM), which effectively reduced the space complexity of TWSVM by constructing two nearest neighbor graphs in the input space. Wang et al. [61] improved LCTSVM to be a fast LCTSVM suitable for large data sets, in which the number of TWSVMs was decreased. Local and Global Regularized Twin SVM (TWSVMLG) [62] not only exploited the local information of the dataset but also considered the local correlation among each local region, where they first pre-constructed a number of local models of the training set and built the decision functions in each local model with a global regularization. Since the relative density degrees reflect the local geometry of the sample manifold and the scatters of the two classes points, Peng and Xu [63] presented the bi-density TWSVM (BDTWSVM) which incorporated the relative density degrees for all training points using the intra-class graph. [64] incorporated a manifold regularization term into LSTWSVM (ManLSTWSVM) to discover the local geometry inside the samples. LSTWSVM via maximum one-class within-class variance, termed as (MWSVM) [65], applied the one-class within-class variance to the classifier, and a localized version (LMWSVM) of MWSVM was further proposed to remove the outliers effectively.

3.1.4 Sparse TWSVMs

Sparse nonparallel SVM (SNSVM) [66], a little difference with NPSVM [27] on the regularization terms used, is a sparse TWSVM since it also took the \(\varepsilon \)-insensitive loss function instead of the quadratic loss function in TWSVM. Peng [67] proposed a rapid sparse TWSVM (STSVM) in the primal space to improve the sparsity and robustness, where for each nonparallel hyperplane, the STSVM employed a back-fitting strategy to iteratively and simultaneously added a support vector. [68, 69] formulated an exact 1-norm linear programming formulation of TWSVM to improve the robustness and sparsity, which leaded to a extremely simple and fast algorithm.

3.1.5 Structural TWSVMs

Qi et al. [70] designed a novel structural TWSVM (\(S\)-TWSVM) only considering one class’s structural information for each model, which was different with all existing structural classifiers such as [71, 72]. This made \(S\)-TWSVM further reduce the computational complexity of the related QPPs, and improved the model’s generalization capacity. A robust minimum class variance TWSVM (RMCV-TWSVM) [73] introduced the variance matrices for the two classes as the regularization term for better generalization performance. Peng and Xu [74] constructed two Mahalanobis distance-based kernels according to the covariance matrices of two classes of data for optimizing the nonparallel hyperplanes, the Mahalanobis distance-based SVM (TMSVM) is suitable especially for the case that the covariance matrices of two classes of data are obviously different. For the TPMSVM [38], Peng et al. [75] presented a structural version (STPMSVM) by focusing on the structural information of the corresponding classes based on the cluster granularity.

3.2 Other Binary TWSVMs

[76] attempted to improve computing time of TWSVM by converting the primal QPPs of TWSVM into smooth unconstrained minimization problems. The smooth reformulations were solved using the well-known Newton-Armijo algorithm. Shao and Deng [77] considered a margin-based TWSVM with unity norm hyperplanes (UNH-MTSVM), the resulted optimal problems were solved efficiently by converting them into smooth unconstrained minimization problems. Ghorai et al. [78] reformulated TWSVM by considering unity norm of the normal vector of the hyperplanes as the constraints, the resulting nonlinear programming problem was solved by sequential quadratic optimization method. A classifier named norm-mixed TWSVM (NMTWSVM) was presented in [79], its main idea was to replace the hinge loss of the other class in the primal problems with the \(L_1\)-norm-based loss. The geometric analysis showed that the dual problems of NMTWSVM can be interpreted as a pair of minimum generalized Mahalanobis-norm problems (MGMNPs) on the two reduced affine hulls(RAHs) composed of two classes of points.

A feature selection method based on TWSVM (FTSVM) was designed in [80], where a multi-objective mixed-integer programming problem was solved by a greedy algorithm, in addition, the linear FTSVM was extended to the nonlinear case. Another feature selection method based on LSTWSVM (FLSTSVM) [81] incorporated a Tikhonov regularization term to the objective of LSTWSVM, and then minimized its 1-norm measure. FLSTSVM can reduce input features for the linear case and determined few kernel functions for the case. [82] treated the kernel selection problem for TWSVM as an optimization problem over the convex set of finitely many basic kernels.

Shao et al. proposed a TWSVM probability model (PTWSVM) [83] to estimate the posterior probability, they first defined a new ranking continues output and then mapped it into probability by training the parameters of an additional sigmoid function. For imbalanced data classification, [84] used under-sampling to give the adaptive weights for each class, which overcomed the bias phenomenon in the TWSVM. Different with standard TWSVMs, [85] constructed two nonparallel hyperplanes simultaneously by solving a single quadratic programming problem, and was consistent between its predicting and training processes. Twin support tensor machine (TWSTM) [86, 87], following the idea of support tensor machine (STM) [88–90], is also an interesting research direction.

3.3 Variants of Twin Support Vector Regressions (TWSVRs)

Some variants of twin support vector machines for regression problems (TWSVRs) are introduced in this section. The training set of the regression problem is given as

$$\begin{aligned} T=\{({x}_1,y_1),\cdots ,({x}_l,y_l)\}\in ({R^n}\times \mathcal{{Y}})^l, \end{aligned}$$
(27)

where \({x}_i\in {R^n},\, y_i\in \mathcal{{Y}}={R},\, i=1,\cdots ,l\). [91] proposed twin support vector regression (TSVR) which was similar to TWSVM in spirit, as it derived a pair of \(\varepsilon \)-insensitive up-bound and down-bound nonparallel planes around the data points. Its lease squares version was developed in [92]. [93] improved the TSVR by formulating it as a pair of linear programming problems instead of QPPs. Weighted TSVR [94] assigned the samples in the different positions with different penalties, which can avoid the over-fitting problem to a certain extent. \(\varepsilon \)-TSVR [95] implemented the structural risk minimization principle by introducing the regularization term in primal problems of TSVR, and the SOR technique was used to solve the optimization problems to speed up the training procedure. [96] adopted the regularization to convert original TSVR into a well-posed problem and employed the \(L_1\)-norm based loss function and regularization to introduce robustness and sparsity simultaneously. Similar to the par-\(\nu \)-SVR [39, 97] proposed an efficient twin parametric insensitive SVR (TPISVR), which was suitable for the case that the noise is heteroscedastic.

The smoothing technique was applied to convert the original constrained minimization problems of TSVR to unconstrained ones such that Newton algorithm with Armijo inexact stepsize could be adopted effectively [98]. A primal version for TSVR (PTSVR) was presented in [99] by introducing the smooth function to approximate its loss function, PTSVR directly optimized the QPPs in the primal space based on a series of sets of linear equations. A least squares version for TSVR (PLSTSVR) was also considered in the primal space [100]. [101] introduced a simple and linearly convergent Lagrangian SVM algorithm for the dual of TSVR. [102] proposed the reduced TSVR (RTSVR) using the notion of rectangular kernels to obtain significant improvements in execution time over the TSVR. Regressors based on TSVR for the simultaneous learning of a function and its derivatives were discussed in [103, 104], and showed their significant improvements in computational time and estimation accuracy.

3.4 Multiclass TWSVMs

To solve the multiple classification problem with the training set

$$\begin{aligned} T=\{(x_1,y_1),\cdots ,(x_l,y_l)\}, \end{aligned}$$
(28)

where \(x_i\in R^n, i=1,\cdots ,l, y_i \in \{1,\cdots ,K\}\) is the corresponding pattern of \(x_i\), there are two types of strategies, one is the “decomposition-reconstruction” strategy [2] by solving a series of smaller optimization problems, while the other one is the “all-together” strategy [105] by solving only one single optimization problem. An interesting model proposed in [106] belonging to the first strategy, termed as multiple birth support vector machine (MBSVM), solved multi-QPPs simultaneously to seek for \(K\) nonparallel hyperplanes

$$\begin{aligned} (w_k\cdot x)+b_k=0, k=1,\cdots , K. \end{aligned}$$
(29)

Compared with the straightforward multiclass extension of TWSVM or GEPSVM [107–109], MBSVM took into account the computational complexity, the “min” decision criterion of TWSVM is changed into the “max” one of MBSVM. The geometric interpretation of MBSVM with \(x\in R^2\) is shown in Fig. 2, where the \(k\)th hyperplane is at least one distance from the \(k\)th class points, and is closer to the other classes, a test pattern is assigned to a class depending on which one it lies farthest to (Fig. 3).

Fig. 3
figure 3

A toy example learned by the linear MBSVM [106]

Full size image

[110] combined the decision tree with the TWSVM together (DTTSVM) for the multi-class classification, which can overcome the possible ambiguous occurred in MBSVM. Twin-KSVC took the advantages of both TSVM and K-SVCR (support vector classification-regression machine for \(k\)-class classification) [111] and evaluated all the training points into an “1-versus-1-versus-rest” structure [112]. A multi-class LSTWSVM based on optimal directed acyclic graph (DAG) was proposed in [113], an average distance measure and a non-repetitive sequence number rearrangement method were offered to reduce the cumulative errors caused by DAG structure.

3.5 Semi-Supervised TWSVMs

Semi-Supervised Learning (SSL) has attracted an increasing amount of interest in the last decade [114]. For the Semi-supervised binary classification problem with the training set

$$\begin{aligned} T=\{(x_1,y_1),\cdots ,(x_l,y_l)\} \cup \{x_{l+1},\cdots ,x_{l+q}\}, \end{aligned}$$
(30)

where \(x_i \in R^n\), \(y_i \in \{-1,1\}\), \(i=1,\cdots ,l\), \(x_i\in R^n\), \(i=l+1,\cdots ,l+q\), and the set \(\{x_{l+1},\cdots ,x_{l+q}\}\) is a collection of unlabeled inputs known to belong to one of the two classes, several novel approaches for making use of the unlabeled data to improve the performance of classifiers have been proposed, in which Laplacian SVM (LapSVM) [115] using the graph Laplacian was a state of the art method. Follow the idea of LapSVM, a novel Laplacian TWSVM (Lap-TSVM) for the SSL problem was proposed in [116], which can exploit the geometry information of the marginal distribution embedded in unlabeled data to construct a more reasonable classifier and be a useful extension of TSVM. Furthermore, by choosing appropriate parameters, Lap-TSVM degenerates to either TSVM or TBSVM. A variant of Lap-TSVM, named as Laplacian smooth TWSVM (Lap-STSVM) was developed in [117]. They converted the constrained QPPs of Lap-TSVM into unconstrained minimization problems (UMPs) in primal space, and the smooth technique was then introduced to make these UMPs twice differentiable, therefore a fast Newton-Armijo algorithm was further designed to solve the UMPs efficiently, which converges globally and quadratically.

The PU problem where the training set consists of a few Positive examples and a large collection of Unlabeled examples, another kind of semi-supervised learning problem, is now gaining more and more attention [118]. Formally, its training set is

$$\begin{aligned} T=\{(x_1,y_1), \cdots , (x_l,y_l)\}\cup \{x_{l+1}, \cdots , x_{l+q}\}, \end{aligned}$$
(31)

where \(x_i\in R^n, y_i=1\), i.e. \(x_i\) is a positive input, \(i=1, \cdots , l\); \(x_i\in R^n\), i.e. \(x_i\) is an unlabeled input known to belong to one of the two classes, \(i=l+1, \cdots , l+q\). For the PU problem, Biased TWSVM (B-TWSVM) based on the Biased SVM (BSVM) [119] was proposed in [120], while [121] applied NPSVM for the PU learning. Both of them firstly converted the PU problem into an unbalance binary classification problem, then applied different weights to the positive examples and the unlabeled examples separately.

3.6 Knowledge-based TWSVMs

In this section, a review of the methods incorporating prior knowledge into TWSVMs, however restricted to the Universum TWSVM, TWSVM with the Privileged information, and Robust TWSVM is given.

Supervised learning problem with Universum samples is a new research subject in machine learning. The concept of Universum sample was firstly introduced in [122], which was defined as the sample not belonging to either class of the classification problem of interest. The authors proposed a new SVM framework, called \(U\)-SVM and their experimental results show that \(U\)-SVM outperforms those SVMs without considering Universum data. Therefore, TWSVM with Universum (called \(U\)-TSVM) was proposed in [123] combining the advantages of TWSVM and \(U\)-SVM. Its weighted version can be found in [124]. A nonparallel SVM that can exploit prior knowledge embedded in the Universum (\(U\)-NSVM) [125] was different with \(U\)-TSVM since it solves one QPP to get two nonparallel hyperplanes simultaneously.

In human learning, there is a lot of teacher information such as explanations, comments, comparisons and so on along with the given examples. Vapnik et al. [126] called this kind of additional prior information as the privileged information, which is only available at the training stage and never available for the test set, i.e, the training set is

$$\begin{aligned} T={(x_{1},x_{1}^{*},y_{1}),\cdots ,(x_{l},x_{l}^{*},y_{l})} \end{aligned}$$
(32)

where \(x_{i}\in R^{n}\),\(x_{i}^{*}\in R^{m}\),\(y_{i}\in \{-1,1\}\),\(i=1,\cdots ,l\). They proposed a new learning model, called Learning Using Privileged Information (LUPI), to accelerate the convergence rate of learninge specially when the learning problem itself is hard. [127] proposed a fast TWSVM using privileged information (called FTSVMPI), and focused on an interesting topic: how to exploit the privileged information to improve the performance of the Visual Tracking Object (VOT) problem.

Some uncertainty is often present in many real-world problems. For example, when the inputs are subjected to measurement errors, it would be better to describe the inputs by uncertainty sets \(\mathcal{X}_i\subset R^n, i=1,\cdots ,l\), since all we know is that the input belongs to the set \(\mathcal{X}_i\), so the training set should become

$$\begin{aligned} T=\{(\mathcal {X}_1,\mathcal{Y}_1), \cdots , (\mathcal {X}_l,\mathcal{Y}_l)\}, \end{aligned}$$
(33)

where \(\mathcal {X}_i\) is a set in \(R^n\), \(\mathcal{Y}_i\in \{-1,1\}\). The goal is to explore a robust model which can deal with such data set. There are many methods of constructing the robust SVMs such as [128, 129]. Robust TWSVM (\(R\)-TWSVM) [130] via second order cone programming (SOCP) formulations for classification was an improved extension of TWSVM, since there were only inner products about inputs in the dual problems which kernel trick can bey directly applied for nonlinear cases and the inverse of matrices were not needed any more.

The prior knowledge in the form of multiple polyhedral sets were incorporated into the linear TWSVM and LSTWSVM, termed as knowledge based TWSVM (KBTWSVM) and knowledge based LSTWSVM (KBLSTWSVM), were formulated in [131]. A 1-norm regularized KBTWSVM resulted in a linear programming was proposed in [132].

3.7 Multi-instance and Multi-task TWSVMs

Multiple-instance learning (MIL), being useful in many applications including text categorization, natural scene classification, image retrieval and so on, has received intense interests recently in the field of machine learning. In MIL framework, the training set consists of positive and negative bags of instances which are points in the \(n\)-dimensional real space \({R^n}\), and each bag contains a set of instances. In each positive training bag, there must be at least one positive instance, whereas a negative bag contains only negative instances. The aim of MIL is to construct a classifier learned from the training set to correctly label unseen bags. A number of MIL methods based on SVMs emerged [133, 134]. Based on TWSVM, [135] extended the idea of MI-SVM [133] to construct the MIL nonparallel classifier (MI-NSVM). The method was mainly divided into two steps: The first step was to generate a spare hyperplane and estimate the score of each instance in positive bags. The second step, MI-NSVM seeked the “most positive” instance of each positive bag by the information obtained in the first step, and then generated the second hyperplane. MI-TWSVM [136] also aimed at generating a positive hyperplane and a negative hyperplane, such that the former one is close to at least one instance (“witness” instance) in every positive bag and is far from all instances belonging to negative bags, and the latter one is close to all instances belonging to negative bags and is far from the “witness” instances in positive bags. Instead of having QPPs, the MI-TWSVM optimization problem were bilevel programming problems (BLPPs). [137] improved MI-TWSVM by implementing the structural risk minimization (SRM) principle and solving a series of QPPs instead of the BLPPs. [138] proposed a least squares version for MIL based on LSTWSVM which used an iterative strategy by solving two linear systems of equations and a QPP alternatively.

Multi-task learning (MTL) is a learning paradigm which seeks to improve the generalization performance of a task with the help of other tasks [139]. When there are relations between the tasks to learn, it can be advantageous to learn all tasks simultaneously instead of following the more traditional approach of learning each task independently of the others. SVMs have been explored for multi-task learning [140, 141], and [142] embeded multi-task learning into TSVMs and made use of the contribution of correlation of tasks.

3.8 Large scale TWSVMs

Considerable efforts have been devoted to the implementation of efficient optimization method for solving the QPP in standard SVMs, such as the chunking and decomposition methods [1, 31, 143–145]. For TWSVMs, though [25, 33] and other authors applied the SOR technique or the coordinate descent method, they in fact took no account of the computation of the inverse matrices and will fail facing the real large scale problems. Since NPSVM [27, 66] skillfully avoided the computation of the inverse matrices and applied the SOR or SMO to solve the QPPs, they can deal with the large scale problems really.

For some applications such as document classification with the data appearing in a high dimensional feature space, linear SVM in which the data are not mapped, has similar performances with nonlinear SVM. For linear SVM, many methods have been proposed in large-scale scenarios such as [146, 147], while for linear TWSVM, \(L_1\)-NPSVM [148] based on the NPSVM [27] and \(L_2\)-TWSVM [149] on ITSVM [26], were designed to deal with large-scale data based on an efficient solver—dual coordinate descent (DCD) method, which is a popular optimization technique, updates one variable at a time by minimizing a single-variable subproblem. Since the dual problems in \(L_1\)-NPSVM or \(L_2\)-TWSVM have the same formulations with that of standard \(L_1\)-SVM or \(L_2\)-SVM, and [147] proposed the DCD method for them, pointed out that the DCD method makes crucial advantage of the linear kernel and outperforms other solvers when the numbers of data and features are both large, therefore the DCD method can by applied for linear TWSVM naturally with several minor modifications.

4 Applications of TWSVMs

As SVMs has many applications, TWSVMs can also be applied into the corresponding fields. This sections reviews the limited applications of TWSVMs because of their few years developments.

Speaker recognition is to decide which person is talking from a group of known speakers, [150] combined TWSVMs with Gaussian Mixture Model (GMM) [151] for text-independent speaker recognition where GMMs were used to extra features. [152] addressed the task of gesture recognition using surface electromyogram (sEMG) data, and proved TWSVM to be an effective approach in meeting the learning problem from multi-class data where patterns in different classes arise from different distributions, since TWSVM is a more natural choice for applying to unbalanced datasets. Human activity recognition (HAR) is an important research branch in computer vision, and [153] proposed a framework for HAR with the combination of local space-time features and LSTWSVM. Speech emotion recognition is used to solve the problem of “how to speak”, just like speaker recognition is proposed to solve “who is speaking”, TWSVM was applied into this problem tentatively [154].

Clustered microcalcifications (MCs) in mammogram can be an indicator of breast cancer, [155] presented a mass detection system based on TWSVM to distinguish the masses from normal breast tissues accurately, [156] extracted combined image features from each image block of positive and negative samples, and trained TWSVM with the 164 dimensional features of each sample to test at every location in a mammogram whether the MCs was present or not. [157] boosted the TWSVM for higher accuracy in MCs detection. A predictive model for heart disease diagnosis using feature selection based on LSTWSVM was developed in [158], where the selection of significant features improved the accuracy. Ding et al. [159] applied TWSVM to the intrusion detection to improve the speed of detection and accuracy.

5 Remarks and Future Directions

This paper has offered an extensive review of TWSVMs, including four basic models: original TWSVM, the improved versions TBSVM, ITSVM and NPSVM. Based on the four models, the extensions and variants of TWSVMs are reviewed, such as the \(\nu \)-TWSVMs, least squares TWSVMs, localized TWSVMs, sparse TWSVMs, structural TWSVMs, and linear programming TWSVMs for the binary classification problems; TWSVRs for the regression problems; Multi-class TWSVMs for the multi-class problems; Semi-supervised TWSVMs for the semi-supervised problems; Knowledge-based TWSVMs for the problems with the Universum set, Priviledged information, or uncertain information; Multi-instance and Multi-task TWSVMs; and also the large scale TWSVMs. Some of these models have already been used in several real-life applications, such as speaker recognition, intrusion detection and etc. Researchers and engineers in data mining, especially in SVMs can benefit from this survey in better understanding the essence of the TWSVMs. In addition, it can also serve as a reference repertory of such approaches.

In this paper, we can see the development of TWSVMs following the way of modifying the corresponding optimization models, since the essence of TWSVMs is to construct appropriate optimization models (linear programming, quadratic programming, nonlinear programming, second order cone programming) for different learning problems. TWSVMs have better generalization ability, are more flexible than TWSVMs because of searching for the nonparallel hyperplanes. However, there’s no such thing as a free lunch. Just as we pointed out for the ITSVM and NPSVM models in Sect. 2, ITSVM sacrifices more model training time than TWSVM to skillfully avoids the computation of the inverse matrices, while NPSVM sacrifices further more model training time than ITSVM to get the sparsity. We can not count on two smaller QPPs to get better performance than one large OPP as the declaration in the original TWSVM, since the costly computation of inverse matrices are not considered.

As we can see, the extensions or variants of TWSVMs were mostly based on the original TWSVMs or TBSVM, so there is a great space for development based on the ITSVM and NPSVM. And new practical problems remaining to be explored present new challenges to TWSVMs to construct new optimization models. These models should also have the same desirable properties as the models in this paper including: good generalization, scalability, simple and easy implementation of algorithm, robustness, as well as theoretically known convergence and complexity [160].