Implementation of latching control in a numerical wave tank with regular waves

Abstract

In order to increase the overall power production efficiency of wave energy technology in the face of sea state variability, the presence of the control is mandatory. A model of the system is required to tune the controller parameters and predict the resulting performances. Even though the relevance of nonlinearities is magnified by the presence of the controller, the device model employed is usually linear. An implementation of control in a fully nonlinear simulation model is desirable, but missing. Hence, this paper proposes to use the fully nonlinear computational fluid dynamics (CFD) environment, implementing the latching control strategy in the open source software OpenFOAM. A case study has been analyzed to highlight the nonlinear behavior of a device under latching control and to evaluate the differences between linear and nonlinear simulation models. The results show that the linear model overestimates the amplitude of motion, and, as a result, the extracted power. Moreover, the choice of the optimal control parameter is significantly affected by the nonlinear effect on the natural period of the device.

1 Introduction

For several countries around the world, the exploitation of ocean wave power may constitute a significant contribution to the diversification of the energy production scenario, increasing the portion of sustainable and renewable resources (Halamay and Simmons 2011; Fusco et al. 2010; Yang et al. 2010). However, in most cases Wave Energy Converters (WECs) are not yet efficient enough to be economically competitive in the renewable energy market. An important role in the achievement of the economic viability is played by the control strategy, able to double the energy harvested (Babarit and Clément 2006).

On the other hand, the ability of the controller to magnify power absorption is extremely sensitive to the ratio of wavelength to device size (Greenhow et al. 1984). A small device tends to have a larger absorbed-power increase than a big device, so its performances gain more benefits from the inclusion of the controller. In order to maximize the power extracted, a WEC must effectively convert energy in a range of frequency as wide as possible. For heaving point absorbers, for example, the resonance frequency of the WEC is usually quite pronounced and the response rapidly decays for frequencies far from resonance. Indeed, the main aim of the control strategy is to address the sea state variability and significantly enlarge the amplitude of motion, especially at frequencies far from the resonance peak. The most common WEC control strategies for linear WEC models are based on a form of complex-conjugate (Nebel 1992) or reactive (Salter 1979) control, which returns the optimal conditions, in the frequency domain, to maximize the energy absorption, as shown in chapter 6 of Falnes (2002). On the other hand, examples of time domain approaches are given by latching (Budal et al. 1979; Babarit and Clément 2006; Kara 2010) and methods based on numerical optimization (Bacelli et al. 2009).

Regardless of which particular control strategy is adopted, a comprehensive model of the system is required and the performance of the controller is highly dependent on the model accuracy. The simplest and common choice is to linearize the system, implicitly assuming small amplitudes of motion. However, under controlled conditions the motion may be exaggerated and, as a consequence, the relevance of nonlinearities increases.

In absence of control, the only external action comes from the waves, whose steepness is physically limited, as shown in chapter 17 of Mehaute (1976). The resulting wave excitation force is smooth and without high-frequency components. Conversely, the controller acts directly on the device with an arbitrary force, limited only by the structural constraints of the system. An example is given by latching control, which imposes a discrete on/off force. Peñalba et al. (2015) implement latching control with both a linear and a partially nonlinear hydrodynamic model and show how the predicted power output and the optimal control calculations are affected by presence/absence of the nonlinear terms. While the linear and nonlinear models produce similar WEC motion in the uncontrolled case, the motions diverge when control is applied. Specifically, nonlinearities becomes relevant when the sharp exciting force of the controller directly influences the dynamics of the device leading to, among other effects, an asymmetric response.

An accurate evaluation of the performance of the controller, as well as a validation of the results of the simulations, may be achieved through experimental tests in the sea or in wave tanks. Bjarte-Larsson and Falnes (2006) tested latching on an axisymmetric floating body in a wave tank and the implementation of the control increased the power captured up to 4.3 times. A comparison between a simulation and tank tests is reported by Durand et al. (2007), where a latching control strategy is applied in a wave tank to the SEAREV device. The controller increased the energy production up to ten times with regular waves, from 50 to 86 % with irregular waves.

Unfortunately, experimental tests are not widely performed because they are time consuming, expensive and require both a device, usually scaled, and a wave tank. A more feasible evaluation tool is represented by the numerical wave tank (NWT) that implements a real tank in a computational fluid dynamics (CFD) environment. The application of the Navier–Stokes equations allows the inclusion of all the nonlinearities while the numerical domain makes possible to simulate the full-scale device and avoid scale effects. On the other hand, CFD has several drawbacks, among which the most relevant are: expensive large clusters needed to perform the computation in a reasonable time, long setup time and the expertise required to produce reliable results, as well as long computational time for each simulation.

Nowadays, in wave energy applications, numerical wave tanks are mainly used to evaluate fluid–structure interaction on one or more floating bodies in operational conditions, to test survivability in extreme conditions (Clauss et al. 2005), to quantify viscous effects in order to identify the terms of the Morrison equation and model an equivalent viscous force (Bhinder et al. 2012) or to provide data for system identification techniques (Davidson et al. 2015b). Even though the experimental results demonstrate the impact of a controller on the system’s dynamics, a real-time control in an NWT is missing. This paper addresses the absence of a control strategy in a CFD environment, implementing latching in the open source software OpenFOAM^®. Rather than focusing on a nonlinear control algorithm, which could be based on the mathematical formulation of Hoskin and Nichols (1986), the objective of the paper is to show that a real-time controller in CFD is implementable and to highlight the prominence of nonlinear WEC behavior under controlled conditions, which leads to a significant difference between optimal latching duration for linear and nonlinear WEC simulation. In particular, the focus is on nonlinearities deriving from the wave–body interaction, therefore only linear waves are analyzed.

Likewise, additional PTO damping has not been included since, even without PTO, the system is already damped enough to avoid unacceptably large oscillations; it will be shown that the maximum oscillation achieved (0.028 m) is just the 22 % of the device radius (see Fig. 11 or Table 1). With no PTO, there is no power extraction, so the objective of the optimization is to exaggerate the amplitude of oscillation. Nevertheless, Babarit et al. (2004) show that, for latching control in a linear system with regular waves, maximization of the amplitude of oscillation is as effective as the maximization of the power extracted.

The reminder of the paper is organized as follows: Sect. 2 presents the mathematical and computational description of the software’s structure while Sect. 3 shows the control strategies available in the proposed latching algorithm. In Sect. 4, results are presented and, in Sect. 5, comparisons are drawn between CFD simulations and linear simulations. In Sect. 6, some conclusions and final remarks are presented.

2 Numerical wave tank

Numerical wave tanks are computer implementations, in either two or three dimensions, of wave tanks (Tanizawa 2000). Having a numerical facility brings several advantages over the real one: a more cost-effective evaluation of motion and power capture, passive access to individual hydrodynamic forces (e.g., restoring or viscous forces) and status variables (e.g., pressure or velocity) in every point of the fluid domain, implementation of ideal constraints and restraints and no need of a real tank and device, so no scale effects. Several drawbacks also exist, among which the most relevant by far is the high computational time, typically 1000 times bigger then the simulation time (Ringwood et al. 2015). Furthermore, the setup of a spatial mesh, which ensures a reasonable compromise between computational time and accuracy, requires time and experience.

The fluid dynamic in CFD is ruled by a set of differential equations called Navier–Stokes equations, chapter 2 of Temam (2001). Under the incompressibility assumption, only the equation of transfer of mass (1) and momentum (2) are utilized:

$$\begin{aligned}&\nabla \cdot \mathbf{u }= 0\end{aligned}$$

(1)

$$\begin{aligned}&\rho \frac{\partial {\mathbf{u }}}{\partial {t}} + \rho \mathbf{u } \cdot \nabla \mathbf{u }= - \nabla p + \nabla \cdot \mathbf T + \rho \mathbf g \end{aligned}$$

(2)

where $\mathbf{u }$ is the fluid velocity, $\rho$ is the fluid density, p is the pressure, $\mathbf g$ is the acceleration of gravity and $\mathbf T$ is the stress deviator, given by.

$$\begin{aligned} \mathbf{T =\mu [\nabla \mathbf{u }+(\nabla \mathbf{u })^T]} \end{aligned}$$

(3)

where $\mu$ is the dynamic viscosity.

The software discretizes the time and space domains in order to form a system of linear algebraic equations. The software utilized in this paper is the open source OpenFOAM, version 2.3.

2.1 OpenFOAM

The development of NWTs in OpenFOAM is a rich research topic and numerous research theses and reports are available (Afshar 2010; Cathelain 2013). In the wave energy field, OpenFOAM has been used to simulate wave energy converters in operational (Palm et al. 2013; Schmitt et al. 2012) and extreme events (Vyzikas et al. 2013) conditions.

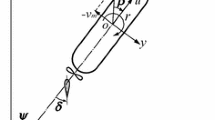
The wave generation application is called waveFoam and was created by Jacobsen et al. (2012) as an extension of the built-in interFoam. The free surface elevation is described by an interface-capturing method known as volume of fluid (VOF) (Hirt and Nicholis 1979). Within the tank, there are three different zones: in the middle region the dynamics are purely governed by the Navier–Stokes equations; hence, this is the actual experimental area of the tank. Upstream, there is the wave generation zone, where the required wave profile is gradually imposed on the fluid domain. Downstream, there is the absorption zone, where the waves are gradually erased to avoid reflections. Figure 1 shows the generic configuration of a numerical wave tank, where the curved profiles in the generation and absorption zones represent the proportion with which the wave profile is imposed on the fluid domain.

Fig. 1

Scheme of a numerical wave tank implemented in OpenFOAM using waveFoam

A further development of the wave generation application is called waveDyMFoam, based on the built-in interDyMFoam, which allows the presence of a floating body thanks to a dynamic mesh that moves and deforms according to the body motion. In the version 2.3 of OpenFOAM, the introduction of the sixDoFRigidBodyMotion solver considerably improves the mechanism taking care of the movement of the body and the consequent deformation of the surrounding mesh. Moreover, constraints and restraints are more reliable and efficient than in the previous versions.

The main reason for the choice of OpenFOAM instead of other CFD commercial software is its flexibility and open source availability. Besides the undeniable relevance of being cost-free, the biggest value is the possibility to access and modify the source code, which allows a deep understanding and total control over the calculations performed by the software.

OpenFOAM is written in C++, which makes straightforward to insert a new customized subroutine into the main structure of the software. Indeed, new compatible applications are easy to create, making the software flexible and adaptable to the user’s needs. In Sect. 2.2, the basic steps to follow to implement a new application are explained, as well as the instructions to download, compile and use the latching control application created by the authors.

2.2 Implementation of latching control

The proposed control algorithm is born as a customized version of the built-in sixDoFRigidBodyMotion, which can be found in the source code folder of OpenFOAM. The original application’s task is to apply Newton’s second law of dynamics, integrating all the forces acting on the body surface, eventually including external restraints, to calculate and update both linear and rotational acceleration, velocity and position. Furthermore, if present, constraints are analytically imposed, directly setting to zero the displacement in the blocked degree of freedom. Note that, in previous versions of OpenFOAM, constraints were indirectly obtained by adding a counteracting force against the resulting force in the direction of the blocked degree of freedom. Even though this approach is theoretically valid, the numerical finite accuracy can cause a defective constraint.

Since every controller essentially acts on the device by means of either restraints or constraints, sixDoFRigidBodyMotion is suitable as the backbone of the new application, implementing the real-time control algorithm. The reader can either code his own control algorithm or download the ready-to-use latching control algorithm available at Giorgi and Ringwood (2015). Details about the control strategy features and options are provided in Sect. 3, while practical instructions are given in the user manual in Giorgi and Ringwood (2015).

3 Latching control

After a brief overview on the latching control given in Sect. 3.1, the control strategy actually implemented in the proposed control algorithm is unfolded. Section 3.2 describes the basic logic of the new source code. Section 3.3 highlights a nonlinear behavior of the natural period with relevant consequences on the latching strategy, leading to an expansion of the control algorithm explained in Sect. 3.4. Finally, in Sect. 3.5, a case study is presented, along with a description of some issues related to the CFD simulation environment.

3.1 Latching control

The purpose of latching control strategy is to force the velocity into phase with the excitation force. An on/off PTO force is applied by means of a latching system, in order to avoid a phase difference between the velocity and the incoming wave excitation force. Referring to Fig. 2, the device is locked at times $t_1$, $t_3$ and $t_5$ at the extrema of displacement, namely when the velocity is zero, and released at times $t_2$ and $t_4$ after a latched duration $T_\mathrm{L}$. The two latching durations, upper position $t_2-t_1$ and lower position $t_4-t_3$, may, in certain cases, preferably be chosen to be different (Falnes and Lillebekken 2003).

Fig. 2

Latching calculations to put position and force in phase. Latching instants at extrema of position P and $-$P: $t_1$, $t_3$ and $t_5$; latching duration: $T_\mathrm{L}$; unlatching instants: $t_2$ and $t_4$

If the wave is regular and monochromatic, with period $T_W$, the natural period $T_{n}$ of the device is known and if the damping is negligible, the control variable $T_\mathrm{L}$ is optimally calculated (Ringwood and Butler 2004) as:

$$\begin{aligned} T_\mathrm{L}=\frac{t_5-t_1}{2}-(t_5-t_4)=\frac{T_W}{2}-\frac{T_\mathrm{n}}{2} \end{aligned}$$

(4)

Equation (4) implicitly suggests that the latching control strategy best suits conditions in which the wave period is bigger than the natural period, with $T_\mathrm{L}>0$. Conversely, another control strategy called declutching is able to control devices facing an incoming wave with period smaller than the natural period (Teillant et al. 2010).

The definition of the natural period in Eq. (4) presents several issues. While, in a linear case, the natural period is a well known and univocal concept, the presence of nonlinearities or large amplitude of motion makes it ambiguous to define. Section 3.3 focuses on the variability of the natural period and the consequences on the choice of the latching duration. Furthermore, Eq. (4) is exact only if damping is absent or negligible. More correctly, the natural period should be substituted by the damped natural period, which approaches the natural period as the damping goes to zero. Section 3.1.1 shows the linear hydrodynamic model approximation of the system and proposes a model order reduction to estimate the influence of the damping on the natural period.

Finally, if the sea state is characterized by polychromatic waves, the requirement of phase accordance between velocity and excitation force becomes blurred, so the optimization criterion is not unique (Babarit et al. 2004). Different targets can be pursued, such as the synchronization of the velocity and excitation peaks (Hals et al. 2002) or the maximization of the absorbed power (Babarit and Clément 2006).

3.1.1 Linear model approximation

The linear equation of motion of a floating body, as in chapter 6 of Newman (1977), is defined in the frequency domain as:

$$\begin{aligned} \{-\omega ^2[M+A(\omega )]+j\omega B(\omega )+G\} x(j\omega )=F_\mathrm{ex}(\omega ), \end{aligned}$$

(5)

where M is the mass, $A(\omega )$ the added mass, $B(\omega )$ the radiation damping, G the stiffness, $F_\mathrm{ex}(\omega )$ is the wave excitation force and x a generic degree of freedom. In the present paper, the hydrodynamic parameters $A(\omega )$ and $B(\omega )$ are calculated by solving the potential problem with the BEM open source software NEMOH.

For the purposes of real-time control, a time domain formulation is needed, obtained applying the Cummins equation (Cummins 1962):

$$\begin{aligned} (M+A_\infty )\ddot{x}(t)+\int _0^tK(t-t')\dot{x}(t')dt'+Gx(t)=f_\mathrm{ex}(t), \end{aligned}$$

(6)

where x is the generic degree of freedom, M is the mass, $A_\infty$ is the infinity frequency added mass asymptote, G is the stiffness, $f_\mathrm{ex}$ is the exciting force and the kernel K of the convolution term is the retardation function. The calculation of K and $A_\infty$ is made applying Ogilvie’s relationships (Ogilvie 1964):

$$\begin{aligned}&K(t)=\frac{2}{\pi }\int _0^\infty B(\omega ){cos}(\omega t)\mathrm{d}\omega ,\end{aligned}$$

(7)

$$\begin{aligned}&A_\infty =\lim _{\omega \rightarrow \infty } A(\omega ). \end{aligned}$$

(8)

Finally, since the direct computation of the integral in (6) is expensive, the convolution term can been replaced by a state space representation (Jefferys 1980) pages 413–438, as showed by Taghipour et al. (2007). In this way, the whole dynamic problem becomes a computationally efficient set of first-order differential equations.

The identification of a state space model is performed using the toolbox provided by Perez and Fossen (2009), which automatically selects a proper order, hereafter called n, to approximate the convolution integral. Therefore, the overall dynamical system order of the system (6) becomes $2 + n$.

In any case, since the oscillatory behavior of a floating object resembles the dynamics of a simple constant mass–damper–spring system, Fusco and Ringwood (2011) propose a second-order approximation, namely reducing the state space order to zero, i.e., the complete system order to two. The reduction is reasonable if the system is described by a dominant pole pair. The evaluation of the relevance of each order is made by means of the Hankel singular values of the complete system $\sigma _i$, which are used to quantify the energy content of each order i (Safonov et al. 1990). If arranged in descending order, namely $\sigma _1 \ge \sigma _2 \ge \cdots \ge \sigma _{n+2}$, the second-order approximation is reliable if $\sigma _2>>\sigma _3$.

The second-order system approximation presents a constant damping term, so Eq. (6) can be rearranged to match the standard second-order dynamical system:

$$\begin{aligned} \ddot{x}+2 \zeta \omega _\mathrm{n} \dot{x} + \omega _\mathrm{n}^2 x = 0, \end{aligned}$$

(9)

where $\zeta <1$ is the damping ratio and $\omega _\mathrm{n}=\frac{2\pi }{T_\mathrm{n}}$ is the natural frequency. Notwithstanding the approximation introduced, the advantage of the order reduction is the possibility to analytically evaluate the effect of damping on the system dynamics. Since the damped natural frequency is defined as

$$\begin{aligned} \omega _\mathrm{d} = \omega _\mathrm{n} \sqrt{1-\zeta ^2}, \end{aligned}$$

(10)

it is smaller than the natural frequency. Consequently, the presence of damping reduces the ideal optimal latching duration:

$$\begin{aligned} T_\mathrm{L} = \frac{T_\omega }{2} - \frac{T_\mathrm{L}}{2} = \frac{T_\omega }{2} - \frac{T_\mathrm{n}}{2 \sqrt{1-\zeta ^2}} \end{aligned}$$

(11)

The approximation error introduced by Eq. (4) is proportional to the damping factor of the non-reduced system, which is not as explicitly accessible as in the standard second-order differential equation (9). The second-order reduction may be of assistance if the whole system is clearly second-order-dominant, namely if the approximation introduced by the order reduction is negligible. Since every case should be assessed for second-order dominance, it is not possible to give to the method a general validity. Therefore, $T_\mathrm{L}$ is not always exactly definable and $T_\mathrm{n}$ is used instead, aware that the actual optimal $T_\mathrm{L}$ will be smaller, accordingly to the damping factor of the system.

3.2 Constant latching duration

The basic latching control algorithm applies to devices subject to monochromatic waves, and utilizes a constant latching duration, which is equal for both positive and negative peaks. Conversely, alternative and adaptive latching duration options are available to deal with nonlinear dynamics, as further explained in 3.4.

The control algorithm allows the user to choose which axis the latching control should be applied to, either in surge (X axis), sway (Y axis) or heave (Z axis) motion. The conventional right-handed coordinate system assumes the incoming wave along the x-axis, the gravity acting on the negative direction of the z-axis and the y-axis oriented according to the right-hand-rule.

Fig. 3

Constant latching duration control strategy. Simulation time: $t_\mathrm{sim}$; time step: $\Delta t$; transition time: $t_\mathrm{transition}$; velocity: v; latching duration $T_\mathrm{L}$; unlatching instant: $t_\mathrm{u}$

In order to be effective, the controller must be able to detect when the latching conditions are verified and actually lock the motion for as long as required by the latching controller. The innovation introduced by the new control algorithm is the dynamical use of constraints to perform the latching act: instead of being applied just at the beginning of the simulation, constraints in the controlled degree of freedom are imposed when the body is latched and removed when the body is released. The timing with which the controller intervenes is defined by the control strategy, whose logic is shown in the flowchart in Fig. 3.

The control algorithm is programmed to apply Newton’s second law of dynamics at every time step $\Delta T$ of the simulation time $t_\mathrm{sim}$ and update the state variables of position, velocity and acceleration. Prior to the application of Newton’s law, the control algorithm sets the constraints accordingly to the latching status.

The initial conditions normally assume the floating body in quiet equilibrium in the numerical wave tank at the still water level. When the simulation starts, the waves are gradually created in the generation zone and travel towards the device which, in turn, begins to move. Hence, the control loop is bypassed for a transition time $t_\mathrm{transition}$, defined by the user, to allow the device motion to reach steady state.

Then, the latching condition of zero velocity at the extrema of displacement needs to be verified. Due to numerical precision, a null velocity is very unlikely, so the multiplication between the values in two successive time steps ($v(t_\mathrm{sim}) \cdot v(t_\mathrm{sim}-\Delta t )$) is checked instead: in the case of an extremum, the product must be either negative or null. Furthermore, when the body is latched, the velocity is exactly set equal to zero, so the null-multiplication-condition is verified as well. Consequently, it is important to asses whether the body has just reached the peak or it was already locked in the extremum from the previous time step, i.e., whether or not the body was latched in the last iteration. In the very first sample point that the controller locks the device, the unlatching instant $t_\mathrm{u}$ is defined by adding the latching duration to the simulation time. The body is kept in position until the latching duration is elapsed, then is freed to escape from the extreme position.

Summing up, use of the latching control algorithm requires the user to declare the type of latching control (constant, alternative or adaptive), the degree of freedom (surge, sway or heave) that is to be latched, the value of latching time and starting time. If some of the parameters are omitted, default values are set in the source code.

3.3 Latching duration and natural period

The main important parameter to choose to perform the latching control is the latching duration. If the incoming wave is monochromatic, Eq. (4) achieves an optimal control, as long as the natural period of the controlled device is known and the damping term $\zeta$ is negligible. If damping is not negligible, then (11) can be used instead. Unfortunately, the definition of a unique characteristic natural period is not straightforward if the linear assumption of small motion is not made, as explained in 3.3.1. Since the amplitude of the motion is exaggerated by the latching control, the small motion hypothesis is generally mistaken.

3.3.1 Natural period

In dynamics, the natural period (or frequency) describes how fast the body oscillates if displaced from an equilibrium position and set free to move. The natural frequency is calculated from the inertia and the stiffness terms of the equation of motion. Equation (5) shows the frequency dependence of the added mass $A(\omega )$ and damping term $B(\omega )$, while the mass M and the stiffness G are constant.

Actually, Eq. (5) is accurate only in a range of motion around the equilibrium, small enough to consider the wetted body surface constant. The added mass (which is the mass of water accelerated by the body motion, therefore depending on the submerged portion of the body) and the hydrostatic stiffness (which depends on the cross section piercing the water) both depend on the instantaneous wetted surface, with the notional dependence shown by A(x(t)) and G(x(t)) in (12), respectively. The natural period, which is defined for a linear case as a time-invariant characteristic of the body, is not a proper descriptor under large motion conditions. A new quantity called the instantaneous natural period is defined by (12), which returns the natural period relative to the actual submerged portion of the body at each time instant. Hence, the instantaneous natural period is able to capture the nonlinear relation between the natural period and the motion of the body.

$$\begin{aligned} T_\mathrm{n}(x(t))= 2 \pi \sqrt{\frac{M+A(x(t))}{G(x(t))}}. \end{aligned}$$

(12)

Consequently, the instantaneous damped natural period depends on the instantaneous natural period as well as on the hydrodynamics of the system.

$$\begin{aligned} T_\mathrm{L}(x(t))= T_\mathrm{n}(x(t))f(B,M,A). \end{aligned}$$

(13)

In 3.3.2 a free decay time series from CFD simulation is used to appreciate the range of variability of the instantaneous natural period.

3.3.2 Free response tests

The natural period is a description of the dynamical behavior of a body left free to move from a position of non-equilibrium. Therefore, a reliable measurement of the actual natural period can be obtained from a free decay test, performed either in a real or numerical tank. While in a linear analysis, eventually inaccurate assumptions are needed to calculate the natural period, here it is directly measured from the time series, which is inclusive of all the nonlinearities instead.

During the evolution of the free decay, both the amplitude and the frequency are changing in time. For the sake of simplicity, the two variables are separated, so that:

$$\begin{aligned} x(t)=A(t)\mathrm{sin}(\omega _\mathrm{n}(t)t+\phi ) \end{aligned}$$

(14)

The natural period is defined as the time lag between two successive homologous (referring to points of equal displacement, a period apart) points of the harmonic function. Since the amplitude is not constant, it is straightforward to sample the natural period at the extrema or the zero-crossings. While a discrete description is valuable, a more precise and continuous trend is required to understand how the nonlinearities gradually modify the dynamics as the amplitude varies. Hence, in order to spot all the couples of consequent homologous points, Eq. (14) needs to be normalized, i.e., divided by the envelope that connects the absolute value of all the peaks and troughs.

As an example, the instantaneous natural period has been calculated for a semisubmerged sphere with radius and draft of 0.125 m, hence with the center of gravity at the free surface height. A heave-free decay is simulated in a CFD environment, starting with the center of gravity at -0.1 m. The resulting instantaneous natural period variations in time are shown via the solid line in Fig. 4. In the same graph, the envelope of the free decay time series is drawn in dotted line, along with the indication of peaks and troughs.

Fig. 4

Instantaneous natural period for a CFD heave-free decay test of a sphere with radius of 0.125 m

As the time elapses, the amplitude of the free decay decreases and the natural period becomes shorter, until it matches the linear natural period, represented by the horizontal dashed line. The transition toward the minimum of 0.69 s is smooth, with a maximum variation of about 7 %, from the highest value of 0.74 s that occurs for an amplitude around 0.1 m. Note a systematic alternation of concavity and convexity, respectively, occurring at the peaks and troughs of the free decay displacement. As a consequence, it is possible to infer that, at equal amplitude, the natural period is relatively longer at positive displacement, than at negative. Indeed, at the right side of Fig. 4, where the steepness of the curve is lower, the variability of the natural period between peaks and troughs is more evident. Further insight can be produced by simulating a free decay from a symmetric initial condition, namely starting from 0.1 m instead of $-$0.1 m. The resulting instantaneous natural period, shown in dash-dot line in Fig. 4, follows the same average trend, but with a symmetric alternation of concavity and convexity, which confirms that at equal magnitude of motion, the natural period is different inside and outside the water. The discrepancy between peaks and troughs becomes smaller as the amplitude decreases. The principal effect responsible for the different natural periods at peaks and troughs is the asymmetric action of the viscous forces, since the body is surrounded by two fluids, mainly water at troughs and mainly air at peaks, with very different viscous coefficients.

Finally, as far as the constant latching duration algorithm is concerned, the instantaneous natural period analysis allows a more effective selection of the latching period. A reasonable forecast of the amplitude of motion acquirable, for example, through a linear simulation, can point to the zone of the envelope in which the body will oscillate under control. Consequently, the corresponding natural period allows the selection of a more suitable latching duration.

3.4 Alternative and adaptive latching durations

Following the discussion about the variability of the natural period in Sect. 3.3.2, the choice of the latching duration is not obvious. Since the instantaneous natural period is systematically longer than the linear one, Eqs. (4) or (11) lead to a shorter latching period. The optimal duration is not clearly defined, since it depends on the amplitude of the motion, which in turn, depends on the latching duration itself. Moreover, the asymmetric behavior between peaks and troughs adds a further degree of complexity. The present control algorithm proposes two options to partially overcome the issues of the non-constant natural period: alternative and adaptive latching control strategies.

The alternative latching control aims to provide more flexibility to the control algorithm, allowing the definition of two different latching periods for peaks and troughs. Even though the choice is still arbitrary, an instantaneous natural period analysis of a free decay test, as in Fig. 4, may be of assistance. Since the natural period at peaks is longer than at troughs, typically the latching duration should be shorter at positive extrema.

The second option available is the adaptive latching control, which is an optimization tool used to find out the latching period that maximizes the amplitude of oscillation of the controlled body. A similar approach has already been applied by Peñalba et al. (2015) to overcome the uncertainty of the latching duration due to a partially nonlinear model.

The optimization loop is based on the assumption of the existence and uniqueness of an optimal point, which is the only maximum of a convex performance function. As widely explained in 3.3.2, the presence of nonlinearities decreases the optimal latching duration. On the other hand, a null value for the latching period implies absence of control, which is implicitly not optimal, unless the natural period is the same of the wave period. The uniqueness of the optimal solution is not straightforward to prove, but a comparison with linear case can bring confidence: constant latching duration control has been implemented in a linear simulation model with several latching periods in order to draw the performance curve in Fig. 5.

Fig. 5

Performance curve of latching control using a linear simulation for a sphere with radius of 0.125 m

The graph in Fig. 5 validates the assumption of uniqueness of the optimal point in a linear model, equal to 0.205 s, correspondent to an equivalent natural period of 0.709 s. The optimal latching duration is highlighted by a circle marker on the top of the convex curve of Fig. 5.

Also in Fig. 5, the square marker represents the linear undamped approximation calculated by Eq. (4). As expected, the damping makes the actual optimal latching duration smaller than the undamped, in this case 3.8 % smaller.

The model order reduction using the Hankel singular values as estimators of the significant order of the system, proposed in 3.3.1, has been applied to approximate the linear model with a second-order differential equation and evaluate the damped natural frequency. The ratio of the second and third-order Hankel singular values, about 43, is big but not enough to give absolute confidence in the reduction. As a matter of fact, the method was successfully applied by Fusco and Ringwood (2011) to geometries with ratio ranging between 230 and 3204. Nevertheless, the reduction suggests a value of damping factor $\zeta$ of about 0.1, which in turn make the damped natural period rise from 0.693 to 0.698 s.

The calculation of the optimal point in the linear case is made possible by the low computational cost of the simulations. A similar approach in CFD is not feasible, due to the huge computational effort required by each simulation.

The approach pursued by the adaptive control algorithm is to tune the latching period within just one simulation run, aiming to maximize the displacement of the body. The first latching duration is an educated guess based, for example, on the linear or the instantaneous natural period. When latching is applied, the amplitude gradually increases, either monotonically or with an intermediate maximum, and stabilizes to a steady value. As the amplitude changes, the period of motion adapts accordingly and, after a transient, stabilizes, matching the forcing wave period. Likewise, when a modification to the latching duration is carried out, both the amplitude and the response period experience a transient that ultimately leads to a steady state. Clearly, the transient is longer when the latching is applied for the first time than when the latching period is adapted. The adaptive algorithm’s task is to wait for the steady state to occur, then update the latching period in order to increase the response of the device, taking into account the records of previous modifications.

The adaptive strategy code is nested in the constant algorithm shown in Fig. 3. The constant latching duration algorithm takes care of applying the control when peaks occur, using the latching period previously established by the adaptive algorithm. As shown in Fig. 6, the adaptive strategy is coded right before the latching algorithm and eventually modifies the latching duration.

Fig. 6

Adaptive latching duration control strategy. Latching duration: $T_\mathrm{L}$; latching duration increment: $\Delta T_\mathrm{L}$

The adaptive strategy is divided in two phases: it first identifies when the period and amplitude are stable, then modifies the latching duration. The steadiness is achieved when the motion period matches the wave period and the amplitude is constant, both within the percentage tolerances set either by the user or by default. Once the transient has elapsed, the stable value of the amplitude is recorded and compared with the last stable value in memory, in order to ascertain whether the last modification of the latching duration increased the stable amplitude. Assuming the convexity of the performance function, similar to Fig. 5, the latching duration is progressively reduced, with a certain step $\Delta T_\mathrm{L}$, as long as the performance improves. Conversely, a worsening happens if the maxima has been exceeded, so the direction of research is inverted and the step is halved to refine the quest.

3.5 Case study

In order to actually show the performance of the latching control algorithm and to highlight the strengths and weaknesses of the CFD implementation, a case study is presented. The CFD simulations are carried out in both 3D and 2D, hence the body is, respectively, a sphere (3D simulations) and a circle (2D simulations) of radius 0.125 m and draft of 0.125 m. The device is constrained to move in the heave direction. The incoming wave is a linear harmonic function with constant amplitude and period in order to clearly show the nonlinear effects and the action of the adaptive latching algorithm. The wave amplitude is 0.015 m, such that the oscillation of the body is comparable to its dimension, highlighting nonlinearities. The wave period is 1.118 s, longer than the natural period of both the sphere and the circle, which are between 0.671 s and 0.894 s, allowing latching to be an effective controller, as explained in 3.1.

A schematic representation of the device within the Numerical Wave Tank is given in Fig. 1. For all the details about the CFD implementation in OpenFOAM, such as the Numerical Wave Tank, the mesh, the solver, the boundary conditions, etc., refer to Davidson et al. (2015a). A more detailed description of the boundary conditions is presented in the appendix. Due to the small characteristic length of the device, the Reynolds number is about $2 \cdot 10^4$ and the flow can be assumed as laminar. This assumption is in agreement with the experiments of Zurkinden et al. (2014) and Bhinder et al. (2011).

Generally, the definition and meshing of the computational domain has the main consequences on the success and quality of the simulation. The most relevant issues related to a controlled floating object are analyzed. The risk of failure due to over-deformation of the cells is particularly important when control is applied, since the numerous big amplitudes of motion caused by the controller stress the whole mesh around the device. On the other hand, the accuracy of the generated waves depends both on the cell dimension at the free surface elevation and on the size of the generation and absorption zones. A rule of thumb is that the generation zone has to be between two and three times the wave length. In the present case study, the wave length is 1.95 m, which means at least 3.9 m for the generation zone. The resulting mesh is presented in Fig. 7. As described in detail by Davidson et al. (2015a), the central region contains a high-density mesh, that horizontally stretches with distance away from the device. Furthermore, the free surface region presents a high-density mesh in the vertical direction. A boundary layer of finer mesh has been added around the floater in order to describe correctly the viscous effects. The thickness of the boundary layer has been determined using the Blasius solution, chapter 9 of Kundu et al. (2011), resulting in a total thickness of 7.6 mm, divided with ten grid points.

Fig. 7

Computational mesh of the numerical wave tank domain. Central region with high-density mesh; free surface region with high vertical density mesh

Doubtless, the biggest impact on the computational load is made by the number of dimensions simulated, namely two or three, where the third dimension is horizontal and perpendicular to the incoming wave direction. The 2D-boundary conditions are such that all the equations are solved within the plane. As a consequence, the equivalent three-dimensional counterpart is a cylinder of infinite length along the third dimension.

In the simulations performed for this paper, in equal hardware conditions, the simulation time required by a 3D simulation is approximately 500 times bigger than its homologous in 2D. In absolute terms, 60 s of 3D simulation typically requires the order of magnitude of several days or weeks of computation. Such a long time makes prohibitive to run a wide range of diverse simulations.

Therefore, the main focus is on the 2D simulations, since the shorter computational time makes possible to change several parameters and analyze the behavior of the control algorithm. Section 4 shows the performances of the constant and adaptive latching duration control applied to the two-dimensional case study. Anyway, one single 3D latching simulation, along with other 2D simulations, has been used in Sect. 5 to draw a comparison against a linear model.

4 Results

The results of the 2D case study are presented. By means of the free decay analysis described in 3.3.2, the instantaneous natural period has been found to range between 0.827 and 0.783 s. A basic constant latching duration control is applied with a latching duration of 0.145 s, corresponding to the nonlinear natural period of 0.827 s. The resulting time series is shown in Fig. 8.

Fig. 8

Constant latching duration control of a circle of radius 0.125 m using a 2D CFD simulation, with regular wave (height: 0.015 m, period: 1.118 s) and latching duration of 0.145 s

The controller is activated after 6.5 s, in order to wait for the wave to arrive and excite steadily the body. When latching is applied, the amplitude increases, reaches a maximum and decreases toward a stable value. The improvement in amplitude achieved by the controller in this case is of the 38 %.

In the steady unlatched condition, the period of motion is the same of the wave. When latching is applied, the period suddenly increases and then is forced to match the excitation period again. Figure 9 shows the decay of the period against the number of peaks after the beginning of the latching.

Fig. 9

Decay of the period of motion of the response in Fig. 8 when latching control is applied. The horizontal axis represents the number of peaks from the beginning of latching

The adaptive latching duration control calculation of Fig. 6 has been applied, initialized with a latching duration of 0.145 s, corresponding to the nonlinear natural period of 0.827 s. After 9 modifications of the latching duration, the resulting optimum point has been identified at 0.1146 s, leading to an increment of amplitude of 49 %. Figure 10 shows the progression of the optimization: the vertical bars indicate the modification steps of the latching duration, while the line graph represents the corresponding stable amplitude achieved. The horizontal axis shows the simulation time when the stable amplitude is reached. Note that, in order to define the latching duration with a four-digit resolution, the simulation time step must be smaller or equal to 0.0005 s.

Fig. 10

Iterations of the adaptive latching duration control algorithm: the horizontal axis represents the simulation time when the stable amplitude is reached and a modification to the latching duration is performed

Fig. 11

Performance curve of latching control using a two-dimensional CFD simulation for a circle of radius 0.125 m

As a first step, the latching duration is decreased, because the nonlinear natural period is longer than the linear. Then, as long as the stable amplitude increases the latching duration is decreased. Conversely, every time the stable amplitude decreases, the research of the optimal latching duration is inverted and refined. The graph in Fig. 10 shows that the optimization algorithm effectively converges.

The foundations of the adaptive algorithm are built on the hypothesis of convexity of the performance curve, assuming the full nonlinear CFD to behave similarly to the linear case shown in Fig. 5. In order to validate such assumption, the performance curve has been reconstructed using several constant latching duration simulations at different latching periods. The results are shown in Fig. 11.

As expected, the performance trend presents an unique peak, occurring for the very same latching period pointed by the adaptive algorithm. Moreover, the optimal latching duration for the CFD fully nonlinear model is smaller than the optimal latching duration for the linear model. The graph highlights the amplitude gained with the linear natural period of 0.783 s, i.e., latching duration of 0.168 s. Finally, the performance achieved with latching duration of 0.145 s is closer to the optimal than to the linear, validating the approach of the instantaneous natural period analysis. Table 1 summaries the amplitudes and percentage improvements obtained with the three choices of latching duration, namely linear natural period, nonlinear instantaneous natural period, optimized latching period with the adaptive algorithm. Table 1 shows that the controller efficiency is quite sensitive to the latching duration, making the physical implementation troublesome. For example, a 15 % relative difference of latching duration between 0.168 and 0.145 s causes a 30 % degradation in efficiency. Previous work has studied the sensitivity to latching duration (Babarit and Clement 2009), which is mainly due to the sharp edges and abrupt modification of the control force. Note that controllers other than latching may implement a similar force characteristic (Bacelli and Ringwood 2015). Implementing the exact latching duration in a real device can be quite difficult due to the delay between the instant when latching is commanded and the instant when the latching system actually locks the device. Various strategies have been tested in order to mitigate such difficulties: Henriques et al. (2012) utilize the threshold unlatching criterion while Durand et al. (2007) advance the latching/unlatching instants to cover the latching system response delay.

Table 1 Latching control performances using a two-dimensional CFD simulation for a circle of radius 0.125 m

Fig. 12

Figure 11 constant latching duration control of a sphere of radius 0.125 m using a linear simulation, with regular wave (height: 0.015 m, period: 0.118 s) and latching duration of 0.205 s

Fig. 13

Figure 12 constant latching duration control of a sphere of radius 0.125 m using a 3D CFD simulation, with regular wave (height: 0.015 m, period: 0.118 s) and latching duration of 0.205 s

5 Discussion

The implementation of latching control in CFD is valuable for being able to include all the nonlinearities and reproduce results more realistic than the linear model ones. Nevertheless, the huge computational cost makes prohibitive an intensive application, especially in an early design stage. On the other side, a more suitable usage can be to provide a benchmark to validate and evaluate the results of linear or partially nonlinear simulation models, eventually defining a range of reliability in which the linear model is acceptable. Indeed, Sect. 5.1 compares the results of a linear model with the outcome of CFD.

5.1 Comparison with linear model

The 3D case study has been simulated in CFD in order to make a comparison with the linear simulation model. The latching duration has been chosen equal to 0.205 s, matching the linear optimal latching duration showed in Fig. 5. The resulting linear and CFD time series are shown, respectively, in Figs. 12 and 13.

The first evident difference is in the transient shape: while the linear simulation shows a monotonic growth towards the steady value, the CFD time series presents an oscillatory behavior with a visible maximum and minimum before stabilizing. When the dynamics elapses, the steady amplitude of motion in CFD is equal to 0.074 m, smaller than the 0.084 m of the linear model. Furthermore, the transient in CFD lasts in about 33 s, 3 times longer than in the linear simulation, which reaches the steady state in less than 11 s. The amplitude transient is linked to a significant period of motion transient, shown in Fig. 14.

Fig. 14

Figure 13 decay of the period of motion of the response in Fig. 13 when latching control is applied. The horizontal axis represents the number of peaks from the beginning of latching

Fig. 15

Figure 14 response amplitude operators of horizontal cylinders with 0.125 m radius and length ranging from 0.25 to 2.5 m

Section 4 showed several two-dimensional results that need to be compared as well. Since the hydrodynamic matrices needed for the linear simulations are computable only for 3D geometries, a direct comparison requires the BEM software to simulate an infinite long cylinder. With a practical point of view, a cylinder is considered infinitely long when a variation of length doesn’t produce a variation of response. Indeed, Fig. 15 shows the asymptotic trend of the response amplitude operator (RAO), which is the transfer function between the surface elevation and the displacement of the body.

Therefore, control has been applied to a long horizontal cylinder of 2.5 m. The relative improvements achieved with respect to the unlatched motion are summarized in Table 2. As in Sect. 3.4 for the sphere, the actual optimal latching duration is smaller than the linear approximation, respectively 0.132 and 0.168 s. The relative difference in latching duration is about 21.3 %, considerably bigger than the 3.8 % of the sphere. The bigger discrepancy is coherent with the higher damping that an infinite long cylinder provides to the system.

Table 2 Comparison between latching performances in linear and CFD simulations

Table 3 Boundary conditions for the 3D numerical wave tank using OpenFOAM 2.3

The presence of viscous losses and nonlinearities causes the CFD improvements to be considerably lower than the linear for every latching duration. The overestimation of the amplitude in the linear model leads to a too optimistic prediction of the power caption under control. Notwithstanding the importance of an accurate prediction of the motion, the key feature to highlight is the different optimal latching duration. While the best linear performance happens at 0.132 s with an improvement of 62 %, the CFD simulation shows a lower improvement of 49 % at a smaller latching duration of 0.1146 s.

As far as the controller is concerned, the main purpose of the simulation model is to reveal the optimal latching duration for the real device. An inaccurate simulation model is not only unable to effectively predict the response, but also points to a latching duration which, even though is optimal for the simulation model, is suboptimal for the real device. Since the CFD model is more accurate than the linear model, the main advantage of having the latching control algorithm implemented in CFD is to indicate a latching duration that suits better the real device.

6 Conclusions

The controller performances and parameters are strictly related to the simulation model and its accuracy. The reliability, as well as the complexity of a model depend on the ability of describing nonlinear behavior. The simplest and computational lightest model is linear, while CFD is able to include all the nonlinearities, at the prize of a huge computational load. The matter of fact is that nonlinearities are magnified by the control, which exaggerates the amplitude of motion and applies abrupt forces directly on the device. While linearization can be acceptable with the uncontrolled device, it becomes an oversimplification when control is applied. Nevertheless, control has never been applied in a CFD environment. In this paper, latching control has been implemented in the CFD open source software OpenFOAM.

The results confirm that founding the latching control on a linear model is misleading and not optimal. Primarily, the amplitudes calculated by the linear model are too optimistic, leading to an overestimation of the power extraction. Moreover, the optimal latching duration pointed out by the linear model is inadequate to maximize the performances of the real device. As a matter of fact, the optimal latching duration depends on the natural period, which is not constant and unique as in the linear approximation. On the contrary, the nonlinear natural period is enlarged by the damping of the system and varies along with the displacement of the device. An optimization tool has been coded in CFD in order to find the actual optimal latching duration, which is smaller than the linear due to the bigger natural period.

Appendix

The boundary conditions of the 3D numerical wave tank are summarized in Table 3. Taking advantage of the symmetry of the problem, only half of the tank is simulated.The names of the boundaries are self-explanatory while the four fields that need to be defined are the phase fraction ($\alpha$), the velocity U, the dynamic pressure ($p_d=\frac{1}{2} \rho \left| U\right| ^2$) and the displacement of the cells (pointDisplacement). The phase fraction $\alpha$ ranges from 0 (only air) to 1 (only water).

The names of the boundaries refer to version 2.3 of OpenFOAM (OpenFOAM 2015). Calling $\Phi$ the general field (either $\alpha$, U, $p_d$ or pointDisplacement), the boundary conditions are the following:

• symmetryPlane: it defines the boundary as a symmetry plane.

• fixedValue (0): it sets $\Phi$ to zero.

• zeroGradient: normal gradient of $\Phi$ is zero.

• waveAlpha: input wave surface elevation determined by waves2Foam (Jacobsen et al. 2012).

• waveVelocity: input wave velocity determined by waves2Foam (Jacobsen et al. 2012).

• inletOutlet: zeroGradient in case of outflow, fixedValue (0) in case of inflow.

• pressureInletOutletVelocity: a zeroGradient condition is applied for outflow while for inflow U is evaluated from the flux.

• totalPressure: total pressure $p_\mathrm{T} = p_0 + \frac{1}{2} \rho \left| U\right| ^2$ is fixed, where $p_0$ is the reference pressure and $\rho$ is the density; when U changes, $p_0$ is adjusted accordingly.

• movingWallVelocity: the normal of the patch value is replaced so that the flux across the patch is zero.

• fixedFluxPressure: the pressure gradient is adjusted such that the flux on the boundary is that specified by the velocity boundary condition.

• calculated: the displacement of the cell is calculated according to the Newton’s second law of dynamics.

In the case of a 2D simulation, which is a one-cell-thick 3D simulation, the boundary condition for every field of the boundary front and back is called empty. As a result, the third dimension will be neglected during the calculations.