1 Introduction

The Material Point Method (MPM) has proven to be successful in solving complex engineering problems that involve large deformations, multi-phase interactions and history-dependent material behaviour. Over the years, MPM has been applied to a wide range of applications, including modelling of failure phenomena in single- and multi-phase media [1, 35, 40], crack growth [14, 20] and snow and ice dynamics [12, 31, 34]. Within MPM, a continuum is discretised by defining a set of Lagrangian particles, called material points, which store all relevant material properties. An Eulerian background grid is adopted on which the equations of motion are solved in every time step. The solution on the background grid is then used to update all material point properties such as displacement, velocity and stress. In this way, MPM incorporates both Eulerian and Lagrangian descriptions. Similarly to other combined Eulerian–Lagrangian techniques, MPM attempts to avoid the numerical difficulties arising from nonlinear convective terms associated with an Eulerian problem formulation, while at the same time preventing grid distortion, typically encountered within mesh-based Lagrangian formulations (e.g. [10, 32]).

Classically, MPM uses piecewise-linear Lagrange basis functions, also known as ‘tent’ functions. However, the gradients of these basis functions are discontinuous at element boundaries. This leads to the so-called grid-crossing errors [2] when material points cross this discontinuity. Grid-crossing errors can significantly influence the quality of the numerical solution and may eventually lead to a lack of convergence (e.g. [28]). Different methods have been developed to mitigate the effect of grid-crossings. For example, the Generalised Interpolation Material Point (GIMP) [2] and Convected Particle Domain Interpolation (CPDI) [25] methods eliminate grid-crossing inaccuracies by introducing an alternative particle representation. The GIMP method represents material points by particle-characteristic functions and reduces to standard MPM, when the Dirac delta function centred at the material point position is selected as the characteristic function. For multivariate cases, a number of versions of the GIMP method are available such as the uniform GIMP (uGIMP) and contiguous-particle GIMP (cpGIMP) methods. The CPDI method extends GIMP in order to accurately capture shear distortion. Much research has been performed to further improve the accuracy of the CPDI approach and increase its range of applicability [16, 22, 26]. On the other hand, the Dual Domain Material Point (DDMP) method [41] preserves the original point-mass representation of the material points, but adjusts the gradients of the basis functions to avoid grid-crossing errors. The DDMP method replaces the gradients of the piecewise-linear Lagrange basis functions in standard MPM by smoother ones. The DDMP method with sub-points [7] proposes an alternative manner for numerical integration within the DDMP algorithm.

The B-spline Material Point Method (BSMPM) [28, 29] solves the problem of grid-crossing errors completely by replacing piecewise-linear Lagrange basis functions with higher-order B-spline basis functions. B-spline and piecewise-linear Lagrange basis functions possess many common properties. For instance, they both satisfy the partition of unity, are non-negative and have a compact support. The main advantage of higher-order B-spline basis functions over piecewise-linear Lagrange basis function is, however, that they have at least \(C^0\)-continuous gradients which preclude grid-crossing errors from the outset. Moreover, spline basis functions are known to provide higher accuracy per degree of freedom as compared to \(C^0\)-finite elements [15]. On structured rectangular grids, adopting B-spline basis functions within MPM not only eliminates grid-crossing errors but also yields higher-order spatial convergence [3, 11, 28, 29, 37]. Previous research also demonstrates that BSMPM is a viable alternative to the GIMP, CPDI and DDMP methods [11, 19, 30, 39]. While the CPDI and DDMP methods can be used on unstructured grids [16, 22, 41], to the best of our knowledge, BSMPM for unstructured grids does not yet exist. This implies that its applicability to real-world problems is limited compared to the CPDI and DDMP methods.

In this paper, we propose an extension of BSMPM to unstructured triangulations to combine the benefits of B-splines with the geometric flexibility of triangular grids. The proposed method employs quadratic Powell–Sabin (PS) splines [23]. These splines are piecewise higher-order polynomials defined on a particular refinement of any given triangulation and are typically used in computer-aided geometric design and approximation theory [9, 18, 24, 27]. PS-splines are \(C^1\)-continuous and hence overcome the grid-crossing issue within MPM by design. We would like to remark that although this paper focuses on PS-splines, other options such as refinable \(C^1\) splines [21] can be used to extend MPM to unstructured triangular grids. The proposed PS-MPM approach is analysed based on several benchmark problems.

The paper is organised as follows. In Sect. 2, the governing equations are provided together with the MPM solution strategy. In Sect. 3, the construction of PS-spline basis functions and their application within MPM is described. In Sect. 4, the obtained numerical results are presented. In Sect. 5, conclusions and recommendation are given.

2 Material Point Method

We will summarise the MPM as introduced by Sulsky et al. [32] to keep this work self-contained. First, the governing equations are presented, afterwards the MPM strategy to solve these equations is introduced.

2.1 Governing equations

The deformation of a continuum is modelled using the conservation of linear momentum and a material model. It should be noted that MPM can be implemented with a variety of material models that either use the rate of deformation (i.e. the symmetric part of the velocity gradient) or the deformation gradient. However, for this study it is sufficient to consider the simple linear-elastic and neo-Hookean models that are based on the deformation gradient. Using the Einstein summation convention, the system of equations in a Lagrangian frame of reference for each direction \(x_k\) is given by

$$\begin{aligned}&\frac{\partial u_k}{\partial t} = v_k, \end{aligned}$$
(1)
$$\begin{aligned}&\rho \frac{\partial v_k}{\partial t} = \frac{\partial \sigma _{kl}}{\partial x_l}+\rho g_k, \end{aligned}$$
(2)
$$\begin{aligned}&D_{kl} = \delta _{kl} + \frac{\partial u_k}{\partial x^0_l},\end{aligned}$$
(3)
$$\begin{aligned}&\sigma _{kl} = {\left\{ \begin{array}{ll} \frac{\lambda }{J} D_{kl} {{\,\mathrm{tr}\,}}\left( E_{kl}\right) + \frac{2\mu }{J} D_{kl}E_{kl} &{} \text {for linear-elastic materials,}\\ \frac{\lambda \ln (J)}{J}\delta _{kl}+\frac{\mu }{J}\left( D_{km}D_{lm} - \delta _{kl} \right) &{} \text {for neo-Hookean materials.} \end{array}\right. } \end{aligned}$$
(4)

where \(u_k\) is the displacement, t is the time, \(v_k\) is the velocity, \(\rho \) is the density, \(g_k\) is the body force, \(D_{kl}\) is the deformation gradient, \(\delta _{kl}\) is the Kronecker delta, \(\sigma _{kl}\) is the stress tensor, \({\varvec{x}}^0\) is the position in the reference configuration, \(\lambda \) is the Lamé constant, \(E_{kl}\) is the strain tensor defined as \(\frac{1}{2}\left( D_{kl} + D_{lk} \right) - \delta _{kl}\), J is the determinant of the deformation gradient and \(\mu \) is the shear modulus. Equations 2 and 4 describe the conservation of linear momentum and the material model, respectively.

Initial conditions are required for the displacement, velocity and stress tensor. The boundary of the domain \(\varOmega \) can be divided into a part with a Dirichlet boundary condition for the displacement and a part with a Neumann boundary condition for the traction:

$$\begin{aligned}&u_k(\varvec{x},t) =U_k(\varvec{x},t)\quad \text {on }\partial \varOmega _u, \end{aligned}$$
(5)
$$\begin{aligned}&\sigma _{kl}(\varvec{x},t)\, n_l = \tau _k(\varvec{x},t)\quad \text {on }\partial \varOmega _\tau , \end{aligned}$$
(6)

where \(\varvec{x} = [\,x_1\,\, x_2\,]^T\) and \(\varvec{n}\) is the unit vector normal to the boundary \(\partial \varOmega \) and pointing outwards. We remark that the domain \(\varOmega \), its boundary \(\partial \varOmega = \partial \varOmega _u\cup \partial \varOmega _\tau \) and the normal unit vector \(\varvec{n}\) may all depend on time.

For solving the equations of motion in the Material Point Method, the conservation of linear momentum in Eq. 2 is needed in its weak form. For the weak form, Eq. 2 is first multiplied by a continuous test function \(\phi \) that vanishes on \(\partial \varOmega _u\) and is subsequently integrated over the domain \(\varOmega \):

$$\begin{aligned} \int _\varOmega \phi \rho a_k \,\mathrm {d}\varOmega =\int _{\varOmega } \phi \frac{\partial \sigma _{kl}}{\partial x_l}\, \mathrm {d}\varOmega + \int _\varOmega \phi \rho g_k \,\mathrm {d}\varOmega , \end{aligned}$$
(7)

in which \(a_k=\frac{\partial v_k}{\partial t}\) is the acceleration. After applying integration by parts, the Gauss integration theorem and splitting the boundary into Dirichlet and Neumann part, the weak formulation becomes

$$\begin{aligned} \int _\varOmega \phi \rho a_k \,\mathrm {d}\varOmega = \int _{\partial \varOmega _\tau } \phi \tau _k\, \mathrm {d}S -\int _\varOmega \frac{\partial \phi }{\partial x_l} \sigma _{kl}\, \mathrm {d}\varOmega + \int _\varOmega \phi \rho g_k \,\mathrm {d}\varOmega , \end{aligned}$$
(8)

whereby the contribution on \(\partial \varOmega _u\) equals zero, as the test function vanishes on this part of the boundary.

2.2 Discretised equations

Equation 8 can be solved using a finite element approach by defining \(n_{\text {bf}}\) basis functions \(\phi _i\) \((i = 1, \dots , n_{\text {bf}})\). The acceleration field \(a_k\) is then discretised as a linear combination of these basis functions:

$$\begin{aligned} a_k(\varvec{x},t) = \sum _{j=1}^{n_{\text {bf}}} \hat{a}_{k,j}\phi _j(\varvec{x}), \end{aligned}$$
(9)

in which \(\hat{a}_{k,j}\) is the time-dependent \(j^{th}\) acceleration coefficient corresponding to basis function \(\phi _j\). Substituting Eq. 9 into Eq. 8 and expanding the test function in terms of the basis functions \(\phi _i\) leads to

$$\begin{aligned}&\int _\varOmega \phi _i\rho \left( \sum _{j=1}^{n_{\text {bf}}} \hat{a}_{k,j}\phi _j\right) \,\mathrm {d}\varOmega \nonumber \\&\quad = \int _{\partial \varOmega _\tau } \phi _i \tau _k\, \mathrm {d}S - \int _\varOmega \frac{\partial \phi _i}{\partial x_l} \sigma _{kl}\, \mathrm {d}\varOmega + \int _\varOmega \phi _i\rho g_k \,\mathrm {d}\varOmega , \end{aligned}$$
(10)

which holds for \(i=1,\dots , n_{\text {bf}}\). By exchanging summation and integration, this can be rewritten in matrix-vector form as follows:

$$\begin{aligned}&\sum _{j=1}^{n_{\text {bf}}}\underbrace{\left( \int _\varOmega \phi _i\rho \phi _j\,\mathrm {d}\varOmega \right) }_{M_{ij}} \hat{a}_{k,j}\nonumber \\&= \underbrace{\int _{\partial \varOmega _\tau } \phi _i \tau _k\, \mathrm {d}S}_{F_{k,i}^\mathrm{trac}} - \underbrace{\int _\varOmega \frac{\partial \phi _i}{\partial x_l} \sigma _{kl}\, \mathrm {d}\varOmega }_{F_{k,i}^\mathrm{int}} + \underbrace{\int _\varOmega \phi _i\rho g_k \,\mathrm {d}\varOmega }_{F_{k,i}^\mathrm{body}}, \end{aligned}$$
(11)
$$\begin{aligned}&\Rightarrow \varvec{M}\varvec{\hat{a}}_{k}= \varvec{F}_k^\mathrm{trac} -\varvec{F}_k^\mathrm{int} +\varvec{F}_k^\mathrm{body}, \end{aligned}$$
(12)

where \(\varvec{M}\) denotes the mass matrix, \(\varvec{\hat{a}}_{k}\) the coefficient vector for the acceleration, while \(\varvec{F}_k^\mathrm{trac}\), \(\varvec{F}_k^\mathrm{int}\) and \(\varvec{F}_k^\mathrm{body}\) denote, respectively, the traction, internal and body force vector in the \(x_k\)-direction. When density, stress and body force are known at time t, the coefficient vector \(\varvec{\hat{a}}_k\) is found from Eq. 12. The properties of the continuum at time \(t+\varDelta t\) can then be determined using the acceleration field at time t.

2.3 Solution procedure

Within MPM, the continuum is discretised by a set of particles that store all its physical properties. At each time step, the particle information is projected onto a background grid, on which the momentum equation is solved. Particle properties and positions are updated according to this solution, as illustrated in Fig. 1.

Fig. 1
figure 1

One time step in the MPM procedure. Projection of particle properties onto the basis functions of the background grid (left). Update of particle properties based on the solution on the background grid (middle). Resetting the grid (right)

Full size image

To solve Eq. 12 at every time step, the integrals in Eq. 11 have to be evaluated. Since the material properties are only known at the particle positions, these positions are used as integration points for the numerical quadrature, and the particle volumes V are adopted as integration weights. Assume that the total number of particles is equal to \(n_p\). Here, subscript p corresponds to particle properties. A superscript t is assigned to particle properties that change over time. The mass matrix and force vectors are then defined by

$$\begin{aligned}&M^t_{ij}= \sum _{p=1}^{n_p} \underbrace{V_p^t \rho _p^t}_{m_p} \phi _i(\varvec{x}_p^t) \phi _j(\varvec{x}_p^t), \end{aligned}$$
(13)
$$\begin{aligned}&F^{\mathrm{trac},t}_{k,i} = \sum _{p=1}^{n_{p}} \phi _i(\varvec{x}_{p}^t)\, f^{\mathrm{trac},t}_{k,p}, \end{aligned}$$
(14)
$$\begin{aligned}&F^{\mathrm{int},t}_{k,i} = \sum _{p=1}^{n_p} V_p^t \frac{\partial \phi _i}{\partial x_m}(\varvec{x}_p^t)\,\sigma _{mk,p}^t \end{aligned}$$
(15)
$$\begin{aligned}&F^{\mathrm{body},t}_{k,i} = \sum _{p=1}^{n_p} \underbrace{V_p^t \rho _p^t}_{m_p} \phi _i(\varvec{x}_p^t) g_k, \end{aligned}$$
(16)

in which \(m_p\) denotes the particle mass, which is set to remain constant over time, guaranteeing conservation of the total mass. The coefficient vector \(\varvec{\hat{a}}_k^t\) at time t for the \(x_k\)-direction is determined by solving

$$\begin{aligned} \varvec{M}^{t}\varvec{\hat{a}}_{k}^t=\left( \varvec{F}_k^{\mathrm{trac},t} -\varvec{F}_k^{\mathrm{int},t} +\varvec{F}_k^{\mathrm{body},t}\right) . \end{aligned}$$
(17)

Unless otherwise stated, Eq. 17 is solved adopting the consistent mass matrix. Next, the reconstructed acceleration field is used to update the particle velocity:

$$\begin{aligned} v_{k,p}^{t+\varDelta t}=v_{k,p}^{t}+\varDelta t \, a_k^t\left( \varvec{x}_p^t\right) = v_{k,p}^{t}+\varDelta t\sum _{j=1}^{n_{\text {bf}}} \hat{a}_{k,j}^{t} \phi _j\left( \varvec{x}_p^t\right) . \end{aligned}$$
(18)

The semi-implicit Euler-Cromer scheme [5] is adopted to update the remaining particle properties. First, the velocity field \(v_k^{t+\varDelta t}\) is discretised as a linear combination of the same basis functions, similar to the acceleration field (Eq. 9):

$$\begin{aligned} v_k^{t+\varDelta t}(\varvec{x})= \sum _{j=1}^{n_{\text {bf}}} \hat{v}_{k,j}^{t+\varDelta t}\phi _j(\varvec{x}), \end{aligned}$$
(19)

in which \(\varvec{\hat{v}}_{k}^{t+\varDelta t}\) is the velocity coefficient vector for the velocity field at time \(t+\varDelta t\) in the \(x_k\)-direction. The coefficient vector \(\varvec{\hat{v}}_{k}^{t+\varDelta t}\) is then determined from a density weighted \(L_2\)-projection onto the basis functions \(\phi _i\). This results in the following system of equations:

$$\begin{aligned} \varvec{M}^t\varvec{\hat{v}}^{t+\varDelta t}_k=\varvec{P}^{t+\varDelta t}_k, \end{aligned}$$
(20)

where \(\varvec{M}^t\) is the same mass matrix as defined in Eq. 13. \(\varvec{P}_{k}^{t+\varDelta t}\) denotes the momentum vector with the coefficients given by

$$\begin{aligned} {P}^{t+\varDelta t}_{k,i} = \sum _{p=1}^{n_p} \underbrace{V_p^t \rho _p^t}_{m_p} v_{k,p}^{t+\varDelta t}\phi _i(\varvec{x}_p). \end{aligned}$$
(21)

Particle properties are subsequently updated in correspondence with Eqs. 1–4. First, the deformation gradient and its determinant are obtained:

$$\begin{aligned} \varvec{D}_{p}^{t+\varDelta t}= & {} \left( \varvec{I}+\varvec{\varepsilon }_{p}^{t+\varDelta t}\varDelta t\right) \varvec{D}_{p}^t, \end{aligned}$$
(22)
$$\begin{aligned} J_p^{t+\varDelta t}= & {} \det (\varvec{D}_p^{t+\varDelta t}). \end{aligned}$$
(23)

Here, \(\varvec{I}\) denotes the identify matrix and \(\varvec{\varepsilon }_{p}^{t+\varDelta t}\) denotes the symmetric part of the velocity gradient:

$$\begin{aligned} \varepsilon _{kl,p}^{t+\varDelta t}= \frac{1}{2}\sum _{j=1}^{{n_{\text {bf}}}}\left( \hat{v}_{k,j}^{t+\varDelta t} \frac{\partial \phi _j}{\partial x_l}(\varvec{x}_p^t)+ \hat{v}_{l,j}^{t+\varDelta t} \frac{\partial \phi _j}{\partial x_k}(\varvec{x}_p^t) \right) . \end{aligned}$$
(24)

For linear-elastic materials, the particle stresses are computed as follows:

$$\begin{aligned} E_{kl,p}^{t+\varDelta t}= & {} \frac{1}{2}\left( D_{kl,p}^{t+\varDelta t}+D_{lk,p}^{t+\varDelta t}\right) - \delta _{kl}, \end{aligned}$$
(25)
$$\begin{aligned} \sigma _{kl,p}^{t+\varDelta t}= & {} \lambda \delta _{kl} {{\,\mathrm{tr}\,}}\left( E_{kl,p}^{t+\varDelta t}\right) + 2\mu E_{kl,p}^{t+\varDelta t}. \end{aligned}$$
(26)

For neo-Hookean materials, the stresses are obtained from

$$\begin{aligned} \sigma _{kl,p}^{t+\varDelta t}= \frac{\lambda \ln (J_p^{t+\varDelta t})}{J_p^{t+\varDelta t}}\delta _{kl} + \frac{\mu }{J_p^{t+\varDelta t}}\left( D_{km,p}^{t+\varDelta t}D_{lm,p}^{t+\varDelta t}-\delta _{kl}\right) . \end{aligned}$$
(27)

The determinant of the deformation gradient is used to update the volume of each particle. Based on this volume, the density is updated in such way that the mass of each particle remains constant:

$$\begin{aligned} V_p^{t+\varDelta t}= & {} J_p^{t+\varDelta t}V_p^0, \end{aligned}$$
(28)
$$\begin{aligned} \rho _p^{t+\varDelta t}= & {} m_p/V_p^{t+\varDelta t}. \end{aligned}$$
(29)

Finally, particle positions and displacements are updated from the velocity field:

$$\begin{aligned} x_{k,p}^{t+\varDelta t}= & {} x_{k,p}^{t} +\varDelta t \sum _{i=1}^{{n_{\text {bf}}}} v_{k,i}^{t+\varDelta t} \phi _i(\varvec{x}_p^t), \end{aligned}$$
(30)
$$\begin{aligned} u_{k,p}^{t+\varDelta t}= & {} u_{k,p}^{t} +\varDelta t \sum _{i=1}^{{n_{\text {bf}}}} v_{k,i}^{t+\varDelta t} \phi _i(\varvec{x}_p^t). \end{aligned}$$
(31)

The described MPM can be numerically implemented by performing the steps in Eqs. 13–31 in each time step in the shown order. Note that all steps can be applied with a variety of basis functions, without any essential difference in the algorithm. In this paper, we investigate the use of Powell–Sabin spline basis functions, which are described in the next section.

Fig. 2
figure 2

A triangular grid (left) and a possible PS-refinement (right). The molecule \(\varOmega _i\) around vertex \(V_i\) is marked grey. (Color figure online)

Full size image
Fig. 3
figure 3

Top left: the PS-points of the middle vertex, marked with red dots, and a possible control triangle containing all PS-points. Other subfigures: the three PS-splines associated with this control triangle. (Color figure online)

Full size image

3 Powell–Sabin spline basis functions

In this section, the construction and essential properties of Powell–Sabin (PS) spline basis functions are summarised. For the full construction process and the proofs of the properties, we refer to the publication by Dierckx [8, 9]. The considered PS-splines are piecewise quadratic splines with global \(C^1\)-continuity. They are defined on arbitrary triangulations, have local support and possess the properties of non-negativity and partition of unity. Several examples of PS-splines are shown in Fig. 3.

3.1 Powell–Sabin grid refinement

To construct PS-splines on an arbitrary triangulation, a Powell–Sabin refinement is required, dividing each of the original main-triangles into six sub-triangles as follows (see also Fig. 2).

  1. 1.

    For each triangle \(t_j\), choose an interior point \(Z_j\) (e.g. the incentre), such that if triangles \(t_j\) and \(t_m\) have a common edge, the line between \(Z_j\) and \(Z_m\) intersects the edge. The intersection point is called \(Z_{jm}\).

  2. 2.

    Connect each \(Z_j\) to the vertices of its triangle \(t_j\) with straight lines.

  3. 3.

    Connect each \(Z_j\) to all edge points \(Z_{jm}\) with straight lines. In case \(t_j\) is a boundary element, connect \(Z_j\) to an arbitrary point on each boundary edge (e.g. the edge middle).

The area consisting of the main-triangles around \(V_i\) is referred to as the molecule \(\varOmega _i\) of \(V_i\) (see Fig. 2). Each PS-spline is associated with a main vertex \(V_i\) and will be defined on the molecule \(\varOmega _i\).

3.2 Control triangles

For each main vertex \(V_i\), the set of PS-points is given by the union of \(V_i\) and the sub-triangle edge midpoints directly around it, see Fig. 3. A control triangle for \(V_i\) is then defined as a triangle that contains all its PS-points. Note that this control triangle is not uniquely defined. However, it preferably has a small area to ensure good stability properties of the resulting PS-splines [8].

A sufficiently good control triangle can be constructed by considering only control triangles with two or three edges shared with the convex hull of the PS-points and taking the one with smallest surface. Further details about the implementation of such an algorithm can be found in [6].

Each control triangle defines three basis functions, all associated with vertex \(V_i\) and the molecule \(\varOmega _i\). Therefore, the basis functions are indexed \(\phi _i^q\) (\(i=1,\dots , n_v,\, q=1,2,3\)), where i indicates the vertex \(V_i\), \(n_v\) the number of vertices and q the local index. Each basis function \(\phi _i^q\) is uniquely defined by a triplet \((\alpha _i^q, \beta _i^q, \gamma _i^q)\), containing the value and gradient of \(\phi _i^q\) in its associated vertex \(V_i\),

$$\begin{aligned} \left( \alpha _{i}^q,\beta _{i}^q,\gamma _{i}^q\right) =\left( \phi _i^q(V_i),\frac{\partial \phi _i^q}{\partial x}(V_i),\frac{\partial \phi _i^q}{\partial y}(V_i)\right) . \end{aligned}$$
(32)

The triplets of the three PS-spline basis functions corresponding to vertex \(V_i\) are determined from the control triangle and the position of \(V_i\). Let the Cartesian coordinates of the control triangle vertices be \(Q_i^1=(X_i^1,Y_i^1)\), \(Q_i^2=(X_i^2,Y_i^2)\) and \(Q_i^3=(X_i^3,Y_i^3)\), and the Cartesian coordinates of \(V_i= (x_i,y_i)\). The three triplets are then determined by solving

$$\begin{aligned} \begin{bmatrix} X^1_i &{}\quad X^2_i &{}\quad X^3_i\\ Y^1_i &{}\quad Y^2_i &{}\quad Y^3_i\\ 1 &{}\quad 1 &{}\quad 1 \end{bmatrix} \begin{bmatrix} \alpha ^1_i &{}\quad \beta ^1_i &{}\quad \gamma ^1_i\\ \alpha ^2_i &{}\quad \beta ^2_i &{}\quad \gamma ^2_i\\ \alpha ^3_i &{}\quad \beta ^3_i &{}\quad \gamma ^3_i \end{bmatrix} =&\begin{bmatrix} x_i &{}\quad 1 &{}\quad 0\\ y_i &{}\quad 0 &{}\quad 1\\ 1 &{}\quad 0 &{}\quad 0 \end{bmatrix}. \end{aligned}$$
(33)

The control triangle has a direct geometric interpretation for the triplet. Solving for the triplet \(\left( \alpha _{i}^q,\beta _{i}^q,\gamma _{i}^q\right) \) of a basis function \(\phi _i^q\) corresponds geometrically to ‘lifting’ up control triangle vertex \(Q_i^q\) of the control triangle in the z-direction to 1, and evaluating the height and gradient of the resulting plane at the location of \(V_i\), as shown Fig. 4.

Fig. 4
figure 4

A control triangle lifted to \(z=1\) in one of its vertices for determining a triplet of a basis function. The location in the lifted plane above the vertex \(V_i\) in the middle is marked with a dot; the value and gradient there correspond to the triplet of the associated basis function

Full size image

3.3 Bernstein–Bézier formulation for quadratic splines

From the triplet \(\left( \alpha _{i}^q,\beta _{i}^q,\gamma _{i}^q\right) \), the PS-spline \(\phi _i^q\) is constructed as a piecewise quadratic polynomial over each sub-triangle in the PS-refinement in barycentric coordinates. Cartesian coordinates (x, y) can be converted to barycentric coordinates \((\eta _1,\eta _2,\eta _3)\) with respect to the considered triangle vertices \((x_1,y_1)\), \((x_2,y_2)\), \((x_3,y_3)\) as follows (see also Fig. 5, left):

$$\begin{aligned} \begin{bmatrix} x_1 &{}\quad x_2 &{}\quad x_3 \\ y_1 &{}\quad y_2 &{}\quad y_3 \\ 1 &{}\quad 1 &{}\quad 1 \end{bmatrix} \begin{bmatrix} \eta _1 \\ \eta _2 \\ \eta _3 \end{bmatrix} = \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}. \end{aligned}$$
(34)
Fig. 5
figure 5

Barycentric coordinates with respect to the sub-triangle vertices (left) and the Bézier ordinates of a quadratic polynomial \(b(\varvec{\eta })\) (right), schematically represented at the same location

Full size image
Fig. 6
figure 6

The molecule around a vertex \(V_i\) (left) and one of the main-triangles in the molecule (right). The locations of the middle vertex Z and the edge vertices R are marked with respect to the vertices \(v_1\), \(v_2\) and \(v_3\). \(v_1(=V_i)\) is also marked with the barycentric coordinates with respect to the control triangle

Full size image

Next, we define 6 quadratic Bernstein polynomials \(B_{i,j,k}\) for each sub-triangle in barycentric coordinates,

$$\begin{aligned}&B_{i,j,k}(\varvec{\eta }) = \frac{2!}{i!j!k!}\eta _1^i\eta _2^j\eta _3^k, \text {with } i,j,k\in \{0,1,2\},\nonumber \\&\text {and}\,\, i+j+k=2, \end{aligned}$$
(35)

which are non-negative and form a partition of unity. Any desired quadratic polynomial \(b(\varvec{\eta })\) can be uniquely constructed as a linear combination of the 6 quadratic Bernstein polynomials \(B_{i,j,k}\) over a sub-triangle,

$$\begin{aligned} b(\varvec{\eta })=\sum _{\begin{array}{c} i+j+k=2,\\ i,j,k\in \{0,1,2\} \end{array}}b_{i,j,k}B_{i,j,k}(\varvec{\eta }), \end{aligned}$$
(36)

where \(b_{i,j,k}\) are called the Bézier ordinates. The desired quadratic polynomial can thus be fully defined by its Bézier ordinates, which can be schematically represented by associating Bézier ordinate \(b_{i,j,k}\) with barycentric coordinates \(\left( \tfrac{i}{2},\tfrac{j}{2},\tfrac{k}{2}\right) \), as shown in Fig. 5.

3.4 Construction of PS-splines

Next, consider the molecule \(\varOmega _i\) around a vertex \(V_i\) and one of the main-triangles \(t_j\) in the molecule, as depicted in Fig. 6. The grey main-triangle has been divided into 6 sub-triangles in the PS-refinement. In each of the sub-triangles, the 6 locations with barycentric coordinates \(\left( \tfrac{i}{2},\tfrac{j}{2},\tfrac{k}{2}\right) ,\,i+j+k=2,\, i,j,k\in \{0,1,2\}\) have been marked. Denote the vertices of the main-triangle by \(v_1\), \(v_2\) and \(v_3\), with \(v_1\) \((=V_i)\) the middle vertex of the considered molecule, and \(v_2\) and \(v_3\) be indexed counter-clockwise. Let the centre vertex, Z, of the grey triangle has barycentric coordinates \(Z=(a,b,c)\) with respect to vertices \(v_1\), \(v_2\) and \(v_3\). Furthermore, let the edge vertices R have barycentric coordinates \(R_{12}=(\lambda _1,\lambda _2,0)\), \(R_{23}=(0,\mu _2,\mu _3)\) and \(R_{13}=(\nu _1,0,\nu _3)\) with respect to \(v_1\), \(v_2\) and \(v_3\), as denoted in Fig. 6. Finally, let \(v_1\) have barycentric coordinates \(v_1=(\alpha _i^1,\alpha _i^2,\alpha _i^3)\) with respect to the control triangle vertices \(Q_i^1\), \(Q_i^2\) and \(Q_i^3\). These values of \(\alpha \) also correspond to the first values of the three triplets of the basis functions associated with this molecule, see Equation (33).

Finally, the three basis function \(\phi _i^q,\, q=1,2,3\), associated with vertex \(V_i\), are defined by their Bézier ordinates on each of the sub-triangles within the molecule of \(V_i\). The Bézier ordinates of a basis function \(\phi _i^q\) are shown in Fig. 7. The coefficients in the figure are given in terms of the triplet \((\alpha ,\beta ,\gamma )=(\alpha _i^q,\beta _i^q,\gamma _i^q)\) of the considered basis function \(\phi _i^q\) and the barycentric coordinates of \(Z=(a,b,c)\), \(R_{12}=(\lambda _1,\lambda _2,0)\), \(R_{13}=(\nu _1,0,\nu _3)\), and the Cartesian coordinates of the considered triangle \(v_1=(x_1,y_1)\), \(v_2=(x_2,y_2)\) and \(v_3=(x_3,y_3)\) as follows,

$$\begin{aligned}&L=\,\alpha +\frac{1-\lambda _1}{2}\overline{\beta },\nonumber \\&L'=\,\alpha +\frac{1-\nu _1}{2}\overline{\gamma }, \nonumber \\&\tilde{L}=\,\alpha +\frac{b}{2}\overline{\beta }+\frac{c}{2}\overline{\gamma }, \end{aligned}$$
(37)

with

$$\begin{aligned} \overline{\beta }= & {} \beta (x_2-x_1)+\gamma (y_2-y_1) \quad \text {and}\nonumber \\ \overline{\gamma }= & {} \beta (x_3-x_1)+\gamma (y_3-y_1). \end{aligned}$$
(38)

The resulting PS-splines corresponding to the shown control triangle of vertex \(V_i\) are shown on the associated molecule in Fig. 3.

Fig. 7
figure 7

The Bézier ordinates for basis function \(\phi _i^1\), corresponding to the vertex \(V_i\) considered in Fig. 6. There are three different basis functions, note that for each of these basis functions, \(\alpha \), \(\beta \) and \(\gamma \) should correspond with the triplet \((\alpha ^q,\beta ^q,\gamma ^q)\) corresponding to PS-triangle vertex \(Q_q\)

Full size image

3.5 Projecting on PS-splines and lumping within PS-MPM

In this section, we show by numerical experiments that the projection on PS-splines leads to third-order spatial convergence in the \(L_2\)-error between an analytic function and its projection. Furthermore, we also investigate the effect of performing a projection on PS-splines using a lumped variant of the mass matrix instead of the consistent one. Lumping of the mass matrix is often used in MPM with piecewise-linear basis functions, but we will show that lumping is less suitable for MPM with PS-spline basis function when no special measures are taken.

We consider the projection of a two-dimensional sine function onto a basis of PS-splines, using a consistent and a lumped mass matrix, respectively. The results are also compared with a projection onto a basis of piecewise-linear basis functions. We project the function \(f=\sin (x/\pi )\sin (y/\pi )\) on the unit square onto a basis of PS-splines using a standard \(L_2\)-projection:

$$\begin{aligned}&\hat{f}(x,y) = \sum _{j=1}^{n_{\text {bf}}}c_j\phi _j(x,y);\nonumber \\&\sum _{j=1}^{n_{\text {bf}}}\underbrace{\left( \int _\varOmega \phi _i\phi _j\,\mathrm {d}\varOmega \right) }_{M_{ij}} c_j= \underbrace{\int _\varOmega \phi _i f \,\mathrm {d}\varOmega }_{b_i}. \end{aligned}$$
(39)

The entries of the mass matrix \(\varvec{M}\) and the right-hand side \(\varvec{b}\) are evaluated using high-order Gauss integration such that the integration error is insignificant. Finally, we may obtain the projection \(\hat{f}\) by either solving \(\varvec{M}\varvec{c}=\varvec{b}\) consistently, or by using the lumped mass matrix, \(b_i = c_i/\tilde{M}_{ii}\), in which the lumped mass matrix \(\varvec{\tilde{M}}\) has been created by lumping all the mass of each row onto its diagonal element, \(\tilde{M}_{ii}=\sum _{j=1}^{n_{\text {bf}}}M_{ij}\), \(\tilde{M}_{ij}= 0\) for \(i\ne j\). A basis of PS-splines, and of piecewise-linear functions were adopted, respectively, both defined on a structured triangulation.

Fig. 8
figure 8

Error in the function value (left) and x-derivative (right) when projecting onto a basis of PS-splines (PS) and piecewise-linear functions (PL), using a consistent (cons.) and a lumped mass matrix

Full size image
Fig. 9
figure 9

The vibrating bar benchmark (top) and the initial particle configuration (bottom)

Full size image

Figure 8 shows the \(L_2\)-error in the function value and x-derivative for various refinements of the grid. When using a consistent mass matrix, the expected orders of convergence are obtained for piecewise-linear basis functions and PS-spline basis functions, both in the function value and the x-derivative. The use of a lumped mass matrix leads to a first-order accurate approximation of the function value for both types of basis functions. However, the x-derivative does not converge at all when adopting a lumped mass matrix within a PS-spline basis. As the gradient of the reconstructed field is often used in MPM (e.g. Eq. 24), lumping within PS-MPM will often lead to spatial oscillations as will be shown in more detail in Sect. 4.3.

4 Numerical results

To validate the proposed PS-MPM, several benchmarks involving large deformations are considered. The first benchmark describes a thin vibrating bar, where the displacement is caused by an initial velocity field. For this benchmark, PS-MPM on a structured triangular grid is compared with a reference solution. A second benchmark considers a unit square undergoing axis-aligned displacement with known analytical solution. The spatial convergence of PS-MPM on an unstructured grid is determined for this benchmark. The third benchmark describes a solid column under self-weight. In this benchmark, we investigate the use of a lumped mass matrix in PS-MPM to stabilise the simulation when part of the original domain becomes empty. We will show that a fully lumped mass matrix within PS-MPM leads to spatial oscillations, as expected from Sect. 3.5. Instead, we propose the use of a partially lumped mass matrix to mitigate these oscillations. Throughout this section, coordinates in the current configuration are denoted by (x, y) and in the reference configuration by \((x^0,y^0)\).

4.1 Vibrating bar

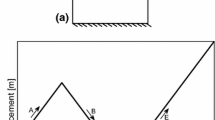
In this section, a thin linear-elastic vibrating bar is considered with both ends fixed. A one-dimensional UL-FEM [36] solution on a very fine grid serves as reference. The grid used for PS-MPM and the initial particle positions are shown in Fig. 9.

The bar is modelled with density \(\rho =25\,{\mathrm{kg/m}}^3\), Young’s modulus \(E=50\,{\mathrm{Pa}}\), Poisson ratio \(\nu = 0\), length \(L=1\, {\mathrm{m}}\), width \(W=0.05\,{\mathrm{m}}\) and initial maximum velocity of \(0.1\,{\mathrm{m/s}}\). The chosen parameters result in a maximum normal strain in the x-direction of approximately \(7\%\). At the left and right boundary, homogeneous Dirichlet boundary conditions are imposed for both x- and y-displacement, whereas at the top and bottom boundary, a homogeneous Dirichlet boundary condition is imposed only for the y-displacement, and a free-slip boundary condition for the x-direction. The initial displacement equals zero, but an initial x-velocity profile is set to \(v_x(x^0,y^0) = 0.1\sin (x^0\pi /L)\). The initial y-velocity is equal to zero.

The time step size for the simulation is \(\varDelta t = 5\cdot 10^{-3}\) s. The Courant number for two-dimensional problems is defined as \(C = \tfrac{2\varDelta t}{h}\sqrt{E/\rho }\), in which h is the typical element length, and \(\sqrt{E/\rho }\) is the characteristic wave speed. Due to the ambiguity of h for a PS-refinement on an unstructured triangular grid, we estimate the average edge length of the sub-triangles by \(h\approx 0.025\) m. In this case, the Courant number is \(C\approx 0.56< 1\), satisfying the CFL condition [4].

Fig. 10
figure 10

Displacement of the particle initially positioned at \((x^0,y^0) \approx (0.5\) m, 0.025 m) over time (left) and the stress component \(\sigma _{xx}\) along the bar at \(t=2.5\) s (right)

Full size image

Figure 10 shows the displacement in the middle of the bar over time and the stress profile through the entire bar at the end of the simulation. Although a relatively coarse PS-MPM grid and few particle are used, the method yields accurate results and a smooth stress profile.

Fig. 11
figure 11

Energy in the vibrating bar with large deformations (above), and for small deformations (below). Both are compared with a sampled reference solution

Full size image

In case of small and large deformations, the energy in the system over time is shown in Fig. 11. Results for small deformations have been obtained by setting the initial maximum velocity equal to \(0.001\, {\mathrm{m/s}}\). In the limit of small deformations, the PS-MPM solution is described exactly by a harmonic oscillator, and the simulation with small deformations is indeed in good agreement with the (sampled) exact solution. For large deformations, however, the solution is no longer perfectly periodic. Nonetheless, the energy over time obtained with PS-MPM strongly resembles the UL-FEM reference solution. Only after 7 s, the PS-MPM simulation shows oscillations in the energy which are not present with UL-FEM. A visible decay in total energy due to numerical dissipation is only observed for simulation times larger than 15 s.

4.2 Axis-aligned displacement on an unstructured grid

In this section, we consider two-dimensional axis-aligned displacement on the unit square (\(L \times W\), with \(L=W=1\) m) to investigate the grid-crossing error and spatial convergence of PS-MPM on an unstructured grid. An analytical solution for this problem is constructed using the method of manufactured solutions: the analytical solution is assumed a priori, and the corresponding body force is calculated accordingly. This benchmark has been adopted from [25] and [38]. The analytical solution for the displacement in terms of the reference configuration is given by

$$\begin{aligned} u_x= & {} u^0\sin \left( 2\pi x^0\right) \sin \left( \sqrt{E/\rho ^0}\,\pi t\right) , \end{aligned}$$
(40)
$$\begin{aligned} u_y= & {} u^0\sin \left( 2\pi y^0\right) \sin \left( \sqrt{E/\rho ^0}\,\pi t+\pi \right) . \end{aligned}$$
(41)

Here, \(\rho ^0=10^3\,{\mathrm{kg/m}}^3\), \(u^0 =0.05\,{\mathrm{m}}\) and Young’s modulus \(E=10^7\,{\mathrm{Pa}}\). The corresponding body forces [25] are

$$\begin{aligned} g_x= & {} \pi ^2 u_x\left( \frac{4\mu }{\rho ^0}-\frac{E}{\rho ^0}-4\frac{\lambda \left[ \ln (D_{xx}D_{yy})-1\right] -\mu }{\rho ^0 D_{xx}^2}\right) , \nonumber \\\end{aligned}$$
(42)
$$\begin{aligned} g_y= & {} \pi ^2 u_y\left( \frac{4\mu }{\rho ^0}-\frac{E}{\rho ^0}-4\frac{\lambda \left[ \ln (D_{xx}D_{yy})-1\right] -\mu }{\rho ^0 D_{yy}^2}\right) ,\nonumber \\ \end{aligned}$$
(43)

in which the Lamé constant \(\lambda \), the shear modulus \(\mu \) and the normal components of the deformation gradient \(D_{xx}\) and \(D_{yy}\) are defined as

$$\begin{aligned}&\lambda = \frac{E\nu }{(1+\nu )(1-2\nu )},\quad \quad \mu = \frac{E}{2(1+\nu )}, \end{aligned}$$
(44)
$$\begin{aligned}&D_{xx} = 1+2u^0\pi \cos (2\pi x^0)\sin \left( \sqrt{E/\rho ^0}\,\pi t\right) , \end{aligned}$$
(45)
$$\begin{aligned}&D_{yy} = 1+2u^0\pi \cos (2\pi y^0)\sin \left( \sqrt{E/\rho ^0}\,\pi t+\pi \right) . \end{aligned}$$
(46)

Here, \(\nu = 0.3\) and all solutions are again given with respect to the reference configuration.

Fig. 12
figure 12

The exact solution in which particles (marked with dots) move back and forth along the marked vectors (left) and the unstructured grid with the initial particle configuration (right)

Full size image
Fig. 13
figure 13

The interpolated particle stress in the x-direction at \(t=0.016\)s

Full size image

This benchmark was simulated with standard MPM and PS-MPM, using an unstructured triangular grid with material points initialised uniformly over the domain, as shown in Fig. 12. A time step size of \(\varDelta t = 2.25 \cdot 10^{-4}\) s was chosen, which results in a Courant number of \(C\approx 0.72\). For the adopted parameters, the imposed solution in Eqs. 40–41 has period \(T=0.02\) s.

4.2.1 Grid-crossing error

First, it is shown that the grid-crossing error typical for standard MPM does not occur in PS-MPM, by comparing the normal horizontal stress resulting from these methods (see Fig. 13). The configurations for PS-MPM and standard MPM contain the same number of particles (5120, 4 times as many as in Fig. 12) and a comparable number of basis functions, 289 for standard MPM and 243 for PS-MPM. As expected, the stress field in standard MPM suffers severely from grid-crossing, whereas with PS-MPM a smooth stress field is observed. The same conclusion can also be drawn when investigating individual particle stresses over time, as is shown in Fig. 14. For this figure, the particle positioned at \((x^0,y^0)\approx (0.25\) m,0.47 m) has been traced throughout the simulation. The figure depicts the stress and trajectory of the particle. For standard MPM, it is observed that the stress profile is highly oscillatory, resulting in a disturbed trajectory. PS-MPM shows no oscillations, but only a small offset, which was found to disappear upon further refinement of the grid.

Fig. 14
figure 14

The stress (left) and movement (right) of a single particle over time (in seconds) for both standard MPM and PS-MPM compared to the exact solution

Full size image

4.2.2 Spatial convergence

PS-MPM with quadratic basis functions is expected to show third-order spatial convergence. To determine the spatial convergence, the time averaged root-mean-squared (RMS) error is used:

$$\begin{aligned} \text {RMS-error} = \sqrt{\frac{\sum _{i=1}^{n_t}\sum _{p=1}^{n_p} |x_p(t_i)-\hat{x}_p(t_i)|^2}{n_p n_t}}, \end{aligned}$$
(47)

where \(n_t\) denotes the total number of time steps of the simulation. Under the assumption that the spatial error is much larger than the error produced by the numerical integration and time-stepping scheme, the spatial convergence of standard MPM and PS-MPM is determined by varying the typical element length h. This length was defined as the average edge length for standard MPM and the average sub-triangle edge length for PS-MPM. It has been observed that the time-integration error is indeed sufficiently small, but the number of particles required for an adequately accurate integration increases rapidly as h decreases.

Fig. 15
figure 15

Spatial convergence (top) and convergence in the number of particles per element (ppe) (bottom) for both standard MPM (left) and PS-MPM (right)

Full size image

Figure 15 shows the spatial convergence of both standard MPM and PS-MPM for different numbers of particles per element on an unstructured grid. Provided that a sufficient number of particles is adopted, standard MPM shows second-order spatial convergence, and PS-MPM converges with third order. Both orders of convergence correspond to the order of the projection-error, as shown in Sect. 3.5. Besides higher-order spatial convergence, PS-MPM also results in a smaller RMS-error compared to standard MPM, even for the coarsest grid.

To achieve the optimal convergence order for both standard MPM and PS-MPM, the number of integration particles required increases rapidly, as the integration error otherwise dominates the total error, as shown in Fig. 15. Note that the convergence rate in the number of particles for both standard MPM and PS-MPM is measured to be of first order. However, for a fixed typical element length h and number of particles per element, the use of PS-MPM leads to a lower RMS-error, illustrating the higher accuracy per degree of freedom. The inaccurate integration in MPM due to the use of particles as integration points is known to limit the spatial convergence. Different measures have been proposed to decrease the quadrature error in MPM based on function reconstruction techniques like MLS [13], cubic splines [37] and Taylor least squares [39]. The combination of PS-MPM with function reconstruction techniques to obtain optimal convergence rates with a moderate number of particles is subject to future research to further improve PS-MPM for practical applications.

4.3 Column under self-weight

In the previous examples, we considered PS-MPM with a consistent mass matrix. However, lumping of the mass matrix is common practice in many applications of MPM, as it speeds up the simulation and increases the numerical stability. In case elements become (almost) empty, the consistent mass matrix in Eq. 13 has very small entries and becomes ill-conditioned, leading to stability issues, which is a well-known phenomena in MPM [32]. Using a lumped version of the mass matrix to solve for the acceleration and velocity fields is known to overcome the ill-conditioning [32]. However, as explained in Sect. 3.5, lumping within PS-splines can cause spatial oscillations. We show that this is indeed the case and propose an alternative based to lumping to overcome the ill-conditioning of the mass matrix while mitigating spatial oscillations as much as possible.

First, we demonstrate that the standard lumping technique is poorly suited for PS-MPM, by considering a solid column under self-weight, as shown in Fig. 16. The column in this exemplary benchmark is modelled as a linear-elastic material. It is fixed in all directions at the bottom, and completely free at the top. At the left and right boundary, we impose a free-slip boundary condition for movement in the y-direction, but the displacement in the x-direction is fixed to be zero. The column is compressed by gravity due to its self-weight.

Fig. 16
figure 16

The column and a discretisation with the expected material point positions at \(t=0\) and \(t=0.186\)

Full size image

The solid column is modelled with density \(\rho =1\cdot 10^3\,{\mathrm{kg/m}}^3\), Young’s modulus \(E=1\cdot 10^5\,{\mathrm{Pa}}\), Poisson ratio \(\nu =0\), gravitational acceleration \(g=-9.81\, {\mathrm{m/s}}^2\), height \(H=1\,{\mathrm{m}}\) and width \(W=0.1\,{\mathrm{m}}\). The maximum strain when adopting these parameters is approximately \(18\%\). Figure 16 illustrates the grid considered for this benchmark as well as the particle positions at maximal deformation.

Due to the fact that part of the grid becomes empty, the use of a consistent mass matrix leads to stability issues with unlumped PS-MPM. The use of a lumped mass matrix within PS-MPM restores the stability, but causes spatial oscillations in the stress profile, as was also discussed in Sect. 3.5. The oscillations degrade the solution of the displacement and velocity as well, as shown in Fig. 17 (left column). Since these spatial oscillations are typical for lumped PS-MPM, common remedies to solve problems due to lumping the mass matrix, like the momentum formulation method [33] or distribution coefficient method [17], do not reduce the spatial oscillations in lumped PS-MPM. Instead, we propose the use of partial lumping.

Fig. 17
figure 17

A comparison of fully lumped PS-MPM (left) and partially lumped PS-MPM (right) for simulation of a solid column up to \(t=2.5\) s. For the energy graphs, \(E_{kin}\) denotes kinetic energy, \(E_{pot}\) the potential energy due to strain, \(E_{grav}\) the gravitational energy and \(E_{tot}\) the total energy

Full size image

4.3.1 Partial lumping to mitigate spatial oscillations

As full lumping within PS-MPM causes spatial oscillations, we will instead consider a partial-lumping approach to overcome the stability issues due to almost empty elements, while at the same time minimising spatial oscillations due to lumping. Partial lumping only lumps those rows responsible for the ill-conditioning. These rows typically correspond to the basis functions in the part of the grid where very few particles are left. By only lumping these few rows, the simulation is stabilised, while introducing a much smaller lumping error compared to full lumping. Note that the choice of rows to lump is crucial to ensure stability. Lumping more rows increases the robustness of the simulation, but decreases the accuracy. The trade-off between stability and accuracy within partially lumped PS-MPM should be reconsidered for each benchmark.

Fig. 18
figure 18

The equilibrium stress at individual particles in a damped solid column. The numerical solutions were determined with fully lumped and partially lumped PS-MPM at \(t=10\) s, at which the solution was in equilibrium

Full size image

For the column under self-weight, we implemented partial lumping by lumping all rows corresponding to a basis function with at least one empty main-triangle in its molecule. Additional empty elements are added at the top of the column, to ensure that the top-most basis functions are always lumped. Figure 17 (right column) shows the displacement and velocity of a particle over time, as well as the stress profile at \(t=2.5\) s obtained with partially lumped PS-MPM. Compared to the results obtained with fully lumped PS-MPM, shown in Fig. 17 (left), the stress profile, the velocity and displacement over time significantly improve. Furthermore, the total energy fluctuates less for partially lumped PS-MPM than for fully lumped PS-MPM and also shows less numerical dissipation. However, for very long simulations, partially lumped PS-MPM requires smaller time steps than fully lumped PS-MPM in order to remain stable.

Finally, we compared the equilibrium solution for the stress profile in the solid column with partial and full lumping. The analytical equilibrium solution is given by [41]:

$$\begin{aligned} \sigma _{yy}(y^{eq}) = \sigma _{yy}(0) \frac{(1-y^{eq}/H)+\kappa (y^{eq}/H)}{1-\kappa (1-\kappa )(y^{eq}/H)}, \end{aligned}$$
(48)

where \(y^{eq}\) refers to the equilibrium position of the particles. Furthermore, \(\sigma _{yy}(0) = H\rho g\) and \(\kappa = \frac{\sigma _{yy}(0)}{2E}\). To obtain the static solution based on the dynamic calculations, a damping term has been added:

$$\begin{aligned} \varvec{F}^\mathrm{damp}_k = -\alpha \, \text {sign}(\varvec{\hat{v}}_k) \left( \varvec{F}_k^\mathrm{trac} -\varvec{F}_k^\mathrm{int} +\varvec{F}_k^\mathrm{body}\right) \end{aligned}$$
(49)

where, \(\alpha = 0.6\). The damping force damps the PS-MPM solution at each time step in the opposite direction of the velocity field. The equilibrium solution has then been determined by simulating the system with both fully lumped and partially lumped PS-MPM until a stable solution was reached. Both the analytical and numerical static solutions are shown in Fig. 18. For fully lumped PS-MPM, the spatial oscillations in the stress profile remain visible in the equilibrium solution. However, the stress profile of partially lumped PS-MPM is in close agreement with the exact solution.

Hence, the use of partial lumping within PS-MPM combines the advantages of adopting a consistent and lumped mass matrix, while minimising their drawbacks, and thereby improves the overall performance of the method. Future research will focus on techniques to further mitigate or fully overcome the oscillations caused by lumping, in particular when PS-MPM is applied for practical problems.

5 Conclusion

In this paper, we presented an alternative for B-spline MPM suited for unstructured triangulations using piecewise quadratic \(C^1\)-continuous Powell–Sabin spline basis functions. The method combines the benefits of smooth, higher-order basis functions with the geometric flexibility of an unstructured triangular grid. PS-MPM yields a mathematically sound approach to eliminate grid-crossing errors, due to the smooth gradients of the basis functions. As a first validation, a vibrating bar was considered, for which the PS-MPM solution yields accurate results on a relatively coarse grid. Numerical simulations obtained for a unit square undergoing axis-aligned displacement have shown higher-order convergence for the particle stresses and displacements.

The use of a lumped mass matrix to increase stability within PS-MPM leads to spatial oscillations in the stress profile. A partial lumping strategy was proposed to combine the advantages of adopting a consistent and lumped mass matrix, which successfully mitigates this issue. Investigation of alternative unstructured spline technologies, in particular, refinable \(C^1\) splines on irregular quadrilateral grids [21] is underway.