Small-signal stability analysis of photovoltaic generation connected to weak AC grid

Abstract

A small-signal model of photovoltaic (PV) generation connected to weak AC grid is established based on a detailed model of the structure and connection of a PV generation system. An eigenvalue analysis is then employed to study the stability of PV generation for different grid strengths and control parameters in a phase-locked loop (PLL) controller in the voltage source converter. The transfer function of the power control loop in the dq rotation frame is developed to reveal the influence mechanism of PLL gains on the small-signal stability of PV generation. The results can be summarized as follows: ① oscillation phenomena at a frequency of about 5 Hz may occur when the grid strength is low; ② the tuning control parameters of the PLL have a noticeable effect on the damping characteristics of the system, and larger proportional gain can improve the system damping;③ within a frequency range of 4-5 Hz, the PLL controller has positive feedback on the power loop of PV generation. A virtual inductance control strategy is proposed to improve the operational stability of PV generation. Finally, a simulation model of PV generation connected to weak AC grid is built in PSCAD/EMTDC and the simulation results are used to validate the analysis.

1 Introduction

Photovoltaic (PV) generation is an important way to address the environmental challenges of generating electricity from fossil fuels. Due to restricted availability of land and the quality of the solar resource, large-scale PV generation systems in China are mostly located in deserts or semi-deserts where the grid structure is relatively weak, and they are integrated into power systems through voltage source converters (VSCs).

Grid impedance, as an indicator of a weak grid, becomes increasingly important with the increasing capacity of grid-connected PV generation [1, 2]. Output power disturbance of the PV array and grid disturbance will affect the point of common coupling (PCC) voltage and make it unstable. An unstable PCC voltage subsequently affects the dynamics of the VSC control system, and the design of the VSC control system based on the ideal grid conditions is no longer suitable [3, 4]. Therefore, this situation poses challenges to both the control and safe operation of PV generation.

The stability of PV generation connected to a weak grid has been investigated in several works [5,6,7,8,9,10,11,12,13]. The authors in [7, 8] proposed an impedance model of a VSC, which was useful for control dynamics and stability studies. Reference [10] established an equivalent VSC that models the N-paralleled grid-connected VSCs in PV plants and described the coupling effect due to grid impedance. However, this study ignored the impact of the control strategy. Reference [11] proposed a small-signal model to analyze the stability of DC-link voltage control in the VSC, but it did not consider the impacts of other control loops. References [12, 13] pointed out that the instability phenomenon is related to converter control loops such as the phase-locked loop (PLL) controller and the AC terminal controller.

To avoid instabilities caused by the influence of the weak AC grid, [14] decreased the PLL bandwidth to prevent its interaction with other modes of the system and slow it down, [15] changed the parameters of the AC terminal control loop to speed it up. Although the system remained stable according to these methods, the performance of the VSC was very poor. Reference [16] proposed an artificial bus for VSC synchronization, which was equivalent to reducing the grid impedance. However, the method could not perfectly emulate a physical inductance and it may be sensitive to noise.

In contrast to previous research, this paper proposes a small-signal model of PV generation connected to a weak AC grid. An eigenvalue analysis is employed to study the stability of PV generation for different grid strengths and control parameters in the PLL controller. In order to improve the operational stability of PV generation, a virtual inductance control strategy is proposed based on [16]. The main contributions of this paper are as follows.

• 1) A thorough analysis of the dynamics of PV generation connected to a weak grid, and the impacts of the controller parameters on the overall system stability.

• 2) An understanding of the influence mechanism of the PLL control parameters on the small-signal stability of PV generation, based on the transfer function of the power control loops in the dq rotation frame.

• 3) The development of a virtual inductance control strategy to stabilize the performance of PV generation in weak AC grid conditions.

The paper is structured as follows. In Section 2, the configuration of PV generation connected to a weak AC grid is described. Section 3 establishes a small-signal model of PV generation connected to a weak AC grid, including PV array, VSC and grid models. The eigenvalue analysis is presented in Section 4. A virtual inductance control strategy is proposed in Section 5. Section 6 describes case studies of PV generation with the proposed control strategy connected to a weak AC grid. The conclusions are presented in Section 7 to close the paper.

2 Configuration of PV generation connected to weak AC grid

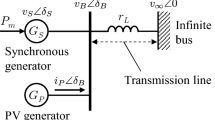
Large-scale PV generation systems are usually far away from load centers and the PV power has to be sent to the main power grid using long distance transmission. When the impedance of the transmission line is significant, the PV generation may be considered to be connected to a weak grid. A simplified but representative model of such a system is shown in Fig. 1 and is used for this study. It has a PV generation system (P₁), a local transmission system (P₂), a long distance transmission system (P₃) and an equivalent circuit of the main grid (P₄).

Fig. 1

Configuration of PV generation connected to a weak AC grid

In Fig. 1, C is the input filter capacitance; U_dc is the DC voltage; L_f is the output filter inductance; C_f is the output filter capacitance; R₁ and L₁ are the resistance and inductance of the local transmission system, respectively; R₂ and L₂ are the resistance and inductance of the long distance transmission system; R_g and X_g are the equivalent resistance and equivalent reactance of the grid; U_t and $\theta_{t}$ are the PCC voltage and its phase; Z_g is the grid impedance; and U_g is the grid voltage. In order to simplify the analysis, the above parameters are referred to the output side voltage level of the VSC.

In Fig. 1, the strength of the AC system is generally described by a short-circuit ratio (SCR), as defined in (1). The AC system is regarded as a weak grid when the R_SCR is lower than 3. From (1), it can be found that the R_SCR decreases with increasing grid impedance.

$$R_{\text{SCR}} = \frac{{S_{ac} }}{{S_{{\rm N}} }} = \frac{{U_{g}^{2} }}{{Z_{g} S_{\text{N}} }}$$

(1)

where S_ac is the short-circuit capacity of the AC system; S_N is the rated power of the PV generation.

In order to simplify the stability analysis of PV generation connected to a weak AC grid, the following assumptions are made:

• 1) The effect of the output filter capacitor C_f is neglected. The AC capacitor in the VSC is responsible for filtering high-frequency harmonics, and this paper focuses on the low-frequency band.

• 2) The effect of the grid resistance R_g is neglected. The resistance of the grid is smaller than the inductance.

• 3) The system is lossless apart from the impact of the resistances included in the model in Fig. 1.

3 Modeling of PV generation connected to weak AC grid

3.1 PV array model

Figure 2 shows the configuration of the PV array, where N_p and N_s are the number of parallel and series connected cells, respectively, and I_PV is the DC current. The U-I characteristic of a PV cell is given by (2), which can be obtained from the manufacturer.

$$I_{o} = I_{sc} \left[ {1 - C_{1} \left( {\text{e}^{{\frac{{U_{dc} }}{{C_{2} U_{oc} }}}} - 1} \right)} \right]$$

(2)

where I_sc is the short-circuit current; U_oc is the open-circuit voltage; C₁ and C₂ are given by (3) and (4).

$$C_{1} = \left( {1 - \frac{{I_{m} }}{{I_{sc} }}} \right)\text{e}^{{ - \frac{{U_{m} }}{{C_{2} U_{oc} }}}}$$

(3)

$$C_{2} = {{\left( {\frac{{U_{m} }}{{U_{oc} }} - 1} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{U_{m} }}{{U_{oc} }} - 1} \right)} {\ln \left( {1 - \frac{{I_{m} }}{{I_{sc} }}} \right)}}} \right. \kern-0pt} {\ln \left( {1 - \frac{{I_{m} }}{{I_{sc} }}} \right)}}$$

(4)

where I_m is the maximum power point current; U_m is the maximum power point voltage. These four parameters are provided by the PV array manufacturer, they can be modified according to (5) when the external conditions change.

$$\left\{ {\begin{array}{*{20}l} {I_{sc} = I_{{sc\text{,ref}}} \frac{S}{{S_{{\text{ref}}} }}(1 + a\Delta T)} \hfill \\ {U_{oc} = U_{{oc\text{,ref}}} \ln (e + b\Delta S)(1 - c\Delta T)} \hfill \\ {I_{m} = I_{{mc\text{,ref}}} \frac{S}{{S_{{\text{ref}}} }}(1 + a\Delta T)} \hfill \\ {U_{m} = U_{{mc\text{,ref}}} \ln (e + b\Delta S)(1 - c\Delta T)} \hfill \\ \end{array} } \right.$$

(5)

where S is the output power of the PV array; subscript ref denotes the reference value; ΔS is the difference; ΔT is the change in temperature from nominal conditions; a, b and c are parameters available from the manufacturer.

Fig. 2

Configuration of PV array

The U_dc-I_PV characteristic of a PV array can be obtained by extending (2) according to the array dimensions:

$$I_{PV} = N_{p} I_{sc} \left[ {1 - C_{1} \left( {\text{e}^{{\frac{{U_{dc} }}{{C_{2} N_{s} U_{oc} }}}} - 1} \right)} \right]$$

(6)

3.2 VSC model and control strategy

Figure 3 shows the topology of the VSC. The mathematical model of VSC is given by (7), which is transformed into a dq frame.

$$\left\{ {\begin{array}{*{20}l} {L_{f} \frac{{{\text{d}}i_{d} }}{{{\text{d}}t}} = U_{d} - U_{td} + \omega L_{f} i_{q} } \hfill \\ {L_{f} \frac{{{\text{d}}i_{q} }}{{{\text{d}}t}} = U_{q} - U_{tq} - \omega L_{f} i_{d} } \hfill \\ {U_{dc} C\frac{{{\text{d}}U_{dc} }}{{{\text{d}}t}} = I_{PV} U_{dc} - U_{td} i_{d} } \hfill \\ \end{array} } \right.$$

(7)

where i_d and i_q are the actual values of the current in the dq frame; U_td and U_tq are the PCC voltages in the dq frame; U_d and U_q are the modulation voltages in the dq frame.

Fig. 3

Topology of VSC

A typical vector control system for a VSC based on the grid voltage is shown in Fig. 4. The DC voltage U_dc and DC current I_PV of PV array are sent to the maximum power point tracking (MPPT) controller to generate the DC voltage reference U_dc,ref. The outer loop in the d frame is the DC voltage controller which produces the current reference i_d,ref for the inner current loop. The outer loop in the q frame is the AC-bus voltage controller which produces the current reference i_q,ref for the inner current loop. The inner current controllers produce modulation signals in the dq frame which are then translated back to the abc frame. θ_pll is the output phase of the PLL.

Fig. 4

Control strategy of VSC

According to Fig. 4, the following equations can be obtained:

$$\left\{ {\begin{array}{*{20}l} {\frac{{\text{d}}x_{1} }{{\text{d}}t} = U_{dc} - U_{{dc,\text{ref}}} } \hfill \\ {\frac{{\text{d}}x_{2} }{{\text{d}}t} = k_{p1} (U_{dc} - U_{{dc,\text{ref}}} ) + k_{i1} x_{1} - i_{d} } \hfill \\ {\frac{{\text{d}}x_{ 5} }{{\text{d}}t} = U_{t} - U_{{t,\text{ref}}} } \hfill \\ {\frac{{\text{d}}x_{3} }{{\text{d}}t} = k_{p5} (U_{t} - U_{{t,\text{ref}}} ) + k_{i5} x_{5} - i_{q} } \hfill \\ {U_{d} = k_{p2} \left[ {k_{p1} (U_{dc} - U_{{dc,\text{ref}}} ) + k_{i1} x_{1} - i_{d} } \right] + k_{i2} x_{2} + U_{td} - \omega Li_{q} } \hfill \\ {U_{q} = k_{p3} \left[ {k_{p5} (U_{t} - U_{{t,\text{ref}}} ) + k_{i5} x_{5} - i_{q} } \right] + k_{i3} x_{3} + U_{tq} + \omega Li_{d} } \hfill \\ \end{array} } \right.$$

(8)

where x₁, x₂, x₃ and x₅ are the state variables; k_p1, k_p2, k_p3 and k_p5 are the proportional gains of the controllers; k_i1, k_i2, k_i3 and k_i5 are the integral gains of the controllers.

Figure 5 shows the working principle of the PLL that is employed to make sure that the d frame is always aligned with the PCC voltage phasor $\dot{U}_{t}$ to synchronize the VSC with the grid. In Fig. 5, $\dot{U}_{t}^{\prime }$ is the actual PCC voltage phasor in the dq frame. When the PLL is exactly locked, $\dot{U}_{t}$ and $\dot{U}_{t}^{\prime }$ should coincide and the angle θ_pllx would then be 0.

Fig. 5

Working principle of PLL

The transformation for the PCC voltage and current from the dq frame to the d’q’ frame is given below. Based on the small-angle assumption that cos(θ_pllx) = 1, sin(θ_pllx) = θ_pllx, (10) can be obtained.

$$\left\{ {\begin{array}{*{20}l} {U_{td}^{\prime } = U_{td} \cos \left( {\theta_{pllx} } \right) - U_{tq} \sin \left( {\theta_{pllx} } \right)} \hfill \\ {U_{tq}^{\prime } = U_{td} \sin \left( {\theta_{pllx} } \right) + U_{tq} \cos \left( {\theta_{pllx} } \right)} \hfill \\ {i_{d}^{\prime } = i_{d} \cos \left( {\theta_{pllx} } \right) - i_{q} \sin \left( {\theta_{pllx} } \right)} \hfill \\ {i_{q}^{\prime } = i_{d} \sin \left( {\theta_{pllx} } \right) + i_{q} \cos \left( {\theta_{pllx} } \right)} \hfill \\ \end{array} } \right.$$

(9)

$$\left\{ {\begin{array}{*{20}l} {U_{td}^{\prime } = U_{td} - U_{tq} \theta_{pllx} } \hfill \\ {U_{tq}^{\prime } = U_{td} \theta_{pllx} + U_{tq} } \hfill \\ {i_{d}^{\prime } = i_{d} - i_{q} \theta_{pllx} } \hfill \\ {i_{q}^{\prime } = i_{d} \theta_{pllx} + i_{q} } \hfill \\ \end{array} } \right.$$

(10)

The control strategy of the PLL is shown in Fig. 6 and (11) can be obtained from it.

$$\left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}x_{pll} }}{{\text{d}t}} = U_{tq} } \hfill \\ {\frac{{{\text{d}}\theta_{pll} }}{{\text{d}t}} = k_{p4} U_{tq} + k_{i4} x_{pll} + \omega_{ 0} } \hfill \\ \end{array} } \right.$$

(11)

where x_pll is the state variable; k_p4 and k_i4 are the PLL parameters.

Fig. 6

Control strategy of PLL

3.3 Grid model

The equivalent circuit of the AC side of PV generation connected to a weak AC grid is shown in Fig. 7, and the Kirchoff voltage law can be written as:

Fig. 7

Equivalent circuit of PV generation connected to AC grid

$$\left\{ \begin{aligned} L_{g} \frac{{{\text{d}}i_{d} }}{{\text{d}t}} = U_{td} - U_{gd} + \omega L_{g} i_{q} \hfill \\ L_{g} \frac{{{\text{d}}i_{q} }}{{\text{d}t}} = U_{tq} - U_{gq} - \omega L_{g} i_{d} \hfill \\ \end{aligned} \right.$$

(12)

$$U_{td}^{\prime } + {\text{j}}U_{tq}^{\prime } = U_{gd} + {\text{j}}U_{gq} + {\text{j}}(i_{d}^{\prime } + {\text{j}}i_{q}^{\prime } )x_{g}$$

(13)

Equations (6)–(13) form a set of differential-algebraic equations, which can accurately describe the behaviour of PV generation connected to a weak grid. In order to develop a small-signal model for the system, the equations must first be linearized around the operating point. Following the detailed derivation procedure shown in Appendix A, the small-signal model of the system is expressed in state-space equations as:

$$\Delta \dot{\varvec{x}} = \varvec{A}\Delta \varvec{x} + \varvec{B}\Delta \varvec{u}$$

(14)

where A is the state matrix defined in Appendix A; B is the input matrix; Δx is the state vectors, which is defined as Δx = [Δx₁, Δx₂, Δx₃, Δx₅, Δx_pll, Δθ_pll, Δi_d, Δi_q, ΔU_dc]^T.

The eigenvalues of the state matrix A supply useful information about the small-signal stability of the system. The participation factor matrix obtained from the left and right eigenvectors gives insight into the relationship between the states and the modes.

3.4 Model validation

In order to validate the small-signal model, the time-domain response of an example PV array and AC grid was calculated using the small-signal model implemented in MATLAB, and compared with the time-domain response calculated using the full nonlinear model simulated on the electromagnetic transient simulation program PSCAD/EMTDC.

The rated power of the PV array is 500 kW, and the controller parameters of the VSC are listed in Table 1. Under a perturbation of illumination, in which the illumination changes from 800 to 1000 W/m² at t = 3 s and from 1000 W/m² back to 800 W/m² at t = 4.5 s, the operation curves calculated by the two models are compared in Fig. 8a. As can be seen from Fig. 8a, there is a deviation between the curves that depends on the sampling time t_mppt of the MPPT controller.

Table 1 Main parameters

Fig. 8

Validation of the small-signal model

In Fig. 4, the DC voltage reference of the VSC is determined by the MPPT controller. The small-signal model established in this paper does not consider the impact of the maximum power tracking controller, while the simulation model in PSCAD includes the maximum power tracking process. Therefore, when the MPPT has a smaller sampling time, it becomes more responsive and the deviation from the small-signal model becomes larger, as shown in Fig. 8a.

Under a perturbation of impedance perturbation, in which the illumination is constant, while the grid inductance changes from 0.2 mH to 0.25 mH at t = 3 s and from 0.25 mH back to 0.2 mH at t = 4.5 s, the operation curves calculated by the two models ae compared in Fig. 8b. They are basically the same because MPPT has no influence on the system’s response to grid impedance.

4 Small-signal stability analysis

4.1 Eigenvalue analysis

In order to obtain the eigenvalues, taking the PV generation system shown in Fig. 1 as an example, the system parameters are shown in Table 1 (all of the parameters are expressed per unit with respect to the output side voltage level of the VSC). Table 2 shows all the system modes with frequency and damping of the oscillation, under the condition that the R_SCR is equal to 1.5. As can be seen from Table 2, the system has two oscillation modes and five damping modes. All the eigenvalues of the system are distributed on the left side of the complex plane, meaning the system is stable.

Table 2 Eigenvalues of state matrix of a PV system connected to a weak grid

Table 3 shows the participation factors of the state variables in each of the modes identified in Table 2. There are nine modes shown in Table 3. The largest participation of state variables is in modes 3, 4 (λ₃, λ₄) and is associated with the DC voltage control. The PLL is related to modes 5, 6 (λ₅, λ₆).

Table 3 Participation factors of state variables in nine modes

4.2 Eigenvalues locus analysis

The factors influencing stability of the system include grid strength and different control parameters in the PLL controller. Their influence will be discussed using the small-signal model of PV generation connected to a weak grid.

The system parameters are shown in Table 1. The eigenvalue locus as the R_SCR varies from 4 to 1.2 is shown in Fig. 9. As the grid strength decreases, it can be seen that λ₂, λ₃, λ₄ and λ₇ move further to the left, λ₁, λ₈ and λ₉ change little, and λ₅ and λ₆ move towards the right-half plane. When the R_SCR reaches 1.2, λ₅ and λ₆ enter the unstable region, and the system becomes unstable. Therefore, the stability of PV generation connected to a weak grid becomes worse with the reduction of grid strength.

Fig. 9

Eigenvalue locus for varying grid strength

When the R_SCR is fixed at 1.5, the eigenvalue locus as the proportional gain of PLL k_p4 varies from 10 to 100 is shown in Fig. 10. As k_p4 increases, it can be seen that λ₃, λ₄, λ₅ and λ₆ move further to the left, while λ₇ moves towards right-half plane. When k_p4 is 10, λ₅ and λ₆ enter the unstable region, so the system becomes unstable.

Fig. 10

Eigenvalue locus for varying k_p4

When k_p4 is fixed at 50, the eigenvalue locus as the integral gain of the PLL k_i4 varies from 100 to 1500 is shown in Fig. 11. As k_i4 increases, it can be seen that λ₃, λ₄ and λ₇ move further to the left, while λ₅ and λ₆ move towards the right-half plane, but do not enter the unstable region.

Fig. 11

Eigenvalue locus for varying k_i4

In conclusion, the decreasing strength of the grid may cause oscillatory phenomena, tuning the proportional gains of PLL controller have a noticeable effect on the damping characteristics of the system, and larger proportional gain of PLL controller could improve the system damping.

4.3 Transfer function of power control loop in dq rotation frame

Based on the eigenvalue analysis above, there is a 4-5 Hz oscillation in the PV generation system when the parameters of PLL controller are not selected properly. To reveal how the PLL control parameters influence the small-signal stability of PV generation, consider that the current control loop bandwidth is much higher than the DC voltage control loop bandwidth. According to the method of [4], the current in the PLL reference frame can track its reference instantaneously (i_d,ref = i_d). The VSC and its control system are simplified as shown in Fig. 12, where P_PV and P_e are the output powers of the PV array and the VSC, respectively.

Fig. 12

Simplified power control loop of VSC

The power control loop in Fig. 12 can be further simplified, as shown in Fig. 13 [4]. The transfer functions G₁(s) and G₂(s) are defined as:

$$G_{ 1} (s) = \frac{{\Delta \theta_{pll} }}{{\Delta i_{d} }} = \frac{{k_{6} k_{p4} {\rm s} + k_{6} k_{i4} }}{{s^{2} - k_{4} k_{p4} {\rm s} - k_{4} k_{i4} }}$$

(15)

$$G_{2} (s) = k_{3} k_{5} + k_{2}$$

(16)

where coefficients k₁ to k₆ are given in detail in Appendix B, and they have specific physical meanings which relate to the structure, parameters and operating conditions of the system. k₁ represents the influence of the q-axis terminal voltage variation on the output active power; k₂, k₄ and k₅ represent the influence of the output of the PLL variation on the output active power, the q-axis terminal voltage and the d-axis terminal voltage, respectively; k₃ represents the influence of the d-axis terminal voltage variation on the output active power; and k₆ represents the influence of the d-axis current variation on the q-axis terminal voltage.

Fig. 13

Further simplified power control loop of VSC

In Fig. 13, the transfer functions G_s(s) and G_m(s) are defined as:

$$G_{s} (s) = k_{1} k_{6}$$

(17)

$$G_{m} (s) = G_{1} (s)(k_{1} k_{4} + G_{2} (s))$$

(18)

According to (15)–(18), the open loop transfer function G_o(s) can be obtained as:

$$G_{o} (s) = \frac{{\Delta P_{e} }}{{\Delta P_{PV} }} = \left( {G_{m} (s){ + }G_{s} (s)} \right)\left( {k_{p1} + \frac{{k_{i1} }}{s}} \right)\frac{1}{{CU_{dc0} {s}}}$$

(19)

By neglecting the effect of the PLL controller dynamics, the Bode diagram of G_o(s) is shown in Fig. 14. It shows that, with decreasing grid strength, the phase margin of G_o(s) decreases and the stability of the system becomes weaker.

Fig. 14

Bode diagram of G_o(s) by neglecting effect of PLL controller dynamics

Considering the effect of the PLL controller dynamics (R_SCR = 1.5), the Bode diagrams of G_s(s), G_m(s) and G_o(s) are shown in Figs. 15 and 16, respectively. As can be seen from Fig. 15, when the proportional gain of the PLL k_p4 becomes 10 and the integral gain of PLL k_i4 becomes 1500, the amplitude of G_m(s) is greater than the amplitude of G_s(s) in the frequency range of 4-5 Hz, and the phase of G_m(s) is approximately equal to 180°. Within the frequency range of 4-5 Hz, the PLL controller has positive feedback on the power loop of PV generation. As can be seen from Fig. 16, with decreasing PLL control parameters, the phase margin of G_o(s) also decreases. The results of the above analysis are consistent with the results of the eigenvalues analysis.

Fig. 15

Bode diagrams of G_s(s) and G_m(s)

Fig. 16

Bode diagram of G_o(s)

5 Virtual inductance control strategy

According to the eigenvalue analysis, we can see that changing the controller parameters can improve the operational stability of PV generation. However, the control loop interactions become obvious under weak AC grid conditions, meaning the parameters should be designed together and existing optimization methods may not be applicable to design them. Therefore, a new simple method involving a virtual inductance control strategy is proposed in this paper, which is equivalent to developing a virtual PCC voltage for VSC synchronization in the control system. The corresponding equivalent circuit is shown in Fig. 17. The relationship between the virtual PCC voltage U_tdq,vir and the PCC voltage U_tdq is given in (20), and U_tdq,vir will be sent to the control system to modify the input value of PLL controller as shown in Fig. 18.

$$\left\{ {\begin{array}{*{20}l} {U_{{td,{\text{vir}}}} = U_{td} + \omega_{pll} L_{\text{vir}} i_{q} } \hfill \\ {U_{{tq,{\text{vir}}}} = U_{tq} - \omega_{pll} L_{\text{vir}} i_{d} } \hfill \\ {L_{\text{vir}} = aL_{g} } \hfill \\ \end{array} } \right.$$

(20)

where a is the virtual control coefficient, 0 ≤ a ≤ 1.

Fig. 17

Equivalent circuit of PV generation connected to the AC grid with a virtual PCC voltage

Fig. 18

Modified control strategy of VSC

In order to explain the influence of the virtual inductance control strategy on the operation stability of PV generation further, U_tdq,vir is introduced to (14) to modify the small-signal model. Comparing with the original matrix A, the four elements A₅₇ = x_g, A₆₇ = k_p4x_g, A₇₈ = 0, A₈₇ = 0 would change to A₅₇ = (1 − a)x_g, A₆₇ = k_p4(1 − a)x_g, A₇₈ = ax_g/L, A₈₇ = − ax_g/L. When a is 0.5, the eigenvalue locus as the R_SCR varies from 4 to 1.2 is shown in Fig. 19, and the eigenvalue locus as the proportional gain of the PLL k_p4 varies from 10 to 100 is shown in Fig. 20. The red eigenvalue locus represents PV generation with the virtual inductance control strategy and the blue eigenvalue locus represents PV generation without the virtual inductance control strategy. Figures 19 and 20 show that the PV generation becomes stable with the virtual inductance control strategy.

Fig. 19

Eigenvalue locus for varying grid strength (a = 0.5)

Fig. 20

Eigenvalue locus for varying k_p4 (a = 0.5)

When VSC adopts the virtual inductance control strategy, the transfer functions G₁(s) and G_m(s) in Section 4 should be modified. G₁(s) and G_m(s) are depicted in (21) and (22) (according to Appendix B, k₆ = x_g). When the R_SCR turns is 1.5, the proportional gain of PLL k_p4 is 10 and the integral gain of PLL k_i4 is 1500, the Bode diagram of G_m(s) with different virtual control coefficients a is shown in Fig. 21. It shows that, when the virtual control coefficient a increases, the amplitude of G_m(s) will be lower than the amplitude of G_s(s) in the frequency range of 4-5 Hz. Compared with the results shown in Fig. 15, the PV generation will become stable when employing a virtual inductance control strategy, and the results of the above analysis are consistent with the eigenvalues analysis.

Fig. 21

Bode diagrams of G_s(s) and G_m(s) with different a

$$G_{ 1} (s) = \frac{{\Delta \theta_{pll} }}{{\Delta i_{d} }} = \frac{{(k_{6} - ax_{g} )k_{p4} s + (k_{6} - ax_{g} )k_{i4} }}{{s^{2} - k_{4} k_{p4} s - k_{4} k_{i4} }}$$

(21)

$$G_{m} (s) = \frac{{( 1- a)x_{g} k_{p4} s + ( 1- a)x_{g} k_{i4} }}{{s^{2} - k_{4} k_{p4} s - k_{4} k_{i4} }}(k_{1} k_{4} + G_{2} (s))$$

(22)

6 Simulation validation

In order to verify the effectiveness of the small-signal analysis, a detailed simulation model of PV generation connected to a weak AC grid is built in PSCAD/EMTDC. The parameters are shown in Table 1.

6.1 Simulation results and analysis

When the proportional gain of PLL k_p4 is 50, and the integral gain of PLL is 1500, Figs. 22 and 23 show the PCC voltage U_t responses, DC voltage U_dc responses, output active power P_e responses and d-axis current i_d responses calculated by the detailed simulation model for a step change of illumination at t = 10 s with different grid strengths.

Fig. 22

Stable waveforms when R_SCR is 1.5

Fig. 23

Unstable waveforms when R_SCR is 1.2

Figure 22 illustrates that the system becomes stable after a step change of illumination when R_SCR = 1.5. Figure 23 illustrates that the system becomes unstable after a step change of illumination when R_SCR = 1.2.

Figure 24 shows the current i_a responses when R_SCR = 1.2. In order to judge the effectiveness of the simulation results, a Prony toolbox is employed using the MATLAB environment to fit the unstable part of i_a (to 18th-order terms). The amplitude, frequency, and damping ratio resulting from the Prony approximate curve are listed in Table 4. It can be seen that the main oscillation frequency is about 5 Hz, which is consistent with the eigenvalue locus analysis in Fig. 9.

Fig. 24

Current i_a responses when R_SCR is 1.2

Table 4 Oscillation modes of i_a in Fig. 24 (to 18th order)

When the R_SCR is 1.5, Figs. 25 and 26 show the PCC voltage U_t responses, DC voltage U_dc responses, output active power P_e responses and d-axis current i_d responses calculated by the detailed simulation model for a step change of illumination at t = 10 s with different PLL gains. In Fig. 25, k_p4 = 100, k_i4 = 1500 and in Fig. 26, k_p4 = 18, k_i4 = 1500.

Fig. 25

Stable waveforms when k_p4 is 100

Fig. 26

Unstable waveforms when k_p4 is 18

Figure 25 illustrates that the system becomes stable after a step change of illumination. Figure 26 illustrates that the system becomes unstable after a step change of illumination.

Figure 27 shows the current i_a responses when k_p4 = 18. As above, a Prony Toolbox employed to fit the unstable part of i_a (to 18th-order terms). The amplitude, frequency, and damping ratio resulting from the Prony approximate curve are listed in Table 5. It can be seen from Table 5 that the main oscillation frequency is also about 5 Hz, which is consistent with the eigenvalue locus analysis in Fig. 10.

Fig. 27

Current i_a responses when k_p4 is 18

Table 5 Oscillation modes of i_a in Fig. 27 (to 18th order)

When the R_SCR is 1.2 and the virtual control coefficient a turns is 0.5, Fig. 28 shows that the PV generation becomes stable with the virtual inductance control strategy, compared with the instability shown in Fig. 23.

Fig. 28

Stable waveforms when R_SCR is 1.2 and virtual control coefficient a is 0.5

When the proportional gain of the PLL k_p41 is 10 and the virtual control coefficient a is 0.5, Fig. 29 shows that the PV generation becomes stable with the virtual inductance control strategy, compared with the instability shown in Fig. 26. These simulation results are consistent with the eigenvalue locus analysis in Fig. 19 and in Fig. 20.

Fig. 29

Stable waveforms when k_p4 is 10 and virtual control coefficient a is 0.5

7 Conclusion

A small-signal model of PV generation connected to a weak grid is presented in this paper. Eigenvalue analysis and the transfer function of the power control loop analyzed in dq rotation frame are employed to study the stability of PV generation with different grid strength and different control parameters in the PLL controller.

The following conclusions can be drawn for the example system parameters used: ① increased output power of a PV unit in a PV generator or decreased grid strength may lead to oscillatory phenomena (R_SCR ≤ 1.2); ② tuning the gains of the PLL in the VSC has a noticeable effect on the damping characteristic of the system, and larger proportional gain of PLL controller (18-100) can improve system damping and enhance the system stability; ③ within the frequency range of 4-5 Hz, the PLL controller has a positive feedback on the power control loop of PV generation.

In order to improve the operation stability of PV generation, the virtual inductance control strategy is presented in this paper. By selecting a proper virtual control coefficient, the virtual inductance control strategy can improve the operational stability of PV generation. The influence of the grid resistance R_g and the MPPT controller on the system stability will be considered in future work.

Appendices

Appendix A

Linearizing (6)–(8) around the operating point leads to (A1) and (A2):

$$\left\{ {\begin{array}{*{20}l} {\frac{{\text{d}}\Delta x_{1} }{{\text{d}}t} = \Delta U_{dc} - \Delta U_{{dc,\text{ref}}} } \hfill \\ {\frac{{\text{d}}\Delta x_{2} }{{\text{d}}t} = k_{p1} \Delta U_{dc} + k_{i1} \Delta x_{1} - \Delta i_{d} } \hfill \\ {\frac{{\text{d}}\Delta x_{3} }{{\text{d}}t} = k_{p5} \Delta U_{t} + k_{i5} \Delta x_{5} - \Delta i_{q} } \hfill \\ {\frac{{\text{d}}\Delta x_{5} }{{\text{d}}t} = \Delta U_{t} } \hfill \\ {\frac{{\text{d}}\Delta x_{pll} }{{\text{d}}t} = \Delta U_{tq} } \hfill \\ {\frac{{\text{d}}\Delta \theta_{pll} }{{\text{d}}t} = k_{p4} \Delta U_{tq} + k_{i4} \Delta x_{pll} } \hfill \\ {L_{f} \frac{{\text{d}}\Delta i_{d} }{{\text{d}}t} = \Delta U_{d} - \Delta U_{td} + \omega L_{f} \Delta i_{q} } \hfill \\ {L_{f} \frac{{\text{d}}\Delta i_{q} }{{\text{d}}t} = \Delta U_{q} - \Delta U_{tq} - \omega L_{f} \Delta i_{d} } \hfill \\ {C\frac{{\text{d}}\Delta U_{dc} }{{\text{d}}t} = \Delta i_{PV} + \frac{{i_{PV0} }}{{U_{dc0} }}\Delta U_{dc} - \frac{{U_{td0} }}{{U_{dc0} }}\Delta i_{d} - \frac{{i_{d0} }}{{U_{dc0} }}\Delta U_{td} } \hfill \\ \end{array} } \right.$$

(A1)

$$\left\{ {\begin{array}{*{20}l} {\Delta U_{d} = k_{p2} k_{p1} (\Delta U_{dc} - \Delta U_{{dc,\text{ref}}} ) + k_{p2} k_{i1} \Delta x_{1} } \hfill \\ \qquad\,\,\,\, { - k_{p2} \Delta i_{d} + k_{i2} \Delta x_{2} + \Delta U_{td} - \omega L_{f} \Delta i_{q} } \hfill \\ {\Delta U_{q} = k_{p3} k_{p5} (\Delta U_{t} - \Delta U_{{t,\text{ref}}} ) + k_{p3} k_{i5} \Delta x_{5} } \hfill \\ \qquad\,\,\,\, { - k_{p3} \Delta i_{q} + k_{i3} \Delta x_{3} + \Delta U_{tq} + \omega L_{f} \Delta i_{d} } \hfill \\ \end{array} } \right.$$

(A2)

Linearizing (10) around the operating point leads to (A3):

$$\left\{ \begin{aligned} &\Delta U_{td}^{{\prime }} = \Delta U_{td} - U_{tq0} \Delta \theta_{pll} \hfill \\ &\Delta U_{tq}^{{\prime }} = U_{td0} \Delta \theta_{pll} + \Delta U_{tq} \hfill \\ &\Delta i_{d}^{{\prime }} = \Delta i_{d} - i_{q0} \Delta \theta_{pll} \hfill \\ &\Delta i_{q}^{{\prime }} = i_{d0} \Delta \theta_{pll} + \Delta i_{q} \hfill \\ \end{aligned} \right.$$

(A3)

Linearizing (13) around the operating point leads to (A4):

$$\left\{ {\begin{array}{*{20}l} {\Delta U_{td}^{{\prime }} = - \Delta i_{q}^{{\prime }} x_{g} } \hfill \\ {\Delta U_{tq}^{{\prime }} = \Delta i_{d}^{{\prime }} x_{g} } \hfill \\ \end{array} } \right.$$

(A4)

Combining (A3) and (A4) gives:

$$\left\{ {\begin{array}{*{20}l} {\Delta U_{td} = - x_{g} \Delta i_{q} + (U_{tq0} - i_{d0} x_{g} )\Delta \theta_{pll} } \hfill \\ {\Delta U_{tq} = x_{g} \Delta i_{d} - (U_{td0} + i_{q0} x_{g} )\Delta \theta_{pll} } \hfill \\ \end{array} } \right.$$

(A5)

Substituting (A2) and (A5) into (A1) leads to (14) in Section 3. The state matrix is as (A6).

$${\varvec{A}} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ {k_{i1} } & 0 & 0 & 0 & 0 & 0 & { - 1} & 0 & {k_{p1} } \\ 0 & 0 & 0 & {k_{i5} } & 0 & {k_{p5} (U_{tq0} - i_{d0} x_{g} )} & 0 & { - (1 + k_{p5} x_{g} )} & 0 \\ 0 & 0 & 0 & 0 & 0 & {(U_{tq0} - i_{d0} x_{g} )} & 0 & { - x_{g} } & 0 \\ 0 & 0 & 0 & 0 & 0 & { - (U_{td0} + i_{q0} x_{g} )} & {x_{g} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {k_{i4} } & { - k_{p4} (U_{td0} + i_{q0} x_{g} )} & {k_{p4} x_{g} } & 0 & 0 \\ {\frac{{k_{p2} k_{i1} }}{{L_{f} }}} & {\frac{{k_{i2} }}{{L_{f} }}} & 0 & 0 & 0 & 0 & { - \frac{{k_{p2} }}{{L_{f} }}} & 0 & {\frac{{k_{p1} k_{p2} }}{{L_{f} }}} \\ 0 & 0 & {\frac{{k_{i3} }}{{L_{f} }}} & {\frac{{k_{p3} k_{i5} }}{{L_{f} }}} & 0 & {\frac{{k_{p3} k_{p5} (U_{tq0} - i_{d0} x_{g} )}}{{L_{f} }}} & 0 & { - \frac{{k_{p3} k_{p5} x_{g} + k_{p3} }}{{L_{f} }}} & 0 \\ 0 & 0 & 0 & 0 & 0 & {t_{1} } & {t_{2} } & {t_{3} } & {t_{4} } \\ \end{array} } \right]$$

(A6)

$$\left\{ {\begin{array}{*{20}l} {t_{1} = - \frac{{i_{d0} }}{{CU_{dc0} }}(U_{tq0} - i_{d0} x_{\text{g}} )} \hfill \\ {t_{2} = - \frac{{U_{td0} }}{{CU_{dc0} }}} \hfill \\ {t_{3} = \frac{{i_{d0} }}{{CU_{dc0} }}x_{g} } \hfill \\ {t_{4} = \frac{1}{C}\left( {\alpha + \frac{{i_{PV0} }}{{U_{dc0} }}} \right)} \hfill \\ \end{array} } \right.$$

(A7)

Appendix B

According to [4], the following equations can be obtained:

$$\left\{ {\begin{array}{*{20}l} {\Delta P_{e} = k_{1} \Delta U_{tq} + k_{2} \Delta \theta_{pll} + k_{3} \Delta U_{td} } \hfill \\ {\Delta U_{tq} = k_{4} \Delta \theta_{pll} + k_{6} \Delta i_{d} } \hfill \\ {\Delta U_{td} = k_{5} \Delta \theta_{pll} + k_{7} \Delta i_{q} } \hfill \\ {\Delta U_{t} = \Delta U_{td} } \hfill \\ \end{array} } \right.$$

(B1)

$$\left\{ {\begin{array}{*{20}l} {k_{1} = U_{{gd0}} /x_{g} } \hfill \\ {k_{2} = U_{{gd0}} U_{{td0}} /x_{g} } \hfill \\ {k_{3} = - U_{{gq0}} /x_{g} } \hfill \\ {k_{4} = - i_{{q0}} x_{g} - U_{{td0}} } \hfill \\ {k_{5} = - i_{{d0}} x_{g} } \hfill \\ {k_{6} = x_{g} } \hfill \\ {k_{7} = - x_{g} } \hfill \\ \end{array} } \right.$$

(B2)