Analysis of small-signal stability of power systems with photovoltaic generators

Abstract

This paper presents a theoretical analysis of the small-signal stability of a power system in which a synchronous generator and a photovoltaic (PV) generator supply power to an infinite bus. The problem considered here is to investigate the existence of the equilibrium points of the system and their stability. In terms of this problem, by focusing on the condition to be satisfied by the equilibrium points and appropriately using the intermediate value theorem, we derive a sufficient condition on the magnitude of the PV current for the existence of the equilibrium points. The condition is given as inequalities with respect to the system parameters. These inequalities show that, if the power system from which the PV generator is removed has equilibrium points, then equilibrium points exist also in the original system as long as the PV current is small. Moreover, we analyze the stability of the equilibrium points and show that the equilibrium points found under our existence condition are asymptotically stable. These results imply that, when the PV current is below a certain level, the existence of the asymptotically stable equilibrium points is preserved even though the PV generator is introduced.

1 Introduction

Modern power systems are characterized by a high penetration of photovoltaic (PV) generators [11]. This is because the increasing use of electricity generated in environmentally friendly ways, such as by using solar energy, is driven by critical concerns over the depletion of fossil fuels and greenhouse gas emissions. Since PV generators convert solar energy directly into electricity, there is no consumption of fossil fuels and hence are no greenhouse gas emissions.

However, the introduction of PV generators affects the performance of power systems. For example, PV penetration degrades the stability of power systems because PV generators do not have the synchronizing torque [6], i.e., internal torque to preserve the synchronization of generators. To solve this problem, many studies have been conducted to date. For instance, a model of a PV generator has been constructed to study the interaction of PV generators with power systems [12]. Other researchers have analyzed the impact of PV penetration on the transient stability [10, 14] and voltage characteristics [1, 7, 13, 16] of power systems. Additionally, controller design for PV systems connected to power grids has been carried out [5, 9, 15].

Our interest in this research is to determine the impact of the penetration of PV generators on the small-signal stability [6] of power systems. This stability indicates the ability of power systems to maintain the synchronization against small disturbances such as variations in loads and power. The motivation for considering the small-signal stability is that this characteristic is fundamental to the problem-free operation of power systems. In fact, a power system without the small-signal stability is destabilized even by small disturbances, which ultimately leads to the disruption of the power supply.

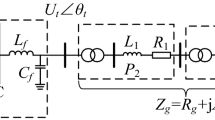
The purpose of this paper is to investigate the impact of PV penetration on the small-signal stability. For this purpose, we consider the system in Fig. 1. This is composed of a synchronous generator, a PV generator, and an infinite bus corresponding to a large system to which the two generators are connected. The generators supply power to the infinite bus through a transmission line. The system in Fig. 1 focuses only on the synchronous generator and the PV generator and thus is suitable for investigating the direct impact of PV penetration on the behavior of the synchronous generator. For this system, we consider the stability of the equilibrium points, i.e., the states in which the electrical output of the synchronous generator is in balance with the mechanical input to it, as the small-signal stability. We then address the problem of verifying the existence of the equilibrium points and analyzing their stability.

Fig. 1

Power system $\varSigma$ with PV generator

In terms of the above problem, this paper makes two contributions. First, we derive a sufficient condition on the magnitude of the PV current for the existence of the equilibrium points. As a result, we show that, if the power system from which the PV generator is removed has equilibrium points, then equilibrium points exist also in the original system as long as the PV current is small. The key idea behind this result is to employ the intermediate value theorem. A straightforward method for solving our problem would be to derive the equilibrium points and clarify their properties. However, deriving the equilibrium points is difficult because it is necessary to solve a nonlinear equation with trigonometric functions and their inverses from the presence of the PV generator. We address this difficulty by focusing on the condition to be satisfied by the equilibrium points and by appropriately using the intermediate value theorem. Second, we analyze the stability of the equilibrium points of the system in Fig. 1 and characterize those equilibrium points that are asymptotically stable. We consequently show that the equilibrium points found under the existence condition derived above are asymptotically stable; that is, the first contribution provides an existence condition of asymptotically stable equilibrium points. This result and the above discussion enable us to conclude that, when the PV current is below a certain level, the small-signal stability is preserved even though the PV generator is introduced.

Before closing this section, we give three remarks on this paper.

First, we note the difference between the results of this paper and those of previous studies. Four previous studies have considered the impact of PV penetration on the small-signal stability [2, 3, 8, 17]. In these studies, the authors have used system models given by the linearization around certain operating points, i.e., equilibrium points. That is, they have implicitly assumed that the target systems have equilibrium points. Contrary to this, we focus on the loss of equilibrium points as the impact of PV penetration on power systems and derive a condition for the existence of equilibrium points. In addition, we clarify the relation between the existence condition and the stability of equilibrium points. In these respects, the contributions of this paper are distinct from those of the previous studies.

Second, this paper presents an analytical result on the small-signal stability by considering the simplified system in Fig. 1. In the field of power engineering, researchers have often focused on stability analysis methods based on numerical computation and have applied their proposed methods to specific systems (see, e.g., [3, 8, 17]). Thus, for other systems with different parameter values, we cannot obtain any insight unless the analysis methods are again used. In addition, to investigate the effects of the parameter values on the systems, we have to use the analysis methods for various parameter values, which requires considerable time and effort. By contrast, this paper presents a stability condition as inequalities with respect to the parameters of the system in Fig. 1. As a result, we clarify that the system in Fig. 1 has the property mentioned above. This property is essential in the sense that it holds regardless of the values of the system parameters. Moreover, our stability condition allows us to estimate the magnitude of the PV current such that the small-signal stability is guaranteed, in advance. This is useful to construct a PV-integrated power system that is small-signal stable. The analytical result of this paper has these advantages, compared with results based on numerical computation.

Finally, this paper is based on our conference paper [4], but differs from it in the following points. First, this paper includes the full explanations and the rigorous proofs of the main results, omitted from [4]. Second, we ensure that the paper is self-contained by showing the detailed derivation of the dynamics of the target system given in the Japanese paper [10]. Third, we present additional numerical examples to verify our result.

Notation

Let $\mathbb {R}$, $\mathbb {R}_{+}$, and $\mathbb {R}_{0+}$ be the real number field, the set of positive real numbers, and the set of nonnegative real numbers, respectively. We use 0 to represent both the zero scalar and the zero vector. We denote by $a\angle \theta$ the complex number with the absolute value a and the argument $\theta$. Finally, the following properties [18] for trigonometric functions and their inverses are used in this paper:

$$\begin{aligned}&\sin (\cos ^{-1}x)=\sqrt{1-x^2}, \end{aligned}$$

(1)

$$\begin{aligned}&\sin (\tan ^{-1}y)=\dfrac{y}{\sqrt{1+y^2}}, \end{aligned}$$

(2)

$$\begin{aligned}&\cos (\cos ^{-1}x)=x, \end{aligned}$$

(3)

$$\begin{aligned}&\cos (\tan ^{-1}y)=\dfrac{1}{\sqrt{1+y^2}}, \end{aligned}$$

(4)

where $-1\le x \le 1$ and $-\infty \le y\le \infty$.

2 Problem formulation

2.1 System description

Consider the power system $\varSigma$ in Fig. 1, composed of the synchronous generator $G_S$, the PV generator $G_P$, and an infinite bus.

For the power system $\varSigma$, we impose the following assumptions.

• The phase angle of the current of $G_P$ for the infinite bus voltage tracks $\delta _B$, i.e.,  the phase angle of the voltage of the bus to which $G_P$ is connected.

• The magnitude of the PV current is constant.

The former implies that $G_P$ has a power conditioning unit. The latter is satisfied if the dynamics of $G_S$ is sufficiently faster than that of $G_P$. In addition, we regard $G_S$ as the combination of a voltage source and reactance.

Then, the dynamics of the system $\varSigma$ (i.e.,  the generator $G_S$) is described by

$$\begin{aligned} M\ddot{\delta }_S(t)=P_m-P_e(\delta _S(t))-D\dot{\delta }_S(t), \end{aligned}$$

(5)

where $\delta _S(t)\in \mathbb {R}$ is the phase angle of the voltage of $G_S$ for the infinite bus voltage, $M\in \mathbb {R}_+$ is the moment of inertia, $P_m\in \mathbb {R}$ is the mechanical input, and $D\in \mathbb {R}_+$ is the damping coefficient. The variable $P_e(\delta _S(t))\in \mathbb {R}$ is the electrical output defined as

$$\begin{aligned}&P_e(\delta _S(t)) \nonumber \\&:=\frac{v_Sv_\infty \sin \delta _S(t)-r_Lv_Si_P\cos (\delta _S(t)-\delta _B(\delta _S(t)))}{r_S+r_L}, \end{aligned}$$

(6)

where $v_S,v_\infty \in \mathbb {R}_+$ are the magnitude of the voltages of $G_S$ and the infinite bus, $r_S,r_L\in \mathbb {R}_+$ are the reactance of $G_S$ and the transmission line, $i_P\in \mathbb {R}_{0+}$ is the magnitude of the current of $G_P$, and

$$\begin{aligned}&\delta _B(\delta _S(t)):= \nonumber \\&{\left\{ \begin{array}{ll} \cos ^{-1}\left( \dfrac{-r_Sr_Li_P}{\sqrt{(r_Lv_S\sin \delta _S(t))^2+(r_Lv_S\cos \delta _S(t)+r_Sv_\infty )^2}}\right) \\ -\phi (\delta _S(t)) \qquad \qquad \qquad \qquad \qquad \mathrm{if}~\sin \delta _S(t)\ne 0, \\ \sin ^{-1}\left( \dfrac{r_Sr_Li_P}{r_Lv_S\cos \delta _S(t)+r_Sv_\infty }\right) \qquad \, \mathrm{if}~\sin \delta _S(t)=0, \end{array}\right. } \end{aligned}$$

(7)

for

$$\begin{aligned}&\phi (\delta _S(t)):= \nonumber \\&{\left\{ \begin{array}{ll} \tan ^{-1}\left( \dfrac{r_Lv_S\cos \delta _S(t)+r_Sv_\infty }{r_Lv_S\sin \delta _S(t)}\right) \qquad \quad \, \mathrm{if}~\sin \delta _S(t)>0, \\ \pi +\tan ^{-1}\left( \dfrac{r_Lv_S\cos \delta _S(t)+r_Sv_\infty }{r_Lv_S\sin \delta _S(t)}\right) \quad \mathrm{if}~\sin \delta _S(t)<0. \end{array}\right. } \end{aligned}$$

(8)

Equation (5) is given as the swing equation. The derivations of (6) and (7) are based on [10]. The details are given in Appendix A.

2.2 Stability analysis problem

2.2.1 Motivating examples

Based on [6], we select the system parameters as $M:=0.0186\,\mathrm{s^2}$, $P_m:=1.15\,\mathrm{pu}$, $D:=0.00531\,\mathrm{s}$, $v_S:=1.12\,\mathrm{pu}$, $v_\infty :=0.995\,\mathrm{pu}$, $r_S:=0.300\,\mathrm{pu}$, and $r_L:=0.500\,\mathrm{pu}$. Figure 2 shows the time responses of the system $\varSigma$ with $i_P:=0.2\,\mathrm{pu}$ and $i_P:=0.5\,\mathrm{pu}$, where $(\delta _S(0),\dot{\delta }_S(0)):=(1,0)$. We see that $\delta _S(t)$ with $i_P:=0.2\,\mathrm{pu}$ converges but that with $i_P:=0.5\,\mathrm{pu}$ does not.

To clarify the reason, we focus on the equilibrium points of the system $\varSigma$. Let $[\delta _S(t)\ \ \dot{\delta }_S(t)]^\top$ be the state variable vector. Then, (5) yields the following state equation of $\varSigma$:

$$\begin{aligned} \frac{d}{dt} \begin{bmatrix} \delta _S(t) \\ \dot{\delta }_S(t) \end{bmatrix} =\begin{bmatrix} \dot{\delta }_S(t) \\ \dfrac{1}{M}\left( P_m-P_e(\delta _S(t))-D\dot{\delta }_S(t)\right) \end{bmatrix}. \end{aligned}$$

(9)

From (9), the equilibrium points of $\varSigma$ are of the form $[\delta _{S}^\star \ \ 0]^\top$ where $\delta _{S}^\star \in \mathbb {R}$ is a solution to

$$\begin{aligned} P_m=P_e(\delta _S). \end{aligned}$$

(10)

Thus, if the curve of $P_e(\delta _S)$ in (6) intersects with the straight line $P_e(\delta _S)=P_m$, then there exists an equilibrium point of $\varSigma$. In Fig. 3, the plots of $P_e(\delta _S)$ with $i_P:=0.2\,\mathrm{pu}$ and $i_P:=0.5\,\mathrm{pu}$ and the straight line $P_e(\delta _S)=P_m$ are depicted by the solid and dotted curves and the thin line, respectively. We see that the curve of $P_e(\delta _S)$ with $i_P:=0.2\,\mathrm{pu}$ intersects with the straight line $P_e(\delta _S)=P_m$ but that with $i_P:=0.5\,\mathrm{pu}$ does not. This means that the existence of the equilibrium points of $\varSigma$ depends on $i_P$, which gives rise to the results in Fig. 2.

Fig. 2

Time responses of $\varSigma$ with $i_P:=0.2\,\mathrm{pu}$ and $i_P:=0.5\,\mathrm{pu}$

2.2.2 Problem to be considered

Motivated by these examples, we consider the following problem.

Problem 1

For the power system $\varSigma$,

• (a) find a condition on $i_P$ for the existence of the equilibrium points;

• (b) if an equilibrium point exists, then check its stability.

Fig. 3

Plots of $P_e(\delta _S)$ with $i_P:=0.2\,\mathrm{pu}$ and $i_P:=0.5\,\mathrm{pu}$

Remark 1

A straightforward method for solving Problem 1 is to directly solve (10) and clarify the properties of the equilibrium points; however, solving (10) is difficult. This is because $P_e(\delta _S)$ contains the nonlinear term due to the presence of the PV generator $G_P$, i.e.,  $r_Lv_Si_P\cos (\delta _S(t)-\delta _B(\delta _S(t)))$ that includes trigonometric functions and their inverses, from (6) to (8). Although one may think that the system $\varSigma$ is simple, this fact makes the problem challenging.

3 Existence of equilibrium points

In this section, we address (a) in Problem 1. To this end, we first derive a condition to avoid the singular points of the system $\varSigma$. Based on this, we present a condition for the existence of the equilibrium points.

3.1 Condition for avoiding singular points

Because of $\cos ^{-1}(\cdot )$ and $\sin ^{-1}(\cdot )$ in (7), the system $\varSigma$ has singular points where the absolute values of the arguments of $\cos ^{-1}(\cdot )$ and $\sin ^{-1}(\cdot )$ are greater than one. We address this issue by presenting a condition on $i_P$ to avoid the singular points of $\varSigma$.

Lemma 1

If $\,i_P$ satisfies

$$\begin{aligned} i_P\le \frac{|r_Lv_S-r_Sv_\infty |}{r_Sr_L}, \end{aligned}$$

(11)

then the power system $\varSigma$ has no singular points, i.e.,

$$\begin{aligned} \left| \dfrac{-r_Sr_Li_P}{\sqrt{(r_Lv_S\sin \delta _S)^2+(r_Lv_S\cos \delta _S+r_Sv_\infty )^2}}\right| \le 1 , \end{aligned}$$

(12)

for every $\delta _S\in \mathbb {R}$ satisfying $\sin \delta _S\ne 0$ and

$$\begin{aligned}&\left| \dfrac{r_Sr_Li_P}{r_Lv_S\cos \delta _S+r_Sv_\infty }\right| \le 1, \end{aligned}$$

(13)

for every $\delta _S\in \mathbb {R}$ satisfying $\sin \delta _S=0$.

Proof

The inequality (12) holds if

$$\begin{aligned} \left( \dfrac{-r_Sr_Li_P}{\sqrt{(r_Lv_S\sin \delta _S)^2+(r_Lv_S\cos \delta _S+r_Sv_\infty )^2}}\right) ^2 \le 1. \end{aligned}$$

(14)

We can rewrite (14) as

$$\begin{aligned} (r_Sr_Li_P)^2&\le (r_Lv_S\sin \delta _S)^2+(r_Lv_S\cos \delta _S+r_Sv_\infty )^2, \end{aligned}$$

which yields

$$\begin{aligned} i_P&\le \frac{\sqrt{(r_Lv_S\sin \delta _S)^2+(r_Lv_S\cos \delta _S+r_Sv_\infty )^2}}{r_Sr_L}\nonumber \\&=\frac{\sqrt{r_L^2v_S^2+r_S^2v_\infty ^2+2r_Sr_Lv_Sv_\infty \cos \delta _S}}{r_Sr_L}, \end{aligned}$$

(15)

because of $r_S,r_L\in \mathbb {R}_+$ and $i_P\in \mathbb {R}_{0+}$. Since $\cos \delta _S\ge -1$ for every $\delta _S\in \mathbb {R}$, the right-hand side of (15) is greater than or equal to $\left( \sqrt{r_L^2v_S^2+r_S^2v_\infty ^2-2r_Sr_Lv_Sv_\infty }\right) /(r_Sr_L)$ for every $\delta _S\in \mathbb {R}$. Thus, we obtain

$$\begin{aligned} i_P&\le \frac{\sqrt{r_L^2v_S^2+r_S^2v_\infty ^2-2r_Sr_Lv_Sv_\infty }}{r_Sr_L} \\&=\frac{\sqrt{(r_Lv_S-r_Sv_\infty )^2}}{r_Sr_L}, \end{aligned}$$

which implies that (12) holds for every $\delta _S\in \mathbb {R}$ under (11). In addition, by choosing $\delta _S$ such that $\sin \delta _S=0$ in (12), we can show that (13) holds for every $\delta _S\in \mathbb {R}$ satisfying $\sin \delta _S=0$ under (11). This completes the proof. $\square$

3.2 Main result

Now, we derive the condition under which the equilibrium points of the system $\varSigma$ exist.

As explained in Sect. 2.2.1, $\varSigma$ has an equilibrium point if (10) has a solution. From (6)–(8) and Lemma 1, $P_e(\delta _S)$ is a continuous function for $\delta _S\in (0,\pi )$ under (11). Therefore, it follows from the intermediate value theorem that if there exist a $\delta _{S}^-\in (0,\pi )$ and a $\delta _{S}^+\in (\delta _{S}^-,\pi )$ satisfying

$$\begin{aligned} P_e(\delta _{S}^-)<P_m, \end{aligned}$$

(16)

$$\begin{aligned} P_e(\delta _{S}^+)>P_m, \end{aligned}$$

(17)

then there exists at least one equilibrium point on $(\delta _{S}^-,\delta _{S}^+)\times \{0\}$ (where $\{0\}$ corresponds to $\dot{\delta }_S=0$), as illustrated in Fig. 4. Hence, we derive a condition on $i_P$ to achieve (16) and (17) for given $\delta _S^-$ and $\delta _S^+$.

Based on this idea, we obtain the following result.

Theorem 1

For the power system $\varSigma$, assume that (11) holds. If there exist a $\delta _{S}^-\in (0,\pi /2)$ and a $\delta _{S}^+\in (\delta _{S}^-,\pi /2]$ satisfying the following two conditions, then there exists at least one equilibrium point on $(\delta _{S}^-,\delta _{S}^+)\times \{0\}$.

$\mathrm {(}C1\mathrm {)}$ :

$c_0(\delta _{S}^-)<0$ and $c_0(\delta _{S}^+)>0$,

$\mathrm {(}C2\mathrm {)}$ :

$i_P< \alpha _{21}(\delta _{S}^+)$,

where

$$\begin{aligned}&c_0(\delta _S):=\dfrac{v_Sv_\infty \sin \delta _S}{r_S+r_L}-P_m, \end{aligned}$$

(18)

$$\begin{aligned}&\alpha _{21}(\delta _{S}):= \dfrac{-c_{12}(\delta _{S})-\sqrt{c_{12}^2(\delta _{S})-4c_2(\delta _{S})c_0(\delta _{S})}}{2c_2(\delta _{S})}, \end{aligned}$$

(19)

for

$$\begin{aligned}&c_{12}(\delta _S):= \dfrac{-r_Lv_S(r_Lv_S+r_Sv_\infty \cos \delta _S)}{(r_S+r_L)\sqrt{f(\delta _S)}}, \end{aligned}$$

(20)

$$\begin{aligned}&c_2(\delta _S):=\dfrac{-r_S^2r_L^2v_Sv_\infty \sin \delta _S}{(r_S+r_L)f(\delta _S)}, \end{aligned}$$

(21)

$$\begin{aligned}&f(\delta _S):=r_L^2v_S^2+r_S^2v_\infty ^2+2r_Sr_Lv_Sv_\infty \cos \delta _S. \end{aligned}$$

(22)

Fig. 4

Idea of analysis

Proof

Using a trigonometric addition formula for (6) gives

$$\begin{aligned}&P_e(\delta _S)=\dfrac{v_Sv_\infty \sin \delta _S}{r_S+r_L} \nonumber \\&-\frac{r_Lv_Si_P(\cos \delta _S\cos (\delta _B(\delta _S))+\sin \delta _S\sin (\delta _B(\delta _S)))}{r_S+r_L}. \end{aligned}$$

(23)

If $\delta _S\in (0,\pi /2]$, then $\sin \delta _S> 0$. Furthermore, from Lemma 1, (12) holds for every $\delta _S\in (0,\pi /2]$ under (11). Thus, by substituting the first equations of (7) and (8) into (23) and using (1)–(4), we obtain

$$\begin{aligned} P_e(\delta _S)=c_2(\delta _S)i_P^2+c_1(\delta _S,i_P)i_P+c_0(\delta _S)+P_m, \end{aligned}$$

(24)

where

$$\begin{aligned}&c_1(\delta _S,i_P) \nonumber \\&:= -\dfrac{r_Lv_S(r_Lv_S+r_Sv_\infty \cos \delta _S)\sqrt{f(\delta _S)-r_S^2r_L^2i_P^2}}{(r_S+r_L)f(\delta _S)}. \end{aligned}$$

(25)

First, we derive a condition corresponding to (16). Based on (11), we substitute $i_P=|r_Lv_S-r_Sv_\infty |/(r_Sr_L)$ into the right-hand side of (25), which provides

$$\begin{aligned} c_{11}(\delta _S)&:= -\dfrac{r_Lv_S(r_Lv_S+r_Sv_\infty \cos \delta _S)}{r_S+r_L} \nonumber \\&\quad \ \ \times \dfrac{\sqrt{2r_Sr_Lv_Sv_\infty (\cos \delta _S+1)}}{f(\delta _S)}. \end{aligned}$$

(26)

By the definition, $f(\delta _S)$ is positive for every $\delta _S\in (0,\pi /2]$ because of $\cos \delta _S\ge 0$. This and $\cos \delta _S\ge 0$ (for every $\delta _S\in (0,\pi /2]$) imply that $c_1(\delta _S,i_P)\le c_{11}(\delta _S)$ for every $i_P\in \mathbb {R}_{0+}$ satisfying (11) if $\delta _S\in (0,\pi /2]$. Thus, it follows from (24) that

$$\begin{aligned} P_e(\delta _S)\le c_2(\delta _S)i_P^2+c_{11}(\delta _S)i_P+c_0(\delta _S)+P_m, \end{aligned}$$

(27)

for every $i_P\in \mathbb {R}_{0+}$ satisfying (11) subject to $\delta _S\in (0,\pi /2]$. Replacing $\delta _S$ in (27) with $\delta _S^-$ gives

$$\begin{aligned} c_2(\delta _S^-)i_P^2+c_{11}(\delta _S^-)i_P+c_0(\delta _S^-) < 0, \end{aligned}$$

(28)

as a sufficient condition for (16).

Second, we derive a condition corresponding to (17). Based on $i_P\in \mathbb {R}_{0+}$, we substitute $i_P=0$ into the right-hand side of (25), which provides $c_{12}(\delta _S)$ in (20). Then, similar to the first case, we can show that $c_1(\delta _S,i_P)\ge c_{12}(\delta _S)$ for every $i_P\in \mathbb {R}_{0+}$ satisfying (11) under $\delta _S\in (0,\pi /2]$. Applying this to (24) yields

$$\begin{aligned} P_e(\delta _S)\ge c_2(\delta _S)i_P^2+c_{12}(\delta _S)i_P+c_0(\delta _S)+P_m, \end{aligned}$$

(29)

for every $i_P\in \mathbb {R}_{0+}$ satisfying (11) subject to $\delta _S\in (0,\pi /2]$. Replacing $\delta _S$ in (29) with $\delta _S^+$ gives

$$\begin{aligned} c_2(\delta _S^+)i_P^2+c_{12}(\delta _S^+)i_P+c_0(\delta _S^+) > 0, \end{aligned}$$

(30)

as a sufficient condition for (17).

In summary, if (28) and (30) hold, then (16) and (17) hold. Thus, if (28) and (30) hold for a $\delta _{S}^-\in (0,\pi /2)$ and a $\delta _{S}^+\in (\delta _{S}^-,\pi /2]$, then there exists at least one equilibrium point on $(\delta _{S}^-,\delta _{S}^+)\times \{0\}$ as described at the beginning of this section. Inequalities (28) and (30) have a solution under (C1), which is expressed as (C2). The derivation of (C2) is shown in Appendix B. This completes the proof. $\square$

Theorem 1 gives a sufficient condition on $i_P$ such that the system $\varSigma$ has equilibrium points. Condition (C1) guarantees that there exists at least one equilibrium point on $(\delta _{S}^-,\delta _{S}^+)\times \{0\}$ in the case of $i_P:=0$. In fact, by substituting $i_P=0$ to (6) and considering (18), we can show that $c_0(\delta _{S}^-)<0$ and $c_0(\delta _{S}^+)>0$ correspond to (16) and (17), respectively. On the other hand, condition (C2) holds when $i_P$ is sufficiently small. In fact, since $\alpha _{21}(\delta _S^+)$ is a positive real number as shown in Lemma 3 in Appendix B, there exists an $i_P>0$ satisfying (C2) for a given $\delta _{S}^+$. Hence, Theorem 1 means that if the power system given by removing $G_P$ from $\varSigma$ has equilibrium points, then the existence of the equilibrium points of $\varSigma$ is guaranteed as long as $i_P$ is sufficiently small.

We comment on the choice of $\delta _S^-$ and $\delta _S^+$. To use Theorem 1, we need to appropriately choose a $\delta _{S}^-\in (0,\pi /2)$ and a $\delta _{S}^+\in (\delta _{S}^-,\pi /2]$. A good choice is to let $\delta _S^-$ and $\delta _S^+$ be a sufficiently small positive number and $\pi /2$, respectively. The reason is that finding the equilibrium points becomes easier as the difference between $\delta _S^+$ and $\delta _S^-$ increases as shown in Fig. 4. In this method, we only have to check (C1) and (C2) for one pair consisting of a $\delta _S^-$ and a $\delta _S^+$.

3.3 Example

Consider again the system $\varSigma$ handled in Sect. 2.2.1, where $i_P:=0.2\,\mathrm{pu}$. Then, (11) in Lemma 1 is calculated as $i_P\le 1.74\,\mathrm{pu}$ and thus is satisfied. For $\delta _{S}^-:=0.01$ and $\delta _{S}^+:=\pi /2$, (18) provides $c_0(\delta _{S}^-)=-1.14$ and $c_0(\delta _{S}^+)=0.243$, from which condition (C1) in Theorem 1 holds. Moreover, since $\alpha _{21}(\delta _{S}^+)$ is calculated as $\alpha _{21}(\delta _{S}^+)=0.375$ from (19), condition (C2) is $i_P<0.375\,\mathrm{pu}$ and $i_P:=0.2\,\mathrm{pu}$ satisfies it. Hence, there exists at least one equilibrium point on $(0.01,\pi /2)\times \{0\}$ from Theorem 1.

Meanwhile, we see from Fig. 3 that when $i_P:=0.2\,\mathrm{pu}$, the system $\varSigma$ has an equilibrium point on $(0.01,\pi /2)\times \{0\}$, i.e., $[1.17\ \ 0]^\top$, which demonstrates the above result.

4 Stability of equilibrium points

Next, we address (b) in Problem 1. That is, we analyze the stability of the equilibrium points of the system $\varSigma$.

4.1 Main result

We introduce the new state variable vector $x(t):=[\delta _S(t)-\delta _S^\star \ \ \dot{\delta }_S(t)]^\top \in \mathbb {R}^2$ to shift the equilibrium point $[\delta _{S}^\star \ \ 0]^\top$ to $x=0$. Although the system $\varSigma$ is a hybrid system from (7) and (8), if $\sin \delta _S^\star > 0$, then there exists a set containing $x=0$ on which $\varSigma$ can be regarded as a non-hybrid system. In this case, it follows from (6), the first equations of (7) and (8), and (9) that the linearized system around $x=0$ is expressed as

$$\begin{aligned} \dot{x}(t)=Ax(t), \end{aligned}$$

(31)

where

$$\begin{aligned} A:= \begin{bmatrix} 0&1 \\ a_{21}(\delta _S^\star )&-\dfrac{D}{M} \end{bmatrix}, \end{aligned}$$

(32)

for

$$\begin{aligned} a_{21}(\delta _S^\star )&:=-\frac{v_Sv_\infty \cos \delta _S^\star }{M(r_S+r_L)} -\frac{r_Lv_Si_P\sin (\delta _S^\star -\delta _B(\delta _S^\star ))}{M(r_S+r_L)} \nonumber \\&\qquad \times \Biggl ( 1-\frac{1}{f(\delta _S^\star )} \biggl ( \frac{r_S^2r_L^2v_Sv_\infty i_P\sin \delta _S^\star }{\sqrt{f(\delta _S^\star )-r_S^2r_L^2i_P^2}} \nonumber \\&\qquad +r_L^2v_S^2+r_Sr_Lv_Sv_\infty \cos \delta _S^\star \biggr ) \Biggr ). \end{aligned}$$

(33)

An investigation of the eigenvalues of the matrix A enables us to analyze the stability of the equilibrium point $[\delta _{S}^\star \ \, 0]^\top$ (satisfying $\sin \delta _S^\star > 0$).

As a result, we obtain the following theorem.

Theorem 2

For the power system $\varSigma$, assume that (11) holds and there exists the equilibrium point $[\delta _S^\star \ \ 0]^\top$ satisfying $\sin \delta _S^\star > 0$. Then, the equilibrium point is asymptotically stable if $\ \delta _S^\star \in (0,\pi /2)$.

Proof

From (32), the eigenvalues $\lambda _1$ and $\lambda _2$ of A are given by

$$\begin{aligned}&\lambda _1 =\dfrac{-D-\sqrt{D^2+4a_{21}(\delta _S^\star )M}}{2M}, \end{aligned}$$

(34)

$$\begin{aligned}&\lambda _2 =\dfrac{-D+\sqrt{D^2+4a_{21}(\delta _S^\star )M}}{2M}. \end{aligned}$$

(35)

Therefore, it follows from $M,D\in \mathbb {R}_+$ that the equilibrium point $[\delta _S^\star \ \ 0]^\top$ is asymptotically stable if $a_{21}(\delta _S^\star )< 0$. The proof of $a_{21}(\delta _S^\star )<0$ is shown in Appendix C, which proves the theorem. $\square$

Theorem 2 characterizes the asymptotically stable equilibrium points of the system $\varSigma$. This result means that the equilibrium points found by Theorem 1 are asymptotically stable. That is, Theorem 1 presents a sufficient condition for the existence of the asymptotically stable equilibrium points.

4.2 Examples

Consider again the system $\varSigma$ handled in Sect. 2.2.1. As given in Sect. 3.3, a condition for the existence of the equilibrium points is $i_P<0.375\,\mathrm{pu}$.

For $i_P:=0.1,0.2,0.3\,\mathrm{pu}$ satisfying the above condition, we calculate $\delta _S^\star$ in the interval $(0,\pi )$ by numerically solving (10) and then obtain $\lambda _1$ and $\lambda _2$ in (34) and (35). The result is summarized in Table 1 where $j:=\sqrt{-1}$. We see that the equilibrium points satisfying $\delta _S^\star \in (0,\pi /2)$ are asymptotically stable because the real parts of the corresponding $\lambda _1$ and $\lambda _2$ are negative. This demonstrates Theorem 2.

As an example of the time response of the system $\varSigma$, that with $i_P:=0.3\,\mathrm{pu}$ is presented in Fig. 5, where $(\delta _S(0),\dot{\delta }_S(0)):=(1.2,-0.3)$ and the thin line expresses $\delta _S=1.31$, i.e., $\delta _S^\star$ in the asymptotically stable equilibrium point. It turns out that $\delta _S(t)$ converges to $\delta _S^\star$.

Table 1 Stability of equilibrium points ($\circ$: asymptotically stable; $\times$: unstable)

Fig. 5

Time response of $\varSigma$ with $i_P:=0.3\,\mathrm{pu}$

5 Conclusion

This paper has examined the existence of equilibrium points and their stability for a power system with a PV generator. By focusing on a property of the equilibrium points and using the intermediate value theorem, we have derived a condition under which the equilibrium points exist. Furthermore, we have characterized the asymptotically stable equilibrium points and have proven that these points are found by the existence condition. These results not only clarify the effect of PV penetration on small-signal stability, but are also useful to construct a power system with a PV generator with asymptotically stable equilibrium points.

Although this paper has presented a solution to the stability analysis problem, other problems remain to be addressed. For example, it would be necessary to extend our result to power systems consisting of multiple synchronous generators and PV generators. In addition, our result would have to be extended to controller design for power systems with PV generators.

Appendices

A Derivations of (6) and (7) [10]

Let $ae^{j\theta }$ be the complex number with the absolute value a and the argument $\theta$, where $e^{j\theta }=\cos \theta +j\sin \theta$. In addition, let $\overline{z}$ be the complex conjugate of the complex number z.

Consider the power system $\varSigma$ in Fig. 1. We have

$$\begin{aligned} \frac{v_Se^{j\delta _S}-v_Be^{j \delta _B}}{jr_S}+i_Pe^{j\delta _B}= \frac{v_Be^{j \delta _B}-v_\infty }{jr_L}, \end{aligned}$$

(36)

as a circuit equation. This can be rewritten as

$$\begin{aligned} v_B = \frac{r_Lv_Se^{j (\delta _S-\delta _B)}+jr_Sr_Li_P+r_Sv_\infty e^{- j\delta _B}}{r_S+r_L}. \end{aligned}$$

(37)

Thus, the complex power of the generator $G_S$ is given by

$$\begin{aligned}&v_Se^{j\delta _S}\frac{v_Se^{-j\delta _S}-\overline{v_B}e^{-j\delta _B}}{-jr_S}\nonumber \\&=\frac{v_Sv_\infty \sin \delta _S-r_Lv_Si_P\cos (\delta _S-\delta _B(\delta _S))}{r_S+r_L} \nonumber \\&\quad +j\,\Biggr ( -\frac{v_Sv_\infty \cos \delta _S+r_Lv_Si_P\sin (\delta _S-\delta _B(\delta _S))}{r_S+r_L} \nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \quad +\frac{v_S^2}{r_S}-\frac{r_Lv_S^2}{r_S(r_L+r_S)}\Biggl ) . \end{aligned}$$

(38)

By focusing on the real part of the right-hand side of (38), we obtain (6).

Next, we derive (7). From $v_B\in \mathbb {R}_+$, $\delta _B$ is determined so that the imaginary part of the right-hand side of (37) is equal to zero. Hence, we obtain

$$\begin{aligned}&r_Lv_S\sin (\delta _S-\delta _B)+r_Sr_Li_P+r_Sv_\infty \sin (-\delta _B) \nonumber \\&= r_Lv_S(\sin \delta _S\cos \delta _B-\cos \delta _S\sin \delta _B) \nonumber \\&\quad +r_Sr_Li_P-r_Sv_\infty \sin \delta _B \nonumber \\&= r_Lv_S\sin \delta _S\cos \delta _B \nonumber \\&\quad -(r_Lv_S\cos \delta _S+r_Sv_\infty )\sin \delta _B+r_Sr_Li_P \nonumber \\&=0, \end{aligned}$$

(39)

where the first equality is given by a trigonometric addition formula. For (39), we consider the following two cases.

• (a) Case of$\sin \delta _S\ne 0$: Combining $\cos \delta _B$ and $\sin \delta _B$ in (39) yields

  $$\begin{aligned}&\sqrt{(r_Lv_S\sin \delta _S)^2+(r_Lv_S\cos \delta _S+r_Sv_\infty )^2} \nonumber \\&\qquad \times \cos ( \delta _B +\phi (\delta _S)) =-r_Sr_Li_P. \end{aligned}$$

  (40)

  Equation (40) implies the first equation of (7).

• (b) Case of$\sin \delta _S= 0$: By substituting $\sin \delta _S= 0$ into (39), we obtain the second equation of (7).

From (a) and (b), (7) is derived.

B Derivation of (C2) in Theorem 1

1.1 B.1 Preliminary

We prepare the following lemma.

Lemma 2

Consider $c_{12}(\delta _S)$, $c_{2}(\delta _S)$, and $c_{11}(\delta _S)$ in (20), (21), and (26). These are negative for every $\delta _S\in (0,\pi /2]$.

Proof

From (20)–(22), (26), and $\sin \delta _S>0$ and $\cos \delta _S \ge 0$ for every $\delta _S\in (0,\pi /2]$, we prove the lemma. $\square$

Lemma 2 leads to the following result.

Lemma 3

Consider $\alpha _{21}(\delta _S)$ in (19). Let

$$\begin{aligned}&\alpha _{22}(\delta _{S}):=\dfrac{-c_{12}(\delta _{S})+\sqrt{c_{12}^2(\delta _{S})-4c_2(\delta _{S})c_0(\delta _{S})}}{2c_2(\delta _{S})}, \end{aligned}$$

(41)

$$\begin{aligned}&\alpha _{11}(\delta _{S}):=\dfrac{-c_{11}(\delta _{S})-\sqrt{c_{11}^2(\delta _{S})-4c_2(\delta _{S})c_0(\delta _{S})}}{2c_2(\delta _{S})}. \end{aligned}$$

(42)

Then, the following statements hold.

• (a) For every $\delta _{S}^+\in (0,\pi /2]$ satisfying $c_0(\delta _S^+)>0$ in (C1) in Theorem 1, $\alpha _{21}(\delta _S^+)$ and $\alpha _{22}(\delta _S^+)$ are positive and negative real numbers, respectively.

• (b) For every $\delta _{S}^-\in (0,\pi /2)$ satisfying $c_0(\delta _S^-)<0$ in (C1) and $c_{11}^2(\delta _{S}^-)-4c_2(\delta _{S}^-)c_0(\delta _{S}^-)>0$, $\alpha _{11}(\delta _S^-)$ is a negative real number.

Proof

(a) From $\delta _S^+\in (0,\pi /2]$ and Lemma 2, we obtain $c_{12}(\delta _S^+)<0$ and $c_2(\delta _S^+)<0$. This and $c_0(\delta _S^+)>0$ imply

$$\begin{aligned} -c_{12}(\delta _{S}^+)-\sqrt{c_{12}^2(\delta _{S}^+)-4c_2(\delta _{S}^+)c_0(\delta _{S}^+)}<0, \end{aligned}$$

where $c_{12}^2(\delta _S^+)-4c_2(\delta _S^+)c_0(\delta _S^+)>0$ is noted. Thus, it follows from (19) and $c_2(\delta _S^+)<0$ that $\alpha _{21}(\delta _S^+)$ is a positive real number. Meanwhile, (41), $c_{12}(\delta _S^+)<0$, $c_2(\delta _S^+)<0$, and $c_{12}^2(\delta _S^+)-4c_2(\delta _S^+)c_0(\delta _S^+)>0$ show that $\alpha _{22}(\delta _S^+)$ is a negative real number. This completes the proof of (a).

(b) From $\delta _S^-\in (0,\pi /2)$ and Lemma 2, we have $c_{2}(\delta _S^-)<0$ and $c_{11}(\delta _S^-)<0$. Therefore, it follows from $c_0(\delta _S^-)<0$ that

$$\begin{aligned} -c_{11}(\delta _{S}^-)-\sqrt{c_{11}^2(\delta _{S}^-)-4c_2(\delta _{S}^-)c_0(\delta _{S}^-)}>0, \end{aligned}$$

where $c_{11}^2(\delta _{S}^-)-4c_2(\delta _{S}^-)c_0(\delta _{S}^-)>0$ is used. This, together with (42) and $c_{2}(\delta _S^-)<0$, proves (b). $\square$

Lemma 3 provides the properties of the solutions to the quadratic equations

$$\begin{aligned}&c_2(\delta _S^-)i_P^2+c_{11}(\delta _S^-)i_P+c_0(\delta _S^-)=0, \end{aligned}$$

(43)

$$\begin{aligned}&c_2(\delta _S^+)i_P^2+c_{12}(\delta _S^+)i_P+c_0(\delta _S^+)=0. \end{aligned}$$

(44)

By using these properties, we derive (C2) in Theorem 1 in the next section.

1.2 B.2 Main part

Condition (C2) is given as a solution to the simultaneous inequalities of (28) and (30). In what follows, we solve each inequality and then show (C2).

1.2.1 B.2.1 Solution to (28)

First, we consider (43). This has three types of solutions depending on the value of $c_{11}^2(\delta _S^-)-4c_2(\delta _S^-)c_0(\delta _S^-)$. Hence, (28) also has three types of solutions, which are described as follows.

• (a) Case of$c_{11}^2(\delta _S^-)-4c_2(\delta _S^-)c_0(\delta _S^-)>0$: Equation (43) has the two real solutions $i_P=\alpha _{11}(\delta _S^-)$ and $i_P=\alpha _{12}(\delta _S^-)$ where

  $$\begin{aligned} \alpha _{12}(\delta _{S}):=\dfrac{-c_{11}(\delta _{S})+\sqrt{c_{11}^2(\delta _{S})-4c_2(\delta _{S})c_0(\delta _{S})}}{2c_2(\delta _{S})}. \end{aligned}$$

  (45)

  We should notice that $\alpha _{12}(\delta _S^-)<\alpha _{11}(\delta _S^-)$ from $c_{2}(\delta _S^+)<0$ in the proof of Lemma 3. This fact and $c_2(\delta _S^+)<0$ show that a solution to (28) is expressed as

  $$\begin{aligned} i_P<\alpha _{12}(\delta _S^-)\ \ \mathrm{or} \ \ i_P>\alpha _{11}(\delta _S^-). \end{aligned}$$

  (46)

• (b) Case of$c_{11}^2(\delta _S^-)-4c_2(\delta _S^-)c_0(\delta _S^-)=0$: The solution to (43) is $i_P=-c_{11}(\delta _{S}^-)/(2c_2(\delta _{S}^-))$. Therefore, it follows from $c_2(\delta _S^-)<0$ in the proof of Lemma 3 that $i_P\ne -c_{11}(\delta _{S}^-)/(2c_2(\delta _{S}^-))$ solves (28). This means that (28) holds for every $i_P\in \mathbb {R}_{0+}$ since $-c_{11}(\delta _{S}^-)/(2c_2(\delta _{S}^-))<0$ from $c_{11}(\delta _{S}^-)<0$ in the proof of Lemma 3 and $c_2(\delta _S^-)<0$.

• (c) Case of$c_{11}^2(\delta _S^-)-4c_2(\delta _S^-)c_0(\delta _S^-)<0$: There are no real solutions to (43), which implies that (28) holds for every $i_P\in \mathbb {R}_{0+}$ because of $c_2(\delta _S^-)<0$.

1.2.2 B.2.2 Solution to (30)

We next consider (44). Since $c_{12}^2(\delta _S^+)-4c_2(\delta _S^+)c_0(\delta _S^+)>0$ as shown in the proof of Lemma 3, (44) has the two real solutions $i_P=\alpha _{21}(\delta _S^+)$ and $i_P=\alpha _{22}(\delta _S^+)$. This and $c_2(\delta _S^+)<0$ imply that

$$\begin{aligned} \alpha _{22}(\delta _S^+)<i_P<\alpha _{21}(\delta _S^+) \end{aligned}$$

(47)

solves (30) because $\alpha _{22}(\delta _S^+)<\alpha _{21}(\delta _S^+)$ from Lemma 3.

1.2.3 B.2.3 Solution to (28) and (30)

The solution to be obtained satisfies both (28) and (30). Thus, from the above discussion, we consider the following three cases.

• (a) Case of$c_{11}^2(\delta _S^-)-4c_2(\delta _S^-)c_0(\delta _S^-)>0$: From (46) and (47), a solution to (28) and (30) is given by $i_P>\alpha _{11}(\delta _S^-)$ and $\alpha _{22}(\delta _S^+)<i_P<\alpha _{21}(\delta _S^+)$. Therefore, by noting $\alpha _{11}(\delta _S^-)<0$, $\alpha _{21}(\delta _S^+)>0$, and $\alpha _{22}(\delta _S^+)<0$ in Lemma 3, we obtain (C2) in Theorem 1.

• (b) Case of$c_{11}^2(\delta _S^-)-4c_2(\delta _S^-)c_0(\delta _S^-)=0$: As mentioned in (b) in Appendix B.2.1, (28) holds for every $i_P\in \mathbb {R}_{0+}$. Hence, in a similar way to that in (a), we obtain (C2) as a solution to (28) and (30).

• (c) Case of$c_{11}^2(\delta _S^-)-4c_2(\delta _S^-)c_0(\delta _S^-)<0$: Similar to (b), we obtain (C2) as a solution to (28) and (30).

From (a)–(c), we derive (C2) in Theorem 1.

C Proof of $a_{21}(\delta _S^\star )< 0$ in proof of Theorem 2

We show $a_{21}(\delta _S^\star )< 0$ by considering the following three cases for $\sin (\delta _S^\star -\delta _B(\delta _S^\star ))$ in $a_{21}(\delta _S^\star )$ in (33).

1.1 C.1 Case of $\sin (\delta _S^\star -\delta _B(\delta _S^\star ))>0$

If $\delta _S^\star \in (0,\pi /2)$, then $\sin (\delta _S^\star )> 0$. Furthermore, Lemma 1 means that (12) holds for every $\delta _S^\star \in (0,\pi /2)$ subject to (11). Thus, the first equations of (7) and (8), and (1)–(4) provide

$$\begin{aligned} \sin (\delta _S^\star -\delta _B(\delta _S^\star )) =&-\dfrac{r_Sr_Li_P(r_Lv_S+r_Sv_\infty \cos \delta _S^\star )}{f(\delta _S^\star )} \nonumber \\&+ \frac{r_Sv_\infty \sin \delta _S^\star \sqrt{f(\delta _S^\star )-r_S^2r_L^2i_P^2}}{f(\delta _S^\star )}. \end{aligned}$$

(48)

From a similar discussion to that in the proof of Theorem 1, $f(\delta _S^\star )>0$ holds for every $\delta _S^\star \in (0,\pi /2)$. Hence, (48) and $\sin (\delta _S^\star -\delta _B(\delta _S^\star ))>0$ imply

$$\begin{aligned}&r_Sv_\infty \sin \delta _S^\star \sqrt{f(\delta _S^\star )-r_S^2r_L^2i_P^2} \nonumber \\&\qquad \qquad \qquad \qquad >r_Sr_Li_P(r_Lv_S+r_Sv_\infty \cos \delta _S^\star ). \end{aligned}$$

(49)

For $a_{21}(\delta _S^\star )$ in (33), (49) yields

$$\begin{aligned} \frac{r_S^2r_L^2v_Sv_\infty i_P\sin \delta _S^\star }{\sqrt{f(\delta _S^\star )-r_S^2r_L^2i_P^2}}&= \frac{r_S^3r_L^2v_Sv_\infty ^2 i_P\sin ^2\delta _S^\star }{r_Sv_\infty \sin \delta _S^\star \sqrt{f(\delta _S^\star )-r_S^2r_L^2i_P^2}} \nonumber \\&< \frac{r_S^3r_L^2v_Sv_\infty ^2 i_P\sin ^2\delta _S^\star }{r_Sr_Li_P(r_Lv_S+r_Sv_\infty \cos \delta _S^\star )} \nonumber \\&= \frac{r_S^2r_Lv_Sv_\infty ^2 \sin ^2\delta _S^\star }{r_Lv_S+r_Sv_\infty \cos \delta _S^\star }. \end{aligned}$$

(50)

In addition, we obtain

$$\begin{aligned}&\frac{1}{f(\delta _S^\star )}\left( \frac{r_S^2r_L^2v_Sv_\infty i_P\sin \delta _S^\star }{\sqrt{f(\delta _S^\star )-r_S^2r_L^2i_P^2}}+r_L^2v_S^2+r_Sr_Lv_Sv_\infty \cos \delta _S^\star \right) \nonumber \\&< \frac{1}{f(\delta _S^\star )}\left( \frac{r_S^2r_Lv_Sv_\infty ^2 \sin ^2\delta _S^\star }{r_Lv_S+r_Sv_\infty \cos \delta _S^\star } +r_L^2v_S^2+r_Sr_Lv_Sv_\infty \cos \delta _S^\star \right) \nonumber \\&= \frac{1}{f(\delta _S^\star )} \left( \frac{r_Lv_S(r_S^2v_\infty ^2 \sin ^2\delta _S^\star +(r_Lv_S+r_Sv_\infty \cos \delta _S^\star )^2)}{r_Lv_S+r_Sv_\infty \cos \delta _S^\star } \right) \nonumber \\&= \frac{r_Lv_S}{r_Lv_S+r_Sv_\infty \cos \delta _S^\star } \nonumber \\&< 1, \end{aligned}$$

(51)

where the first inequality is derived by (50) and $f(\delta _S^\star )>0$ for every $\delta _S^\star \in (0,\pi /2)$, the second and third equalities are given by a simple calculation and (22), respectively, and the last inequality follows from $\cos \delta _S^\star > 0$ for every $\delta _S^\star \in (0,\pi /2)$. This, together with (33), $\cos \delta _S^\star > 0$, and $\sin (\delta _S^\star -\delta _B(\delta _S^\star ))>0$, shows $a_{21}(\delta _S^\star )< 0$.

1.2 C.2 Case of $\sin (\delta _S^\star -\delta _B(\delta _S^\star ))<0$

In a similar way to that in the previous section, we have

$$\begin{aligned} \frac{r_S^2r_L^2v_Sv_\infty i_P\sin \delta _S^\star }{\sqrt{f(\delta _S^\star )-r_S^2r_L^2i_P^2}} > \frac{r_S^2r_Lv_Sv_\infty ^2 \sin ^2\delta _S^\star }{r_Lv_S+r_Sv_\infty \cos \delta _S^\star }, \end{aligned}$$

(52)

instead of (50). Thus, similar to (51), we obtain

$$\begin{aligned}&\frac{1}{f(\delta _S^\star )}\left( \frac{r_S^2r_L^2v_Sv_\infty i_P\sin \delta _S^\star }{\sqrt{f(\delta _S^\star )-r_S^2r_L^2i_P^2}}+r_L^2v_S^2+r_Sr_Lv_Sv_\infty \cos \delta _S^\star \right) \nonumber \\&> \frac{r_Lv_S}{r_Lv_S+r_Sv_\infty \cos \delta _S^\star }. \end{aligned}$$

(53)

This and (33) provide

$$\begin{aligned} a_{21}(\delta _S^\star )&< -\frac{v_Sv_\infty \cos \delta _S^\star }{M(r_S+r_L)} -\frac{r_Lv_Si_P\sin (\delta _S^\star -\delta _B(\delta _S^\star ))}{M(r_S+r_L)} \nonumber \\&\quad \;\times \Biggl ( 1-\frac{r_Lv_S}{r_Lv_S+r_Sv_\infty \cos \delta _S^\star } \Biggr ) \nonumber \\&= -\frac{1}{M(r_S+r_L)} \left( v_Sv_\infty \cos \delta _S^\star + r_Lv_Si_P \right. \nonumber \\&\quad \times \left( -\dfrac{r_Sr_Li_P(r_Lv_S+r_Sv_\infty \cos \delta _S^\star )}{f(\delta _S^\star )} \right. \nonumber \\&\quad \left. + \frac{r_Sv_\infty \sin \delta _S^\star \sqrt{f(\delta _S^\star )-r_S^2r_L^2i_P^2}}{f(\delta _S^\star )}\right) \nonumber \\&\quad \left. \times \left( 1- \frac{r_Lv_S}{r_Lv_S+r_Sv_\infty \cos \delta _S^\star } \right) \right) \nonumber \\&= -\frac{1}{M(r_S+r_L)} \left( v_Sv_\infty \cos \delta _S^\star \right. -\dfrac{r_S^2r_L^2v_Sv_\infty i_P^2\cos \delta _S^\star }{f(\delta _S^\star )} \nonumber \\&\quad \left. +\dfrac{r_S^2r_Lv_Sv_\infty i_P\sin \delta _S^\star \cos \delta _S^\star \sqrt{f(\delta _S^\star )-r_S^2r_L^2i_P^2}}{f(\delta _S^\star )(r_Lv_S+r_Sv_\infty \cos \delta _S^\star )} \right) ,\nonumber \\ \end{aligned}$$

(54)

where the first inequality is obtained from (53) and $\sin (\delta _S^\star -\delta _B(\delta _S^\star ))<0$, the second equality follows from (48), and the last one is given by a simple calculation. Thus, we obtain

$$\begin{aligned}&a_{21}(\delta _S^\star )<-\frac{1}{M(r_S+r_L)} \left( v_Sv_\infty \cos \delta _S^\star \right. \nonumber \\& -\dfrac{(r_Lv_S-r_Sv_\infty )^2v_Sv_\infty \cos \delta _S^\star }{f(\delta _S^\star )} \nonumber \\& \left. +\dfrac{r_S^2r_Lv_Sv_\infty i_P\sin \delta _S^\star \cos \delta _S^\star \sqrt{f(\delta _S^\star )-r_S^2r_L^2i_P^2}}{f(\delta _S^\star )(r_Lv_S+r_Sv_\infty \cos \delta _S^\star )} \right) \nonumber \\&= -\frac{1}{M(r_S+r_L)} \left( \dfrac{2r_Sr_Lv_S^2v_\infty ^2 \cos \delta _S^\star (\cos \delta _S^\star +1)}{f(\delta _S^\star )} \right. \nonumber \\& \left. +\dfrac{r_S^2r_Lv_Sv_\infty i_P\sin \delta _S^\star \cos \delta _S^\star \sqrt{f(\delta _S^\star )-r_S^2r_L^2i_P^2}}{f(\delta _S^\star )(r_Lv_S+r_Sv_\infty \cos \delta _S^\star )} \right) \nonumber \\&<0, \end{aligned}$$

(55)

where the first inequality is derived by (11) and $f(\delta _S^\star )>0$ for every $\delta _S^\star \in (0,\pi /2)$, the second equality is given by (22), and the last inequality follows from $\sin \delta _S^\star > 0$, $\cos \delta _S^\star > 0$, and $f(\delta _S^\star )>0$ for every $\delta _S^\star \in (0,\pi /2)$. From (55), the proof is completed.

1.3 C.3 Case of $\sin (\delta _S^\star -\delta _B(\delta _S^\star ))=0$

As a direct consequence of (33) and $\cos \delta _S^\star > 0$ for every $\delta _S^\star \in (0,\pi /2)$, $a_{21}(\delta _S^\star )< 0$ is established.