1 Introduction

Dual active bridge (DAB) DC-DC converters have several advantages, such as bidirectional power flow, high power density, easy implementation of zero-voltage switching, convenient access to cascading and parallelism. As a result, these converters are widely used in the distributed generation systems [1,2,3], DC-micro-grid systems [4], electric vehicle charging systems [5,6,7,8], energy storage systems [9, 10], and power electronic transformers in railway locomotive applications [11, 12].

In applications mentioned above, it is significant to achieve robust dynamic performances of DAB DC-DC converters under challenging circumstances, such as input voltage fluctuation, output load disturbance, and etc. Various advanced control schemes have been proposed to enhance the dynamic response. Firstly, dynamic characteristics of DAB DC-DC converters were analyzed by the small-signal modeling and the discrete-time average modeling methods [13,14,15]. A feed-forward compensation strategy [16], which feedbacks the load current to the control system, was used to improve transient response of DAB DC-DC converters in the load disturbance conditions. However, a table lookup is essential for the feed-forward strategy, which makes it less applicable in complex operation conditions. Besides, a model-based phase-shift (MPS) control was also developed to improve dynamic response under load disturbance [17, 18]. Meanwhile, high efficiency is another critical requirement for DAB DC-DC converters. Switching strategies utilizing off-line computation have capability in minimizing power losses [19, 20]. However, consecutive optimal control cannot be realized by these strategies. Reducing current stress and power reflow in a DAB DC-DC converter can increase efficiency as well [21]. Extended phase shift (EPS) control, which is able to largely improve efficiency by reducing current stress, was introduced in [4]. However, when EPS control was adopted to DAB DC-DC converters, there usually exists slow dynamic response issues.

Direct power control (DPC) scheme is a popular active solution to enhance dynamic performance of AC-DC or DC-AC converters [22, 23]. It is well known for its strong abilities to improve dynamic and static performances of power converters. However, there are few reports about the DPC scheme applied in DAB DC-DC converters so far.

By combing EPS control with DPC control, a hybrid scheme EPS-DPC is proposed in this paper. The EPS-DPC scheme unites high efficiency of EPS and great dynamic performance of DPC. As a result, the DAB DC-DC converter using EPS-DPC has advantages in both high efficiency and outstanding dynamic performance.

The paper is organized as follows. SPS and EPS control schemes are introduced and compared in detail in Section 2. In Section 3, EPS-DPC control is proposed, and its derivation from combination of EPS and DPC is included as well. Theoretical comparison of dynamic response performance in EPS and SPS was demonstrated in Section 4. A scale-down DAB DC-DC converter prototype was designed and built to test performance of the proposed EPS-DPC scheme, the EPS control with traditional voltage-loop (EPS-TVL), and the single phase shift (SPS) control with traditional voltage-loop (SPS-TVL). And a comparison of experimental results was carried out in Section 5. Conclusions are drawn from theoretical analysis and experimental results comparison, and then summarized in Section 6.

2 Theoretical analysis of single phase shift and extend phase shift controls

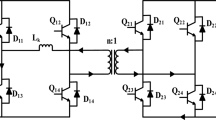
A typical topology of a DAB DC-DC converter is shown in Fig. 1, and its equivalent model under phase shift control is shown in Fig. 2.

Fig. 1
figure 1

DAB DC-DC converter topology

Full size image
Fig. 2
figure 2

Equivalent model of DAB DC-DC converter with phase shift control

Full size image

In Fig. 2, L is the total inductance of the transformer leakage inductor and auxiliary inductor; U ab and U cd are the output pulse voltages of H 1-bridge and H 2-bridge respectively; U L is the voltage across the inductor, while i L is the current through the inductor; n is the transformer voltage conversion ratio.

The main waveforms of a DAB DC-DC converter with SPS control are shown in Fig. 3, where T S is the switching period, D is the phase shift ratio between S1S3 and S5S7.

Fig. 3
figure 3

Waveforms of DAB DC-DC converters with SPS control

Full size image

It can been seen in Fig. 3 that i L is out of phase with U ab during t 0 to t 01 and t 2 to t 23 intervals in a switching period. Thus, the transmission power is negative during these intervals, and it is defined as power reflow. Transmission power P, power reflow Q S and current stress i PS of DAB DC-DC converters with SPS control can be expressed as:

$$\left\{ \begin{aligned} P{ = }\frac{{nT_{\text{S}}^{{}} U_{\text{in}}^{{}} U_{\text{o}}^{{}} }}{2L}D ( 1 { - }D )\hfill \\ Q_{\text{S}} = \frac{{nT_{\text{S}}^{{}} U_{\text{in}}^{{}} U_{\text{o}}^{{}} }}{16L(k + 1)}[k + (2D - 1)]^{2} \hfill \\ i_{\text{PS}}^{{}} = \frac{{nT_{\text{S}}^{{}} U_{\text{o}}^{{}} }}{2L}(2D - 1 + k) \hfill \\ \end{aligned} \right.$$
(1)

where k is the voltage ratio and k = U in/(nU o). P, Q S and i PS given in (1) can be further simplified into (2).

$$\left\{ \begin{aligned} p{ = }\,\frac{P}{{P_{\text{N}}^{{}} }} = 4D ( 1 { - }D )\hfill \\ q_{\text{S}} = \frac{{Q_{\text{S}} }}{{P_{\text{N}}^{{}} }} = \frac{{[k + (2D - 1)]^{2} }}{2(k + 1)} \hfill \\ i_{\text{ps}}^{{}} = \frac{{i_{\text{PS}}^{{}} }}{{i_{\text{PN}}^{{}} }} = 2(2D - 1 + k) \hfill \\ \end{aligned} \right.$$
(2)

where P N and i PN are:

$$\left\{ \begin{aligned} P_{\text{N}}^{{}} = \frac{{nT_{\text{S}}^{{}} U_{\text{in}}^{{}} U_{\text{o}}^{{}} }}{8L} \hfill \\ i_{\text{PN}}^{{}} = \frac{{nT_{\text{S}}^{{}} U_{\text{o}}^{{}} }}{4L} \hfill \\ \end{aligned} \right.$$
(3)

The main waveforms of DAB DC-DC converters with EPS control [4] are shown in Fig. 4. D 1 is the phase shift ratio between S1 and S3; D 2 is the phase shift ratio between S3 and S5, S7.

Fig. 4
figure 4

Waveforms of DAB DC-DC converters with EPS control

Full size image

Similarly, transmission power P, power reflow Q E and current stress i PE of the DAB DC-DC converter with EPS control can be expressed as:

$$\left\{ \begin{aligned} P = \frac{{nT_{\text{S}}^{{}} U_{\text{in}}^{{}} U_{\text{o}}^{{}} }}{4L}(D_{1}^{{}} + 2D_{2}^{{}} - D_{1}^{2} - 2D_{2}^{2} - 2D_{1}^{{}} D_{2}^{{}} ) \hfill \\ Q_{\text{E}} = \frac{{nT_{\text{S}}^{{}} U_{\text{in}}^{{}} U_{\text{o}}^{{}} [k(1 - D_{1} ) + (2D_{2} - 1)]^{2} }}{16L(k + 1)} \hfill \\ i_{\text{PE}}^{{}} = \frac{{nT_{\text{S}}^{{}} U_{\text{o}}^{{}} }}{2L}[k(1{ - }D_{1}^{{}} ) + 2D_{1}^{{}} + 2D_{2}^{{}} - 1] \hfill \\ \end{aligned} \right.$$
(4)

Then, P, Q E and i PE can be simplified as:

$$\left\{ \begin{aligned} p = 2(D_{1}^{{}} + 2D_{2}^{{}} - D_{1}^{2} - 2D_{2}^{2} - 2D_{1}^{{}} D_{2}^{{}} ) \hfill \\ q_{\text{E}} = \frac{{[k(1 - D_{1} ) + (2D_{2} - 1)]^{2} }}{2(k + 1)} \hfill \\ i_{\text{pe}}^{{}} = 2[k(1{ - }D_{1}^{{}} ) + 2D_{1}^{{}} + 2D_{2}^{{}} - 1] \hfill \\ \end{aligned} \right.$$
(5)

In order to reduce current stress and power reflow of SPS control, a constrained optimization method is adopted [4] under EPS control, and phase-shift ratios D 1 and D 2 can be calculated with respect to D under the same transmission power circumstance. Phase-shift ratio D 1 can be calculated as follow.

$$D_{1}=\left\{ \begin{aligned} & \frac{1-\sqrt{2(1-2D)^2-1}}{2} {\quad} {\quad} {K < 2, 0 \leq D < (2-{\sqrt{2}})/4}\\ &\frac{1+\sqrt{2(1-2D)^2-1}}{2} {\quad}{\quad} {K \geq 2, 0 \leq D < (2-{\sqrt{2}})/4}\\ &\sqrt{2}(1-2D)/2 {\quad} {\quad} {\quad} {\quad}{\,\,\,\,}(2-\sqrt{2})/4 \leq D < {1/2}\end{aligned}\right.$$
(6)

Similarly, phase-shift ratio D 2 can be calculated as follow.

$$D_{2}=\left\{ \begin{aligned} &{0} {\quad}{\quad}{\quad}{\quad}{\quad}{\quad}{\quad}{\,\,\,\,\,\,\,}{\quad}{0 \leq D < (2-{\sqrt{2}})/4}\\ &\frac{1-{\sqrt{2}}(1-2D)}{2} {\quad}{\,\,\,\,\,\,\,\,\,\,\,}(2-\sqrt{2})/4 \leq D < {1/2} \end{aligned}\right.$$
(7)

According to (6) and (7), the relationship between D 1 and D 2 can be derived as:

$$D_{2}=\left\{ {\begin{array}{*{20}l} {0} & {0 \le D < \left( {2 - \sqrt 2 } \right)/4} \\ \frac{1}{2} - D_{1}^{{}} & {\left( {2 - \sqrt 2 } \right)/4 \le D < 1/2} \\ \end{array} } \right.$$
(8)

In addition, according to (2), the simplified current stress i ps and the simplified power reflow q S in SPS control are functions of the simplified transmission power p, which are given in (9).

$$\left\{ \begin{aligned} & i_{\text{ps}}^{{}} = 2\left( {k - \sqrt {1 - p} } \right) \\ &q_{\text{S}} = \frac{{k - \sqrt {1 - p} }}{2(k + 1)} \hfill \\ \end{aligned} \right.$$
(9)

Similarly, according to (5) and (12), the simplified current stress i pe and the simplified power reflow q E in EPS control can be written in functions of the simplified transmission power p as follows.

$$ i_{\text{pe}}^{{}} = \left\{ \begin{aligned}& k + (2 - k)\sqrt {1 - 2p} {\quad} {\quad} \,{0 \le p \le \frac{1}{2}} \\ &2k - k\sqrt {2 - 2p} {\qquad} {\qquad} {\frac{1}{2} < p \le 1} \hfill \\ \end{aligned} \right.$$
(10)
$$q_{\text{E}}^{{}} = \left\{ \begin{aligned} &\frac{{\left[ {k\left( {1 + \sqrt {1 - 2p} } \right) - 2} \right]^{2} }}{ 2(k + 1)} {\qquad} {0 \le p \le \frac{1}{2}} \\ &\frac{{\left[ {k\left( {1 - \sqrt {\frac{1 - p}{ 2}} } \right) - 2\sqrt {\frac{1 - p}{ 2}} } \right]^{2} }}{ 2(k + 1)} {\quad} {\frac{1}{2} < p \le 1} \hfill \\ \end{aligned}\right.$$
(11)

According to (9)–(11), in SPS and EPS schemes, characteristics of the simplified current stress and simplified power reflow with respect to the unified transmission power p are shown in Fig. 5.

Fig. 5
figure 5

Characteristics comparison between SPS and EPS controls

Full size image

It can be seen from Fig. 5a that both the simplified power reflows in SPS and EPS schemes increase with voltage conversion ratio k. Under the same k value, the power reflow with SPS control continuously increases with the increasing of p, while the power reflow with EPS control decreases firstly and then increases with p increasing. In the full range of k from 0 to 1, q E of EPS is always smaller than q S of SPS, which validates that EPS can effectively reduce power reflow, compared with SPS. In addition, it can be concluded from Fig. 5b that both current stresses in SPS and EPS schemes increase with transmission power p at various voltage conversion ratios k. Comparison results indicate that EPS reaches smaller current stress than SPS. In conclusion, compared with SPS control, EPS control has advantages in reducing the power reflow and current stress of DAB DC-DC converters at the same time.

3 Hybrid scheme of EPS control and DPC scheme

DPC scheme is one of the classical control strategies to improve dynamic performances of power converters [22, 23]. Since the desired output voltage is always related to the transmission power in voltage-source converters, the transmission power is an important parameter for power converters. The series inductance L, the switching period T S and the transformer voltage ratio n can be considered as constant values in the DAB DC-DC converters. Thus, according to (4), the desired transmission power p * in EPS-DPC scheme can be defined as:

$$ \begin{aligned} p_{{}}^{*} = \frac{4L}{{nT_{\text{S}}^{{}} }}p \mathop {}\nolimits_{{}} = U_{\text{in}}^{{}} U_{\text{o}}^{{}} (D_{1}^{{}} + 2D_{2}^{{}} - D_{1}^{2} - 2D_{2}^{2} - 2D_{1}^{{}} D_{2}^{{}} ) \hfill \\ \end{aligned} $$
(12)

Combining (8) and (12), the phase-shift ratios D 1 can be expressed with p * as:

$$ D_{1}^{{}} = \left\{ \begin{aligned} &\frac{1}{2}{\kern 1pt} + \sqrt {\frac{1}{4} - \frac{{2p_{{}}^{*} }}{{U_{\text{o}}^{{}} U_{\text{in}}^{{}} }}} {\quad}0 \le p_{{}}^{*} < \frac{{U_{\text{o}}^{{}} U_{\text{in}}^{{}} }}{8},k \ge 2 \hfill \\& \frac{1}{2} - \sqrt {\frac{1}{4} - \frac{{2p_{{}}^{*} }}{{U_{\text{o}}^{{}} U_{\text{in}}^{{}} }}} {\quad}0 \le p_{{}}^{*} < \frac{{U_{\text{o}}^{{}} U_{\text{in}}^{{}} }}{8},k < 2 \hfill \\ &\sqrt {\frac{1}{2} - \frac{{2p_{{}}^{*} }}{{U_{\text{o}}^{{}} U_{\text{in}}^{{}} }}} {\quad} {\quad}{\,}{\,}{\,}\frac{{U_{\text{o}}^{{}} U_{\text{in}}^{{}} }}{8} \le p_{{}}^{*} \le \frac{{U_{\text{o}}^{{}} U_{\text{in}}^{{}} }}{4} \hfill \\ \end{aligned} \right. $$
(13)

Similarly, the phase-shift ratios D 2 can be expressed with p * as:

$$D_{2}^{{}} = \left\{ \begin{aligned} &0{\quad}{\quad}{\quad}{\quad}{\quad}{\quad}{\quad}{\quad} {\,} 0 \le p_{{}}^{*} < \frac{{U_{\text{o}}^{{}} U_{\text{in}}^{{}} }}{8} \hfill \\ &\frac{1}{2}- \sqrt {\frac{1}{2} - \frac{{2p_{{}}^{*} }}{{U_{\text{o}}^{{}} U_{\text{in}}^{{}} }}} {\quad}{\,\,}\frac{{U_{\text{o}}^{{}} U_{\text{in}}^{{}} }}{8} \le p_{{}}^{*} \le \frac{{U_{\text{o}}^{{}} U_{\text{in}}^{{}} }}{4} \hfill \\ \end{aligned} \right.$$
(14)

According to (14), characteristics of phase-shift ratios and the desired transmission power with uniformization can be seen in Fig. 6.

Fig. 6
figure 6

Characteristics of phase-shift ratios and desired transmission power

Full size image

From Fig. 6, it is clear that when p * is smaller than 0.125U in U o, the phase-shift ratio D 2 is equal to zero; and then, with the increase of p *, the phase-shit ratio D 2 gradually increases, and it reaches 0.5 when p * = 0.25U in U o. Differently, when p * is smaller than 0.125U in U o, there are two variation trends of the phase-shift ratio D 1. When k is smaller than 2, D 1 increases along with p *. In contrary, when k is equal to or larger than 2, D 1 decreases as p * increases. Moreover, when p * is larger than 0.125U in U o, D 1 gradually decreases and down to zero when p * increases to 0.25U in U o.

The optimized phase-shift ratios in the EPS-DPC scheme can be obtained from (14) as well. Figure 7 shows the overall procedure flowchart which is used to estimate the optimized values D 1 and D 2, where p * is the output of the voltage outer loop PI controller and represents the unified transmission power reference.

Fig. 7
figure 7

Calculating procedure of optimal phase-shift ratios in EPS-DPC scheme

Full size image

Moreover, according to (8), D 2 can be expressed with respect to D 1 in the EPS control system. In order to implement the close-loop control of the EPS control, combining (6)–(8), and D 1 and D 2 can be expressed by the output of the PI controller as follows.

$$ D_{1}^{{}} = \left\{ \begin{aligned} &1 / 2 { - }PI_{\text{out}}^{{}} {\quad}0 \le p_{{}}^{*} 1/4,k \ge 2 \hfill \\ {\kern 1pt} &PI_{\text{out}}^{{}} {\quad}{\quad}{\,\,\,\,\,\,\,}0 \le PI_{\text{out}}^{{}} {\kern 1pt} {\quad}1/4,k 2 \hfill \\ &1 / 2 { - }PI_{\text{out}}^{{}}{\quad}1/4 \le p_{{}}^{*} \le 1/2 \hfill \\ \end{aligned} \right.$$
(15)
$$ D_{2}^{{}} = \left\{ \begin{aligned}& 0{\qquad} {\quad} {\kern 1pt} {\,\,}0 \le PI_{\text{out}}^{{}} {\kern 1pt} 1/2 \hfill \\ &PI_{\text{out}} {\qquad} 1/4 \le p_{{}}^{*} \le 1/2 \hfill \\ \end{aligned} \right.$$
(16)

4 Dynamic response performance comparison of EPS and SPS

It is essential to analyze the main influence factors on the transmission power. During the dynamic response process, the inductor current may contain DC bias current, which should be considered when calculating the transient transmission power. For a DAB DC-DC converter with SPS control, if the inductor current includes a DC bias component, it has waveforms shown in Fig. 8.

Fig. 8
figure 8

Waveforms of DAB DC-DC converters with DC bias current under SPS control

Full size image

According to Fig. 8, with different initial values of the inductor current i L (t 0), the transmission power can be expressed as:

$$\begin{aligned} P&= \frac{1}{{T_{\text{S}}^{{}} }}\int_{{t_{0}^{{}} }}^{{t_{4}^{{}} }} {U_{\text{ab}}^{{}} (t)(i_{L}^{'} (t) - I){\text{d}}t} \hfill \\ \quad\mathop {}\limits^{{}} &= \frac{1}{{T_{\text{S}}^{{}} }}\int_{{t_{0}^{{}} }}^{{t_{4}^{{}} }} {U_{\text{ab}}^{{}} (t)i_{L}^{'} (t) - U_{\text{ab}}^{{}} (t)I{\text{d}}t} \hfill \\ \end{aligned}$$
(17)

where i ’ L (t) is the AC component of inductor current i L ; I is the DC component of i L . Since the H 1-bridge output voltage waveform U ab(t) is a symmetrical square-wave in positive and negative half periods, with amplitude U in, the integral value of component U ab(t)I in the right side of (17) is zero, and the transmission power P is indicated by U in, U o and D in form of (18).

$$P\,=\,\frac{{U_{\text{in}} U_{\text{o}} D ( 1- D )T_{\text{S}}^{{}} }}{ 2nL}$$
(18)

Comparing (1) and (18), it is obvious that P is determined by U in, U o, D, T S, n and L under SPS control no matter what condition the converter operates in. Similarly, the transmission power with EPS control is also only related to the circuit parameters and the phase-shift ratios regardless its operating circumstances.

So, in order to reach the desired output voltage of the DAB DC-DC converter, the desired transmission power obtained from the PI controller can be directly used to calculate the command phase-shift ratios D 1 and D 2, which are able to improve the dynamic responses of this converter, compared with the traditional PI controller.

In particular, according to (12)–(14), when the input voltage is changed, the corresponding phase-shift ratios D 1 and D 2 can be quickly obtained, because the desired transmission power p * is unchanged with the same load resistance. The waveforms of dynamic procedure under EPS-DPC scheme are shown in Fig. 9.

Fig. 9
figure 9

Waveforms of dynamic procedure under EPS-DPC scheme

Full size image

According to Fig. 9, when the input voltage U in steps up and down, the desired transmission power p* will keep the same since the output voltage U o will not change visibly with capacitance C 2. Then, the phase-shift ratios D 1 and D 2 can be calculated by (14) to maintain the same transmission power p *, and the output voltage U o will keep in the desired output voltage U *o . Therefore, the EPS-DPC scheme can achieve better dynamic performances of the DAB DC-DC converter.

Moreover, according to (12)–(14), the output voltage U o is used to describe the phase-shift ratios D 1 and D 2, which can act as a negative feedback to calculate the phase-shift ratios D 1 and D 2. Hence, the EPS-DPC scheme can also improve the dynamic performances when the load resistance is changed.

5 Experimental results comparison and analysis of EPS-DPC, SPS-TVL and EPS-TVL

Based on a scale-down DAB DC-DC converter prototype, SPS-TVL, EPS-TVL and EPS-DPC are compared in details. Corresponding block diagrams of these control strategies are given in Figs. 10, 11 and 12. It can be noticed that, in EPS-TVL and EPS-DPC, there is one extra voltage sensor to measure the input voltage when compared with the SPS-TVL scheme.

Fig. 10
figure 10

Block diagram of SPS-TVL scheme

Full size image
Fig. 11
figure 11

Block diagram of EPS-TVL scheme

Full size image
Fig. 12
figure 12

Block diagram of EPS-DPC scheme

Full size image

In order to verify the aforementioned theoretical analysis, an experimental hardware prototype of a DAB DC-DC converter is designed with a TMS320F28335 DSP controller of Texas Instruments [24]. The main parameters of the adopted DAB DC-DC converter are listed in Table 1. An experimental comparison of the proposed EPS-DPC scheme, EPS-TVL and SPS-TVL control schemes is carried out on the prototype.

Table 1 Electrical parameters of experimental prototype
Full size table

Figure 13 show the experimental waveforms of current stress and efficiency with respect to the input voltage U in for these three schemes, respectively. It can be noticed in Fig. 13a that EPS-DPC scheme and EPS-TVL scheme present similar results and achieve lower current stress comparing with SPS-TVL scheme. In addition, from Fig. 13b, it is clear that compared with the SPS-TVL control, the EPS-DPC scheme and EPS-TVL control can achieve higher efficiency, especially in high input voltage condition. Thus, it can be summarized that the EPS-DPC and EPS-TVL control schemes can achieve better current stress suppression and higher efficiency in high input voltage condition, compared with SPS-TVL.

Fig. 13
figure 13

Experimental waveforms of current stress and efficiency with respect to input voltage U in in three control schemes

Full size image

Start-up process performance of three schemes was compared. When the experimental parameters are set as R = 15 Ω, U in = 60 V and U *o  = 40 V. Figure 14 shows experimental results of the input voltage, the inductor current and the output voltage in the DAB DC-DC converter system during start-up process for three schemes. It is clear in Fig. 14 that the start-up time is 370, 313, 100 ms in the SPS-TVL, EPS-TVL and EPS-DPC schemes, respectively. Thus, the EPS-DPC control has realized faster dynamic response than the others. Moreover, in the EPS-DPC, there is no overshoot in the output voltage during start-up process, and the current stress through transformer is much lower.

Fig. 14
figure 14

Experimental results during start-up process

Full size image

Dynamic responses to input voltage fluctuation in three schemes were studied. When the experimental parameters are set as R = 20 Ω and U *o  = 40 V, Figs. 15 and 16 show experimental results of the input voltage, the output voltage and inductor current in the DAB DC-DC converter with the input voltage step-change, where the input voltage U in steps down from 80 V to 70 V in Fig. 15, and conversely in Fig. 16. The SPS-TVL control in Figs. 15a and 16a and the EPS-TVL control in Figs. 15b and 16b take a relatively long settling time (over 100 ms) in both the input voltage step-down and step-up conditions for the output voltage to reach the desired value. In contrary, for the EPS-DPC scheme in Figs. 15c and 16c, the output voltage is almost unchanged during the input voltage step-change, which means its settling time is pretty short. In a word, the EPS-DPC scheme can keep the output voltage constant, and achieve outstanding dynamic behavior when the input voltage fluctuation occurs. Furthermore, the current stresses in EPS-DPC and EPS-TVL control schemes are smaller than that in SPS-TVL control scheme as well.

Fig. 15
figure 15

Experimental results when input voltage steps down from 80 V to 70 V

Full size image
Fig. 16
figure 16

Experimental results when input voltage steps up from 70 V to 80 V

Full size image

Comparison on dynamic responses to load disturbance of three schemes was carried out. When the experimental parameters are set as U in = 65 V and U *o  = 40 V, Figs. 17 and 18 show experimental results of the input voltage, the output voltage and inductor current in the adopted DAB DC-DC converter with a load step-change, where the load steps from 15 to 20 Ω in Fig. 17, and conversely in Fig. 18. In SPS-TVL control in Figs. 17a and 18a and EPS-TVL control in Figs. 17b and 18b, the transient responses of the output voltage are slow, with a relatively long settling time (over 100 ms) in both the load step-down and step-up conditions. The EPS-TVL control is a bit better in dynamic performances than the SPS-TVL control though. However, the EPS-DPC scheme in Figs. 17c and 18c outstands the EPS-TVL and SPS-TVL by short settling time (below 100 ms) when the load disturbance occurs.

Fig. 17
figure 17

Experimental results when the load steps up from 15 to 20 Ω

Full size image
Fig. 18
figure 18

Experimental results when load steps down from 20 to 15 Ω

Full size image

6 Conclusion

In order to improve both efficiency and the output dynamic response of DAB DC-DC converters, a hybrid control scheme combining the extend-phase-shift control and direct power control is proposed in this paper. For DAB DC-DC converter applications, the proposed EPS-DPC, the EPS-TVL and the SPS-TVL schemes are analyzed and compared in detail. A scale-down experimental prototype test is utilized to compare performances of these three control schemes and verify benefits of the proposed EPS-DPC. The conducted studies conclude that the proposed EPS-DPC scheme has following salient features:

  1. 1)

    EPS-DPC scheme can achieve the best dynamic performance under start-up process, input voltage fluctuation, and load disturbance circumstances when compared with SPS-TVL and EPS-TVL.

  2. 2)

    EPS-DPC, as well as EPS-TVL, can realize higher converter efficiency than SPS-TVL, especially in relatively high input voltage conditions.