1 Introduction

A voltage source inverter is widely used in renewable energy power generation systems and micro-grids in order to ensure a high-quality grid current [1,2,3]. However, the pulse width modulation (PWM) of the inverter produces many switching harmonics in the grid current. Thus, to limit these current harmonics according to standards such as IEEE Std 929-2000, an L or LCL filter is needed [4,5,6]. Compared with the L filter, the LCL filter with or without a harmonic trap in [5, 6] can provide much higher attenuation of switching harmonics with reduced volume and weight so that the power density is increased. Unfortunately, the LCL inherent resonance complicates its control. The passive damping (PD) method with an extra resistor is simple, but it causes power losses [7,8,9,10]. Alternatively, active damping (AD) with extra control algorithms has been widely studied.

Existing AD strategies include filter-based AD, feedback-based AD with the feedback of extra voltage and current states, and weighted average control of the two inductor currents. Filter-based AD improves stability by adding a digital filter next to the current controller [11,12,13,14,15,16]. For feedback-based AD, the state used for feedback can be the capacitor current [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32], the capacitor voltage [33,34,35,36], the inverter-side current [37], the grid current [38,39,40,41] or a combination of multiple states [42,43,44,45,46,47,48,49,50]. Among the feedback-based AD methods, proportional feedback of capacitor current is widely studied during last decade due to its simple implementation. For weighted average control, using the weighted average of the grid current and the inverter-side current, the LCL resonance is avoided [51,52,53,54,55,56,57]. All these control strategies have been reported to suppress the LCL resonance. Nevertheless, only a few comparative studies have been reported.

In [11], Dannehl et al. conducted a comparative study of filter-based AD with several different kinds of digital filters on the forward path, but differences with respect to other AD strategies were not revealed. In [33], by means of equivalent graph transformation, the concept of a virtual resistor revealed the relationship of PD and AD with capacitor voltage or current feedback. In [34], an effective analysis method unifying the inner feedback loop of capacitor current and voltage was presented. The studies in [33, 34] were limited to AD with feedback of the capacitor state. In [58], Xu et al. analyzed the basic principles of single-state feedback AD based on the capacitor current, capacitor voltage or grid current. The common features of single-state feedback-based ADs were found, but the differences among them and the differences with respect to other kinds of AD were not presented.

In summary, links between various strategies have not been released to the public by the previous work on LCL-resonance damping. The AD mechanisms studied in this paper will help to clarify the relationships among different strategies, and to derive novel strategies. A review of existing resonance damping strategies for AD is elaborated, and some novel ones are derived. Section 2 briefly describes the LCL resonance in the grid-connected inverter and analyses the mechanisms of AD strategies based on the state feedback. Sections 3 and 4 review the strategies for single-state and multi-state feedback, respectively. Section 5 investigates the robustness, implementation costs and impact of AD on grid current distortion with different strategies. Finally, Section 6 concludes this study.

2 Mechanisms of state feedback control to damp LCL resonance

2.1 Resonance of LCL filters in grid-connected inverters

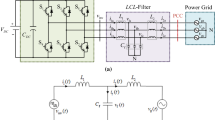
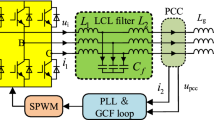
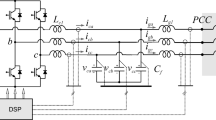
Figure 1 shows the structure of a grid-connected LCL-filtered inverter which consists of the inverter-side inductor L 1, capacitor C 1 and grid-side inductor L 2. The voltage and current state parameters in the LCL filter are marked; u dc is the dc-link voltage, u inv is the output voltage of the inverter bridge, and u g is the grid voltage. Depending on different practical applications, u dc can be the output of a photovoltaic array, the output of a DC-DC converter or the DC bus voltage in the micro-grid system. As shown in Table 1, transfer functions from u inv to every voltage or current state have a pair of non-damped poles at the resonance frequency (f res = ω res/2π) so that a resonance peak exists. For instance, Bode plots for i L1 and i L2 are shown in Fig. 2.

Fig. 1
figure 1

Grid-connected LCL-filtered inverter

Full size image
Table 1 Transfer functions from inverter output to every state
Full size table
Fig. 2
figure 2

Bode plots of transfer functions from u inv to i L1 and i L2

Full size image

Subject to the number of states participating in resonance damping, existing AD strategies are classified as single-state or multi-state feedback control.

2.2 Basic principles of single-state feedback control

2.2.1 Feedback compensation

The typical feedback compensation structure given in Fig. 3 indicates that a resonant term G(s) can be controlled by the correct feedback H(s).

Fig. 3
figure 3

Typical control structure of feedback compensation

Full size image

Assuming that G(s) exhibits a resonant peak at ω res, the closed-loop frequency response at ω res is expressed as:

$$\frac{{C({\text{j}}\omega_{\text{res}} )}}{{R({\text{j}}\omega_{\text{res}} )}} = \frac{{G({\text{j}}\omega_{\text{res}} )}}{{1 + G({\text{j}}\omega_{\text{res}} )H({\text{j}}\omega_{\text{res}} )}}$$
(1)

where G(jω res) approximates infinity and H(jω res) is the gain of active damping feedback at ω res.

Feedback control theory indicates that feedback compensation would suppress the inherent resonance peak if the real part of 1 + G(jω)H(jω) around ω res is greater than zero. Moreover, for the control in Fig. 3, the resonance peak in C(s) is highly damped once negative feedback (i.e., G(jω res)H(jω res) > 0) is achieved. The deeper the negative feedback, the higher the damping of the peak.

A unified control structure based on single-state feedback compensation is given in Fig. 4. The outer loop tracks the reference current i ref while the inner loop is the feedback compensation aiming to damp the resonance. In Fig. 4, u is the output of the current controller G c(s), x represents one of the voltage and current states in the LCL filter, u m is the modulation wave (i.e, the PWM reference), and k PWM stands for the transfer function from u m to u inv. Based on the principle of feedback compensation, detailed investigations of the proper H(s) for each state will be presented later.

Fig. 4
figure 4

Unified current control structure with active damping based on single-state feedback compensation

Full size image

2.2.2 Cascade compensation

Besides AD based on feedback compensation, cascade (series) compensation is another feasible solution to damp the resonance peak. Cascade compensation is obtained by moving H(s) in Fig. 3 onto the forward path, giving the structure shown in Fig. 5.

Fig. 5
figure 5

Typical control structure of cascade compensation

Full size image

Another kind of AD is then derived. Its basic principle is to directly mitigate the peak at ω res. Thus, H(s) should have an extremely low gain at ω res. Then, incorporating the LCL-filtered inverter, the unified control structure based on single-state cascade compensation is given in Fig. 6. Cascade compensation is directly implemented in the closed-loop control of i L1 or i L2.

Fig. 6
figure 6

Unified current control structure with active damping based on single-state cascade compensation

Full size image

2.3 Basic principles of multi-state feedback control

Multi-state feedback control is achieved by a suitable linear combination of several states. On the one hand, feedback of the combination of states generates a novel state whose zeros can be assigned. On the other hand, the combined state feedback changes the poles of the system characteristic equation. Then, there are two basic strategies, zero placement and pole placement.

2.3.1 Zero-placement strategy

The unified control scheme of multi-state feedback control with the zero-placement strategy is shown in Fig. 7, where state x f is a combination of the voltage and current states denoted as x 1, x 2, …, x i with weights f 1(s), f 2(s), …, f i (s), respectively [54].

Fig. 7
figure 7

Unified current control structure of multi-state feedback based on zero-placement strategy

Full size image

The transfer function from u inv to x f is the weighted sum of two or more transfer functions in Table 1:

$$G_{{u_{\text{inv}} }}^{{x_{\text{f}} }} (s) = f_{1} (s)G_{{u_{\text{inv}} }}^{{x_{1} }} (s) + f_{2} (s)G_{{u_{\text{inv}} }}^{{x_{2} }} (s) + \cdots + f_{i} (s)G_{{u_{\text{inv}} }}^{{x_{i} }} (s)$$
(2)

The combination does not change the poles of (2) while a couple of conjugate zeros can be placed at ω res to cancel the unstable resonance poles in the denominator. That is, the basic principle for the states x 1, x 2, …, x i and the weights f 1(s), f 2(s), …, f i (s) can be expressed as:

$$\left. {(s^{2} + \omega_{\text{res}}^{ 2} )G_{{u_{\text{inv}} }}^{{x_{\text{f}} }} (s)} \right|_{{s = \pm {\text{j}}\omega_{\text{res}} }} = 0$$
(3)

where the left side is the simplest form with the common divisor \((s^{2} + \omega_{\text{res}}^{ 2} )\) removed. When (3) is satisfied, the simplest form of the transfer function from u inv to x f is:

$$G_{{u_{\text{inv}} }}^{{x_{\text{f}} }} (s) = \frac{N(s)}{D(s)}$$
(4)

where the numerator and denominator only contain the positive exponential of s.

The lowest order of the transfer functions in Table 1 is 2. Thus, for the sake of simplifying the control design, the order of (4) should be less than 2. Both N(s) and D(s) should be composed of only s 1 and s 0. Accordingly, the transfer function has three forms: ① the order of N(s) is 1 while that of D(s) is 0; ② N(s) and D(s) are 1 or 0 at the same time; ③ the order of N(s) is 0 while that of D(s) is 1. Among these forms, the third one ensures that only a few harmonics exist in x f and is most easily realized. Therefore, the transfer function from u inv to x f should be:

$$G_{{u_{\text{inv}} }}^{{x_{\text{f}} }} (s) = \frac{1}{Ls + R}$$
(5)

where L and R stand for the coefficient of s 1 and s 0. This transfer function represents a grid-connected inverter with an L filter, where x f stands for the current through the inductor, L is the inductance and R denotes the negligible parasitic resistance. In summary, with the zero-placement strategy, an L-filtered grid-connected inverter is virtually constructed from the LCL-filtered one so that current control is effected as control of the L-filtered inverter current x f [52, 54].

2.3.2 Pole-placement strategy

The pole-placement strategy aims to directly assign all the system poles by the proper choice of state feedback. Figure 8 gives its general control block. Multi-state feedback uses a linear combination of several states. In total, there are 18 kinds of state feedback as shown in (6) where P, I and D stand for proportional, integral and derivative feedback, respectively. The number of states participating in the pole-placement can be 2, 3 or 4 [42,43,44,45,46,47,48,49].

Fig. 8
figure 8

Unified current control structure of multi-state feedback based on pole-placement strategy

Full size image
$$\begin{aligned} \hfill x_{\text{f}} = F\left\{ {\left[ {\begin{array}{*{20}c} {i_{L1} } & {u_{L1} } & {\begin{array}{*{20}c} {i_{C1} } & {u_{C1} } & {i_{L2} } & {u_{L2} } \\ \end{array} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} P \\ I \\ D \\ \end{array} } \right]} \right\} \\ \hfill = F(i_{L1} P + i_{L1} I + i_{L1} D + u_{L1} P + u_{L1} I \\ \hfill + \cdots + u_{L2} P + u_{L2} I + u_{L2} D) \\ \end{aligned}$$
(6)

3 Overview of resonance damping strategies with single-state feedback

For active damping based on single-state feedback, in order to make a negative feedback at ω res, the open-loop phase responses from u to all the current and voltage states at ω res need first to be clarified. Then, the requirement of the feedback term H(s) will be obtained.

3.1 Phase characteristics around resonance frequency

Neglecting low-frequency components in u g, u C1 equals u L2. Thus, according to the relationship between current and voltage of inductors and capacitors, i C1 has a lead of 180° over i L2 (that is, the phases of i C1 and i L2 are opposite). In addition, because ω res is larger than ω f, the impedance of C 1 at ω res is much smaller than that of L 2. Therefore, the phase of i L1 around ω res is the same as that of i C1 (i.e., with 180° lead over i L2, as demonstrated by Fig. 2), but the amplitude of i L1 is smaller than that of i C1 according to Kirchhoff’s current law. At ω res, due to conjugate resonance poles, a sharp 180° lag occurs. Accordingly, assuming the phase of u inv is 0°, phase variation trends of all the current states around ω res are given in Fig. 9 (the dashed arrows show the increasing trend of ω). Then, considering that the voltage of the inductor is 90° ahead of its current and the capacitor voltage is 90° behind its current, the phases of the voltage states are also given in Fig. 9.

Fig. 9
figure 9

Phase characteristics of current and voltage states around resonance frequency (i.e., ω res ± Δω)

Full size image

3.2 Strategies based on feedback compensation

3.2.1 AD subject to different options of single state

Based on Sect. 2.2 and Fig. 9, it is easy to obtain the basic requirements for damping the resonance peak as well as to find a suitable AD feedback, as given in Table 2. For instance, in the following, the capacitor current is chosen as an example to explain the principle, while similar discussions on other states are not given. Recall the inner-loop control in Fig. 4 with x = i C1 (in other words, Fig. 3 with R(s) = u and C(s) = i C1). As can be seen in Fig. 9, the phases of i C1 around ω res are always in the first and fourth quadrants. The real part of the transfer function from u m to i C1 in Fig. 4 (i.e., G(s) in Fig. 3) around ω res is always positive. Thus, the gain of H(s) at ω res should be positive for negative feedback, and the attenuation of the LCL resonance peak is higher with a larger gain of H(s). Considering (1), to make the peak below 0 dB, H(jω res) should be much larger than 1.

Table 2 Overview of existing resonance damping strategies based on single-state feedback
Full size table

AD strategies based on feedback compensation are in essence the same while their differences mainly lie in the choice of states for feedback. Typical applications of proportional i C1 feedback can be found in [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34]. For 1st-order derivative feedback of u C1, a high-pass filter (HPF) with a similar response is an alternative solution [35]. Feedback of u L1 does have the ability of LCL resonance damping, but the measurement of u L1 is difficult. For i L2, assuming H(s) = ks 2, the peak can be damped [38,39,40,41], but the high-order derivative is hard to implement with high reliability in practice. Thus, a novel AD based on i L2 feedback is proposed in [39], by using a modified HPF with an optimized parameter design. For feedback of u L2, the difference from u C1 feedback is the low-frequency dynamic, considering that u C1 is u L2 + u g.

3.2.2 Digital control delay impact

In a digital control system, the delay always exists between the signal sampling and the reloading of u m. If the sampling is at the beginning of the control cycle and the PWM reference is reloaded at the end, the control delay reaches one period (also called one-sample delay). Moreover, the PWM inverter behaves as a zero-order hold. That is, k PWM in the digital control system is:

$$\begin{aligned} k_{\text{PWM}} = \left| {k_{\text{PWM}} } \right|e^{{ - sT_{\text{d}} }} \cdot \frac{{1 - e^{{ - sT_{\text{s}} }} }}{{sT_{\text{s}} }} \\ \approx \left| {k_{\text{PWM}} } \right|e^{{ - sT_{\text{d}} }} e^{{ - s{{T_{\text{s}} } \mathord{\left/ {\vphantom {{T_{\text{s}} } 2}} \right. \kern-0pt} 2}}} = \left| {k_{\text{PWM}} } \right|e^{{ - s(T_{\text{d}} + {{T_{\text{s}} } \mathord{\left/ {\vphantom {{T_{\text{s}} } 2}} \right. \kern-0pt} 2})}} \\ \end{aligned}$$
(7)

where T s is the sampling period; T d is the delay between the sampling and the reloading of the PWM reference. The control delay causes a considerable phase lag at ω res which is related to ω res and the sampling frequency f s = 1/T s. The phase lag of (7) at ω res is:

$$\varphi_{\text{lag}} = 2{{\uppi }}\frac{{T_{\text{d}} + {{T_{\text{s}} } \mathord{\left/ {\vphantom {{T_{\text{s}} } 2}} \right. \kern-0pt} 2}}}{{T_{\text{s}} }} \cdot \frac{{f_{\text{res}} }}{{f_{\text{s}} }} = 2{{\uppi }}\frac{{T_{\text{d}} + {{T_{\text{s}} } \mathord{\left/ {\vphantom {{T_{\text{s}} } 2}} \right. \kern-0pt} 2}}}{{T_{\text{s}} }}\alpha$$
(8)

Clearly, a larger α or T d yields a larger phase lag. Note that α is always smaller than 1/2.

In fact, the delay in (7) could turn the original negative feedback to a positive one. For instance, for i C1 feedback, if the phase lag caused by the control delay is larger than 90°, H(s) (here, k) multiplied by k PWM at ω res is no longer positive. In this case, the proportional feedback of i C1 is no longer a negative one so that AD based on i C1 feedback becomes unstable. Moreover, if the lag exceeds 270°, H(s) multiplied by k PWM at ω res turns positive again. This indicates that positive proportional feedback of i C1 will be unstable if the phase lag of the control delay satisfies:

$$\frac{{{\uppi }}}{2} \le \varphi_{\text{lag}} \le \frac{{3{{\uppi }}}}{2}$$
(9)

With the use of (8) this implies:

$$\left( {\frac{1}{4\alpha } - \frac{1}{2}} \right)T_{\text{s}} \le T_{\text{d}} \le \left( {\frac{3}{4\alpha } - \frac{1}{2}} \right)T_{\text{s}}$$
(10)

For instance, with one-sample delay (i.e., T d = T s), the resonance still exists if α is between 1/6 and 1/2, as also analyzed in [26,27,28,29,30,31,32, 34]. If (10) is fulfilled, the feedback AD in Fig. 4 produces two unstable poles in the open-loop transfer function from i ref to i L1 or i L2, yielding some difficulties for robust design [27, 31].

3.3 Strategies based on cascade compensation

3.3.1 AD for inverter-side or grid current control

Cascade compensation is directly implemented in the closed-loop control of i L1 or i L2 in Fig. 6. Generally, a standard current controller G c(s) such as proportion integration (PI) or proportional derivative (PR) yields a negligible phase lag at ω res. If the control delay is not considered, i L1 closed-loop control can guarantee stable operation in [59, 60], and it is unnecessary to use a notch filter as H(s) to damp the LCL peak. For i L2 closed-loop control without control delay, a notch filter is needed because phase matching at ω res is difficult to realize.

3.3.2 Digital control delay impact

Given that the major feature of the delay is the phase lag, the delay behaves as a phase compensator so that single-loop control can work stably in some cases. For instance, for T d = T s, i L2 closed-loop control cannot easily stabilize the inverter because of insufficient phase lag at ω res when α is lower than 1/6 (c.f. (10)). Figure 10 shows open-loop Bode plots with different α. According to the Nyquist stability criterion [11], when α is 0.15, the system is unstable because there is a −180° crossing at the frequency where the gain is above 0 dB; conversely, when α is 0.25 or 0.35, the system is stable. The situation for i L1 closed-loop control is opposite to that for i L2 closed-loop control because of the different phases of i L1 and i L2 as depicted in Figs. 2 and 9. In summary, for low ω res, it is possible to use i L1 closed-loop control, while it is hard for the i L2 closed-loop control to be stable. For high ω res, i L1 closed-loop control is no longer stable, while i L2 closed-loop control works well [11, 12, 26, 61,62,63].

Fig. 10
figure 10

Open-loop bode plots with only i L2 closed-loop control

Full size image

When the delay cannot provide proper phase matching for damping the resonance, the gain H(s) in Fig. 6 is needed. The performance with three kinds of H(s) are studied in [11]. The lead-lag or low-pass digital filter can introduce a slight lead or lag in phase so that phase matching can be further adjusted. The notch filter damps the resonance through direct magnitude adjustment as long as it has an extremely low gain at ω res. Filter-based AD has been broadly discussed in [11,12,13,14,15,16].

4 Overview of resonance damping strategies with multi-state feedback

4.1 Multi-state feedback control based on zero-placement

4.1.1 Choices of state feedback for zero-placement

In Fig. 7, at least, two states are required to facilitate the zero-placement. Based on the principle in Sect. 2.3.1, several possible combinations can be obtained. Detailed derivations can be found in [54]. It is found that both weighted average control (WAC) and split capacitor current (LCCL) control in [51,52,53,54,55] are typical applications and use exactly the same weights. In WAC, x 1 is i L1, x 2 is i L2, f 1(s) equals L 1/(L 1 + L 2), and f 2(s) equals L 2/(L 1 + L 2). With the use of Kirchhoff’s current law, the split capacitor current in [51] also equals f 1(s)i L1 + f 2(s)i L2.

4.1.2 Drawbacks of zero-placement based strategy

The zero-placement current control is effected as control of an L-filtered inverter, but it is stressed that i L2 is the final output current of the high-order inverter system. The transfer function from x f to i L2 can be expressed as:

$$G_{{x_{\text{f}} }}^{{i_{L2} }} (s) = \frac{{\omega_{\text{res}}^{ 2} }}{{s^{2} + 2\xi \omega_{\text{res}} s + \omega_{\text{res}}^{2} }}$$
(11)

where ξ is the slight damping related to the parasitic resistor. The resonance poles are still observed in the final output. Therefore, zero-placement does not solve the potential resonance in i L2 [56]. If the proportional gain of G c(s) is increased, the control bandwidth increases, but the peak produced by the under-damped conjugate poles also increases. The solid line in Fig. 11 shows the Bode plot of the closed-loop transfer function from i ref to i L2 with only the zero-placement current control. The peak occurs at ω res (L 1 = 1 mH, L 2 = 1 mH, C 1 = 10 μF). Thus, the inverter with only zero-placement works stably with no resonance harmonics if the harmonic interference, especially around ω res, are negligible. However, if there are significant disturbances (e.g., a sudden change of current reference), resonance harmonics will be aroused.

Fig. 11
figure 11

Characteristics of grid current with different zero-placement

Full size image

4.1.3 Improvements of zero-placement based strategy

As discussed in Sect. 3.2, AD strategies based on single-state feedback compensation are able to damp the resonance peak. When combined with single-state feedback AD, an improved zero-placement based control structure is obtained, as shown in Fig. 12. The main disadvantage of introducing the feedback of x AD is the need to sample an extra current or voltage. Thus, AD should avoid the need for an extra state if possible. For instance, when x 1 and x 2 are i L1 and i L2, x AD can be one of {i C1, i L1, i L2}, considering that the difference between i L1 and i L2 is exactly i C1 [56]. The dashed line in Fig. 11 shows the characteristic of i L2 with the improved strategy, and the resonance peak is highly suppressed.

Fig. 12
figure 12

Unified structure of improved zero-placement based strategies with extra active damping

Full size image

4.1.4 Control delay impact

The interval between x 1 sampling and x 2 sampling is denoted as T d1, and that between x 2 sampling and PWM reloading is denoted as T d2. The transfer function from u inv to x f in Fig. 12 can be expressed as:

$$G_{{u_{\text{inv}} }}^{{x_{\text{f}} }} (s) = f_{1} (s)G_{{u_{\text{inv}} }}^{{x_{1} }} (s)e^{{ - sT_{{{\text{d}}1}} }} + f_{2} (s)G_{{u_{\text{inv}} }}^{{x_{2} }} (s)$$
(12)

The delay time T d2 does not affect the generation of the novel state x f, but T d1 does. If T d1 is large, cancelling the resonance poles in (12) is not possible unless the weight f 1(s) or f 2(s) contains a corresponding exponential factor. Luckily, for a digital signal processor (DSP) with a clock frequency of hundreds of megahertz, the time interval between sequential sampling of two signals is negligible so that zero-pole cancellation at the resonance frequency in (12) is still fulfilled approximately.

However, for the extra active damping loop in Fig. 12, the control delay will have a non-negligible impact on its performance, as discussed in Sect. 3.2.

4.2 Multi-state feedback control based on pole-placement

It should be noted that conventional full state feedback control in [44] and the slide mode control in [50] are the typical implementation of (6) with the use of proportional feedback of i L1, i L2 and u C1. This kind of multi-state feedback control requires sampling several current and voltage signals. Generally, according to the relationships among the current and voltage states, the choice of states is indeed flexible [49]. For instance, for full state feedback control, proportional feedback of u C1 can be replaced by integral feedback of i C1 due to the inherent relation between i C1 and u C1. The choice of state feedback can be optimized to reduce the number of sensors.

Studies [42] and [49] treat k PWM as 1 with no delay. However, the control delay which exists in k PWM will make the locations of poles vary from the expected ones. To solve this inconvenience, in [42], researchers try to use the Smith predictor to eliminate the delay impact. For the pole-placement design in the z-domain, another way is to take account the control delay by introducing an extra state. For instance, considering that the control delay appears as z −1, the inverter output voltage was included in the state vector [44,45,46,47,48], and several parameter design methods for full state feedback control were proposed in [45, 46, 48].

Table 3 gives a general overview of the existing multi-state feedback strategies.

Table 3 Overview of existing resonance damping strategies based on multi-state feedback
Full size table

5 Discussions

In practice, the question is how to choose appropriately for a specific application from so many available current control strategies. Firstly, stability and robustness have to be assured. Secondly, different strategies require different numbers of sensors. Thirdly, using different states for feedback might yield different abilities to suppress low-order grid current harmonics depending on the low-frequency components of the selected states.

5.1 Stability and robustness improvement

System instability related to LCL resonance can be solved by single-state or multi-state feedback AD. When control delays do not exist, the existing current control strategies with AD have all been proved to work very well for any LCL parameters [18,19,20,21,22,23,24, 34, 39, 60].

Recently, many researchers paid special attention to stability and robustness in the presence of some non-ideal factors. It is concluded in Sects. 3 and 4 that control delay impacts on single-state feedback AD a lot while it has negligible impact on multi-state feedback AD. Besides delay, in practical application the filter parameters may vary from their design values and the grid at the PCC has non-negligible impedance. The studies in [6, 27,28,29,30,31,32], and [64,65,66,67,68] showed that the resonance frequency is significantly reduced when the filter parameters and the grid impedance are varied.

5.1.1 Single-state feedback AD

For i C1 feedback AD (a typical single-state feedback AD), the theoretical derivations in [27,28,29,30,31,32] discussed the detailed design principle to maintain stability and showed that dual-loop current control could be stable even when the inner-loop AD was unstable (i.e., α fulfills (10)). However, a sharp decrease of ω res, challenged this robustness. Improving the stability of inner-loop AD was critical for improving robustness [31]. Thus, considering that digital delay causes instability of inner-loop AD, delay compensation should be used to improve stability and robustness [27, 31].

Implementating delay compensation is no longer complex nowadays. Several delay compensation methods have been proposed:

  1. 1)

    Given that α is equal to f res/f s, increasing f s can put α outside the range in (10).

  2. 2)

    According to (8), reducing T d can reduce the phase lag. Then the critical value of α is increased so that a filter with a high ω res will become easier to damp. Adjusting the sampling instant or the reloading instant of u m [27, 28] can greatly reduce T d; but aliasing in the sampling process should be treated properly, as discussed in [69, 70]. A modified duty cycle generation method based on area equivalence proposed in [71] can also greatly reduce T d. The multi-sampling method in [72] can reduce the delay to some extent.

  3. 3)

    A digital filter featuring phase advance is also a possible way to compensate phase lag, including the lead filter [29, 30], the high-pass filter [31], the second-order generalized integrator (SOGI) [73, 74] and so on. The study in [31] compared some delay compensation methods and recommended reducing T d as a promising choice.

5.1.2 Single-state cascade AD

Studies discussed in Sect. 3.3 show that stability with single-state cascade AD relies too much on accurate system information including the delay time and the real resonance frequency. Therefore, when the filter parameters and the grid impedance vary widely, stability may be seriously affected. Figure 13 shows the inverter output waveform with notch-filtered AD [11] with L 1 = L 2 = 1 mH and C 1 = 10 μF (the following sections will also use these parameters). Before 85 ms, the inverter works well; however, many resonance harmonics are aroused after the grid impedance increases.

Fig. 13
figure 13

Current waveform with notch-filter AD subjected to the step change of grid impedance value

Full size image

The study in [13] tried to design the notch frequency away from the default resonance frequency so that notch-filter AD worked stably when the grid impedance varied within a certain range. In order to maintain a high robustness in the case of widely varying grid impedance, [14] proposed to adjust the notch frequency by estimating the grid impedance on- or off-line. To avoid using grid impedance estimation, [75] used a hybrid method which comprised passive damping and notch filter AD. The robustness with single-state cascade AD was enhanced, but the power loss was increased.

5.1.3 Multi-state feedback AD

Pole-placement based multi-state feedback is robust because of the full controllability of the inverter dynamics, as analyzed in [44, 46, 50]. However, for zero-placement based multi-state feedback, the weights f 1(s) and f 2(s) closely relate to the filter parameters. For instance, in the WAC, f 1(s) and f 2(s) depend on L 1 and L 2. If the real value of L 1 or L 2 varies, the cancellation of unstable resonance poles will be affected. Thus, in [56], an improved WAC with extra i C1 feedback (i.e., x AD = i C1 in Fig. 12) is used for high robustness. Figure 14 shows the current waveform with improved zero-placement and extra AD control in the case that L 1 varies away from its default value (i.e., the real L 1 is 1.1 mH). Before 45 ms, only zero-placement current control is enabled and a large number of resonance harmonics are stimulated by the mismatch of filter and control parameters. Once the extra AD is enabled, the resonance is eliminated rapidly.

Fig. 14
figure 14

Current waveform with the improved zero-placement strategy in the case of mismatched filter parameters

Full size image

5.2 Implementation costs

The number of sensors is an important contributor to implantation costs, and depends on the choice of current for tracking i ref and the choice of states for damping control. Table 4 shows the required sensors for existing current control strategies. Generally speaking, multi-state feedback based control requires more sensors than the single-state feedback based control. Especially for a three-phase inverter, too many high-precision sensors are needed for multi-state feedback. Among all the existing control strategies, grid current outer-loop control with grid current AD in [39, 40], grid current single-loop control with filter-based AD and inverter-side current single-loop control with filter-based AD [11, 12] need to sample only one current for current control. To minimize the number of sensors for multi-state feedback control, estimation algorithms should be used. Recently, studies in [76, 77] and [78,79,80,81,82,83] separately gave some good examples for slide model control and full-state feedback control.

Table 4 Comparisons of robustness, sensors and grid current distortions with different strategies
Full size table

Usually, sampling and control are implemented in digital signal processing (DSP). More time is available for calculation if the sampling frequency is much lower than the DSP clock. Considering that the sampling frequency is usually several to dozens of kHz and the DSP clock is hundreds of MHz [4,5,6, 11, 12, 19], the calculation can all be finished within one sampling period.

5.3 Current distortion caused by grid voltage harmonics

Grid voltage distortion is the main cause of grid current distortion. Recall the LCL filter structure in Fig. 1. Kirchhoff’s current and voltage laws tell:

$$\left\{ \begin{aligned} u_{C1} = u_{L2} + u_{\text{g}} \hfill \\ i_{L1} = i_{C1} + i_{L2} \hfill \\ \end{aligned} \right.$$
(13)

Without considering the current control loop, the low-order voltage harmonics in u g occur in u C1. Given that i C1 has an inherent relation with u C1, i C1 also has low-order current harmonics related to the grid voltage harmonics. Furthermore, according to the second equation in (13), i L1 also relates closely to the grid voltage harmonics. A similar argument applies to u L1. In summary, compared with feedback of u L2 or i L2, the feedback of u C1, i C1, i L1 or u L1 will add considerable information about grid voltage harmonics into the control loop so the grid current quality can be improved.

The above deduction can also be derived theoretically. When state feedback is used, the grid voltage impact can be directly observed through the transfer function from u g to i L2. Recall Fig. 8. Clearly, the u C1, i C1, i L1 and u L1 feedback loops all have no contact with the forward path from u g to i L2 through −1/L 2 s, while the i L2 and u L2 feedback loops have contact. Therefore, according to Mason’s gain formula, extra terms which are related to the feedback of u C1, i C1, i L1 and u L1 will occur in the numerator of the transfer function from u g to i L2. Consequently, grid voltage harmonics in the case of u C1, i C1, i L1 and u L1 feedback will have extra impact on the grid current quality. For this reason, the full feedforward method uses a 1st-order derivative feedforward of u g to improve the grid current quality in [19] and [47]. The above investigations are also synthesized in Table 4.

In order to show the effect of different choices of x on grid current distortion, Fig. 15 provides some grid current waveforms with the single-state control in Fig. 4 and identical control parameters when x is u C1 or u L2. The grid voltage contains 5% 5th and 7th voltage harmonics. It is found that the grid current with AD feedback of u C1 is noticeably distorted, so the above deduction is verified.

Fig. 15
figure 15

Distorted grid current waveforms with different feedback AD

Full size image

5.4 Summary

In order to improve the inverter performance as well as to minimize the implementation cost, current control strategies should exhibit a high robustness, require as few sensors as possible and have negligible impact on grid current distortion. Table 4 gives a general overview.

For the single-state strategies, existing studies mainly focused on improving robustness with the capacitor current AD. But such AD requires an additional sensor and has some adverse impact on grid current distortion. Future studies on improving AD when sampling only the grid current may be necessary, considering that minimal sensors are required and the impact of such AD on low-order grid current distortion is negligible.

Multi-state feedback strategies all need many sensors so the cost is relatively high, especially for three-phase systems. Besides, the multi-state feedback strategies have some adverse impact on the suppression of low-order grid current harmonics because of the use of capacitor voltage, capacitor current, or inverter-side current feedback. But it is noted that these strategies (except those with WAC) are very robust. Thus, recent studies focused on reducing the implementation cost.

6 Conclusions

In this study, the basic principles for resonance damping are analyzed. Existing LCL resonance damping strategies are sorted into four categories, i.e., single-state feedback compensation, single-state cascade compensation, multi-state zero-placement and multi-state pole-placement. Instability caused by the LCL filter can be solved by state feedback with any of the above four mechanisms. Then, a systematic study is provided to reveal not only the similarities but also differences among various LCL-resonance damping strategies. On the basis of the basic control mechanisms, some novel or improved strategies can be derived. Lastly, a comparative investigation of existing strategies has been done in order to reveal the future focus of research on LCL-resonance damping. The objective is simultaneously to improve the inverter performance, e.g., robustness and grid current harmonics rejection, and to minimize the implementation cost.