1 Introduction

The penetration of Distributed Generation (DG) using Voltage-Source-Converter (VSC) continuously increases over the past few decades [1, 2]. It is a main characteristic of new power-electronics-enabled power system. Diverse renewable energy resources are integrated into the grid with VSC as the interface, for example the photovoltaic, the wind power, and the fuel cell. In addition, VSCs are also used in the energy storage system and the high-voltage dc (HVDC) transmission system [3, 4]. Consequently, VSCs are becoming increasingly important component in the modern power system. Compared with the traditional SG, VSCs lack rotating inertia and damping property which play a significant role in ancillary services for grid dynamic performance and stability [5, 6]. With the penetration of VSC-based DG increasing, the overall system inertia and damping are dramatically decreased which can lead to potential small-signal power angle stability problem [7], which is characterized by the low-frequency oscillations of angular frequency and active power, and threatens the stable operation.

In order to analyze the small-signal stability of modern power system with VSCs, a promising solution is to establish SG-equivalent model for the VSCs [8,9,10,11,12]. It is the classic Phillips-Heffron model, which characterizes the SG dynamics with inertia, synchronizing and damping coefficients [13, 14]. Based on the Phillips-Heffron model, the well-developed small-signal stability theories in traditional power system can be applied in the modern power system with VSCs. For the voltage-controlled (VC) VSCs [15], the droop controlled VSC and traditional SG is proved to have an equivalent dynamic in the electro- mechanical time scale [8]. The Phillips-Heffron model of the VC-VSC has been successfully applied to the synchronization and stability analysis for microgrid with multiple VSCs [12]. The classic Kuramoto oscillator theory can be applied in this case, which is originally applied for the stability analysis of the traditional power system based on multiple SGs [16]. Besides the VC-VSCs, a lot of VSCs are operated in current-controlled (CC) mode because of the simplicity of its control strategy and the adequate utilization of the renewable energy [17, 18]. Nevertheless, the equivalence between the dynamic characteristics of the CC-VSC and the traditional SG has been hardly studied. As for the CC-VSCs, it is often regarded as an ideal current source and the dynamic of phase-locked-loop (PLL) is always overlooked. Such assumptions only hold true in strong grid with low penetration level of VSCs [11, 19]. The CC-VSC is considered to affect the small-signal stability of the system indirectly just by altering the steady state operation point of the SGs [19]. The interactive mechanism between the CC-VSC and the SGs has not been addressed. Some researches point out that the dynamic of PLL can significantly affect the system synchronization and stability [20,21,22,23,24], especially in the weak-grid system. As the penetration increasing, the effect of CC-VSCs on system stability becomes more prominent. Most of the researches investigate the effect of CC-VSCs on small-signal stability of the modern power system including CC-VSCs and SGs based on the system synthesis with the eigenvalues calculation of the whole system [19, 25,26,27]. The high-order mathematical model of the whole system is complicated, and the physical explanation of the VSC dynamic can hardly be recognized [26, 27]. Thus it is inconvenience to obtain the direct principle for the parameter optimizations of the CC-VSC to improve the small-signal stability [11].

This paper presents a Phillips-Heffron model for the CC-VSC considering the dynamics of PLL. It reveals that the corresponding physical interpretation of the dynamic behavior of CC-VSC based on the equivalence with SG. Thus it promotes the cognition about the CC-VSC from the perspective of the traditional SG-based power system, and bridges the gap between the CC-VSC and the mature theories of traditional power system. It is also essential for the parameter design of the CC-VSCs from the perspective of small-signal stability of the modern power system including VSCs and SGs. An introduction about the architecture and control of PLL-based CC-VSC is presented in Section 2. It is followed by the definition of “current angle” in Section 3, and the relationship between the current angle and the power angle is also quantified. This provides a foundation for Section 4 in which the Phillips-Heffron model for the CC-VSC is presented, by highlighting the virtual electromechanical swing process. Based on the proposed model, the dynamic performance of the CC-VSC is analyzed by using the theory and method of traditional SG-based power system. Section 5 gives an application of the proposed Phillips-Heffron model of the CC-VSC in small-signal stability analysis, as well as the parameter optimizations of the CC-VSC. Section 6 is dedicated to simulation verification for the dynamic performance and stability analysis.

2 Configuration and control of CC-VSC

Figure 1 shows the configuration and control scheme of a grid-connected power electronic generation unit based on a CC-VSC. It includes the dc power source, the grid-tied inverter, the passive filter, the transmission line, and the grid. The voltage source on the DC side can be energy storage system, fuel cells, or photovoltaic with energy storage, so the DC-link dynamic can be ignored. U dc is the voltage of the DC capacitor. The grid-tied inverter is integrated to the point of common coupling (PCC) via an L-type filter, as shown in Fig. 1. It is also feasible to employ an LCL-type filter, but it is equivalent to the L-type filter in electromechanical time scale [11]. The transmission line is denoted by the inductance L. The terminal voltage of the VSC is u PCC and u g is the grid voltage.

Fig. 1
figure 1

Structure and control diagram of CC-VSC

Full size image

With the assistance of PLL, current and voltage variables can be transformed from the abc stationary frame to the dq synchronous rotational frame and vice versa. The real and imaginary components of the current are regulated by a proportional-integral (PI) controller in the synchronous reference frame. In Fig. 1, two dq domains are defined respectively [20]. One is the system dq domain utilizing the actual phase-angle of the phasor \(\tilde{U}_{\text{PCC}}\). The variables of the system dq domain are all marked by the superscript s. The other one is the converter dq domain which applies the output angle of the PLL for dq transformation. The variables of the converter dq domain are all marked by the superscript c. The output angle of the PLL is normally aligned with the actual phase-angle of \(\tilde{U}_{\text{PCC}}\), and the converter dq frame is in accord with the system dq domain. However, when the system suffers a disturbance, the disturbance will propagate to the output angle of the PLL. Consequently, the disturbance will further result in the output power fluctuation, because the output current control depends on the converter dq domain which is determined by the PLL.

Though there are many kinds of structures of PLL, these PLLs are extensions of the conventional synchronous reference frame (SRF) PLL which is described by the diagram in Fig. 2 [28]. The SRF-PLL is commonly used as an essential building block in the CC-VSCs to estimate the grid frequency and phase. If not considering the unbalanced grid faults, the results drawn from the conventional SRF-PLL are applicable since all the types of PLL share the same phase-locking principle and the PLL model [28, 29]. Therefore, the conventional SRF-PLL is used in this paper for analysis. It is worth mentioning that the parameter J in Fig. 2 is defined to represent a virtual inertia coefficient in the subsequent SG-equivalent modeling.

Fig. 2
figure 2

Diagram of conventional SRF-PLL

Full size image

For the generation units based on CC-VSCs, the PLL dynamic may be set in 1 Hz to 30 Hz [30, 31], considering the tradeoff between rapid tracking and disturbance rejection. The PLL dynamic plays a key role in the energy conversion process in the electromechanical time scale [20,21,22,23,24]. The current tracking dynamic may in 300~400 Hz [26], and it can be ignored in the electromechanical dynamic investigation. Therefore, the PLL dynamic is the main factor in the subsequent SG-equivalent modeling.

3 Definition of current angle for CC-VSC

Recently, the concept of “virtual rotor angle” of VC-VSC is presented from the SG-equivalent perspective [32]. For the voltage source, such as SG and VC-VSC, the rotor angle or virtual rotor angle can uniquely determine the power. Thus they can also be regarded as power angle. However, CC-VSC is a current source, which is different from the voltage source. Therefore, it is necessary to define a new concept for the CC-VSC from the SG-equivalent perspective.

As shown in Fig. 1, the CC-VSC needs to be connected to a reference voltage \(\tilde{U}_{\text{g}}\). Its output current is \(\tilde{I}\) and the terminal voltage is \(\tilde{U}_{\text{PCC}}\). In this system, the reference variable is \(\tilde{U}_{\text{g}}\), the independent variable is \(\tilde{I}\), and the dependent variable is \(\tilde{U}_{\text{PCC}}\). For a traditional voltage- source-based system, the independent variable is the terminal voltage of the voltage source, and the dependent variable is its output current. This is a basic difference, and it is also the foundation of the subsequent definition of current angle.

As shown in Fig. 3, the angle between the current of CC-VSC and the grid voltage is defined as “current angle”, and it is represented by the symbol δ i . The angle between \(\tilde{U}_{\text{PCC}}\)and \(\tilde{U}_{\text{g}}\)is δ, which is regarded as the rotor angle or the power angle in the traditional voltage-source-based system. The symbol φ represents the power-factor angle. The relationship among them is shown in (1).

Fig. 3
figure 3

Phasor diagram of CC-VSC-based system

Full size image
$$\delta = \delta_{i} { + }\varphi$$
(1)

Comparing the Fig. 3a and b, it is revealed the active power depends on the current angle δ i instead of δ, as shown in (2).

$$P = \frac{3}{2}U_{\text{g}} I\cos \delta_{i}$$
(2)

For the power system based on CC-VSC, the current angle δ i can uniquely determine the power, but the relationship between current angle and power is different from that between the traditional power angle and power. For example, if the current angle increases, the active power decreases. The incremental formula is shown in (3).

$$\Delta P = - \frac{3}{2}U_{\text{g}} I\sin \delta_{i0} \Delta \delta_{i}$$
(3)

For the traditional voltage-source-based system, the power angle δ can uniquely determine the power, and the incremental formula is shown in (4).

$$\Delta P = \frac{3}{2}\frac{{U_{\text{PCC}} U_{\text{g}} }}{{X_{L} }}\cos \delta_{0} \Delta \delta$$
(4)

Then, the quantitative relationship between the current angle in CC-VSC-based system and the traditional power angle can be derived, as shown in (5).

$$\left\{ \begin{aligned} \Delta \delta = K_{\text{C}} \Delta \delta_{i} \hfill \\ K_{\text{C}} = - \tan \delta_{i0} \tan \delta_{0} \hfill \\ \end{aligned} \right.$$
(5)

The relationship establishes the connection between the CC-VSC and the voltage source, such as SG and VC-VSC. It will be applied in the stability analysis of multi-machine power system including CC-VSCs and the voltage source.

4 Phillips-Heffron model of CC-VSC

4.1 Small-signal modeling of PLL-based CC-VSC

Based on the proposed current angle, a Phillips-Heffron model is established for the generation unit with CC-VSC, considering the dynamic of PLL in the weak grid. As previously stated, this paper focuses on the dynamics in the electromechanical time scale. For the CC-VSC, the current-loop bandwidth in PWM-based VSC systems is overwhelming higher than the grid frequency (50 Hz). It provides a precise fundamental frequency current tracking, so the CC-VSC behaves as a current source accurately following the current reference. However, the current control is based on the reference frame provided by the PLL, which significantly influences the actual output current and power. Therefore, the electromechanical dynamic of PLL is very important for the generation unit with CC-VSC.

As shown in Fig. 1, the q-axis component of the terminal voltage \(\tilde{U}_{\text{PCC}}\) is the input of the PLL. The terminal voltage of the CC-VSC can be represented in (6). It consists of two parts: the grid voltage and the voltage drop on the transmission line.

$$\tilde{U}_{\text{PCC}} = jX_{L} \tilde{I} + \tilde{U}_{\text{g}}$$
(6)

In the process of small-signal modeling, the amplitude of current and the amplitude of grid voltage are assumed to be the value before the disturbance and to keep constant. Because this paper focuses on the small-signal stability analysis, the modeling is based on algebraic differential equations and the effect of frequency dynamic on the transmission line is overlooked [14]. As shown in Fig. 4a, the graphical analysis procedure of the q-axis component of \(\tilde{U}_{\text{PCC}}\)is given, under the steady state condition. The output angle of the PLL is θ 0. It is aligned with the actual phase-angle of \(\tilde{U}_{\text{PCC}}\), so the converter dq frame is in accord with the actual terminal voltage of CC-VSC. The corresponding current angle is represented as δ i0.

Fig. 4
figure 4

Vector diagram

Full size image

As shown in Fig. 4a, the q-axis component of \(\tilde{U}_{\text{PCC}}\)can be represented in (7).

$$u_{q} = IX_{L} \sin \left[ {\left( {\frac{\pi }{2} + \varphi + \theta_{0} } \right) - \theta_{0} } \right] + U_{\text{g}} \sin \left( {0 - \theta_{0} } \right)$$
(7)

The first item in (7) depicts the upward arrow line parallel to the q-axis of PLL in Fig. 4a, and the second item depicts the downward arrow line. These two arrow lines in the reverse direction have the equal length. Thus the q-axis component of \(\tilde{U}_{\text{PCC}}\) is zero under the steady state condition.

When the system suffers disturbances, the output angle of the PLL is not aligned with the actual phase-angle of \(\tilde{U}_{\text{PCC}}\). Figure 4b shows the graphical analysis procedure of the q-axis component of \(\tilde{U}_{\text{PCC}}\). The output angle of the PLL is θ 0 + ∆θ. The corresponding current angle is δ i0+∆δ i , since the current phase depends on the reference frame provided by the PLL. Therefore, the increment of current angle is equal to the increment of the output angle of the PLL, as shown in (8).

$$\Delta \delta_{i} = \Delta \theta$$
(8)

Synthetically considering Fig. 4a and b, the q-axis component of \(\tilde{U}_{\text{PCC}}\)can be represented in (9).

$$u_{q} = IX_{L} \cos \varphi - U_{\text{g}} \sin \theta$$
(9)

where θ is the output angle of the PLL, which can also be represented as δ i +φ.

As shown in (9), the first item depicts the upward arrow line in Fig. 4b, and the second item depicts the downward arrow line. These two arrow lines in the reverse direction do not have the equal length. Thus the q-axis component of \(\tilde{U}_{\text{PCC}}\) is not zero under the dynamic state condition, which means the PLL will suffer the process of dynamic adjustment. According to the diagram of the PLL in Fig. 2, the dynamic behavior of the PLL can be depicted in (10).

$$\left\{ \begin{aligned} Js\omega &= \left( {sk_{\text{p}} + k_{\text{i}} } \right)u_{q} \hfill \\ s\theta &= \omega \hfill \\ \end{aligned} \right.$$
(10)

Substituting (9) into (10), the equivalent swing equation can be obtained:

$$\left\{ \begin{array}{l} Js\omega = k_{\text{i}} IX_{L} \cos \varphi - k_{\text{i}} U_{\text{g}} \sin \theta - k_{\text{p}} U_{\text{g}} \cos \theta \cdot \omega \hfill \\ \,\, s\theta = \omega \hfill \\ \end{array} \right.$$
(11)

According to (7), it is obvious that equation (12) can be set up under the steady state condition.

$$k_{\text{i}} IX_{L} \cos \varphi - k_{\text{i}} U_{\text{g}} \sin \theta_{0} = 0$$
(12)

The virtual mechanical torque which acts as the accelerating torque in the equivalent swing equation can be obtained. The virtual electromagnetic torque which acts as the decelerating torque in the equivalent swing equation can also be obtained. Both of them are given in (13).

$$\left\{ \begin{aligned} T_{\text{vm}} &= k_{\text{i}} IX_{L} \cos \varphi \hfill \\ T_{\text{ve}} &= k_{\text{i}} U_{\text{g}} \sin \left( {\delta_{i} + \varphi } \right) \hfill \\ \end{aligned} \right.$$
(13)

For the CC-VSC, the current tracking dynamic can be ignored in the electromechanical dynamic investigation, and the current amplitude is an independent variable. Therefore, it is reasonable to assume that the virtual mechanical torque keeps constant. Thus the corresponding incremental equation of the CC-VSC can be obtained in (14) resembling the Phillips-Heffron modeling of traditional SG, which is suitable for small-signal stability analysis.

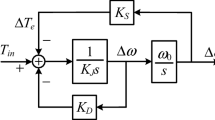
$$\left\{ \begin{aligned} Js\Delta \omega &= - k_{\text{i}} U_{\text{g}} \cos \theta_{0} \Delta \delta_{i} - k_{\text{p}} U_{\text{g}} \cos \theta_{0} \Delta \omega \hfill \\ s\Delta \delta_{i} &= \Delta \omega \hfill \\ \end{aligned} \right.$$
(14)

According to (14), the diagram of the Phillips-Heffron model of CC-VSC can be presented in Fig. 5.

Fig. 5
figure 5

Diagram of the Phillips-Heffron model of CC-VSC

Full size image

Likewise, for the proposed Phillips-Heffron model of CC-VSC, the corresponding equivalent inertia K J, equivalent synchronizing coefficient K S, and equivalent damping coefficient K D can be obtained as:

$$\left\{ \begin{array}{l} K_{\text{J}} = J \hfill \\ K_{\text{S}} = k_{\text{i}} U_{\text{g}} \cos \theta_{0} \hfill \\ K_{\text{D}} = k_{\text{p}} U_{\text{g}} \cos \theta_{0} \hfill \\ \end{array} \right.$$
(15)

Resembling the Phillips-Heffron modeling of traditional SG, the equivalent inertia K J denotes the power cost for altering the angular frequency of the CC-VSC. The synchronizing coefficient K S reflects the performance supporting machine-grid synchronism. As shown in (15), the integral regulator of PLL leads to the synchronizing property, which takes charge of restoring the operation point when it deviates from its steady state. The damping coefficient K D represents the capability for damping the oscillation of angular frequency. It is apparent in (15) that proportional regulator of PLL in CC-VSC generates the effect of damping. If J, k p and k i are all positive, K J, K S and K D will be positive correspondingly under the condition of normal operating point (cosθ 0>0). That means the VSC is equipped with certain inertia, damping and synchronizing ability. These parameters are important physical concepts to represent the dynamic characteristics of the SG in the classical stability theory.

According to Fig. 2, the relationship in (16) can also be revealed, which gives the definition of the equivalent energy serving for inertia response in CC-VSCs.

$$\psi = \frac{1}{s} \cdot u_{q}$$
(16)

Substituting (9) into (16):

$$s\psi = IX_{L} \cos \varphi - U_{\text{g}} \sin \theta$$
(17)

Consequently, the linearized form of (17) can be obtained. By replaceing ∆θ with ∆δ i according to (8), the incremental equation of ψ can be obtained as (18).

$$s\Delta \psi = - U_{\text{g}} \cos \theta_{0} \Delta \delta_{i}$$
(18)

Then, substituting the quantitative relationship between the current angle and the traditional power angle,which is given in (5), into (17), the relationship between ∆ψ and the traditional power angle can be derived, as shown in (19).

$$s\Delta \psi = U_{\text{g}} \cos \theta_{0} \cot \delta_{i0} \cot \delta_{0} \cdot \Delta \delta$$
(19)

It is revealed in (19) that the increment ∆ψ is the integral of traditional power angle increment ∆δ. Likewise, it is the integral of power increment, which is the so-called energy from the perspective of physical meaning. Therefore, the variable ψ in Fig. 2 is defined as equivalent energy in this paper. It describes the extra energy which the CC-VSC supplies for the inertia response.

4.2 Small-signal stability mechanism of CC-VSC

The traditional small-signal stability mechanism of SG-based single machine infinite bus system can also be applied to analyze the small-signal stability mechanism of the corresponding CC-VSC system, since the Phillips- Heffron model of CC-VSC has been established resembling the traditional SG. As stated in [14], for the traditional SG-based single machine infinite bus system, the system characteristic equation can be obtained according to the Phillips-Heffron model, as shown in (20).

$$s^{2} + \frac{{K_{\text{D}} }}{{K_{\text{J}} }}s + \frac{{K_{\text{S}} }}{{K_{\text{J}} }} = 0$$
(20)

Thus, the natural frequency ω n and the damping ratio ζ can be expressed in (21).

$$\left\{ \begin{aligned} \omega_{\text{n}} &= \sqrt {\frac{{K_{\text{S}} }}{{K_{\text{J}} }}} \hfill \\ \zeta &= \frac{1}{2} \frac{{K_{\text{D}} }}{{\sqrt {K_{\text{S}} K_{\text{J}} } }} \hfill \\ \end{aligned} \right.$$
(21)

The conclusion above is also suitable for the CC-VSC system. Considering the equivalent inertia, synchronizing coefficient and damping coefficient of the Phillips- Heffron model of CC-VSC as shown in (15), the following conclusions can be deduced. It can be readily seen in (15) that the CC-VSC will possess a larger inertia with the value of J increasing. As a result, both the natural frequency and the damping ratio will decreases according to (21). With a large integral coefficient k i of the PLL, the equivalent synchronizing coefficient K S is also large, thus the natural frequency will increase while the damping ratio will decrease. In addition, if the proportional coefficient k p of the PLL is larger, the equivalent damping coefficient K D is larger, which means that the damping ratio will increase, and the current angle as well as the angular frequency will turn into steady state with a quicker dynamic response process.

Besides the parameters of PLL, other factors such as the output power, the grid voltage and the impedance of transmission line also play an important role on the small- signal stability. When the output power of CC-VSC is large, it means that the steady-state angle θ 0 between the terminal voltage of CC-VSC and the grid voltage is large. It is also the steady-state power angle δ 0 in traditional power system. As demonstrated in (15), it is obvious that the large θ 0 makes the stability deteriorate, by degrading the damping performance and the synchronizing ability. Likewise, the amplitude of grid voltage can also influence the small-signal stability, by altering the value of equivalent synchronizing coefficient and damping coefficient. When the grid voltage dips, both the damping performance and the synchronizing ability will be weakened according to (15). It also helps explain why the CC-VSC system tends to lose its stability when suffering voltage sag. An important parameter of the system configuration is the impedance of the transmission line which is represented by an inductor L in Fig. 1. A large inductance indicates a large virtual mechanical torque, as shown in (13). Under the condition of the steady state, the virtual mechanical torque is equal to the virtual electromagnetic torque which is also represented in (13). Thus, it is inferred that the steady-state angle θ 0 is large with the large inductance. As mentioned above, the large θ 0 degrades the damping performance and the synchronizing ability of the CC-VSC system. Therefore, it is evident that larger inductance of transmission line is unfavorable, because it will lead to weaker small-signal stability. The traditional power system theory also presents that the compactness of electrical link between two interconnected power sources depends on the inductance of the transmission line: if the linking inductance is larger, the electrical connection will be weaker, and the stability will get worse.

From the perspective of the energy which the CC-VSC provides for the inertia response, the small-signal stability can also be analyzed as following.

Substituting (16) into the dynamic behavior of PLL in (10), the linearized equation can be achieved in (22).

$$J\Delta \omega = \left( {sk_{\text{p}} + k_{\text{i}} } \right)\Delta \psi$$
(22)

Generally, only the incremental relationship represented by the linearized equation is considered for small-signal stability analysis [11]. By manipulating (22) and substituting ∆ω for s∆δ, the following equation can be obtained:

$$\frac{J}{\Delta \psi } = \frac{{k_{\text{p}} }}{{\Delta \delta_{i} }} + \frac{{k_{\text{i}} }}{\Delta \omega }$$
(23)

Plainly stated in the linearized relationship shown in (23), the equivalent energy ψ is related to not only the angular frequency ω but also the current angle δ i . Further analysis of the result shows that a larger virtual inertia J implies more energy supporting inertia response in the CC-VSC system when other parameters are unaltered. It is revealed that more energy is required from the DC-side of the CC-VSC with a larger virtual inertia, thus the design of virtual inertia can’t be arbitrary and it is limited by the physical property of the DG on the DC-side. Although the increase of the control parameters k p and k i is beneficial to enhancing the damping performance and the synchronizing ability as stated above, it will also cause negative effect to a certain extent. As shown in (23), the instantaneous fluctuation of the current angle δ i may be very large if the proportional coefficient k p of PLL increases to a extreme degree. Analogously, there will be a considerable instantaneous fluctuation of the angular frequency with a large integral coefficient k i. Therefore, the parameter selection of k p and k i also need tradeoff, considering the damping performance and the synchronizing ability, as well as the instantaneous fluctuation of current angle and angular frequency.

5 Model application in small-signal stability analysis

5.1 Model application in a two-machine power system

In this section, the proposed Phillips-Heffron model is applied in a two-machine power system, as shown in Fig. 6. As we known, both Virtual SG (VSG) controlled VC-VSC and droop controlled VC-VSC can be regarded as an equivalent SG [8, 9]. Therefore, microgrid constructed by multiple VC-VSCs would be tantamount to a SG with large capacity, which is called “master SG” in this paper with inertia K J1, damping coefficient K D1 and synchronizing coefficient K S1. The PLL-based CC-VSC is regarded as a Phillips-Heffron model with K J2, K D2 and K S2 in the following analysis. The two-machine system including a CC-VSC and a voltage source is the basic configuration of multiple-machine system.

Fig. 6
figure 6

Structure of two-machine power system

Full size image

For small-signal analysis of the two-machine power system, the corresponding linearized model which is also known as the incremental equation can be obtained in (24).

$$\left\{ \begin{aligned} \frac{{{\text{d}}\Delta \delta_{1} }}{{{\text{d}}t}} &= \omega_{0} \Delta \omega_{1} \hfill \\ K_{{{\text{J}}1}} \frac{{{\text{d}}\Delta \omega_{1} }}{{{\text{d}}t}} &= - K_{{{\text{S}}1}} \left( {\Delta \delta_{1} - K_{\text{C}} \Delta \delta_{2} } \right) - K_{{{\text{D}}1}} \Delta \omega_{1} \hfill \\ \frac{{{\text{d}}\Delta \delta_{2} }}{{{\text{d}}t}} &= \Delta \omega_{2} \hfill \\ K_{{{\text{J}}2}} \frac{{{\text{d}}\Delta \omega_{2} }}{{{\text{d}}t}} &= - K_{{{\text{S}}2}} \left( {\Delta \delta_{2} - \Delta \delta_{1} } \right) - K_{{{\text{D}}2}} \Delta \omega_{2} \hfill \\ \end{aligned} \right.$$
(24)

In (24), ∆δ 1 and ∆ω 1 are the phase increment and frequency increment of the master SG which represents the microgrid. ∆δ 2 and ∆ω 2 are the current angle increment and frequency increment of the CC-VSC. ω 0 is the synchronous angular frequency of the grid.

It is worth noting that there is a coefficient K C in the calculating process of the frequency dynamic of the master SG. It is the conversion ratio between the current angle of the CC-VSC and the traditional power angle, as shown in (5). From the synchronous torque items in (24), it can be observed that there is a difference between the voltage source, namely the master SG, and the current source, namely the CC-VSC. The reason is that there is distinction between their synchronizing mechanisms. For the voltage sources, their phase synchronization depends on the exchange of active power which actuates the frequency change. However, for the current source, its phase synchronization aiming to the voltage reference depends on the PLL. As shown in (15), its synchronizing ability is related to the control parameter of PLL instead of the exchange of active power. Therefore, the variation of the current angle ∆δ 2 should be converted into the variation of traditional power angle when calculating the synchronous torque for the master SG. The quantitative relationship shown in (5) represents the effects of the current angle of CC-VSC on the phase and the angular frequency of the voltage source connected with it.

Taking ∆δ 1, ∆ω 1, ∆δ 2 and ∆ω 2 as state variables, the small-signal model of the two-machine power system can be written in a state-space form as shown in (25).

$$\left[ {\begin{array}{*{20}c} {\Delta \dot{\delta }_{1} } \\ {\Delta \dot{\omega }_{1} } \\ {\Delta \dot{\delta }_{2} } \\ {\Delta \dot{\omega }_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 & {\omega_{0} } & 0 & 0 \\ { - \frac{{K_{{{\text{S}}1}} }}{{K_{{{\text{J}}1}} }}} & { - \frac{{K_{{{\text{D}}1}} }}{{K_{{{\text{J}}1}} }}} & {\frac{{K_{{{\text{S}}1}} }}{{K_{{{\text{J}}1}} }}K_{\text{C}} } & 0 \\ 0 & 0 & 0 & 1 \\ {\frac{{K_{{{\text{S}}2}} }}{{K_{{{\text{J}}2}} }}} & 0 & { - \frac{{K_{{{\text{S}}2}} }}{{K_{{{\text{J}}2}} }}} & { - \frac{{K_{{{\text{D}}2}} }}{{K_{{{\text{J}}2}} }}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\Delta \delta_{1} } \\ {\Delta \omega_{1} } \\ {\Delta \delta_{2} } \\ {\Delta \omega_{2} } \\ \end{array} } \right]$$
(25)

5.2 Stability analysis of two-machine power system

As mentioned above, droop controlled VC-VSC can be regarded as an equivalent SG [8, 9]. Since there are more and more droop controlled VC-VSCs applied in microgrid as voltage sources, droop controlled VC-VSC is taken as a typical example of the master SG in this paper. As stated in [8], the corresponding equivalent inertia K J1, equivalent synchronizing coefficient K S1, and equivalent damping coefficient K D1 can be deduced as (26). In (26), T f is the filtering time constant in the droop control, and k P is the power-frequency droop coefficient. U 1 is the terminal voltage amplitude of the VC-VSC itself, and U 2 is the amplitude of the voltage at the other end of the transmission line. X L is also the reactance of the transmission line, and δ 0 is the steady-state phase difference between U 1 and U 2.

$${\kern 1pt} \left\{ \begin{aligned} K_{{{\text{J}}1}} &= {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{T_{\text{f}} }}{{k_{\text{P}} }} \hfill \\ K_{{{\text{S}}1}} &= {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{3}{2}\frac{{U_{1} U_{2} }}{{X_{L} }}\cos \delta_{0} \hfill \\ K_{{{\text{D}}1}} &= {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{{k_{\text{P}} }} \hfill \\ \end{aligned} \right.$$
(26)

Parameters of the two-machine power system are given in Table 1. As stated above, the two-machine system including a CC-VSC and a voltage source is the basic configuration of multiple-machine system. The stability analysis based on the two-machine system is both representative and typical. Therefore, it is regarded as the basic case to investigate the small-signal stability in this part.

Table 1 Parameters of two-machine power system
Full size table

Figure 7a shows the trajectories of the eigenvalues along with the virtual inertia of the PLL, namely the equivalent inertia coefficient of the CC-VSC, increasing from 0.05 to 0.2. The direction of the arrow represents the variation trend of system eigenvalues. Since the parameter J changes with equal space, the effect of the equivalent inertia on the eigenvalues is stronger at the sparse sections of the eigenvalue trajectories, while the effect of the equivalent inertia on the eigenvalues is weaker at the serried sections of the eigenvalue trajectories. As shown in Fig. 7a, there are two pairs of conjugate eigenvalues in the two-machine power system. According to the sensitivity analysis [14], it is revealed that the conjugated eigenvalues #1 and #2 are sensitive to the state variables ∆δ 2 and ∆ω 2 and the conjugated eigenvalues #3 and #4 are sensitive to the state variables ∆δ 1 and ∆ω 1 when the parameter J is less than 0.16. In this parameter range, the frequency of the oscillation mode which is dominated by the CC-VSC decreases gradually, while the damping ratio gets worse with the parameter J increasing. In the parameter range 0.16 ≤ J ≤ 0.2, all the eigenvalues are influenced by the state variables ∆δ 1, ∆ω 1, ∆δ 2 and ∆ω 2 together and there is little difference between the strengths of influence. It is obvious that the conjugated eigenvalues #3 and #4 move to the right half plane significantly in this parameter range with the parameter J increasing. The critical value of the parameter J is about 0.18. When the equivalent inertia coefficient of the CC-VSC is larger than 0.18 in this case, the two-machine system will be unstable. It implies that the equivalent inertia of the CC-VSC can’t be designed too large relative to the inertia of the voltage source which it connected to.

Fig. 7
figure 7

Trajectories of eigenvalues

Full size image

Figure 7b shows the trajectories of the eigenvalues with the decrease of the parameter k p, which will cause the decrease of the equivalent damping coefficient of the CC-VSC. According to the sensitivity analysis, it is revealed that the conjugated eigenvalues #1 and #2 are sensitive to the state variables ∆δ 2 and ∆ω 2 and the conjugated eigenvalues #3 and #4 are sensitive to the state variables ∆δ 1 and ∆ω 1. From the trajectories of the eigenvalues in Fig. 7b, it can be observed that the frequency of the oscillation modes almost not affected by the variation of the parameter k p. Nevertheless, damping ratio of the oscillation modes is reduced with the parameter k p decreasing, especially the oscillation mode dominated by the state variables ∆δ 2 and ∆ω 2 of the CC-VSC. As shown in Fig. 7b, eigenvalues of the two-machine system move into the unstable region when the parameter k p is less than 0.16.

Figure 7c demonstrates the trajectories of the eigenvalues as the synchronizing coefficient of CC-VSC decreasing which is caused by the decrease of the parameter k i. According to the sensitivity analysis, it is revealed that the conjugated eigenvalues #1 and #2 are sensitive to the state variables ∆δ 2 and ∆ω 2 and the conjugated eigenvalues #3 and #4 are sensitive to the state variables ∆δ 1 and ∆ω 1 when the parameter k i is larger than 90. In this parameter range, the frequency of the oscillation mode which is dominated by the CC-VSC decreases gradually, while the damping ratio increases with the parameter k i decreasing. In the parameter range from 90 to 50, all the eigenvalues are influenced by the state variables ∆δ 1, ∆ω 1, ∆δ 2 and ∆ω 2 together and there is little difference between the strengths of influence. As shown in Fig. 7c, the conjugated eigenvalues #3 and #4 move to the right half plane significantly in this parameter range with the parameter k i decreasing. When the parameter k i of the CC-VSC is less than 55 in this case, the two-machine system will be unstable.

It is worth mentioning that the purpose of the stability analysis based on the two-machine system presented above is providing a basic reference case for the small-signal stability analysis of multiple-machine system. Actually, it can be observed that the amount increasing of the CC-VSCs in the multiple-machine system is equivalent to the inertia decreasing of the master SG which acts as the voltage reference in the basic two-machine system through the similar analysis. The inertia decreasing of the master SG means that the relative inertia of the CC-VSC increases, which may cause the eigenvalues moving to the right half plane and threat to the system stability. It can be easily validated, for example the stability has a tendency to deteriorate when the penetration of DGs increases or the grid gets weaker for application in engineering. Due to the limited space, the detailed discussion about other multiple-machine systems is not presented here, but the relative conclusions can be deduced according to the stability analysis presented above.

6 Simulation verifications

6.1 Validation of Phillips-Heffron model of CC-VSC

In order to verify the proposed Phillips-Heffron model of the CC-VSC, a simulation of one-machine infinite-bus power system is performed, as illustrated in Fig. 1. In the simulation, the DC side is connected to a constant voltage source, which facilitates focusing on the electromechanical dynamic of PLL. The control structure is also illustrated in Fig. 1 which applies the usual PI control scheme with the assistant of SRF-PLL. The main parameters are given in Table 2.

Table 2 Parameters for simulation
Full size table

In these following simulation results, sub-graph (a) depicts the angular frequency ω of the PLL-based CC-VSC. The variation of equivalent energy ψ supporting inertia response of the CC-VSC and the output active power P of the VSC are illustrated in sub-graph (b) and (c), respectively. The reactive current reference of VSC is always set to zero. The active current reference i * d is originally set to 105A (the corresponding output power of three-phase VSC is about 50 kW), and generates a 5% step disturbance at the time of 1.1 s.

Figure 8 illustrates the influence of the virtual inertia J on the dynamic behavior of CC-VSC. As shown in Fig. 8, it is obvious that the oscillation of ω decreases with the virtual inertia J increasing. It means that the larger virtual inertia coefficient is able to withstand abrupt fluctuation of the angular frequency ω. If the virtual inertia of the CC-VSC is too small, the instantaneous fluctuation of the angular frequency will be large. The ability to maintain the system frequency can be regulated by designing the virtual inertia coefficient J. However, the stronger ability of frequency stabilization is at the cost of larger fluctuation of the output power of CC-VSC, and the corresponding equivalent energy ψ supporting inertia response, as shown in Fig. 8. It is also coherent with the theoretical analysis given in (16). As shown in (16), if the virtual inertia J is larger, the fluctuation of the equivalent energy ∆ψ will be large, so as the corresponding active power ∆P.

Fig. 8
figure 8

Effect of J on small-signal stability of the CC-VSC

Full size image

Figure 9 illustrates the influence of the proportional gain of PLL on the damping characteristic of CC-VSC. Distinctly, oscillations of the angular frequency, the equivalent energy ψ and the output active power are mitigated with the parameter k p increasing. It is indicated that larger k p provides a better damping capability, which is coherent with the theoretical analysis given in (15).

Fig. 9
figure 9

Effect of k p on small-signal stability of the CC-VSC

Full size image

Figure 10 shows the impact of the integral gain k i of the PLL on the synchronizing ability of CC-VSC. As shown in Fig. 10, the angular frequency, the equivalent energy ψ as well as the corresponding output power are able to draw near to each steady state value more quickly, with the increase of k i. It is revealed that larger k i indicates stronger synchronizing ability in accordance with (15). As stated in Section 4, the natural frequency will increase while the damping ratio will decrease with the parameter k i increasing. So it can also be observed that the oscillation amplitudes of ω, ψ, and P get higher with the integral gain k i increasing in Fig. 10.

Fig. 10
figure 10

Effect of k i on small-signal stability of the CC-VSC

Full size image

6.2 Validation of stability analysis based on proposed model

Simulation based on the two-machine power system is also performed to demonstrate the validity of the proposed Phillips-Heffron model of CC-VSC for multi-machine application in Section 5. System configuration is illustrated in Fig. 6. The main parameters are given in Table 1. It is worth to note that the “master SG” which represents the microgrid is implemented as a droop- controlled VC-VSC in the simulation.

In these following simulation results, the output active power of CC-VSC is set to 20kW and the reactive power is zero. At the time of 5.1s, the voltage of the microgrid generates a 5° phase jump as a disturbance. Figure 11 illustrates the influence of the inertia coefficient of CC-VSC on the small-signal stability of the two-machine system. Figure 11a depicts the situation when the inertia of CC-VSC is relatively small (J = 0.05), Fig. 11b shows the situation with a larger inertia (J = 0.15), and Fig. 11c shows the situation when the inertia is larger than the critical value shown in Fig. 7a. There is a coupling oscillation between the angular frequency of master SG, namely ω 1, and the angular frequency of CC-VSC, namely ω 2. The coupling oscillation is relatively slow with a large inertia of the CC-VSC, while the frequency of the coupling oscillation mentioned above is higher with a small inertia, comparing the Fig. 11a and b. It is also revealed that, with the inertia of the CC-VSC increasing, the small-signal stability of the system is deteriorated, regardless of the suppression of the instantaneous frequency fluctuation of CC-VSC itself. From Fig. 11c, it can be see that the system will become unstable after the equivalent inertia of the CC-VSC exceeds the critical value.

Fig. 11
figure 11

Frequency dynamic with the inertia coefficient of the CC-VSC increasing

Full size image

As shown in Fig. 12, the coupling frequency dynamic of the two-machine system will be affected by the damping coefficient of the CC-VSC. As shown in Fig. 12a, with a large damping coefficient (k p = 3), the convergence of the frequency oscillation is fast. While the damping coefficient of the CC-VSC is decreased (k p = 1), the frequency oscillation gets more obvious, which implies a poor stability. With the parameter k p further decreasing and exceeding the critical value in Fig. 7b, the angular frequency of both the CC-VSC and the master SG keep sustained divergent oscillating.

Fig. 12
figure 12

Frequency dynamic with the damping coefficient of the CC-VSC decreasing

Full size image

The influence of the synchronizing coefficient of the CC-VSC is illustrated in Fig. 13. Compared with the Fig. 13b, Fig. 13a has a relatively poor performance of the system stability with a large synchronizing coefficient (k i = 300) of the CC-VSC. The frequency oscillation is more obvious than that in Fig. 13b when the disturbance occurs, especially the frequency dynamic of the CC-VSC itself. Moreover, the frequency of the coupling oscillation is higher with the large synchronizing coefficient, which is also in accordance with the analysis in Section 5. After the synchronizing coefficient of the CC-VSC is reduced (k i = 150) appropriately, the frequency oscillation of the system is suppressed in a certain extent. Nevertheless, as mentioned in the theoretical analysis in Section 5, with the parameter k i further decreasing and exceeding the critical value in Fig. 7c, the system will be unstable. This situation is shown in Fig. 13c with a very small synchronizing coefficient (k i = 50) of the CC-VSC.

Fig. 13
figure 13

Frequency dynamic with the synchronizing coefficient of the CC-VSC decreasing

Full size image

7 Conclusion

Considering the differences and relations between the CC-VSC and the voltage source, the concept of current angle is proposed for the CC-VSC, similar to the rotor angle of traditional SG. By using the current angle, a Phillips-Heffron model for the CC-VSC is presented, considering the dynamic of phase-locked-loop (PLL) in the weak grid. Then the dynamics of the CC-VSC in the electromechanical time scale is represented by the famous inertia, synchronizing and damping coefficients, and the small-signal stability of a CC-VSC-based single machine infinite bus system is analyzed by means of the traditional theory of power system. It is found that: 1) The CC-VSC can imitate the traditional SGs to implement equivalent inertia by designing the parameter J in the PLL; 2) Within certain limits, the CC-VSC possesses strong capabilities for damping oscillations and supporting machine-grid synchronism, if k p and k i are large; 3) On the contrary, these capabilities will be weakened with the output active power increasing or the connection inductance increasing.

Based on the relationship between the current angle and the traditional power angle, the proposed Phillips- Heffron model of the CC-VSC can be applied in the multiple-machine system. Taking the two-machine power system as a basic case, the small-signal stability analysis is investigated. It is revealed that the inertia, the damping and synchronizing coefficient of CC-VSC will influence the coupling oscillation of the whole system. Based on the proposed model and the theoretical analysis, parameter optimization of the CC-VSCs can be achieved from the perspective of the small-signal stability of the modern power system including VSCs and SGs.