1 Introduction

Every bridge has certain restriction for the vehicle load and length. When the limit exceeds, permit has to be sought from the competent authority to pass the vehicle through the bridge. Weigh bridges are installed at important sections of highways to restrict the overloaded vehicles to enter the bridge. Presently, weigh-in-motion system in use can estimate the axle loads. But it incurs high cost of installation and maintenance. Accuracy is also affected by the speed of vehicle and unevenness of the pavement. It is to be mentioned that vehicle and bridge are integral parts of transportation system. The performance of one is affected by the performance of other and vice versa. Their behavior is coupled due to forces at contact points. For given structural configuration, construction materials, and road surface condition, the physical parameters of vehicle also play a significant role in bridge dynamic behavior. Traditionally, the bridge design load is calculated by magnifying static live load with impact factor. Days are not far when complete moving load time history would be necessary to check the design of long-span bridges. Recognizing the practical significance of the research on moving load identification, efforts have been made to estimate vehicle load from the bridge dynamic response using various techniques to improve the accuracy.

For the determination of axle load, weigh-in-motion system using instrumented bridge was developed by Moses [1]. Clayton and Peter [2] investigated truck weights from the perspective of regulatory limits. Accurate knowledge of dynamic forces acting on the built-up bridges is important to know the remaining service life. The interaction of moving vehicles with bridge has attracted the attention of many researchers for predicting their behavior by analytical and numerical techniques. However, it is difficult to measure the interaction force directly as their dynamics are coupled with both temporal and spatial variation. Theoretical model of bridge–vehicle interaction was developed by Green and Cebon [3] and Yang and Yau [4] within the limitations of linear dynamics. The determination of vehicle parameters from bridge response measurement requires a development of forward and an inverse scheme. The inverse solution is usually iterative in nature, whereas forward scheme may adopt an analytical or numerical approach depending on the bridge–vehicle model and degree of complexity involved. Yu and Chan [5] reviewed the recent works on moving load identification on bridges. Connor and Chan [6] employed least square method to estimate equivalent static load and their dynamic variation with time based on bridge response measurement. Vehicle–bridge interaction was ignored in the system model. An interpretive method was developed by Law et al. [7] where bridge has been modeled as an assembly of lumped masses, and Chan et al. [8] improved the model using Euler Bernouli continuous system. He also conducted laboratory experiments for the identification of moving mass from measured strain [9]. Later on, Law and Fang [10] proposed a theoretical optimal state estimation with the use of dynamic programming, by which moving load could be identified, overcoming the difficulties of ill conditioning of state matrix in time and frequency domain approach mentioned in Refs [11, 12]. Moving load identification in multi-span beams was also reported in Refs. [13, 14], where the effect of noise, number of vibration modes, and effect of support flexibility for non-rigid bearings were considered. Recently, Wu and Law [15] adopted stochastic finite-element-based method for moving load identification and further, they presented a new approach of vehicle axle load identification using Karhunen–Loeve expansion of stochastic process with irregular road surface [16]. In the last two decades, system identification using various numerical and experimental techniques has been tried in the field of structural engineering. Ghanem and Shinozuka [17] reviewed different identification algorithms and studied their applications to structures subjected to earthquake excitation. Shinozuka and Ghanem [18] verified different identification algorithms based on data obtained during controlled experiments on physical model. Deng and Cai [19] used genetic algorithm to identify parameters of vehicles moving on bridges. Development of Bayesian state estimation methodologies has added a new dimension in system identification involving various uncertainties [20]. Most important Bayesian estimation is Kalman filtering which is applicable to linear models and Gaussian type of uncertainties, and can be regarded as the stepping stone for the development of particle filtering method. In the last decade, the particle filter method based on conditional probability theory has attracted many researchers in the field of communication engineering, robotics, image processing, and ecology to estimate state of the system and hidden parameters from noisy signals/data [21–23]. Weerts et al. [24] applied particle filtering for state updating in rainfall–runoff models in hydrological applications. Schon et al. [25] reported on the computational complexity that increases with state dimension and suggested a marginalization technique to improve particle filtering which was then successfully used to an integrated navigation system of Swedish aircraft. Chatzi and Smyth [26] considered sensor heterogeneity for system identification of three degree of freedom system using unscented Kalman filter and particle filter technique. Narsella and Manohar [27] employed finite-element-based particle filter method for system identification with multiple sensor data for structural health monitoring purpose. Use of particle filter technique to estimate damage in vibrating beams without prior information of undamaged state has been documented by Pokale and Gupta [28]. Ching et al. [29] and Nasrella and Manohar [30] applied a particle filter method for state as well as system parameter estimation of dynamic systems implementing finite-element model in forward scheme with deterministic excitation. It was concluded that particle filter method can provide consistent result for non-linear models also.

Literatures available on the identification of moving load parameters on bridges using particle filter technique are scanty. Further researches are necessary to establish the popularity of the particle filter technique in vehicle–bridge coupled dynamics in the presence of stochasticity of contact forces. It was realized by researchers that particle filtering technique is computationally expensive, as a large number of response samples are required to obtain converged results. Although particle filter technique may take care of model inaccuracies, forward solution of mathematical model of the dynamic system with iterative or numerical schemes consumes lot of time to detect hidden parameters in the signal. In view of this fact, it would be advantageous if an idealized but quite accurate physical model is evolved which enables closed-form solutions to be interfaced with the iterative process of the particle filtering technique. In the present paper, a forward solution of the bridge–vehicle coupled system for non-homogeneous pavement input has been obtained in closed form to enable rapid generation of samples, required in the iterative algorithm to overcome the demerits of the existing particle filter method. Since accelerometers are the most practically used sensors, the simulated acceleration time history has been used to illustrate the approach with idealized model of bridge and vehicle. It may be noted that most of the authors limited their study to the estimation of gross vehicle weight from the bridge dynamic response. The effect of vehicle suspensions on the bridge dynamic response has been recognized by Green et al. [31], where they observed that use of soft and well-damped suspension produces smaller dynamic wheel loads on the bridge pavement. Moreover, estimation of vehicle suspension and tyre parameters, in indirect way, is also helpful to vehicle owners since a suitable maintenance policy may be worked out from the knowledge of current status. The present study formulates a coupled bridge–vehicle system using continuum approach, where parameters of bridge and vehicle in combined way influence the system output and, therefore, governs the moving force time history on the bridge. Particle filtering technique along with semi-analytical scheme has been used to estimate not only vehicle body mass but also tyre mass, suspension stiffness, suspension damping, tyre stiffness, and tyre damping. The identified vehicle parameters have been used to reconstruct interaction force time history and compared with the true value. The algorithm used in the present study along with semi-analytical method of sample generation has been tested by comparing the results with theoretical and experimental results available in published literatures. The identification technique used in the paper has also been examined in the presence of noise with response samples at different locations, vehicle velocity, and bridge surface roughness. The effect of range of the parameters to construct prior probability density function on the efficiency of the method is also discussed.

2 Bridge–vehicle dynamic interaction

2.1 Bridge–vehicle system equations

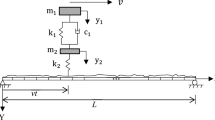
In particle filtering technique, it is necessary that forward problem of the bridge–vehicle model can be solved by adopting suitable scheme. The choice of model depends on the purpose of analysis, computational cost, and desired accuracy. Usually, transverse dimension of bridge deck is small compared to its span, and therefore a simplified beam model is a suitable option to establish a clear connection between bridge response and other influencing parameters [32], especially in case of implementing a computationally intensive method for the estimation of system parameters using large number of response samples in stochastic dynamics. The simpler model when tuned to fundamental natural frequency of the real bridge is expected to predict dynamic behavior similar to real structure. In the present study, a single-span bridge has been idealized as Euler–Bernoulli beam of uniform cross section and damping properties. Vehicle has been modeled as a lumped sprung mass m v, and the mass of wheel, tyre, and part of the suspension is referred to as the unsprung mass m w. The characteristics of the vehicle suspension system have been assumed to be linear. The bridge–vehicle model is shown in Fig. 1.

Fig. 1
figure 1

Bridge-vehicle Model

Full size image

All translatory motions are assumed to be positive in upward direction. The sprung mass m v is subjected to heave motion z 1 in vertical direction, and the vertical displacement of unsprung mass m w is subjected to z 2. The vehicle body and the unsprung mass are connected by suspension system comprising spring element of stiffness k v and dashpot with damping constant c v, respectively. Tyre stiffness and damping are k t and c t, respectively. It may be noted that the vertical degrees of freedom z 1 , z 2 and bridge deflection y(x,t) are measured with reference to their respective static equilibrium position at any time instant t. The equation of motion for the vehicle is coupled with the bridge equation of motion through the interaction force existing at the contact point of the two systems.

The governing differential equations of motion of the two lumped masses can be written as

$$ m_{\text{v}} \textit{\"{Z}}_{1} (t)\, + \,c_{\text{v}} \left\{ {\dot{Z}_{1} (t)\, - \,\dot{Z}_{2} (t)} \right\}\, + \,k_{\text{v}} \left\{ {Z_{1} (t)\, - \,Z_{2} (t)} \right\}\, = \,0, $$
(1)
$$ m_{\text{w}} \textit{\"{Z}}_{2} (t)\, + \,k_{t} \,\,\left\{Z_{2} (t)\, - \,y(x_{\text{c}} ,\,t)\, - \,h(x_{\text{c}} )\right\}\, + \,k_{\text{v}} \,\,\left\{Z_{2} (t)\, - \,Z_{1} (t)\right\} + \,c_{\text{v}} \,\,\left\{\dot{Z}_{2} (t)\, - \,\dot{Z}_{1} (t)\right\} + \,c_{t} \left[ {\dot{Z}_{2} (t)\, - \,\left\{ {\dot{y}(x_{\text{c}} ,t)\, + \,\dot{h}(x_{\text{c}} )} \right\}} \right]\, = \,0, $$
(2)

where h(x) is the pavement roughness at a distance x from the reference station and x c denotes the location of wheel contact form the same reference station. The governing equation of transverse motion of the beam can be written as

$$ {\text{EI}}\frac{{\partial^{4} y(x,t)}}{{\partial x^{4} }} + m_{\text{b}} \frac{{\partial^{2} y(x,t)}}{{\partial t^{2} }} + c_{\text{b}} \frac{\partial y(x,t)}{\partial t} = \,f_{c} (x,t), $$
(3)

where m b, EI, and c b represent the mass per unit length, flexural rigidity of bridge, and viscous damping per unit length of bridge, respectively. Assuming tyre remains in contact with the bridge at all times, interaction force (f c ≥ 0) in space and time variable can be expressed as

$$ \begin{gathered} f_{\text{c}} (x,t) = - \left[ {k_{\text{t}} \left\{ {z_{2} (t) - y(x,t) - h(x)} \right\} + c_{\text{t}} \left\{ {\dot{z}_{2} (t) - \dot{y}(x,t) - \dot{h}(x)} \right\}} \right]\,\delta (x - x_{\text{c}} )\, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \{ m_{\text{w}} + m_{\text{v}} \} g\delta (x - x_{\text{c}} ),\,\,\,\,\,\,\,\,\, \hfill \\ \end{gathered} $$
(4)

where δ is the Dirac delta function having the following property

$$ \int\limits_{ - \infty }^{\infty } {f(x)} \,\delta (x - x_{\text{c}} )\text{d}x = f(x_{\text{c}} ). $$
(5)

2.2 Bridge deck roughness

In the present study, we introduce a roughness, which is non-homogeneous in space even though vehicle velocity is constant, by adopting the following equation:

$$ h(x) = h_{\text{m}} (x) + \sum\limits_{s = 1}^{N} {\varsigma_{s} \,\,\cos (2\pi \,\,\varOmega_{s} x + \theta_{s} )} , $$
(6)

where h(x) is the deck surface unevenness which includes two parts. The first part h m(x) is a deterministic mean which may represent construction defects, pot holes, approach slab settlement, expansion joints, development of corrugation, etc. The second part of Eq. (6) is a Gaussian process [33] with a random phase angle θ s uniformly distributed from 0 to 2π. N is the number of terms used to build up the road surface roughness,ς s is the amplitude of cosine wave, Ω s is the spatial frequency (rad/m) within the interval [Ω L , Ω U] where Ω L , Ω U are lower and upper cut-off frequencies of spatial unevenness, respectively. The parameters ς s and Ω s are computed as

$$\varsigma_{s} = {\sqrt{{2S(\varOmega_{s}}})\Delta \varOmega } \,\,\,\,;\varOmega_{s} = \varOmega_{\text{L}} + \left( {s - \frac{1}{2}} \right)\Delta \varOmega; \, \Delta \varOmega = \frac{{(\varOmega_{\text{U}} - \varOmega_{\text{L}} )}}{N}. $$
(7)

In Eq. (7), S(.) is the power spectral density function (m3/rad) at spatial frequency Ω s of road surface roughness. The index ‘s’ refers to a discrete point inside the frequency range Ω L to Ω U, where power spectral density of road roughness is to be known. In the present study, power spectral density function has been expressed as [34]

$$ S(\varOmega_{s} ) = S(\varOmega_{0} ) \times \left( {\frac{{\varOmega_{s}^{{}} }}{{\varOmega_{0}^{{}} }}} \right)^{ - 2} , $$
(8)

where Ω 0 is referred as discontinuity frequency and is taken as 1/2π (rad/m).

On examination of Eq. (8), it is revealed that at very low spatial frequency (Ω s  → 0), the power spectral density becomes unbounded, i.e., S(Ω s ) → ∞. In view of this, Yin et al. [35] suggested an improved equation as follows:

$$ S(\varOmega_{s} ) = S(\varOmega_{0}^{{}} ) \times \frac{{\varOmega_{0}^{2} }}{{\varOmega_{s}^{2} + \varOmega_{\text{L}}^{2} }}. $$
(9)

The PSD function given by Eq. (9) has been adopted in the present study.

2.3 Discretization of bridge equations of motion

Using mode superposition technique, the bridge deflection in flexure has been shown by Meriovitch [36] as

$$ y(x,t) = \sum\limits_{k = 1}^{\infty } {\varphi_{k} (x)q_{k} (t)} , $$
(10)

where \( \phi_{k} \left( x \right) \) is the flexural mode of the beam for simply supported boundary condition and q k (t) is the generalized co-ordinates in the kth mode. The natural frequencies of simply supported bridge can be obtained as [36]

$$ \omega_{k} = \sqrt {\frac{\text{EI}}{{m_{\text{b}} }}(\frac{k\pi }{L})^{4} } , $$
(11)

where \( \omega_{k} \) is the bridge natural frequency in the kth mode, and EI, m b, and L represent flexural rigidity, mass per unit length, and span of the bridge, respectively.

The mass normalized mode shape is given by [36]

$$ \varphi_{k} (x) = \sqrt {\frac{2}{{m_{\text{b}} L}}} \sin \frac{k\pi x}{L}. $$
(12)

Now, substituting Eq. (10) in Eq. (3) and multiplying both sides of the equation by \( \phi_{j} \left( x \right) \) and then integrating with respect to x from 0 to L with the use of orthogonality conditions, the equation of motion can be discretized in normal co-ordinates as

$$ \textit{\"{q}}_{k} (t) + 2\xi_{k} \omega_{k} \dot{q}_{k} (t) + \omega_{k}^{2} q_{k} (t) = Q_{k} (t),\;\left({k = 1, 2, 3\ldots} \right), $$
(13)

where \( \xi_{k} \) is the modal damping ratio in the kth mode. In practical application, the number of modes is to be limited to a finite size.

The generalized force (Q k ) of bridge in flexure [36] is given as

$$ Q_{k} (t) = \frac{1}{{M_{k} }}\int\limits_{0}^{L} {f_{c} (x,t)\varphi_{k} (x)\text{d}x} , $$
(14)

where the term M k is generalized mass in the kth mode [36] given by

$$ M_{k} = \int\limits_{0}^{L} {m_{b} \varphi_{k}^{2} (x)\text{d}x.} $$
(15)

Substituting Eq. (4) in Eq. (14) and using property of Dirac delta function, the generalized force in the kth of mode of bridge transverse vibration has been worked out as

$$ \begin{gathered} Q_{k} (t) = - \frac{1}{{M_{k} }}\left[ {k_{t} \left\{ {z_{2} (t) - \sum\limits_{k = 1}^{{n_{\text{b}} }} {\varphi_{k} (x_{\text{c}} )q_{k} (t)} - h(x_{\text{c}} )} \right\}\varphi_{k} (x_{\text{c}} )} \right. \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\, + c_{t} \left\{ {\dot{z}_{2} (t) - \sum\limits_{k = 1}^{{n_{b} }} {\varphi_{k} (x_{\text{c}} )\dot{q}_{k} (t)} - Vh^{\prime}(x_{\text{c}} )} \right\}\varphi_{k} (x_{\text{c}} ) - \{ m_{\text{w}} + m_{\text{v}} \} g\varphi_{k} (x_{\text{c}} ), \hfill \\ \end{gathered} $$
(16)

in which g denotes acceleration due to gravity and (′) represents space derivative.

2.4 Solution of forward problem

The system Eqs. (1), (2), and (13) are coupled second-order ordinary differential equations. Theoretically, there is infinite number of modes in continuous system. However, for practical purpose, the number of modes has to be truncated to a finite size. Considering first ‘n b’ flexural modes of the beam, the number of coupled equations then becomes n = 2 + n b. The system equations can be expressed in matrix notation as

$$ [\varvec{M}]\{\varvec{\textit{\"{r}}}(t)\} + [\varvec{C}(t)]\{\dot{\varvec{r}}(t)\} + [\varvec{K}(t)]\{\varvec{r}(t)\} = \{\varvec{F}(t)\}, $$
(17)

where {r(t)} = {z 1(t), z 2(t) q 1 (t), q 2(t)…, q n (t)}T is the response vector, {F(t)} is the generalized stochastic force vector. [M], [C(t)], and [K(t)] are the system mass, damping, and stiffness matrix, respectively, of size (2 + n b) × (2 + n b). It may be noted that due to coupling of bridge–vehicle equations, the stiffness and damping matrix becomes time dependent due to change of wheel contact position on the bridge with time. The ‘n’ system equations are now recast into a 2n-dimensional first-order state-space form [37] as given below:

$$ \{ \dot{\varvec{P}}(t)\} + [\varvec{A}(t)]\{ \varvec{p}(t)\} = \{ \varvec{P}(t)\} , $$
(18)

where

$$ \{ \varvec{p}(t)\} = \left\{ {\frac{{\dot{\varvec{r}}(t)}}{{\varvec{r}(t)}}} \right\};\quad[\varvec{A}(t)] = \left\{ {\begin{array}{*{20}c} {\frac{{[\varvec{M}]^{ - 1} [\varvec{C}(t)]}}{{ - [\varvec{I}]}}} & {\frac{{[\varvec{M}]^{ - 1} [\varvec{K}(t)]}}{{[{\mathbf{0}}]}}} \\ \end{array} } \right\};\quad\{ \varvec{P}(t)\} = \left\{ {\frac{{[\varvec{M}]^{ - 1} \{ \varvec{F}(t)\} }}{{\{ {\mathbf{0}}\} }}} \right\}, $$
(19)

Here, {p(t)} is the state vector, [A(t)] is the state matrix, [I] is an identity matrix, {P(t)} is the augmented excitation vector, and [0] is a null vector or matrix. This form is suitable for bridge–vehicle interaction problems, since suspension damping is not small and diagonalization of damping matrix as in case of Rayleigh’s damping may not be fully convincing. Let the eigenvalues of the state matrix [A(t)] be α 1 , α 2 , α 3 …α 2n and the corresponding complex conjugate eigenvectors be {u}1, {u}2, {u}3…{u}2n Defining modal matrix [U(t)] and using linear transformation {p(t)} = [U(t)]{v(t)} in Eq. (19), along with orthogonality condition of the complex eigen vectors, the decoupled first-order system is given below:

$$ \dot{v}_{j} (t) + \alpha_{j} v_{j} (t) = R_{j} (t),\,\,\,\,\,\,\,\,\,\,j = 1,2,3 \ldots 2n, $$
(20)

where

$$ R_{j} = \sum\limits_{s = 1}^{n} {u^{\prime}_{js} } \sum\limits_{k = 1}^{n} {m^{\prime}_{sk} F_{k} (t)} , $$
(21)

where \({u^{\prime}_{js} }\) denotes the elements in the inverse of the matrix [U(t)] and \({m^{\prime}_{sk} }\) denotes the elements in the inverse of matrix [M]. Using Fourier–Stieltjes transform [37], Eq. (21) can be written in frequency domain as

$$ R_{j} (\omega ) = \sum\limits_{s = 1}^{n} {u^{\prime}_{js} } \sum\limits_{k = 1}^{n} {m^{\prime}_{sk} \int\limits_{ - \infty }^{\infty } {\exp ( - i\omega t)} \,\text{d}[\,F_{k} (\omega )]} . $$
(22)

The general solution of Eq. (20) may now be expressed as

$$ v_{j} (t) = X_{0j} \exp ( - \alpha_{j} t) + \int\limits_{ - \infty }^{\infty } {H_{j} (\omega ,t)} R_{j} (\omega )\text{d}\omega , $$
(23)

where X 0j are constants of integration to be determined from the initial conditions. H j (ω,t) is the transient frequency response function given by [37]

$$ H_{j} (\omega ,t) = \frac{1}{{ - i\omega + \alpha_{j} }}\exp ( - i\omega t). $$
(24)

Using Eqs. (22), (24) in Eq. (23) and then utilizing linear transformation of generalized coordinate to physical coordinate, the original response vector {r(t)} may be expressed as

$$ \begin{aligned} r_{m} (t) = \sum\limits_{j = 1}^{2n} {u_{m + n,j} X_{0j} \exp ( - \alpha_{j} t)} + \sum\limits_{j = 1}^{2n} {u_{m + n,j} \sum\limits_{s = 1}^{n} {u^{\prime}_{js} } } \sum\limits_{k = 1}^{n} {m^{\prime}_{sk} } \quad \int_{ - \infty }^{\infty } {F_{k} (\tau )\left[ {\frac{1}{{2\uppi}}\int\limits_{ - \infty }^{\infty } {\frac{\exp [i\omega (\tau - t)]}{{ - i\omega + \alpha_{j} }}} \text{d}\omega } \right]} \,\text{d}\tau , \quad m = 1,2,3 \ldots \ldots n. \hfill \\ \end{aligned} $$
(25)

The first term of Eq. (25) represents homogeneous solution of the system equation due to initial condition, and the second term of the equation represents particular solution due to imposed dynamic force.

Using Cauchy’s residue theorem [38], the general solution of Eq. (25) now can be expressed in compact form

$$ r_{m} (t) = \sum\limits_{j = 1}^{2n} {u_{m + n,j} X_{0j} \exp ( - \alpha_{j} t)} + \sum\limits_{j = 1}^{2n} {u_{m + n,j} \sum\limits_{s = 1}^{n} {u^{\prime}_{js} } } \sum\limits_{k = 1}^{n} {m^{\prime}_{sk} } I_{jk} , $$
(26)

where

$$ I_{jk} = \int_{0}^{t} {\exp [\alpha_{j} (\tau - t)]F_{k} (\tau )} \text{d}\tau , $$
(27)

in which t is the bridge loading time defined as t = x/V, x being the distance traversed by the vehicle at instant t and V being the constant speed of the vehicle. When the vehicle is at the point of exit, then t = L/V where L is the span of the bridge.

Closed-form expressions for the components of the above integral which generates each of the response samples have been developed and given in Appendix-1. The response samples thus form complete ensemble of the process. Averaging across the ensemble at each time step yields mean \( \mu_{Y} \left( {t_{k} } \right) \) and standard deviation σ Y (t k ) of response process Y.

3 Identification of vehicle parameters

This paper presents the applicability of particle filter to identify the unknown vehicle parameters and provides an estimate of time-dependent moving load on the bridge. The main idea of this method is to estimate the unknown vehicles parameters from the available bridge response measurements. Since both the unknown parameters and the observation data are contaminated by noise, complete information of the parameters is possible if we can construct the probability density function of unknown parameters conditioned on the available bridge response measurement, called posterior probability density function. Vehicle parameters to be identified include sprung mass, unsprung mass, suspension stiffness, suspension damping, tyre stiffness, and tyre damping. Bridge parameters and the vehicle forward velocity are taken to be known.

The basic principle of particle filter method is to represent the required posterior density function of unknown vehicle parameters by a set of random samples (particles) with associated weights, and to compute the estimates based on these samples and weights. As the number of samples becomes very large, this Monte Carlo characterization becomes an equivalent representation of the posterior probability function, and the solution approaches the optimal Bayesian estimate [39]. The system states r l are assumed to propagate according to the system equation

$$ r_{l + 1} = g_{l} \,(r_{l} ;\,\varPhi {}_{l}\,,\eta_{l} ),\,\,\,\,\,\,\,l = 0,1,2,3 \ldots . \, N_{t} , $$
(28)

where l represents the discretized time dimension and N t is the number of time instants considered. \(\varPhi_l\) Є R d is a d-dimensional vehicle parameters vector which is considered as constant, r l Є R n is a n-dimensional vector denoting the state of the system, and a model noise η l Є R m is the discretized m-dimensional vector of a sequence of independent and identically distributed random variables. The noise is assumed to be independent of past and current state with known probability density function. g l (.) is a system transition function.

When the system measurements become available, the system states are related to these measurements via the observation equation given below:

$$ Z_{l} = f_{l} (r_{l} ;\varPhi_{l} \,,\zeta_{l} )\,\,;\,\,\,\,\,\,\,\,l = 0, \, 1, \, 2, \, 3 \ldots . \, N_{t} , $$
(29)

where Z l Є R p is a p-dimensional bridge response measurement vector, a measurement noise ζ l Є R s is a s-dimensional vector of a sequence of independent and identically distributed random variables, and f l (.) is a non-linear function that relates the measurements to the system state.

Since, state of the system is dependent on system parameters {Φ}, observation equation can be rewritten as

$$ Z_{l} = f_{l} \,(\varPhi_{l} \,,\zeta {}_{l}\,),\;\,\,\,\,\,\,\,l = 0, \, 1, \, 2, \, 3 \ldots \, N_{t} . $$
(30)

Vehicle parameters identification problem can now be considered as being equivalent to the determination of the posterior probability density function p(Φ l |Z l ). According to Bayesian theorem, p(Φ l |Z l ) can be written as [39]

$$ p(\varPhi_{l} |Z_{l} ) = \frac{{p(Z_{l} |\varPhi_{l} )p(\varPhi_{l} )}}{{\int {p(Z_{l} |\varPhi_{l} )p(\varPhi_{l} )\text{d}\varPhi_{l} } }}, $$
(31)

where \( p(\varPhi_{l} |Z_{l} ) \) is the posterior PDF, \( p(Z_{l} |\varPhi_{l} ) \) is the likelihood of individual parameters, \( p (\varPhi) \) is the prior probability density function, and \( \int {p(Z_{l} |\varPhi_{l} )p(\varPhi_{l} )\text{d}\varPhi_{l} } \) the normalizing parameter, respectively.

Thus knowing posterior PDF p(Φ l |Z l ) first few moments of the vehicle parameters Φ l , conditioned on bridge response measurement Z l , at each time step can be determined. The particle filtering algorithm for identifying vehicle parameters has been implemented by the following principal operations [39]:

(i) Prediction: Draw N p random samples of vehicle parameters \( \{ \varPhi_{0j} \}_{l = 1}^{{N_{l} }} \) from the assumed PDF \( \{ p(\varPhi_{0l} )\}_{l = 1}^{{N_{l} }} \).

(ii) Forward Solution: Determine bridge response using present closed-form expressions at time step l. If N l is sufficiently large, these estimates are approximately distributed as \( \{ p(f_{l} \,[\varPhi_{0l} ]|Z_{l} )\}_{l = 1}^{{N_{l} }} \) .

(iii) Updating: Once the measurements are available for different measurement locations (i = 1,2,3….N m ) at time l, evaluate the likelihood corresponding to all the samples.

This implies that one needs to evaluate \( \{ p(Z_{l} |f_{l} \,[\varPhi_{0l} ])\}_{l = 1}^{{N_{l} }} . \)

For the lth measurement, calculate the weighting function as

$$ w_{l} = \frac{{p(Z_{l} |\varPhi_{il}^{*} )}}{{\sum\nolimits_{j = 1}^{{N_{p} }} {p(Z_{l} |\varPhi_{il}^{*} )} }}. $$
(32)

The discrete mass probability function for the next iteration is defined as

$$ P(\varPhi_{lj} = f_{l} \,[\varPhi_{0j} ]) = w_{j} . $$
(33)

(iv) Resampling: From the discrete mass distribution function, a new set of N p samples of Φ lj is generated. This constitutes the posterior estimates of Φ lj . The mean of estimates is obtained by averaging across the ensemble.

Set l = l+1 and if l < N t , then go to the step (ii) and repeat other steps, otherwise stop. In this way, the filtering is carried out for the entire available time history of measurements.

4 Results and discussions

In this study, particular attention is given to examine the applicability of particle filter method in identifying vehicle parameters (sprung mass, unsprung mass, suspension stiffness, suspension damping, tyre stiffness, and tyre damping) on measured bridge dynamic response. Since no physical experiments have been undertaken, the measured response samples have been synthetically generated using the present analytical expression with artificial noise added to it to mimic field data. The ends of the bridge are simply supported. The following data for bridge and vehicle have been assumed to simulate measured response:

Bridge span (L) = 20 m; mass (m b) = 11.15 × 10 kg/m; flexural rigidity (EI) = 1.695 × 1010 N-m2; Speed range in which vehicle movement is considered is 40–80 km/h; Vehicle mass (m v) = 18,000 kg; wheel mass (m w) = 1,500 kg; suspension stiffness (k v) = 3.6 × 107 N/m; Suspension damping (c v) = 7.2 × 104 N-sec/m; tyre stiffness (k t) = 0.9 × 107 N/m; and tyre damping (c t) = 0.7 × 104 N-sec/m. For modeling deck surface roughness, the values of spectral roughness coefficient (ς) have been taken as 2 × 10−6–18 × 10−6 m2/(m/cycle) according to International Organization for Standardization (ISO-8608) specifications for the class of different road conditions [40]. The lower and upper limits of the spatial frequencies of the road profile are taken as ω L = 0.01 cycle/m and ω U = 3 cycle/m. The cut-off spatial frequencies are chosen in view of the practical size of tyre. The forward problem has been solved using closed-form solution given in Sect. 2.4, and above data have been employed to generate bridge dynamic responses.

With the assumed parameters as above, time histories of response (displacement, velocity, and acceleration) at three different locations (at L/4, L/2, and 3L/4) have been obtained, and the response time series are made corrupted by addition of artificial noise. In generating response samples to mimic measured data, vehicle parameters, bridge roughness profile and vehicle speed, have been taken as known quantities. The focus is on demonstrating whether the simulated (measured) data used as input to the particle filter be able to estimate the values of the vehicle parameters and to what precision. With identified vehicle parameters and known bridge sectional and material properties, state has been estimated and used to reconstruct dynamic tyre force imposed on the bridge during movement of the vehicle.

4.1 Response statistics of bridge

Response statistics have been found by a semi-analytical solution of forward problem which is intended to assist particle filtering algorithm to identify vehicle parameters. We first present the mean displacement, velocity, and acceleration of the bridge at one-fourth, half, and three-fourth of span (Figs. 2, 3, and 4). Corresponding standard deviations are shown in Figs. 5, 6, and 7, respectively. Vehicle velocity is taken as 60 km/h (16.67 m/sec). These results are obtained from the present analytical formulations laid down in Sect. 2. No noise has been added at this stage. However, measured data will be considered in the particle filter algorithm by adding different levels of noise in the simulated response sample using closed-form expressions.

Fig. 2
figure 2

Mean displacement of bridge at different locations

Full size image
Fig. 3
figure 3

Mean velocity of bridge at different locations

Full size image
Fig. 4
figure 4

Mean acceleration of bridge at different locations

Full size image
Fig. 5
figure 5

Standard deviation of bridge displacement response at different locations

Full size image
Fig. 6
figure 6

Standard deviation of bridge velocity response at different locations

Full size image
Fig. 7
figure 7

Standard deviation of bridge acceleration at different locations

Full size image

The mean quantities of mid-span response is larger compared to other span locations. Due to variation of roughness in random manner, the response magnitudes at other points are also different. The frequency of oscillation for the mean response at different locations shown in Figs. 2, 3, and 4 are not varying as the vehicle wheel is excited by same frequency due to uniform velocity considered in the presentation of the results here. Standard deviation values shown in Figs. 5 and 7 do not show any definite pattern of variation.

4.2 Comparison of vehicle load estimation with published results

Main focus of the present study is to estimate vehicle parameters from bridge dynamic response using particle filtering technique. Before conducting a parametric study for the vehicle parameters to be identified, a comparative study of the results obtained by particle filtering approach with published results obtained by different identification techniques has been carried out.

4.2.1 Comparison with the results of numerical study

First, we present a comparative study with the method proposed by Law et al. [41] based on simulated data to judge the efficiency of particle filter approach for moving load identification. The loading on the bridge pavement used by them was a deterministic harmonic function composed of two different frequencies as given below:

$$ f(t) = 121\,\,\,[1 - 0.1\sin (10\rho \pi t) + 0.05\sin (50\pi t)]{\text{kN}} . $$
(34)

The result of Ref. [41] was based on interpretive method. The comparison is shown in Table 1. It may be noted that percentage error increases with the vehicle speed. Besides, it has been observed that poor surface condition of the bridge produces more error in the estimation. The same patterns have been found even in the present method. However, particle filter method gives improved estimate of the gross axle load in all cases as compared to the interpretive method. Further, gross axle force time history has been reconstructed from the estimated vehicle parameters by considering same bridge surface condition and vehicle speed as assumed by Law et al. [41]. Comparison of reconstructed force time history with the assumed time varying axle load is shown in Fig. 8. It may be seen that high fluctuation of moving force about the reference loading has been produced at the end of time history in the results obtained by Law et al. [41]. This might be due to the fact that high-frequency component of random unevenness could not be properly filtered out with the sampling frequency considered in the earlier study. However, the high-frequency component could not disturb the estimation of moving load when particle filter technique has been used in the present study. This resulted higher accuracy in parameter estimation.

Table 1 Comparison of the estimate of gross vehicle weight with published results [41]
Full size table
Fig. 8
figure 8

Comparison of reconstructed dynamic axle load with published result in Ref. [41]

Full size image

4.2.2 Comparison with the results of experimental study

The second comparative study has been done with the experimental data from Law et al. [7]. They conducted a laboratory experiment with a model car having a total mass (M c) 7.1 kg being pulled at a speed of 3.102 m/s over a simply supported beam of span 3.376 m. The model bridge was a flat bar having cross-sectional dimension of 100 mm × 25 mm. The mass and flexural rigidity of the beam were 24.12 kg/m and 63.4 kNm2, respectively. Other details of experiments can be found in Ref [7]. Accelerometers were mounted on the beam at 1/4, 1/2, and 3/4 span. Sampling frequency was 256 Hz. Acceleration record at 3/4th of the span experimentally obtained in Ref. [7] was taken as measured data in particle filter method for estimating the mass of the model car. The progress of iteration with updated estimation as obtained in the present study is shown in Fig. 9. The result shows that the filtering process converges at the 57th of iteration to a mass value of 7.26 kg. The error has been estimated as 2.25 %. This demonstrates successful application of particle filter method for the estimation of moving mass when experimentally acquired data are utilized in the algorithm.

Fig. 9
figure 9

Progressive estimate of model car mass using experimental data [7] and its comparison with true value

Full size image

4.3 Influence of various factors on vehicle parameter identification

The particle filter method is now applied to estimate the unknown vehicle parameters which include sprung mass, unsprung mass, suspension stiffness, suspension damping, tyre mass, stiffness, and damping. Only acceleration response of the bridge has been used as in most of the practical situation, accelerometers are common type of sensors. The analytically computed time history has been contaminated by the addition of artificial noise to mimic field data. The mean and standard deviation values of the vehicle parameters are calculated at each stage of iteration at each time step of the synthetically generated time history. The progress of iteration and its convergence are presented in the subsequent sub-sections taking various factors into considerations.

4.3.1 Effect of bridge response measurement location

The bridge acceleration measurement at different locations along the span has been used as input to the particle filter algorithm. Vehicle parameters as well as dynamic interaction force are estimated. In both the cases, standard deviation approaches very low value at a certain number of iteration which implies that the algorithm has achieved convergence. The progress of estimation of mean and standard deviation has been displayed in the form of graphical plot of estimated parameters versus corresponding number of iterations (Figs. 10, 11, 12, 13, 14, 15). Result shows that measurement taken other than the mid span takes a longer iteration to achieve convergence. Percentage error has been calculated for different measurement inputs as shown in Table 2. The results are obtained when response samples from analytical model are contaminated by 5 % noise. The effect of noise level on the algorithm has been tested by adding 10 % noise also. Table 3 shows the percentage error as well as number of iteration required to converge, when noise level is increased. Result shows that mid-span response gives the best estimate for the vehicle parameters as well as dynamic interaction force identification. The reconstructed mean and standard deviation of dynamic force induced in the bridge with identified parameters is shown in Fig. 16. The result reveals that bridge response measurement at mid span gives around 2%–5 % error, while measurement other than mid span leads to 4%–10 % error.

Fig. 10
figure 10

Progressive estimate of vehicle mass

Full size image
Fig. 11
figure 11

Progressive estimate of wheel mass

Full size image
Fig. 12
figure 12

Progressive estimate of vehicle suspension stiffness

Full size image
Fig. 13
figure 13

Progressive estimate of vehicle suspension damping

Full size image
Fig. 14
figure 14

Progressive estimate of tyre stiffness

Full size image
Fig. 15
figure 15

Progressive estimate of tyre damping

Full size image
Table 2 Effect of response measurement location on indentified vehicle parameters
Full size table
Table 3 Effect of different noise levels on the estimated vehicle parameters
Full size table
Fig. 16
figure 16

Comparison of a mean and b standard deviation of identified and true dynamic interaction force using acceleration data at different locations

Full size image

4.3.2 Effect of assumption of the prior PDF p(Φ 0)

In the absence of any information about the unknown parameters, it is assumed that the prior PDF p(Φ 0) is uniformly distributed within a range [Φ L, Φ U]. Two different cases have been considered to specify the range within which random particles are generated assuming uniform probability density function p(Φ 0).

Case-1: Keeping the lower and the upper limits with large variation from the true value.

Case-2: When the lower and upper limits are not widely apart from the actual value.

The ranges of values of the parameters assumed for the above two cases are mentioned in Tables 4, 5, 6. In these two cases, the number of particles N p  = 1,000 and artificial noise is taken to be 5 % of the simulated maximum bridge dynamic response. The mean and standard deviation are observed at each stage of iteration and stop when standard deviation becomes less than equal to tolerance. Identified vehicle–bridge interaction force is shown in Fig. 17 simultaneously comparing with the true value of dynamic interaction force. It has been found that a wrong choice of p(Φ 0) does not necessarily lead to wrong estimates by the particle filter identification method. However, a crude assumption of the prior probability density is found to consume longer time to achieve convergence. Assumption based on the first case of prior density function leads to 3%–5 % error, while the second case assumption gives 2%–4 % error.

Table 4 Range of mass of vehicle and wheel mass to construct prior PDF
Full size table
Table 5 Range of suspension stiffness and tyre stiffness to construct prior PDF
Full size table
Table 6 Range of suspension damping and tyre damping to construct prior PDF
Full size table
Fig. 17
figure 17

Comparison of a mean and b standard deviation of identified and true dynamic interaction force for different ranges of values used to construct prior PDF p(Φ0)

Full size image

4.3.3 Effect of different vehicle velocities

The identification algorithm has been examined from the measured response for different vehicle speeds over the bridge. The response samples have been generated at 60 km/h (16.67 m/s) and 80 km/h (22.20 m/s) of vehicle speed. The sampling time interval in measured response sample (after adding 5 % artificial noise) has been initially chosen as 0.02 s. This time interval was not satisfactory in case of vehicle moving at higher speed. The reason may be that vehicle leaves the bridge in a shorter time span generating less number of data points that are available in the working of a particle filter algorithm. Number of iteration required to get convergence and percentage error is tabulated in Table 7. It has been found that lower speed gives better estimate but it requires more number of iteration to achieve the convergence.

Table 7 Performance of the algorithm at different vehicle speeds (V)
Full size table

4.3.4 Effect of different roughness conditions

Bridge deck surface irregularity has been considered in the identification of vehicle parameters based on ISO specification [40] for different conditions—good, average, and poor. Among the three conditions, results show that good condition gives the best estimate with less number of iterations which is given in Tables 8, 9, 10. This may be attributed to the reason that noise effect in dynamic input for the case of rougher pavement increases, requiring more number of iterations for convergence. This is in conformity with the results obtained when artificial noise level increased from 5 % to 10 % as stated in Sect. 4.3.1.

Table 8 Identification of mass of vehicle and wheel for different road conditions
Full size table
Table 9 Identification of stiffness and damping of vehicle suspension for different road conditions
Full size table
Table 10 Identification of stiffness and damping of tyre for different road conditions
Full size table

4.4 Comparison of CPU processing time for estimation of vehicle parameters with numerically generated samples

The efficiency of the proposed analytical approach for the forward scheme in the identification of vehicle parameters has been judged by comparing the CPU processing time when numerically simulated samples are used. For numerical scheme, Newmark’s method [42] has been adopted. Three different sampling frequencies 300, 500, and 700 Hz have been used to compare the convergence rate. A personal computer with Inte l(R) Core (TM) i3-2120 CPU 3.3 GHz and 4.0 GB RAM has been employed for all computations. Vehicle speed 60 km/h (16.67 m/s) and poor bridge deck surface condition [40] have been considered for the study. The results are presented in Table 11. It has been found that sampling frequency affects the estimation accuracy for both the method of solutions. Higher sampling frequency leads to lower error in vehicle parameters estimation as shown in Table 11. Since several parameters are estimated simultaneously, the CPU processing time is also different for each parameter. The overall time requirement for the parameter estimation has been found to be decreased by 27 %, while average accuracy has been increased by 24 % due to the use of present semi-analytical method in forward scheme of Particle Filtering approach. This again demonstrates the superiority of particle filter method when combined with analytical method for generations of response samples.

Table 11 Comparison of computer processing time for estimation of vehicle parameters
Full size table

5 Conclusions

In the present study, particle filtering combined with a semi-analytical method has been outlined for the identification of vehicle parameters as it passes over a simply supported bridge. The deck surface roughness has been considered as a non-homogeneous random process in spatial domain. Comparison of the results obtained by present study using particle filter method with published results has shown higher accuracy. The dynamic interaction force time history has been reconstructed with the identified parameters and compared with true value. Effect of different measurement locations along the bridge span and artificially added noise has been investigated. The accuracy of the proposed method has been checked by considering two different cases of prior density function selection. A comparative study of computational time required in particle filter method using present semi-analytical scheme and numerical scheme has been performed. Some of the major findings and recommendations on the applicability of particle filter technique for vehicle parameter identification are given below:

(1) Response measurement location has greater influence on the accuracy and computational time required in application of particle filtering technique. For simply supported single-span bridge like the one being presented, mid-span sensor data may be the better option.

(2) For identification of vehicle parameters with greater accuracy and within short time, response picked up at lower vehicle movement would be preferable for the implementation of particle filtering method.

(3) Rough bridge deck surface would require more time for the convergence of the result. The same conclusion is also valid for increased noise level in response data.

(4) The initial wrong choice of parameters of prior probability density function does not eventually lead to wrong estimate, except that the convergence time would increase. This would imply that an idealized bridge model amenable for a closed-form solution of the response, in case of linear problem, may save much computational time.

(5) Choice of sampling frequency governs the time of convergence. Higher sampling frequency leads to the increased accuracy at the cost of increased CPU processing time in the estimation of system parameters.

(6) The present semi-analytical method used in generation of response samples brings rapid convergence and higher accuracy as compared to existing numerical methods.