1 Introduction

There are many systems existing in the form of networks, such as social networks, biological networks, World Wide Webs, and so on. Because these networks are with high complexity, they are named “complex networks” [1]. According to the quick spreading of application fields, the research of complex networks has become one of the most important intersecting fields of multi-subjects, and the modeling and simulation of complex networks has been paid more and more attention to. As an important aspect, many statistical descriptors of complex networks have been proposed, such as average path length, clustering coefficient, degree distribution, betweenness, entropy, etc., [2] in which entropy is an interesting conception. Some entropy descriptors have also been defined, such as entropy of the degree distribution, target entropy, search information entropy, and road entropy, etc. [3, 4]. Although the unprecedented progress has been achieved, these descriptors cannot describe the degree dependence relationship, which is also an important characteristic for modeling and simulation of complex networks.

In this paper, we propose a new entropy descriptor for complex networks named degree dependence entropy (DDE), describe the constructing process, and interpret the reasonableness of the DDE descriptor through the simulation experiments. The simulation results show that the DDE descriptor can reflect the complexity of degree dependence relationship in complex networks, which is meaningful for networked modeling and simulation. The rest of this paper is organized as follows: the complex networks and information entropy is reviewed in Sects. 2 and 3. Sections 4 and 5 describe the construction of degree dependence matrices and the proposed DDE descriptor. The experiments and discussion are discussed in Sect. 6. Finally, the conclusions are given in Sect. 7.

2 Complex networks

Qian Xue-sen gave a strict definition for complex networks as: networks with part or all characteristics of self-organization, self-similarity, attractor, small world and scale-free can be called the complex networks. It also can be generalized as networks producing high complexity, and the complexity is mainly presented as following points:

  1. (i)

    The structure is complex. The number of vertices is large, and the structure of networks produces many different characteristics.

  2. (ii)

    The network is evolutional. Mainly networks represent the appearance and disappearance of vertices. Take the world-wide network for example, the web page or link may appear or disconnect at any time, which changes the network structure continuously.

  3. (iii)

    The types of links are diverse. The weights between vertices are different and may have direction.

  4. (iv)

    The network is with dynamics complex. The set of vertices may belong to the non-linear dynamics system, and the vertex state will change complex.

  5. (v)

    The vertices are various. Vertices of complex networks can represent anything, for example, vertices of the human relationship complex networks represent different individuals, and the vertices of world-wide complex networks represent different web pages.

  6. (vi)

    The complexity is the fusion of multi-level complexities, which will affect each other and lead to unpredictable result.

Based on the characteristics above, many researches have been done on complex networks, and information entropy is one of the most interesting fields, which will be investigated in this paper.

3 Information entropy

Information entropy is a conception of information theory proposed by Shannon [5]. Shannon defined information as “the reduction of entropy”, viz. “the reduction of uncertainty of a system”, and firstly proposed the quantitative description method for information. Suppose X = {x 1, x 2, ···, x n } is a discrete random variable, the appearance probability of information source given by X is denoted as p i  = p(x i ), i = 1, 2, ···, n, and \( \sum\limits_{i = 1}^{n} {p_{i} } = 1 \). Then the information entropy of information source X can be expressed as

$$ H(X) = \sum\limits_{i = 1}^{n} {p_{i} \log_{2} \frac{1}{{p_{i} }}} = - k\sum\limits_{i = 1}^{n} {p_{i} \ln p_{i} } , $$
(1)

where H(X) is a value expressing the global characteristic of information source, and k = log2 e is the Boltzmann constant.

Information entropy can be seen as a measurement of the order of a system, the higher the information entropy, the more information content is, and the less uncertain of X.

4 Construction of degree dependence matrices

Information entropy has some excellent characteristics, which can be used for the singularity detection or irregularity judgment in many engineerings [6, 7] and signal analysis fields [8, 9]. If there are multiple states existing in the detected signal or system (denoted by X), the higher H(X) will indicate the less uniform of X and more singular, otherwise the lower H(X) will indicate the less singular. Hence we can use information entropy to establish analyse models and measure the complexity of a system. In this paper, we compose the degree dependence matrices to express the degree dependence situation of a network.

Suppose a undirected complex network A has N vertices expressed as v 1, v 2, ···, v N , and k i is the degree of v i . Let D N×N is the shortest path length matrix of A, where D ij is the shortest path between v i and v j . For each shortest path length d, we compose a degree dependence matrix \( {\user2{P}}^{d} \) as

$$ P_{mn}^{d} = \# \{ (v_{i} ,v_{j} )|D_{ij} = d,\quad k_{i} = m,\quad k_{j} = n,\quad i = 1,2, \cdots ,N,\quad j = 1,2, \cdots ,N\} , $$
(2)

where #{·} denotes the number of elements in the set.

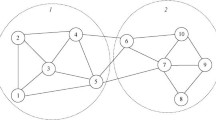
Equation (2) denotes the degree dependence situation between pairs of vertices when the shortest path length between them is d. Take the network shown in Fig. 1 as an example:

Fig. 1
figure 1

Example network

Full size image

The degrees and the shortest path lengths between all pairs of vertices are shown in Eqs. (3) and (4).

$$ {\user2{K}} = (k_{1} ,k_{2} ,k_{3} ,k_{4} )^{\text{T}} = (1,3,2,2)^{\text{T}} , $$
(3)
$$ {\user2{D}} = \left[ {\begin{array}{*{20}c} 0 & 1 & 2 & 2 \\ 1 & 0 & 1 & 1 \\ 2 & 1 & 0 & 1 \\ 2 & 1 & 1 & 0 \\ \end{array} } \right]. $$
(4)

Then we should compute the elements of \( {\user2{P}}^{d} \), using one element \( P_{23}^{1} \) as an example, it is computed as

$$ \begin{aligned} P_{23}^{1} & = \# \{ (v_{i} ,v_{j} )|D_{ij} = 1, \quad k_{i} = 2,\quad k_{j} = 3,\quad i = 1,2,3,4,\quad j = 1,2,3,4\} \\ & = \# \{ (v_{3} ,v_{2} ),(v_{4} ,v_{2} )\} \\ & = 2. \\ \end{aligned} $$
(5)

Then we can achieve the whole degree dependence matrix when d = 1 as shown in Eq. (6):

$$ \varvec{P}^{1} = \left[ {\begin{array}{*{20}c} 0 & 0 & 1 & 0 \\ 0 & 2 & 2 & 0 \\ 1 & 2 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right]. $$
(6)

Further, in order to normalize the matrix, we transfer Eq. (2) to the normalized form:

$$ P_{mn}^{d} = {{P_{mn}^{d} } \mathord{\left/ {\vphantom {{P_{mn}^{d} } {N^{2} }}} \right. \kern-0pt} {N^{2} }}. $$
(7)

The matrix is symmetric, and we can achieve all the degree dependence matrices for the other different d in the same way.

5 Degree dependence entropy based on degree dependence matrices

For the undirected complex network A, suppose A is connective, we have obtained all the degree dependence matrices of A. Then we can define the DDE (E DDE) as Eq. (8):

$$ E_{\text{DDE}} (P^{d} ) = \sum\limits_{m = 1}^{N} {\sum\limits_{n = 1}^{N} {P_{mn}^{d} \log } } P_{mn}^{d} . $$
(8)

For each complex network, at most N DDEs can be obtained. However the number of DDEs N′ is much less than N in most actual situation, viz. N′ ≪ N due to the small world characteristic.

Obviously, DDE is a quantitative statistical characteristic of complex networks. From the construction of degree dependence matrices and the intrinsic meanings of information entropy, we can indicate that the DDE can reflect the degree dependence relationship and corresponding characteristic in certain extent. When the degree dependence relationship is complex, the DDE values will be high; when the degree dependence relationship is uniform, the DDE values will be low.

6 Simulation experiments and result analysis

In order to exam the reasonableness of the proposed descriptor for complex networks, we calculate the DDEs of different type networks, including: the nearest-neighbor coupled network (regular network) (vertices number: N = 1,000, neighbors number of each vertex: B = 20), ER random graph (N = 1,000, average degree of vertices: T = 20), WS small-world network (N = 1,000, B = 20, replacement probability p = 0.0001 − 1), and BA scale-free network (N = 1,000, T = 20, vertices number of initial ER graph: \( N_{\text{I}} = 20 \), initial probability of lines: \( p_{\text{I}} = 0.1 \)).

In the first experiment, we compute the DDEs of different complex network types. The DDE values of them are shown in Table 1, and the corresponding curves are shown in Fig. 2 (only the non-zero DDEs are denoted).

Table 1 DDE values of different type networks
Full size table
Fig. 2
figure 2

DDE curves of different type networks

Full size image

From Table 1 and Fig. 2, it can be seen that DDE is increasing with the increasing of random. Because regular network is with the most definite degree dependence relationship, it has the lowest DDEs on all shortest distances. For WS small-world networks, when p = 0.1 the DDE values are higher than p = 0.01, which also indicates that higher DDE values mean less regularity, and the DDE values of ER random network are much higher than both of them. Specially, for BA scale-free networks, because there are some key vertices owning most shortest paths passing by them, the degree dependence relationship will be particularly uniform, and it has the highest DDEs.

In the second experiment, we compare the DDEs of WS small-world networks under different replacement probability p. The results are shown in Fig. 3.

Fig. 3
figure 3

DDE curves of WS small-world networks with different p

Full size image

From Fig. 3, for each curve (corresponding the shortest path length d) with the increasing of p, the random is increasing, and the degree dependence relationship is becoming more and more complex, so the network’s DDE is increasing. Further, the DDE values are increasing much more quickly when p is small. It can be explained that the degree dependence relationship grows quickly when p is not too big, and when p is bigger than a threshold the degree dependence relationship will not get much orderless. The shortest path lengths is becoming shorter and shorter with the increasing of p. For example, in this experiment the longest shortest path length is d = 4 when p = 0.2. This appearance is also accordance with the WS small-world networks’ characteristics, which also confirms the reasonableness of the proposed DDE descriptor.

At last, the DDE curves of WS small-world networks with different p on the log–log coordinate is shown in Fig. 4. And all of the curves approach to straight lines well, which is also an interesting phenomenon to be studied deeply in the future.

Fig. 4
figure 4

DDE curves of WS small-world networks with different p on log–log coordinate

Full size image

7 Conclusions

A quantitative statistical characteristic DDE descriptor for complex networks is proposed in this paper. In the progress, we put forward the degree dependence matrices under different shortest path lengths, and then extract DDEs from the matrices. At last the reasonableness is demonstrated through simulation experiments. Simulation results show that the DDE can reasonably reflect the complexity of degree dependence relationship and corresponding characteristic, which can be seen as a meaningful quantitative characteristic of complex networks, and it can supply better accordance for modeling and simulation of complex networks.