1 Introduction

The role played by flow characteristics of blood in arteries in the development of arterial disease is widely accepted [1, 2]. Particularly, Wall Shear Stress (WSS) acts as an important regulator of endothelial dysfunction [3] and it was extensively reported to be associated with the initiation and development of atherosclerosis. Research has shown that high WSS as a localized phenomenon, usually maximum at geometric non-uniformities like bifurcations and curvatures [4], and has a significant influence on local haemodynamics. Also, the necessity of using realistic arterial models in vivo or in vitro studies is well recognized [5].

Investigation of flow in arterial models had challenges associated with rheological models to be used [6]. To overcome the difficulty in the prediction of the rheological behaviour of blood, researchers had proposed different ways to perform haemodynamic analysis [7]. Blood was considered as a Newtonian fluid as the shear rates are higher than 100 s−1 in small arteries [8,9,10,11]. Use of non–Newtonian rheological models in cardiovascular computational fluid dynamics (CFD) is becoming more attractive due to the availability of robust computational tools. Steinman [12] enumerated the assumptions in blood flow modelling and performed analysis on its impact on computational haemodynamics. Cross [13] proposed a non–Newtonian blood viscosity model which was completely dedicated to shear thinning behaviour. These shortcomings were overcome by Bird–Carreau and Carreau–Yasuda models, which allowed for limiting behaviour at high shear viscosities, which was more widely observed in cardiovascular flows. In both Bird–Carreau and Carreau–Yasuda models, it could be noted that these models behave as Newtonian fluid when the time constant is zero, i.e. when the viscosity is constant with time. Gijsen et al. [14] showed that the shear thinning effect controls the non–Newtonian behaviour of the blood flow. Kumar et al.[15] discussed blood flow in an asymmetrical fusiform artery subjected to pulsatile flow inlet conditions using Carreau–Yasuda rheological model to mimic behaviour of blood. It was observed that the Carreau–Yasuda rheological model attracted significant attention from mathematicians and engineers due to its wide range of applications in quantifying the non–Newtonian behaviour of blood. Guerra et al. [16] used Cross and Carreau–Yasuda models along with the Data Assimilation approach and could successfully reconstruct flow profiles on 3D arterial models. Abugattas et al. [17] used a variational multiscale finite element approach to study the flow through bifurcations by comparing the behaviour of three constitutive rheological models, viz. power law, Cross and Carreau–Yasuda model. They concluded not to carry out a study based on shear stress using the Newtonian model; however, the Cross and Carreau–Yasuda model is preferred as it is bounded by zero and infinite shear rate viscosities.

The deformation of the arterial model was solved by using linear momentum equations [18, 19]. Research showed that the assumption of linear elastic artery material was computationally inexpensive and agreed well with the experimental study [20, 21]. Many researchers also used the hyperelastic material model [22, 23]which enables to capture of the stiffening and incompressibility behaviour under high strain. However, for patient-specific simulation, the application of this model is scarce due to the non-availability of material information such as composition and fibre orientation. The use of different elasticity models did not show any dramatic changes in the results when compared to the linear elastic model [24].

Blagojevic et al. [25] presented a theoretical basis by calculating blood flow in a coronary artery model by emphasizing plaque development based on the oscillatory shear index (OSI). OSI is a temporal variation of low and high WSS. The bifurcations and curvatures were more susceptible to low WSS, and in these locations OSI was higher, indicating higher flow recirculation [26].

Another cause leading to stroke is hypertension. Hypertension leads to increased arterial deformation and WSS at certain locations leading to plaque rupture [27]. Milad et al. [28] experimentally studied that the increased stenosis severity led to negative WSS and oscillatory shear in the post-stenotic region and increased angular phase difference between WSS and circumferential stress at the stenosis neck. The evaluated parameters helped identify the potential location for plaque growth and arterial remodelling. To understand the effect of arterial distensibility and hypertension, a fully coupled FSI analysis was performed. The results helped to understand the plaque growth and arterial remodelling phenomenon [29, 30]. In the previous study, the influence of arterial distensibility and different stages of hypertension on a stenosed carotid artery was studied by considering blood as Newtonian fluid [31].

The effect of blood flow on the arterial wall and vice versa were studied using the FSI method. The two domains were linked using a coupling scheme like the Arbitrary Lagrange–Eulerian (ALE) method, where the mesh deformation of one domain adheres to the boundary of another domain [19, 32,33,34,35]. A fully coupled FSI analysis is typically transient and captures the domain behaviour over a time period. Elasticity and compliance of the vessel wall are important characteristics of the arterial system, and hence only CFD study neglecting the arterial compliance was not recommended [36]. FSI analysis controls the finite volume-based CFD and structural FEA methods by coupling the physics of fluid and solid domains through FEA and CFD solvers [37]. The physical phenomena that were not easily measured such as the initiation of atherosclerosis, progression, and diagnosis could be studied by using FSI [38, 39].

The study of realistic artery models, both diseased and normal, is necessary to understand the underlying haemodynamics related to atherosclerosis. The effect of volume flow waveform inlet on the abdominal aortic aneurysms[40] and arterial branches [41, 42] studied the effect of volume flow rate inlet waveforms. The induced wall shear stress distribution was validated through PIV measurements, and they suggested the sensitivity of wall shear stress distribution and growth rate was near the aneurysm geometry. Low WSS and high OSI and longer Relative Residence Time (RRT) were associated with the development and progression of atherosclerosis [43].

Based on the extensive literature review of previous studies, it was observed that there has not been any significant research on the effect of blood rheology and blood pressure on the carotid artery bifurcation. In this paper, an FSI study is performed on a 3D patient-specific normal and stenosed carotid artery model. The effect of hypertension and the rheological model is observed on the anatomical geometry. The Carreau–Yasuda model is used to represent non–Newtonian behavior. The computational study involved four blood pressure cases, normal (120/80 mm Hg), prehypertension (120–139/80–89), stage 1 hypertension (140–159/90–99 mm Hg), stage 2 hypertension (≥ 160/ ≥ 100 mm Hg) [31].

2 Materials and methods

2.1 Geometric model generation

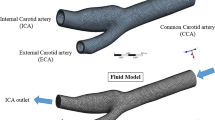
The data acquired from CT scan was imported as DICOM files to Mimics (Materialise, Leuven, Belgium), a medical image processing tool to convert into a computational model. The images are imported and a new mask was created using customized threshold values and by editing the mask slice by slice and separated from the surrounding tissues. Subsequently, the segment was grown by using the region growing tool through which a 3D mask was generated (Fig. 1). The boundary, interior, and greyscale strength of the region of interest serve as broad descriptors. Thus, the three types of segmentation are threshold based, edge based, and region based. Each pixel was assessed using the threshold-based method in accordance with the greyscale value that represents the scans' intensity. Later, smoothing processes were carried out by using a sufficient number of iterations to eliminate sharp corners and edges and carry out surface rendering operations. After the model's appropriateness was confirmed, a solid model was created in CATIA using a stereolithographic file (.stl) that was exported from it. A CAD software program called CATIA was used to import the stereolithography file format that MIMICS provided. The 3D models of fluid and artery were created independently since the FSI comprises structural and fluid models that depict blood and elastic arteries, respectively. The steps involved in creating the 3D model are described here. Similar to this, a 3D model of the arterial wall was created using a uniform wall thickness of 0.7 mm to mimic the elastic artery.[44,45,46]. Figure 2 shows the steps involved in generating a meshed carotid artery model used in this study. Both models were meshed using ten nodes tetrahedral elements for both fluid and solid models.

Fig. 1
figure 1

CT images of the carotid artery in different planes and generated 3D model of the normal carotid artery (top), and stenosed carotid artery (bottom) showing Common, Internal, and External Carotid artery. The highlighted region (white dots) indicates a single slice of the CT image in coronal, transverse, and sagittal planes highlighting the carotid artery region

Full size image
Fig. 2
figure 2

Step-by-step procedure of generating the computational domain, a DICOM images from CT scan imported to mimics to visualize the area of interest, b 3D mask generated from the available data, c 3D mask imported to 3 MATIC to smoothen and edit the surface mask, d edited surface mask in CATIA to create a 3D volume and imported to ANSYS and mesh the volume for FSI analysis

Full size image

2.2 Mathematical modelling and computational setup

The general computational domain in an FSI analysis consists of both fluid and solid domain, interface between fluid and solid, and inlet and outlet boundary conditions. The conservation of mass is a balance between mass entering a surface of a control volume and mass leaving a surface of the same control volume. This is summarized as shown below [47]

$$\frac{D\rho }{{Dt}} + \rho \nabla .v = 0$$
(1)

where ρ is density, t is time, and v is the fluid velocity.

The above continuity equation is rewritten in Arbitrary Lagrange Eulerian (ALE) framework as

$$\frac{\partial \rho }{{\partial t}} + \nabla \;\rho \left( {v - v_{c} } \right) = 0$$
(2)

where vc is grid velocity.

The law of conservation of momentum is obtained from Newton’s second law, \(\sum F = ma\), where \(\sum F\) is the sum of all forces on a control volume. There are two types of forces, body force, and surface force. For an incompressible flow,

$$\rho \frac{Dv}{{Dt}} = Body force + Surface force$$
(3)

where \(\frac{Dv}{{Dt}}\) is the acceleration.

The momentum equation can be written as

$$\rho \frac{\partial v}{{\partial t}} + \rho \left( {v\;\nabla } \right)v = \nabla \;\left( {\rho \Upsilon \nabla v} \right)$$
(4)

where \(\Upsilon\) is diffusivity.

The above momentum equation is rewritten in the ALE framework as

$$\rho \frac{\partial v}{{\partial t}} + \rho \left( {\left[ {v - v_{c} } \right]\;\nabla } \right)v = \nabla \;\left( {\rho \Upsilon \nabla v} \right)$$
(5)

The governing equation for the solid domain is written in Lagrangian reference as

$$Md + Cd + Kd = F$$
(6)

where d is the displacement, M is mass, C is damping, K is stiffness, and F is force.

The governing equation of fluid in the ALE framework is written as

$$\underbrace {{\frac{\partial \rho \emptyset }{{\partial t}}}}_{Temporal\;term} + \underbrace {{\nabla \;\left( {\rho \left[ {v - v_{c} } \right]\phi } \right)}}_{Convection\;term} - \underbrace {{\nabla \;\left( {\rho \Upsilon_{\phi } \nabla \emptyset } \right)}}_{Diffusion\;term} = \underbrace {{S_{\emptyset } \left( \emptyset \right)}}_{Source\;term}$$
(7)

where \(\emptyset\) is transport variable, \(\Upsilon_{\phi }\) diffusivity, and \(S_{\emptyset }\) is source term.

In the finite volume method, the governing equations must satisfy the control volume \({V}_{P}\) around point P, therefore, writing the above equation in integral form

$$\mathop \smallint \limits_{t}^{t + \Delta t} \left\{ {\underbrace {{\frac{\partial }{\partial t}\smallint \rho \emptyset dV_{P} }}_{Temporal term} + \underbrace {{\smallint \nabla \cdot \left( {\rho \left[ {v - v_{c} } \right]\emptyset dV_{P} } \right)}}_{Convection term} - \underbrace {{\smallint \nabla \cdot \left( {\rho {\Upsilon }_{\phi } \nabla \emptyset } \right)dV_{P} }}_{Diffusion term}} \right\} = \mathop \smallint \limits_{t}^{t + \Delta t} \left\{ {\underbrace {{\smallint S_{\emptyset } \left( \emptyset \right)dV_{P} }}_{Source term}} \right\}$$
(8)

The temporal term is discretized using second-order backward Euler scheme, and the convection term is discretized using Gauss Theorem [48].

The relations for stress tensors is given as

$$\sigma_{f} = - p_{f} + 2\mu \varepsilon \left( {v_{f} } \right)$$
(9)

where μ is the dynamic viscosity of the fluid, \(p_{f}\) is the Lagrange multiplier corresponding to incompressibility constraint in (1), and (vf) is the strain–rate tensor.

The boundary conditions on the fluid–solid interface are assumed to be

$$\sigma _{f} n = \sigma _{s} n,~\;v_{f} = v_{s} ~\;{\text{on}}\;\Gamma _{t}^{0}$$
(10)

where n is a normal unit vector to the interface \(\Gamma_{t}^{0}\). This implies a no-slip condition for flow and that the interface forces are balanced.

The governing equations were solved using Ansys CFX 19.0, and the structural analysis was performed using Ansys Structural 19.0 module (Ansys Inc., Canonsburg, PA). As the Reynolds number was below 500 for both the models, the flow is considered to be laminar.

The iterative method used by Ansys CFX for the FSI coupling solution is Dirichlet/Neumann approach. It means the fluid equation is imposed with Dirichlet boundary conditions like displacement and velocity at the interface. At the same time, Neumann boundary conditions such as forces are applied to the solid equation.

The standard procedure of calculation in the FSI problem is summarized in Fig. 3. Similar work has been performed by Kamakoti et al. and Wall et al. [49, 50].

Fig. 3
figure 3

Flow chart showing standard FSI solution procedure

Full size image

The next step is to solve the flow field to get

$$\tilde{P}_{m + 1}^{n + 1} = F\left( {\tilde{d}_{m + 1}^{n + 1} } \right)$$
(11)

where P is the fluid pressure and F is the fluid load.

The fluid load obtained is transferred to a solid solver and the corresponding load to be applied to the solid solver is estimated (Figs. 4, 5)

$$\tilde{P}_{m + 1}^{n + 1} = \omega \left( {\tilde{P}_{m + 1}^{n + 1} } \right)$$
(12)
Fig. 4
figure 4

A meshed computational model of the normal artery (top), and stenosed artery (bottom) used in the study showing tetrahedral elements and inflation boundary layer

Full size image
Fig. 5
figure 5

Grid independence study a and time sensitivity study b to determine optimum mesh size and optimum time step for FSI analysis

Full size image

where \(\omega\) is applied under-relaxation factor.

The solid governing equation is solved to get

$$\tilde{d}_{m + 1}^{n + 1} = S\left( {\tilde{P}_{m + 1}^{n + 1} } \right)$$
(13)

where S represents solid.

The deformation of the fluid domain is estimated which corresponds to the solid solution obtained from the previous step given as

$$d_{m + 1}^{n + 1} = \left( {1 - \omega } \right)\tilde{d}_{m + 1}^{n + 1} + \omega d_{m + 1}^{n + 1}$$
(14)

It should be noted that \(\tilde{d}_{m + 1}^{n + 1}\) is not the final solution but only an estimated solution for fluid calculation at coupling level m + 1.

The solution is converged if the following condition is satisfied

$$r^{n + 1,s} < \varepsilon_{0} , \;r^{n + 1,s} = d_{m + 1}^{n + 1} - d_{m}^{n + 1}$$
(15)
$$r^{n + 1,f} < \varepsilon_{0} , \;r^{n + 1,f} = P_{m + 1}^{n + 1} - P_{m}^{n + 1}$$
(16)

where r is the residual and \(\varepsilon_{0}\) is the tolerance for determining convergence. f and s denote fluid and solid, respectively.

The criteria to determine the convergence of the FSI solution are given as [51]

$$Convergence = \frac{{\log \left( {\frac{{ \in_{x} }}{{ \in_{\min } }}} \right)}}{{\log \left( {\frac{{ \in_{\max } }}{{ \in_{\min } }}} \right)}}$$
(17)

where \(\in_{x}\) is the norm of interface quantities transferred between two domains, \(\in_{\min }\) is the convergence criteria specified in the coupling setup, and \(\in_{\max }\) is the divergence limit. If \(\in_{x} < \in_{\min }\), then the solution is converged.

One of the reasons behind the intimal thickening was found to be the oscillatory flow during the diastolic phase of a cardiac cycle. To recognize the risk zones, the Oscillatory shear index was considered as per the previous study[31] given as

$$OSI = 0.5 \times \left( {1 - \frac{{\left| {\mathop \smallint \nolimits_{0}^{T} \overrightarrow {WSS} dt} \right|}}{{\mathop \smallint \nolimits_{0}^{T} \left| {\overrightarrow {WSS} } \right|dt}}} \right)$$
(18)

where T is the time period of the cardiac cycle. OSI measures the time-averaged variations of the shear stress without considering the shear stress in an immediate neighbourhood of a specific point[52].

In the present study, a linear elastic material model was selected for the artery with an Elastic modulus of 0.9 MPa and Poisson’s ratio of 0.45 [53]. The results between the Newtonian and Carreau–Yasuda model were compared. The fluid flow model in Newtonian model has a dynamic viscosity of 0.004 Pa s and density of 1060 kg/m3, while the Carreau–Yasuda viscosity model is considered as,

$$\frac{{\mu - \mu_{\infty } }}{{\mu_{0} - \mu }} = \left[ {1 + \left( {\lambda \gamma } \right)^{a} } \right]^{{\frac{{\left( {n - 1} \right)}}{a}}}$$
(19)

where \(\mu_{\infty } = 0.0022 Pa s,\) is high shear viscosity, \(\mu_{0} = 0.022 Pa s,\) is low shear viscosity, \(\lambda = 0.1105 s,\) is the time constant, \(n = 0.392\) is the power-law index, and \(= 0.644\) is Yasuda exponent [14]. The computational model was modelled in CATIA V5 (3D modelling software) and imported into Ansys CFX (version 19.0) and meshed with 10 node tetrahedral elements. To capture near wall quantities, inflation with 12-point refinement with smooth transition were imposed. Meshed model is shown in Fig. 4.

2.3 Boundary conditions

The 3D normal and stenosed carotid artery models were considered to interpret the haemodynamics under four different blood pressure conditions. Nodes at the ends of the structural model were fixed, and the remaining nodes were free to move [54, 55]. A velocity profile applied at the inlet and pressure at the artery outlets are shown in Fig. 6. For both the inlet velocity and outlet pressure, the values obtained are used to generate a polynomial equation and this was used in the Fourier series equation to generate the necessary pulse wave. Fourier series, as defined in Eq. 20, was implemented to get the temporal velocity and pressure waveform equations. The Fourier coefficients were obtained from an initial approximate waveforms of six harmonics which is found to be optimum to obtain the desired waveform [31]. For FSI, the surface of the artery in contact with the lumen is defined as fluid–solid interface for data transfer.

$$F\left( t \right) = A_{m} + \mathop \sum \limits_{n = 1}^{N} \left( {A_{n} \cos \left( {n\omega t} \right) + B_{n} \sin \left( {n\omega t} \right)} \right)$$
(20)
Fig. 6
figure 6

Applied inlet velocity profile extracted from ultrasound Doppler data (top) and outlet pressure profiles applied at the internal and external carotid artery branches

Full size image

3 Results

3.1 Mesh convergence and time step sensitivity study

A time step sensitivity test was carried out for 3 cardiac cycles of 0.8 s each, and an optimum time step was obtained during the transient analysis. The last cycle of the three cardiac cycles was used to capture the haemodynamic parameters like WSS and Velocity[56]. The computational model of both stenosed and normal carotid artery was subjected to a time step sensitivity test. Time steps based on the step size of 50, 100, 125, 160, and 200 for both stenosed and normal carotid artery were performed for normal blood pressure and based on this, an ideal time step of 100, i.e. 0.008 s was chosen to perform the analysis as shown in Fig. 5(b).

A grid independence test was performed to obtain the optimum grid size for the study. Figure 5(a) shows the average deformation and average velocity plots for different grid sizes. An optimum mesh density of 105,963 solid and 323,514 fluid elements for the normal artery model and a mesh density of 205,938 solid and 215,208 fluid elements for the stenosed artery model were chosen in the study. 

3.2 Wall shear stress

Variation of WSS for one cardiac cycle was considered at different planes as shown in Fig. 7. To evaluate the risk of atherosclerosis, the planes were considered at different locations of the carotid artery exposed to low WSS and high OSI which were considered as critical regions, at the CCA, carotid sinus, and the region where the CCA bifurcates into ICA and ECA [57].

Fig. 7
figure 7

Locations to capture temporal haemodynamic parameters. Planes are selected such that it represents CCA, bifurcation zone, and sudden reduction and increase in cross-sectional area in normal (left), and stenosed (right) carotid artery

Full size image

Figure 8 shows the bar chart highlighting the maximum WSS magnitude in normal and stenosed carotid artery models considering both Newtonian and Carreau–Yasuda viscosity models. The WSS was reduced with an increase in the blood pressure due to increased deformation of the artery and increased peripheral resistance in the artery.

Fig. 8
figure 8

Maximum WSS magnitude

Full size image

Figure 9 shows the variation of maximum WSS for one cardiac cycle at the location of the planes considered in the stenosed carotid artery. Similarly, Fig. 10 shows the temporal variation of WSS in the normal carotid artery. The WSS was maximum at the divider wall of the bifurcation, and due to flow diversion, recirculation zones are generated at the outer wall of the ICA near carotid bulb which extends until the end of the curved ICA. The recirculation zone was more prominent in the Carreau–Yasuda model and extends towards the inner wall of the ICA as shown in Fig. 11. Table 1 shows the maximum WSS magnitudes at different blood pressures for both Newtonian and Carreau–Yasuda models.

Fig. 9
figure 9

Temporal WSS variations in the stenosed carotid artery at planes located at downstream of CCA (Plane 1), carotid sinus (Plane 2), the neck of stenosis (Plane 3), and at post-stenotic region (Plane 4). The WSS increases at the downstream, and the maximum is at the neck of the stenosis and reduces post-stenosis

Full size image
Fig. 10
figure 10

Temporal WSS variations in the normal carotid artery at planes located at downstream of CCA (Plane 1), carotid sinus (Plane 2), and the flow divider region (Plane 3). Like the stenosed artery, the WSS is low at the CCA and highest at the flow divider

Full size image
Fig. 11
figure 11

Flow recirculation zones in normal and stenosed carotid arteries

Full size image
Table 1 Maximum WSS (Pa) magnitudes in normal and stenosed carotid artery
Full size table

The magnitude of WSS decreases with increased blood pressure, and the Newtonian model predicts lower WSS compared to Carreau–Yasuda model.

3.3 Oscillatory shear index

The oscillatory shear index (OSI), originally introduced by Ku et al. [58], is aimed at quantifying the degree of deviation of the WSS from its average direction during the heart beat cycle due to either secondary and reverse flow velocity components occurring in pulsatile flow. Although the formation of plaque was dependent on many other factors, the oscillatory shear stress was more appropriate while dealing with oscillatory blood flow [59]. According to many experimental investigations [60,61,62], the plaque formation was at the location where there was the maximum shear oscillation. Figures 12 and 13 illustrate OSI distribution for stenosed and normal carotid artery, respectively, subjected to different blood pressures.

Fig. 12
figure 12

OSI contours on the stenosed carotid artery model. Maximum OSI is at the carotid sinus and at the region downstream of the stenosis where the flow reversals are maximum. (a) NBP, (b) HBP 1, (c) HBP 2, and (d) HBP 3

Full size image
Fig. 13
figure 13

OSI contours on the normal carotid artery model. Maximum OSI is at the carotid sinus and at the base of the ECA where the flow reversals are maximum. (a) NBP, (b) HBP 1, (c) HBP 2, and (d) HBP 3

Full size image

4 Discussion

Modelling of fluid dynamics and characterization of near wall phenomenon accurately is important to understand the initiation and progression of atherosclerotic lesion in arterial models and also to predict the changes that occur during variation in blood pressure, and blood rheology. The results in this research indicate that there are significant differences up to 35% in WSS between Newtonian and Carreau–Yasuda models. As shown in Table 1, in normal carotid artery, an increase of 2% and 3.5% and an increase of 3% and 5% in stenosed model is observed between Newtonian and Carreau Yasuda models, respectively. The Carreau–Yasuda model shows higher WSS compared to the Newtonian model due to higher velocity gradients, whereas the Newtonian model presents higher viscosities near the wall [17]. The magnitudes of WSS are significantly higher in the Carreau–Yasuda model in all the phases of the cardiac cycle due to the fact that the dynamic viscosity of the Carreau–Yasuda model stays significantly higher compared to the Newtonian fluid throughout the cardiac cycle. The WSS over the last cardiac cycle, as shown in Figs. 9 and 10 where there is considerable lower WSS values by 30% at peak systole for Newtonian fluid compared to Carreau–Yasuda model. The results show high values of WSS at the flow divider region which forces the blood to separate between the branches. The flow decelerates in this area creating high velocity gradients near the outer wall. It has been shown previously that the flow encounters deviation to the inner walls of the ICA and ECA and the results reinforce this detail. The results are in agreement with works of Moradicheghamahi et al. [63]. The WSS results conveys that the measurements considering Newtonian fluid underestimate the WSS. This underestimation is specific for the current applied flow parameters. Different values of viscosity can lead to different estimation; however, it should be kept in mind that temporal change of the shear rate will change the viscosity of the non-Newtonian fluid. To determine the load on vessels, the non-Newtonian effect cannot be neglected.

The OSI does not vary with blood pressures or viscosity models. Emphasis was on OSI distribution during three phases of the cardiac cycle (Peak systole, early diastole and late diastole). It was evident from the figures that the OSI was maximum at the outer wall of the ICA near the carotid sinus, and at the base of the ECA which may be a likely location for development of plaque. The OSI distribution patterns were not significantly altered by varying the blood pressure and the viscosity models. The higher OSI defines the regions of flow recirculation occurring in circular pattern at the outer wall of the ICA and distal inner wall of the ICA. The OSI contours emphasize that the elevated OSI tend to occur at the sites of impingement of flow and the mean WSS divergence regions at the distal end of recirculation zones. It was also predominant where reverse flow meets the dominant flow direction at the outer wall of the ECA below the stenosis. OSI was maximum in the regions where flow streamline meets along the front and back of the ICA and where there was a vortex formation adjacent to the wall as observed during the late diastole phase of the cardiac cycle. The Newtonian and Carreau–Yasuda viscosity models did not show significant difference in the OSI contours. The OSI distributions suggest the low magnitude of WSS was captured with the OSI. The OSI contours also show large variation among the two carotid artery models. For both models, the high OSI was found near the inner wall of the ICA. The high level of OSI indicates detrimental flow condition, and the regions with an OSI magnitude of > 0.2 are prone to vascular dysfunction [64]. Additionally, the region near the outer wall of the ECA adjacent to the stenosis showed higher OSI compared to the normal carotid artery model.

The three-dimensional CFD and FSI analysis revealed that increased blood pressure leads to reduced maximum wall shear stress and higher recirculation zones in critical areas in the carotid artery that were captured by solving the flow field using three-dimensional fully coupled FSI analysis. The thorough investigation of 2 different subject specific cases demonstrated the potential of numerical FSI simulations to understand the detailed haemodynamics in normal and diseased conditions, such as entry and exit of flow velocity near the stenosis, swirling of flow post stenosis and at the carotid sinus, post-stenotic arterial wall deformations, WSS at the neck and across the stenosis and at the carotid sinus. All these variables were not under the purview of imaging diagnostic techniques. Although accurate investigations were dependent on arterial wall, flow assumptions, boundary conditions, numerical approximations, and FSI simulations with few approximations provided an overall flow pattern and haemodynamic behaviour similar to clinical observations. The numerical simulation of subject specific models for different blood pressures will certainly be useful in understanding the haemodynamic variations and possible outcomes.

5 Conclusions

The findings of this study have improved our knowledge of how blood flow at the carotid artery bifurcation is affected by blood pressure and blood rheology. The study also emphasized the role that FSI plays in assisting with the identification of cardiovascular physiology in both healthy and stenotic carotid arteries. Increased blood pressure resulted in lower maximum wall shear stress and higher recirculation zones in important parts of the carotid artery, according to three-dimensional CFD and FSI analysis. These areas were identified by solving the flow field using three-dimensional fully coupled FSI analysis.

The major conclusions from the analysis are as follows:

  1. 1.

    In FSI analysis, the WSS magnitude predicted by the Newtonian model was lower compared to the Carreau–Yasuda model due to the shear thinning behaviour captured by the Carreau–Yasuda model.

  2. 2.

    The flow recirculation zone was mainly observed in the carotid sinus region in the normal carotid artery model, whereas in the stenosed carotid artery, it was also seen in the post-stenotic region due to sudden increase in the cross-section regions that correspond to low-WSS regions as areas prone to atherosclerosis.

  3. 3.

    The oscillatory shear index was mainly model specific, as there was no significant difference in the distribution between different blood pressure conditions.

  4. 4.

    The results showed that the formation of atherosclerotic plaque in regions such as the posterior wall of the carotid sinus was high as the WSS was lower.