Skip to main content
SpringerLink
Log in

Numerical analysis of a microfluidic mixer and the effects of different cross-sections and various input angles on its mixing performance

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

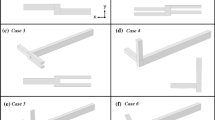
Micromixers have better efficiency in terms of both the time-scale of chemical kinetics and diffusive transport compared to the conventional macro-mixers. The mixing efficiency in micromixers is an important performance indicator in mixers. This paper presents a numerical study of how the design of a micromixer along with the design of the mixing process affects the mixing efficiency. Specifically, two different types of cross-sections of the channel in micromixers, namely circular and rectangular cross-sections, together with the inlet angle of the channel, were studied. The process parameters, such as the inlet velocity of fluids and diffusion coefficient, were studied as well. The result shows that the circular cross-section can sustain a large pressure difference without undergoing any remarkable distortion and deformation, and it can achieve better performance. The result further indicates that the inlet velocity and diffusion coefficient have significant effects on mixing efficiency; specifically, the low inlet velocity and high diffusion coefficient value can lead to a better mixing performance. However, different input angles alone could not make the mixing efficiency change noticeably. In other words, the mixing performance of such micromixers relies more on the inlet velocity and diffusion coefficient than on the fluid flow angle in the inlet.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20

Similar content being viewed by others

Notes

  1. Called mixing length.

Abbreviations

A :

Cross-sectional area (m2)

C :

Concentration of reagents (mol/m3)

D :

Diffusion coefficient (m2/s)

F :

Force (N)

f :

Mole fraction (–)

j :

Diffusion (mol/s m2)

I :

Identity matrix (–)

L :

Microchannel length (m)

\(M_{i}\) :

Mixing efficiency (%)

R :

Change in concentration rate (mol/s m3)

U :

Velocity (m/s)

\(\rho\) :

Density (kg/m3)

\(\mu\) :

Viscosity (Pa s)

\(\sigma\) :

Standard deviation (–)

References

  1. Ouyang P, Tjiptoprodjo R, Zhang W, Yang G (2008) Micro-motion devices technology: the state of arts review. Int J Adv Manuf Technol 38(5–6):463–478

    Article  Google Scholar 

  2. Yao X, Fang J, Zhang W (2018) A further study on the analytical model for the permeability in flip-chip packaging. J Electron Packag 140(1):011001

    Article  Google Scholar 

  3. Kwang HS, Kwon Y, Choe J (2006) Microreaction technology in practice. Stud Surf Sci Catal 159:649–652

    Article  Google Scholar 

  4. Lei L, Bergstrom D, Zhang B, Zhang H, Yin R, Song K-Y, Zhang W (2017) Micro/nanospheres generation by fluid-fluid interaction technology: a literature review. Recent Pat Nanotechnol 11(1):15–33

    Article  Google Scholar 

  5. Nayak A (2014) Analysis of mixing for electroosmotic flow in micro/nano channels with heterogeneous surface potential. Int J Heat Mass Transf 75:135–144

    Article  Google Scholar 

  6. Liang Y, Weihs GF, Wiley D (2014) Approximation for modelling electro-osmotic mixing in the boundary layer of membrane systems. J Membr Sci 450:18–27

    Article  Google Scholar 

  7. Wang Y, Zhe J, Chung BTF, Dutta P (2008) A rapid magnetic particle driven micromixer. Microfluid Nanofluid 4:375–389

    Article  Google Scholar 

  8. Alizadeh A, Zhang L, Wang M (2014) Mixing enhancement of low-Reynolds electro-osmotic flows in microchannels with temperature-patterned walls. J Colloid Interface Sci 431:50–63

    Article  Google Scholar 

  9. Campisi M, Accoto D, Damiani F, Dario P (2009) A soft-lithographed chaotic electrokinetic micromixer for efficient chemical reactions in lab-on-chips. J Micro Nano Mech 5:69–76

    Article  Google Scholar 

  10. Chen CK, Cho CC (2008) Electrokinetically driven flow mixing utilizing chaotic electric fields. Microfluid Nanofluid 5(6):785–793. https://doi.org/10.1007/s10404-008-0286-4

    Article  Google Scholar 

  11. Deng B, Tian Y, Yu X, Song J, Guo F, Xiao Y, Zhang Z (2014) Laminar flow mediated continuous single-cell analysis on a novel poly (dimethylsiloxane) microfluidic chip. Anal Chim Acta 820:104–111. https://doi.org/10.1016/j.aca.2014.02.033

    Article  Google Scholar 

  12. Wang H, Iovenitti P, Harvey E, Masood S (2003) Numerical investigation of mixing in microchannels with patterned grooves. J Micromech Microeng 13(6):801–808. https://doi.org/10.1088/0960-1317/13/6/302

    Article  Google Scholar 

  13. Papadopoulos V, Kefala I, Kaprou G, Kokkoris G, Moschou D, Papadakis G, Gizeli E, Tserepi A (2014) A passive micromixer for enzymatic digestion of DNA. Microelectron Eng 124:42–46

    Article  Google Scholar 

  14. Le The H, Le Thanh H, Dong T, Ta BQ, Tran Minh N, Karlsen F (2015) An effective passive micromixer with shifted trapezoidal blades using wide Reynolds number range. Chem Eng Res Des 93:1–11. https://doi.org/10.1016/j.cherd.2014.12.003

    Article  Google Scholar 

  15. Farahinia A, Jamaati J, Niazmand H, Zhang WJ (2019) Investigation of an electro-osmotic micromixer with heterogeneous zeta-potential distribution at the wall. Eng Res Express 1(1):015024. https://doi.org/10.1088/2631-8695/ab3a15

    Article  Google Scholar 

  16. Buchegger W, Wagner C, Lendl B, Kraft M, Vellekoop M (2011) A highly uniform lamination micromixer with wedge shaped inlet channels for time resolved infrared spectroscopy. Microfluid Nanofluid 10:889–897

    Article  Google Scholar 

  17. Huang MZ, Yang RJ, Tai CH, Tsai CH, Fu LM (2006) Application of electrokinetic instability flow for enhanced micromixing in cross-shaped microchannel. Biomed Microdev 8:309–315

    Article  Google Scholar 

  18. Zhang K, Guo S, Zhao L, Zhao X, Chan HL, Wang Y (2011) Realization of planar mixing by chaotic velocity in microfluidics. Microelectron Eng 88(6):959–963. https://doi.org/10.1016/j.mee.2010.12.029

    Article  Google Scholar 

  19. Neerincx PE, Denteneer RPJ, Peelen S, Meijer HEH (2011) Compact mixing using multiple splitting, stretching, and recombining flows. Macromol Mater Eng 296:349–361

    Article  Google Scholar 

  20. Alam A, Afzal A, Kim KY (2014) Mixing performance of a planar micromixer with circular obstructions in a curved microchannel. Chem Eng Res Des 92(3):423–434. https://doi.org/10.1016/j.cherd.2013.09.008

    Article  Google Scholar 

  21. Bhattacharyya S, Bera S (2015) Combined electroosmosis-pressure driven flow and mixing in a microchannel with surface heterogeneity. Appl Math Model 39(15):4337–4350. https://doi.org/10.1016/j.apm.2014.12.050

    Article  MathSciNet  MATH  Google Scholar 

  22. Kamali R, Mansoorifar A, Dehghan Manshadi MK (2014) Effect of baffle geometry on mixing performance in the passive micromixer. Trans Mech Eng 38(M2):351–360

    Google Scholar 

  23. Farahinia A, Zhang WJ (2019) Numerical investigation into the mixing performance of micro T-mixers with different patterns of obstacles. J Braz Soc Mech Sci Eng 41(11):491–504. https://doi.org/10.1007/s40430-019-2015-1

    Article  Google Scholar 

  24. Hardt S, Pennemann H, Schönfeld F (2006) Theoretical and experimental characterization of a low-Reynolds number split-and-recombine mixer. Microfluid Nanofluid 2(3):237–248. https://doi.org/10.1007/s10404-005-0071-6

    Article  Google Scholar 

  25. Hessel V, Löwe H, Schönfeld F (2005) Micromixers—a review on passive and active mixing principles. Chem Eng Sci 60(8–9):2479–2501

    Article  Google Scholar 

  26. Farahinia A, Jamaati J, Niazmand H (2019) Investigation of slip effects on electroosmotic mixing in heterogeneous microchannels based on entropy index. SN Appl Sci 1(7):728–740. https://doi.org/10.1007/s42452-019-0751-6

    Article  Google Scholar 

  27. Nguyen N, Wu Z (2005) Micromixers—a review. J Micromech Microeng 15:R1–R16. https://doi.org/10.1088/0960-1317/15/2/R01

    Article  Google Scholar 

  28. Yang S-M, Chen F, Yin D, Zhang H, Yin R, Zhang B, Zhang W (2018) Flow-free droplet-based platform for spiral-striated polymorphic structure of periodical crystalline agglomerates. Microfluid Nanofluid 22(10):114. https://doi.org/10.1007/s10404-018-2137-2

    Article  Google Scholar 

  29. Jamaati J, Farahinia A, Niazmand H (2015) Investigation of mixing in electroosmotic micromixers using Nernst–Planck equations. Modares Mech Eng 15(4):203–213

    Google Scholar 

  30. Jamaati J, Farahinia A, Niazmand H (2015) Mixing investigation in combined electroosmotic/pressure-driven micromixers with heterogeneous wall charges. Modares Mech Eng 15(7):297–306

    Google Scholar 

  31. Bhagat AAS, Peterson ET, Papautsky I (2007) A passive planar micromixer with obstructions for mixing at low Reynolds numbers. J Micromech Microeng 17(5):1017

    Article  Google Scholar 

  32. Yoshimura M, Shimoyama K, Misaka T, Obayashi S (2019) Optimization of passive grooved micromixers based on genetic algorithm and graph theory. Microfluid Nanofluid 23(3):30

    Article  Google Scholar 

  33. Jamaati J, Farahinia A, Niazmand H (2015) Numerical investigation of electro-osmotic flow in heterogeneous microchannels. Modares Mech Eng 15(3):260–270

    Google Scholar 

  34. Farahinia A, Jamaati J, Niazmand H (2017) Study of slip effect on electro-osmotic micromixer performance based on entropy index. Amirkabir J Mech Eng 49(3):535–548. https://doi.org/10.22060/mej.2016.776

    Article  Google Scholar 

  35. Zhendong L, Yangcheng L, Jiawei W, Guangsheng L (2012) Mixing characterization and scaling-up analysis of asymmetrical T-shaped micromixer: experiment and CFD simulation. Chem Eng J 181:597–606

    Article  Google Scholar 

  36. Shi X, Xiang Y, Wen L-X, Chen J-F (2012) CFD analysis of flow patterns and micromixing efficiency in a Y-type microchannel reactor. Ind Eng Chem Res 51(43):13944–13952

    Article  Google Scholar 

  37. Jamaati J, Niazmand H, Renlsizbulut M (2013) Investigation of electrokinetic mixing in 3D non-homogenous microchannels. J Comput Appl Res Mech Eng 3(1):41–52

    Google Scholar 

  38. Haghighinia A, Movahedirad S (2019) Fluid micro-mixing in a passive microchannel: comparison of 2D and 3D numerical simulations. Int J Heat Mass Transf 139:907–916. https://doi.org/10.1016/j.ijheatmasstransfer.2019.05.084

    Article  Google Scholar 

  39. Qaderi A, Jamaati J, Bahiraei M (2019) CFD simulation of combined electroosmotic-pressure driven micro-mixing in a microchannel equipped with triangular hurdle and zeta-potential heterogeneity. Chem Eng Sci 199:463–477. https://doi.org/10.1016/j.ces.2019.01.034

    Article  Google Scholar 

  40. Ait Mouheb N, Malsch D, Montillet A, Solliec C, Henkel T (2012) Numerical and experimental investigations of mixing in T-shaped and cross-shaped micromixers. Chem Eng Sci 68(1):278–289. https://doi.org/10.1016/j.ces.2011.09.036

    Article  Google Scholar 

  41. Conlisk AT (2012) Essentials of micro-and nanofluidics: with applications to the biological and chemical sciences. Cambridge University Press, Cambridge

    Book  Google Scholar 

  42. Atkins P, De Paula J (2011) Physical chemistry for the life sciences. Oxford University Press, USA

    Google Scholar 

  43. Baccar N, Kieffer R, Charcosset C (2009) Characterization of mixing in a hollow fiber membrane contactor by the iodide–iodate method: numerical simulations and experiments. Chem Eng J 148(2–3):517–524

    Article  Google Scholar 

  44. Chen JM, Horng TL, Tan WY (2006) Analysis and measurements of mixing in pressure-driven microchannel flow. Microfluid Nanofluid 2(6):455–469. https://doi.org/10.1007/s10404-006-0092-9

    Article  Google Scholar 

  45. Wong SH, Ward MC, Wharton CW (2004) Micro T-mixer as a rapid mixing micromixer. Sens Actuators B Chem 100(3):359–379

    Article  Google Scholar 

  46. Jain M, Rao A, Nandakumar K (2013) Numerical study on shape optimization of groove micromixers. Microfluid Nanofluid 15(5):689–699

    Article  Google Scholar 

  47. Yazdi AA, Sadeghi A, Saidi MH (2015) Electrokinetic mixing at high zeta potentials: ionic size effects on cross stream diffusion. J Colloid Interface Sci 442:8–14

    Article  Google Scholar 

  48. Mondal B, Mehta SK, Patowari PK, Pati S (2019) Numerical study of mixing in wavy micromixers: comparison between raccoon and serpentine mixer. Chem Eng Process Process Intensif 136:44–61. https://doi.org/10.1016/j.cep.2018.12.011

    Article  Google Scholar 

  49. Giere S, Iliescu T, John V, Wells D (2015) SUPG reduced order models for convection-dominated convection–diffusion–reaction equations. Comput Methods Appl Mech Eng 289:454–474. https://doi.org/10.1016/j.cma.2015.01.020

    Article  MathSciNet  MATH  Google Scholar 

  50. Knobloch P, Tobiska L (2009) On the stability of finite-element discretizations of convection-diffusion-reaction equations. IMA J Numer Anal 31(1):147–164. https://doi.org/10.1093/imanum/drp020

    Article  MathSciNet  MATH  Google Scholar 

  51. Golbabai A, Kalarestaghi N (2018) Improved localized radial basis functions with fitting factor for dominated convection-diffusion differential equations. Eng Anal Bound Elem 92:124–135. https://doi.org/10.1016/j.enganabound.2017.10.008

    Article  MathSciNet  MATH  Google Scholar 

  52. Sanderse B, Misra S, Dubinkina S, Henkes RAWM, Oosterlee CW (2018) Numerical simulation of roll waves in pipelines using the two-fluid model. In: Paper presented at the 11th North American conference on multiphase production technology, Banff, Canada, 2018/12/10

  53. Matsunaga T, Lee H-J, Nishino K (2013) An approach for accurate simulation of liquid mixing in a T-shaped micromixer. Lab Chip 13(8):1515–1521

    Article  Google Scholar 

  54. Khaydarov V, Borovinskaya E, Reschetilowski W (2018) Numerical and experimental investigations of a micromixer with chicane mixing geometry. Appl Sci 8(12):2458

    Article  Google Scholar 

  55. Celik IB (2008) Procedure for estimation and reporting of discretization error in CFD applications. ASME J Fluids Eng 1(6):1–7

    Google Scholar 

  56. Lee CY, Lin C, Hung M, Ma R, Tsai CH, Lin CH, Fu LM (2006) Experimental and numerical investigation into mixing efficiency of micromixers with different geometric barriers. In: Materials science forum. Trans Tech Publ, pp 391–396

  57. Lobasov AS, Minakov AV, Kuznetsov VV, Rudyak VY, Shebeleva AA (2018) Investigation of mixing efficiency and pressure drop in T-shaped micromixers. Chem Eng Process Process Intensif 134:105–114. https://doi.org/10.1016/j.cep.2018.10.012

    Article  Google Scholar 

  58. Viktorov V, Nimafar M (2013) A novel generation of 3D SAR-based passive micromixer: efficient mixing and low pressure drop at a low Reynolds number. J Micromech Microeng 23(5):055023

    Article  Google Scholar 

  59. Raza W, Hossain S, Kim K-Y (2018) Effective mixing in a short serpentine split-and-recombination micromixer. Sens Actuators B Chem 258:381–392. https://doi.org/10.1016/j.snb.2017.11.135

    Article  Google Scholar 

  60. Feng X, Ren Y, Sun H, Chen X, Zhang K, Jia Y, Hou L, Xiao M, Jiang H (2019) Effect of vortex on mass transport and mixing in microcapillary channels. Chem Eng J 362:442–452

    Article  Google Scholar 

Download references

Acknowledgements

The authors gratefully acknowledge the Department of Mechanical at the University of Saskatchewan for providing the research facilities. As well, the research is made possible to the first author by the Saskatchewan Innovation & Opportunity Scholarship (2019–2020) and the Devolved Graduate Scholarships.

Funding

This research work is not supported by any funding agency.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, University of Saskatchewan, Saskatoon, Canada

    A. Farahinia & W. J. Zhang

Authors
  1. A. Farahinia
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. W. J. Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Farahinia.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Technical Editor: Daniel Onofre de Almeida Cruz, D.Sc.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Farahinia, A., Zhang, W.J. Numerical analysis of a microfluidic mixer and the effects of different cross-sections and various input angles on its mixing performance. J Braz. Soc. Mech. Sci. Eng. 42, 190 (2020). https://doi.org/10.1007/s40430-020-02275-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-020-02275-9

Keywords

Search

Navigation