Skip to main content

Advertisement

SpringerLink
Log in

Bending, buckling and vibration analysis of functionally graded non-uniform nanobeams via finite element method

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

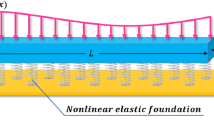
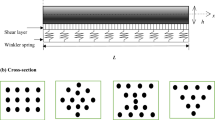
In the current study, bending, buckling and vibration behaviours of functionally graded in depth direction non-uniform nanobeams are investigated in the framework of nonlocal strain gradient theory. Material variation is assumed through the thickness and modelled using exponential, sigmoid and power-law functions. Moreover, cross-sectional variation is also considered using exponential and power-law functions. Using these general non-uniformity and non-homogeneity in conjunction with nonlocal strain gradient theory, a general beam is modelled. For this general model, equations of motion are derived using Hamilton’s principle and solved by using a novel technique in combining finite element method with Lagrangian interpolation technique, Gaussian quadrature method and Wilson’s Lagrangian multiplier method. Mechanical behaviour of such structures is fully explained with parametric study for all three cases of bending, buckling and vibration response. It is shown that combination of material variation, non-uniformity and scale effects has a significant effect in changing the mechanical behaviour of such structures in both static and dynamic cases.

Graphical abstract

.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Müller E, Drašar Č, Schilz J, Kaysser WA (2003) Functionally graded materials for sensor and energy applications. Mater Sci Eng, A 362(1):17–39. https://doi.org/10.1016/S0921-5093(03)00581-1

    Article  Google Scholar 

  2. Udupa G, Rao SS, Gangadharan KV (2014) Functionally graded composite materials: an overview. Procedia Mater Sci 5:1291–1299. https://doi.org/10.1016/j.mspro.2014.07.442

    Article  Google Scholar 

  3. Schulz U, Peters M, Bach FW, Tegeder G (2003) Graded coatings for thermal, wear and corrosion barriers. Mater Sci Eng, A 362(1):61–80. https://doi.org/10.1016/S0921-5093(03)00579-3

    Article  Google Scholar 

  4. Pompe W, Worch H, Epple M, Friess W, Gelinsky M, Greil P, Schulte K (2003) Functionally graded materials for biomedical applications. Mater Sci Eng, A 362(1):40–60. https://doi.org/10.1016/S0921-5093(03)00580-X

    Article  Google Scholar 

  5. Shahba A, Rajasekaran S (2012) Free vibration and stability of tapered Euler–Bernoulli beams made of axially functionally graded materials. Appl Math Model 36(7):3094–3111. https://doi.org/10.1016/j.apm.2011.09.073

    Article  MathSciNet  MATH  Google Scholar 

  6. Shahba A, Attarnejad R, Hajilar S (2011) Free vibration and stability of axially functionally graded tapered Euler–Bernoulli beams. Shock Vib 18(5):683–696. https://doi.org/10.3233/SAV-2010-0589

    Article  Google Scholar 

  7. Fang JS, Zhou D (2016) Free vibration analysis of rotating axially functionally graded tapered Timoshenko beams. Int J Struct Stab Dyn 16(05):1550007. https://doi.org/10.1142/S0219455415500078

    Article  MathSciNet  MATH  Google Scholar 

  8. Kumar S, Mitra A (2015) Large amplitude free vibration analysis of axially functionally graded tapered rotating beam by energy method. In: Sinha JK (ed) Vibration engineering and technology of machinery. Springer, Cham, pp 473–483. https://doi.org/10.1007/978-3-319-09918-7_42

    Chapter  Google Scholar 

  9. Calim FF (2016) Transient analysis of axially functionally graded Timoshenko beams with variable cross-section. Compos B Eng 98:472–483. https://doi.org/10.1016/j.compositesb.2016.05.040

    Article  Google Scholar 

  10. Lin J, Li J, Guan Y, Zhao G, Naceur H, Coutellier D (2018) Geometrically nonlinear bending analysis of functionally graded beam with variable thickness by a meshless method. Compos Struct 189:239–246. https://doi.org/10.1016/j.compstruct.2018.01.063

    Article  Google Scholar 

  11. Dehrouyeh-Semnani AM (2018) On the thermally induced non-linear response of functionally graded beams. Int J Eng Sci 125:53–74. https://doi.org/10.1016/j.ijengsci.2017.12.001

    Article  MathSciNet  Google Scholar 

  12. Dehrouyeh-Semnani AM (2017) On boundary conditions for thermally loaded FG beams. Int J Eng Sci 119:109–127. https://doi.org/10.1016/j.ijengsci.2017.06.017

    Article  MathSciNet  Google Scholar 

  13. Xu Y, Yu T, Zhou D (2014) Two-dimensional elasticity solution for bending of functionally graded beams with variable thickness. Meccanica 49(10):2479–2489. https://doi.org/10.1007/s11012-014-9958-1

    Article  MathSciNet  MATH  Google Scholar 

  14. Duy HT, Van TN, Noh HC (2014) Eigen analysis of functionally graded beams with variable cross-section resting on elastic supports and elastic foundation. Struct Eng Mech 52(5):1033–1049. https://doi.org/10.12989/sem.2014.52.5.1033

    Article  Google Scholar 

  15. Shi ZF, Chen Y (2004) Functionally graded piezoelectric cantilever beam under load. Arch Appl Mech 74(3):237–247. https://doi.org/10.1007/s00419-004-0346-5

    Article  MATH  Google Scholar 

  16. Wattanasakulpong N, Prusty BG, Kelly DW (2011) Thermal buckling and elastic vibration of third-order shear deformable functionally graded beams. Int J Mech Sci 53(9):734–743. https://doi.org/10.1016/j.ijmecsci.2011.06.005

    Article  Google Scholar 

  17. Şimşek M (2010) Fundamental frequency analysis of functionally graded beams by using different higher-order beam theories. Nucl Eng Des 240(4):697–705. https://doi.org/10.1016/j.nucengdes.2009.12.013

    Article  Google Scholar 

  18. Aydogdu M, Taskin V (2007) Free vibration analysis of functionally graded beams with simply supported edges. Mater Design 28(5):1651–1656. https://doi.org/10.1016/j.matdes.2006.02.007

    Article  Google Scholar 

  19. Piovan MT, Sampaio R (2009) A study on the dynamics of rotating beams with functionally graded properties. J Sound Vib 327(1):134–143. https://doi.org/10.1016/j.jsv.2009.06.015

    Article  Google Scholar 

  20. Şimşek M (2016) Buckling of Timoshenko beams composed of two-dimensional functionally graded material (2D-FGM) having different boundary conditions. Compos Struct 149:304–314. https://doi.org/10.1016/j.compstruct.2016.04.034

    Article  Google Scholar 

  21. Pydah A, Batra RC (2017) Shear deformation theory using logarithmic function for thick circular beams and analytical solution for bi-directional functionally graded circular beams. Compos Struct 172:45–60. https://doi.org/10.1016/j.compstruct.2017.03.072

    Article  Google Scholar 

  22. Wang ZH, Wang XH, Xu GD, Cheng S, Zeng T (2016) Free vibration of two-directional functionally graded beams. Compos Struct 135:191–198. https://doi.org/10.1016/j.compstruct.2015.09.013

    Article  Google Scholar 

  23. Pydah A, Sabale A (2017) Static analysis of bi-directional functionally graded curved beams. Compos Struct 160:867–876. https://doi.org/10.1016/j.compstruct.2016.10.120

    Article  Google Scholar 

  24. Lü CF, Chen WQ, Xu RQ, Lim CW (2008) Semi-analytical elasticity solutions for bi-directional functionally graded beams. Int J Solids Struct 45(1):258–275. https://doi.org/10.1016/j.ijsolstr.2007.07.018

    Article  MATH  Google Scholar 

  25. Şimşek M (2015) Bi-directional functionally graded materials (BDFGMs) for free and forced vibration of Timoshenko beams with various boundary conditions. Compos Struct 133:968–978. https://doi.org/10.1016/j.compstruct.2015.08.021

    Article  Google Scholar 

  26. Rajasekaran S, Khaniki HB (2018) Free vibration analysis of bi-directional functionally graded single/multi-cracked beams. Int J Mech Sci 144:341–356. https://doi.org/10.1016/j.ijmecsci.2018.06.004

    Article  Google Scholar 

  27. Nejad MZ, Hadi A (2016) Non-local analysis of free vibration of bi-directional functionally graded Euler–Bernoulli nano-beams. Int J Eng Sci 105:1–11. https://doi.org/10.1016/j.ijengsci.2016.04.011

    Article  MathSciNet  Google Scholar 

  28. Chong ACM, Yang F, Lam DC, Tong P (2001) Torsion and bending of micron-scaled structures. J Mater Res 16(4):1052–1058. https://doi.org/10.1557/JMR.2001.0146

    Article  Google Scholar 

  29. Ruoff RS, Qian D, Liu WK (2003) Mechanical properties of carbon nanotubes: theoretical predictions and experimental measurements. C R Phys 4(9):993–1008. https://doi.org/10.1016/j.crhy.2003.08.001

    Article  Google Scholar 

  30. Rudd RE, Broughton JQ (1999) Atomistic simulation of MEMS resonators through the coupling of length scales. J Model Simul Microsyst 1(29):29–38

    Google Scholar 

  31. Liebold C, Müller WH (2016) Comparison of gradient elasticity models for the bending of micromaterials. Comput Mater Sci 116:52–61. https://doi.org/10.1016/j.commatsci.2015.10.031

    Article  Google Scholar 

  32. Lei J, He Y, Guo S, Li Z, Liu D (2016) Size-dependent vibration of nickel cantilever microbeams: experiment and gradient elasticity. AIP Adv 6(10):105202. https://doi.org/10.1063/1.4964660

    Article  Google Scholar 

  33. Motz C, Schöberl T, Pippan R (2005) Mechanical properties of micro-sized copper bending beams machined by the focused ion beam technique. Acta Mater 53(15):4269–4279. https://doi.org/10.1016/j.actamat.2005.05.036

    Article  Google Scholar 

  34. Deng W, Li L, Hu Y, Wang X, Li X (2018). Thermoelastic damping of graphene nanobeams by considering the size effects of nanostructure and heat conduction. J Therm Stress. 24 Jul 2018 (published online). https://doi.org/10.1080/01495739.2018.1466669

    Article  Google Scholar 

  35. Kröner E (1967) Elasticity theory of materials with long range cohesive forces. Int J Solids Struct 3(5):731–742. https://doi.org/10.1016/0020-7683(67)90049-2

    Article  MATH  Google Scholar 

  36. Eringen AC (1983) On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J Appl Phys 54(9):4703–4710. https://doi.org/10.1063/1.332803

    Article  Google Scholar 

  37. Eringen AC (2002) Nonlocal continuum field theories. Springer, Berlin. https://doi.org/10.1007/b97697

    Book  MATH  Google Scholar 

  38. Fleck NA, Muller GM, Ashby MF, Hutchinson JW (1994) Strain gradient plasticity: theory and experiment. Acta Metall Mater 42(2):475–487. https://doi.org/10.1016/0956-7151(94)90502-9

    Article  Google Scholar 

  39. Lam DCC, Yang F, Chong ACM, Wang J, Tong P (2003) Experiments and theory in strain gradient elasticity. J Mech Phys Solids 51(8):1477–1508. https://doi.org/10.1016/S0022-5096(03)00053-X

    Article  MATH  Google Scholar 

  40. Bergman RM (1968) Asymptotic analysis of some plane problems of the theory of elasticity with couple stresses. Theory Elast Semilinear Mater 32(6):1070–1074. https://doi.org/10.1016/0021-8928(68)90035-X

    Article  Google Scholar 

  41. Toupin RA (1962) Elastic materials with couple-stresses. Arch Ration Mech Anal 11(1):385–414. https://doi.org/10.1007/BF00253945

    Article  MathSciNet  MATH  Google Scholar 

  42. Mindlin RD, Tiersten HF (1962) Effects of couple-stresses in linear elasticity. Arch Ration Mech Anal 11(1):415–448. https://doi.org/10.1007/BF00253946

    Article  MathSciNet  MATH  Google Scholar 

  43. Lim CW, Zhang G, Reddy JN (2015) A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation. J Mech Phys Solids 78:298–313. https://doi.org/10.1016/j.jmps.2015.02.001

    Article  MathSciNet  MATH  Google Scholar 

  44. Farokhi H, Ghayesh MH (2015) Nonlinear motion characteristics of microarches under axial loads based on modified couple stress theory. Arch Civ Mech Eng 15(2):401–411. https://doi.org/10.1016/j.acme.2014.12.012

    Article  Google Scholar 

  45. Dai HL, Wang YK, Wang L (2015) Nonlinear dynamics of cantilevered microbeams based on modified couple stress theory. Int J Eng Sci 94:103–112. https://doi.org/10.1016/j.ijengsci.2015.05.007

    Article  MathSciNet  Google Scholar 

  46. Dehrouyeh-Semnani AM, Dehrouyeh M, Zafari-Koloukhi H, Ghamami M (2015) Size-dependent frequency and stability characteristics of axially moving microbeams based on modified couple stress theory. Int J Eng Sci 97:98–112. https://doi.org/10.1016/j.ijengsci.2015.09.003

    Article  MathSciNet  Google Scholar 

  47. Li YS, Feng WJ, Cai ZY (2014) Bending and free vibration of functionally graded piezoelectric beam based on modified strain gradient theory. Compos Struct 115:41–50. https://doi.org/10.1016/j.compstruct.2014.04.005

    Article  Google Scholar 

  48. Sahmani S, Bahrami M, Ansari R (2014) Nonlinear free vibration analysis of functionally graded third-order shear deformable microbeams based on the modified strain gradient elasticity theory. Compos Struct 110:219–230. https://doi.org/10.1016/j.compstruct.2013.12.004

    Article  Google Scholar 

  49. Hosseini M, Bahaadini R (2016) Size dependent stability analysis of cantilever micro-pipes conveying fluid based on modified strain gradient theory. Int J Eng Sci 101:1–13. https://doi.org/10.1016/j.ijengsci.2015.12.012

    Article  Google Scholar 

  50. Khaniki HB, Hosseini-Hashemi S (2017) The size-dependent analysis of multilayered microbridge systems under a moving load/mass based on the modified couple stress theory. Eur Phys J Plus 132(5):200. https://doi.org/10.1140/epjp/i2017-11466-0

    Article  Google Scholar 

  51. Dehrouyeh-Semnani AM, Nikkhah-Bahrami M (2015) The influence of size-dependent shear deformation on mechanical behavior of microstructures-dependent beam based on modified couple stress theory. Compos Struct 123:325–336. https://doi.org/10.1016/j.compstruct.2014.12.038

    Article  Google Scholar 

  52. Khaniki HB, Rajasekaran S (2018) Mechanical analysis of non-uniform bi-directional functionally graded intelligent micro-beams using modified couple stress theory. Mater Res Express 5(5):055703. https://doi.org/10.1088/2053-1591/aabe62

    Article  Google Scholar 

  53. Dehrouyeh-Semnani AM, Dehrouyeh M, Torabi-Kafshgari M, Nikkhah-Bahrami M (2015) A damped sandwich beam model based on symmetric–deviatoric couple stress theory. Int J Eng Sci 92:83–94. https://doi.org/10.1016/j.ijengsci.2015.03.007

    Article  Google Scholar 

  54. Dehrouyeh-Semnani AM, Mostafaei H, Nikkhah-Bahrami M (2016) Free flexural vibration of geometrically imperfect functionally graded microbeams. Int J Eng Sci 105:56–79. https://doi.org/10.1016/j.ijengsci.2016.05.002

    Article  MathSciNet  Google Scholar 

  55. Reddy JN (2007) Nonlocal theories for bending, buckling and vibration of beams. Int J Eng Sci 45(2):288–307. https://doi.org/10.1016/j.ijengsci.2011.11.011

    Article  MATH  Google Scholar 

  56. Aydogdu M (2009) A general nonlocal beam theory: its application to nanobeam bending, buckling and vibration. Physica E 41(9):1651–1655. https://doi.org/10.1016/j.physe.2009.05.014

    Article  Google Scholar 

  57. Moradweysi P, Ansari R, Hosseini K, Sadeghi F (2018) Application of modified Adomian decomposition method to pull-in instability of nano-switches using nonlocal Timoshenko beam theory. Appl Math Model 54:594–604. https://doi.org/10.1016/j.apm.2017.10.011

    Article  MathSciNet  Google Scholar 

  58. Lei Y, Adhikari S, Friswell MI (2013) Vibration of nonlocal Kelvin–Voigt viscoelastic damped Timoshenko beams. Int J Eng Sci 66:1–13. https://doi.org/10.1016/j.ijengsci.2013.02.004

    Article  MathSciNet  MATH  Google Scholar 

  59. Khaniki HB, Hosseini-Hashemi S (2017) Dynamic response of biaxially loaded double-layer viscoelastic orthotropic nanoplate system under a moving nanoparticle. Int J Eng Sci 115:51–72. https://doi.org/10.1016/j.ijengsci.2017.02.005

    Article  MathSciNet  Google Scholar 

  60. Ebrahimi F, Barati MR, Zenkour AM (2018) A new nonlocal elasticity theory with graded nonlocality for thermo-mechanical vibration of FG nanobeams via a nonlocal third-order shear deformation theory. Mech Adv Mater Struct 25(6):512–522. https://doi.org/10.1080/15376494.2017.1285458

    Article  Google Scholar 

  61. Daneshmehr A, Rajabpoor A, Hadi A (2015) Size dependent free vibration analysis of nanoplates made of functionally graded materials based on nonlocal elasticity theory with high order theories. Int J Eng Sci 95:23–35. https://doi.org/10.1016/j.ijengsci.2015.05.011

    Article  MathSciNet  Google Scholar 

  62. Hashemi SH, Khaniki HB (2017) Dynamic behavior of multi-layered viscoelastic nanobeam system embedded in a viscoelastic medium with a moving nanoparticle. J Mech 33(5):559–575. https://doi.org/10.1017/jmech.2016.91

    Article  Google Scholar 

  63. Khaniki HB (2018) On vibrations of nanobeam systems. Int J Eng Sci 124:85–103. https://doi.org/10.1016/j.ijengsci.2017.12.010

    Article  MathSciNet  Google Scholar 

  64. Arefi M (2018) Analysis of a doubly curved piezoelectric nano shell: nonlocal electro-elastic bending solution. Eur J Mech A/Solids 70:226–237. https://doi.org/10.1016/j.euromechsol.2018.02.012

    Article  MathSciNet  MATH  Google Scholar 

  65. Aria AI, Biglari H (2018) Computational vibration and buckling analysis of microtubule bundles based on nonlocal strain gradient theory. Appl Math Comput 321:313–332. https://doi.org/10.1016/j.amc.2017.10.050

    Article  MathSciNet  Google Scholar 

  66. Xu XJ, Wang XC, Zheng ML, Ma Z (2017) Bending and buckling of nonlocal strain gradient elastic beams. Compos Struct 160:366–377. https://doi.org/10.1016/j.compstruct.2016.10.038

    Article  Google Scholar 

  67. Ebrahimi F, Barati MR (2018) Damping vibration analysis of graphene sheets on viscoelastic medium incorporating hygro-thermal effects employing nonlocal strain gradient theory. Compos Struct 185:241–253. https://doi.org/10.1016/j.compstruct.2017.10.021

    Article  Google Scholar 

  68. Mohammadi K, Rajabpour A, Ghadiri M (2018) Calibration of nonlocal strain gradient shell model for vibration analysis of a CNT conveying viscous fluid using molecular dynamics simulation. Comput Mater Sci 148:104–115. https://doi.org/10.1016/j.commatsci.2018.02.036

    Article  Google Scholar 

  69. Nematollahi MS, Mohammadi H, Nematollahi MA (2017) Thermal vibration analysis of nanoplates based on the higher-order nonlocal strain gradient theory by an analytical approach. Superlattices Microstruct 111:944–959. https://doi.org/10.1016/j.spmi.2017.07.055

    Article  Google Scholar 

  70. Sahmani S, Aghdam MM (2018) Nonlocal strain gradient beam model for postbuckling and associated vibrational response of lipid supramolecular protein micro/nano-tubules. Math Biosci 295:24–35. https://doi.org/10.1016/j.mbs.2017.11.002

    Article  MathSciNet  MATH  Google Scholar 

  71. Ghayesh MH, Farajpour A (2018) Nonlinear coupled mechanics of nanotubes incorporating both nonlocal and strain gradient effects. Mech Adv Mater Struct. https://doi.org/10.1080/15376494.2018.1473537

    Article  Google Scholar 

  72. Ghayesh MH, Farajpour A (2018) Nonlinear mechanics of nanoscale tubes via nonlocal strain gradient theory. Int J Eng Sci 129:84–95. https://doi.org/10.1016/j.ijengsci.2018.04.003

    Article  MathSciNet  Google Scholar 

  73. Li L, Hu Y, Li X (2016) Longitudinal vibration of size-dependent rods via nonlocal strain gradient theory. Int J Mech Sci 115:135–144. https://doi.org/10.1016/j.ijmecsci.2016.06.011

    Article  Google Scholar 

  74. Li L, Tang H, Hu Y (2018) The effect of thickness on the mechanics of nanobeams. Int J Eng Sci 123:81–91. https://doi.org/10.1016/j.ijengsci.2017.11.021

    Article  MathSciNet  Google Scholar 

  75. Li L, Hu Y (2017) Post-buckling analysis of functionally graded nanobeams incorporating nonlocal stress and microstructure-dependent strain gradient effects. Int J Mech Sci 120:159–170. https://doi.org/10.1016/j.ijmecsci.2016.11.025

    Article  Google Scholar 

  76. Li L, Li X, Hu Y (2016) Free vibration analysis of nonlocal strain gradient beams made of functionally graded material. Int J Eng Sci 102:77–92. https://doi.org/10.1016/j.ijengsci.2016.02.010

    Article  Google Scholar 

  77. Şimşek M (2016) Nonlinear free vibration of a functionally graded nanobeam using nonlocal strain gradient theory and a novel Hamiltonian approach. Int J Eng Sci 105:12–27. https://doi.org/10.1016/j.ijengsci.2016.04.013

    Article  MathSciNet  Google Scholar 

  78. Li X, Li L, Hu Y, Ding Z, Deng W (2017) Bending, buckling and vibration of axially functionally graded beams based on nonlocal strain gradient theory. Compos Struct 165:250–265. https://doi.org/10.1016/j.compstruct.2017.01.032

    Article  Google Scholar 

  79. Ebrahimi F, Barati MR (2017) A nonlocal strain gradient refined beam model for buckling analysis of size-dependent shear-deformable curved FG nanobeams. Compos Struct 159:174–182. https://doi.org/10.1016/j.compstruct.2016.09.058

    Article  Google Scholar 

  80. Khaniki HB, Hosseini-Hashemi S (2017) Buckling analysis of tapered nanobeams using nonlocal strain gradient theory and generalized differential quadrature method. Mater Res Express 4(6):065003. https://doi.org/10.1088/2053-1591/aa7111

    Article  Google Scholar 

  81. Khaniki HB, Hosseini-Hashemi S, Nezamabadi A (2017) Buckling analysis of nonuniform nonlocal strain gradient beams using generalized differential quadrature method. Alex Eng J. https://doi.org/10.1016/j.aej.2017.06.001

    Article  Google Scholar 

  82. Bakhshi Khaniki H, Hosseini-Hashemi Sh (2017) Dynamic transverse vibration characteristics of nonuniform nonlocal strain gradient beams using the generalized differential quadrature method. Eur Phys J Plus 132:500. https://doi.org/10.1140/epjp/i2017-11757-4

    Article  Google Scholar 

  83. Rajasekaran S, Khaniki HB (2017) Bending, buckling and vibration of small-scale tapered beams. Int J Eng Sci 120:172–188. https://doi.org/10.1016/j.ijengsci.2017.08.005

    Article  MathSciNet  Google Scholar 

  84. Rajasekaran S, Bakhshi Khaniki H (2018) Finite element static and dynamic analysis of axially functionally graded nonuniform small-scale beams based on nonlocal strain gradient theory. Mech Adv Mater Struct. https://doi.org/10.1080/15376494.2018.1432797

    Article  Google Scholar 

  85. Rajasekaran S (2017) Nonlocal theory of buckling of tapered nano columns under self weight and an axial tip load using Matrix Based Chebyshev Spectral Collocation (MBCSC). J Struct Eng 44(1):1–10

    Google Scholar 

  86. Reddy JN (1993) An introduction to the finite element method, vol 2, no 2.2. McGraw-Hill, New York

  87. Wilson EL (1996) Three-dimensional static and dynamic analysis of structures. Computers and Structures Inc, Berkeley

    Google Scholar 

  88. Şimşek M, Yurtcu HH (2013) Analytical solutions for bending and buckling of functionally graded nanobeams based on the nonlocal Timoshenko beam theory. Compos Struct 97:378–386. https://doi.org/10.1016/j.compstruct.2012.10.038

    Article  Google Scholar 

  89. Pinarbasi S (2012) Buckling analysis of nonuniform columns with elastic end restraints. J Mech Mater Struct 7(5):485–507. https://doi.org/10.2140/jomms.2012.7.485

    Article  Google Scholar 

  90. Eltaher MA, Emam SA, Mahmoud FF (2013) Static and stability analysis of nonlocal functionally graded nanobeams. Compos Struct 96:82–88. https://doi.org/10.1016/j.compstruct.2012.09.030

    Article  Google Scholar 

  91. Eltaher MA, Emam SA, Mahmoud FF (2012) Free vibration analysis of functionally graded size-dependent nanobeams. Appl Math Comput 218(14):7406–7420. https://doi.org/10.1016/j.amc.2011.12.090

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors sincerely thank the reviewers for their valuable suggestions to improve the standard of the manuscript.

Author information

Authors and Affiliations

  1. Visiting Faculty of Civil Engineering, PSG College of Technology, Coimbatore, Tamil Nadu, 641004, India

    Sundaramoorthy Rajasekaran

  2. School of Mechanical Engineering, Iran University of Science and Technology, Narmak, Tehran, 16846-13114, Iran

    Hossein Bakhshi Khaniki

Authors
  1. Sundaramoorthy Rajasekaran
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hossein Bakhshi Khaniki
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hossein Bakhshi Khaniki.

Additional information

Technical Editor: Wallace Moreira Bessa, D.Sc.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Rajasekaran, S., Khaniki, H.B. Bending, buckling and vibration analysis of functionally graded non-uniform nanobeams via finite element method. J Braz. Soc. Mech. Sci. Eng. 40, 549 (2018). https://doi.org/10.1007/s40430-018-1460-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-018-1460-6

Keywords

Search

Navigation