1 Introduction

Acquiring valid information on planetary interiors is an elusive scientific objective hampered by the obvious impossibility of in situ measurements and a handful of non-trivial complications.

In case of the Earth the presence of a relatively large magnetic field and its changes are helpful in studying the internal processes of the planet, since the main geomagnetic field observed at the surface originates from dynamo processes of the fluid outer core. Mathematical representation of the field and its slow gradual change to unprecedented accuracy are obtained from ground based observations and satellite missions.

This paper intends to provide a short summary of our present knowledge on the generating processes of the main geomagnetic field along with the scientific inquiries which have revealed these pieces of information. The main difficulties or constraints concerning each area of investigation are briefly described as well. On the basis of these, the paper demonstrates the raison d’être of a machine learning based approach of the problem of core field reconstruction.

The main conclusion of the study points to the necessity of a global source model of the core field, which is at present missing as a tool of gaining and validating information on the geodynamo, especially at processes of shorter spatial scales.

2 Recent knowledge on consistency and composition of the core: geomagnetic dynamo aspects

First indications to a liquid central region within the Earth’s interior come from the determination of a shadow-zone affecting seismic shear waves by Oldham (1906), who already attributed this to a solid–liquid phase transition from the mantle to the core.

Gutenberg (1912) provided a depth for the Core Mantle Boundary (CMB) at approximately 2900 km based on the seismic velocity profiles.

Lehmann (1936) found that the core can be further separated to a fluid outer and a liquid inner part by discovering faint signals of P waves (reflected from the surface of the inner core) that can be detected within the shadow-zone.

This allows for a thick spherical shell mainly of liquid metal for any field generation process to play a role in the geodynamo, though we shall see that it is not entirely metal and that such processes may extend beyond this region (see the end of this section).

The findings presented above used seismic wave propagation to derive information about the general structure of Earth’s core. Seismic wave properties and propagation characteristics, wavelet distortion along the path are useful also in the empirical determination of the density distribution of Earth’s interior.

Assuming a spherically symmetric Earth in hydrostatic equilibrium, a density-depth profile inside the Earth interior can be estimated using the Adams-Williamson equation Eq. (1) using the measured velocity of shear and compressional waves (Gubbins and Roberts 1987).

$$ln\left( {\frac{\rho \left( r \right)}{{\rho_{0} }}} \right) = - \mathop \int \limits_{{r_{0} }}^{r} \frac{g\left( r \right)}{\phi \left( r \right)}dr$$
(1)

here \(g\left( r \right)\) is the gravitational acceleration at radius \(r\), \(\phi \left( r \right)\) is a seismic parameter combining the shear and compressional wave velocities as a function of depth, \(r_{0}\) is the radius of Earth, \(\rho_{0}\) is the mean near-surface density of the Earth, and \(\rho \left( r \right)\) is assigned to the density-depth profile.

To gain a more reliable understanding of the state of the core, more complex Earth models were developed (Bullen and Haddon 1967; Dziewonski and Anderson 1981) providing depth profiles of elastic properties, gravitational acceleration, density and pressure. These make use of Eq. (1) accompanied by other geodetic and seismological properties of the Earth such as periods of its eigenmodes and moments of inertia. Acquiring these profiles helps in identifying other important semi-empirical derived functions, e.g. the temperature profile by the density jump \(\Delta \rho\) across the ICB of 0.6 to 1.0 g/cm3 (Davies et al. 2015), which is mainly a result of an increased concentration of light elements, affecting the melting point (see below).

Thus, we have summarized pieces of evidence from seismology that support the existence of a fluid core and a solid inner core, and yield profiles of density, pressure and gravitational acceleration. These are generally considered to be the most well defined physical quantities of the core, whereas other key parameters derived partly by using these basic quantities, such as the electrical and thermal conductivity and the dynamic viscosity of the core are the least certain (Gans 1972).

These key physical parameters can be specified by ab initio calculations, shock wave or diamond anvil cell experiments.

Gans (1972) gave an estimation of the dynamic viscosity using seismic properties and the properties of iron at the melting point on the CMB. The estimated values were in the range of ~ 3–19 × 10−3 (Pas) which is in either case much closer to that of water than that of Earth’s mantle. Its relevance is in the vigorousness of the convection in the geodynamo (see Sect. 5).

One of the latest measurements of the electrical resistivity of liquid iron at core conditions is that of Ohta et al. (2016), which translates into a conductivity of ~ 6 × 105–106 (S/m). The importance of this result is the varying intensity of field generation (see Sect. 5 and below), and the amount of screening it can cause when recovering time-dependent systems within the core.

The review article of Davies et al. (2015) summarizes experimental thermal conductivity estimations assuming different core compositions ranging between 100 and 170 (W/mK), much higher than previously thought. This impacts both the behavior of the geodynamo (see Sect. 5) and its evolution (see below).

Temperature values at the CMB can be experimentally approximated and were found to be between 3100 and 3500 °C by Nomura et al. (2014).

In this article temperature values at the boundaries are given also for the ICB, which can be constrained by the density profile (as seen above), between ~ 5800 and 6300 °C.

In light of these uncertain quantities some important information on energy balance and the formation of the geodynamo is briefly noted here.

Wood et al. (2006) explained how crystallization of the compounds had to start to begin forming a solid phase region in the centre as the core cooled down. As described later it turned out that such a process has a profound impact on why the geodynamo can exist.

It is worth mentioning that Song and Richards (1996) argued the inner core overtakes other parts of the Earth in rotational velocity, a phenomenon which could also have left its mark on geomagnetic records. Whether or not this is the case has been a matter of debate up until today (Vidale 2019).

Nakagawa and Tackley (2008) came to the conclusion that the CMB has a significant spatial variation in heat flow with respect to its effect on the field generation in the core.

Though most models trying to reproduce the operation of the geodynamo still assume uniform boundaries, core-mantle interactions and the control of the mantle on the geodynamo are subject to frontier research works (e.g. Olson et al. 2010).

The main sources of energy for convection are heat and buoyancy. Heat was released by the formation of the core, during the differentiation of lighter and heavier elements (Horedt 1980). It is also supplied by the solidification of the inner core as latent heat is being released during the crystallization (Buffett 2003). It is debated whether radioactive isotopes such as 40K could produce internal heat contributing to these sources (Blanchard et al. 2017).

When considering sources of buoyancy, findings on the composition and properties of the medium in the core need inspection.

The idea of a dominantly iron core originates from a long time ago (e.g. Barnett 1924). Iron is important with respect to the geodynamo for its thermal and electrical conductivity (see below).

Equally important is the finding made first by Gessmann et al. (2001) that light elements, such as silicon could be diluted in an iron-rich core.

Besides producing heat, crystallization of the inner core acts as a major source of buoyancy sustaining the dynamo action, since during the solidification light elements are expelled into the bottom of the liquid core (Kutzner and Christensen 2000). Before the formation of the inner core, the geodynamo could have been mainly powered by secular cooling (Landeau et al. 2017).

One of the main obstacles of a consistent understanding of the evolution of the geodynamo and the age of the inner core is the challenge mounted by experimentally reproducing circumstances inside the geodynamo (see above and in Sect. 4). Direct measurements of the thermal and electrical properties of iron at high temperature are still rare. They are the source of a major contradiction: though there is a large scatter of results, most direct measurements show a relatively high thermal conductivity of iron at core conditions, and a temperature profile closer to subadiabatic, putting the age of the inner core to roughly 1 Ga (Davies et al. 2015), while paleointensity measurements suggest an older inner core and a much lower thermal conductivity for liquid iron (Tarduno et al. 2015).

However, there are currently no unequivocal findings supported by paleomagnetism on when the inner core formation took place.

Landeau et al. (2017) found that the strength of the axial octupole field could be a good indicator of inner core nucleation. Biggin et al. (2015) suggested that field intensity variations roughly 1.3 Ga ago can be a sign of inner core formation, but this too is doubted by others such as Ohta et al. (2016).

Further deepening the mystery of geomagnetism and the structural history of the core is the age of the geodynamo itself: It is known that silicate melts can also attain enhanced convective properties. In the early history of the Earth, a magma ocean could have been present at the lowermost mantle, complicating the evolution of the geodynamo while making it possible to operate as early on as 4.5 Ga (Ziegler and Stegman 2013).

As for the energy budget of the core, another peculiar feature which is difficult to reproduce and not clearly understood is that the magnetic energy of the geodynamo could be as much as 4 orders of magnitude larger than its kinetic energy (Zimmerman et al. 2014) [see Eq. (10)].

Most importantly, difficulties in estimating key variables such as the electrical and thermal conductivities manifest themselves in geodynamo modeling by an uncertain relative importance and time scales of diffusion (magnetic decay) and the advective field generation, an uncertain contribution of chemical and thermal convection as driving mechanisms, and an uncertain structure of the convection (Gubbins et al. 2015) (see also Eq. (10) in Sect. 5.).

3 Core field models and characteristics

Models of the core field generally use a spherical harmonic (SH) expansion of the potential from data recorded in point measurements, leading to a physics based interpolation of the field under the assumption of an insulating mantle (Gubbins and Bloxham 1987). These are either included in complex geomagnetic models incorporating satellite and ground observatory data such as CHAOS (Finlay et al. 2016) and GRIMM (Lesur et al. 2008), or long time-span models mostly based on paleomagnetic records, such as GUFM-1 (Jackson et al. 2000) and CALS3k (Korte and Constable 2011). The below Eqs. (2) to (3) were used to derive the geomagnetic reference field model IGRF-12 (Finlay et al. 2015).

$$V^{i} = a\mathop \sum \limits_{n = 1}^{{N_{i} }} \mathop \sum \limits_{m = 0}^{n} g_{n}^{m} \cos \left( {m\phi } \right) + h_{n}^{m} \sin \left( {m\phi } \right)\left( {\frac{a}{r}} \right)^{n + 1} P_{n}^{m} \left( {\cos \left( \theta \right)} \right)$$
(2)
$$V^{e} = a\mathop \sum \limits_{n = 1}^{2} \mathop \sum \limits_{m = 0}^{n} q_{n}^{m} \cos \left( {mT_{d} } \right) + s_{n}^{m} \sin \left( {mT_{d} } \right)\left( {\frac{a}{r}} \right)^{n + 1} P_{n}^{m} \left( {\cos \left( {\theta_{d} } \right)} \right) + a\mathop \sum \limits_{n = 1}^{2} q_{n}^{0,GSM} R_{n}^{0} \left( {R,\theta ,\phi } \right)$$
(3)

\(V^{i}\) in Eq. (2) gives the internal and \(V^{e}\) in Eq. (3) the external geomagnetic potentials. \(N_{i}\) is the maximum degree of internal expansion and the external expansion is limited to degree 2 (\(g, h, q, s\) are the Gauss coeffitients, \(P_{n}^{m}\) are Schmidt-normalized associated Legendre polinomials, \(a\) is Earth’s radius). The ring current in Eq. (3) is represented in solar magnetic coordinates (SM), other more remote magnetospheric sources are given in geocentric solar magnetospheric (GSM) coordinates in the second term.

Despite of the long-term dominance of the axial dipole field, deviations from it are actually required for the existence of the geodynamo (see Sect. 4.). The dipole field has at present an 11.5° tilt from the rotational axis, and amounts to as much as 90% of the total geomagnetic field spectrum. The most significant feature of the non-dipole field is a region in the South Atlantic, where the total geomagnetic main field is significantly weaker than at its surroundings. Hartmann and Pacca (2009) demonstrated that it can be described mostly by quadrupole and octupole terms (n = 2, 3) in Eq. (2). Finding out what kind of processes inside a geodynamo could result in the formation of this so-called South Atlantic Anomaly are frontier research issues (Pavón-Carrasco and DeSantis 2016).

When intending to describe the geodynamo one should keep in mind that determining what part of the geomagnetic field is actually produced by it is not a trivial problem to solve.

This is mainly due to the following complications:

Even sources of long wavelength signals in the geomagnetic SH spectrum used for modeling are difficult to be separated as internal fields [\(g_{1}^{0}\) in Eq. (2)], as they are contaminated by short-term variations coming mostly from the magnetospheric ring current [\(q_{1}^{0}\) in Eq. (3)] (Langel 1993). Attempts at advancing the modeling of magnetic effect of the ring current and therefore allowing a more reliable distinction between internal and external fields were carried out by numerous authors from Fukushima and Kamide (1973) to Fok et al. (2001) and Pick and Korte (2018).

Observatory information on the main field is known to be polluted mainly by external variations and the corresponding secondary fields induced within the solid Earth in the subdecadal time period band (Wardinski and Holme 2011).

When accepting Eq. (2) it has to be taken into account that this representation as a potential calculated inside an insulating mantle allows no toroidal magnetic fields (\(\varvec{B}_{T} = \nabla \times \left( {\varvec{T}r} \right)\)) outside the core, meaning we can have little idea on how such fields can be arranged inside it.

At satellite altitude, the potential theory noted above is violated and a rotational field component should be added.

At high geomagnetic latitudes field models are generally characterized by higher uncertainty because of un-modelled external fields (Mandea and Olsen 2006).

In addition to these, the derivation of geomagnetic models is itself ill-posed and often achieved by ad-hoc regularizations to achieve convergence of field model spectra.

4 Existence of the geodynamo

One of the main evidences of paleomagnetism with profound implications on the origins of the geomagnetic field comes from dating the oldest rock samples containing remanent magnetization which can be as old as 3.4 Ga (McElhinny and Senanayake 1980). This implies an internal geomagnetic field of significant magnitude having been produced at least since then. It is a strong argument supporting the existence of the geodynamo as some kind of regeneration mechanism is required to sustain a field for such a long time (Usui et al. 2009).

Polarity reversals found mainly in the oceanic crust first by Cox (1969) and described in detail by e.g. Sahy et al. (2019) display relatively long lasting magnetic periods termed chrons. These periods display nearly identical magnetizations in the basaltic crust except for the orientation. This observation is particularly difficult to reconcile with any other explanation than a self-sustaining dynamo, because it requires the existence of two states \(\varvec{B}\left( r \right)\) and \(- \varvec{B}\left( r \right)\) which equally satisfy the solution of the induction equation Eq. (4) and it has a rather well observed example in case of the solar dynamo (Merrill and McFadden 1990).

Zollner in 1871 was the first researcher who came up with the idea that features of the geomagnetic field may be at least partially explained by electric currents flowing inside a liquid core (Roberts 2007b), but unfortunately his ideas didn’t meet much attention until Larmor (1919) suggested that with an initial seed field \(\varvec{B}_{0}\) it could be possible that a magnetic field is sustained by currents in the conducting liquid even in the absence of that field provided that they flow in an appropriate path. What he suggested has been essentially a liquid metal dynamo [originally for the Sun, but soon many realized it could apply to the Earth and other planets as well (Elsasser 1946)]. Larmor’s ideas are explained in more detail in Kreuzahler et al. (2017).

$$\partial_{t} \varvec{B} = \nabla \times \left( {\varvec{u} \times \varvec{B}} \right) + \eta \nabla^{2} \varvec{B}$$
(4)

Like in many other branches of physics describing the possible processes precede the description of their physical reasons. This is extremely important when demonstrating (or denying) the existence of a sustainable dynamo in liquid metal, because only specifically organized geometries of currents can possibly lead to a dynamo action. In case of freely moving liquids this obstacle is in itself difficult to overcome (Roberts 2007a).

Thus, we can ask the question: What kind of paths can currents take in order to sustain the dynamo action in a liquid conductor? Answering it is the objective when solving the so-called kinematic dynamo problem, only dealing with the description of such possible current and flow configurations.

A more recent argument about the importance of kinematic dynamos in understanding the actual geodynamo comes from Stefani and Tretter (2018).

Since the advent of Larmor’s idea, many theoreticians have cast doubt over the possibility of any planetary or stellar magnetic fields produced by dynamos. Many objections seemingly disproving the possibility of liquid metal dynamos in general came in the form of proven statements as follows.

Two dimensional magnetic fields cannot be maintained by a dynamo (Cowling 1957).

Stationary axisymmetric magnetic fields cannot be maintained by a dynamo (Cowling 1934).

This last argument made by Cowling is especially relevant as it seems to contradict the dominantly dipolar and axial nature of the geomagnetic field but its importance starts to wane when one realizes that it’s neither perfectly axial, nor steady (Merrill and McFadden 1990). However, observations of the magnetic field of Saturn redirected some attention to the theorem, given that it is the only planet considered to have a nearly perfectly axisymmetric magnetic field, which in addition seems to be outstandingly stationary (Davis and Smith 1990). Finding an explanation for this situation, which supports the planetary dynamo theory is subject to intensive frontier research (Stanley and Bloxham 2016).

An important constraint in providing a conclusive evidence supporting planetary dynamos is the lack of laboratory experimental proof. There have been a number of laboratory experiments some of which did result in a self-sustaining dynamo listed in Table 1, but none of them can be acknowledged as a scaled-down demonstration of the actual geodynamo. Moreover, experiments using liquids inside a spherical domain have not yielded a self-sustaining dynamo process yet (Christensen 2019). However, given the complexity of the actual convectively driven core dynamo realistic expectations should be of different setups demonstrating its different features, such as the role of α and Ω effects (see Sect. 5.) in field generation and inertial modes (Wei et al. 2011; Zimmerman et al. 2014).

Table 1 More recent laboratory dynamo experiments and their relevance with respect to reproducing features of the actual geodynamo
Full size table

There have been a handful of experiments providing relevant information on how the geodynamo works.

Onset of self-sustaining dynamo action in conducting fluids were observed in the Riga experiment by Gailitis et al. (2003) and the Karlsruhe experiment by Müller et al. (2008). Both experiments used liquid sodium as the conducting medium and observed a dynamo process at magnetic Reynolds numbers still low compared to that of the Earth [for comparison, see Eq. (10)]. The Karlsruhe dynamo produced an equatorial dipole field which was generated by the α2 effect (Rädler et al. 1998) and it was in agreement with the mean-field prediction about the onset of the dynamo action.

5 Operation of the geodynamo

Paleomagnetic evidences of the inner core formation and its impact on the behavior of the core dynamo were presented in Sect. 2. Evidences for reversals were discussed in Sect. 4.

Variations in the geomagnetic polarity are also key paleomagnetic pieces of information with respect to how the geodynamo works. The frequency and magnitude of these changes is an important characteristic of Earth’s dynamo process. Polarity reversals and less persistent changes of the poles called excursions occur rather erratically, which is difficult to reproduce in simulations (see the end of this section). An outstanding example of this is the long period of normal polarity configuration in the Cretaceous (Cretaceous Normal Superchron) without any traces of reversal, albeit still presenting significant variability (Granot et al. 2012). The last reversal occurred approximately 773 ka ago and more recent studies suggest it could be a longer, more complex process to finish, then previously thought (Singer et al. 2019). The best documented recent excursion (Laschamp event) briefly resulted in a fully reversed state and occurred ~ 41ky ago (Nowaczyk et al. 2012).

One of the main challenges associated to understanding this behavior is of answering whether the current morphological changes in the main field we observe can lead to an excursion or even a reversal (Pavón-Carrasco and DeSantis 2016; Brown et al. 2018). Valet and Fournier (2016) summarize transitional features of the field deduced mainly from paleomagnetic records which may accompany an impending reversal. The strongest such feature is a large and systematic decrease in field intensity, more controversial are occurrences of field intensity oscillations and preferred regions where geomagnetic poles tend to move toward during a reversal. Nevertheless, achieving this objective is severely hampered both by problems in acquiring reliable transitional paleomagnetic data and difficulties in mid- to long-term predictions of the field behavior (see the end of this section).

The first observational evidence that the geomagnetic field shows a long-term trend came as early as 1635 by Gellibrand (Alexandrescu et al. 1996; Roberts 2007b), long before a global observatory network and measurements of the field becoming frequent all over the world.

It is not self-evident how these observed (local and global) changes in the field could provide information on the operation of the geodynamo, e.g. Gauss attributed the secular variation (SV) to the solidification of the crust (Roberts 2007b), and a significant part of the SV spectrum can be attributed to the solar cycle and accompanying inductive effects in the mantle. However, Langel et al. (1986) argued that most of these changes can arise internally as a result of advection and diffusion of the field inside the core (see below).

The westward drift of the non-dipole features of the main field was observed already by Halley in 1692 (Thompson 1989), and later studies showed that it can be a result of field advection in the core as well as MHD waves (see the discussion of Magneto-Coriolis waves).

Jerks are more recently discovered short-term variations of the geomagnetic field first discovered by Courtillot (1978) and validated later by Malin et al. (1983). The first suggestion that these short accelerations of the SV are actually features of the main field and come from processes inside the geodynamo was made by Malin and Hodder (1982), followed by other colleagues (Alexandrescu et al. 1995; Le Huy et al. 1998; Bloxham et al. 2002).

Some very recent results suggest that jerks could actually provide unique local information on the configuration of the core field and density anomalies by describing them as localized MHD waves (see the discussion of Alfvén waves).

It is interesting to note that general information about flow velocities in the core and indirectly about the torsional oscillations (see below) can be acquired from long period changes in the length of day using the conservation of angular momentum of the core-mantle system (Jault et al. 1988; Dumberry and Bloxham 2006; Gillet et al. 2010).

A more thorough understanding of the general properties of field generation and the geodynamo itself necessitate significant advances in theory and computation.

Parker (1955) described how the amplification of the field is possible inside a rotating fluid, giving two fundamental solutions of the kinematic dynamo problem. The α effect comes as a result of radial flows amplifying the poloidal magnetic fields. The Ω effect, on the other hand, acts to amplify the toroidal magnetic fields by zonal flows. How and to what extent these type of effects actually operate inside the geodynamo is still a matter of research and debates (Reshetnyak 2016).

Answering the central question of the kinematic dynamo theorem (see Sect. 4.) mainly means searching for the solutions of Eq. (4) with prescribed flows independent of \(\varvec{B}\). Such solutions which can be relevant in the Earth’s case are briefly listed here.

In the simplest relevant case assuming an infinitely conductive medium, whatever flow is given, the field lines and the local strength of the field should be contained in it (Roberts 2007a). This frozen flux approximation Eq. (5) is important not only for kinematic dynamos but for the MHD theory in general (see below). Many studies investigated how valid this assumption could be in case of the geodynamo. For example, Metman et al. (2018) found that magnetic diffusion can explain secular variation just about as well as the frozen flux approximation.

$$d_{t} \varvec{B} = \varvec{B} \cdot \nabla \varvec{u} - \varvec{B}\nabla \cdot \varvec{u}$$
(5)

Parker (1955) constructed a kinematic dynamo model in which the rotating fluid can regenerate a dipole field via the effect of small-scale convective vortexes on a large-scale toroidal magnetic field, inducing the poloidal magnetic field (described above as the α effect).

Steenbeck and Krause (1966) has used a formulation for his dynamo models that distinguish between large-scale and small-scale flows. This mean-field dynamo theorem is relevant when attributing the regeneration of the large-scale field to small-scale processes as sources (see Sect. 6).

Braginsky and Roberts (1987) demonstrated that a dynamo can regenerate the field with both the α and Ω effects at play. That required a prescribed helicity field and buoyancy force. This has had relevant implications also on theoretical studies up until now (Gilbert and Vanneste 2019).

$$\partial_{t} B_{rCMB} = - \nabla_{h} \left( {u_{hCMB} B_{rCMB} } \right)$$
(6)

Exploiting the imposition of the frozen flux approximation [Eq. (5)] on the radial component of the induction equation [Eq. (4)] already leads to a possibility of inverting velocities at the CMB from the radial component of the estimated SVCMB derived from SV data at the surface [Eq. (6)] (Bloxham 1988). This yields a valuable information on the geodynamo, and even applying such assumptions, can lead to more accurate forecasts of SV than fields produced by linear extrapolations of time-dependent IGRF model coefficients (Beggan et al. 2014).

In order to gain more in-depth knowledge of the complex phenomena attached to the hydromagnetic system reproducing the field, the MHD dynamo theory was developed. This theory aims at explaining and analyzing the main forces behind the operation of liquid dynamos and seeks solutions to the coupled momentum and induction equations (Roberts 2007a).

For diffusionless processes in the core (Eq. 5) (infinite conductivity assumption) Alfvén’s wave equation describes one possible motion of magnetic field lines.

Inside the core there should be no perceivable Alfvén waves present as their amplitude vanishes at larger length scales. One special kind of such waves is an exceptional case termed torsional oscillations which work as an effect of the Coriolis force on the field lines (Gubbins and Roberts 1987).

Another exception challenging this assumption may be Aubert and Finlay (2019) who consider the geomagnetic jerks being a proof of localized Alfvén wave packets elevated to the CMB by sudden buoyancy variations inside the geodynamo.

Taylor in 1963 showed that the effect of the Lorentz force vanishes in the limit of rapid rotation (\(Ro \ll 1\) in Eq. (7)) over cylindrical surfaces around the rotational axis (Roberts 2007a). This is called the rotational dynamo constraint. Taylor also proved that under low viscosity conditions far from boundary layers in rotating systems columnar flows invariant to the axis of rotation (commonly referred to as Taylor columns) may prevail. Dumberry and Bloxham (2003) examined how effectively these laws could be at work in the Earth’s core. They suggested that Earth’s dynamo should be in a quasi-Taylor state where the rotational constraint can be considered valid except for torsional oscillations.

Magneto-Coriolis (MC) waves are another phenomena of the same fashion which quite possibly are an integral part of the operation of the geodynamo. They could be derived from the coupling of the momentum and the induction equations (Eqs. (7), (9)). As their propagation time and velocities indicate, a type of MC waves could be the reason for the detected geomagnetic westward drift (Hori et al. 2015).

A central problem of the MHD theory is associated with how the flow would behave in the presence of the nonlinearly acting Lorentz force (Busse 1977) as well as with an increasing flow velocity and a low viscosity (Zhang and Jones 1997; Guervilly et al. 2019). A steady flow assumption results in field generation taking place in current sheets of diminishing thickness. That implies more compact regions of field generation in more vigorous flows, which has been confirmed in many numerical computations (see below).

Formulated in e.g. Calkins (2018) the quasi-geostrophic (QG) assumption is an important practical approach to the MHD theory, attempting to describe a more realistic operation in the so-called rapidly rotating dynamic regime.

$$\partial_{t} \varvec{u}^{g} + \frac{1}{Ro}\hat{\varvec{z}} \times \varvec{u}^{a} = \frac{ - 1}{{Ro^{2} }}\nabla \left( {p^{a} } \right) + M\varvec{B}\nabla \varvec{B} + {{\Gamma }}\theta \hat{\varvec{z}} + \frac{1}{Re}\nabla^{2} \varvec{u}^{g}$$
(7)
$$\partial_{t} \theta = \nabla \left( {\varvec{u}\theta } \right) + \frac{1}{Pe}\nabla^{2} \theta$$
(8)
$$\partial_{t} \varvec{B} = \nabla \times \left( {\varvec{u} \times \varvec{B}} \right) + \frac{1}{Rm}\nabla^{2} \varvec{B}$$
(9)

Equations (7)–(9) are essentially the governing equations of the Oberbeck-Boussinesque approximation but keeping only the geostrophic parts in Eq. (7) except for the ageostrophic flow velocity \(\varvec{u}^{a}\) in the Coriolis-term and the pressure term (Gillet et al. 2011).

In formulas (7)–(9) the notation of other variables stand for \(\hat{\varvec{z}}\) the axial unit vector, \(p^{a}\) the (ageostrophic) pressure, \(\varvec{B}\) the magnetic induction vector, \(\theta\) the temperature.

The dimensionless numbers in Eqs. (7)–(9) are defined as follows:

$$Ro = \frac{U}{{2{{\Omega }}l}} \approx 10^{ - 6} - 10^{ - 7} ,\quad M = \frac{{B^{2} }}{{\rho \mu U^{2} }} \approx 10^{2} - 10^{5} ,\quad {\Gamma } = \frac{{g\alpha {{\Delta }}Tl}}{{U^{2} }} \approx 10^{5} - 10^{7} ,\quad Re = \frac{Ul}{\nu } \approx 10^{9} - 10^{11} , \quad Pe = \frac{Ul}{\kappa } \approx 1 - 10^{2} ,\quad Rm = \frac{Ul}{\eta } \approx 10^{2} - 10^{4}$$
(10)

\(Ro\) describes the ratio of the inertial and Coriolis forces, \(M\) is the ratio of manetic to kinetic energy density, \({{\Gamma }}\) is the buoyancy number which along with \(Re\) indicates a very vigorous convection (it can be related to the Rayleigh and Ekman numbers not used here, which are even higher). \(Re\) and \(Rm\) describe the ratio of inertial to viscous forces and magnetic induction to magnetic diffusion respectively, \(Pe\) represents the ratio of advective to diffusive heat transport rate. The ranges in Eq. (10) are given using the quantities (\(\rho ,\kappa ,{{\Delta }}T,\sigma\)) discussed in Sect. 2 and those featured in Davies et al. (2015), Gillet et al. (2010) and Finlay and Amit (2011). These numbers represent the uncertain information about the behavior of the geodynamo due to the high inaccuracies in the estimations of key physical parameters.

Gillet et al. (2011) argue that for SV time scales the QG assumption holds well in the core dynamo.

This formulation also has a very beneficial property, making it possible to essentially recover internal velocities when velocities at the boundary layer (CMB) are determined. On the other hand, it also implicitly assumes that those recovered velocities account for most of the field generation processes which may or may not be the case (Schaeffer et al. 2016).

Nonetheless, the approach led to most of today’s competing and promising geodynamo simulations.

The first dynamo simulation relevant for the geomagnetic field was the astrophysical 3D MHD simulation of Gilman and Miller (1981). Simulations intending to replicate specifically the processes inside the geodynamo were performed by Glatzmaier and Roberts (1995) and Kageyama and Sato (1995). These were significant milestones in acquiring relevant information on the geodynamo, as reproducing time variations of the main field such as westward drifting of the non-dipole field and polarity reversals came within reach. In Table 2, we listed some significant milestones since then in achieving more realistic and relevant simulations.

Table 2 More recent geodynamo simulations and their relevance with respect to the operation of the actual geodynamo
Full size table

Uncertainties and difficulties about inferencing the general state of Earth’s core field and the properties of the core were mentioned in the preceding sections. Here, many complications in acquiring information on geodynamo operation are described in short.

When solving Eq. (6) one should notice that there are two velocity components at each point on the CMB surface to compute for one corresponding \(B_{rCMB}\). Furthermore, motions along lines of \(B_{rCMB} = 0\) cannot be determined, as they yield no SV for a given epoch. Such a problem is severely ill-posed, and could have many equivalent solutions as shown by e.g. Bloxham (1989), Beggan and Whaler (2008). Non-uniqueness applies to geodynamo inferences using geodynamo simulations as well, attempts at alleviating such kind of difficulties were made by e.g. Aubert and Fournier (2011).

Recent simulations are slowly but firmly getting closer to replicating circumstances inside the actual geodynamo, yet they still have shortcomings in some aspects. It is uncertain when simulations could fully embrace the strongly time-dependent processes associated with the actual geodynamo (Zhang and Gubbins 2000), and somewhat curiously, the more they are scalable to Earth’s internal relations, the less frequently they tend to produce reversals (Takahashi et al. 2005). It is to be noted that the frequency of reversals and excursions may also depend on the boundary conditions of the system (see Sect. 2).

This is further complicated when deriving the scaling parameters of Eqs. (7)–(9), not only by having highly inaccurate values of key physical input parameters, but also by their orders of magnitude. In Sect. 2, estimations are listed and the corresponding dimensionless numbers are given in Eq. (10). As shown in Eq. (10), while being uncertain, values of the kinematic viscosity still put \(Pm = Rm/Re\sim1\) and \(Ek = \sqrt {Ro/Re}\) well in the range of \(\sim10^{15}\).

This feature of the hydromagnetic convection inside the geodynamo effectively prohibits accurate long-term (polarity reversal, century long forecast) predictions of the evolution of the geomagnetic field even beyond the current computational power (Hulot et al. 2010).

Another factor which arises with the uncertainties of these numbers is the question about the physical relevance of simulations, namely, whether the actual balance of forces is represented in the models (Schwaiger et al. 2019).

However, simulations do achieve significant amount of convergence to the Earth-like state (Aubert 2019), some even claiming to be in the so-called asymptotic regime (Aubert et al. 2017) (listed in Table 2)., In this case large-scale features of the MHD flow don’t change significantly with the growing vigorousness, and large-scale processes could perhaps be interpreted in simulation results without diverging from the actual solution characteristics in case of the Earth.

This is important to note since findings in simulations such as Kageyama et al. (2008) and Miyagoshi et al. (2011) featured in Table 1 could provide valuable information when inferring the actual field produced by the geodynamo.

We saw in Sect. 3 that geomagnetic field models could provide valid information on the core field for up to SH degree 14. This has implications when applying this truncation to the induction equation. It is estimated that neglecting the effect of small-scale flows and fields in influencing the field evolution has a larger impact on the precision of the solutions than neglecting field diffusion (Eymin and Hulot 2005; Pais and Jault 2008). This problem affects core surface flow solutions as well as inferences using simulations (Gillet et al. 2009; Matsui and Buffett 2013; Aubert 2019).

Last but not least, an obstacle arises when directly addressing any field generation process in the core which varies in time, due to the highly conductive medium in which it is embedded (see Sect. 2). This screening effect is a result of field diffusion in Eq. (4) and was addressed in detail by e.g. Bullard (1948) and Gubbins (1996). It effectively constrains the detectability of source signals based on their depth, spatial extension and the characteristic frequency of their time-variation. The effect can be characterized by a skin depth

$$\delta_{w} = \left( { \frac{{\tau_{Pj}^{l} }}{{\mu_{0} \sigma }}} \right)^{1/2}$$
(11)

where \(\tau_{Pj}^{l}\) is the poloidal decay time of the structure, related to its spatial scales (described by \(l, j\)). This generally means that significant spatially averaged information on a field generated deep within the core should originate only from a top ‘layer’ of a couple of hundreds of kilometres.

6 Introducing the concept of an equivalent source model

Gaining information on processes in the geodynamo and predicting its behavior has recently started to rely on the coupling noted in Sect. 5. This property of the QG approach allows the inference of the distribution of the internal parameters of the system from surface data (or, in general, interpolating them between sparse measurements) (Fournier et al. 2010). These parameters can then be fed back into the simulations for predictive modeling in a technique called data assimilation, originally used in meteorology (Talagrand 1997). The disadvantage of this technique lies in the instabilities of ensemble modelling and the complex statistical properties (covariances) of simulated parameters relied on during computations (Sanchez et al. 2018). In spite of these challenges, such predictive models already outperform simple extrapolations and show a reasonable decade-long accuracy in hindcasting (Aubert 2015).

One outcome of this review is that a comprehensive and detailed examination of source models for the geomagnetic core field is largely missing from the literature as well as current approaches and studies.

Simple source models of the main geomagnetic field have been investigated in the following works known to the authors (presented in chronological order):

Mayhew and Estes (1983) developed an equivalent source dipole technique for the sole purpose of comparing such models to the standard SH models of the main field. In their study, they fix the dipoles’ radial position or attitude and emphasize that the results cannot have an appropriate physical interpretation.

Langel (1987) examined the possibility of reconstructing Earth’s magnetic field by the superimposed fields of simple magnetic dipoles or current loops. He noted that the use of current loops was not perfect. In particular, he pointed out that any representation in terms of dipoles or current loops has an equivalent representation in terms of spherical harmonics, the initial placement of the dipoles or current loops had to be carefully chosen for the solution to properly converge, and any model solution would be non-unique (in an unconstrained case infinitely many sets of sources could produce the same surface field).

De Santis and Qamili (2010) constructed a magnetic monopole model for mapping the behavior of the South Atlantic anomaly but they did not explain how this physically unrealistic source can provide useful information about it.

Ladynin (2014) constructed a straightforward source model consisting of dipoles, though its simple estimation procedure (successively fitting the dipoles for the residuals) leaves a large room for equivalent solutions and renders the solution physically implausible.

Another outcome points to the issues emerging from these studies.

On one hand e the authors note that even though such models do not directly represent the true field generation processes, this is not to imply that they are unable to discover useful information related to them. A renewed interest in equivalent source approaches can help contributing to the current advances by independently constraining some important pieces of information in a relatively simple way. Carefully chosen a priori considerations of source models, probably coupled to estimations of the large-scale material flow and the magnetic diffusion of source fields, have the potential to provide valuable information and alleviate the shortcomings and limitations gathered in the previous sections, such as:

  1. (1)

    Allowing for a much simpler, straightforward insight than the less direct approach of inferences using complex simulations and statistical relations (see above).

  2. (2)

    Resulting in more accurate representations of fields produced by vigorous flows (see Sect. 5).

  3. (3)

    Yielding more constraints on how small-scale fields can be configured in the core (see Sect. 5) and how they can contribute to inaccuracies in the simulations as fields of larger spatial wavelengths than the cutoff degree.

  4. (4)

    Yielding more constraints on the magnitude and arrangement of toroidal magnetic fields in the core, which remain an important hidden factor in the field generation process (see Sect. 3).

  5. (5)

    Indirectly helping to resolve the issue related to the origin of disproportionately high magnetic energies in the core (see Sect. 2) by extending our understanding of the magnitude and configuration of the internal field.

  6. (6)

    Yielding constraints on some of the important physical parameters (see Sect. 2), e.g. the electrical conductivity, by validating in what magnitudes can currents be present in the core.

  7. (7)

    Mitigating the problem of uncertain dimensionless numbers (see Sects. 2 and 5) via constraining the dynamic regime in which the geodynamo can operate by selecting geometries for paths of currents resulting in the best fitting physically relevant solution.

  8. (8)

    Providing information on the regeneration mechanisms of the field inside the actual geodynamo in terms of identifying the main sources of the dynamo action (see Sect. 5) and paths of electric currents suitable for field regeneration (see Sect. 4), including the disputed relative importance of small-scale processes (see Sect. 5).

  9. (9)

    Providing insight into the magnitude and relative importance of field diffusion, and electromagnetic screening [see Eq. (11)], supposing that diffusion of the source field configuration is incorporated in a suitable way, such as in Metman et al. (2018).

On the other hand, it is acknowledged that even with well-defined constraints, the simplicity of sources models drafted above doesn’t necessarily transform the recovery-problem to a well-posed estimation.

Hence, inverse source modeling in this case leads to an implementation of machine learning methods: They aid in solving ill-posed problems without the need to explicitly include the complex relations between every source parameter and input field data in the estimation (Kim and Nakata 2018). Therefore, it is possible to search for only specific source parameters without ignoring the effects of others on the solution.

7 Preliminary test results

To demonstrate the abilities of such an algorithm in separating and recovering magnetic sources based on their fields recorded at a given surface, results of an estimation performed using synthetic data are presented here. The forward problem assumed 10 filamentary current loops of varying size and current intensity, positioned and aligned randomly within a spherical shell domain having the dimensions of Earth’s outer core. As additional a priori constraints, loops were not allowed to be located directly underneath each other and their surrounding medium was assumed to be a perfect insulator, meaning that in this simple case no diffusive effects were included (see Sect. 6).

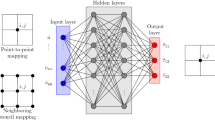
The program solves the inverse problem in two main stages: a deep learning based image segmentation and a genetic algorithm based parameter estimation. The main reason behind this dissection is computational efficiency and the optimization of neural network model accuracy in term of training set size.

Deep neural networks, such as U-Net are still most effective at addressing differentiable image processing problems with a network architecture and training set of limited size, such as segmentation and source detection. In this case that part of the solution yielded only the number and spatial arrangement of the synthetic sources. Genetic algorithms (GA) on the other hand can robustly recover the relatively high number of features (parameters) of a given source configuration (Haiping et al. 2019).

In the first phase, normalized logarithmic radial magnetic field data on the shell surface at a depth corresponding to that of the CMB (see Fig. 4 in the “Appendix”) were fed into a modified version of U-Net (Ronnenberger et al. 2015) as inputs. The network contained four layers with 64, 128, 256 and 512 channels respectively. This type of convolutional neural network architecture is generally used for image segmentation. It consists of two paths: a compression path for extracting features from the image and an expanding path upscaling the features by bilinear upsampling to produce the pixel-level segmentation. To achieve that, crops of the extracted features are copied from each stage of the first path to that of the second path.

The above implementation of the basic U-Net architecture was put to use here only for segmenting the geographic distribution of the sources given the input field. Training was carried out on an NVIDIA GeForce MX130 GPU using 100 input and ground truth images produced by synthetic field data of 5–15 randomly set-up current loops as sources.

Input CMB field data were sampled for segmentation into images containing 45 × 90 pixels using uniform sampling, resulting in a Mercator map of the spherical surface data. Besides, investigation of segmenting different projections is intended to establish how significantly polar distortions could be at play. With the growing number of layers in a network a less significant effect is expected. For stability reasons, U-Net was trained not for exactly pinpointing sources but for finding their approximate location using smoothed source maps such as the ground truth shown in Fig. 1.

Fig. 1
figure 1

True geographic positions of the synthetic current loops (left) and those recovered by U-Net (right) The color scale corresponds to the probability of source detection on the map. The asterisk marks a mismatching true and recovered source. (Color figure online)

Full size image

Estimating the surface component of source locations based on their ambient field given on that same surface can seem to be deceivingly simple, as dipolar source fields which are radially aligned can be well corresponded to a source position. In other cases though, the inversion becomes ill-conditioned (e.g. it becomes difficult to separate between one tilted source and two sources having magnetic moments perpendicular to the surface). As it appears in figures Figs. 1 and 4, the U-Net segmentation can overcome these difficulties along with clearly outlining sources at different depths (the source in the middle of Fig. 4 is much closer to the surface than all the others and therefore produces a much stronger signal). However, one source highlighted with an asterisk in Fig. 1 has a noticeably high positional error in the recovery. This means that despite the a priori constraints, not all equivalences can be eliminated, arising from the above ambiguities of the inversion (see Sect. 6). The authors suggest conducting further research in mitigating these issues.

Though now widely applied for image processing, for source separation, this architecture has exclusively been used on audio input signals (Meseguer-Brocal and Peeters 2019), thus being the first such application on images known to the authors.

After testing the trained network, the segmented source map was used to provide the GA the number of sources to recover and an initial surface distribution in the second phase. To do that, assignment of sources was carried out automatically by selecting local maxima on the segmented output image (see Fig. 1). Normalized CMB radial field data along with surface field component data were provided to the GA estimation as stable reference values in the loss function in order to fully recover the geometry, the current intensity and direction of each source.

The GA estimation was set with 16 populations having a 2% mutation rate, a 4% rate of exchange (migration) between randomly selected populations at every 10th iteration (Haiping et al. 2019) and a population size of 64 solutions. The above computation was performed in parallel execution using 16 CPUs and in this example took approximately 4 h to finish. The 4 h runtime consisted of 2000 consecutive iterations.

The two stages of the machine learning framework proposed here are described in more detail in Fig. 2.

Fig. 2
figure 2

Flowchart of the inversion framework featuring the two main phases

Full size image

Figure 3 presents the results of the full recovery: The actual and recovered current loops and their spatial positions inside the shell.

Fig. 3
figure 3

True (red) and recovered (blue) current systems in a synthetic computation within the southern and northern hemispheres of the spherical computational domain. The yellow sphere in the middle represents the inner core. Red arrows in the middle of the loops mark their orientations relative to the hypothetical north. (Color figure online)

Full size image

U-Net was built, trained and tested here using python’s neural network framework pytorch (Paszke et al. 2019) and the GA code was written in MATLAB (© 1994–2020 The MathWorks, Inc.).

8 Conclusions

An inquiry on the applicability of machine-learning based approaches in the research of the main geomagnetic field is proposed based on a summary of progress in terms of inferencing field generation processes of the geodynamo. For this purpose, a preliminary framework has been set up presenting the functionality of such a method on synthetic data with Earth-like geometric arrangement.