Skip to main content

Advertisement

SpringerLink
Log in

Numerical simulation and analysis of the Swift–Hohenberg equation by the stabilized Lagrange multiplier approach

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

Abstract

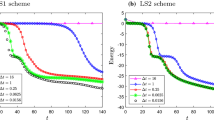
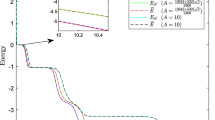
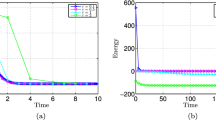
In this work, we develop linear, first- and second-order accurate, and energy-stable numerical scheme for the Swift–Hohenberg (SH) equation. An auxiliary variable (Lagrange multiplier) is used to control the nonlinear term so that the linear temporal scheme can be easily constructed. To further achieve the accuracy with large time steps, a proper stabilized term is adopted. For the first-order time-accurate scheme, the backward Euler approximation is adopted. The Crank–Nicolson (CN) and explicit Adams–Bashforth (AB) approximations are applied to achieve temporally second-order accuracy. We analytically perform the estimations of the semi-discrete solvability, the energy stability with respect to the original and pseudo-energy functionals, and the convergence error. To numerically solve the resulting discrete system of equations, we use an efficient linear multigrid method. We present various two- (2D) and three-dimensional (3D) computational examples to demonstrate the accuracy and energy stability of the proposed scheme.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  • Abbaszadeh M, Khodadadian A, Parvizi M, Dehghan M, Heitzinger C (2019) A direct meshless local collocation method for solving stochastic Cahn-Hilliard-Cook and stochastic Swift-Hohenberg equations. Eng Anal Bound Elem 98:253–264

    Article  MathSciNet  Google Scholar 

  • Christov CI, Pontes J (2002) Numerical scheme for Swift-Hohenberg equation with strict implementation of Lyapunov functional. Math Comput Model 35:87–99

    Article  MathSciNet  Google Scholar 

  • Church JM, Guo Z, Jimack PK, Madzvamuse A, Promislow K, Wetton B, Wise SM, Yang F (2019) High accuracy benchmark problems for Allen-Cahn and Cahn-Hilliard dynamics. Commun Comput Phys 26:947–972

    Article  MathSciNet  Google Scholar 

  • Dehghan M, Abbaszadeh M (2017) The meshless local collocation method for solving multi-dimensional Cahn-Hilliard, Swift-Hohenberg and phase field crystal equations. Eng Anal Bound Elem 78:49–64

    Article  MathSciNet  Google Scholar 

  • Dong L, Wang C, Zhang H, Zhang Z (2020) A positivity-preserving second-order BDF scheme for the Cahn-Hilliard equation with variable interfacial parameters. Commun Comput Phys 28:967–998

    Article  MathSciNet  Google Scholar 

  • Elder KR, Viñals J, Grant M (1992) Ordering dynamics in the two-dimensional stochastic Swift–Hohenberg equation. Phys Rev Lett 68:3024–3027

    Article  Google Scholar 

  • Feng W, Guo Z, Lowengrub JS, Wise SM (2018) A mass-conservative adaptive FAS multigrid solver for cell-centered finite difference methods on block-structured locally-cartesian grids. J Comput Phys 352:463–497

    Article  MathSciNet  Google Scholar 

  • Gao Y, Li R, Mei L, Lin Y (2020) A second-order decoupled energy stable numerical scheme for Cahn-Hilliard-Hele-Shaw system. Appl Numer Math 157:338–355

    Article  MathSciNet  Google Scholar 

  • Gomez H, Nogueira X (2012) A new space-time discretization for the Swift-Hohenberg equation that strictly respects the Lyapunov functional. Commun Nonlinear Sci Numer Simul 17:4930–4946

    Article  MathSciNet  Google Scholar 

  • Guillén-González F, Tierra G (2013) On linear schemes for the Cahn-Hilliard diffuse interface model. J Comput Phys 234:140–171

    Article  MathSciNet  Google Scholar 

  • Haken H (1983) Advanced synergetics. Springer, Berlin

    Book  Google Scholar 

  • Hutt A, Atay FM (2005) Analysis nonlocal neural fields for both general and gamma-distributed connectivities. Physica D 203:30–54

    Article  MathSciNet  Google Scholar 

  • Kim J, Kang K, Lowengrub J (2004) Conservative multigrid methods for the Cahn-Hilliard fluids. J Comput Phys 193:511–543

    Article  MathSciNet  Google Scholar 

  • Kudryashov NA, Sinelshchikov DI (2012) Exact solutions of the Swift–Hohenberg equation with dispersion. Commun Nonlinear Sci Numer Simul 17:26–34

    Article  MathSciNet  Google Scholar 

  • Lee HG (2017) A semi-analytical Fourier spectral method for the Swift-Hohenberg equation. Comput Math Appl 74:1885–1896

    Article  MathSciNet  Google Scholar 

  • Lee HG (2019) An energy stable method for the Swift-Hohenberg equation with quadratic-cubic nonlinearity. Comput Methods Appl Mech Engrg 343:40–51

    Article  MathSciNet  Google Scholar 

  • Li H, Ju L, Zhang C, Peng Q (2018) Unconditionally energy stable linear schemes for the diffuse interface method with Peng-Robinson equation of state. J Sci Comput 75:993–1015

    Article  MathSciNet  Google Scholar 

  • Li N, Lin P, Gao G (2019) Energy law preserving finite element scheme for the Cahn-Hilliard equation with dynamic boundary conditions. Commun Comput Phys 26:1490–1509

    Article  MathSciNet  Google Scholar 

  • Liu H, Yin P (2019) Unconditionally energy stable DG scheme for the Swift-Hohenberg equation. J Sci Comput 81:789–819

    Article  MathSciNet  Google Scholar 

  • Nikolay NA, Ryabov PN (2016) Analytical and numerical solutions of the generalized dispersive Swift-Hohenberg equation. Appl Math Comput 286:171–177

    MathSciNet  MATH  Google Scholar 

  • Sarmiento AF, Espath LFR, Vignal P, Dalcin L, Parsani M, Calo VM (2018) An energy-stable generalized-\(\alpha \) method for the Swift-Hohenberg equation. J Comput Appl Math 344:836–851

    Article  MathSciNet  Google Scholar 

  • Shivanian E, Abbasbandy S (2020) Pseudospectral meshless radial point interpolation for generalized biharmonic equation in the presence of Cahn-Hilliard conditions. Comput Appl Math 39:148

    Article  MathSciNet  Google Scholar 

  • Staliunas K, Sánchez-Morcillo VJ (1998) Dynamics of phase domain in the Swift–Hohenberg equation. Phys Lett A 241:28–34

    Article  Google Scholar 

  • Su J, Fang W, Yu Q, Li Y (2019) Numerical simulation of Swift-Hohenberg equation by the fourth-order compact scheme. Comput Appl Math 38:54

    Article  MathSciNet  Google Scholar 

  • Swift J, Hohenberg PC (1977) Hydrodynamic fluctuation at the convective instability. Phys Rev A 15:319–328

    Article  Google Scholar 

  • Viñals J, Hernández-Garca E, San MM, Toral R (1991) Numerical study of the dynamical aspects of pattern selection in the stochastic Swift–Hohenberg equation in one dimension. Phys Rev A 44:1123–1133

    Article  Google Scholar 

  • Wise S, Kim J, Lowengrub J (2007) Solving the regularized, strongly anisotropic Cahn-Hilliard equation by an adaptive nonlinear multigrid method. J Comput Phys 226:414–446

    Article  MathSciNet  Google Scholar 

  • Xi H, Viñals J, Gunton JD (1991) Numerical solution of the Swift–Hohenberg equation in two dimensions. Phys A 177:356–365

    Article  Google Scholar 

  • Xu Z, Yang X, Zhang H, Xie Z (2019) Efficient and linear schemes for anisotropic Cahn-Hilliard model using the Stabilized-Invariant Energy Quadratization (S-IEQ) approach. Comput Phys Commun 238:36–49

    Article  MathSciNet  Google Scholar 

  • Yang X (2016) Linear, first and second order and unconditionally energy stable numerical schemes for the phase field model of homopolymer blends. J Comput Phys 327:294–316

    Article  MathSciNet  Google Scholar 

  • Yang J, Kim J (2020) An unconditionally stable second-order accurate method for systems of Cahn-Hilliard equations. Commun Nonlinear Sci Numer Simulat 87:105276

    Article  MathSciNet  Google Scholar 

  • Yang X, Zhang G (2020) Convergence analysis for the Invariant Energy Quadratization (IEQ) schemes for solving the Cahn-Hilliard and Allen-Cahn equations with general nonlinear potential. J Comput Sci 82:55

    Article  MathSciNet  Google Scholar 

  • Zhang J, Yang X (2019) Numerical approximations for a new \(L^2\)-gradient flow based phase field crystal model with precise nonlocal mass conservation. Comput Phys Commun 243:51–67

    Article  MathSciNet  Google Scholar 

  • Zhu G, Kou J, Sun S, Yao J, Li A (2019) Numerical approximation of a phase-field surfactant model with fluid flow. J Sci Comput 80:223–247

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The corresponding author (J.S. Kim) was supported by Korea University Grant. The authors thank the reviewers for constructive and helpful comments on the revision of this article.

Author information

Authors and Affiliations

  1. School of Computer Science and Engineering, Sun Yat-sen University, Guangzhou, 510275, China

    Junxiang Yang

  2. Department of Mathematics, Korea University, Seoul, 02841, Republic of Korea

    Junseok Kim

Authors
  1. Junxiang Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Junseok Kim
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Junseok Kim.

Additional information

Communicated by Frederic Valentin.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, J., Kim, J. Numerical simulation and analysis of the Swift–Hohenberg equation by the stabilized Lagrange multiplier approach. Comp. Appl. Math. 41, 20 (2022). https://doi.org/10.1007/s40314-021-01726-w

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40314-021-01726-w

Keywords

Mathematics Subject Classification

Search

Navigation