Skip to main content
SpringerLink
Log in

Riemann–Hilbert problems of a six-component fourth-order AKNS system and its soliton solutions

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

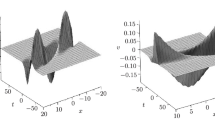
Abstract

Associated with a \(4\times 4\) matrix spectral problem, a six-component AKNS soliton hierarchy is presented, together with the first three nonlinear soliton systems. From an equivalent spectral problem, a kind of Riemann–Hilbert problems is formulated for a six-component system of fourth-order AKNS equations in the resulting AKNS hierarchy. Soliton solutions to the considered system of coupled fourth-order AKNS equations are worked out from a reduced Riemann–Hilbert problem where an identity jump matrix is taken.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Ablowitz MJ, Clarkson PA (1991) Solitons, nonlinear evolution equations and inverse scattering. Cambridge University Press, Cambridge

    Book  Google Scholar 

  • Ablowitz MJ, Kaup DJ, Newell AC, Segur H (1974) The inverse scattering transform-Fourier analysis for nonlinear problems. Stud Appl Math 53:249–315

    Article  MathSciNet  Google Scholar 

  • Belokolos ED, Bobenko AI, Enol’skii VZ, Its AR, Matveev VB (1994) Algebro-geometric approach to nonlinear integrable equations. Springer, Berlin

    MATH  Google Scholar 

  • Chen ST, Zhou RG (2012) An integrable decomposition of the Manakov equation. Comput Appl Math 31:1–18

    Article  MathSciNet  Google Scholar 

  • Doktorov EV, Leble SB (2007) A dressing method in mathematical physics. Mathematical physics studies, vol 28. Springer, Dordrecht

  • Dong HH, Zhao K, Yang HW, Li YQ (2015) Generalised \((2+1)\)-dimensional super MKdV hierarchy for integrable systems in soliton theory. East Asian J Appl Math 5:256–272

    Article  MathSciNet  Google Scholar 

  • Dong HH, Guo BY, Yin BS (2016) Generalized fractional supertrace identity for Hamiltonian structure of NLS-MKdV hierarchy with self-consistent sources. Anal Math Phys 6:199–209

    Article  MathSciNet  Google Scholar 

  • Drinfeld VG, Sokolov VV (1982) Equations of Korteweg–de Vries type, and simple Lie algebras. Sov Math Dokl 23:457–462

    Google Scholar 

  • Fokas AS, Lenells J (2012) The unified method: I. Nonlinearizable problems on the half-line. J Phys A Math Theor 45:195201

    Article  MathSciNet  Google Scholar 

  • Freeman NC, Nimmo JJC (1983) Soliton solutions of the Korteweg–de Vries and Kadomtsev–Petviashvili equations: the Wronskian technique. Phys Lett A 95:1–3

    Article  MathSciNet  Google Scholar 

  • Geng XG, Wu JP (2016) Riemann–Hilbert approach and N-soliton solutions for a generalized Sasa–Satsuma equation. Wave Motion 60:62–72

    Article  MathSciNet  Google Scholar 

  • Gerdjikov VS (2005) Geometry, integrability and quantization. In: Mladenov IM, Hirshfeld AC (eds) Proceedings of the 6th international conference (Varna, June 3–10, 2004). Softex, Sofia, pp 78–125

  • Gesztesy F, Holden H (2003) Soliton equations and their algebro-geometric solutions: \((1+1)\)-dimensional continuous models. Cambridge University Press, Cambridge

    Book  Google Scholar 

  • Guo M, Fu C, Zhang Y, Liu JX, Yang HW (2018) Study of ion-acoustic solitary waves in a magnetized plasma using the three-dimensional time-space fractional Schamel–KdV equation. Complexity 2018:6852548. https://doi.org/10.1155/2018/6852548

  • Hirota R (2004) The direct method in soliton theory. Cambridge University Press, New York

    Book  Google Scholar 

  • Hu BB, Xia TC, Ma WX (2018) Riemann–Hilbert approach for an initial-boundary value problem of the two-component modified Korteweg–de Vries equation on the half-line. Appl Math Comput 332:148–159

    MathSciNet  Google Scholar 

  • Kawata T (1984) Riemann spectral method for the nonlinear evolution equation. In: Advances in nonlinear waves, vol I. Research Notes in Mathematics, vol 95. Pitman, Boston, pp 210–225

  • Lax PD (1968) Integrals of nonlinear equations of evolution and solitary waves. Commun Pure Appl Math 21:467–490

    Article  MathSciNet  Google Scholar 

  • Ma WX (1992a) A new hierarchy of Liouville integrable generalized Hamiltonian equations and its reduction. Chin Ann Math Ser A 13:115–123

    MathSciNet  MATH  Google Scholar 

  • Ma WX (1992b) A new hierarchy of Liouville integrable generalized Hamiltonian equations and its reduction. Chin J Contemp Math 13:79–89

    MathSciNet  Google Scholar 

  • Ma WX (1995) Symmetry constraint of MKdV equations by binary nonlinearization. Phys A 219:467–481

    Article  MathSciNet  Google Scholar 

  • Ma WX (2002) Complexiton solutions to the Korteweg–de Vries equation. Phys Lett A 301:35–44

    Article  MathSciNet  Google Scholar 

  • Ma WX (2009) Variational identities and applications to Hamiltonian structures of soliton equations. Nonlinear Anal Theory Methods Appl 71:e1716–e1726

    Article  MathSciNet  Google Scholar 

  • Ma WX (2011) Generalized bilinear differential equations. Stud Nonlinear Sci 2:140–144

    Google Scholar 

  • Ma WX (2018a) Conservation laws by symmetries and adjoint symmetries. Discrete Contin Dyn Syst Ser S 11:707–721

    MathSciNet  MATH  Google Scholar 

  • Ma WX (2018b) Riemann–Hilbert problems and N-soliton solutions for a coupled mKdV system. J Geom Phys 132:45–54

    Article  MathSciNet  Google Scholar 

  • Ma WX, Chen M (2006) Hamiltonian and quasi-Hamiltonian structures associated with semi-direct sums of Lie algebras. J Phys A Math Gen 39:10787–10801

    Article  MathSciNet  Google Scholar 

  • Ma WX, Fuchssteiner B (1996) Integrable theory of the perturbation equations. Chaos Solitons Fractals 7:1227–1250

    Article  MathSciNet  Google Scholar 

  • Ma WX, You Y (2005) Solving the Korteweg–de Vries equation by its bilinear form: Wronskian solutions. Trans Am Math Soc 357:1753–1778

    Article  MathSciNet  Google Scholar 

  • Ma WX, Zhou RG (2002) Adjoint symmetry constraints leading to binary nonlinearization. J Nonlinear Math Phys 9(Suppl 1):106–126

    Article  MathSciNet  Google Scholar 

  • Ma WX, Zhou Y (2018) Lump solutions to nonlinear partial differential equations via Hirota bilinear forms. J Differ Equ 264:2633–2659

    Article  MathSciNet  Google Scholar 

  • Ma WX, Xu XX, Zhang YF (2006) Semi-direct sums of Lie algebras and continuous integrable couplings. Phys Lett A 351:125–130

    Article  MathSciNet  Google Scholar 

  • Ma WX, Yong XL, Qin ZY, Gu X, Zhou Y (2016a) A generalized Liouville’s formula. Preprint

  • Ma WX, Zhou Y, Dougherty R (2016b) Lump-type solutions to nonlinear differential equations derived from generalized bilinear equations. Int J Mod Phys B 30:1640018

    Article  MathSciNet  Google Scholar 

  • Ma WX, Yong XL, Zhang HQ (2018) Diversity of interaction solutions to the \((2+1)\)-dimensional Ito equation. Comput Math Appl 75:289–295

    Article  MathSciNet  Google Scholar 

  • Magri F (1978) A simple model of the integrable Hamiltonian equation. J Math Phys 19:1156–1162

    Article  MathSciNet  Google Scholar 

  • Manakov SV (1974) On the theory of two-dimensional stationary self-focusing of electromagnetic waves. Sov Phys JETP 38:248–253

    Google Scholar 

  • Matveev VB (1992) Generalized Wronskian formula for solutions of the KdV equations: first applications. Phys Lett A 166:205–208

    Article  MathSciNet  Google Scholar 

  • Matveev VB, Salle MA (1991) Darboux transformations and solitons. Springer, Berlin

    Book  Google Scholar 

  • Novikov SP, Manakov SV, Pitaevskii LP, Zakharov VE (1984) Theory of solitons: the inverse scattering method. Consultants Bureau, New York

    MATH  Google Scholar 

  • Satsuma J, Ablowitz MJ (1979) Two-dimensional lumps in nonlinear dispersive systems. J Math Phys 20:1496–1503

    Article  MathSciNet  Google Scholar 

  • Shchesnovich VS (2002) Perturbation theory for nearly integrable multicomponent nonlinear PDEs. J Math Phys 43:1460–1486

    Article  MathSciNet  Google Scholar 

  • Shchesnovich VS, Yang J (2003) General soliton matrices in the Riemann–Hilbert problem for integrable nonlinear equations. J Math Phys 44:4604–4639

    Article  MathSciNet  Google Scholar 

  • Tu GZ (1989) The trace identity, a powerful tool for constructing the Hamiltonian structure of integrable systems. J Math Phys 30:330–338

    Article  MathSciNet  Google Scholar 

  • Wang DS, Zhang DJ, Yang J (2010) Integrable properties of the general coupled nonlinear Schrödinger equations. J Math Phys 51:023510

    Article  MathSciNet  Google Scholar 

  • Wang XR, Zhang XE, Zhao PY (2014) Binary nonlinearization for AKNS-KN coupling system. Abstr Appl Anal 2014:253102. https://doi.org/10.1155/2014/253102

    Article  MathSciNet  Google Scholar 

  • Xiao Y, Fan EG (2016) A Riemann–Hilbert approach to the Harry-Dym equation on the line. Chin Ann Math Ser B 37:373–384

    Article  MathSciNet  Google Scholar 

  • Xu XX (2010) An integrable coupling hierarchy of the \(\text{ MKdV }_-\) integrable systems, its Hamiltonian structure and corresponding nonisospectral integrable hierarchy. Appl Math Comput 216:344–353

    MathSciNet  MATH  Google Scholar 

  • Yu J, Zhou RG (2006) Two kinds of new integrable decompositions of the mKdV equation. Phys Lett A 349:452–461

    Article  MathSciNet  Google Scholar 

  • Zhang Y, Dong HH, Zhang XE, Yang HW (2017) Rational solutions and lump solutions to the generalized \((3 +1)\)-dimensional shallow water-like equation. Comput Math Appl 73:246–252

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The work was supported also in part by the 111 project of China (B16002), the China state administration of foreign experts affairs system under the affiliation of North China Electric Power University, Natural Science Fund for Colleges and Universities of Jiangsu Province under the grant 17KJB110020, and the Distinguished Professorships by Shanghai University of Electric Power, China and North-West University, South Africa. The author would also like to thank S. Batwa, X. Gu, X.Z. Hao, S. Manukure, M. Mcanally, Y.L. Sun, F.D. Wang, H. Wang, X.L. Yong, H.Q. Zhang and Y. Zhou for their valuable discussions.

Author information

Authors and Affiliations

  1. Department of Mathematics, Zhejiang Normal University, Jinhua, 321004, Zhejiang, China

    Wen-Xiu Ma

  2. Department of Mathematics and Statistics, University of South Florida, Tampa, FL, 33620-5700, USA

    Wen-Xiu Ma

  3. College of Mathematics and Systems Science, Shandong University of Science and Technology, Qingdao, 266590, Shandong, China

    Wen-Xiu Ma

  4. College of Mathematics and Physics, Shanghai University of Electric Power, Shanghai, 200090, China

    Wen-Xiu Ma

  5. Department of Mathematical Sciences, International Institute for Symmetry Analysis and Mathematical Modelling, North-West University, Mafikeng Campus, Private Bag X2046, Mmabatho, 2735, South Africa

    Wen-Xiu Ma

Authors
  1. Wen-Xiu Ma
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wen-Xiu Ma.

Additional information

Communicated by Pierangelo Marcati.

The work was supported in part by NSFC under the Grants 11371326, 11301331 and 11371086; and NSF under the Grant DMS-1664561.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ma, WX. Riemann–Hilbert problems of a six-component fourth-order AKNS system and its soliton solutions. Comp. Appl. Math. 37, 6359–6375 (2018). https://doi.org/10.1007/s40314-018-0703-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40314-018-0703-6

Keywords

Mathematics Subject Classification

Search

Navigation