Closed Loop Guidance During Close Range Rendezvous in a Three Body Problem

Abstract

The paper presents a novel application of the State Dependent Riccati Equation (SDRE) guidance approach with state constraints for a chaser spacecraft in the close proximity of a passive target. The dynamics are described by full 6 degree of freedom rigid-body relative motion. The final trajectory is defined by a passively safe approaching cone, which acts as path constraint and follows the attitude motion of target. A Near Rectilinear Halo Orbit in the Earth-Moon system is the selected rendezvous scenario to fully validate the proposed solution, even though the parameters related to the constraints and weighting functions are kept as general as possible, thus applicable to other similar missions.

Introduction

In the past few years there has been an increased interest in space exploration. In particular, the International Space Exploration Roadmap was proposed in February 2018 [1] indicating, as objectives, a permanent return to the Moon, and unmanned and manned missions to Mars.

Within this context, an international effort is undergoing to plan a mission to the Moon consisting in a target space station located in a near rectilinear halo orbit (NRHO) about the L2 Lagrangian points of the Earth - Moon system, and a lunar lander equipped with a rover collecting lunar samples and bringing them back to the station, to later be returned to Earth [2]. There are many advantages in using a NRHO, such as stability of the orbit with low $\Delta V$ for station-keeping, continuous visibility from Earth for communications, low periselene altitude, etc. However rendezvous and berthing dynamics and control require in depth study primarily because of the non Keplerian environment the vehicles will move in, where classical control strategies based on linearized two-body dynamics no longer apply.

The rendezvous mission considered here consists of a series of orbital maneuvers and controlled trajectories, which successively bring the active vehicle (chaser) close and eventually into contact with the passive vehicle (target). The complexity of the rendezvous approach results from the multitude of conditions and constraints that must be fulfilled. The target station may impose safety zones, approach-trajectory corridors and hold points along the way to verify the chaser’s trajectory accuracy, and to switch between appropriate sensor suites. Any dynamic state (position and velocities, attitude and angular rates) of the chaser vehicle outside the nominal limits of the approach trajectory could lead to collision with the target, a situation dangerous for crew and vehicle integrity [3].

The problem of control of rendezvous dynamics in Earth’s orbit has been studied since the 1960s’ [4, 5] and performed in the past, starting with the Apollo program, the historical 1975 Apollo - Soyuz mission, and occurring at the present time with the activities related to the international space station. While long range rendezvous and phasing are generally automated, most of the close range rendezvous is still performed manually [6, 7]. Traditionally, rendezvous and proximity operations are performed using open-loop maneuver planning techniques, and ad hoc error corrections. Examples of constrained maneuvers include the thrust magnitude constraints, constraints on the approaching spacecraft to maintain its position within a Line-of-Sight (LOS) cone emanating from the docking port on the target platform, and constraints on the terminal translation velocity for soft-docking are proposed for instance in [8,9,10].

From a guidance and control standpoint, several methods can be found in the literature. Some of the studies use terminal sliding mode control, which enables a time-fixed process with the flight prescribed a priori [11]. A fixed-time glideslope guidance algorithm on a quasi-periodic halo orbit can be found in [12]. Another interesting reference on guidance algorithms for low Earth orbit (LEO) is [13], where linear optimal regulator control combined with proportional navigation was proposed. Hartley and coworkers applied model predictive control techniques for a Keplerian rendezvous [14]. An application of H-infinity control can be found in [5], which shows good performance for the case of elliptic orbit, provided linearization bounds are maintained.

A State Dependent Riccati Equation (SDRE) method provides a systematic approach for solving the infinite horizon optimal control of nonlinear systems, avoiding the solution of the associated Hamilton-Jacobi-Bellman partial differential equation, generally unpractical. The technique guarantees local stability and optimality, robustness with respect to non-modeled dynamics and uncertainties, as well as real time implementation. SDRE effectiveness has been proven extensively on a wide variety of applications, see [15] for instance. The method has been also used for relative motion control in a classical two-body scenarios with good results in the control of translation-attitude coupling [16, 17]. The paper proposes and verifies a State Dependent Riccati Equation technique as an effective approach to the close range rendezvous in a three-body problem, with particular reference to the future Artemis program. To the authors’ knowledge, this is a novel application due to the nature of the underlying dynamics, except perhaps for the work in [18], where the authors proved the efficiency of SDRE for a station-keeping and reorientation for formation flight in a Sun - Earth scenario, with solar pressure perturbations.

The paper is organized as follow: the mathematical model of relative motion of two spacecraft is provided in Sect. 2. Section 3 describes the motion constraints introduced in the State Dependent Riccati Equation general algorithm. The guidance structure for the problem and numerical examples are presented in Sect. 4 and conclusions in Sect. 5.

Equations of Motion

This section summarizes the relative motion dynamics in the restricted three body problem. More details can be found in [19] and [20], among others. Although general in nature, the application in the paper will be based on the proposed Lunar Orbital Platform Gateway (LOP-G) consisting of a a space station in a lunar NRHO orbit, and a Lunar Ascent Element (LAE) returning from the Moon for berthing with the station. They will be also referred to as target and chaser respectively. The chaser spacecraft is the only actively controlled element.

Relative Translation

Let us consider two spacecraft performing a rendezvous maneuver. The two spacecraft are subjected to the gravitational action of the two primary bodies (in this case Earth and Moon).

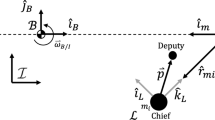
The relative motion between the two vehicles is described with respect to a widely used reference system $\mathcal {L}: \begin{Bmatrix}\mathbf {R}_t; \hat{\mathbf {i}},\hat{\mathbf {j}}, \hat{\mathbf {k}} \end{Bmatrix}$, local-vertical local-horizon (LVLH), which is appropriate for control design, with the unit vector defined as follows:

$$\begin{aligned} \hat{\mathbf {i}} = \hat{\mathbf {j}} \times \hat{\mathbf {k}},\quad \hat{\mathbf {j}} = -\frac{\mathbf {h}_{t/m}}{h_{t/m}}, \quad \hat{\mathbf {k}} = -\frac{\mathbf {r}_{mt}}{r_{mt}} \end{aligned}$$

(1)

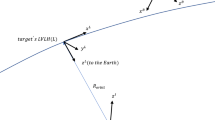
where $\mathbf {r}_{mt}$ is the target position with respect to the Moon-centered rotating frame, with magnitude $r_{mt} = ||\mathbf {r}_{mt}||$, $\mathbf {h}_{t/m} = \mathbf {r}_{mt} \times \left[ \dot{\mathbf {r}}_{mt} \right] _{\mathcal {M}}$ is the target angular momentum with respect to the Moon, with magnitude $h_{t/m} = ||\mathbf {h}_{t/m}||$. In general, the unit vectors $\hat{\mathbf {i}}, \hat{\mathbf {j}},\hat{\mathbf {k}}$ are also known as V-bar, H-bar e R-bar (strictly speaking defined only for Keplerian motion). Note that if we introduce the $\mathcal {M}: \begin{Bmatrix}\mathbf {R}_m; \hat{\mathbf {i}}_m,\hat{\mathbf {i}}_m, \hat{\mathbf {i}}_m \end{Bmatrix}$ frame centered in the center of mass of Moon, the unit vectors $\hat{\mathbf {i}}_m -\hat{\mathbf {j}}_m$ lie in the moon orbital plane:

$$\begin{aligned} \hat{\mathbf {i}}_m = -\frac{\mathbf {r}_{em}}{r_{em}}, \quad \hat{\mathbf {j}}_m = \hat{\mathbf {k}}_m \times \hat{\mathbf {i}}_m,\quad \hat{\mathbf {k}}_m = -\frac{\mathbf {h}_{m/e}}{h_{m/e}}, \end{aligned}$$

(2)

Also, $\mathbf {r}_{em}$ is the Moon position with respect to the Earth, $r_{em} = ||\mathbf {r}_{em}||$, $\mathbf {h}_{m/e} = \mathbf {r}_{em} \times \left[ \dot{\mathbf {r}}_{em} \right] _{\mathcal {I}}$ is the specific angular momentum of the Moon with respect to the Earth, and $h_{m/e} = ||\mathbf {h}_{m/e}||$. The equations describing the dynamics of the relative position between the two spacecraft, in the LVLH frame, are taken from [19] and are shown below:

Fig. 1

Reference frames

$$\begin{aligned} \begin{aligned} \begin{bmatrix} \ddot{\varvec{\rho }}\end{bmatrix}_{\mathcal {L}} + 2\varvec{\omega }_{l/i} \times \begin{bmatrix} \dot{\varvec{\rho }} \end{bmatrix}_{\mathcal {L}} + \begin{bmatrix} \dot{\varvec{\omega }}_{l/i} \end{bmatrix}_{\mathcal {L}} \times \varvec{\rho } + \varvec{\omega }_{l/i} \times \left( \varvec{\omega }_{l/i} \times \varvec{\rho } \right) = \mu _m \left( \frac{\mathbf {r}_{mt}}{r_{mt}^3} - \frac{\mathbf {r}_{mc}}{r_{mc}^3} \right) + \mu _e \left( \frac{\mathbf {r}_{et}}{r_{et}^3} - \frac{\mathbf {r}_{ec}}{r_{ec}^3} \right) \end{aligned} \end{aligned}$$

(3)

Referring to Fig. 1a we have:

$$\begin{aligned} \mathbf {r}_{mc} = \mathbf {r}_{mt} + \varvec{\rho },\quad \mathbf {r}_{et} = \mathbf {r}_{mt} + \mathbf {r}_{em}, \quad \mathbf {r}_{ec} = \mathbf {r}_{et} + \varvec{\rho } \end{aligned}$$

In Eq. (3) we have the relative position $\varvec{{\rho }}$, and its derivatives with respect to the LVLH frame; the angular velocity $\mathbf {\omega }_{l/i}$ of the LVLH frame with respect to the inertial frame, and the target and chaser positions with respect to the Moon-centered frame $\mathbf {r}_{mt}$, $\mathbf {r}_{mc}$, respectively.

The proposed target orbit is shown in Fig. 2, with the average period of 7 days, and aposelene and periselene distances of 70,000 km and 6,000 Km, respectively.

Fig. 2

NRHO target orbit

The close range rendezvous and berthing are assumed to occur during aposelene passage for safety reasons, since the target’s velocity is the lowest, this also allows for the simplification of the equations. In this case in fact, the approximation of the primary bodies revolving in circular orbits, (Circular Restricted Three-Body Problem CR3BP assumption) appears appropriate [21]. With this assumption, the number of time-varying parameters in Eq. (3) reduce. Indeed $\mathbf {r}_{em}$ is constant, ${\omega }_{m/i} = n \hat{\mathbf {k}}_m$ and $\left[{\omega}_{m/i} \right] _{\mathcal M} = {0}$. The use of equations derived from CR3BP, while still nonlinear, allows the reduction of variables with respect to the elliptical case. In fact for target information we only need: $\mathbf{r}_{mt}, \left[ \mathbf{r}_{mt} \right]_{\mathcal L}$.

Relative Attitude

In the study of rendezvous operations, during long range approach, the translational motion is considered sufficient to describe the relative distance propagation and even the design of a reference trajectory. As the chaser moves near the target, attitude and attitude rates dynamics and control become of paramount importance for the safety of the maneuver as well as the precision required during the final phase (be that either berthing or docking). The procedure adopted here consists of a separate computation of chaser and target attitude, since the latter is undergoing passive motion [22].

Chaser Attitude

The chaser spacecraft (LAE) is the part of the lander, and will depart the Moon’s surface once the ground operations are complete. It is assumed to be cylindrical, and its side view is depicted in Fig. 3. Its preliminary configuration can be found in [23].

Fig. 3

Chaser side view

With reference to the body fixed frame $\mathcal {C}$ shown in Fig. 1c, which has the origin in the center of mass of the rigid chaser spacecraft and axes parallel to the principal axes of inertia, the attitude dynamics are given by:

$$\begin{aligned} \mathbb {I}\dot{\varvec{\omega }} + \varvec{\omega } \times \mathbb {I}\varvec{\omega } = \mathbf {N} \end{aligned}$$

(4)

where $\mathbf {N}$ is torque vector, $\mathbb {I}$ is the inertia matrix and $\varvec{\omega }$ is the angular velocity of the rotating frame. Note that $\varvec{\omega }$ is defined with respect to the inertial frame, and it can be computed as:

$$\begin{aligned} \varvec{\omega } = \varvec{\omega }_{c/i} = \varvec{\omega }_{c/l} + \varvec{\omega }_{l/i} \end{aligned}$$

where $\varvec{\omega }_{c/l}$ is the angular velocity of chaser with respect to $\mathcal {L}$ and $\varvec{\omega }_{l/i}$ is the angular velocity of $\mathcal {L}$ with respect to inertial frame. The kinematic motion can be described by standard Euler angles and by means of quaternions as well. In this work the following definition was used: $q_1 =\cos (\frac{\theta }{2})$, $q_i =e_i \sin (\frac{\theta }{2})$ with $i = 2,3,4$; where $\mathbf {e} = \left[ e_2,\; e_3,\; e_4 \right] ^\top$ is the Euler rotation eigenaxis and $\theta$ is the rotation angle around $\mathbf {e}$. The differential relationship between quaternions and angular velocity is given by:

$$\begin{aligned} \begin{aligned} \dot{\mathbf {q}}_{c/l}&= \frac{1}{2} \begin{bmatrix} 0 &{} -\varvec{\omega }_{c/l}^\top \\ \varvec{\omega }_{c/l} &{} - [\varvec{\omega }_{c/l}]^\times \end{bmatrix} \mathbf {q}_{c/l}\\&=\frac{1}{2}\mathbf {Q}(\varvec{\omega }_{c/l})\mathbf {q}_{c/l} \end{aligned} \end{aligned}$$

(5)

with $\mathbf {q}_{c/l}$ the quaternion that describes the relative attitude between $\mathcal {C}$ and $\mathcal {L}$, and $[\cdot ]^\times$ denotes the operator that transforms a vector into the associated antisymmetric matrix. The set of differential equations given by Eqs. (4) and (5) provide the nonlinear attitude model of chaser [24].

Target Attitude

For the target’s attitude we take as reference the international space station (ISS) dynamics, which is attitude controlled using a two sided limit cycle controller, and has a sawtooth profile. This motion can be modelled as an harmonic oscillator [22] and described in Eq. (6) below using quaternion formulation:

$$\begin{aligned} \begin{bmatrix} \dot{\mathbf {q}}_{t/l} \\ \dot{\varvec{\omega }}_{t/l} \end{bmatrix} = \begin{bmatrix} \frac{1}{2}\mathbf {Q}(\varvec{\omega }_{t/l}) &{} \varvec{0}_{4 \times 3} \\ -\mathbf {K}_{qt} &{} \varvec{0}_{3 \times 3} \end{bmatrix} \begin{bmatrix} \mathbf {q}_{t/l} \\ \varvec{\omega }_{t/l} \end{bmatrix} \end{aligned}$$

(6)

where $\mathbf {q}_{t/l}$ is the quaternion that describes the attitude of target body frame with respect to LVLH, $\dot{\mathbf {q}}_{t/l}$ is the time derivative of quaternion, $\varvec{\omega }_{t/l}$ is the angular velocity of target with respect to LVLH frame; $\dot{\varvec{\omega }}_{t/l}$ is the angular acceleration of target with respect to LVLH frame, $\mathbf {Q}(\cdot )$ is the matrix that relates the time derivative of the quaternion with the angular velocity, and $\mathbf {K}_{qt}$ is a diagonal matrix containing the eigen frequency for each axis. Note that the fixed target frame is defined similarly to that of the chaser (Fig. 1c).

Relative Attitude

The relative attitude between two rotating objects is based on the difference of the respective angular velocities expressed in an appropriate frame [22]. In this case the difference is expressed in the $\mathcal {C}$ reference:

$$\begin{aligned} \varvec{\omega }_{c/t} = \varvec{\omega }_{c/l} - \mathbf {R}_{cl}(\mathbf {q_{c/l}}) \varvec{\omega }_{t/l} \end{aligned}$$

(7)

$\mathbf {R}_{cl}(\mathbf {q_{c/l}})$ is the matrix that transforms the components of a vector from frame $\mathcal {L}$ to frame $\mathcal {C}$.

$$\begin{aligned} \mathbf {R}_{cl}(\mathbf {q}_{c/l}) = \begin{bmatrix} 1 - 2(q_3^2 + q_4^2) &{} 2(q_2 q_3 + q_1 q_4) &{} 2(q_2 q_4 - q_1 q_3) \\ 2(q_2 q_3 - q_1 q_4) &{} 1 - 2(q_2^2 + q_4^2) &{} 2(q_3 q_4 + q_1 q_2) \\ 2(q_2 q_4 + q_1 q_3) &{} 2(q_3 q_4 - q_1 q_2) &{} 1 - 2(q_2^2 + q_3^2) \end{bmatrix} \end{aligned}$$

(8)

Once the relative angular velocity $\varvec{\omega }_{c/t}$ has been determined, we can compute the derivative of the associated quaternion as: $\dot{\mathbf {q}}_{c/t} = \frac{1}{2}\mathbf {Q}(\varvec{\omega }_{c/t})\mathbf {q}_{c/t}$.

Control Synthesis

As described in the introduction, the SDRE methodology is used to synthesize of a closed loop guidance in the final berthing phase of the mission. A short review of the methodology is described below for clarity’s sake. The reader can refer to [15] and [25], for more details. The next section specializes the general structure to the specific problem addressed by the paper.

Consider a nonlinear regulator problem that minimizes the following quadratic cost function:

$$\begin{aligned} J(\mathbf{x} , \mathbf{u} ) = \frac{1}{2}\int _{0}^{\infty }\left( \mathbf{x} ^\top \mathbf{Q} (\mathbf{x} )\mathbf{x} + \mathbf{u} ^\top \mathbf{R} (\mathbf{x} )\mathbf{u} \right) \,dt \end{aligned}$$

(9)

subjected to nonlinear differential constraints affine in the control of the form:

$$\begin{aligned} \dot{\mathbf{x }} = \mathbf {f(x)} + \mathbf {g(x)} \mathbf {u} \end{aligned}$$

(10)

where $\mathbf {x} \in \mathbb {R}^{n}$ is the system’s state vector (see later for the present application), $\mathbf {u} \in \mathbb {R}^{m}$ is the control vector, $\mathbf {f}: \mathbb {R}^{n} \rightarrow \mathbb {R}^{n}$, $\mathbf {g} \ne \varvec{0}$ $\forall \mathbf {x} \in \mathbb {R}^{n}$; $\mathbf {Q}(\mathbf {x}) \ge 0$ and $\mathbf {R}(\mathbf {x}) > 0$ are the weight matrices of the state vector and the input vector respectively. If the dynamics of the system in Eq. (10) can be written in a pseudo-linear form by the introduction of a State Dependent Coefficient (SDC) as:

$$\begin{aligned} \dot{\mathbf {x}} = \mathbf {A(x)} \mathbf {x} + \mathbf {B(x)} \mathbf {u} \end{aligned}$$

(11)

with state and input matrices functions of the state, then the SDRE control method assumes the form of a LQR-like controller and can be summarized in the following two steps:

• 1. solve the associated state dependent algebraic Riccati equation:

  $$\begin{aligned} \mathbf {A}^\top (\mathbf {x})\mathbf {P}(\mathbf {x}) + \mathbf {P}(\mathbf {x})\mathbf {A}(\mathbf {x}) - \mathbf {P}(\mathbf {x})\mathbf {B}(\mathbf {x})\mathbf {R}^{-1}(\mathbf {x})\mathbf {B}^\top (\mathbf {x})\mathbf {P}(\mathbf {x}) + \mathbf {Q}(\mathbf {x}) \end{aligned}$$

  (12)

• 2. compute the nonlinear state feedback control law, which assumes a full state feedback form:

  $$\begin{aligned} \mathbf {u} = -\mathbf {R}^{-1}(\mathbf {x})\mathbf {B}^\top (\mathbf {x})\mathbf {P}(\mathbf {x})\mathbf {x} \end{aligned}$$

  (13)

In order to obtain a valid solution $\mathbf {P}(\mathbf {x})$ of the algebraic Riccati equation, the pair$\begin{Bmatrix}\mathbf {A}(\mathbf {x});\mathbf {B}(\mathbf {x})\end{Bmatrix}$ must be pointwise stabilizable in the linear sense [15].

• Motion Constraints

The rendezvous maneuvers can be performed by imposing constraints on the relative position and relative velocity of the two spacecraft when they are approaching, especially in the final phase of the rendezvous. This can be incorporated in the general SDRE design as well.

Consider the system described by Eq. (10), with initial conditions $\mathbf {x(0)} = \mathbf {x}_{0} \in \Omega$ and a set of allowable states defined by:

$$\begin{aligned} \Omega = \begin{Bmatrix} \mathbf {x}:\mathbf {l(x)} \le \varvec{0}, \mathbf {l(x)} \in \mathbb {R}^{p}, \mathbf {l(\cdot )} \in C^{1} \end{Bmatrix} \end{aligned}$$

(14)

it is possible to design a controller such that the closed loop system is stable and $\mathbf {x}$ does not exceed $\partial \Omega$, the boundary of $\Omega$, defined by:

$$\begin{aligned} \partial \Omega = \begin{Bmatrix} \mathbf {x}:\mathbf {l(x)} = \varvec{0}, \mathbf {l(x)} \in \mathbb {R}^{p}, \mathbf {l(\cdot )} \in C^{1} \end{Bmatrix} \end{aligned}$$

(15)

The sufficient condition for $\mathbf {x}$ to remain in $\Omega$ is $\nabla \mathbf {l(x)}\dot{\mathbf {x}}=0$. The controller that satisfies these conditions forces the trajectories of the closed loop system to follow the level curves of the $\Omega$ set. Incorporating the constraint as a quadratic term, the cost function becomes:

$$\begin{aligned} J(\mathbf {x}, \mathbf {u}) &{} = J_{0}(\mathbf {x}, \mathbf {u}) + J_{\Omega }(\mathbf {x}, \mathbf {u}) = \\ &{} = \frac{1}{2}\int _{0}^{\infty }\left( \mathbf{x} ^\top \mathbf{Q} (\mathbf{x} )\mathbf{x} + \mathbf{u} ^\top \mathbf{R} (\mathbf{x} )\mathbf{u} \right) \,dt + \frac{1}{2}\int _{0}^{\infty }\left( \mathbf {z}^\top \mathbf {W}_{z}(\mathbf {x})\mathbf {z}\right) \,dt \end{aligned}$$

(16)

The second term on the RHS of the cost function introduces the constraints, and can be represented by the fictitious output $\mathbf {z}$, defined as follow:

$$\begin{aligned} \mathbf {z} = \nabla \mathbf {l(x)} \begin{bmatrix} \mathbf {A(x)}\mathbf {x} + \mathbf {B(x)} \mathbf {u} \end{bmatrix} = \mathbf {C(x)}\mathbf {x} + \mathbf {D(x)} \mathbf {u} \end{aligned}$$

(17)

$\mathbf {W}_z$ is a $p \times p$ matrix, selected such that its i-th element has a large value when $\mathbf {x}$ is near the border of the i-th constraint and small elsewhere. This means that in the cost function the component expressed by $J_{\Omega }(\mathbf {x}, \mathbf {u})$ is predominant with respect to $J_{0}(\mathbf {x}, \mathbf {u})$ when the state does not respect the constraint, and becomes negligible when the constraint is satisfied [16].

In cases when $\nabla \mathbf {l(x)}$ is orthogonal to $\mathbf {B(x)}$, the term $\mathbf {D(x)} = \varvec{0}$. An alternative way of choosing $\mathbf {W}_{z}(\mathbf {x})$ is then to penalize the state, that is the i-th element of the weight assumes a large value when we are in a region of the state space to be penalized and zero otherwise [25].

With the introduction of state constraints, the control law becomes:

$$\begin{aligned} \mathbf {u} = - \mathbf {K}(\mathbf {x})\mathbf {x} = -\begin{bmatrix}\mathbf {K}_{0}(\mathbf {x}) + \mathbf {K}_{\Omega }(\mathbf {x})\end{bmatrix}\mathbf {x} \end{aligned}$$

(18)

where

$$\begin{aligned} \mathbf {K}_{0}(\mathbf {x}) = \bar{\mathbf {R}}^{-1}(\mathbf {x})\mathbf {B}(\mathbf {x})\bar{\mathbf {P}}(\mathbf {x}) \qquad \mathbf {K}_{\Omega }(\mathbf {x}) = \bar{\mathbf {R}}^{-1}(\mathbf {x})\mathbf {D}^{T}(\mathbf {x})\mathbf {W}_{z}(\mathbf {x})\mathbf {C}(\mathbf {x}) \end{aligned}$$

(19)

For the purpose of the present work, the assumption of full state availability was made, when deriving the control law in Eq. (18), that is relative position and rate vectors, attitude quaternions, and angular rate.

If full state is not available to the controller, a discrete state estimate can be considered referring to the work in [26], and improved in [27], in order to avoid possible loss of observability due to the size of selected time intervals. Recalling [27], we consider a stochastic nonlinear system of the form:

$$\begin{aligned} \begin{aligned} \dot{\mathbf{x }} = \mathbf {f(x)} + \mathbf {D} \mathbf {w}\\ \mathbf {y(x)} = \mathbf {h(x)} + \mathbf {v}\ \end{aligned} \end{aligned}$$

(20)

where $\mathbf {w}$ is a Gaussian zero-mean white noise associated with the process, $\mathbf {v}$ is a Gaussian zero-mean measurement noise. By means of Euler’s discretization, with step $\mathbf {T}_{s}$, we have $\mathbf {A}_{k}=\mathbf {I}^{n}+\mathbf {T}_{s}{A}(\hat{x}_{k})$, and $\mathbf {H}_{k}=\mathbf {H}(\hat{x}_{k})$.Where $\mathbf {A}(.)$ is one possible SDC parametrization of a continuous system and $\mathbf {H}(.)$ is a possible SDC parametrization for the output of the system in Eq. (20). The nonlinear discrete time system can be viewed as a frozen-in-time linear equation. Traditionally, there are two formulations of the discrete SDRE estimator based on Kalman filter. Here we use the two-step recursive update (see [27] for details).

SDRE Guidance Law

The general SDRE controller defined in Eqs. (11), (16) and (18) is now detailed in terms of problem specific state dependent coefficient (SDC) parametrization [15], and the definition of state constraints. Numerical results of the SDRE closed loop guidance applied to the cis-lunar rendezvous will be then presented and discussed in the next section.

SDC Parametrization for Translation

The equations of relative motion described by Eq. (3), can be parametrized since all the conditions of existence are guaranteed. Note that the nonlinearities of the system are due to gravitational terms. The term that takes into account the gravitational attraction due to the Moon can be rewritten as follows:

$$\begin{aligned} \mu _m \left( \frac{\mathbf {r}_{mt}}{r_{mt}^3} - \frac{\mathbf {r}_{mc}}{r_{mc}^3} \right) = \begin{bmatrix} -\frac{\mu _m}{r_{mc}^3} &{}0 &{}0 \\ 0&{} -\frac{\mu _m}{r_{mc}^3} &{}0 \\ \gamma _m x &{} \gamma _m y &{} \gamma _m (z - r_{mt}) - \frac{\mu _m}{r_{mc}^3} \end{bmatrix} \varvec{\rho } = \mathbf {A}_m\mathbf {(x)} \varvec{\rho } \end{aligned}$$

(21)

the gravitational attraction due to the Earth is given by:

$$\begin{aligned} \mu _e&\left( \frac{\mathbf {r}_{mt} + \mathbf {r}_{em}}{|| \mathbf {r}_{mt} + \mathbf {r}_{em} ||^3} - \frac{\mathbf {r}_{mt} + \mathbf {r}_{em} +\varvec{\rho }}{|| \mathbf {r}_{mt} + \mathbf {r}_{em} +\varvec{\rho } ||^3} \right) = \mathbf {A}_e\mathbf {(x)} \varvec{\rho } = \nonumber \\&\begin{bmatrix} \gamma _e r_{em}^{\kern 0.1500 em x} (2 r_{em}^{\kern 0.1500 em x} + x) - \frac{\mu _e}{r_{ec}^3} &{} \gamma _e r_{em}^{\kern 0.1500 em x} (2 r_{em}^{\kern 0.1500 em y} + y) &{} \gamma _e r_{em}^{\kern 0.1500 em x} (2 (r_{em}^{\kern 0.1500 em z} - r_{mt}) + z)\\ \gamma _e r_{em}^{\kern 0.1500 em y} (2 r_{em}^{\kern 0.1500 em x} + x) &{} \gamma _e r_{em}^{\kern 0.1500 em y} (2 r_{em}^{\kern 0.1500 em y} + y) - \frac{\mu _e}{r_{ec}^3} &{} \gamma _e r_{em}^{\kern 0.1500 em y} (2 (r_{em}^{\kern 0.1500 em z} - r_{mt}) + z)\\ \gamma _e (r_{em}^{\kern 0.1500 em z} - r_{mt}) (2 r_{em}^{\kern 0.1500 em x} + x) &{} \gamma _e (r_{em}^{\kern 0.1500 em z} - r_{mt}) (2 r_{em}^{\kern 0.1500 em y} + y) &{} \gamma _e (r_{em}^{\kern 0.1500 em z} - r_{mt}) (2 (r_{em}^{\kern 0.1500 em z} - r_{mt}) + z) - \frac{\mu _e}{r_{ec}^3} \end{bmatrix} \varvec{\rho } \end{aligned}$$

(22)

where $\varvec{\rho } = \left[ x \; y \; z \right] ^\top$, $\mathbf {r}_{mt} = \left[ 0\; 0\; -r_{mt} \right] ^\top$, $\mathbf {r}_{mc} = \left[ x \; y \; z-r_{mt} \right] ^\top$, $\mathbf {r}_{em} = \left[ r_{em}^x \; r_{em}^y \; r_{em}^z \right] ^\top$, and

$$\begin{aligned} \begin{aligned} \gamma _m = -\mu _m \frac{(r_{mc}^2 + r_{mt}r_{mc} + r_{mt}^2)}{(r_{mc} + r_{mt})(r_{mc}^3 r_{mt}^2)}, \quad \gamma _e = \mu _e\frac{(r_{ec}^2 + r_{et}r_{ec} + r_{et}^2)}{(r_{ec} + r_{et})(r_{ec}^3 r_{et}^3)} \end{aligned} \end{aligned}$$

The complete parameterization of the relative motion, Eq. (3), becomes:

$$\begin{aligned} \mathbf {A(x)} = \begin{bmatrix} {0}_{3 \times 3} &{} \mathbf {I}_{3 \times 3} \\ -\left[ {\dot\Omega }_{l/i}\right]_{\mathcal L} - \Omega _{l/i}^2 + \mathbf {A}_m\mathbf {(x)} + \mathbf {A}_e\mathbf {(x)} &{} -2 \Omega _{l/i} \end{bmatrix}, \quad \mathbf {B(x)} = \begin{bmatrix} {0}_{3 \times 3} \\ \mathbf {I}_{3 \times 3} \end{bmatrix} \end{aligned}$$

(23)

$\mathbf {x} = \left[ {\rho } \; \dot{\varvec{\rho }} \right] ^\top$ is the state vector, $\left[ {\dot\Omega }_{l/i}\right]_{\mathcal L}$ and $\Omega _{l/i}$ denote the antisymmetric matrices associated to $\left[ {\omega }_{l/i}\right]_{\mathcal L}$ and $\omega _{l/i}$, respectively.

SDC Parametrization for Attitude

Similarly, it is possible to derive a SDC parameterization for the dynamics and kinematics of the chaser’s attitude (see Eqs. (4), and (5)). The parameterization was taken from [28].

$$\begin{aligned} \begin{bmatrix} \frac{\epsilon }{2} &{} 0 &{} 0 &{} 0 &{} -\frac{q_2}{2} &{} -\frac{q_3}{2} &{} -\frac{q_4}{2} \\ 0 &{} \frac{\epsilon }{2} &{} 0 &{} 0 &{} \frac{q_1}{2} &{} -\frac{q_4}{2} &{} \frac{q_3}{2} \\ 0 &{} 0 &{} \frac{\epsilon }{2} &{} 0 &{} \frac{q_4}{2} &{} \frac{q_1}{2} &{} -\frac{q_2}{2} \\ 0 &{} 0 &{} 0 &{} \frac{\epsilon }{2} &{} -\frac{q_3}{2} &{} \frac{q_2}{2} &{} \frac{q_1}{2} \\ a_{11}\frac{q_1}{\mathbf {q}^T\mathbf {q}} &{} a_{11}\frac{q_2}{\mathbf {q}^T\mathbf {q}} &{} a_{11}\frac{q_3}{\mathbf {q}^T\mathbf {q}} &{} a_{11}\frac{q_4}{\mathbf {q}^T\mathbf {q}} &{} 0 &{} 0 &{} 0 \\ a_{12}\frac{q_1}{\mathbf {q}^T\mathbf {q}} &{} a_{12}\frac{q_2}{\mathbf {q}^T\mathbf {q}} &{} a_{12}\frac{q_3}{\mathbf {q}^T\mathbf {q}} &{} a_{12}\frac{q_4}{\mathbf {q}^T\mathbf {q}} &{} 0 &{} 0 &{} 0 \\ a_{13}\frac{q_1}{\mathbf {q}^T\mathbf {q}} &{} a_{13}\frac{q_2}{\mathbf {q}^T\mathbf {q}} &{} a_{13}\frac{q_3}{\mathbf {q}^T\mathbf {q}} &{} a_{13}\frac{q_4}{\mathbf {q}^T\mathbf {q}} &{} 0 &{} 0 &{} 0 \end{bmatrix} \end{aligned}$$

(24)

where $\epsilon = -0.0001$ is a small constant added to the spacecraft quaternion kinematics for numerical reasons in the solution of algebraic Riccati equation. Notice that the addition of $\epsilon$ correction is only an artifact since the quaternions parameters represent only three independent parameters The coefficients $a_{ij}$ are:

$$\begin{aligned} \left[ a_{11},\, a_{12},\, a_{13} \right] ^\top = -\, \mathbb {I}^{-1} \left( \varvec{\omega }_{c/t} \times \mathbb {I}\varvec{\omega }_{c/t}\right) \end{aligned}$$

Constraints and Keep-out-Zone

In the final phase and proximity operations of the rendezvous, the chaser should approach the target from a direction bound by a safety zone for collision avoidance mitigation. Typical constraints for close range are selected as spheres of a given radius (for instance in the Heracles-ESA mission the rendezvous sphere has a 10 Km radius, the approach sphere 2 Km, and the keep-out-zone 0.2 Km, respectively). In this work a simpler cone-like final approach corridor is considered as in [9].

Fig. 4

Approaching cone constraint

Figure 4 shows a qualitative constraint illustration, in which $\mathbf {p}$ is the unit vector of the path direction, and $\beta$ is the maximum cone angle of the corridor and the main design parameter. The constraint geometry is rewritten using Eq. (14) formalism and becomes:

$$\begin{aligned} l(\mathbf {x}) = -\left[{\rho }^\top \right]_{\mathcal T} \cdot \left[ \mathbf {p} \right]_{\mathcal T} + ||{\rho }||_{\mathcal T} \cos {\beta } \le 0 \end{aligned}$$

(25)

where $\mathbf {x} = \left[ {\rho }^\top ,\, \dot{{\rho }}^\top ,\, \mathbf {q}_{c/l}^\top ,\, {\omega }_{c/l}^\top \right] ^\top$ is the system’s state vector. The constraint is represented as a fictitious output as in Eq. (17) expressed in a target $\mathcal {T}$ frame so, as we can see from Eq. (25), the direction of cone axis depends on target’s attitude.

Note that in our case $\nabla l(\mathbf {x}) \bot \mathbf {B}(\mathbf {x})$, so the weight function $\mathbf {W}_z$ was selected to penalize the state when it is far from the imposed constraint. In other words, we chose the weight function that depends on the 3D distance between the chaser’s center of mass and the line described by the unit vector $\mathbf {p}$. In this way, $\mathbf {W}_z$ has a large value when the chaser’s center of mass is far from the cone axis and small value when it is close to, as mentioned earlier.

Results

In this section, numerical simulations are presented to validate the proposed method. The target moves on a NRHO and we simulate rendezvous maneuvers both at the aposelene, as well as in the worst case condition, i.e. close to periselene. Table 1 summarizes the initial conditions. We assume that the attitude motion of the target has a maximum amplitude of 5$^{\circ }$ and the eigen-frequency of Eq. (6) is equal to $k_{qt} = {0.1571}~\text {rad}\, \mathrm {s}^{-1}$ [3]. The chaser is is modeled as a cylinder with inertia matrix $\mathbb {I} = diag(0.0011, 0.0006, 0.0006)$ $kg \cdot km^2$ [20]. The direction vector of the approaching cone is $\left[ \mathbf {p} \right]_{\mathcal T} = \left[ -1,\, 0,\, 0 \right] ^\top$ and the maximum cone angle is set to $\beta =$ 25$^{\circ }$.

Table 1 Initial conditions

The main equations used for motion propagation are those relative to the circular restricted three body problem. For better numerical stiffness the equations are normalized as in [29]; the distances are normalized to the Moon’s orbit semi-major axis, the time in units of the inverse mean motion of the NRHO orbit, and the masses are expressed such as $M_e +M_m =1$. The terminal conditions selected for the tests are $\rho$ $\le$ 1 m for relative position, and $\dot{\rho }$ $\le$ 0.03 m/s for relative velocity. Note that for ESA’s ATV mission concept [30] the constraints were 20 m in relative position, and 0.01 m/s for relative velocity [3]. Simulations were run using Simulink^TM, the guidance and navigation algorithm runs at 1 Hz, and the Dorman-Price integration algorithm was used.

Aposelene Approach

The aposelene is considered the most feasible area for the docking/berthing. Current literature indicates that as the most likely location, and it has been shown that CR3P equations are sufficiently accurate for the dynamic description of the relative motion [6, 21]. In this case, the target has the slowest orbital velocity. The docking/berthing zone is indicated in red in Fig. 2.

The SDRE controller was tested by means of a limited Montecarlo simulation for six different relative distances $\rho ={5, 8, 11, 14, 17, 20}$ Km. For each $\rho$, 20 random uniformly distributed points were selected.

The weighting matrices coefficients used for the translation are:

$$\begin{aligned} \mathbf {Q}_0 = \begin{bmatrix} \mathbf {Q}_p &{} \varvec{0}_{3 \times 3} \\ \varvec{0}_{3 \times 3} &{}3 \cdot \mathbf {I}_{3 \times 3} \end{bmatrix} \qquad \mathbf {Q}_p = 12 \cdot \begin{bmatrix} 10^{5} &{} 0 &{} 0 \\ 0 &{} 10^{6} &{} 0 \\ 0 &{} 0 &{} 10^{5} \end{bmatrix} \end{aligned}$$

(26)

$$\begin{aligned} \mathbf {R}_0 = 10^{-9} \cdot \mathbf {I}_{3 \times 3} \end{aligned}$$

(27)

The constraint matrix depends on distance between cone axis and chaser, and is set as follow:

$$\begin{aligned} \mathbf {W}_{z} = 5 \cdot 10^{4} \cdot \mathbf {f}_{axis}(x,y,z) \end{aligned}$$

(28)

where $\mathbf {f}_{axis}(x,y,z)$ is the classical formula that defines the distance of one point from line in 3D space. All weights were selected by trial and error in order to maximize the accuracy and minimize the control effort.

The position is assumed to be an available measurement, so $\mathbf {H}(\mathbf {x}) = \begin{bmatrix} \mathbf {I}_{3 \times 3} \quad \varvec{0}_{3 \times 3} \end{bmatrix}$. The measurement error is considered as purely random with Gaussian distribution, zero mean and standard deviation $\sigma = 1/3 \times 10^{-2}$ m [16]. The process error model is based on [31], and is considered as purely random with Gaussian distribution, zero mean and standard deviation $\sigma = 1/3 \times 10^{-6}$ $Km/s^2$. The control weighting matrices are the same as in Eq. (27), and the process noise and measurement covariance matrices are given by:

$$\begin{aligned} \mathbf {Q}_f = \begin{bmatrix} \varvec{0}_{3 \times 3} &{} \varvec{0}_{3 \times 3} \\ \varvec{0}_{3 \times 3} &{} 10^{-12}\cdot \mathbf {I}_{3 \times 3} \end{bmatrix} \qquad \mathbf {R}_f = 0.6768 \cdot 10^{-21} \cdot \mathbf {I}_{3 \times 3} \end{aligned}$$

(29)

The initial condition for the error covariance matrix is given by:

$$\begin{aligned} \mathbf {P}_f^0 = \begin{bmatrix} 2.6015 \cdot 10^{-10} \cdot \mathbf {I}_{3 \times 3} &{} \varvec{0}_{3 \times 3} \\ \varvec{0}_{3 \times 3} &{} 0.9820\cdot 10^{-5}\cdot \mathbf {I}_{3 \times 3} \end{bmatrix} \qquad \end{aligned}$$

(30)

The filter initial conditions are:

$$\begin{aligned} \mathbf {x}_f^0 = \mathbf {x}^0 + \begin{bmatrix} \xi _p \\ \xi _v \end{bmatrix} \end{aligned}$$

where $\mathbf {x}^0$ is the real relative position and velocity of chaser, $\xi _p$ and $\xi _v$ are $3 \times 1$ vectors of uniformly distributed random numbers, in the interval (0, 10) [cm] and (0, 1) [cm/s], respectively.

The performance analysis was based on normalized values of position error, error rate and amount of control, over the time of flight period.

$$\begin{aligned} Ie_\rho = \int _{0}^{t_{of}} ||\mathbf {e}_\rho (t) || \, dt \qquad Ie_{\dot{\rho }} = \int _{0}^{t_{of}} ||\mathbf {e}_{\dot{\rho }}(t)|| \, dt \qquad \delta _{v} = \int _{0}^{t_{of}} ||\mathbf {u}_ || \, dt \end{aligned}$$

(31)

where $\mathbf {e}_\rho (t)$, $\mathbf {e}_{\dot{\rho }}(t)$, $\delta _{v}$ are the error vectors respectively between real position and estimated position, real velocity and estimated velocity, and equivalent propellant consumption. Figure 5 shows the relative position between chaser and target from the Montecarlo simulation.

Fig. 5

Relative position, aposelene approach

The time of flight and control effort are shown in Figs. 6 and 7.

Fig. 6

Time of flight vs distance, aposelene approach

Fig. 7

Control effort vs distance, aposelene approach

Table 2 Error indices for aposelene approach

As we can see from Figs. 6 and 7, the total control effort $\delta _{v}$ and time of flight $t_{of}$ increase with increasing relative distance, as expected. In addition, the linearity in Fig. 6 confirms the feasibility of aposelene approach in terms of validity of the equations of motion.

When the chaser initial conditions are not inside the LOS cone and the relative distance is less than 15 Km, the chaser moves very slowly as it reaches the approach corridor. The corresponding standard deviation could be reduced by increasing the number of tests. The average errors in position and rate, between real and estimated values, are shown in Table 2.

To evaluate the attitude behavior at the aposelene, we consider a sample trajectory from those simulated above and shown in Fig. 8. The rendezvous maneuver lasts about 2 hours starting from relative distance of about 11 Km. The results in terms of $\Delta V$ expenditure compare favorably with the results in [32], where different thrust allocation algorithms were used, and the results in [33], where continuous thrust was implemented using the adjoint method.

Fig. 8

Chaser relative trajectory for attitude analysis

For the selected example, the control forces and torques are shown in Figs. 9 and 10, respectively.

Fig. 9

Control effort (torques)

Fig. 10

Control effort (forces)

The large initial values depend on the fact that the chaser is controlling both its translation and rotation, the coupling is noticeable especially along the z axis, with the oscillatory behavior of the z force component. The control amount could be tuned further by changing the weights in the optimization. The angular behavior in terms of quaternions and angular rates is shown in the next figures (See Fig. 11). Figure 9 shows the target and chaser quaternions, while the time histories of chaser and target angular velocities are shown in Fig. 12.

Fig. 11

Attitude quaternions in the LVLH frame

Fig. 12

Angular velocities in the chaser’s body frame

The weighting strategy used to satisfy the constraint imposes a severe penalty on velocity, due to the orthogonality of $\nabla \mathbf {l(x)}\perp \mathbf {B(x)}$. As matter of fact we have initially a high velocity in R-bar and then, when the chaser reaches the axis of the approaching cone, the R-bar component decreases and the V-bar velocity has a plateau, with the chaser moving towards the target.

Periselene Approach

A rendezvous at the periselene of the NRHO orbit is not considered practical for several reasons: first of all the target vehicle is at its maximum speed, thus making the safety requirements very critical and too restrictive, secondly to maintain a desired relative position and velocity, the requirements on $\Delta$V could be too high for the mission. Thirdly the circular restricted three body problem may lose accuracy during propagation. This case is then used only for the purpose of evaluating the behavior of the proposed guidance in a worst case scenario.

The approach zone at the periselene is shown in red in Fig. 13.

Fig. 13

Target orbit at periselene

The Montecarlo simulations were performed with the same parameters used for the aposelene approach. The propagation equations are based on the elliptical restricted three body problem. The resulting trajectories, time of flight, and control effort are shown in Figs. 14, 15, and 16, respectively.

The most significant difference between the two cases is the increase of control amount required to perform the rendezvous at periselene, as suspected. Table 3 shows very similar errors in position and a slightly increase in rate error for the periselene approach. An interesting comparison is shown in Fig. 17. On the left a zoomed set of trajectories obtained using the ER3BP are shown (taken from Fig. 14), while on the right the trajectories are computed using the CR3BP equations. This indicates that the CR3BP equations could be sufficient for the relative motion description, see Table 4. Figure 18 shows the influence of the gain in the weighting matrix $\mathbf{W} _z$ described in Eq. (28). The higher the gain and the faster the trajectory moves towards a rectilinear $V-bar$ path (figure to the right). The numerical values for the two cases are shown in Tables  5 and 6, respectively.

Fig. 14

Relative position, periselene approach

Fig. 15

Time of flight versus distance, Periselene approach

Fig. 16

Control usage versus distance, Periselene approach

Table 3 Error indices for Periselene approach

Fig. 17

Comparison between ER3BP (left) and CR3BP (right) solutions at Periselene

Table 4 Time of flight and control effort difference between ER3BP and CR3BP

Fig. 18

Influence of gain on the weighting Matrix W, low gain (left), high gain (right)

Table 5 Low gain data

Table 6 High gain data

Conclusions

The paper presents a State Dependent Riccati Equation approach to closed loop guidance with state constraints. The technique is applied in a rendezvous scenario between two spacecraft around the Moon in a NRHO environment, due to nonlinear nature of the relative dynamics. The constraints are formulated as a conic area that depends on the target’s attitude, so the chaser’s center of mass must follow the complete target’s motion. Although simulations are based on a somewhat limited Montecarlo analysis, the method provides successful control and feasible $\Delta V$ requirements at the aposelene, and also a satisfactory behavior at the periselene, with additional control effort. The weighting selection on the constraints allows the designer to modify the trajectory in order to acquire quickly a desired $V-bar$ direction, which appears to be desirable in standard rendezvous maneuvers. The mission scenario used for the synthesis is based on current information on the lunar gateway study, thus the numerical data could be subjected to variations in the future, as well as the computational requirements of SDRE, with respect to mission design.