1 Introduction

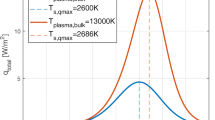
The gas metal arc welding (GMAW) process is widely used in the industry for manufacturing metallic constructions. To develop a better understanding about the process as well as to predict the welding results in advance, the method of computer simulation is increasingly used. The present work is concerned with the area of process simulation as defined in [1], where among other results, the shape of the weld pool, as well as the temperature distribution in the weld pool as well as in the workpiece, is of primary interest. To calculate the accurate shape and size of the weld pool, according to the welding process parameters, a wide range of phenomena need to be accounted for. The phenomena include the resistance in the cables and the wire electrode, the droplet formation and detachment, the arc including anode and cathode boundary layers, the melt pool including convective and conductive heat transfer, melting and solidification enthalpies, and heat conduction within the workpiece. The conditions at the cathode boundary layer pose a very sensitive boundary condition to the magneto-hydrodynamic calculation of the weld pool and as they present the main driving forces together with the effects of the heated, molten droplets. In current works e.g [2, 3], the cathodic heat flux due to the arc is usually treated as a fixed Gaussian density function, Cf. Fig. 1 as originally presented by [4]; the present work proposes a new concept for its description.

Fig. 1
figure 1

Gaussian distribution of heat flux for P = 1.358 [kW]

Full size image

2 Problem statement

It has been shown that under certain circumstances, the cathodic attachment region in an arc discharge can consist of multiple highly mobile cathode spots (CS) [5], whose exact dynamics has remained a mystery and whose properties have so far evaded a reliable fundamental description as their spatio-temporal dimensions are too small to allow for more accurate analysis. However, it is observed that in the absence of an external magnetic field, the spots seem to follow a quasi-stochastic random walk [6]. Therefore, the assumption of a Gaussian distribution can be considered a fair first approach. However, in [7] where the cathode spots have been observed under welding conditions, it is already apparent that the distribution of the cathode spots is concentrated not at the center of the weld pool, where it is the hottest, but rather ring-shaped, with a void at the center. The body of work to describe the cathode spots theoretically is quite extensive; however, most works concern conditions in vacuum arcs [8, 9, e.g.]. Others are concerned with refractory cathodes like tungsten, where the main part of the current is transported by thermionically emitted electrons [10, 11, e.g.]. One theory that was proposed in [12] assumes electron avalanches arising from very high local electric fields due to extreme protrusions on the metal surface. However, on a smooth surface of a liquid melt pool, such protrusions are highly unlikely. In [13], a probabilistic system of cathode spot attachment was already investigated. There is also a theoretical model proposed by the same author for arc cathode attachment [14], which attributes the high observed current densities to ion-enhanced thermo-field emission (Murphy-Good).

In this work, the authors present a concept which is based on the hypothesis that the existence probability of the CS is strongly dependent on evaporation and therefore the heat flux distribution should be coupled to the resulting surface temperature field of the weld pool. In order to achieve a physical coupling, a two-component model has been developed, one for the description of the elementary cathode spot and another one to simulate their movement and distribution on the melted and partially overheated weld pool surface. The simplified model of the elementary CS is based on descriptions of the cathode layer of several authors while assuming non-linear ionization processes, which are treated as a black box. This allows to match the current density to the empirically observed high current densities on volatile materials, which cannot be explained by thermionic emission, as is the case in refractory materials like tungsten. Additionally, it assumes a strong damping effect to the ion-current density, due to evaporation pressure. The model of the CS distribution assigns the potential heat flux of the CS according to the surface temperature to the probability and therefore yields a new distribution for CS, and therefore also heat flux and current density.

3 Model of elementary cathode spot

To gain knowledge of the properties of CS, as well as its conditions of existence, the following model was developed. The main phenomena which were considered to contribute to the net heat flux are the following: heat gains by ion bombardment qion and back diffused electrons qebd and heat losses by thermionic emission qem, evaporation qevap, heat conduction qcond, and radiation qrad. In order to calculate these, the current densities of thermionic electrons, ions, and back-diffused electrons need to be known.

$$ {q}_{\mathrm{CS}}={q}_{\mathrm{cond}}={q}_{\mathrm{ion}}+{q}_{\mathrm{ebd}}-{q}_{\mathrm{evap}}-{q}_{\mathrm{em}}-{q}_{\mathrm{rad}} $$
(1)

The external parameters for the model were dSheath = 10−8 [m] and UD = 10 [V], and the thickness of the cathode sheath and the voltage drop are according to [10]. The heavy particle temperature Th is assumed to equal the surface temperature of the wall Tw due to thermalization with evaporated atoms.

$$ {T}_{\mathrm{h}}={T}_{\mathrm{w}} $$
(2)

The electron temperature in the plasma is assumed to follow from the energy kinetic energy that the electrons gain after the emission from the cathode surface, while losing some energy in a single ionization process. It is therefore estimated as

$$ {T}_e=\frac{\left(e\times {U}_{\mathrm{D}}+{k}_{\mathrm{B}}\times {T}_{\mathrm{W}}-e\times {E}_{\mathrm{ion}}\right)}{3/2\times {k}_{\mathrm{B}}} $$
(3)

with kB as the Boltzmann constant, e as the electron charge, and Eion = 7.9 [eV] ionization energy of iron vapor.

The effective work function was taken as

$$ {A}_{\mathrm{eff}}=A-\Delta A $$
(4)

with A = 4.5 [eV] being the work function for iron and

$$ \Delta A=\sqrt{\frac{e\times {U}_{\mathrm{D}}}{4\pi {\varepsilon}_0{d}_{\mathrm{Sheath}}}} $$
(5)

the lowering of the work function [15], with ε0 as the vacuum permittivity.

The thermionic electron current density is calculated according to the Richardson-Schottky relation [16]

$$ {j}_{\mathrm{e}\mathrm{m}}=e\frac{4\pi {k}_B^2{m}_{\mathrm{e}}}{h^3}{T}_{\mathrm{w}}^2\times \exp \left(-\frac{A-\Delta A}{k_{\mathrm{B}}{T}_{\mathrm{w}}}\right) $$
(6)

with me as the electron mass, h as the Planck constant. The ion-current density is calculated as

$$ {j}_{\mathrm{ion}}={\left({j}_{\mathrm{em}}\times \exp \left(-\frac{P_{\mathrm{vap}}^2}{P_{\mathrm{atm}}^2}\right)\right)}^{1.6} $$
(7)

The exponent of 1.6 is chosen to match the total current density found by Mesyats [17] of jCS = 1 − 3 × 1012 [A/m2], with Pvap as the pressure of vaporized material (Eq. (8) taken from [18]), Patm as the atmospheric pressure, Tb = 3134 [K] as the boiling temperature of iron, Hvap = 347 × 103 [J/mol] as the molar heat of vaporization of iron, and R as the gas constant.

$$ {P}_{\mathrm{vap}}={P}_{\mathrm{atm}}\times \exp \left[\frac{-{H}_{\mathrm{vap}}}{R}\left(\frac{1}{T_{\mathrm{W}}}-\frac{1}{T_{\mathrm{b}}}\right)\right] $$
(8)

Assuming that to generate the ion-current density, atoms are ionized, therefore giving rise to an electron current density of the same magnitude, the thermionic electron emission current density as well as ion-current density can be taken to be a measure for the electron density. The electrons are assumed to be scattered in collisions, but forced back by the electric field; therefore, the back-diffused current density is estimated as

$$ {j}_{\mathrm{ebd}}=\left({j}_{em}+{j}_{\mathrm{ion}}\right)/2\times \exp \left(-\frac{e{U}_{\mathrm{D}}}{k{T}_e}\right) $$
(9)

The total current density is therefore given as

$$ {j}_{\mathrm{CS}}={j}_{\mathrm{ion}}-{j}_{\mathrm{ebd}}+{j}_{\mathrm{em}} $$
(10)

The corresponding heat fluxes are given as

$$ {\displaystyle \begin{array}{c}{\mathrm{q}}_{\mathrm{ion}}=\frac{{\mathrm{j}}_{\mathrm{ion}}}{\mathrm{e}}\ \left[{k}_B\left(2{\mathrm{T}}_{\mathrm{h}}+\frac{{\mathrm{ZT}}_{\mathrm{e}}}{2}-2{\mathrm{T}}_{\mathrm{W}}\right)+\right.\\ {}+\mathrm{Ze}{\mathrm{U}}_{\mathrm{D}}++{\mathrm{E}}_{\mathrm{ion}}-\mathrm{Z}{\mathrm{A}}_{\mathrm{e}\mathrm{ff}}\ \left.\begin{array}{c}\ \\ {}\end{array}\right]\\ {}\approx \frac{j_{ion}}{\mathrm{e}}\left[{k}_B\frac{{\mathrm{T}}_{\mathrm{e}}}{2}+\mathrm{e}{\mathrm{U}}_{\mathrm{D}}+{\mathrm{E}}_{\mathrm{ion}}-{\mathrm{A}}_{\mathrm{e}\mathrm{ff}}\right]\end{array}} $$
(11)

following [10], with Z = 1, considering only the first ionization for simplification.

$$ {q}_{\mathrm{ebd}}=\frac{j_{\mathrm{ebd}}}{e}\left(2k{T}_e+{A}_{\mathrm{eff}}\right) $$
(12)

according to [10].

$$ {q}_{\mathrm{em}}=\frac{j_{\mathrm{em}}}{e}\left(2k{T}_{\mathrm{W}}+{A}_{\mathrm{eff}}\right) $$
(13)

according to [10].

$$ {q}_{\mathrm{evap}}={J}_{\mathrm{vap}}{H}_{\mathrm{vap}}/{M}_{\mathrm{iron}} $$
(14)

following [15], with Miron the molar mass of iron and

$$ {J}_{\mathrm{vap}}={\left(\frac{m_{\mathrm{M}}}{2\pi {k}_{\mathrm{B}}{T}_{\mathrm{w}}}\right)}^{1/2}{P}_{\mathrm{vap}} $$
(15)

the flux of evaporated particles in diffusive mode according to [19].

$$ {q}_{\mathrm{rad}}=\varepsilon \sigma {T}_{\mathrm{w}}^4 $$
(16)

according to [20], with εσ = 5.670367 × 108 [J/(s × m2 × K4)] as the Stefan-Boltzmann constant.

The proposed model states a relationship between the surface temperature and the expected heat flux as well as the current density in case of a cathode spot, see Figs. 2 and 3.

Fig. 2
figure 2

Dependence of heat flux on surface temperature

Full size image
Fig. 3
figure 3

Dependence of heat flux and current density on surface temperature in logarithmic scale

Full size image

4 Model of cathode spot distribution

The distributions for heat flux and current density are calculated by a Monte Carlo scheme, assuming an initial temperature field T0; w(x, y) (Fig. 4) of the front part of a fully developed weld pool surface, a new distribution of CS is selected by sampling locations of single CS without replacement according to a probability P(x, y). The probability at each location is chosen to be directly proportional to the possibly generated heat flux, convoluted with a super-Gauss function to take into account the influence of distance of the anode tip to the cathode, favoring a spot close to the center below the torch (x0, y0), with rx = 3 × 10−3[m], ry = 3 × 10−3 [m], x0 = 3 × 10−3 [m], and y0 = 0 × 10−3 [m]. Here, k = 3/(rxry) is a geometrical parameter, which influences the spreading, similar to a standard deviation.

$$ {P}_{\mathrm{abs}}\left(x,y\right)={q}_{\mathrm{CS}}\left({T}_{\mathrm{w}}\left(x,y\right)\right)\times {e}^{-\left({\left(k\left({\left(x-{x}_0\right)}^2+{\left(y-{y}_0\right)}^2\right)\right)}^2\right)} $$
(17)
$$ P\left(x,y\right)=\frac{P_{\mathrm{abs}}\left(x,y\right)}{\int {P}_{\mathrm{abs}}\left(x,y\right) dxdy} $$
(18)
Fig. 4
figure 4

Initial temperature field

Full size image

The choice of the proportionality of the probability to the possibly generated heat flux arises from the reasoning that for a higher possibly generated heat flux, there should be a larger potential energy available locally. For the non-stable non-equilibrium state to relax to the state of the lowest potential energy, the largest release of energy, i.e., the release of the highest heat flux, is assumed to be most favorable following a least action principle.

The grid size is chosen according to the assumed diameter of the CS of Δx = 5 [μm], i.e., a CS spot area of 25 × 10−12 [m2] and the time step is chosen as Δt = 5 × 10−8 [s] following [5, 14], giving an approximate speed of the CS of vCS = 102 [m/s]. The current density jCS and the heat flux qCS will be calculated according to the cathode surface temperature and applied at the location of the occurring CS.

Initially, a number of CS is generated on the grid, until the total current surpasses a fixed value I = 180 [A]. If the total current is higher than the fixed value of I, the number of CS will be reduced in the next time step, picking according to the inverse probability inherent to each CS, until the total current falls below the fixed value again, etc.

If the spot is not removed, it will move around the grid in the next time step in random direction, only taking into account the probability at its adjacent fields, which is convoluted with a small Gaussian again to take into account the longer distance to diagonal grid cells fdiagonal = 0.0751, fstraight = 0.1238.

At each location where a spot resides (xCS, yCS), the local temperature modification of the surface is treated in a very simplified way. A local temperature gain ∆T(x, y, t) is added to the surface temperature field Tw(x, y) according to a strongly simplifying assumption of transient heat transfer of a point explosion in a homogenous semi-infinite solid.

$$ \Delta T\left(x,y,t\right)=\frac{H_0(t)}{{\left(4\pi \alpha t\right)}^{3/2}\rho {C}_{\mathrm{p}}}\times \exp \left(-\frac{{\left(x-{x}_{\mathrm{CS}}\right)}^2}{4\alpha t}-\frac{{\left(y-{y}_{\mathrm{CS}}\right)}^2}{4\alpha t}\right) $$
(19)

where H0 is the amount of energy, α = κρCp [m2/s] as the thermal diffusivity, κ as the thermal conductivity, ρ as the density, and Cp as the heat capacity, taken from [21], not taking into account the actual local temperature, but assuming a fixed temperature of Tα = 2450 [K] everywhere.

For the calculation of H0, also strong simplifications were applied. To save calculation time, a fixed heat flux of q0 = 1013 [W/m2], following from the maximum heat flux (see Fig. 2) which is also the most probable heat flux due to the choice of (17), was assumed to act for the duration Δt. However, substantial energy losses due to evaporation were calculated according to Eq. (8), Eq. (14), and Eq. (15) with T = 2450 [K] + ∆T(x, y, tlocal) and substracted at a local time step of Δtlocal = 10−9 [s], until the center of ∆T(x, y, tlocal) reached 10 [K], after \( {t}_{H_0;\max }=777\times \Delta t \).

$$ {\displaystyle \begin{array}{l}\mathrm{for}\ t<\Delta t:\\ {}{H}_0(t)=\int \left({q}_0\Delta {x}^2\right) dt\\ {}\mathrm{for}\ t\ge \Delta t:\\ {}{H}_0(t)={H}_0\left(\Delta t\right)-\int {q}_{\mathrm{evap}}(T)\Delta {x}^2{t}^{0.2} dt\end{array}} $$
(20)

The factor t0.2 was added to approximate the spreading of the area of the overheated surface and was chosen as the maximum value that would still allow a numerically stable solution; however, this value would depend on the used time step. The amount of energy lost due to this additional evaporation accounts for approximately 20% of the input energy q0∆x2Δt, where ∆x2 is the area of the CS and ∆t is the considered time step. The final changes remained in \( {T}_w\left(x,y\right)={T}_{0;w}\left(x,y\right)+\Delta T\left(x,y,{t}_{H_0;\mathit{\max}}\right) \). In spatial direction, the additional temperature distribution ∆T(x, y, t) was limited to 29∙Δx in x-direction and 29∙Δy in y-direction, which was considered sufficient to account for the spreading of the local temperature profile until the maximum time \( {t}_{H_0;\max } \). After each time step, the new probabilities from Eq. (17) and Eq. (18) were calculated according to the new Tw(x, y).

A schematic of the algorithm is presented in Fig. 5.

Fig. 5
figure 5

Schematic workflow of the algorithm

Full size image

5 Results

The combined model yields several statements about the simulated cathodic arc attachment in GMAW.

After a calculation time of ∼76 [h] 105 iterations have been processed; therefore, a simulation time of 5 × 10−3 [s] has been calculated. The total average current was I = 181.3 [A]. The total electrical power was P = I × UD = 1.813 [kW]; from that a total of PHeat = 1.358 [kW] has been transferred to the cathode, not accounting for the 20% losses from Eq. (20).

Figure 6 presents the evolution of the probability distribution. The CS will locally heat up the surface to a maximum temperature, thereby modifying the probability distribution, until it becomes very unlikely for a CS to settle there; then, the highest probability for a CS is in between the very hot region and the cold region, following the relationship shown in Fig. 2. Since the coarse heat transfer model does not effectively distribute the heat, the area with “intermediate” temperatures (between maximum and minimum temperatures, i.e., ~ 3000[K]) becomes very narrow and highly concentrated, giving rise to a very thin line. It should be noted that in the bottom picture of Fig. 6, the light blue shading in the area towards the right side (i.e., towards the back of the weld pool) represents a probability that is two orders of magnitude lower than the probability on the pink line. This results in the CS mostly gathering on the pink line, as becomes also apparent from Figs. 7 and 8.

Fig. 6
figure 6

Resulting probability distribution, for time 5 × 10−2, 5 × 10−1, 5 [ms]. The isolines of the liquidus and boiling temperature of the initial temperature distribution are overlaid

Full size image
Fig. 7
figure 7

Resulting heat flux distribution, for time 5 × 10−2, 5 × 10−1, 5 [ms]. The isolines of the liquidus and boiling temperature of the initial temperature distribution are overlaid as well as an indication for the distance traveled by the torch in the lower left corner

Full size image
Fig. 8
figure 8

Resulting current density distribution, for time 5 × 10−2, 5 × 10−1, 5 [ms]. The isolines of the liquidus and boiling temperature of the initial temperature distribution are overlaid

Full size image

The resulting heat flux distribution was calculated as

$$ \frac{\sum_{t=0}^{t\_\mathrm{total}}{q}_{\mathrm{CS}}\left(x,y,t\right)}{t_{\mathrm{total}}} $$
(21)

is presented in Figure 7, with ttotal as the total simulated time. The welding direction is from right to left. It becomes apparent that a sickle shape of the heat flux distribution is present with an emphasis towards the melting front. As the movement of the torch has not been taken into account, an arrow was placed in the figures (lower left) to indicate the movement of the plate according to time-scale and grid resolution, assuming a welding speed of 80 [cm/min]. The distance traveled by the torch after 5 [ms] equals d = 6.67 × 10−4[m].

As the distribution reflects the locations of the CS, the distribution of the current density in Fig. 8 follows the distribution of the heat flux (calculated just as Eq. (21)), however with values about one order of magnitude lower, as expected from the model (Fig. 3).

As the heat transfer model is still over-simplified and as no movement of the torch towards colder areas is taken into account, the distributions do not converge but expand infinitely.

6 Discussion

The proposed concept allows to calculate a new distribution of cathodic heat flux (Figs. 7 and 9) and current density to replace the widely used Gaussian approximation (Fig. 1), taking into account physically in-depth models of cathodic processes and evaporation. It is possible to extend the model to derive from it also a distribution of the arc pressure. However, several drawbacks need to be addressed.

Fig. 9
figure 9

Smoothed, resulting heat flux distribution, for time 5 [ms] as an interpolated 3D surface

Full size image

The concept cannot be considered complete, and one of the main reasons for this is that the solution does not converge. This is due to the lack of a thorough treatment of the heat transfer. However, given a proper model for the heat transfer, it is expected to receive principally similar results, i.e., a peak of the probability of the cathode spots at temperature between the maximum temperature of the weld pool and the cold temperature of the unaffected workpiece. This follows from the relation displayed in Fig. 2 and the assumption of the highest probability of the CS at the location of the highest possible heat flux.

As the understanding of elementary cathode spots in atmospheric conditions is still quite limited, the actual processes of ionic current generation are so far still treated as a black box and calibrated to match empirical values and the presence of oxides is not taken into account either. Also, the model of evaporation should be updated, for example, with a model for rapid vaporization by Knight [22]. As the chosen values from literature for CS area and current per spot could be different for different conditions, the absolute values, presented here, cannot be considered reliable. Also, the occurrence of temperatures at the weld pool surface beyond boiling temperature is not realistic. However, any relation of the heat flux and current density on the surface temperature for an arc cathode which is dominated by ion transfer will have a maximum heat flux or current density at temperatures below the maximum temperature. As the heating will always occur in such way as to heat until the maximum temperature, the highest probability for a cathode spot will always occur between the hottest point at the center and the cool area outside of the weld pool. This mechanism would explain the observations of the cathode spot distribution in [7], where they seem to avoid the hot center.

The heat transfer statement is obviously extremely simplified as it takes into account only an analytical expression of thermal point explosions in an isothermal, semi-infinite half space, with a fixed heat flux and an additional heat loss by evaporation, at each cathode spot location. However, these flaws are not critical and can be overcome, even if they would greatly slow down the calculation. Another more difficult issue is the fact that, although the temperature is modified locally during the presence of a cathode spot, this influence on the resulting values of heat flux and current density from the elementary cathode spot model is not being accounted for. This issue concerns deeply the dynamic nature of the cathode spot and is not addressed by the current approach. However, for a first approach, to study the tendencies of the proposed concept, the assumptions are sufficient to allow showing the feasibility of such model.

Another under-determined parameter is the Gauss function, which is convoluted with the hypothetical heat flux to give the probability in Eq. (17). In reality, the distance between the torch and the workpiece is complicated, as the arc pressure suppresses the liquid surface, which is also varying due to the droplet-transfer process. Also, the whole magneto-hydrodynamic statement of the arc plasma has been neglected as well. However, it is assumed that the displayed tendencies of the distribution might be modified but not suppressed. Additionally, it can be followed from the new distribution, that since the electric field within the arc column is mostly axisymmetric, a strong change of the field lines must occur in the cathode region, giving rise to a very strongly differentiating Lorentz force, which could have a very strong impact on the weld pool hydrodynamics. Also, for a complete hydrodynamic model of the weld pool, the effect of droplets, which carry their own heat and represent their own kind of volumetric heat source, has to be taken into account.

7 Conclusion

In this work, the hypothesis that the cathode area in GMAW is highly dependent on evaporation has been investigated and a novel concept for the calculation of the distribution of heat flux and current density has been proposed. Here, the highest probability for the CS is not at the location with the highest temperature of the weld pool surface, and so the maximum of the resulting calculated heat flux distribution is located much further in front of the hottest area of the weld pool surface. Despite the obvious drawbacks, the proposed concept represents an incremental improvement over the widely used assumption of a purely Gaussian heat-flux distribution, and its effect should be investigated in the frame of a hydrodynamic weld pool calculation.