1 Introduction

As part of the initiative Industry 4.0, digitalization has increasingly become a requirement for manufacturing processes. Therefore, also the simulation of these processes plays a major role in meeting these requirements. The welding simulation can be distinguished, as introduced in [1], into three interconnected areas of process simulation, where the size and shape of the weld pool should be calculated, structural simulation, where the effects of the temperature field upon the entire work piece are calculated, and material simulation, where the properties of the material under the thermal conditions of the process are being calculated. In gas metal arc welding (GMAW) process simulation, the hydrodynamics in the weld pool play a major role in the distribution of the heat and therefore the formation of the weld pool shape. It is therefore important to accurately take into account all driving forces of the liquid melt. One of the drivers is the electromagnetic Lorentz force which scales quadratic with the electric current density. To accurately model this force, the current density in the attachment of the arc to the work piece needs to be taken into account, while this attachment is particularly determined by the cathode sheath processes. However, in current GMAW process simulations, the current density is either assumed to be distributed in a Gaussian way [2, 3] or following directly from the Maxwell equations while ignoring the cathode sheath processes entirely [4,5,6]. It is clear that this represents a simplification that does not reflect the real conditions in the weld pool. In [7], the treatment of the sheath processes is referred to [8]. In this work, as well as in [9] and [10], it is not entirely clear how the cathode sheath is solved, but it seems like the total current density is calculated from the Maxwell equations and the contribution from the thermionic current density is calculated by the Richardson-Dushman equation, while the contribution by the ion flux is simply assumed as the difference between these two values. However, even in this approach, the total current density will be axisymmetric following from the Maxwell equations without the consideration of the cathode sheath. It follows that there is a demand for a method to consider the cathode sheath processes more accurately. In [11], a model for the evaporation-determined arc-cathode coupling in GMAW (EDACC) was presented and its effects were investigated in [12]. In this model, the heat deposition from the plasma to the weld pool is realized by the arc-cathode interaction in the cathode layer and heat transfer by heat conduction plays only a minor role. Nonetheless, the plasma temperature has a crucial role for the ionization degree and the availability of ions, which are mainly responsible for the delivery of heat and current to the cathode. Compared to previous approaches, the consideration of the arc-cathode interaction has a strong influence on the distributions of the current density and the heat flux, which have their maximum value no longer at the position of the highest surface temperature, but rather at intermediate temperatures, resulting in a “ring-like” attachment. Therefore, it is the first model to take into account the influence not only from the arc plasma onto the weld pool but also the influence from the weld pool surface conditions on the attachment of the arc to the cathode, in the conditions present during GMAW.

The present work is intended to make the model more applicable to GMAW process simulation, by presenting a simplified formulation to facilitate an easy step-by-step implementation.

2 Problem statement

The presented model is based on the principle of evaporation-determined arc cathode coupling (EDACC) as it was described in [11]. Therefore, the present work is concerned with the interface between the arc plasma and the weld pool, but does not attempt to describe either the arc plasma or the weld pool formation itself. However, the model was extended with a weighting factor, to adjust the influence of the metal vapor on the local plasma temperature, in order to calibrate for realistic weld pool surface temperatures (see Eq. (4)).

The model is described here following the algorithmic structure to allow for easy implementation in a GMAW weld pool process simulation, rather than for enabling following the physical logic, which was already described in [11]. This means also that constants have been evaluated and noted as numerical values, and all physical units have been omitted.

In order to include the evaluation of the Saha equation in this simplified form, the fraction of the partition sums for first and second ionization of iron was included here as a polynomial valid between 3000 (K) − 25,000(K) for TPlasma, local (see Eq.(5)).

The model can be interpreted as dependent only on the radius of the arc rArc (mm), the weld pool surface temperature Tw (K), and the cathode fall voltage drop UD (V). However, it is formulated in such a way to allow the temperature of the plasma bulk Tplasma, bulk (K) and the iron vapor density of the plasma bulk nFe, bulk (m−3) to serve as input parameters as well, instead of the radius of the arc, thereby allowing for a coupling between an arc plasma simulation and a weld pool simulation.

Finally, the resulting distributions for heat flux and current density can be normalized and multiplied with more empirical values for the arc power PArc and the arc current IArc (see Eq. (17) and Eq. (19)).

The model assumes an arc-pressure of 1.5 atm at the weld pool surface and, like the model presented in [11], only considers singly ionized iron states.

3 Simplified surface heat source model

In order to use the proposed surface heat source model for a weld pool simulation without the consideration of a plasma, a simple approximation for the conditions on the plasma side is being proposed in dependence on the radius of the arc rArc. This radius can be also assumed in a first approximation to equal the width of the weld pool, in a standard DC process. This assumption is justified in the EDACC approach, as the main contributions of the heat flux and the current density will occur on the outer edge of the arc, therefore also determining the edge of the weld pool.

The temperature of the plasma bulk Tplasma, bulk is assumed as a asymmetric 8th-order Gaussian distribution which stretches slightly towards the tail of the weld pool, as indicated in Eq.(1) (see also Fig. 7), which is not to be confused with the heat flux distribution. This assumption derives from the observation in [13] that the temperature at the metal vapor core of the arc is as cold as 6000 (K)–8000 (K) for argon shielding gas. Since it is widely understood that this lowering of the plasma temperature is due to radiation losses in the presence of metal vapor, a similar plasma temperature is assumed in vicinity of the cathode, where metal vapor is also expected to be present to a significant degree.

$$ {T}_{\mathrm{plasma},\mathrm{bulk}}\left(x,y\right)=300\ \left(\mathrm{K}\right)+\left(7000\ \left(\mathrm{K}\right)-300\left(\mathrm{K}\right)\right)\cdotp \left\{\begin{array}{c}{e}^{\left(-150\cdotp {\left(\frac{{\left(x-{x}_0\right)}^2+{\left(y-{y}_0\right)}^2}{{r_{\mathrm{Arc}}}^2}\right)}^4\right)};\mathrm{for}\ x<{x}_0\\ {}{e}^{\left(-150\cdotp {\left(\frac{0.5\cdotp {\left(x-{x}_0\right)}^2+{\left(y-{y}_0\right)}^2}{{r_{\mathrm{Arc}}}^2}\right)}^4\right)};\mathrm{for}\ x>{x}_0:\end{array}\right. $$
(1)

Here, (x, y) are the coordinates of the weld pool surface and (x0, y0) are the positions of the welding torch. The welding direction is in x-direction.

It is possible to assume an influence of background iron vapor atoms in the plasma nFe, bulk, as would be expected in a real GMAW process. There, an iron atom density of 1021 (m−3) was assumed in the vincinity of the cathode. As in pulsed GMAW processes, the iron atom density was measured to be ~ 2.5·1022 (m−3) in the characteristic metal vapor core [14], and the dilution of the iron atoms that would follow from the observed spread over the cathode surface seems reasonable. As the atoms ionize together with the evaporated atoms from the cathode surface at the local plasma temperature TPlasma, local, they also contribute to the ion flux to the cathode and therefore the current and heat transfer. It should be noted that especially for lower cathode surface temperatures (in this case Tw < 1900 (K)), where the evaporation from the cathode is not yet very strong, these background ions can have a dominating influence. Here, for simplicity, the same distribution was assumed as for the plasma bulk temperature (see Eq. (2)).

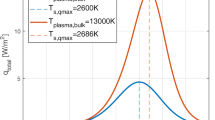
$$ {n}_{\mathrm{Fe},\mathrm{bulk}}\left(x,y\right)={10}^{21}\ \left({m}^{-3}\right)\cdotp \left\{\begin{array}{c}\mathrm{for}\ x<{x}_0:{e}^{\left(-150\cdotp {\left(\frac{{\left(x-{x}_0\right)}^2+{\left(y-{y}_0\right)}^2}{{r_{\mathrm{Arc}}}^2}\right)}^4\right)}\\ {}\mathrm{for}\ x>{x}_0:{e}^{\left(-150\cdotp {\left(\frac{0.5\cdotp {\left(x-{x}_0\right)}^2+{\left(y-{y}_0\right)}^2}{{r_{\mathrm{Arc}}}^2}\right)}^4\right)}\end{array}\right. $$
(2)

Following the reasoning described in [11], the local plasma temperature TPlasma, local is calculated as a mixture between the temperature of the metal vapor (assumed to be equal to the cathode surface temperature TW) and the temperature of the plasma bulk TPlasma, bulk. However, while in [11] the mixture was assumed by equally weighted influence of plasma gas and evaporated metal, this assumption was a bit arbitrary, as the relevant length scales for ionization and the area of saturated metal vapor conditions were never really considered in detail. From the approach for the mixing of the plasma temperatures presented in [11] follows the presented approach (Eq. (3)), but it has been extended to include a weighting factor ω (Eq. (4)), which can increase the influence of the evaporated metal onto the local plasma temperature. This can be also interpreted as a shift of the relevant ionization length towards the evaporating cathode surface. The weighting factor in Eq. (4) was chosen in such a way to scale with the saturated vapor pressure of iron. This newly introduced weighting factor ω allows to calibrate the maximum surface temperature at which a positive heat flux will still be generated, therefore defining the maximum temperature of the weld pool surface. Here, ω is assumed to be proportional to the evaporation pressure due to the Clausius-Clayperon equation and the factor wf = 2500 N/m2 is suggested, which gives rise to a maximum surface temperature of TW, max ≈ 2700 (K). The influence of wf on the heat flux is displayed in Fig. 1. It should be noted that the lower the value for wf is, the lower will be the maximum weld pool surface temperature TW, max; however, also the influence from the background iron atom density nFe, bulk will become more strong, which can be seen in Fig. 1 for temperatures TW < 1900 (K), where the heat flux is almost entirely contributed by these ions. Please keep in mind that all physical units have been omitted in the notation of the equations, here and in the following.

Fig. 1
figure 1

Distribution of qtotal for fixed TPlasma, local in dependence of Tw with influence of weighting factor wf

Full size image
$$ {T}_{\mathrm{Plasma},\mathrm{local}}=\frac{\omega \cdotp {e}^{\left(20.3417-4.2050\cdotp {10}^4\cdotp {T_{\mathrm{w}}}^{-1}\right)}+1.0168\cdotp {10}^3}{\frac{\omega }{T_{\mathrm{w}}}\cdotp {e}^{\left(20.3417-4.2050\cdotp {10}^4\cdotp {T_{\mathrm{w}}}^{-1}\right)}+\frac{1.0168\cdotp {10}^3}{T_{\mathrm{plasma},\mathrm{bulk}}}} $$
(3)
$$ \omega =\frac{P_{\mathrm{vap}}}{\mathrm{w}\mathrm{f}}=\frac{e^{\left(25.3456-4.2050\cdotp {10}^4\cdotp {T_{\mathrm{w}}}^{-1}\right)}}{\mathrm{w}\mathrm{f}} $$
(4)

As the evaporated iron atoms, as well as the iron atoms from the plasma bulk, are assumed to ionize at LTE, the Saha equation was solved as stated in [11]. However, to simplify the procedure, the ratio of the partition sums for neutral and singly ionized iron atoms for different plasma temperatures was approximated here by a 5th-order polynomial, Eq.(5), to allow for a straightforward implementation in the GMAW process simulation. The approximation (Eq. (5)) was retrieved by automatically fitting the ratio of the partition sums in the Saha equations, with values retrieved from [15] (see Fig. 2).

$$ {\displaystyle \begin{array}{l}{P}_{\mathrm{FractionPartitionSum}}\\ {}=1.5074\cdotp {10}^{-21}\cdotp {T_{\mathrm{Plasma},\mathrm{local}}}^5\\ {}\begin{array}{c}-1.2955\cdotp {10}^{-16}\cdotp {T_{\mathrm{Plasma},\mathrm{local}}}^4\\ {}+4.2398\cdotp {10}^{-12}\cdotp {T_{\mathrm{Plasma},\mathrm{local}}}^3\\ {}\begin{array}{c}-6.2329\cdotp {10}^{-8}\cdotp {T_{\mathrm{Plasma},\mathrm{local}}}^2\\ {}+3.1937\cdotp {10}^{-4}\cdotp {T_{\mathrm{Plasma},\mathrm{local}}}^1\\ {}+1.0658\end{array}\end{array}\end{array}} $$
(5)
Fig. 2
figure 2

Polynomic fit for partition sum data from [15] from 3000 (K) to 25,000 (K)

Full size image

This allows to solve for the ion density nion, Eq. (7), while Eq. (6) is just an intermediate step, to keep the clarity in the notation. Both these steps, Eq. (6) and Eq. (7), are following from the Saha equation.

$$ {C}_{S\mathrm{aha}}={P}_{\mathrm{FractionPartitionSum}}\cdotp {T_{\mathrm{Plasma},\mathrm{local}}}^{3/2}\cdotp {e}^{\left(49.9283-\frac{9.1594\cdotp {10}^4}{T_{\mathrm{Plasma},\mathrm{local}}}\right)} $$
(6)
$$ {\displaystyle \begin{array}{c}{n}_{\mathrm{ion}}=-\frac{C_{\mathrm{Saha}}}{2}+\\ {}{C}_{\mathrm{Saha}}\cdotp \sqrt{\frac{\left(\frac{e^{\left(79.3688-\frac{4.2050\cdotp {10}^4}{T_{\mathrm{w}}}\right)}}{4\cdotp {T}_{\mathrm{w}}}+{n}_{\mathrm{Fe},\mathrm{bulk}}\right)}{C_{\mathrm{Saha}}}+\frac{1}{4}}\end{array}} $$
(7)

With the ion density, nion, as a function of the local plasma temperature, it allows to define the local ion current density, Eq.(8), just as in [11].

$$ {j}_{\mathrm{ion}}=2.5208\cdotp {10}^{-18}\cdotp \sqrt{T_{\mathrm{Plasma},\mathrm{local}}+{T}_{\mathrm{w}}}\cdotp {n}_{\mathrm{ion}} $$
(8)

To define the current density due to field-enhanced thermionic emission, the effective work function was defined as described in [11], where the cathode fall voltage drop UD enters in its 8th root.

$$ {A}_{\mathrm{eff}}=5.3333\cdotp {10}^4-0.0022\cdotp \sqrt[4]{n_{\mathrm{ion}}}\cdotp \sqrt[8]{\left({T}_{\mathrm{Plasma},\mathrm{local}}+{T}_{\mathrm{w}}\right)\cdotp {U}_{\mathrm{D}}} $$
(9)
$$ {j}_{\mathrm{em}}={T_{\mathrm{W}}}^2\cdotp {e}^{\left(13.997-\frac{A_{\mathrm{eff}}}{T_{\mathrm{W}}}\right)} $$
(10)

The resulting total current density is then simply the sum of the ion flux and the field-enhanced thermionic emission, Eq.(11), as is the case in [11].

$$ {j}_{total}={j}_{ion}+{j}_{em} $$
(11)

The total heat flux (Eq. (15)) then follows from the energy contributions from the ion flux (Eq. (13)) and the losses by the field-enhanced thermionic emission (Eq. (12)), as well as losses by radiation (Eq. (14)), just as outlined in [11].

$$ {q}_{\mathrm{em}}={j}_{\mathrm{em}}\cdotp \left(8.6250\cdotp {10}^{-5}\cdotp {T}_{\mathrm{W}}+4.6\right) $$
(12)
$$ {q}_{\mathrm{ion}}={j}_{\mathrm{ion}}\cdotp \left(4.3125\cdotp {10}^{-5}\cdotp {T}_{\mathrm{Plasma},\mathrm{local}}+{U}_{\mathrm{D}}+6.9284\right) $$
(13)
$$ {q}_{\mathrm{rad}}={e}^{\left(-\left(\frac{T_{\mathrm{w}}}{442}\right)-13.5321\right)}\cdotp {T_{\mathrm{W}}}^4 $$
(14)
$$ {q}_{total}={q}_{ion}-{q}_{em}-{q}_{rad} $$
(15)

Finally, in order to receive an easy to handle heat source for GMAW process simulation, the resulting heat flux and the current density can be normalized to the total power of the arc (see Eq. (16)). The total power of the arc (Eq.(17)) is suggested as the difference between the total electrical power in the process as supplied by the welding power source UPowerSource ∙ IArc with an efficiency factor of 0.8 and the power of the droplet (Eq. (18)), following [16], as the efficiency factor accounts for resistive power losses in the cables and contacts and for losses due to energy dissipation (radiation and convection) of the arc column to the environment.

$$ {q}_{\mathrm{HS}}\left(x,y\right)={P}_{\mathrm{Arc}}\cdotp \frac{q_{\mathrm{total}}\left(x,y\right)}{\int {q}_{\mathrm{total}}\left(x,y\right) dxdy} $$
(16)
$$ {P}_{\mathrm{Arc}}={U}_{\mathrm{PowerSource}}\cdotp {I}_{\mathrm{Arc}}\cdotp 0.8-{P}_{\mathrm{Droplet}} $$
(17)
$$ {P}_{\mathrm{Droplet}}={c}_{\rho}\cdotp \rho \cdotp \pi \cdotp {r_{\mathrm{wire}}}^2\cdotp {v}_{\mathrm{wire}}\cdotp \left({T}_{\mathrm{Droplet}}-{T}_0\right) $$
(18)

where in Eq. (18), cρ is the simplified the heat capacity of the wire material, ρ is the density of the wire, rwire is the radius of the wire, vwire is the wire feed speed, TDroplet is the average droplet temperature, and T0 is the initial temperature of the wire before heating.

Similarly, also the current density can be normalized to the total current of the arc (Eq. (19)).

$$ {j}_{\mathrm{HS}}\left(x,y\right)={I}_{\mathrm{Arc}}\cdotp \frac{j_{\mathrm{total}}\left(x,y\right)}{\int {j}_{\mathrm{total}}\left(x,y\right) dxdy} $$
(19)

4 Results

The results for the heat source have been exemplified for a typical steady-state weld pool simulation, based in the hydrodynamics model shown in [12]. The process parameters under consideration were UPowerSource = 26.9 (V) and IArc = 200 (A), for a weld pool width of 10.9 (mm), i.e. rArc = 5.45 (mm).

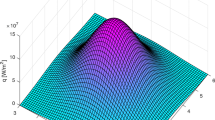
In Fig. 3, the resulting heat flux and surface temperature distributions are shown. It can be seen that the maximum characteristic of the heat flux on the weld pool front is apparent, just as in [12]; however, also a local maximum of the heat flux towards the tail of the weld pool appeared, which has its reason in the consideration in the smooth distribution of Tplasma, bulk, while in [12], the distribution was flat and confined to a specific radius. It should be noted that in this model, the surface flows cannot be considered accurate, as no Marangoni convection was considered. Also visible is, as was already pointed out in [12], a slight local maximum of heat flux close to the center of the attachment, where the influence of the droplets modifies the weld pool surface temperature. Additionally, it can be seen that the considered weighting factor limits the maximum surface temperature to TW, max ≈ 2700 (K) and the EDACC model causes a very even distribution of the surface temperature over the whole area of attachment.

Fig. 3
figure 3

View from the top: weld pool surface EDACC heat flux and surface temperature distribution

Full size image

In Fig. 4, the current density distribution as well as the vector field of the electromagnetic force density on the top surface is displayed. It can be seen that the current density distribution closely resembles the distribution of the heat flux, as the main current transfer mechanism is transport by the ions, which are also responsible for the heating. It can also be seen that the strongest forces act at the weld pool front, with a component of the electromagnetic force density towards the center of the attachment.

Fig. 4
figure 4

View from the top: weld pool surface EDACC current density and surface electromagnetic force density distribution

Full size image

In Fig. 5, the resulting electromagnetic force density on the top surface of the weld pool is displayed in the view of a longitudinal cross-section. It can be seen that the electromagnetic force plane is considerable at the melting front. For comparison, the electromagnetic force density for the same process parameters, but using a Gaussian distribution of the current density instead, is shown in Fig. 6. It can be seen that in this case, the highest electromagnetic forces are below the center of the heat source and the absolute value of the strongest vector is only about half as strong (indicated by the green color).

Fig. 5
figure 5

Longitudinal cross-section with vectors of electromagnetic force density on the top surface and the melting temperature iso-contour line indicated

Full size image
Fig. 6
figure 6

Longitudinal cross-section with vectors of electromagnetic force density on the top surface for the standard Gaussian distribution of the current density, for comparison with Fig. 5

Full size image

It should be noted that the current density, which is parallel to the electric field, is defined to enter along the vertical axis, as would be expected in an electrostatic problem, where the field lines enter the conductive material always in a perpendicular way. However, the problem in question is a magnetostatic problem (i.e., the charge carriers are moving along static field lines), and therefore the condition of electric field lines perpendicular to the conductive surface is not required. On the contrary, it is expected that the electric field lines will be more curved when the arc plasma is considered as well, causing them to turn the direction of the electromagnetic force more towards the vertical axis.

Therefore, the showed results intend to give only an example for the resulting distribution, while the main goal is to enable researchers with expertise in arc plasma and hydrodynamic weld pool simulation, to couple both these simulation domains in a way that is physically meaningful. Even if the physical meaning of the resulting heat flux is reduced to an extend by the normalizations performed in Eq. (16) and Eq. (19), still the characteristics of the attachment can be retrieved anyhow, with the additional advantage of being able to calibrate the model beforehand to the desired weld pool surface temperature by the weighting factor Eq. (4). The approach with a continuously re-adjusting heat source does indeed bear a numerical challenge for the convergence; therefore, a more sophisticated numerical scheme should be considered.

5 Discussion

The presented simplified formulation for a heat source distribution based on the EDACC principle resembles the characteristics of the EDACC arc-cathode attachment. In particular, it should be noted that, while the arc-plasma temperature was assumed as seen in Eq. (1) (see Fig. 7) the resulting heat flux to the weld pool (see Fig.8) does only partially resemble the distribution of the arc plasma temperature. This is due to the influence of the weld pool surface evaporation on the arc-cathode coupling, as explained in [11], and it shows that the heat flux to the weld pool cannot be explained by conductive heat transfer from the arc plasma.

Fig. 7
figure 7

Assumption of 3D distribution of Tplasma, bulk(x, y) from Eq. (1)

Full size image
Fig. 8
figure 8

Resulting heat flux distribution qHS in 3D, the same as in Fig. 3

Full size image

While the choice of the formulation of the model in numerical terms makes it arguably more difficult, to follow the physics, the purpose of the present work is to give a description of a surface heat source model based on the EDACC principle that will allow easy implementation in other GMAW process simulations.

Therefore, the showed results intend to give only an example for the resulting distribution, while the main goal is to enable researchers with expertise in arc plasma and hydrodynamic weld pool simulation, to couple both these simulation domains in a way that is physically meaningful. Even if the physical meaning of the resulting heat flux is reduced to an extend by the normalizations performed in Eq. (16) and Eq. (19), still the characteristics of the attachment can be retrieved anyhow, with the additional advantage of being able to calibrate the model beforehand to the desired weld pool surface temperature by the weighting factor Eq. (4). The approach with a continuously re-adjusting heat source does indeed bear a numerical challenge for the convergence; therefore, a more sophisticated numerical scheme should be considered.

A thorough validation of the presented heat source model in terms of cross-section comparisons can not yet be presented. A first initial spot sample evaluation with a comparison of the EDACC model and with a Gaussian heat source was presented in [12], However, as was discussed there also, the new EDACC formulation gives results, at least for the surface temperature field, which are not physically inconsistent, i.e., where boiling temperature is not exceeded. Another argument in favor of the EDACC model in terms of physical consistency is that when applying the Gaussian heat source, the forces due to the Marangoni effect are often overestimated due to the much larger surface temperatures and resulting temperature gradients, as well as uncertainties on the value of the surface tension which is very sensitive to the chemical composition (see [16]). With the EDACC model and this presented simple formulation, this overestimation is not necessary, because it shows that the current approaches for modeling the weld pool formation (for example, see [17] and [18]) are based on assumptions and parameters, which are adjusted to give the desired result, but which are in principle unphysical or unjustified. Therefore, it should be noted that while it is possible to achieve simulation results that closely resemble real welding experiments that as long as the individual phenomena and their resulting interaction are still insufficiently taken into account, a quantitative validation in terms of a weld pool formation comparison seems to be unreasonable. To understand the interaction of the individual phenomena and especially their dominance in the process of weld pool formation and in the whole system of wire-arc-weld pool, the presented simple formulation of the EDACC model can be helpful.

The most obvious difference to the presented work in [12] is the local attachment of the arc towards the tail of the weld pool. However, as mentioned in Section 4, the Marangoni effect was not included and therefore the flow from the heating zone outward towards the cooler regions was not considered. Such flow would extend the hot parts of the surface towards the tail region of the weld pool, effectively diminishing the attachment in this region.

Also, since the 3D simulation of the arc plasma with accurate description of the electric field lines was not yet considered, the current density is assumed to enter perpendicular to the surface. Therefore, the electromagnetic force density includes a component towards the center of the heat source. However, the real arc will show a steeper entering of the field lines and therefore a smaller component towards the center. This would increase the weight of the Marangoni convection against the convection towards the center at the back of the heating zone that can be observed now. Additionally, this would accelerate the liquid melt towards the bottom, carving it deeper into the base material.

6 Conclusion

The present work proposes a simplified formulation for consideration of a surface heat and current source distribution based on the EDACC principle for GMAW process simulation. It allows to model the processes at the interface between the weld pool and the arc in a physically non-contradicting way (e.g., while keeping the weld pool surface at realistic temperature levels). Therefore, it can be followed that the electromagnetic force density will be considered more accurately, and effects arising from temperature gradients, like the Marangoni effect, will show to be less dominant. This might have an influence on the weld pool convection, especially when considering both the arc plasma as well as the work piece domain. Additionally, it can be calibrated to the weld pool surface temperature and it can take into account the influence of the droplet on the attachment. While it is still not entirely straightforward, how to set the boundary conditions in a coupled arc plasma and weld pool simulation when considering the EDACC principle, the proposed formulation can be applied for stand-alone weld pool simulations where the arc plasma is not yet considered. However, the presented formulation simplifies the applicability of the EDACC approach considerably and might allow a self-consistent coupled simulation in the near future.