Abstract
In the present work, an efficient numerical technique, called q-homotopy analysis transform method (briefly, \(q\)-HATM), is applied to nonlinear Fisher’s equation of fractional order. The homotopy polynomials are employed, in order to handle the nonlinear terms. Numerical examples are illustrated to examine the efficiency of the proposed technique. The suggested algorithm provides the auxiliary parameters \(\hbar\) and \(n\), which help us to control and adjust the convergence region of the series solution. The outcomes of the study reveal that the \(q\)-HATM is computationally very effective and accurate to analyse nonlinear fractional differential equations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Calculus of fractional order is pretty antique subject in mathematics. Fractional derivatives were debut in 1695, as in the question of the extension of meaning. Derivatives and integrals of arbitrary order afford more factual models of the real-world phenomenon [1], than classical calculus. During the twentieth century, a bulky amount of research on fractional calculus published by many pioneers includes Caputo [2], Miller and Ross [3], Podlubny [4], Liao [5], and others.
The problems relating to applications of fractional calculus are located in various connected branches of science and engineering, like finance [6], nanotechnology [7], electrodynamics [8], and many other fields. The analytical and numerical solution of fractional partial differential equations plays a vital role in describing the characters of nonlinear problems that arise in daily life.
In 1937, Fisher proposed a model for the temporal and spatial propagation of a virile gene in an infinite medium, called Fisher’s equation [9]. The simplest and classical case of Fisher’s equation so-called reaction diffusion equation is given by [10]
which basically the Logistic equation and the conjunction of diffusion equation with diffusion factor \(\lambda\) and birth rate \(\mu\). Here, \(u\left( {x,t} \right)\) specifies the state evolution over the spatial–temporal domain characterized by the coordinates \(x\), \(t ,\) respectively. Fisher’s equation is widely used in chemical kinetics [11], Neolithic transitions [12], branching Brownian motion [13], epidemics and bacteria [14] and many other disciplines.
Many researchers studied various techniques like, Adomian decomposition method [15], homotopy perturbation Sumudu transform method [16], Haar wavelet method [17], optimal homotopy asymptotic method [17], homotopy perturbation method [18], Chebyshev spectral collocation method [19], and fractional natural decomposition method [20] to obtain numerical solutions for the Fisher’s equation of fractional order. Recently, Singh et al. [21] introduced and nurtured the new homotopy technique known as \(q\)-HATM to study nonlinear problems (including, classical and arbitrary order) arises in nature [22, 23]. This method is an elegant amalgamation of homotopy algorithm through Laplace transform.
Preliminaries
Here, we recall some definitions and properties of fractional calculus and Laplace transform, which are used in the sequel:
Definition 1
The fractional integral of a function \(f\left( t \right) \in C_{\mu } \left( {\mu \ge - 1} \right)\), of order \(\alpha > 0\) initially defined by Riemann–Liouville is represented as [4]
Definition 2
The fractional derivative of \(f \in C_{ - 1}^{n}\) in the Caputo [2] sense is defined as
Definition 3
The Laplace transform (LT) of a Caputo fractional derivative \(D_{t}^{\alpha } f\left( t \right)\) is represented as [2, 3]
where \(F\left( s \right)\) represents the Laplace transform of the function \(f\left( t \right)\).
Fundamental idea of \(q\)-HATM
To present the fundamental idea of proposed method [24,25,26], we consider a general nonlinear non-homogeneous fractional partial differential equation of the form:
where \(D_{t}^{\alpha } {\mathcal{U}}\left( {x,t} \right)\) represents the fractional derivative of \({\mathcal{U}}\left( {x,t} \right)\) in the Caputo’s sense, \(R\) and \(N\) specifies the linear and nonlinear differential operator, respectively, and \(f\left( {x,t} \right)\) represents the source term. Now, by employing the LT on Eq. (5), we get
On simplifying Eq. (6), we have
According to homotopy analysis method [5], here we define nonlinear operator as
where \(q \in \left[ {0,\frac{1}{n}} \right]\), and \(\varphi \left( {x,t;q} \right)\) is real function of \(x,\;t\) and \(q\).
We construct a homotopy for nonzero auxiliary function \(H\left( {x,t} \right)\) as follows:
where \(L\) be a symbol of the Laplace transform, \(q \in \left[ {0,\frac{1}{n}} \right] \left( {n \ge 1} \right)\) is the embedding parameter, \(\hbar \ne 0\) is an auxiliary parameter, \(\varphi \left( {x,t;q} \right)\) is an unknown function, and \({\mathcal{U}}_{0} \left( {x,t} \right)\) is an initial guess of \({\mathcal{U}}\left( {x,t} \right)\). The following results hold for \(q = 0\) and \(q = \frac{1}{n}\):
respectively. Thus, by amplifying \(q\) from \(0\) to \(\frac{1}{n}\), the solution \(\varphi \left( {x,t;q} \right)\) converge from \({\mathcal{U}}_{0} \left( {x,t} \right)\) to the solution \({\mathcal{U}}\left( {x,t} \right)\). Expanding the function \(\varphi \left( {x,t;q} \right)\) in series form by employing Taylor theorem near to \(q\), one can get
where
On choosing the auxiliary linear operator, the initial guess \({\mathcal{U}}_{0} \left( {x,t} \right),\) the auxiliary parameter \(n, \hbar\) and \(H\left( {x,t} \right)\), the series (11) converges at \(q = \frac{1}{n}\); then it gives one of the solutions of the original nonlinear equation of the form
Now, differentiating the zeroth order deformation Eq. (9) \(m\)-times with respect to \(q\) and then dividing by \(m!\) and finally taking \(q = 0\), which yields
where the vectors are defined as
By virtue of inverse Laplace transform on Eq. (14), we obtain the recursive equation as
where
and
Finally, on solving Eq. (16) we obtain the components of the \(q\)-HATM series solution.
\(q\)-HATM solution for fractional Fisher’s equations
To demonstrate the efficiency and applicability of the proposed algorithm, we consider two examples as an illustration.
Example 4.1
Consider the nonlinear time-fractional Fisher’s equation [16, 20]:
with initial condition
Taking LT on Eq. (19) and then employing the condition given in Eq. (20), we have
Using the proposed algorithm, the nonlinear operator \(N\) to be define as
By adopting the foregoing procedure of \(q\)-HATM, the deformation equation of \(m\)th order at \(H\left( {x,t} \right) = 1\) is given as
where
By plugging inverse Laplace transform on both sides of Eq. (23), we get
On solving the forgoing equations systematically, we arrive at
In this manner, the rest of the iterative components can be obtained. Then, the family of \(q\)-HATM series solution of Eq. (19) is given by
If we set \(\alpha = 1,\; \hbar = - 1\) and \(n = 1\), then the obtained solution \(\mathop \sum \nolimits_{m = 1}^{N} u_{m} \left( {x,y,t} \right)\left( {\frac{1}{n}} \right)^{m}\) converges to the exact solution \(u\left( {x,t} \right) = \frac{1}{{\left( {1 + {\text{e}}^{x - 5t} } \right)^{2} }}\) of the classical order Fisher’s equation as \(N \to \infty .\)
Example 4.2
Consider the one-dimensional generalized fractional order Burgers–Fisher equation [17] at \(\eta = 1,\; \mu = 1\) and \(\beta = 0.01\):
with initial conditions
By performing LT on both sides of Eq. (27) and then make use of conditions provided in Eq. (28), we have
The nonlinear operator \(N\) to be define as
By exercising with this numerical procedure, one can get the deformation equation of the \(m\)th order for \(H\left( {x,t} \right) = 1\), as
where
By applying inverse Laplace transform on Eq. (31), we get
On solving above equation, we have
In this pattern, remaining iterative components can be derived. Finally, the group of \(q\)-HATM series solution of Eq. (27) is given by
Exact solution of Eq. (27) at \(\alpha = 1\) is given by [17]
Numerical results and discussion
In order to verify whether the proposed algorithm leads to greater accuracy, the numerical solutions have been evaluated. From results, we can certainly conclude that the proposed technique provides remarkable exactness in comparison with the method available in the literature [16, 17].
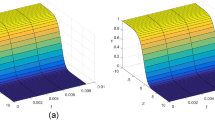
Figure 1 explores the comparison of \(q\)-HATM solution with exact solution and absolute error for Example 4.1. Figure 2 cites the action of solution obtained for Eq. (19) with distinct Brownian motion. Figure 3 depicts the \(q\)-HATM solution for different values of auxiliary parameter \(\hbar\) which helps us to control and adjust the convergence region. Figures 4, 5 and 6 explore the role of \(n\) with respect to \(\hbar\) in \(q\)-HATM solution. In Table 1, we present the comparison between the results obtained by the ADM [15], HPSTM [16] and proposed method with exact solution. Further, it can be observed from Table 2, the absolute error is very tiny.
a Surface of approximate solution. b Surface of exact solution. c Surface of absolute error \(= \left| {u_{{{\text{exa}} .}} - u_{{{\text{app}} . }} } \right|\) at \(\hbar = - 1\), \(n = 1\) and \(\alpha = 1\) for Example 4.1
Plot of q-HATM solution \(u\left( {x,t} \right)\) with respect to \(t\) when \(n = 1, \;\hbar = - 1\) and \(x = 0.5\) with various values of \(\alpha\) for Example 4.1
Plot of q-HATM solution \(u\left( {x,t} \right)\) at \(x = 1, \;n = 1 \;{\text{and}}\; \alpha = 1\) with diverse values of \(\hbar\) for Example 4.1
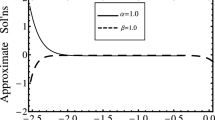
\(\hbar\)-curve drown for the q-HATM solution \(u\left( {x,t} \right)\) at \(x = 0.1, \;t = 0.01\) and \(n = 1\) with various values of \(\alpha\) for Example 4.1
\(\hbar\)-curve drown for the q-HATM solution \(u\left( {x,t} \right)\) at \(x = 0.1, \;t = 0.01\) and \(n = 2\) with diverse values of \(\alpha\) for Example 4.1
\(\hbar\)-curve drown for the q-HATM solution \(u\left( {x,t} \right)\) at \(x = 0.1,\; t = 0.01\) and \(n = 3\) with various values of \(\alpha\) for Example 4.1
Moreover, Fig. 7 cites the nature of \(q\)-HATM solution in comparison with exact solution for Example 4.2; in particular Fig. 7c revels the efficiency of proposed technique in terms of absolute error. Figure 8 explores the validity of Brownian motion, i.e. \(\alpha = 0.90, 0.75, 0. 50\). Figure 9 depicts the \(q\)-HATM solution for different values of auxiliary parameter \(\hbar\) which helps us to control and adjust the convergence region. Lastly, Figs. 10, 11 and 12 represent \(\hbar\)-curves and the horizontal line illustrates the range of convergence for Eq. (27). Further, the efficiency of proposed scheme is drowned in terms of numerical simulations for Example 4.2 which is shown in Table 3 and it clear that the proposed method is very accurate.
a Surface of approximate solution. b Surface of exact solution. c Surface of absolute error \(= \left| {u_{{{\text{exa}} .}} - u_{{{\text{app}} . }} } \right|\) at \(\eta = 1,\;\mu = 1,\;\xi = 0.01,\;\beta = 0.01, \;n = 1, \; \hbar = - 1 \;{\text{and}}\; \alpha = 1\) for Example 4.2
Plot of q-HATM solution \(u\left( {x,t} \right)\) with respect to \(t\) when \(\eta = 1,\mu = 1,\xi = 0.01,\beta = 0.01,n = 1, \hbar = - 1\) and \(x = 0.5\) with diverse values of \(\alpha\) for Example 4.2
Plot of q-HATM solution \(u\left( {x,t} \right)\) at \(\eta = 1,\;\mu = 1,\;\xi = 0.01,\;\beta = 0.01, \;x = 1, \;\alpha = 1\; {\text{and}}\; n = 5\) with diverse values of \(\hbar\) for Example 4.2
\(\hbar\)-curve drown for the q-HATM solution \(u\left( {x,t} \right)\) at \(\eta = 1,\;\mu = 1,\;\xi = 0.01,\;\beta = 0.01, \;n = 1,\;t = 0.01\) and \(\varvec{ }x = 0.5\) with diverse values of \(\alpha\) for Example 4.2 \(.\)
\(\hbar\)-curve drown for the q-HATM solution \(u\left( {x,t} \right)\) at \(\eta = 1,\;\mu = 1,\;\xi = 0.01,\;\beta = 0.01, \;x = 0.5,\; t = 0.01\) and \(n = 2\) with diverse values of \(\alpha\) for Example 4.2
\(\hbar\)-curve drown for the q-HATM solution \(u\left( {x,t} \right)\) at \(\eta = 1,\;\mu = 1,\;\xi = 0.01,\;\beta = 0.01, \;x = 0.5, \;t = 0.01\) and \(n = 3\) with diverse values of \(\alpha\) for Example 4.2
Conclusion
In this study, the \(q\)-homotopy analysis transform method is employed profitably to find the solution for nonlinear time-fractional Fisher’s equation. Two examples are carried out in order to validate and illustrate the efficiency of the method. The results reveal the complete reliability and wide applicability of the proposed technique. Compared to other numerical techniques, the proposed technique requires less amount of computational overhead. Moreover, the method manipulates and controls the series solution, which rapidly converges to the exact solution very efficiently in a short admissible domain. The results obtained, using the \(q\)-HATM, were in good record with results already available in the literature [15,16,17, 27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56].
References
Du, M., Wang, Z., Hu, H.: Measuring memory with the order of fractional derivative. Sci. Rep. 3(3431), 1–3 (2013). https://doi.org/10.1038/srep03431
Caputo, M.: Elasticita e dissipazione. Zanichelli, Bologna (1969)
Miller, K.S., Ross, B.: An introduction to fractional calculus and fractional differential equations. Wiley, New York (1993)
Podlubny, I.: Fractional differential equations. Academic Press, New York (1999)
Liao, S.J.: Homotopy analysis method: a new analytic method for nonlinear problems. Appl. Math. Mech. 19, 957–962 (1998)
Scalar, E., Gorenflo, R., Mainardi, F.: Fractional calculus and continuous time finance. Phys. A 284, 376–384 (2000)
West, B.J., Turalskal, M., Grigolini, P.: Fractional calculus ties the microscopic and macroscopic scales of complex network dynamics. New J. Phys. 17, 1–13 (2015). https://doi.org/10.1088/1367-2630/17/4/045009
Tarasov, V.E.: Fractional vector calculus and fractional Maxwell’s equations. Ann. Phys. 323, 2756–2778 (2008)
Fisher, R.A.: The wave of advance of advantageous genes. Ann. Eugen. 7, 353–369 (1937)
Alquran, M., Al-Khaled, K., Sardar, T., Chattopadhyay, J.: Revisited Fisher’s equation in a new outlook: a fractional derivative approach. Phys. A 438, 81–93 (2015)
Rossa, J., Villaverdeb, A.F., Bangab, J.R., Vazquezc, S., Moranc, F.: A generalized Fisher equation and its utility in chemical kinetics. PNAS 107(29), 12777–12781 (2010)
Ammerman, A.J., Cavalli-Sforza, L.L.: The neolithic transition and the genetics of population in Europe. Princeton University Press, Princeton (1984)
Merdan, M.: Solutions of time-fractional reaction–diffusion equation with modified Riemann–Liouville derivative. Int. J. Phys. Sci. 7(15), 2317–2326 (2012)
Kerke, V.M.: Results from variants of the Fisher equation in the study of epidemics and bacteria. Phys. A 342, 242–248 (2004)
Wazwaz, A.M., Gorguis, A.: An analytic study of Fisher’s equation by using Adomian decomposition method. Appl. Math. Comput. 154, 609–620 (2004)
Abedle-Rady, A.S., Rida, S.Z., Arafa, A.A.M., Adedl-Rahim, H.R.: Approximate analytical solutions of the fractional nonlinear dispersive equations using homotopy perturbation Sumudu transform method. Int. J. Innov. Sci. Eng. Technol. 1(9), 257–267 (2014)
Gupta, A.K., Ray, S.S.: On the solutions of fractional Burgers–Fisher and generalized Fisher’s equations using two reliable methods. Int. J. Math. Math. Sci. (2014). https://doi.org/10.1155/2014/682910
Cherif, M.H., Belghaba, K., Zaine, D.: Homotopy perturbation method for solving the fractional Fisher’s equation. Int. J. Anal. Appl. 10(1), 9–16 (2016)
Khader, M.M., Saad, K.M.: A numerical approach for solving the fractional Fisher equation using Chebyshev spectral collocation method. Chaos Solitons Fractals 110, 169–177 (2018)
Rawashdeh, M.S.: The fractional natural decomposition method: theories and applications. Math. Methods Appl. Sci. 40(7), 2362–2376 (2016)
Singh, J., Kumar, D., Swroop, R.: Numerical solution of time- and space-fractional coupled Burgers’ equations via homotopy algorithm. Alex. Eng. J. 55(2), 1753–1763 (2016)
Veeresha, P., Prakasha, D.G., Baskonus, H.M.: New numerical surfaces to the mathematical model of cancer chemotherapy effect in Caputo fractional derivatives. CHAOS 29(1), 1–13 (2019)
Srivastava, H.M., Kumar, D., Singh, J.: An efficient analytical technique for fractional model of vibration equation. Appl. Math. Model. 45, 192–204 (2017)
Kumar, D., Singh, J., Baleanu, D.: A new numerical algorithm for fractional Fitzhugh–Nagumo equation arising in transmission of nerve impulses. Nonlinear Dyn. 91, 307–317 (2018)
Veeresha, P., Prakasha, D.G., Magesh, N.: Numerical simulation for fractional Jaulent–Miodek equation associated with energy-dependent Schrodinger potential using two novel techniques (2018). arXiv:1810.06311[math.NA]
Prakash, A., Prakasha, D.G., Veeresha, P.: A reliable algorithm for time-fractional Navier–Stokes equations via Laplace transform. Nonlinear Eng. (2019) (Accepted)
Abbasbandy, S., Shivanian, E.: Multiple solutions of mixed convection in a porous medium on semi-infinite interval using pseudo-spectral collocation method. Commun. Nonlinear Sci. Numer. Simul. 16(7), 2745–2752 (2011)
Seyedi, S.H., Saray, B.N., Nobari, M.R.H.: Using interpolation scaling functions based on Galerkin method for solving non-Newtonian fluid flow between two vertical flat plates. Appl. Math. Comput. 269, 488–496 (2015)
Abbasbandy, S., Shivanian, E., Vajravelu, K., Kumar, S.: A new approximate analytical technique for dual solutions of nonlinear differential equations arising in mixed convection heat transfer in a porous medium. Int. J. Numer. Methods Heat Fluid Flow 27(2), 486–503 (2016)
Soltani, L.A., Shivanian, E., Ezzati, R.: Shooting homotopy analysis method: a fast method to find multiple solutions of nonlinear boundary value problems arising in fluid mechanics. Eng. Comput. 34(2), 471–498 (2017)
Seyedi, S.H., Saray, B.N., Ramazani, A.: On the multiscale simulation of squeezing nanofluid flow by a high precision scheme. Powder Technol. 340, 264–273 (2018)
Abbasbandy, S., Magyari, E., Shivanian, E.: The homotopy analysis method for multiple solutions of nonlinear boundary value problems. Commun. Nonlinear Sci. Numer. Simul. 14(9–10), 3530–3536 (2009)
Vosoughi, H., Shivanian, E., Abbasbandy, S.: Unique and multiple PHAM series solutions of a class of nonlinear reactive transport model. Numer. Algorithms 61(3), 515–524 (2012)
Abbasbandy, S., Shivanian, E.: Prediction of multiplicity of solutions of nonlinear boundary value problems: novel application of homotopy analysis method. Commun. Nonlinear Sci. Numer. Simul. 15(12), 3830–3846 (2010)
Abbasbandy, S., Shivanian, E.: Predictor homotopy analysis method and its application to some nonlinear problems. Commun. Nonlinear Sci. Numer. Simul. 16(6), 2456–2468 (2011)
Dehghan, M., Manafian, J.: The solution of the variable coefficients fourth-order parabolic partial differential equations by the homotopy perturbation method. Z. Naturforsch. 64, 420–430 (2009)
Dehghan, M., Manafian, J., Saadatmandi, A.: Solving nonlinear fractional partial differential equations using the homotopy analysis method. Numer. Math. Partial Differ. Equ. J. 26, 448–479 (2010)
Dehghan, M., Manafian, J., Saadatmandi, A.: The solution of the linear fractional partial differential equations using the homotopy analysis method. Z. Naturforsch. 65, 935–949 (2010)
Dehghan, M., Heris, J.M., Saadatmandi, A.: Application of semi-analytic methods for the Fitzhugh–Nagumo equation, which models the transmission of nerve impulses. Math. Meth. Appl. Sci. 33, 1384–1398 (2010)
Dehghan, M., Heris, J.M.: Application of the exp-function method for solving a partial differential equation arising in biology and population genetics. Int. J. Numer. Anal. Model. 21(6), 736–753 (2011)
Foroutan, M., Zamanpour, I., Manafian, J.: Applications of IBSOM and ETEM for solving the nonlinear chains of atoms with long-range interactions. Eur. Phys. J. Plus. 132(421), 1–18 (2017)
Bulut, H., Baskonus, H.M.: The oscillations of solutions of initial value problems for parabolic equations by HPM. Appl. Math. J. 7(53), 2621–2627 (2013). m-hikari
Baskonus, H.M., Bulut, H.: On the numerical solutions of some fractional ordinary differential equations by fractional Adams–Bashforth–Moulton method. Open Math. 13(1), 547–556 (2015)
Baskonus, H.M., Bulut, H.: A Comparison between NTDM and VIM for modified Camassa–Holm and modified Degasperis–Procesi equations. Nonlinear Stud. 22(4), 601–611 (2015)
Baskonus, H.M., Hammouch, Z., Mekkaoui, T., Bulut, H.: Chaos in the fractional order logistic delay system: circuit realization and synchronization. AIP Conf. Proc. 1738, 290005 (2016)
Bulut, H., Yel, G., Baskonus, H.M.: An application of improved Bernoulli sub-equation function method to the nonlinear time-fractional Burgers equation. Turk. J. Math. Comput. Sci. 5, 1–17 (2016)
Gencoglu, M.T., Baskonus, H.M., Bulut, H.: Numerical simulations to the nonlinear model of interpersonal relationships with time fractional derivative. AIP Conf. Proc. 020103(1798), 1–9 (2017)
Yokus, A., Baskonus, H.M., Sulaiman, T.A., Bulut, H.: Numerical simulation and solutions of the two-component second order KdV evolutionary system. Numer. Math. Partial Differ. Equ. J. 34(1), 211–227 (2017)
Ravichandran, C., Jothimani, K., Baskonus, H.M., Valliammal, N.: New results on nondensely characterized integrodifferential equations with fractional order. Eur. Phys. J. Plus. 133(109), 1–10 (2018)
Dokuyucu, M.A., Celik, E., Bulut, H., Baskonus, H.M.: Cancer treatment model with the Caputo–Fabrizio fractional derivative. Eur. Phys. J. Plus. 133(92), 1–7 (2018)
Esen, A., Sulaiman, T.A., Bulut, H., Baskonus, H.M.: Optical solitons to the space-time fractional (1 + 1)-dimensional coupled nonlinear Schrodinger equation. Optik 167, 150–156 (2018)
Yavuz, M., Ozdemir, N., Baskonus, H.M.: Solutions of partial differential equations using the fractional operator involving Mittag–Leffler kernel. Eur. Phys. J. Plus. 133(215), 1–12 (2018)
Sulaiman, T.A., Bulut, H., Yokus, A., Baskonus, H.M.: On the exact and numerical solutions to the coupled Boussinesq equation arising in ocean engineering. Indian J. Phys. (2018). https://doi.org/10.1007/s12648-018-1322-1
Sulaiman, T.A., Yokus, A., Gulluoglu, N., Baskonus, H.M., Bulut, H.: Regarding the numerical and stability analysis of the Sharma–Tosso–Olver equation. ITM Web Conf. 22(01036), 1–9 (2018). https://doi.org/10.1051/itmconf/20182201036. (CPCI-S; ISI Web of Science)
Tekiyeh, R.M., Manafian, J., Baskonus, H.M., Dusunceli, F.: Applications of He’s semi-inverse variational method and ITEM to the nonlinear long-short wave interaction system. Int. J. Adv. Appl. Sci. (2019) (Accepted)
Yokus, A., Sulaiman, T.A., Gulluoglu, M.T., Bulut, H.: Stability analysis, numerical and exact solutions of the (1 + 1)-dimensional NDMBBM equation. ITM Web Conf. 22, 01064 (2018)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Veeresha, P., Prakasha, D.G. & Baskonus, H.M. Novel simulations to the time-fractional Fisher’s equation. Math Sci 13, 33–42 (2019). https://doi.org/10.1007/s40096-019-0276-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40096-019-0276-6