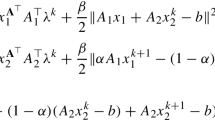New iterative methods for generalized singular-value problems

Abstract

This paper presents two new iterative methods to compute generalized singular values and vectors of a large sparse matrix. To reach acceleration in the convergence process, we have used a different inner product instead of the common one, Euclidean one. Furthermore, at each restart, a different inner product has been chosen by the researchers. A number of numerical experiments illustrate the performance of the above-mentioned methods.

Introduction

There are a number of applications for generalized singular-value decomposition (GSVD) in the literature including the computation of the Kronecker form of the matrix pencil $A - \lambda B$ [5], solving linear matrix equations [1], weighted least squares [2], and linear discriminant analysis [6] to name but a few. In a number of applications like the generalized total least squares problem, the matrices $A$ and $B$ are large and sparse, so in such cases, only a few of the generalized singular vectors corresponding to the smallest or largest generalized singular values are needed. There is a kind of close connection between the GSVD problem and two different generalized eigenvalue problems. In fact, there are many efficient numerical methods to solve generalized eigenvalue problems [8,9,10,11]. In this paper, we will examine the Jacobi–Davidson-type subspace method which is related to the Jacobi–Davidson for the SVD [5], which in turn is inspired by the Jacobi–Davidson method to solve the eigenvalue problem [4]. The main step in Jacobi–Davidson-type method for the (GSVD) is solving the correction equations in an exact manner requiring the solution of linear systems of original size at each iteration. In general, these systems are considered as large, sparse, and nonsymmetrical. For this matter, we use the weighted Krylov subspace process to solve the correction equations in an exact manner, and we show that our proposed method has the feature of asymptotic quadratic convergence.

The paper is organized as follows. In “Preparations”, we will remind the readers of basic definitions of the generalized singular-value decomposition problems and their elementary properties. “A new iterative method for GSVD” introduces our new numerical methods to solve generalized eigenvalue problems together with an analysis of the convergence of these methods. Several numerical examples are presented in “Numerical experiments”. Finally, the conclusions are given in the last section.

Preparations

Definition 2.1

Supposes that $A \in R^{m \times n}$ and $B \in R^{p \times n}$. The generalized singular values of the pair $(A,B)$ are presented as

$$\sum {(A,B) = \left\{ {\sigma \left| {\sigma \ge 0,\,\,\det (A^{\text{T}} A - \sigma^{2} B^{\text{T}} B) = 0} \right.} \right\}} .$$

Definition 2.2

A generalized singular value is called simple if $\sigma_{i} \ne \sigma_{j}$, for all $i \ne j$.

Theorem 2.3

Suppose $A \in R^{m \times n}$, $B \in R^{p \times n}$ , and $m \ge n$ . Here, taking the previous theorem into consideration, we see that there are orthogonal matrices $U_{m \times m}$, $V_{p \times p}$ and a nonsingular matrix $X_{n \times n}$ , such that

$$\begin{aligned} U^{\text{T}} AX = \sum\nolimits_{1} { = {\text{diag}}(\alpha_{1} , \ldots ,\alpha_{n} )} \quad \alpha_{i} \ge 0, \hfill \\ V^{\text{T}} BX = \sum\nolimits_{2} { = {\text{diag}}(\beta_{1} , \ldots ,\beta_{n} )} \quad \beta_{i} \ge 0, \hfill \\ \end{aligned}$$

(1)

where $q = \hbox{min} \{ p,n\}$, $r = {\text{rank}}(B)$ , and $\beta_{1} \ge \cdots \ge \beta_{r} \text{ > }\beta_{r + 1} = \cdots = \beta_{q} = 0$ . If $\alpha_{j} = 0$ for any $j$,$r + 1 \le j \le n$ , then $\sum {(A,B) = \left\{ {\sigma \left| {\sigma \ge 0} \right.} \right\}}$ . Otherwise, $\sum {\left( {A,B} \right) = \left\{ {\frac{{\alpha_{i} }}{{\beta_{i} }}\left| {i = 1, \ldots ,r} \right.} \right\}}$.

Proof

Refer to [3].

Theorem 2.4

Let $A \in R^{n \times n}$, $B \in R^{n \times n}$ have the GSVD:

$$U^{\text{T}} AX = \sum\nolimits_{1} { = {\text{diag}}(\alpha_{i} )} ,\quad V^{\text{T}} BX = \sum\nolimits_{2} { = {\text{diag}}(\beta_{i} )} \,;$$

furthermore, consider it as nonsingular. Here, then, the matrix pencil

$$\left( {\begin{array}{*{20}c} 0 & A \\ {A^{\text{T}} } & 0 \\ \end{array} } \right) - \lambda \left( {\begin{array}{*{20}c} I & 0 \\ 0 & {B^{\text{T}} B} \\ \end{array} } \right)$$

(2)

has eigenvalues $\lambda_{j} = \pm {{\alpha_{j} } \mathord{\left/ {\vphantom {{\alpha_{j} } {\beta_{j} ,\,\,\,j = 1, \ldots ,n}}} \right. \kern-0pt} {\beta_{j} ,\,\,\,j = 1, \ldots ,n}}$ which corresponds to the eigenvectors:

$$\left( \begin{aligned} \,\,\,\,\,\,\,u_{j} \hfill \\ \pm {{x_{j} } \mathord{\left/ {\vphantom {{x_{j} } {\beta_{j} }}} \right. \kern-0pt} {\beta_{j} }} \hfill \\ \end{aligned} \right),\quad j = 1, \ldots ,n$$

(3)

where $u_{j}$ is the ith column of $U$ and $x_{j}$ is the ith column of $X$.

Proof

Refer to [3].

Let $D$ be a diagonal matrix, that is, $D = {\text{diag}}(d_{1} ,d_{2} , \ldots ,d_{n} )$. If $u$ and $v$ are two vectors of $R^{n}$, we define the $D$-scalar product of $(u,v)_{D} = v^{\text{T}} Du.$ which is well defined if and only if the matrix $D$ is positively definite or to say $d_{i} \text{ > }0,\,\,i = 1, \ldots ,n$. The norm associated with this inner product is the $D$-norm $\left\| \cdot \right\|_{D}$ which is defined as $\left\| u \right\|_{D} = \sqrt {\left( {u,u} \right)_{D} } = \sqrt {u^{\text{T}} Du} {\kern 1pt} \;\forall u \in R^{n}$.

As assumption $B$ has full rank, $(x,y)_{{(B^{\text{T}} B)^{ - 1} }} : = y^{\text{T}} (B^{\text{T}} B)^{ - 1} x$ is an inner product, and due to this, the corresponding norm satisfies $\left\| x \right\|^{2}_{{(B^{\text{T}} B)^{ - 1} }} : = (x,x)_{{(B^{\text{T}} B)^{ - 1} }}$. Inspired by the equality $\left\| Z \right\|_{F}^{2} = {\text{trace}}(Z^{\text{T}} Z)$ for a real matrix $Z$, we define the $(B^{\text{T}} B)^{ - 1}$-Frobenius norm of $Z$ by

$$\left\| Z \right\|_{{(B^{\text{T}} B)^{ - 1} ,F}}^{2} = {\text{trace}}(Z^{\text{T}} (B^{\text{T}} B)^{ - 1} Z).$$

(4)

A new iterative method for GSVD

We will advance different extraction methods here which are often more appropriate for small generalized singular values than the standard one from “A new iterative method for GSVD”. Before dealing with these new methods, we should refer to our main idea which is developed considering Krylov subspace methods.

Theorem 3.1

Assume that $\left( {\sigma ,u,v} \right)$ is a generalized singular triple: $Aw = \sigma u$ and $A^{\text{T}} u = \sigma B^{\text{T}} Bw$ , where $\sigma$ is a simple nontrivial generalized singular value, and $\left\| u \right\| = \left\| {Bw} \right\| = 1$ , and suppose that the correction equations

$$P = \left( {\begin{array}{*{20}c} {I - \tilde{u}\tilde{u}^{\text{T}} } & 0 \\ 0 & {I - B^{\text{T}} B\tilde{w}\tilde{w}^{\text{T}} } \\ \end{array} } \right),$$

(5)

are solved exactly in every step. Provided that the initial vectors $(\tilde{u},\tilde{w})$ are close enough to $(u,w)$ the sequence of approximations $(\tilde{u},\tilde{w})$ converges quadratically to $(u,w)$.

Proof

Refer to [4].

Lemma 3.2

Having in mind the Theorem 3.1, now suppose that $m$ steps of the weighted Arnoldi process [7] have been performed on the following matrix:

$$\left( {\begin{array}{*{20}c} {I - uu^{\text{T}} } & 0 \\ 0 & {I - B^{\text{T}} Bww^{\text{T}} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} { - \theta I} & A \\ {A^{\text{T}} } & { - \theta B^{\text{T}} B} \\ \end{array} } \right).$$

(6)

Furthermore, consider the matrix $\widetilde{H}_{m}$ as the Hessenberg matrix, whose nonzero entries are the scalars $\tilde{h}_{i,j}$ , constructed by the Weighted Arnoldi process. Here, we notice that the basis $\widetilde{V}_{m} = \left[ {\tilde{v}_{1} , \ldots ,\tilde{v}_{m} } \right]$ constructed by this algorithm is $D$-orthonormal and we have

$$\widetilde{V}_{m}^{\text{T}} D\widetilde{V}_{m} = I_{m} ,$$

(7)

$$\left( {\begin{array}{*{20}c} {I - uu^{\text{T}} } & 0 \\ 0 & {I - B^{\text{T}} Bww^{\text{T}} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} { - \theta I} & A \\ {A^{\text{T}} } & { - \theta B^{\text{T}} B} \\ \end{array} } \right)\widetilde{V}_{m} = \widetilde{V}_{m + 1} \left( {\begin{array}{*{20}c} {\widetilde{H}_{m} } \\ {h_{m + 1,m} e_{m}^{\text{T}} } \\ \end{array} } \right).$$

(8)

Proof

See [4].

We know that similar to Krylov methods, the mth $(m \ge 1)$ iterate $x_{m} = \left[ {s_{m} ,t_{m} } \right]^{t}$ of the weighted-FOM and weighted-GMRES methods belong to the affine Krylov subspace:

$$\left( {\begin{array}{*{20}c} {s_{0} } \\ {t_{0} } \\ \end{array} } \right) + \kappa_{m} \left( {\left( {\begin{array}{*{20}c} {I - uu^{\text{T}} } & 0 \\ 0 & {I - B^{\text{T}} Bww^{\text{T}} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} { - \theta I} & A \\ {A^{\text{T}} } & { - \theta B^{\text{T}} B} \\ \end{array} } \right),\left( {\begin{array}{*{20}c} {r_{0}^{\left( s \right)} } \\ {r_{0}^{\left( t \right)} } \\ \end{array} } \right)} \right).$$

(9)

Now, it is the time to prove our main theorem.

Theorem 3.3

Considering Theorem 3.1, $m$ steps of the weighted Arnoldi process have been run on (7). Here, the iterate $x_{m} = \left[ {s_{m} ,t_{m} } \right]^{t}$ is the exact solution of the correction equation:

$$P\left( {\begin{array}{*{20}c} { - \theta I} & A \\ {A^{\text{T}} } & { - \theta B^{\text{T}} B} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} s \\ t \\ \end{array} } \right) = - r,\,\quad \,s{ \bot }\tilde{u},\quad \,t{ \bot }\tilde{w}.$$

(10)

Proof

The iterate $x_{m}^{\text{WF}}$ of the weighted-FOM method is selected, because its residual is $D$-orthonormal or

$$\left( {\begin{array}{*{20}c} {r_{m}^{(s)} } \\ {r_{m}^{(t)} } \\ \end{array} } \right)^{\text{WF}} { \bot }_{D} \,\,\kappa_{m} \left( {\left( {\begin{array}{*{20}c} {I - uu^{\text{T}} } & 0 \\ 0 & {I - B^{\text{T}} Bww^{\text{T}} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} { - \theta I} & A \\ {A^{\text{T}} } & { - \theta B^{\text{T}} B} \\ \end{array} } \right),\left( {\begin{array}{*{20}c} {r_{0}^{\left( s \right)} } \\ {r_{0}^{\left( t \right)} } \\ \end{array} } \right)} \right).$$

(11)

The iterate $x_{m}^{\text{WG}}$ of the weighted-GMRES method is selected to lessen the residual $D$-norm in (9). Here, we notice that it is the solution of the least squares problem:

$${\text{minimize}}_{{\left[ {s,t} \right]^{t} \in \left( {4.4} \right)}} \left\| {\left( {\begin{array}{*{20}c} {A\tilde{w} - \theta \tilde{u}} \\ {A^{\text{T}} \tilde{u} - \theta B^{\text{T}} B\tilde{w}} \\ \end{array} } \right) - P\left( {\begin{array}{*{20}c} { - \theta I} & A \\ {A^{\text{T}} } & { - \theta B^{\text{T}} B} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} s \\ t \\ \end{array} } \right)} \right\|_{D} .$$

(12)

In these methods, we use the $D$-inner product and the $D$-norm to calculate the solution in the affine subspace (9) and we create a $D$-orthonormal basis of the Krylov subspace:

$$\kappa_{m} \left( {\left( {\begin{array}{*{20}c} {I - uu^{\text{T}} } & 0 \\ 0 & {I - B^{\text{T}} Bww^{\text{T}} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} { - \theta I} & A \\ {A^{\text{T}} } & { - \theta B^{\text{T}} B} \\ \end{array} } \right),\left( {\begin{array}{*{20}c} {r_{0}^{(s)} } \\ {r_{0}^{(t)} } \\ \end{array} } \right)} \right).$$

(13)

by the weighted Arnoldi process. An iterate $x_{m}$ of these two methods can be transcribed as

$$\left( {\begin{array}{*{20}c} {s_{m} } \\ {t_{m} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {s_{0} } \\ {t_{0} } \\ \end{array} } \right) + \widetilde{V}_{m} \left( {\begin{array}{*{20}c} {y_{m}^{(s)} } \\ {y_{m}^{(t)} } \\ \end{array} } \right),$$

where $y_{m} \in R^{m}$.

Therefore, the matching residual $r_{m} = \left[ {r_{m}^{(s)} ,r_{m}^{(t)} } \right]^{t}$ satisfies

$$\begin{aligned} \left( {\begin{array}{*{20}c} {r_{m}^{(s)} } \\ {r_{m}^{(t)} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {A\tilde{w} - \theta \tilde{u}} \\ {A^{\text{T}} \tilde{u} - \theta B^{\text{T}} B\tilde{w}} \\ \end{array} } \right) - \left( {\begin{array}{*{20}c} {I - uu^{\text{T}} } &\quad 0 \\ 0 &\quad {I - B^{\text{T}} Bww^{T} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} { - \theta I} & A \\ {A^{\text{T}} } & { - \theta B^{\text{T}} B} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {s_{m} } \\ {t_{m} } \\ \end{array} } \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\, = \left( {\begin{array}{*{20}c} {A\tilde{w} - \theta \tilde{u}} \\ {A^{\text{T}} \tilde{u} - \theta B^{T} B\tilde{w}} \\ \end{array} } \right) - P\left( {\begin{array}{*{20}c} { - \theta I} & A \\ {A^{\text{T}} } & { - \theta B^{\text{T}} B} \\ \end{array} } \right)\left( {\left( {\begin{array}{*{20}c} {s_{0} } \\ {t_{0} } \\ \end{array} } \right) + \widetilde{V}_{m} \left( {\begin{array}{*{20}c} {y_{m}^{(s)} } \\ {y_{m}^{(t)} } \\ \end{array} } \right)} \right), \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\, = \left( {\begin{array}{*{20}c} {r_{0}^{\left( s \right)} } \\ {r_{0}^{\left( t \right)} } \\ \end{array} } \right) - P\left( {\begin{array}{*{20}c} { - \theta I} & A \\ {A^{\text{T}} } & { - \theta B^{\text{T}} B} \\ \end{array} } \right)\widetilde{V}_{m} \left( {\begin{array}{*{20}c} {y_{m}^{(s)} } \\ {y_{m}^{(t)} } \\ \end{array} } \right), \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\, = \widetilde{V}_{m + 1} \left( {\beta e_{1} - \left( {\begin{array}{*{20}c} {\widetilde{H}_{m} } \\ {h_{m + 1,m} e_{m}^{\text{T}} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {y_{m}^{(s)} } \\ {y_{m}^{(t)} } \\ \end{array} } \right)} \right), \hfill \\ \end{aligned}$$

where $\beta = \left\| {r_{0} } \right\|_{D}$, $r_{0} = \left[ {r_{0}^{(s)} ,r_{0}^{(t)} } \right]^{t} ,$ and $e_{1}$ is the first vector of the canonical basis.

At this point, the weighted-FOM method entails finding the vector $y_{m}^{\text{WF}} = \left[ {y_{m}^{(s)} ,y_{m}^{(t)} } \right]^{t}$ solution of the problem:

$$\widetilde{V}_{m}^{\text{T}} D\widetilde{V}_{m + 1} (\beta e_{1} - \widetilde{H}_{m} y_{m}^{\text{WF}} ) = 0,$$

which is equal to solve

$$\widetilde{H}_{m} y_{m}^{\text{WF}} = \beta e_{1} .$$

(14)

To the extent that the weighted-GMRES method is considered, the matrix $\widetilde{V}_{m + 1}$ is $D$-orthonormal, so we have

$$\begin{aligned} \left\| {r_{m} } \right\|_{D}^{2} = \left\| {\widetilde{V}_{m + 1} (\beta e_{1} - \widetilde{H}_{m} y_{m} )} \right\|_{D}^{2} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\, = \left\| {\beta e_{1} - \widetilde{H}_{m} y_{m} } \right\|_{2}^{2} , \hfill \\ \end{aligned}$$

and problem (12) is condensed to find the vector $y_{m}^{\text{WG}}$ solution of the minimization problem:

$${\text{minimize}}_{{y \in R^{m} }} \left\| {\beta e_{1} - \widetilde{H}_{m} y} \right\|_{2} .$$

(15)

We can reach the solution of (14) and (15) with the use of the QR decomposition of the matrix $\widetilde{H}_{m}$, as for the FOM and GMRES algorithms.

When $m$ is equal to the degree of the minimal polynomial of

$$\left( {\begin{array}{*{20}c} {I - uu^{\text{T}} } & 0 \\ 0 & {I - B^{\text{T}} Bww^{\text{T}} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} { - \theta I} & A \\ {A^{\text{T}} } & { - \theta B^{\text{T}} B} \\ \end{array} } \right)$$

for $r_{0} = [r_{0}^{(s)} ,r_{0}^{(t)} ]^{t}$, the Krylov subspace (13) will be invariant. Therefore, the iterate $x_{m} = [s_{m} ,t_{m} ]^{t}$ gained by both methods is the exact solution of the correction Eq. (10).■

It is time to write the main algorithm in this paper now. The following algorithm applies FOM, GMRES, weighted-FOM, and weighted-GMRES processes to solve the correction Eq. (10) and as a final point to solve the generalized singular-value decomposition problem. They are represented as F-JDGSVD, G-JDGSVD, WF-JDGSVD, and WG-JDGSVD.

As Algorithm 3.1 displays, there are two loops in this algorithm. One of them computes the largest generalized singular value called the outer iteration, and the other called the inner iteration solves the system of linear equation at each iteration. Numerical tests indicate that there is a significant relation between parameter $m$ and the norm of residual vector and the computational time.

Convergence

We will now demonstrate that the method we have proposed has asymptotically quadratic convergence to generalized singular values when the correction equations are solved in an exact manner and tend toward linear convergence when they are solved with a sufficiently small residual reduction.

Theorem 3.4

Having in mind Theorem 3.3, suppose that $m$ steps of the weighted Arnoldi process have been performed on (6) and $x_{m} = [s_{m} ,t_{m} ]^{\text{T}}$ is the exact solution of the correction Eq. (10). Provided that he initial vectors $(\tilde{u},\tilde{w})$ are close enough to $(u,w)$ , the sequence of approximations $(\tilde{u},\tilde{w})$ converges quadratically to $(u,w)$.

Proof

Suppose

$${\text{A}} = \left( {\begin{array}{*{20}c} 0 & A \\ {A^{T} } & 0 \\ \end{array} } \right),\,\quad {\text{B}} = \left( {\begin{array}{*{20}c} I & 0 \\ 0 & {B^{T} B} \\ \end{array} } \right)$$

and $P$ are like what you have seen in (5). Let $\left[ {s_{m} ,t_{m} } \right]^{T}$ with $s_{m} \bot \tilde{u}$ and $t_{m} \bot \tilde{w}$ be the exact solution to the correction equation:

$$P({\text{A}} - \theta {\text{B}})\left( {\begin{array}{*{20}c} {s_{m} } \\ {t_{m} } \\ \end{array} } \right) = - r.$$

(16)

Besides, let $\alpha u = \tilde{u} + s,\,\,\,s \bot \tilde{u}$, and $\beta w = \tilde{w} + t,\,\,\,t \bot \tilde{w}$, for certain scalars $\alpha$ and $\beta$, satisfy (15); note that these decompositions are possible meanwhile $u^{\text{T}} \tilde{u} \ne 0$ and $w^{\text{T}} \tilde{w} \ne 0$ because of the assumption that the vectors $(\tilde{u},\tilde{w})$ are close to $(u,w)$. Projecting (16) yields

$$P({\text{A}} - \theta {\text{B}})\left( {\begin{array}{*{20}c} s \\ t \\ \end{array} } \right) = - r + P\left( {\begin{array}{*{20}c} {(\mu_{1} - \theta )s} \\ {(\mu_{2} - \theta )B^{\text{T}} Bt} \\ \end{array} } \right).$$

(17)

Subtracting (16) from (17) gives

$$P({\text{A}} - \theta {\text{B}})\left( {\begin{array}{*{20}c} {s - s_{m} } \\ {t - t_{m} } \\ \end{array} } \right) = P\left( {\begin{array}{*{20}c} {(\mu_{1} - \theta )s} \\ {(\mu_{2} - \theta )B^{\text{T}} Bt} \\ \end{array} } \right).$$

Thus for $(\tilde{u},\tilde{w})$ close enough to $(u,w)$, $P({\text{A}} - \theta {\text{B}})$ is a bijection from $\tilde{u}^{ \bot } \times \tilde{w}^{ \bot }$ onto itself. Together with

$$\begin{aligned} \mu_{1} &= \tilde{u}^{\text{T}} A(\tilde{w} + t) = \theta + O\left( {\left\| t \right\|} \right), \hfill \\ \mu_{2} &= (\tilde{w} + t)^{\text{T}} A^{\text{T}} (\tilde{u} + s)/\left\| {B(\tilde{w} + t)} \right\|^{2} = \theta + O\left( {\left\| s \right\| + \left\| t \right\|} \right), \hfill \\ \end{aligned}$$

this implies asymptotic quadratic convergence:

$$\left\| {\left( \begin{aligned} \alpha u - (\tilde{u} + s_{m} ) \hfill \\ \beta w - (\tilde{w} + t_{m} ) \hfill \\ \end{aligned} \right)} \right\| = \left\| {\left( {\begin{array}{*{20}c} {s - s_{m} } \\ {t - t_{m} } \\ \end{array} } \right)} \right\| = O\left( {\left\| {\left( \begin{aligned} s \hfill \\ t \hfill \\ \end{aligned} \right)} \right\|^{2} } \right).$$

Numerical experiments

In this section, we look for the largest generalized singular value, using the following default options of the proposed method:

Maximum dimension of search spaces	$30$
Maximum iterations to solve correction equation	$10$
Fix target until $\left\| r \right\| \le \varepsilon$	$0.01$
Initial search spaces	Random

Example 4.1

The matrix pair $(A,B)$ is constructed, such that that they are similar to experiments as [7]. We choose two diagonal matrices of dimension $n = 1000$. For $j = 1,2, \ldots ,1000$

$$C = {\text{diag}}(c_{j} ),\quad c_{j} = {{\left( {n - j + 1} \right)} \mathord{\left/ {\vphantom {{\left( {n - j + 1} \right)} {2n}}} \right. \kern-0pt} {2n}},\,\quad S = \sqrt {1 - C^{2} } ,$$

$$D = {\text{diag}}(d_{j} ),\quad d_{j} = \left\lceil {{j \mathord{\left/ {\vphantom {j {250}}} \right. \kern-0pt} {250}}} \right\rceil + r_{j}$$

where the $r_{j}$ uniformly distributed on the interval $(0,1)$ and $\left\lceil \cdot \right\rceil$ denotes the ceil function. We take

$$A = Q_{1} CDQ_{2} ,\quad B = Q_{1} SDQ_{2}$$

where $Q_{1}$ and $Q_{2}$ are two random orthogonal matrices. The estimated condition numbers of $A$ and $B$ are $4.4e2$ and $5.7e0$, respectively (Table 1).

Table 1 Implementation of Algorithm 3.1 for $\left( {A,B} \right)$ with different values of $m$

We can see that by increasing the value of $m$, the number of outer and inner iterations decreases. Therefore, the consuming time also decreases. But not that if $m$ is very large, the number of iterations increases because of loosing the orthogonality property. This example is given to show the improvement brought by the weighted methods ${\text{WF-JDGSVD}}$ and ${\text{WG-JDGSVD}}$ is simultaneously on the relative error and on the computational time (Fig. 1).

Fig. 1

Errors plot created by F-JDGSVD, G-JDGSVD, WF-JDGSVD, and WG-GSVD

From figure one, we can see that the suggested method WG-JDGSVD is more accurate form the other methods.

Example 4.2

In this experiment, we take $A \, = \, CD$ and $B \, = \, SD$ of various dimension $n = 400, \, 800, \, 1000, \, 1200.$

This example is given to show the performance of two new methods on the large sparse problems. In this test, we have difficulties in computing the largest singular value for ill-conditioned matrices $A$ and $B$. We note that in this experiments, due to the ill-conditioning of $A$ and $B$, it turned out to be advantageous to turn of the Krylov option.

Example 4.3

Consider the matrix pair $(A,B)$, where $A$ is selected from the university of Florida sparse matrix collection [8] as lp-ganges. This matrix arises from a linear programming problem. Its size is $1309 \times 1706$ and it has a total of $Nz \, = \, 6937$ nonzero elements. The estimated condition number is $2.1332e4$, and $B$ is the $1309 \times 1706$ identity matrix (Tables 2, 3).

Table 2 Implementation of Algorithm 3.1 for $(A,B)$ with various dimensions and $m = 6$

Table 3 Implementation of Algorithm 3.1 for $\left( {A,B} \right)$ with different values of $m$

We should mention that, for all considered Krylov subspaces sizes, each weighted method converges in less iterations and less time than its corresponding standard method. The convergence of F-JDGSVD and G-JDGSVD is slow, and we have linear asymptotic convergence. However, the two WF-JDGSVD and WG-JDGSVD methods have quadratic asymptotic convergence, because the correction Eq. (10) is solved exactly.

Remark 4.4

From the above examples and tables, we can see that the two suggested methods are more accurate than G-JDGSVD and F-JDGSVD for the same value m, but its computational times are often a little longer than G-JDGSVD and F-JDGSVD. Therefore, we can use WF-JDGSVD and WG-GSVD if the computational time is less important.

Remark 4.5

The algorithm we have described finds the largest generalized singular triple. We can compute multiple generalized singular triples of the pair $(A,B)$ using a deflation technique. Suppose that $U_{f} = \left[ {u_{1} , \ldots ,u_{f} } \right]$ and $W_{f} = \left[ {w_{1} , \ldots ,w_{f} } \right]$ contain the already found generalized singular vectors, where $BW_{f}$ has orthonormal columns. We can check that the pair of deflated matrices

$$\hat{A}: = (I - U_{f} U_{f}^{\text{T}} )A(I - W_{f} W_{f}^{\text{T}} B^{\text{T}} B)\quad {\text{and}}\quad \hat{B}: = B(I - W_{f} W_{f}^{\text{T}} B^{\text{T}} B)$$

(18)

has the same generalized singular values and vectors as the pair $(A,B)$ (see [3]).

Example 4.6

In generalized singular-value decomposition, if $B = I_{n}$, the $n \times n$ identity matrix, we get the singular value of $A$. ${\text{SVD}}$ has important applications in image and data compression. For example, consider the following image.

This image is represented by a $1185 \times 1917$ matrix $A$. Which we can then decompose via the singular-value decomposition as $A = U\sum V^{\text{T}}$ where $U$ is $1185 \times 1185$, $\sum$ is $1185 \times 1917$, and $V$ is $1917 \times 1917$. The matrix $A$, however, can also be written as a sum of rank 1 matrices $A = \sum\nolimits_{j = 1}^{r} {\sigma_{j} u_{j} v_{j}^{\text{T}} }$, where $\sigma_{1} \ge \sigma_{2} \ge \cdots \ge \sigma_{r} \text{ > }0$ are the $r$ nonzero singular value of $A$. In digital image processing, any matrix $A$ of order $m \times n(m \ge n)$ generally has a large number of small singular values. Suppose there are $(n - k)$ small singular values of $A$ that can be neglected (Fig. 2).

Fig. 2

Original image

Then, the matrix $A_{k} = \sigma_{1} u_{1} v_{1}^{\text{T}} + \sigma_{2} u_{2} v_{2}^{\text{T}} + \cdots + \sigma_{k} u_{k} v_{k}^{\text{T}}$ is a very good approximation of $A$, and such an approximation can be adequate. Even when $k$ is chosen much less then $n$, the digital image corresponding to $A_{k}$ can be very close to the original image. Below are the subsequent approximations using various numbers of singular values.

The observation on those examples, we found when $k \le 20$, the images are blurry but with the increase of singular values, when their numbers are about $50$, we have a good approach to the original image.

Conclusions

In this paper, we have suggested two new iterative methods, namely, WF-JDGSVD and WG-JDGSVD, for the computation of some of the generalized singular values and corresponding vectors. Various examples studied illustrate these methods. To accelerate the convergence, we applied the Krylov subspace method for solving the correction equations in large sparse problems. In our methods, we see the existence of asymptotically quadratic convergence, because the correction equations are solved exactly. In the meantime, the correction equations in F-JDGSVD and G-JDGSVD methods are solved inexactly for large sparse problems, so we have linear convergence.

As the amount of the WF-JDGSVD and WG-JDGSVD methods is not much larger than that of the F-JDGSVD and G-JDGSVD methods, and as the weighted methods need less iterations to convergence, the parallel version of the weighted methods seems very interesting. From the tables and the figures, we see that when m increases, the suggested methods are more accurate than the previous methods; moreover, by increasing the dimension of the matrix, two suggested methods are applicable; this results are supported by convergence theorem which shows the asymptotically quadratic convergence to generalized singular values.