Introduction

In the study of the breakup of 17F into proton + 16O, some potential model for 17F has been used previously such as Woods–Saxon potential with spin–orbit and coulomb potentials [1] and M3Y interaction model [2]. Solution of the Schrodinger equation including the above potentials has been done by the numerical methods in the above-mentioned works. This is because analytical solution of these equations is not possible. However, some theoretical groups have tried to solve these Schrodinger equations analytically. For example, Pahlavani et al. have solved the Schrodinger equation including Woods–Saxon potential with spin–orbit and centrifugal terms by Nikiforov–Uvarov method [3]. They did not include the coulomb term to their calculations. Adding the coulomb potential (here for r < R C ; R C  = spherical nucleus radius) and solution of the Schrodinger equation by Nikiforov–Uvarov method is the main goal of the present work. In our previous works we have used the NU method to solve the Schrodinger equation with different potentials such as angle-dependent potential [4], Energy-dependent potential [5]; Dirac equation with NU method such as Hartmann potential [6]; Duffin–Kemmer–Petiau (DKP) equation with NU method such as Woods–Saxon potential [7], Hulthen vector potential [8] and Klein–Gordon equation with NU method such as energy-dependent potential [9]. Here, we have extended the Ref. [3] by adding a coulomb term to its potential. Adding this potential enhances the difficulty of the problem very much. Thus, we had to change the transformations and other formulas of the Ref. [3] to be able to solve the Schrodinger equation. Finally, energy eigenvalues and corresponding eigenfunctions obtained.

Parametric NU method

This powerful mathematical tool could be used to solve the second-order differential equations. Considering the following differential equation [10–12]

$$\psi_{n}^{{\prime \prime }} \left( s \right) + \frac{{\tilde{\tau }\left( s \right)}}{\sigma \left( s \right)}\psi_{n}^{{\prime }} \left( s \right) + \frac{{\tilde{\sigma }\left( s \right)}}{{\sigma \left( s \right)^{2} }}\psi_{n} \left( s \right) = 0 ,$$
(1)

where \(\sigma \;(z)\) and \(\tilde{\sigma }(z)\) are polynomials of second order at most, and \(\tilde{\tau }(z)\) is a first-order polynomial. To make the application of the NU method simpler and the checking of the validity of solution unnecessary, we present a shortcut for the method. We begin the method by writing the general form of the Schrodinger-like Eq. (1) as

$$\psi_{n}^{{\prime \prime }} \left( s \right) + \left( {\frac{{c_{1} - c_{2} s}}{{s(1 - c_{3} s)}}} \right)\psi_{n}^{{\prime }} \left( s \right) + \left( {\frac{{ - p_{2} s^{2} + p_{1} s - p_{0} }}{{s^{2} (1 - c_{3} s)^{2} }}} \right)\psi_{n} \left( s \right) = 0 ,$$
(2)

where the wave functions \(\psi_{n} (s)\) satisfies

$$\psi_{n} \left( s \right) = \phi \left( s \right)y_{n} \left( s \right) .$$
(3)

By comparing Eq. (3) with its counterpart Eq. (2), one can obtain

$$\tilde{\tau }(s) = c_{1} - c_{2} s,\begin{array}{*{20}c} {} & {\sigma (s)} \\ \end{array} = s(1 - c_{3} s),\begin{array}{*{20}c} {} & {\tilde{\sigma }(s)} \\ \end{array} = - p_{2} s^{2} + p_{1} s - p_{0} .$$
(4)

According to the NU method [10], one can obtain the bound state energy equation as [11, 12]

$$c_{2} n - (2n + 1)c_{5} + (2n + 1)(\sqrt {c_{9} } + c_{3} \sqrt {c_{8} } ) + n(n - 1)c_{3} + c_{7} + 2c_{3} c_{8} + 2\sqrt {c_{8} c_{9} } = 0 ,$$
(5)

where

$$\begin{aligned} c_{4} &= \frac{1}{2}(1 - c_{1} ), \hfill \\ c_{5} &= \frac{1}{2}(c_{2} - 2c_{3} ), \hfill \\ c_{6} &= c_{5}^{2} + p_{2} , \hfill \\ c_{7} &= 2c_{4} c_{5} - p_{1} \hfill \\ c_{8} &= c_{4}^{2} + p_{0} , \hfill \\ c_{9} &= c_{3} (c_{7} + c_{3} c_{8} ) + c_{6} . \hfill \\ \end{aligned}$$
(6)

In addition, we also find that:

$$\rho (s) = s^{{c_{10} }} (1 - c_{3} s)^{{c_{11} }}$$
(7)
$$\varphi (s) = s^{{c_{12} }} (1 - c_{3} s)^{{c_{13} }}$$
(8)
$$c_{12} > 0,c_{13} > 0$$
$$y_{n} (s) = P_{n}^{{(c_{10} ,c_{11} )}} (1 - 2c_{3} s),c_{10} > - 1,c_{11} > - 1$$
(9)

are necessary in calculating the wave functions

$$\psi_{nl} (s) = N_{nl} s^{{c_{12} }} (1 - c_{3} s)^{{c_{13} }} P_{n}^{{(c_{10} ,c_{11} )}} (1 - 2c_{3} s) ,$$
(10)

where \(P_{n}^{(\mu ,\nu )} (x),\mu > - 1,\nu > - 1,x \in \left[ { - 1,1} \right]\) are Jacobi polynomials. All undefined constant parameters are as follows [13]:

$$\begin{aligned} c_{10} &= c_{1} + 2c_{4} + 2\sqrt {c_{8} } \hfill \\ c_{11} &= 1 - c_{1} - 2c_{4} + \frac{2}{{c_{2} }}\sqrt {c_{9} } \hfill \\ c_{12} &= c_{4} + \sqrt {c_{8} } \hfill \\ c_{13} &= - c_{4} + \frac{1}{{c_{3} }}(\sqrt {c_{9} } + c_{5} ), \hfill \\ \end{aligned}$$
(11)

where

$$c_{3} \ne 0,\;c_{13} > 0,\;c_{12} > 0,\;s \in [1,1/c_{13} ]\;\,{\text{and}}\,\;\quad c_{13} \ne 0 .$$
(12)

Solutions of Schrodinger equation

We treat 17F as the combination of a proton and an inert 16O core with spin 0 [1]. Schrodinger equation for the N-particles which interact with each other can be written as [17, 18]:

$$\frac{{\hbar^{2} }}{2\mu }\left[ {\frac{{{\text{d}}^{2} }}{{{\text{d}}r^{2} }} + \frac{D - 1}{r}\frac{\text{d}}{{{\text{d}}r}} - \frac{{l\left( {l + D - 2} \right)}}{{r^{2} }}} \right]R\left( r \right) + V\left( r \right)R\left( r \right) = {\text{ER}}\left( r \right) ,$$
(13)

where D = 3N − 3. Here, D, l, and N denote, respectively, the space dimension, total angular momentum and the number of particles, \(\mu\) is one of particle masses, and x is the hyper-radius. If we write this equation for 17F as the combination of a proton and an inert 16O core with spin 0 (we have two-particle systems. Thus, N = 2 and then we find D = 3), we find the radial part of the Schrodinger equation as,

$$\frac{{{\text{d}}^{2} R\left( r \right)}}{{{\text{d}}r^{2} }} + \frac{2}{r}\frac{{{\text{d}}R\left( r \right)}}{{{\text{d}}r}} + \frac{2\mu }{{\hbar^{2} }}\left[ {E - V\left( r \right) - \frac{{\hbar^{2} l\left( {l + 1} \right)}}{{2\mu r^{2} }}} \right]R\left( r \right) = 0 .$$
(14)

The potential profile contain the following terms.

1. Woods–Saxon:

$$V_{\text{WS}} = \frac{{ - V_{0} }}{{1 + e^{{\frac{{(r - R_{0} )}}{a}}} }}$$
(15)

We have used V 0 = 42.71 MeV for 17F atom [3]. There, V 0 is defined as 40.5 + 0.13A MeV, where A is the mass number of nuclei (here 17 for 17F). R 0 is radius of the spherical nucleus and a = 0.65 fm is surface diffuseness.

Woods–Saxon potential has vast applications in description of both spherical and deformed nuclei in nuclear and particle physics. Analytic solution of Schrödinger equation with Woods–Saxon potential is very useful which provide for us invaluable theoretical results. DKP equation is also solved analytically by means of NU method a vector deformed Woods–Saxon potential [18]. However, scientist have solved the Woods–Saxon potential for S states (l = 0), exactly and also by some approximation they have also found the solutions for any l states. [19–22]

2. Spin–orbit term as,

$$V_{LS} \left( r \right) = V_{LS}^{(0)} \left( {\frac{{r_{0} }}{\hbar }} \right)^{2} \frac{1}{r}\left[ {\frac{\text{d}}{{{\text{d}}r}}\frac{1}{{1 + e^{{\frac{{(r - R_{0} )}}{a}}} }}} \right]\left( {\vec{L}.\vec{S}} \right)$$
(16)

where we have used \(V_{LS}^{(0)} = 0.44V_{0}\).

3. Coulomb term,

$$V_{C} (r) = \left\{ \begin{aligned} &\frac{{e^{2} }}{{R_{C} }}\left[ {3 - \left( {\frac{r}{{R_{C} }}} \right)^{2} } \right]\quad r \le R_{C} \hfill \\ &\frac{{8e^{2} }}{r}\quad r \le R_{C} \hfill \\ \end{aligned} \right.$$
(17)

Here we have solved the Schrodinger equation for r < R C . By using of the change of variable as \(\psi \left( r \right) = rR(r)\) we have,

$$\frac{{{\text{d}}\psi }}{{{\text{d}}r}} = R(r) + r\frac{{{\text{d}}R(r)}}{{{\text{d}}r}}.$$
(18)

Then the Schrodinger equation becomes,

$$\frac{{{\text{d}}^{2} \psi (r)}}{{{\text{d}}r^{2} }} + \frac{2\mu E}{{\hbar^{2} }}\psi (r) - \frac{2\mu V(r)}{{\hbar^{2} }}\psi (r) - \frac{{l\left( {l + 1} \right)}}{{r^{2} }}\psi (r) = 0 .$$
(19)

Now, complete Schrodinger equation reads,

$$\begin{aligned} &\frac{{{\text{d}}^{2} \psi \left( r \right)}}{{{\text{d}}r^{2} }} + \frac{2\mu E}{{\hbar^{2} }}\psi \left( r \right) - \frac{2\mu }{{\hbar^{2} }}\left[ {\frac{{ - V_{0} }}{{1 + e^{{\frac{{\left( {r - R_{0} } \right)}}{a}}} }}} \right. \hfill \\ &\quad + V_{LS}^{\left( 0 \right)} r_{0}^{2} \frac{1}{r}\left( {\frac{\text{d}}{{{\text{d}}r}}\frac{1}{{1 + e^{{\frac{{\left( {r - R_{0} } \right)}}{a}}} }}} \right)\left( {j\left( {j + 1} \right) - l\left( {l + 1} \right) - \frac{3}{4}} \right) + \left. {\frac{{3e^{2} }}{{\pi \varepsilon_{0} R_{C} }} - \frac{{e^{2} r^{2} }}{{\pi \varepsilon_{0} R_{C}^{3} }}} \right]\psi \left( r \right) \hfill \\ &\quad - \frac{{l\left( {l + 1} \right)}}{{r^{2} }}\psi \left( r \right) = 0 .\hfill \\ \end{aligned}$$
(20)

We need another change of variable as \(s = e^{ - \delta r}\), which leads,

$$\frac{{{\text{d}}\psi (r)}}{{{\text{d}}r}} = \frac{{{\text{d}}\psi (r)}}{{{\text{d}}s}} \times \frac{{{\text{d}}s}}{{{\text{d}}r}} = - \delta s\frac{{{\text{d}}\psi (r)}}{{{\text{d}}s}}$$
(21)
$$\frac{{{\text{d}}^{2} \psi (r)}}{{{\text{d}}r^{2} }} = \delta^{2} s^{2} \frac{{{\text{d}}^{2} R(s)}}{{{\text{d}}s^{2} }} + \delta^{2} s\frac{{{\text{d}}R(s)}}{{{\text{d}}s}} .$$
(22)

We define \(\delta = \frac{1}{a}\), \(q = e^{{\delta R_{0} }}\), \(V_{0}^{{\prime }} = V_{0} q\) and \(V_{LS}^{{{\prime }0}} = V_{LS}^{0} q\). We have used the following approximation too,

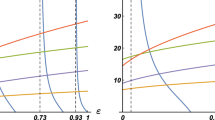
$$\frac{1}{{r^{2} }} \approx \delta^{2} \left( {\frac{{e^{ - \delta r} }}{{1 - e^{ - \delta r} }}} \right)^{2} .$$
(23)

To find the best value of the \(\delta\) we have changed the \(\delta\) and plotted both side of the above equation several times and found the best \(\delta\) to be 0.4 fm−1. Figure 1 shows two sides of the above equation to obtain \(\delta\). By using the later change of variable the Schrodinger equation reads,

$$\begin{aligned} &\delta^{2} s^{2} \frac{{{\text{d}}^{2} R(s)}}{{{\text{d}}s^{2} }} + \delta^{2} s\frac{{{\text{d}}R(s)}}{{{\text{d}}s}} + \left(\frac{2\mu E}{{\hbar^{2} }} + \frac{{2\mu V_{0}^{{\prime }} }}{{\hbar^{2} }}\left( {\frac{s}{1 + qs}} \right) \hfill \right.\\ &\quad \left.+ \frac{{\mu r_{0}^{2} V_{LS}^{{{\prime 0}}} \delta^{2} }}{{\hbar^{2} }}\left( {j\left( {j + 1} \right) - l\left( {l + 1} \right) - \frac{3}{4}} \right)\frac{{s^{2} }}{{(1 - s)(1 + qs)^{2} }} \hfill \right.\\ &\quad \left.- \frac{{6\mu e^{2} }}{{\pi \varepsilon_{0} \hbar^{2} R_{C} }} + \frac{{2\mu e^{2} }}{{\pi \varepsilon_{0} \hbar^{2} R_{C}^{3} \delta^{2} }}\frac{{(1 - s)^{2} }}{{s^{2} }} - l\left( {l + 1} \right)\delta^{2} \frac{{s^{2} }}{{(1 - s)^{2} }}\right)\\ &\quad \times R(s) = 0. \hfill \\ \end{aligned}$$
(24)
Fig. 1
figure 1

Left hand side (LHS) and right hand side (RHS) of the Eq. (23) to obtain \(\delta\)

Full size image

After some simplifications we have,

$$\begin{aligned} &\frac{{{\text{d}}^{2} R(s)}}{{{\text{d}}s^{2} }} + \frac{1}{s}\frac{{{\text{d}}R(s)}}{{{\text{d}}s}} + \left(\frac{{\frac{2\mu E}{{\hbar^{2} \delta^{2} }}(1 - s)^{2} + \frac{{2\mu V_{0}^{{\prime }} }}{{\hbar^{2} \delta^{2} }}\frac{{s(1 - s)^{2} }}{1 + qs}}}{{s^{2} (1 - s)^{2} }} \hfill \right.\\ &\quad \left.+ \frac{{\frac{{\mu r_{0}^{2} V_{LS}^{{{\prime }0}} }}{{\hbar^{2} }}\left( {j\left( {j + 1} \right) - l\left( {l + 1} \right) - \frac{3}{4}} \right)\frac{{s^{2} (1 - s)}}{{(1 + qs)^{2} }} - \frac{{6\mu e^{2} }}{{\pi \varepsilon_{0} \hbar^{2} R_{C} \delta^{2} }}(1 - s)^{2} }}{{s^{2} (1 - s)^{2} }} \hfill \right.\\ &\quad \left.+ \frac{{\frac{{2\mu e^{2} }}{{\pi \varepsilon_{0} \hbar^{2} R_{C}^{3} \delta^{4} }}\frac{{(1 - s)^{4} }}{{s^{2} }} - l\left( {l + 1} \right)s^{2} }}{{s^{2} (1 - s)^{2} }}\right)R(s) = 0. \hfill \\ \end{aligned}$$
(25)

Here, we present a new procedure with which we can convert the Schrodinger equation with any shape of the potential profile into the NU type equation. To use the NU method we convert the numerator of the potential term to a second-order polynomial. For this purpose we have used the following approximations which we have found through numerical fitting,

$$\frac{{s(1 - s)^{2} }}{1 + qs} = 0.006595579s^{2} - 0.0132710857s + 0.0067413175.$$
(26)

Figure 2a shows the two sides of the equation above. As it is clear, this approximation is extremely good. We have also used from

$$\frac{{s^{2} (1 - s)}}{{(1 + qs)^{2} }} = - 3.3579988\; \times \;10^{ - 9} s^{2} - 0.432019240084\; \times \;10^{ - 4} s + 0.4341808999\; \times \;10^{ - 4} .$$
(27)
Fig. 2
figure 2

a Left hand side (LHS, filled circle line) and right hand side (RHS, filled square line) of the Eq. (26) to show the accuracy of the approximation (27). b Same as a but for Eq. (27). b Same a but for Eq. (28)

Full size image

Figure 2b shows the two sides of the equation above. As it is clear, this approximation is extremely good. We have also used from

$$\frac{{(1 - s)^{4} }}{{s^{2} }} = 0.981s^{2} - 3.537s + 3.4.$$
(28)

Figure 2c shows the two sides of the equation above. As it is clear, this approximation is extremely good. To convert the last Schrodinger equation to the N-U type Schrodinger equation,

$$\psi_{n}^{{\prime \prime }} \left( s \right) + \frac{{\tilde{\tau }\left( s \right)}}{\sigma \left( s \right)}\psi_{n}^{{\prime }} \left( s \right) + \frac{{\tilde{\sigma }\left( s \right)}}{{\sigma \left( s \right)^{2} }}\psi_{n} \left( s \right) = 0$$
(29)
$$\psi_{n}^{{\prime \prime }} (s) + \left( {\frac{1 - s}{s(1 - s)}} \right)\psi_{n}^{{\prime }} (s) + \left( {\frac{{ - \gamma s^{2} + \beta s - \varepsilon^{2} }}{{s^{2} (1 - s)^{2} }}} \right)\psi_{n} (s) = 0.$$
(30)

We define three parameters \(\varepsilon\), \(\beta\), \(\gamma\) as follows:

$$\begin{aligned} - \gamma &= \frac{2\mu E}{{\hbar^{2} \delta^{2} }} + \frac{{2\mu V_{0}^{{\prime }} }}{{\hbar^{2} \delta^{2} }}(0.006595579) \hfill \\ &\quad + \frac{{\mu V_{LS}^{{{\prime }0}} r_{0}^{2} \left( {j\left( {j + 1} \right) - l\left( {l + 1} \right) - \frac{3}{4}} \right)}}{{\hbar^{2} }}( - 3.3579988\; \times \;10^{ - 9} ) \hfill \\ &\quad - \frac{{6\mu e^{2} }}{{\pi \varepsilon_{0} \hbar^{2} R_{C} \delta^{2} }} + \frac{{2\mu e^{2} }}{{\pi \varepsilon_{0} \hbar^{2} R_{C}^{3} \delta^{4} }}(0.981) - l(l + 1) \hfill \\ \end{aligned}$$
(31)
$$\begin{aligned} \beta &= \frac{4\mu E}{{\hbar^{2} \delta^{2} }} + \frac{{2\mu V_{0}^{{\prime }} }}{{\hbar^{2} \delta^{2} }}(0.0132710857) \hfill \\ &\quad + \frac{{\mu V_{LS}^{{{\prime }0}} r_{0}^{2} \left( {j\left( {j + 1} \right) - l\left( {l + 1} \right) - \frac{3}{4}} \right)}}{{\hbar^{2} }}(0.432019240084\; \times \;10^{ - 4} ) \hfill \\ &\quad + \frac{{12\mu e^{2} }}{{\pi \varepsilon_{0} \hbar^{2} R_{C} \delta^{2} }} - \frac{{2\mu e^{2} }}{{\pi \varepsilon_{0} \hbar^{2} R_{C}^{3} \delta^{4} }}(3.537) \hfill \\ \end{aligned}$$
(32)
$$\begin{aligned} - \varepsilon^{2} &= \frac{2\mu E}{{\hbar^{2} \delta^{2} }} + \frac{{2\mu V_{0}^{{\prime }} }}{{\hbar^{2} \delta^{2} }}(0.0067413175) \hfill \\ &\quad + \frac{{\mu V_{LS}^{{{\prime }0}} r_{0}^{2} \left( {j\left( {j + 1} \right) - l\left( {l + 1} \right) - \frac{3}{4}} \right)}}{{\hbar^{2} }}(0.4341808999\; \times \;10^{ - 4} ) \hfill \\ &\quad - \frac{{6\mu e^{2} }}{{\pi \varepsilon_{0} \hbar^{2} R_{C} \delta^{2} }} + \frac{{6.8\mu e^{2} }}{{\pi \varepsilon_{0} \hbar^{2} R_{C}^{3} \delta^{4} }} \hfill \\ \end{aligned}$$
(33)

Now we write \(\beta\), \(\gamma\) as function of \(\varepsilon\),

$$\begin{aligned} \gamma &= \varepsilon^{2} + \frac{{\mu V_{0}^{{\prime }} }}{{\hbar^{2} \delta^{2} }}(0.000291477) \hfill \\&\quad + \frac{{\mu V_{LS}^{{{\prime }0}} r_{0}^{2} \left( {j\left( {j + 1} \right) - l\left( {l + 1} \right) - \frac{3}{4}} \right)}}{{\hbar^{2} }}(0.434214479888\; \times \;10^{ - 4} ) \hfill \\ &\quad + \frac{{4.838\mu e^{2} }}{{\pi \varepsilon_{0} \hbar^{2} R_{C}^{3} \delta^{4} }} + l(l + 1) \to \gamma = \varepsilon^{2} + A \hfill \\ \end{aligned}$$
(34)
$$\begin{aligned} \beta &= 2\varepsilon^{2} + \frac{{0.0004230986\mu V_{0}^{{\prime }} }}{{\hbar^{2} \delta^{2} }} \hfill \\ &\quad+ \frac{{\mu V_{LS}^{{{\prime }0}} r_{0}^{2} \left(j\left( {j + 1} \right) - l\left( {l + 1} \right) - \frac{3}{4}\right)}} {{\hbar^{2} }}\\ &\quad \times (0.436342559716 \times 10^{ - 4} ) \hfill \\ &\quad + \frac{{6.526\mu e^{2} }}{{\pi \varepsilon_{0} \hbar^{2} R_{C}^{3} \delta^{4} }} \to \beta = 2\varepsilon^{2} + B \hfill \\ \end{aligned}$$
(35)

Based on what we have described above in the N-U section, we can find the following second-order polynomial:

$$\begin{aligned} &n - (2n + 1)\left( { - \frac{1}{2}} \right) + (2n + 1)\left( {\sqrt {\gamma - \beta + \varepsilon^{2} + \frac{1}{4}} + \varepsilon } \right) \hfill \\ &\quad + n(n + 1) - \beta + 2\varepsilon^{2} + 2\varepsilon \sqrt {\gamma - \beta + \varepsilon^{2} + \frac{1}{4}} = 0. \hfill \\ \end{aligned}$$
(36)

After some simplifications we have,

$$\begin{aligned} &\left[ {4\left( {A - B + \frac{1}{4}} \right) - (2n + 1)^{2} } \right]\varepsilon^{2} + 2(2n + 1)\left[ {2A - B - n^{2} - n} \right]\varepsilon \hfill \\ &\quad + \left[ {(2n + 1)^{2} \left( {A - B + \frac{1}{4}} \right) - \left( {n^{2} + n + \frac{1}{2} - B} \right)^{2} } \right] = 0 \hfill \\ \end{aligned}$$
(37)
$$h_{2} \varepsilon^{2} + h_{1} \varepsilon + h_{0} = 0.$$
(38)

By solving this equation and obtaining the \(\varepsilon\) we will wined the energies E as,

$$\begin{aligned} E_{nlj}& = \frac{{ - \hbar^{2} \delta^{2} }}{2\mu }\left(\varepsilon^{2} + \frac{{2\mu V_{0}^{{\prime }} }}{{\hbar^{2} \delta^{2} }}(0.0067413175) \hfill \right.\\&\quad \left. + \frac{{\mu V_{LS}^{{{\prime }0}} r_{0}^{2} \left( {j\left( {j + 1} \right) - l\left( {l + 1} \right) - \frac{3}{4}} \right)}}{{\hbar^{2} }}(0.4341808999 \times 10^{ - 4} ) \hfill \right.\\&\quad \left. - \frac{{6\mu e^{2} }}{{\pi \varepsilon_{0} \hbar^{2} R_{C} \delta^{2} }} + \frac{{6.8\mu e^{2} }}{{\pi \varepsilon_{0} \hbar^{2} R_{C}^{3} \delta^{4} }}\right) \hfill \\ \end{aligned}$$
(39)

Ground state energy of the 17F can be obtained by using of \(j = \frac{5}{2}\) n = 0, l = 2 and the first excited states can be calculated by using of the \(j = \frac{1}{2}\) n = 1, l = 0. Table 1 shows the results obtained in this work and Refs. [14, 16]. As it is clear from the Table 1, good accuracy in our work has been achieved. However, we have calculated the \(\frac{1}{2}^{ + }\) state energy with more accuracy (our absolute error = 0.023 MeV, Hagen et al. absolute error = 0.0918 MeV) while Hagen et al. have calculated the \(\frac{5}{2}^{ + }\) state energy with higher accuracy (our absolute error = 0.71 MeV, Hagen et al. absolute error = 0.0337 MeV). Now, the wave functions can be obtained through,

$$\psi (s) = y(s)\phi (s)$$
(40)
$$\rho (s) = s^{1 + 2\varepsilon } (1 - s)^{{2\sqrt {\gamma - \beta + \varepsilon^{2} + \frac{1}{4}} }}$$
(41)
$$\phi (s) = s^{\varepsilon } (1 - s)^{{\left( {\sqrt {\gamma - \beta + \varepsilon^{2} + \frac{1}{4}} - \frac{1}{2}} \right)}}$$
(42)
$$y_{n} (s) = P_{n}^{{\left( {1 + 2\varepsilon ,2\sqrt {\gamma - \beta + \varepsilon^{2} + \frac{1}{4}} } \right)}} (1 - 2s)$$
(43)
$$\psi_{nl} (s) = N_{nl} s^{\varepsilon } (1 - s)^{{\sqrt {\gamma - \beta + \varepsilon^{2} + \frac{1}{4}} + \frac{1}{2}}} \times P_{n}^{{(1 + 2\varepsilon ,2\sqrt {\gamma - \beta + \varepsilon^{2} + \frac{1}{4}} )}} (1 - 2s) ,$$
(44)

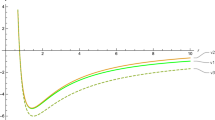
where \(P_{n}^{(\mu ,\nu )} (x),\mu > - 1,\nu > - 1,x \in \left[ { - 1,1} \right]\) are Jacobi polynomials. \({5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0pt} 2}^{ + }\) state and \({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}^{ + }\) state wave functions are presented in the Fig. 3a, b, respectively. As we can see in these figures, good agreement exists. We have used the parameters of the [3], since they lead to the energies closer to the experimental values which we have presented in the Table 1.

Table 1 Comparison of the energies obtained in this work with ab initio computation [14] and experimental values [16]
Full size table
Fig. 3
figure 3

a Normalized 5/2+ state wave function which we have calculated (filled circle line) compared with [15] (filled square line) as a function of the radius r (fm). b Normalized 1/2+ state wave function which we have calculated (filled circle line) compared with Ref. [15] (filled square line) as a function of the radius r (fm)

Full size image

Conclusion

In this study, the non-relativistic radial Schrodinger equation solved for Wood–Saxon potential together with coulomb potential (for r < R C ; R C  = spherical nucleus radius), spin–orbit interaction and centrifugal term through a new hybrid numerical fitting Nikiforov–Uvarov method. For this purpose, by using approximate expansion of 1/r 2 different than that used by Pahlavani et al., Schrodinger equation has been transformed to the analytically solvable differential equation of NU method. Good agreement with experimental values is obtained. We have calculated the 1/2+ state energy with more accuracy (our relative error = 0.023 MeV and Hagen et al. relative error = 0.0918 MeV), while Hagen et al. have calculated the 5/2+ state energy with higher accuracy (our relative error = 0.71 MeV and Hagen et al. relative error = 0.0337 MeV). Our obtained wave functions are in agreement with Kim et al.’s too.